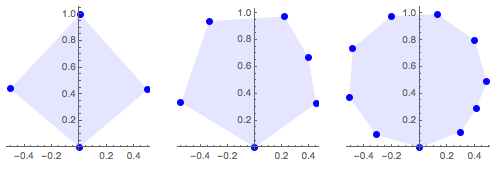
Trouvez le petit polygone le plus grand
Trouvez le polygone ayant l'aire maximale parmi les polygones ayant 
côtés et un diamètre 
.
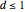Dans la version 11 de Mathematica, FindMinimum ajoute un solveur IPOPT pour résoudre des problèmes d'optimisation sous contrainte à grande échelle de manière plus efficace.
Appelez n le nombre de sommets du polygone.
n = 50;Soit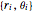 
, les coordonnées polaires du sommet 
ème du polygone.
vars = Join[Array[r, n], Array[\[Theta], n]];Ils satisfont les contraintes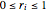 
, 
, 
, 
.
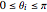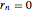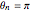varbounds =
Join[Table[0 <= r[i] <= 1, {i, n - 1}], {r[n] == 0},
Table[0 <= \[Theta][i] <= Pi, {i, n - 1}], {\[Theta][n] == Pi}];L'aire du polygone correspond à la somme des aires des triangles dont les sommets 
, 
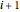et 
(l'origine).
area = 1/2 Sum[
r[i] r[i + 1] Sin[\[Theta][i + 1] - \[Theta][i]], {i, 1, n - 1}];La distance entre deux sommets ne doit pas dépasser 1.
constr1 =
Flatten[Table[
0 < r[i]^2 + r[j]^2 -
2 r[i] r[j] Cos[\[Theta][i] - \[Theta][j]] <= 1, {i, 1,
n - 1}, {j, i + 1, n}], 2];En raison de l'ordre des sommets, les contraintes suivantes existent également.
constr2 = Table[\[Theta][i] <= \[Theta][i + 1], {i, 1, n - 1}];Choisissez les points initiaux pour les variables.
x0 = vars /. {r[i_] ->
4. i (n + 1 - i)/(n + 1)^2, \[Theta][i_] -> \[Pi] i/n};Maximisez la zone soumise à des contraintes.
sol = FindMaximum[{area, constr1, constr2, varbounds},
Thread[{vars, x0}]];Convertissez en coordonnées cartésiennes.
rectpts =
Table[FromPolarCoordinates[{r[i], \[Theta][i]}], {i, 1, n}] /.
sol[[2]];Tracez la solution.
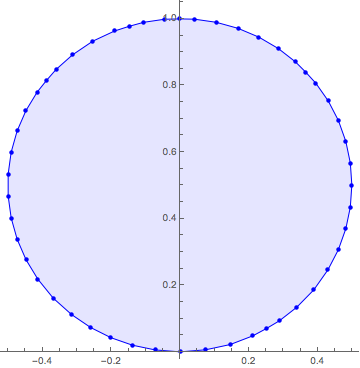
Show[ListPlot[rectpts, PlotStyle -> {Blue, PointSize -> Medium}],
Graphics[{Opacity[.1], Blue, EdgeForm[Blue], Polygon[rectpts]}],
AspectRatio -> 1, ImageSize -> Medium]
