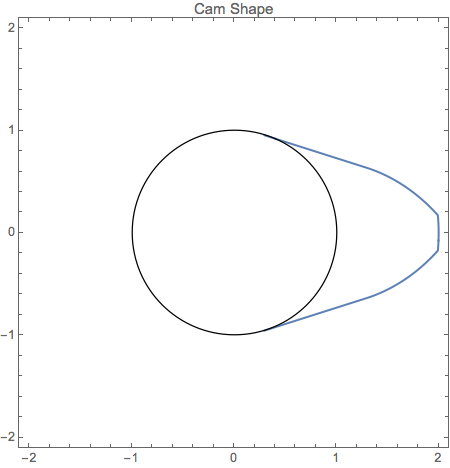
Optimieren Sie die Form eines Nockens: Neu in Wolfram Language 11

Optimieren Sie die Form eines Nockens

Entwerfen Sie die Form eines konvexen Nockens mit maximaler Fläche der Ventilöffnung für eine Drehung des Nockens und Bedingungen auf die Radien des Nockens.

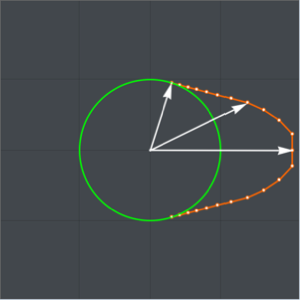
Wir nehmen an, dass die Form des Nockens auf 6π/5 seines Umfanges die Form eines Kreises mit Radius r_min hat und über die verbleibenden 4π/5 symmetrisch geformt ist.

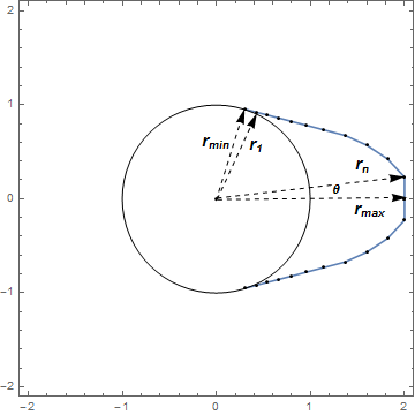
Die Entwurfsvariablen r_i, i=1, …, n repräsentieren den Radius des Nockens zu gleich voneinander entfernten Winkeln θ in einem Winkel von 2π/5, der oberen Hälfte des nicht-kreisförmigen Teils des Nockens.

In[1]:=

n = 100; vars = Array[r, n];

Jeder Radius r_i muss im Intervall 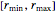liegen.

In[2]:=

rmin = 1; rmax = 2;
varbounds = Table[rmin <= r[i] <= rmax, {i, 1, n}];

Geben Sie den oben definierten Winkel θ an.

In[3]:=

\[Theta] = 2 Pi/(5 (n + 1));

Konvexitätsbedingungen werden durch das Ungleichungssystem 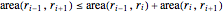ausgedrückt.

In[4]:=

convexconstri = (1/2) r[i - 1] r[i + 1] Sin[2 \[Theta]] <= 
   (1/2) r[i - 1] r[i] Sin[\[Theta]] + (1/2) r[i] r[
      i + 1] Sin[\[Theta]];

Durch 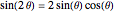kann das System wie folgt anders ausgedrückt werden. Beachten Sie, dass 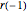der Radius eines Punkts auf dem kreisförmigen Teil des Nockens und daher gleich wie 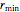ist.

In[5]:=

convexconstr = 
  Table[2 r[i - 1] r[i + 1] Cos[\[Theta]] <= 
     r[i] (r[i - 1] + r[i + 1]), {i, 0, n}] /. {r[-1] -> rmin, 
    r[0] -> rmin, r[n + 1] -> rmax};

Eine Bedingung für die Änderungsrate des Radius wird bezüglich des Parameters α als 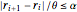ausgedrückt.

In[6]:=

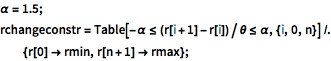
\[Alpha] = 1.5; rchangeconstr = 
 Table[-\[Alpha] <= (r[i + 1] - r[i])/\[Theta] <= \[Alpha], {i, 0, 
    n}] /. {r[0] -> rmin, r[n + 1] -> rmax};

Es wird angenommen, dass die Zielfunktion (Öffnungsbereich des Ventils) eine einfachere lineare Beziehung zu den Entwurfsvariablen r_i, gegeben als π r_v ²(r₁+…+r_n)/n, hat, wobei r_v eine Konstante in Bezug auf die Geometrie des Ventils ist.

In[7]:=

rv = 1;
objfun = Pi rv^2 (1/n) Sum[r[i], {i, 1, n}];

Wählen Sie Anfangspunkte für die Variablen.

In[8]:=

initpts = Table[.5 (rmin + rmax), {i, 1, n}];

Lösen Sie das Maximierungsproblem.

In[9]:=

sol = FindMaximum[
   Join[{objfun}, varbounds, convexconstr, rchangeconstr], 
   Thread[vars, initpts]];

Beachten Sie, dass einige der größten Radien das Maximum 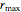haben.

In[10]:=

Table[r[i], {i, 95, 100}] /. sol[[2]]

Out[10]=

Plotten Sie die Lösung.

Den kompletten Wolfram Language-Input zeigen

In[11]:=

solpts1 = 
  Table[{r[i] Cos[-2. Pi/5 + \[Theta] i], 
      r[i] Sin[-2. Pi/5. + \[Theta] i]}, {i, -1, n + 2}] /. {r[-1] -> 
      rmin, r[0] -> rmin, r[n + 1] -> rmax, r[n + 2] -> r[n]} /. 
   sol[[2]];
solpts2 = Map[{#[[1]], -#[[2]]} &, Reverse@solpts1];
solpts = Join[solpts1, solpts2];
Show[ListLinePlot[solpts, PlotRange -> {{-2.1, 2.1}, {-2.1, 2.1}}, 
  PlotLabel -> "Cam Shape", AspectRatio -> 1, Axes -> False, 
  Frame -> True], Graphics[{Circle[{0., 0.}, 1.]}], 
 ImageSize -> Medium]

Out[11]=