Wolfram 语言™

优化凸轮的形状

在对凸轮的半径加以约束的条件下，设计凸性凸轮的形状，使凸轮旋转一周时阀门开启面积最大.

假设凸轮的形状是在其周长的 角度上半径为 r_min 的圆弧，在余下的 角度上形状对称.

设计变量 r_i, i=1, …, n 表示在凸轮非圆周部分的上半部分的 的角度内，以等角距 θ 分布的凸轮半径.

In[1]:=

n = 100; vars = Array[r, n];

每个半径 r_i 都被约束在区间 中.

In[2]:=

rmin = 1; rmax = 2; varbounds = Table[rmin <= r[i] <= rmax, {i, 1, n}];

输入上面定义的角度 θ.

In[3]:=

\[Theta] = 2 Pi/(5 (n + 1));

凸性约束被表示为不等式组 .

In[4]:=

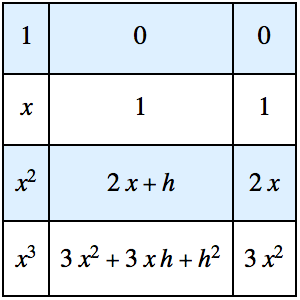
convexconstri = (1/2) r[i - 1] r[i + 1] Sin[2 \[Theta]] <= (1/2) r[i - 1] r[i] Sin[\[Theta]] + (1/2) r[i] r[ i + 1] Sin[\[Theta]];

通过应用 ，不等式组可重新表示如下. 注意 为凸轮的圆周部分上一个点的半径，因而与 相等.

In[5]:=

convexconstr = Table[2 r[i - 1] r[i + 1] Cos[\[Theta]] <= r[i] (r[i - 1] + r[i + 1]), {i, 0, n}] /. {r[-1] -> rmin, r[0] -> rmin, r[n + 1] -> rmax};

用参数 α 来表示对半径变化率的约束，其形式为 .

In[6]:=

\[Alpha] = 1.5; rchangeconstr = Table[-\[Alpha] <= (r[i + 1] - r[i])/\[Theta] <= \[Alpha], {i, 0, n}] /. {r[0] -> rmin, r[n + 1] -> rmax};

一般假定目标函数（阀门开启面积）与设计变量 r_i 有一个简单的线性关系，由 π r_v ²(r₁+…+r_n)/n 给出，其中 r_v 是一个与阀门几何形状相关的常数.

In[7]:=

rv = 1; objfun = Pi rv^2 (1/n) Sum[r[i], {i, 1, n}];

选择变量的初始点.

In[8]:=

initpts = Table[.5 (rmin + rmax), {i, 1, n}];

求解最大值问题.

In[9]:=

sol = FindMaximum[ Join[{objfun}, varbounds, convexconstr, rchangeconstr], Thread[vars, initpts]];

注意有几个最大半径为最大值 .

In[10]:=

Table[r[i], {i, 95, 100}] /. sol[[2]]

Out[10]=

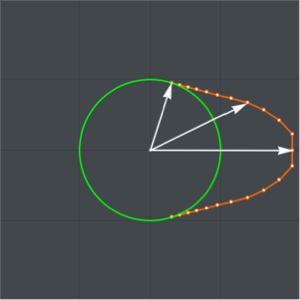
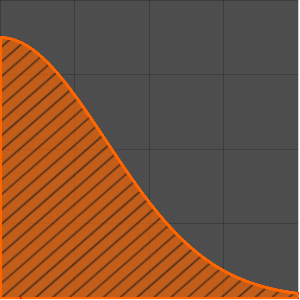
画出解的图形.

In[11]:=

solpts1 = Table[{r[i] Cos[-2. Pi/5 + \[Theta] i], r[i] Sin[-2. Pi/5. + \[Theta] i]}, {i, -1, n + 2}] /. {r[-1] -> rmin, r[0] -> rmin, r[n + 1] -> rmax, r[n + 2] -> r[n]} /. sol[[2]]; solpts2 = Map[{#[[1]], -#[[2]]} &, Reverse@solpts1]; solpts = Join[solpts1, solpts2]; Show[ListLinePlot[solpts, PlotRange -> {{-2.1, 2.1}, {-2.1, 2.1}}, PlotLabel -> "Cam Shape", AspectRatio -> 1, Axes -> False, Frame -> True], Graphics[{Circle[{0., 0.}, 1.]}], ImageSize -> Medium]

Out[11]=