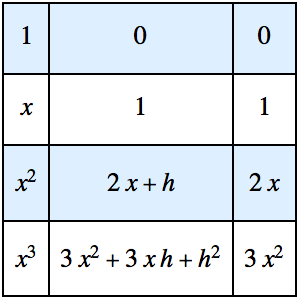
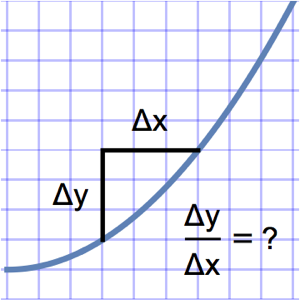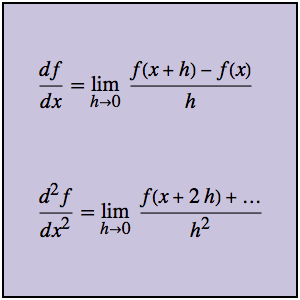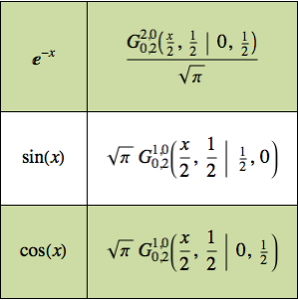Оптимизация формы кулочка

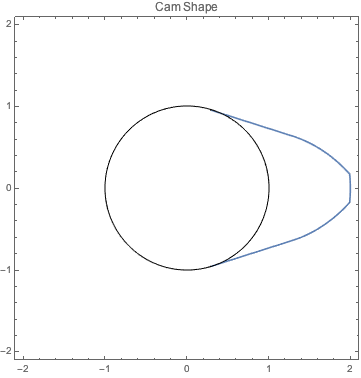
Спроектировать форму выпуклой бочки валка, чтобы максимизировать площадь отверстия клапана для одного вращения бочки валка с ограничениями радиусa.

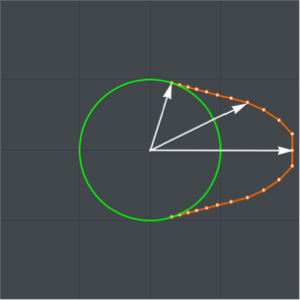
Предположим, что форма бочки валка кругообразная с углом 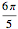, что её окружность с радиусом r_min, и что она симметрично сформирована для оставшихся .

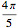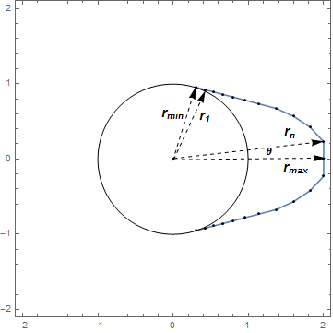
Расчётные параметры r_i, i=1, …, n представляют радиус бочки валка на равноудалённых углах θ, распределённых в рамках угла 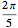верхней части некругообразной части бочки валка.

In[1]:=

n = 100; vars = Array[r, n];

Каждый радиус r_i лежит на отрезке .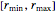

In[2]:=

rmin = 1; rmax = 2; varbounds = Table[rmin <= r[i] <= rmax, {i, 1, n}];

Ввести угол θ, определённый выше.

In[3]:=

\[Theta] = 2 Pi/(5 (n + 1));

Ограничения на выпуклость выражены системой неравенств .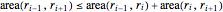

In[4]:=

convexconstri = (1/2) r[i - 1] r[i + 1] Sin[2 \[Theta]] <= (1/2) r[i - 1] r[i] Sin[\[Theta]] + (1/2) r[i] r[ i + 1] Sin[\[Theta]];

Используя 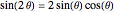, система неравенств может быть выражена в ином формате. Заметьте, что 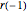является радиусом точки на кругообразной части бочки валка и потому равна .

In[5]:=

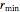convexconstr = Table[2 r[i - 1] r[i + 1] Cos[\[Theta]] <= r[i] (r[i - 1] + r[i + 1]), {i, 0, n}] /. {r[-1] -> rmin, r[0] -> rmin, r[n + 1] -> rmax};

Ограничение скорости изменения радиуса выражено параметром α, как в .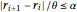

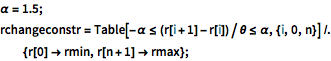
In[6]:=

\[Alpha] = 1.5; rchangeconstr = Table[-\[Alpha] <= (r[i + 1] - r[i])/\[Theta] <= \[Alpha], {i, 0, n}] /. {r[0] -> rmin, r[n + 1] -> rmax};

Целевая функция (площадь отверстия клапана) предполагает наличие простого линейного отношения с расчётными параметрами r_i при условии, что π r_v ²(r₁+…+r_n)/n, где r_v является постоянной величиной, относящейся к геометрическому строению клапана.

In[7]:=

rv = 1; objfun = Pi rv^2 (1/n) Sum[r[i], {i, 1, n}];

Выберать начальные точки для переменных.

In[8]:=

initpts = Table[.5 (rmin + rmax), {i, 1, n}];

Решить задачу максимизации.

In[9]:=

sol = FindMaximum[ Join[{objfun}, varbounds, convexconstr, rchangeconstr], Thread[vars, initpts]];

Hекоторые самые большие радиусы максимальны, .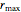

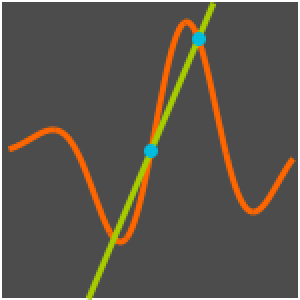
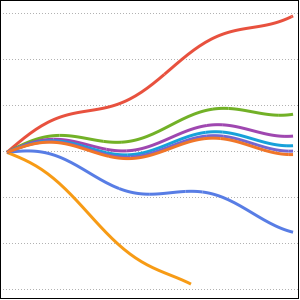
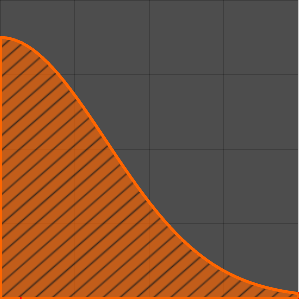
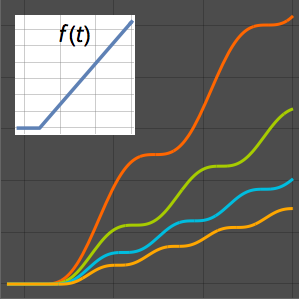
In[10]:=

Table[r[i], {i, 95, 100}] /. sol[[2]]

Out[10]=

Отобразить решение данной задачи на графике.

In[11]:=

solpts1 = Table[{r[i] Cos[-2. Pi/5 + \[Theta] i], r[i] Sin[-2. Pi/5. + \[Theta] i]}, {i, -1, n + 2}] /. {r[-1] -> rmin, r[0] -> rmin, r[n + 1] -> rmax, r[n + 2] -> r[n]} /. sol[[2]]; solpts2 = Map[{#[[1]], -#[[2]]} &, Reverse@solpts1]; solpts = Join[solpts1, solpts2]; Show[ListLinePlot[solpts, PlotRange -> {{-2.1, 2.1}, {-2.1, 2.1}}, PlotLabel -> "Cam Shape", AspectRatio -> 1, Axes -> False, Frame -> True], Graphics[{Circle[{0., 0.}, 1.]}], ImageSize -> Medium]

Out[11]=