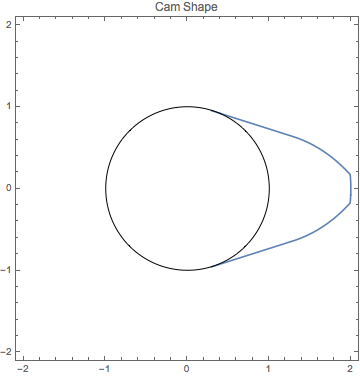
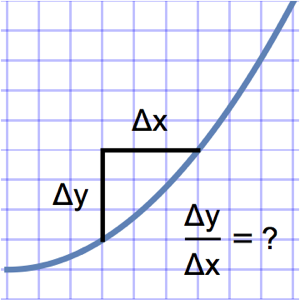カムの形状を最適化する
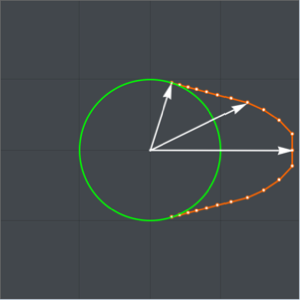
カムの1回転に対する弁の開口が最大化されるよう，カムの半径に制約条件を付けて凸状カムの形状を設計する．
カムの形状は，半径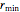 
の円周の角度
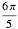では円であり，残りの
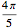上では対称な形であると想定する．
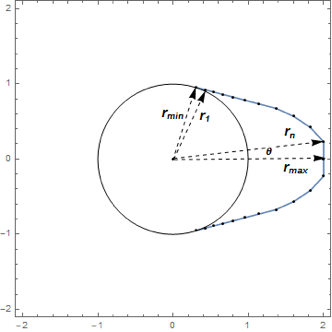
設計変数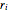 
, 
, 
, 
, 
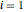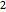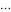, は角度
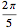，つまりカムの円状の部分ではない上半分に分布した等間隔の角度 
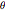でのカムの半径を表す．
In[1]:=
n = 100; vars = Array[r, n];それぞれの半径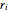 
は，区間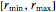
になければならない．
In[2]:=
rmin = 1; rmax = 2;
varbounds = Table[rmin <= r[i] <= rmax, {i, 1, n}];上で定義された角度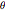 
を入力する．
In[3]:=
\[Theta] = 2 Pi/(5 (n + 1));凸性制約は不等式系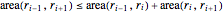
により表される．
In[4]:=
convexconstri = (1/2) r[i - 1] r[i + 1] Sin[2 \[Theta]] <=
(1/2) r[i - 1] r[i] Sin[\[Theta]] + (1/2) r[i] r[
i + 1] Sin[\[Theta]];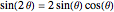
を使うと，系は下のように再表現することができる． 
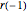はカムの円状の部分にある点の半径なので 
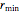に等しいということに注目のこと．
In[5]:=
convexconstr =
Table[2 r[i - 1] r[i + 1] Cos[\[Theta]] <=
r[i] (r[i - 1] + r[i + 1]), {i, 0, n}] /. {r[-1] -> rmin,
r[0] -> rmin, r[n + 1] -> rmax};半径の変化率に対する制約は，パラメータ α で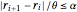
として表される．
In[6]:=
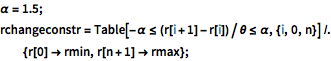
\[Alpha] = 1.5; rchangeconstr =
Table[-\[Alpha] <= (r[i + 1] - r[i])/\[Theta] <= \[Alpha], {i, 0,
n}] /. {r[0] -> rmin, r[n + 1] -> rmax};目的関数（弁の開口部）は，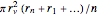
（
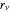は値の幾何学に関連した定数）として与えられる設計変数 
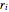と単純な線形関係を持つと想定される．
In[7]:=
rv = 1;
objfun = Pi rv^2 (1/n) Sum[r[i], {i, 1, n}];変数の初期点を選ぶ．
In[8]:=
initpts = Table[.5 (rmin + rmax), {i, 1, n}];最大化問題を解く．
In[9]:=
sol = FindMaximum[
Join[{objfun}, varbounds, convexconstr, rchangeconstr],
Thread[vars, initpts]];最大の半径のうちのいくつかは最大の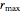 
である．
In[10]:=
Table[r[i], {i, 95, 100}] /. sol[[2]]Out[10]=
解をプロットする．
完全なWolfram言語入力を表示する
Out[11]=
