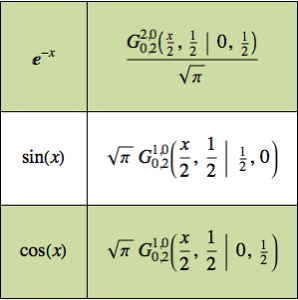ランプ強制関数を使って常微分方程式を解く

純粋なランプ応答を計算する．

In[1]:=

sol = DSolveValue[{x''[t] + a^2 x[t] == Ramp[t - a], x[0] == 0, x'[0] == 0}, x[t], t, Assumptions -> a > 0] // FullSimplify

Out[1]=

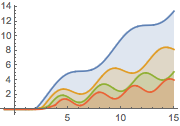
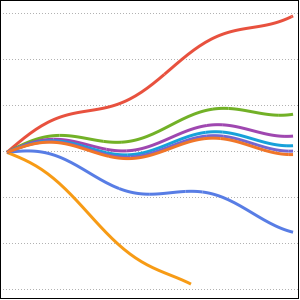
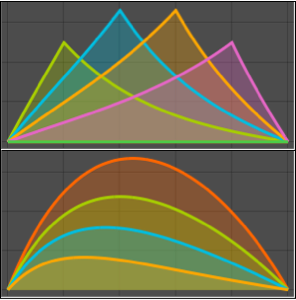
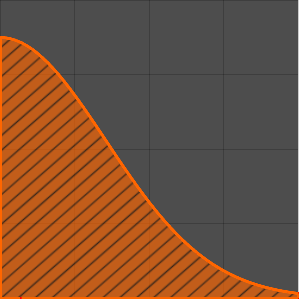
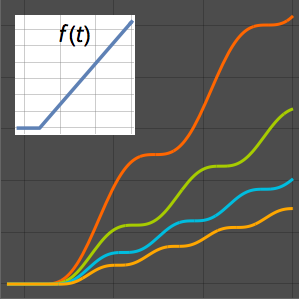
パラメータ a のさまざまな値に対する解をプロットする．

In[2]:=

Plot[Table[sol, {a, 1, 2, 0.3}] // Evaluate, {t, -1, 15}, Filling -> Axis]

Out[2]=

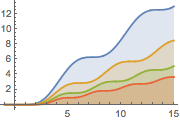
ランプと衝撃力を組み合せる．

In[3]:=

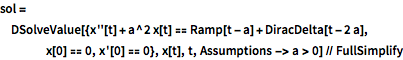
sol = DSolveValue[{x''[t] + a^2 x[t] == Ramp[t - a] + DiracDelta[t - 2 a], x[0] == 0, x'[0] == 0}, x[t], t, Assumptions -> a > 0] // FullSimplify

Out[3]=

In[4]:=

Plot[Table[sol, {a, 1, 2, 0.3}] // Evaluate, {t, -1, 15}, Filling -> Axis]

Out[4]=