Calcule a aceleração da gravidade

A aceleração da gravidade pode ser calculada medindo o período de um pêndulo 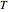e seu comprimento 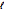usando 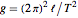. A incerteza na média de cinco medições repetidas do período é modelado com uma BatesDistribution.

In[1]:=

\[Mu]T = Quantity[2, "Seconds"]; \[CapitalDelta]T = Quantity[0.01, "Seconds"]; period\[ScriptCapitalD] = BatesDistribution[ 5, {\[Mu]T - \[CapitalDelta]T/2, \[Mu]T + \[CapitalDelta]T/2}]

Out[1]=

O comprimento do pêndulo foi medido utilizando uma régua com resolução de 1 mm, assim sua incerteza é modelada com um UniformDistribution.

In[2]:=

\[Mu]len = Quantity[1, "Meters"]; \[CapitalDelta]len = UnitConvert[Quantity[1, "mm"], "Meters"]; len\[ScriptCapitalD] = UniformDistribution[{\[Mu]len - \[CapitalDelta]len/ 2., \[Mu]len + \[CapitalDelta]len/2.}]

Out[2]=

A incerteza na medida da aceleração da gravidade.

In[3]:=

g\[ScriptCapitalD] = TransformedDistribution[ (2 \[Pi])^2 len/T^2, {len \[Distributed] len\[ScriptCapitalD], T \[Distributed] period\[ScriptCapitalD]}]

Out[3]=

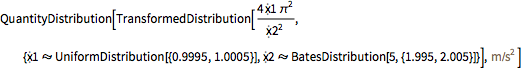
Compare com uma aproximação linear.

In[4]:=

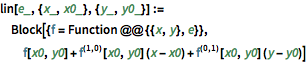
lin[e_, {x_, x0_}, {y_, y0_}] := Block[{f = Function @@ {{x, y}, e}}, f[x0, y0] + \!\(\*SuperscriptBox[\(f\), TagBox[ RowBox[{"(", RowBox[{"1", ",", "0"}], ")"}], Derivative], MultilineFunction->None]\)[x0, y0] (x - x0) + \!\(\*SuperscriptBox[\(f\), TagBox[ RowBox[{"(", RowBox[{"0", ",", "1"}], ")"}], Derivative], MultilineFunction->None]\)[x0, y0] (y - y0)]

In[5]:=

lin\[ScriptCapitalD][\[ScriptCapitalD]_] := NormalDistribution[Mean[\[ScriptCapitalD]], StandardDeviation[\[ScriptCapitalD]]]

In[6]:=

gApprox\[ScriptCapitalD] = TransformedDistribution[ lin[(2 Pi)^2 len/ T^2, {len, \[Mu]len}, {T, \[Mu]T}], {len \[Distributed] lin\[ScriptCapitalD][len\[ScriptCapitalD]], T \[Distributed] lin\[ScriptCapitalD][period\[ScriptCapitalD]]}]

Out[6]=

Calcule a aceleração média usando as distribuições exatas e linearizadas.

In[7]:=

{\[Mu]g, \[Mu]gApprox} = {NExpectation[g, g \[Distributed] g\[ScriptCapitalD]], NExpectation[g, g \[Distributed] gApprox\[ScriptCapitalD]]}

Out[7]=

Calcule as escalas de incerteza.

In[8]:=

{\[Sigma]g, \[Sigma]gApprox} = {Sqrt[ NExpectation[(g - \[Mu]g)^2, g \[Distributed] g\[ScriptCapitalD]]], StandardDeviation[gApprox\[ScriptCapitalD]]}

Out[8]=

Ache a estimativa de amostragem do intervalo de confiança de 90% para a aceleração medida.

In[9]:=

confidenceInterval = Quantile[RandomVariate[g\[ScriptCapitalD], 10^6], {0.05, 0.95}]

Out[9]=

In[10]:=

NProbability[First[confidenceInterval] < x < Last[confidenceInterval], x \[Distributed] g\[ScriptCapitalD]]

Out[10]=