A equação do tempo

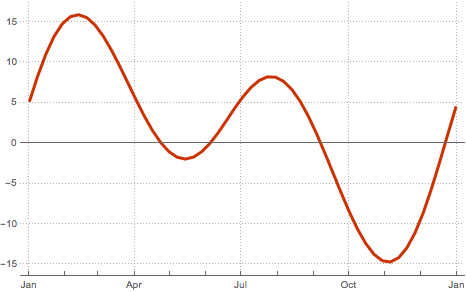
Devido à excentricidade da órbita da Terra e a inclinação do eixo da Terra em relação ao plano da órbita, o movimento aparente do sol varia ao longo do ano. Isto induz uma variação no tempo medido por um relógio solar (tempo solar aparente) em relação a um relógio mais preciso, por exemplo, determinado pela rotação aparente das estrelas fixas (hora sideral). Esta diferença é conhecida como a Equação do Tempo.

SiderealTime retorna valores de tempo sideral como quantidades de unidades mistas, usando MixedUnit.

In[1]:=

SiderealTime[]

Out[1]=

In[2]:=

SiderealTime[]; QuantityUnit[%]

Out[2]=

O tempo sideral é na verdade um ângulo, e portanto pode ser convertido em outras unidades angulares.

In[3]:=

UnitConvert[SiderealTime[], "AngularDegrees"]

Out[3]=

A Equação do Tempo é determinada pelo movimento do Sol, conforme dado pela SunPosition. Calcule valores semanais ao meio-dia GMT.

In[4]:=

dates = DateRange[ DateObject[{2015, 1, 1}, TimeObject[{12, 0}, TimeZone -> 0], TimeZone -> 0.`], DateObject[{2015, 12, 31}, TimeObject[{12, 0}, TimeZone -> 0], TimeZone -> 0.`], 7];

In[5]:=

sunpos = SunPosition[GeoPosition[{0, 0}], dates, CelestialSystem -> "Equatorial"]

Out[5]=

Use SiderealTime para calcular a ascensão reta no meridiano de Greenwich para as mesmas datas semanais.

In[6]:=

stime = SiderealTime[GeoPosition[{0, 0}], dates]

Out[6]=

Por fim, encontre os valores correspondentes da Equação do Tempo como a diferença entre a ascensão reta do Sol e o tempo sideral ao meio-dia durante todo o ano. Mostre o resultado em minutos.

In[7]:=

equationoftime = UnitConvert[(TimeSeriesMap[First, sunpos] - stime), "MinutesOfRightAscension"]

Out[7]=

Os valores absolutos da Equação do Tempo podem ser maiores do que 15 minutos.

In[8]:=

MinMax[equationoftime]

Out[8]=

In[9]:=

DateListPlot[equationoftime, GridLines -> Automatic, Axes -> True, PlotTheme -> "Web"]

Out[9]=