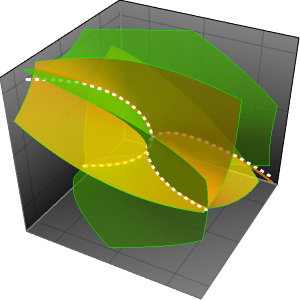
급수해 계산하기(AsymptoticDSolveValue)
선형상미분방정식은 그 방정식의 통상점 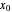 부근의 테일러 급수 전개
부근의 테일러 급수 전개 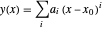 에 의해 근사할 수 있습니다. 이 예에서는 AsymptoticDSolveValue를 사용하여 이러한 근사를 구하는 방법을 설명합니다.
에 의해 근사할 수 있습니다. 이 예에서는 AsymptoticDSolveValue를 사용하여 이러한 근사를 구하는 방법을 설명합니다.
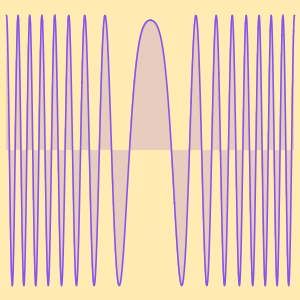
Cos를 정의하는 상미분방정식의 테일러 다항식 근사를 계산합니다.
높은 차수를 지정하여 근사 범위를 향상시킵니다.
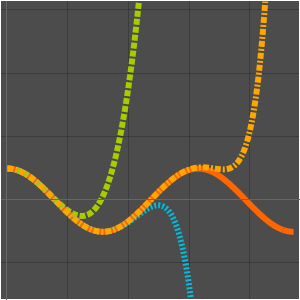
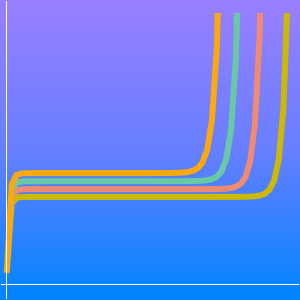
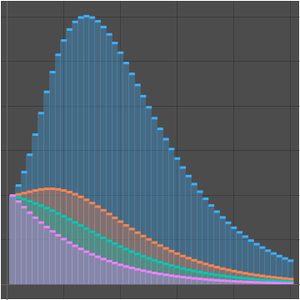
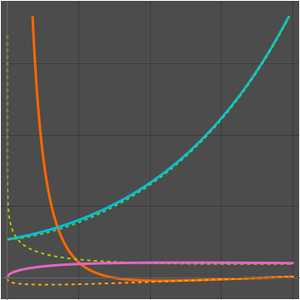
근사의 차수로 범위의 변화를 조사합니다.
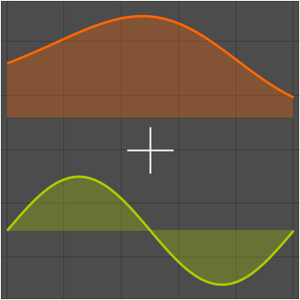
통상점 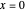 에서 선형상미분방정식 계의 테일러 근사를 계산합니다.
에서 선형상미분방정식 계의 테일러 근사를 계산합니다.
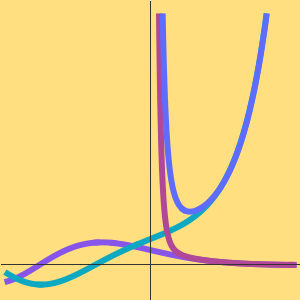
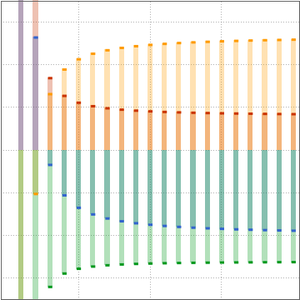
다음의 예와 같이, 테일러 근사는 다수의 경우 분석 계수를 가지는 비선형상미분방정식에 대해 계산할 수 있습니다.
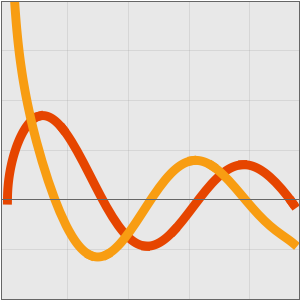
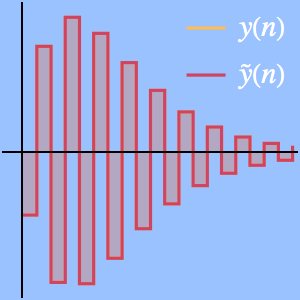
해에 의해 주어진 연속 근사를 그래프로 그립니다.