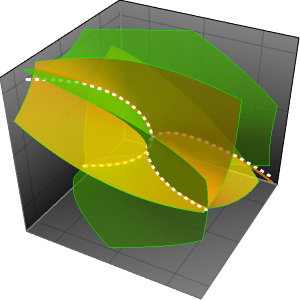
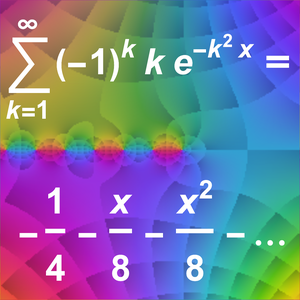점근 근사 검증하기
함수 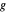 가 기준점에 가까워짐에 따라 소실되는 상대 오차를 갖는 함수
가 기준점에 가까워짐에 따라 소실되는 상대 오차를 갖는 함수 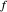 를 근사하면,
를 근사하면, 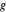 는
는 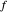 와 점근적으로 등가(AsymptoticEquivalent)라고(
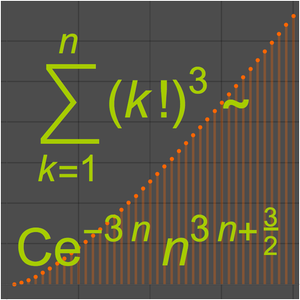
와 점근적으로 등가(AsymptoticEquivalent)라고(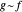 라고 쓰이기도 한다)합니다. 자주 쓰이는 예로, 계승 함수에 대한 스털링(Stirling)의 근사를 들 수 있습니다.
라고 쓰이기도 한다)합니다. 자주 쓰이는 예로, 계승 함수에 대한 스털링(Stirling)의 근사를 들 수 있습니다.
상대 오차가 제로에 접근하기 때문에, 함수의 비율은 1에 가까워집니다.
스털링 근사는 상대 오차가 0에 가까워지면 절대 오차는 무한대로 다가갑니다.
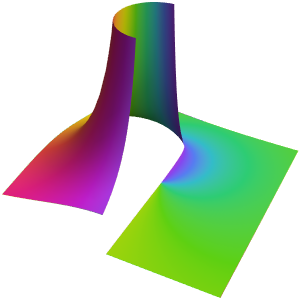
테일러 급수는 점근 근사를 줍니다.
로랑 급수 역시 점근 근사를 줍니다.
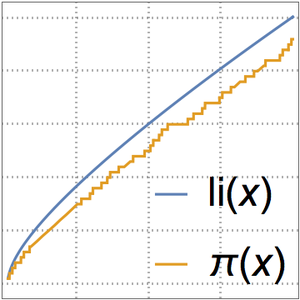
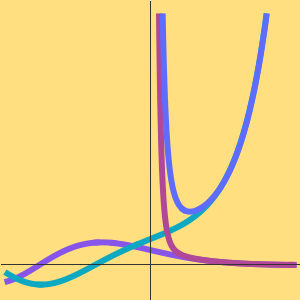
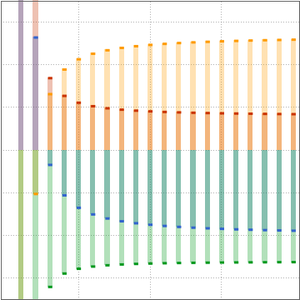
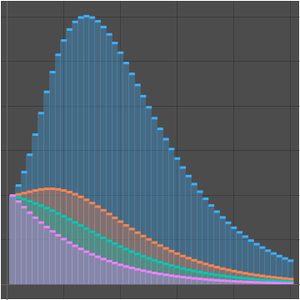
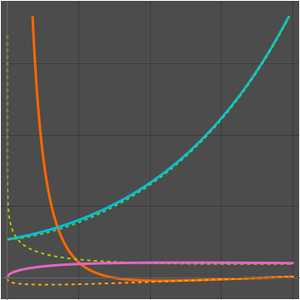
소수 정리에 따르면, 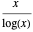 는 소수 계수 함수
는 소수 계수 함수 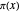 의 점근 근사입니다.
의 점근 근사입니다.
로그 적분 함수 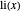 로 더 나은 근사가 주어집니다.
로 더 나은 근사가 주어집니다.
소수 계수 함수와 두 개의 근사를 비교합니다.