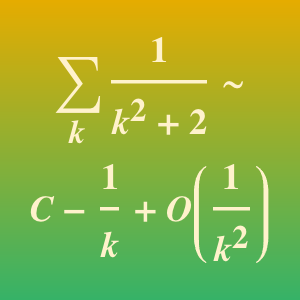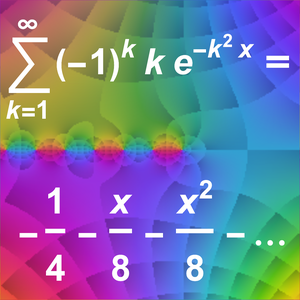점근 전개 생성하기(AsymptoticDSolveValue)
선형상미분방정식은 그 방정식의 불확정 특이점 근처의 일반 점근 급수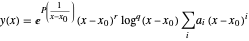 
에 의해 근사할 수 있습니다. 이 예에서는 AsymptoticDSolveValue를 사용하여 이러한 근사를 구하는 방법을 설명합니다. 점근 급수의 지수 인자는 불확정 특이점 근처에서 해의 급속한 성장, 감쇠, 또는 진동을 파악해야 합니다.
불확정 특이점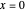 
에서 선형 일차 상미분방정식의 점근 근사를 계산합니다.
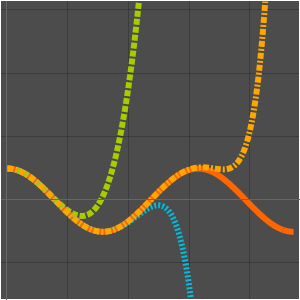
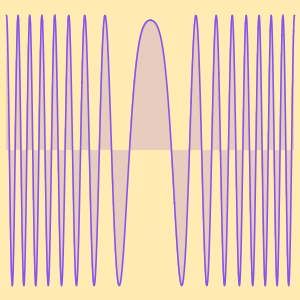
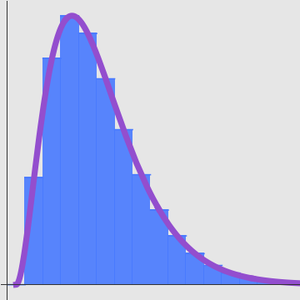
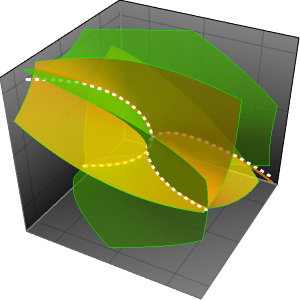
해에 의해 주어진 연속 근사를 그래프로 그립니다.
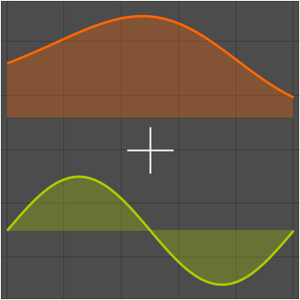
에어리(Airy) 방정식은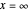 
에서 불확정 특이점을 갖습니다.
불확정 특이점으로 근사 전개를 계산합니다.
표준적 에어리 함수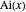 
의 Infinity에서의 급수와 비교하면 위는 
, 
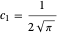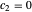에 대응합니다.
함수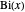 
는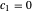 
, 
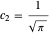에 해당합니다.
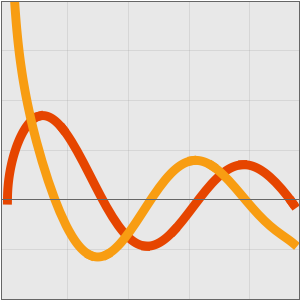
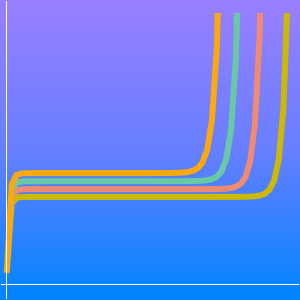
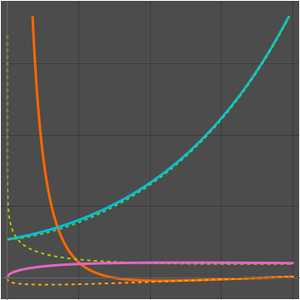
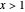값에 대해서 점근 전개는 빠르고 좋은 근사를 줍니다.
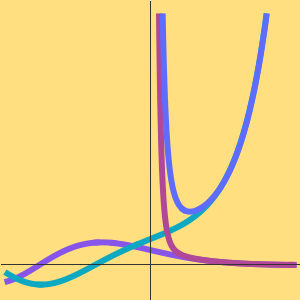
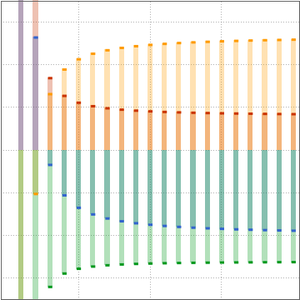
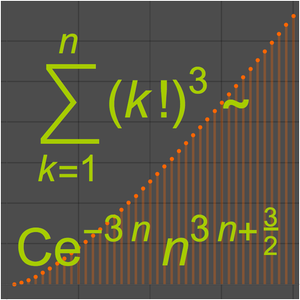
불확정 특이점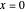 
에서 선형 고차 상미분방정식의 점근 근사를 구합니다.
