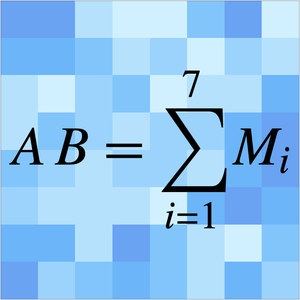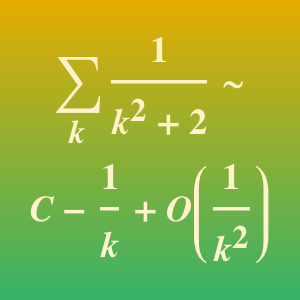求计算复杂度
在谈到算法的运行时间时，通常将最简单的函数 AsymptoticEqual (big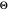 
) 赋予精确运行时间函数。 陈述这种相等关系的另一种方式是每个函数都 AsymptoticLessEqual (big 
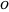) 和 AsymptoticGreaterEqual (big 
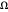) 另一个函数。下面以 Strassen 算法为例，对这些概念进行说明，该算法是发现的第一个 subcubic 矩阵乘法算法。
该算法包括四个步骤：将每个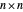 
矩阵分割为 4 个子矩阵，从 8 个子矩阵形成 14 个线性组合，将这 7 对组合相乘，并对 7 个结果求和。因此，计算乘法的时间 
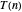将是分割矩阵的恒定时间 
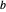，在第二步和第四步形成线性组合所用的时间 
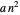，以及第三步花费的时间 
。
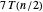求递归关系式。
尽管结果有点儿复杂，但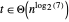 
。
同样地，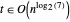
和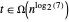 
。
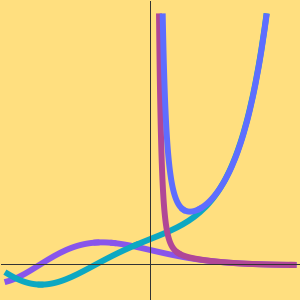
注意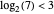 
，所以算法是 subcubic 的。
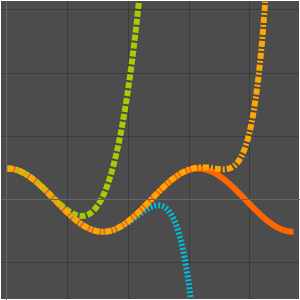
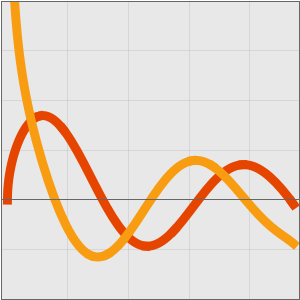
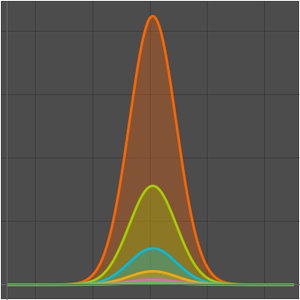
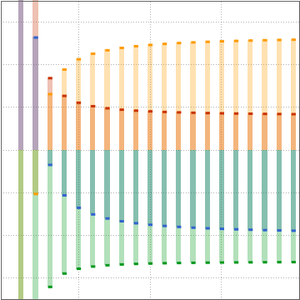
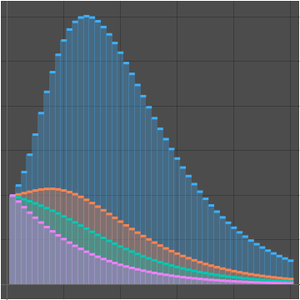
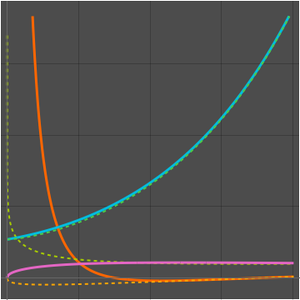
比较原始立方算法和 Strassen 算法的增长率。
