Wolfram 语言™

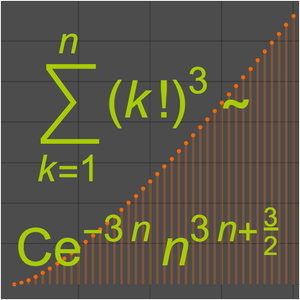
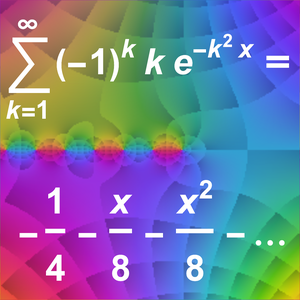探索发散渐近展开式 (AsymptoticIntegrate)

通常以发散级数的形式给出渐近展开式。一般情况下，发散级数的前几个项为问题提供了极好的近似，但如果包括更多的项，近似的质量会恶化。下面的例子中，一个取决于参数的定积分说明了这种现象。

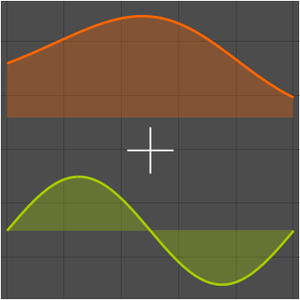
考虑以下定积分的级数展开式。

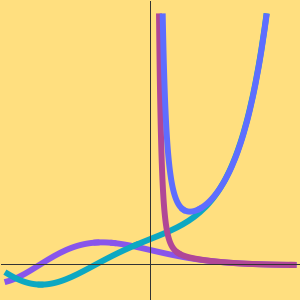
对于所有非零的 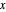值，级数发散。

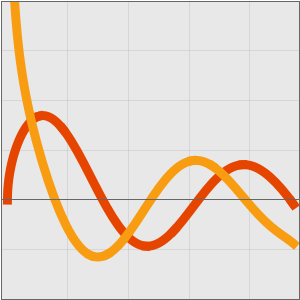
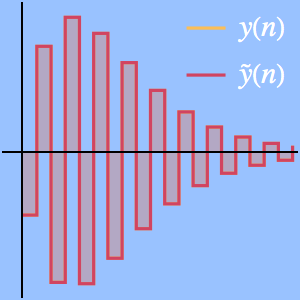
虽然级数是发散的，但它为积分提供了极好的渐近逼近。例如，以下数值比较表明近似是相当准确的。

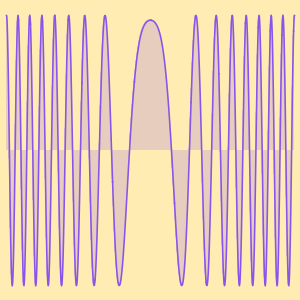
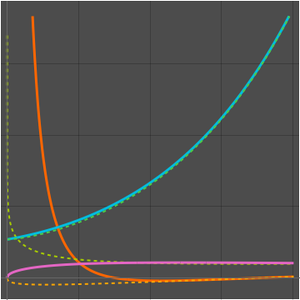
如果包含更多的项，近似则不再准确，对于渐近级数，这是很常见的行为。

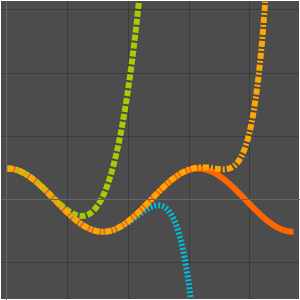
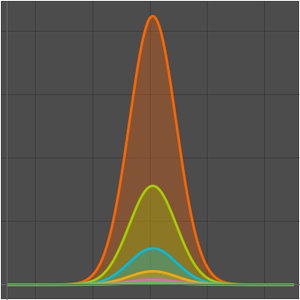
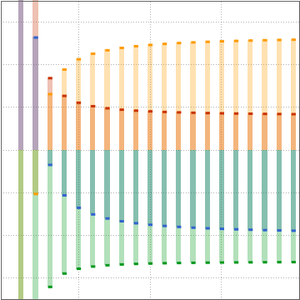
下图显示，对于固定的 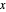值，当项的数量在一定范围（取决于 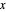）内时，渐近级数提供了很好的近似。当项的数量超出此范围时，近似开始发散。

用 Integrate 或 Regularization 获取精确结果。