Geometrischer Schwerpunkt
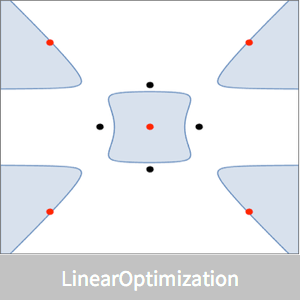
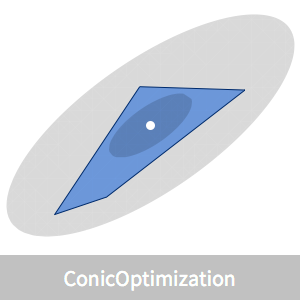
Ein konvexes Polygon kann als Schnittpunkt von Halbebenen dargestellt werden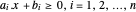 
. Der geometrische Schwerpunkt kann als Punkt innerhalb des Polygons definiert werden, der das Produkt der Abstände zu den Seiten maximiert. Der Abstand eines Punktes 
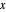im Polyeder zu allen Seiten ist 
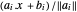, und so ist der geometrische Schwerpunkt 
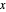, wodurch 
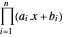maximiert wird.
Dieses Beispiel veranschaulicht die Anwendung der exponentiellen Kegel-Optimierung mit ConicOptimization um das analytische Zentrum zu finden, und wie die Ungleichheitsdarstellung eines Polygons mit LinearOptimization extrahiert werden kann.
Nehmen Sie ein konvexes Polygon her.
Extrahieren Sie die Koeffizienten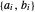 
für jede Seite.
Die dem Polygon entsprechenden skalaren Ungleichungen sind:
Um das Problem als konvexe Minimierung auszudrücken, nehmen Sie ein Protokoll und drehen Sie das Vorzeichen der Zielfunktion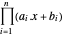 
um. Die transformierte Zielfunktion ist 
.
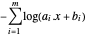Da eine Summe von Logarithmen konkav ist, ist das negative Vorzeichen konvex und daher kann die Hilfsvariable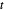 
als Zielfunktion mit 
unter der Bedingung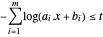 
eingeführt werden.
Visualisieren Sie die Position des geometrischen Schwerpunkts.
Es gibt einfache Formeln, die die eingeschriebenen und umhüllenden Ellipsen mit dem Schwerpunkt als Mittelpunkt angeben.
