Centro analítico
Un polígono convexo puede ser representado como intersecciones de planos medios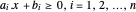 
. El centro analítico puede ser definido como un punto dentro del polígono que maximiza el producto de las distancias a los lados. La distancia de un punto 
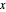en el poliedro a cada lado es 
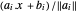, y por lo tanto el centro analítico es 
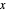, que maximiza 
.
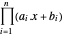Este ejemplo demuestra cómo se pueden usar las restricciones cónicas exponenciales con ConicOptimization para encontrar el centro analítico, y cómo se puede extraer la representación de desigualdad para un polígono usando LinearOptimization.
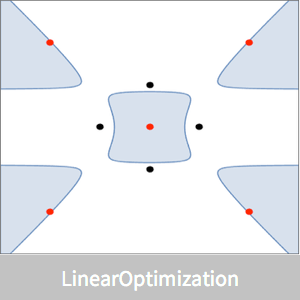
Tome un polígono convexo.
Extraiga los coeficientes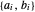 
de cada lado.
Las desigualdades escalares que corresponden al polígono son:
Para expresar el problema como una minimización convexa, tome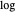 
y anule el objetivo 
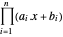. El objetivo transformado es 
.
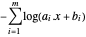Debido a que una suma de logaritmos es cóncava, la anulación es convexa, por lo cual se puede introducir una variable auxiliar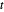 
como la función objetivo con 
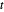sujeta a la restricción to 
.
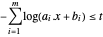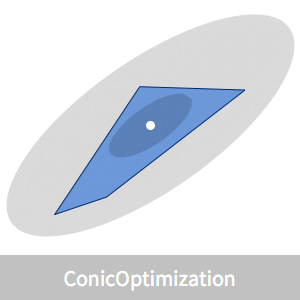
Visualice la ubicación del centro analítico.
Existen fórmulas simples que proporcionan los elipsoides inscritos y de cobertura que se centran en el centro analítico.
