解析的中心
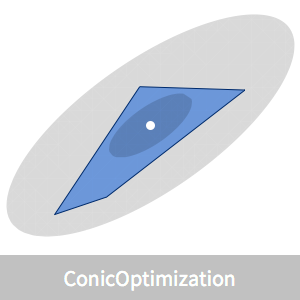
凸多角形は半平面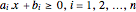 
の交差として表すことができる．解析的中心は，辺までの距離の積を最大化する多角形内部の点として定義することができる．多面体内部の点 
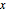から各面までの距離は
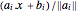であるため，解析的中心は
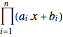を最大化する 
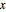である．
この例は，指数関数的な錐制約をConicOptimizationで使って，解析的中心を求め，LinearOptimizationを使って多角形の不等式表現を抽出する方法を示す．
凸多角形を取る．
各辺の係数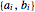
を抽出する．
多角形に対応するスカラー不等式は以下の通りである．
問題を凸最小化として表すために，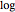
を取り目的関数
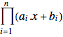を否定する．変換された目的関数は
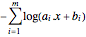である．
対数の和は凹であり，その否定は凸なので，補助変数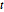 
は，制約条件
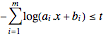のもとで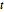 
の目的関数として導入される．
解析的中心の位置を可視化する．
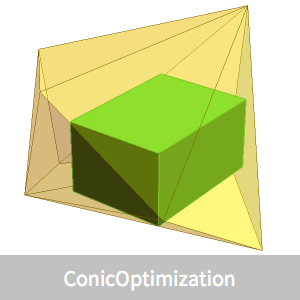
解析的中心を中心とする内接楕円体と被覆楕円体を与える簡単な式がある．
