Centro analítico
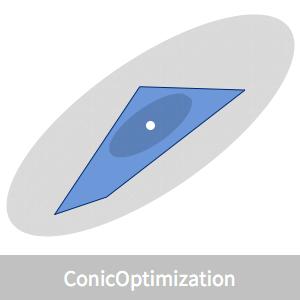
Um polígono convexo pode ser representado como interseções de meio-planos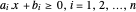 
. O centro analítico pode ser definido como um ponto dentro do polígono que maximiza o produto das distâncias para os lados. A distância de um ponto 
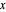no poliedro de cada lado é 
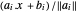, e assim o centro analítico é 
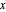, que maximiza 
.
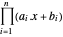Este exemplo monstra como restrições de cone exponencial podem ser usadas com ConicOptimization para encontrar o centro analítico, assim como a representação da desigualdade para um polígono pode ser extraída usando LinearOptimization.
Considere um polígono convexo.
Extraia os coeficientes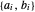 
para cada lado.
As desigualdades escalares correspondentes ao polígono são:
Para expressar o problema como uma minimização convexa, use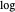 
e negue o objetivo 
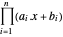. O objetivo transformado é 
.
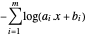Como uma soma de logaritmos é côncava, a negação é convexa e, portanto, uma variável auxiliar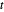 
pode ser introduzida como a função objetiva com 
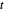sujeita à restrição 
.
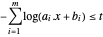Visualize a localização do centro analítico.
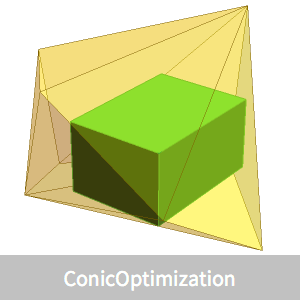
Existem fórmulas simples que especificam os elipsóides inscritos e envolventes que estão centralizados no centro analítico.
