Robust Data Fitting
Find a robust fit to nonlinear discrete data by minimizing 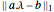 .
.
This example demonstrates how a fitting problem can easily be converted to an optimization problem using matrices, vector variables and vector inequalities.
Generate some noisy data with outliers.
Fit the data using the basis functions 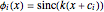 . The approximating model will be
. The approximating model will be  .
.
The function DesignMatrix can be used to get the design matrix 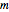 with elements
with elements 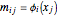 .
.
The response is the second element of each data point.
Minimize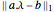 by introducing a vector variable s such that each component of s satisfies
by introducing a vector variable s such that each component of s satisfies  so that
so that 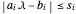 . The condition can be expressed for all components at once using VectorLessEqual.
. The condition can be expressed for all components at once using VectorLessEqual.
The norm  is convex, so with the conditions
is convex, so with the conditions 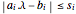 , minimizing
, minimizing 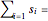 Total[s] is equivalent to minimizing the norm
Total[s] is equivalent to minimizing the norm  .
.
Equations with explicit numerical values may be used to define parameter values. Here, the parameters 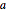 and
and 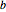 are defined in terms of the design matrix and the response.
are defined in terms of the design matrix and the response.
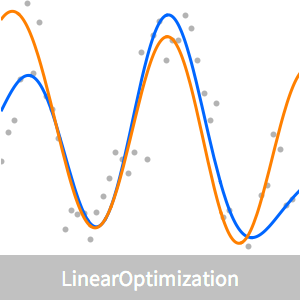
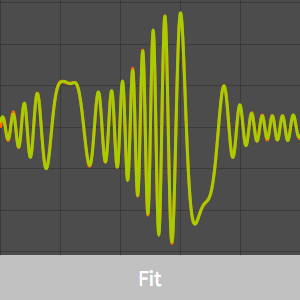
Visualize the fit.
Compare the approximating model with the least squares fit.
Note that both of these fits can be done directly with Fit. The L1 fit is done with the following.
The least squares fit is the default for Fit and is done with the following.