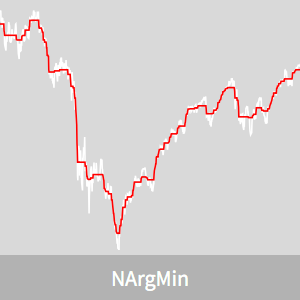
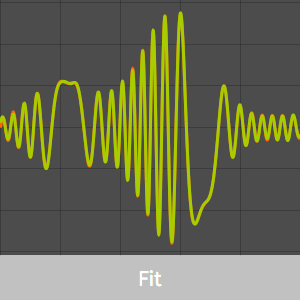
강력한 데이터 맞춤
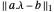을 최소화함으로써 비선형 이산 데이터에 대한 강력한 맞춤을 구합니다.
이 예는 행렬, 벡터 변수, 벡터 부등식을 사용하여 맞춤 문제를 최적화 문제로 쉽게 변환하는 방법을 보여줍니다.
특이한 값을 가진 노이즈 데이터를 생성합니다.
기저함수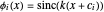 
를 사용하여 데이터를 맞춥니다. 근사 모델은 
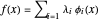입니다.
함수 DesignMatrix를 사용하여 요소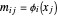 
의 계획 행렬 
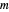을 얻을 수 있습니다.
해당 응답은 각 데이터 포인트의 제2요소입니다.
벡터 변수 s를 도입해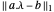 
을 최소화합니다. s의 각 요소는 
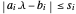가 되도록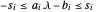 
을 만족시키면, 모든 요소는 VectorLessEqual을 사용하여 한 번에 나타낼 수 있습니다.
노름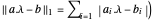 
는 볼록이므로 
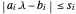일 때,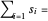 
Total[s]를 최소화하는 것은 노름 
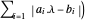을 최소화하는 것과 동일합니다.
명시적인 수치값을 가진 방정식을 사용하여 매개변수 값을 정의 할 수 있습니다. 개인은 계획 행렬과 응답에 대한 매개 변수 a와 b를 정의합니다.
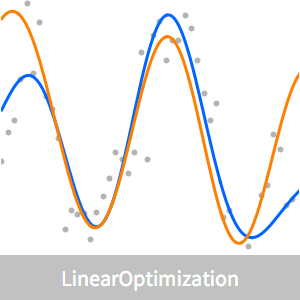
맞춤을 시각화합니다.
근사 모델을 최소 제곱 맞춤과 비교합니다.
이러한 맞춤은 모두 Fit에서 직접할 수 있습니다. L1 맞춤은 다음과 같이 합니다.
최소 제곱 맞춤은 Fit의 기본이며, 다음과 같이 이루어 집니다.
