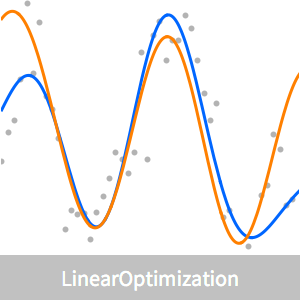
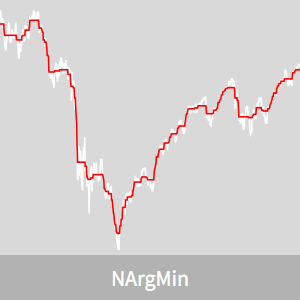
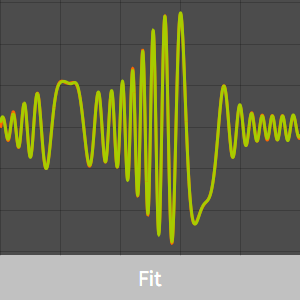
Ajuste de datos sólidos
Encuentre un ajuste sólido para datos discretos no lineales minimizando 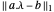 .
.
Este ejemplo demuestra cómo un problema de ajuste puede ser convertido fácilmente en un problema de optimización usando matrices, variables vectoriales e inequidades vectoriales.
Genere algunos datos ruidosos con valores atípicos.
Ajuste los datos usando las funciones básicas 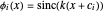 . El modelo aproximado será
. El modelo aproximado será 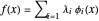 .
.
La función DesignMatrix puede ser usada para obtener la matriz de diseño 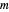 con elementos
con elementos 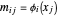 .
.
La respuesta es el segundo elemento de cada punto de datos.
Minimice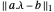 introduciendo una variable vectorial s de manera que cada componente de s cumpla con
introduciendo una variable vectorial s de manera que cada componente de s cumpla con 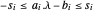 para que
para que 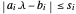 . La condición puede ser expresada para todos los componentes a la vez usando VectorLessEqual.
. La condición puede ser expresada para todos los componentes a la vez usando VectorLessEqual.
La norma 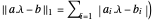 es convexa, así que con las condiciones
es convexa, así que con las condiciones 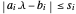 , minimizar
, minimizar 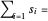 Total[s] es equivalente a minimizar la norma
Total[s] es equivalente a minimizar la norma 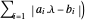 .
.
Las ecuaciones con valores numéricos explícitos pueden ser usadas para definir valores de parámetro. Aquí, los parámetros 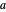 y
y 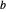 son definidos en términos de la matriz de diseño y la respuesta.
son definidos en términos de la matriz de diseño y la respuesta.
Visualice el ajuste.
Compare el modelo de aproximación con el ajuste de mínimos cuadrados.
Note que ambos ajustes pueden realizarse directamente con Fit. El ajuste L1 se realiza con lo siguiente.
El ajuste de mínimos cuadrados es predeterminado para Fit y se realiza con lo siguiente.