Ajustement robuste des données
Recherchez un ajustement robuste aux données discrètes non linéaires en minimisant 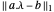 .
.
Cet exemple démontre comment un problème d'ajustement peut facilement être converti en un problème d'optimisation en utilisant des matrices, des variables vectorielles et des inégalités vectorielles.
Générez des données bruitées avec des valeurs aberrantes.
Ajustez les données en utilisant les fonctions de base 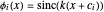 . Le modèle approximatif sera
. Le modèle approximatif sera 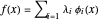 .
.
La fonction DesignMatrix permet d'obtenir le design de la matrice 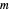 avec les éléments
avec les éléments 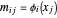 .
.
La réponse correspond au deuxième élément de chaque point de données.
Minimisez 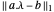 en introduisant une variable vectorielle s de sorte que chaque composante de s satisfasse
en introduisant une variable vectorielle s de sorte que chaque composante de s satisfasse 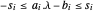 de sorte que
de sorte que 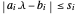 . La condition peut être exprimée pour toutes les composantes à la fois en utilisant VectorLessEqual.
. La condition peut être exprimée pour toutes les composantes à la fois en utilisant VectorLessEqual.
La norme 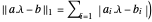 est convexe, donc avec les conditions
est convexe, donc avec les conditions 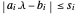 , minimiser
, minimiser 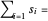 Total[s] équivaut à minimiser la norme
Total[s] équivaut à minimiser la norme 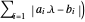 .
.
Les équations avec des valeurs numériques explicites peuvent être utilisées pour définir les valeurs des paramètres. Ici, les paramètres 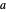 et
et 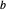 sont définis en fonction du design de la matrice et de la réponse.
sont définis en fonction du design de la matrice et de la réponse.
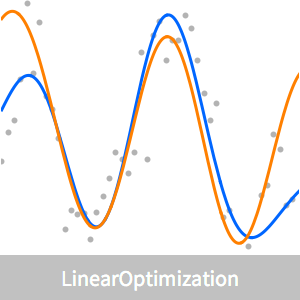
Visualisez l'ajustement.
Comparez le modèle approximatif avec l'ajustement des moindres carrés.
Remarquez que ces deux ajustements peuvent être effectués directement avec Fit. L'ajustement L1 se fait de la manière suivante :
L'ajustement des moindres carrés correspond à l'ajustement par défaut pour Fit et se fait de la manière suivante :