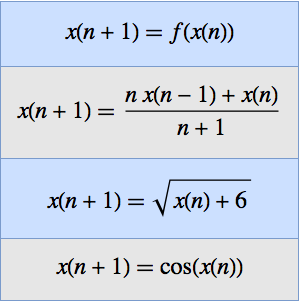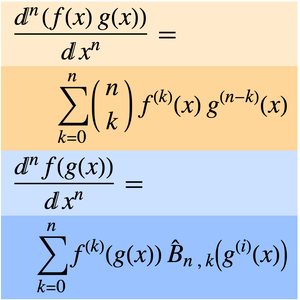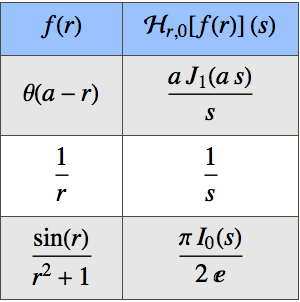数列の極限を求める
数列の極限は微積分ではよく出てくるもので,対応する関数の極限がない場合でも存在することがある.以下の例で示すように,バージョン12のDiscreteLimit関数を使うと,閉形式で与えられた数列または形式的な演算子で指定された数列の極限を計算することができる.
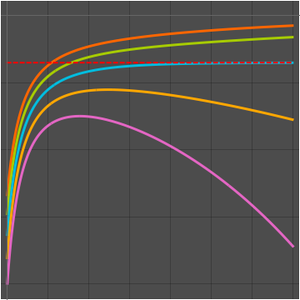
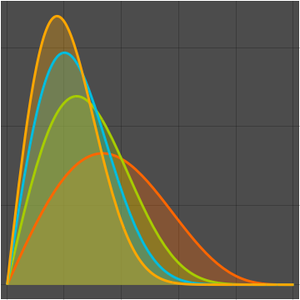
数列の極限を求める.
数列を可視化する.
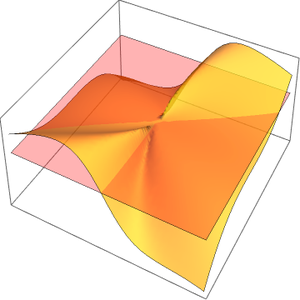
多変量数列の極限を求める.
数列を可視化する.
次の例では,極限についてのロピタル(L'Hôpital)の定理の離散版であるシュトルツ・チェザロ(Stolz–Cesàro)の定理を使う.
ネストされたInactive総和の極限を求める.
Inactive連分数の極限を求める.
次の例は,関数の極限は存在しないかもしれないが対応する数列の極限は存在するということを示している.
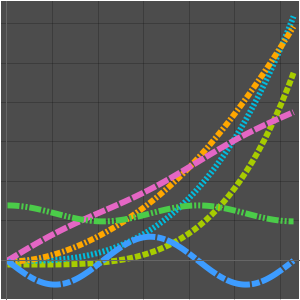
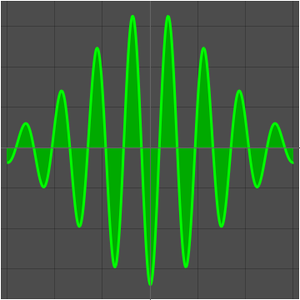
三角関数を定義する.
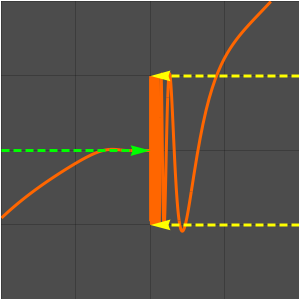
関数および,整数で関数をサンプリングして得られた数列をプロットする.
ここで関数の極限は存在しない.
これは,関数の値が-1と1の間で振動するからである.
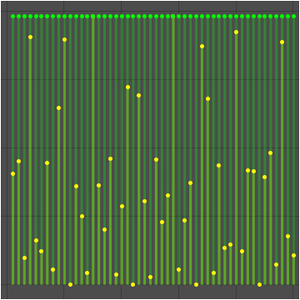
しかし,数列の極限は存在する.
これは,数列はすべてのサンプル点において一定だからである.