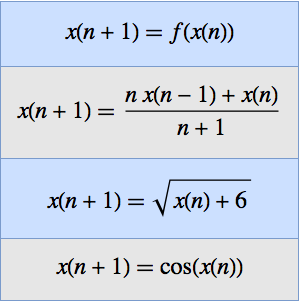数列の下限と上限を求める
数列の下限と上限は常に存在するという利点があるが,数列の極限は例外的な場合にのみ存在する.次の例で示すように,振動数列の下限と上限を計算することができるアルゴリズムと新関数がこのたび初めて加わった.
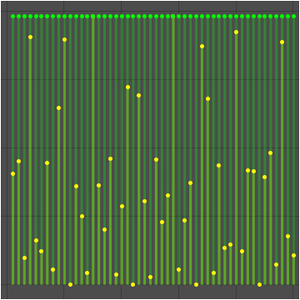
数列の下限を求める.
数列の上限を求める.
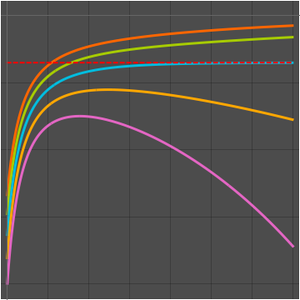
以下の数列の極限は存在する.
したがって,極限は数列の上限と下限の両方に対して同じである.
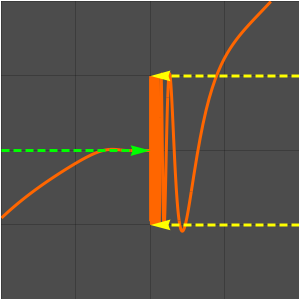
以下の数列の極限は存在しない.
これは,偶数の部分数列と奇数の部分数列が異なる極限に収束するからである.
したがって,数列の下極限と上極限は等しくはない.