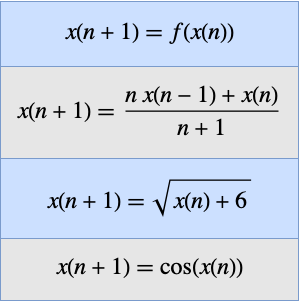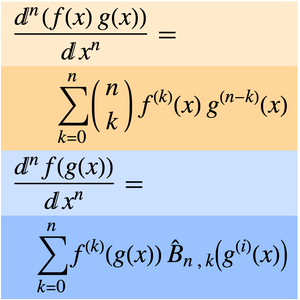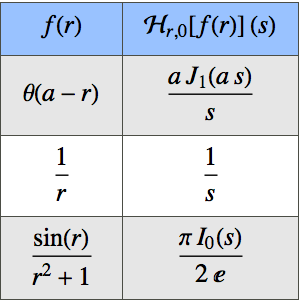求序列的极限
微积分中经常出现序列的极限,即使相应的函数极限不存在,序列的极限也可能存在。12 版中的 DiscreteLimit 函数可用来计算以解析形式给出的或由正式运算符指定的序列的极限,如下例所示。
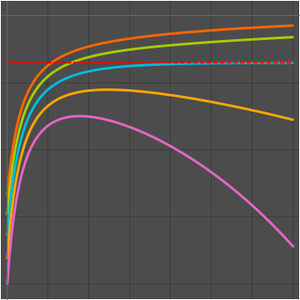
求序列的极限。
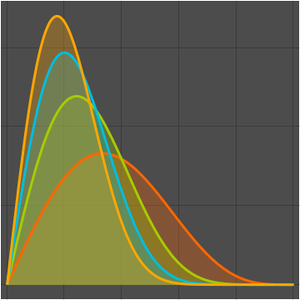
可视化序列。
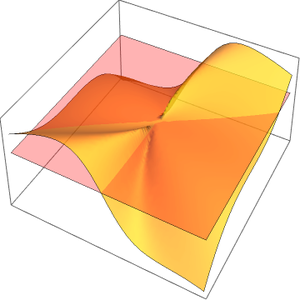
求多变量序列的极限。
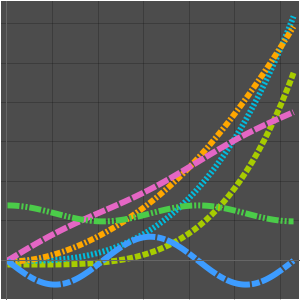
可视化序列。
下面的例子使用 Stolz–Cesàro 规则,即求极限的 L'Hôpital 规则的离散版本。
求嵌套 Inactive 和的极限。
求 Inactive 连分数的极限。
下面的例子说明了函数的极限可能不存在,但相应的序列的极限却存在。
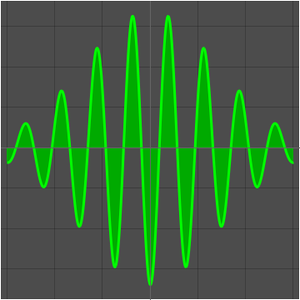
定义一个三角函数。
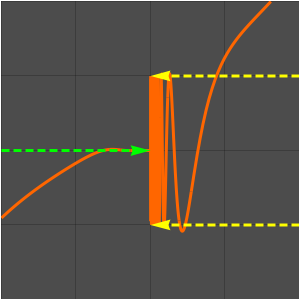
绘制函数和通过在整数处对函数进行采样而获得的序列。
函数的极限不存在。
这是因为函数的值在 -1 和 1 之间振荡。
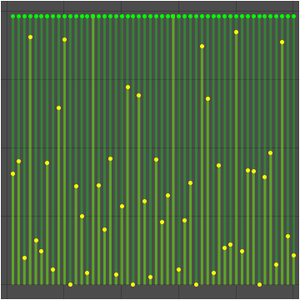
然而,序列的极限却存在。
这是因为序列在所有采样点都是常数。