Euklids Elemente
Eine der ältesten und einflussreichsten mathematischen Abhandlungen aller Zeiten ist Die Elemente, ein dreizehnteiliges Werk des griechischen Mathematikers Euklid von Alexandria. Die in Die Elemente beschriebenen Konstruktionen können in der Wolfram Language mit GeometricScene dargestellt und mit RandomInstance visualisiert werden.
In Postulat 1 in Buch I heißt es, dass man bei zwei beliebigen Punkten 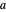 und
und 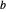 ein gleichseitiges Dreieck mit
ein gleichseitiges Dreieck mit 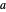 und
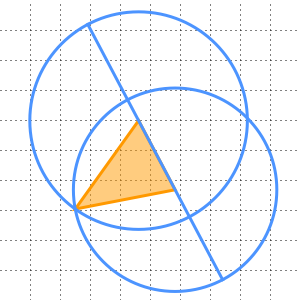
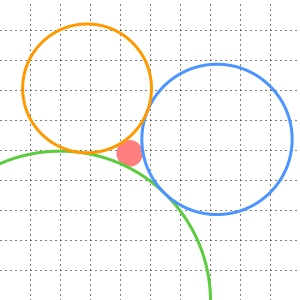
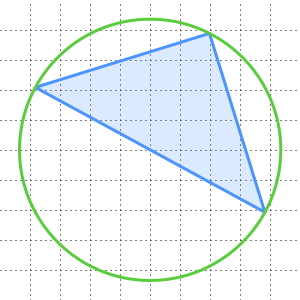
und 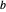 als zwei seiner Knoten konstruieren kann. Zeichnen Sie zwei Kreise, die auf
als zwei seiner Knoten konstruieren kann. Zeichnen Sie zwei Kreise, die auf 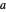 und
und  zentriert sind und deren Radien gleich dem Abstand zwischen ihnen sind. Dann bildet ihr Schnittpunkt
zentriert sind und deren Radien gleich dem Abstand zwischen ihnen sind. Dann bildet ihr Schnittpunkt 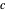 den dritten Eckpunkt eines solchen gleichseitigen Dreiecks.
den dritten Eckpunkt eines solchen gleichseitigen Dreiecks.
Postulat 22 von Buch I verallgemeinert Postulat 1, indem es besagt, dass es für alle positiven Größen 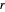 ,
, 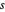 und
und 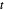 , für die
, für die 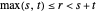 gilt, es ein Dreieck mit den Seitenlängen
gilt, es ein Dreieck mit den Seitenlängen 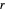 ,
, 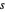 und
und 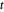 gibt.
gibt.
Wählen Sie positive Zufallszahlen für 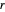 ,
, 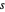 und
und 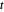 , sodass
, sodass 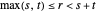 .
.
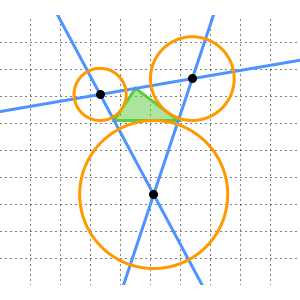
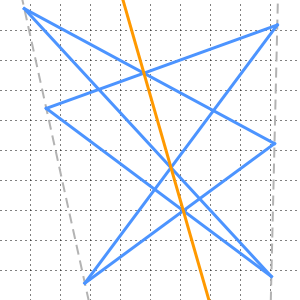
Bilden Sie diese geometrische Struktur wie folgt: Ziehen Sie eine Gerade durch die Punkte  ,
,  ,
, 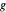 und
und 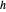 in dieser Reihenfolge, wobei
in dieser Reihenfolge, wobei 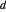 und
und 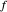 den Abstand
den Abstand 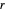 zueinander haben,
zueinander haben, 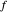 und
und 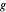 den Abstand
den Abstand 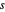 und
und 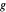 und
und 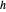 den Abstand
den Abstand 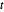 zueinander haben. Zeichnen Sie den Kreis mit Mittelpunkt
zueinander haben. Zeichnen Sie den Kreis mit Mittelpunkt 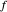 , der durch
, der durch 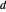 geht, sowie den Kreis mit Mittelpunkt
geht, sowie den Kreis mit Mittelpunkt 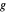 , der durch
, der durch 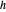 geht. Wenn
geht. Wenn 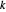 einer der Punkte ist, wo diese Kreise einander schneiden, dann ist
einer der Punkte ist, wo diese Kreise einander schneiden, dann ist 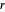 der Abstand zwischen
der Abstand zwischen 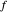 und
und 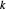 ,
, 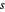 ist der Abstand zwischen
ist der Abstand zwischen 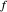 und
und 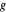 , und
, und 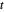 ist der Abstand zwischen
ist der Abstand zwischen 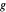 und
und 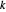 . Daher bilden die Punkte
. Daher bilden die Punkte 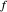 ,
, 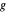 und
und 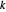 ein Dreieck.
ein Dreieck.