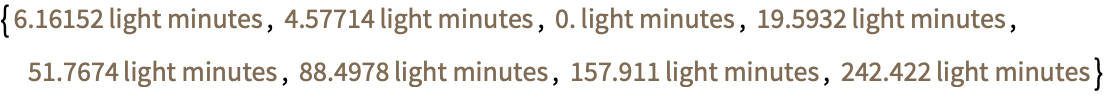| 17 | Units |
As soon as you’re dealing with real-world quantities, it’s inevitable that you’ll run into units. In the Wolfram Language, you can enter quantities with units using  .
.
Enter a quantity of time in units of hours:
Press the check mark to accept the interpretation:
You can use InputForm to see how the Wolfram Language internally represents this.
Show the internal form of a quantity:
In[1]:=
Out[1]=
You can always enter quantities directly like this, or you can use  , either for the whole thing, or just for the units.
, either for the whole thing, or just for the units.
The Wolfram Language knows about all the 10,000 or so common kinds of units. UnitConvert converts between them.
Convert from hours to minutes:
In[2]:=
Out[2]=
You can do arithmetic with quantities even if they have different units.
Add a length in feet to one in centimeters:
In[3]:=
Out[3]=
Divide one length by another:
In[4]:=
Out[4]=
Use dollars in a computation:
In[5]:=
Out[5]=
Multiply a price per pound by a weight in kilograms:
In[6]:=
Out[6]=
You can convert between currencies. The Wolfram Language always knows the latest conversion rate.
In[7]:=
Out[7]=
There are many places where units show up. Another example is in angles—and this is such a common case that the Wolfram Language lets you handle it in a special way. You can enter an angle like 30 degrees either as 30 Degree, or as 30°, where the ° can be typed as deg .
Display a string rotated by 30 degrees:
In[8]:=
Out[8]=
If you leave off the Degree or °, the Wolfram Language will assume you’re talking about radians, which go from 0 to 2π (about 6.28) around a circle, rather than degrees, which go from 0 to 360.
π/2 radians is equivalent to 90°:
In[9]:=
Out[9]=
Make a list of rotations in degrees from 0 to 360:
In[10]:=
Out[10]=
There’s lots to do with angles. For example, AnglePath gives the path you’d follow if you successively turned by a sequence of angles.
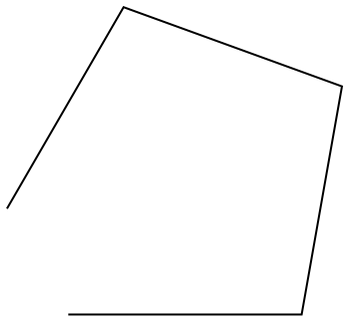
Start off horizontal, then turn three times by 80°:
In[11]:=
Out[11]=
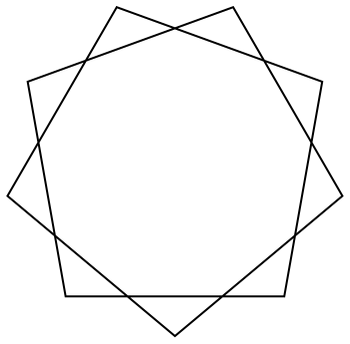
Keep turning by 80° and you’ll eventually get back to where you started:
In[12]:=
Out[12]=
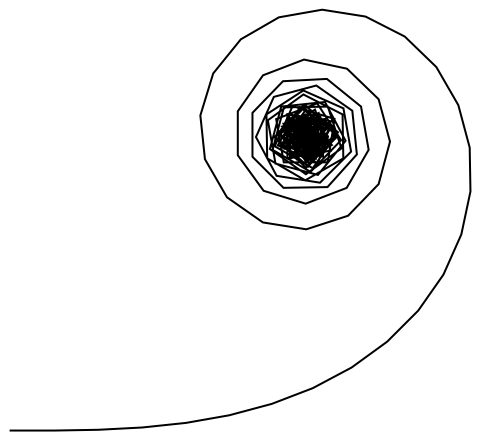
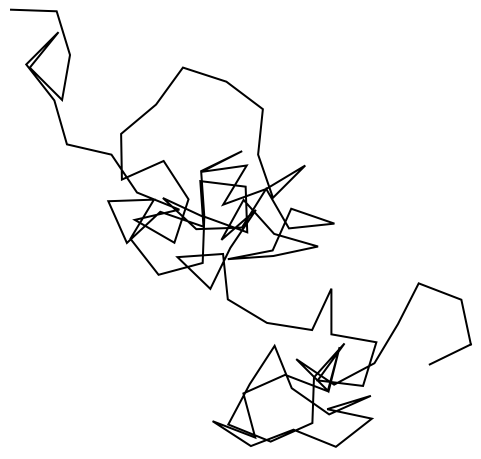
If you keep increasing the angle, you get an interesting pattern:
In[13]:=
Out[13]=
| UnitConvert[quantity,unit] | convert between units | |
| CurrencyConvert[amount,unit] | convert between currencies | |
| 30 Degree | angle in degrees | |
| 30° | angle in degrees entered with deg | |
| Rotate[expr,angle] | rotate on the screen | |
| AnglePath[{angle1,angle2,...}] | path derived from a sequence of turns |
17.1Convert 4.5 lbs (pounds) to kilograms. »
17.2Convert 60.25 mph to kilometers per hour. »
17.3Find the height of the Eiffel Tower in miles. »
17.4Find the height of Mount Everest divided by the height of the Eiffel Tower. »
17.5Find the mass of the Earth divided by the mass of the Moon. »
17.6Convert 2500 Japanese yen to US dollars. »
17.7Find the total of 35 ounces, 1/4 ton, 45 lbs and 9 stone in kilograms. »
17.8Get a list of the distances to each planet using the "DistanceFromEarth" property, and convert all the results to light minutes. »
17.13Make graphics of the path obtained by turning a constant angle 100 times, controlling the angle from 0° to 360° with a Manipulate. »
17.14Make graphics of the path obtained by successively turning by the digits of 2^10000 multiplied by 30°. »
+17.1Convert 4.3 light years to furlongs. »
+17.2Convert 20,000 leagues to miles. »
+17.5Generate a list of letters of the alphabet, each randomly rotated. »
+17.6Generate graphics for a path obtained by turning 100 times through a random number of degrees between 0 and 360. »
What unit abbreviations does the Wolfram Language understand?
Pretty much any common abbreviation, whether it’s miles/hr or mph or mi/h, etc. (If you’re wondering if an abbreviation will work, just try it.)
Does the Wolfram Language pick units based on what country I’m in?
Yes. For example, it’ll tend to use inches if you’re in the US, and centimeters if you’re in continental Europe.
Do I have to be connected to the network to use units?
Only to interpret input like 5kg. If you type Quantity[5, "Kilograms"] you don’t need the network—except to deal with units like currencies whose values are always changing.
What can I do if my unit conversion gives me an exact fraction but I want a decimal number?
Use the function N[...] to find a decimal approximation. Or add a decimal point to a number in your input. We’ll talk more about this in Section 23.
Why don’t I get the same result for the currency conversion example?
- The Wolfram Language handles all 160 or so standard currencies (including ones like bitcoin). If necessary, you can use the ISO currency code (USD, UKP, etc.) to specify a currency.
- Degree isn’t a function; like Red, Green, etc. it’s a symbol. We’ll talk more about these later.
- AnglePath implements “turtle graphics” familiar from languages like Logo and Scratch.
- AnglePath3D generalizes AnglePath to 3D, allowing for “flying turtles”, spacecraft simulations, etc.