| 30 | Rearranging Lists |
It’s common for lists that come out of one computation to have to be rearranged before going into another computation. For example, one might have a list of pairs, and need to convert it into a pair of lists, or vice versa.
Transpose a list of pairs so it becomes a pair of lists:
In[1]:=
Out[1]=
Transpose the pair of lists back to a list of pairs:
In[2]:=
Out[2]=
“Thread” across the elements of two lists:
In[3]:=
Out[3]=
Partition takes a list, and partitions it into blocks of a specified size.
Partition a 12-element list into blocks of size 3:
In[4]:=
Out[4]=
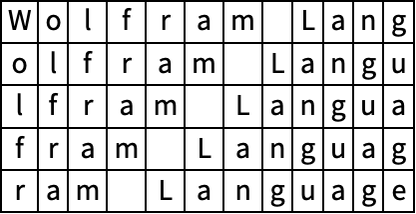
Partition a list of characters to display them in a grid:
In[5]:=
Out[5]=

If you don’t tell it otherwise, Partition breaks a list up into non-overlapping blocks. But you can also tell it to break the list into blocks that have some specified offset.
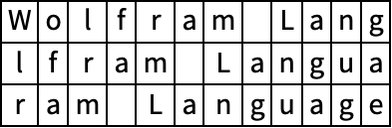
Partition a list into blocks of size 3 with offset 1:
In[6]:=
Out[6]=
In[7]:=
Out[7]=
Use an offset of 2 instead:
In[8]:=
Out[8]=
Make a list of lists from digits of successive integers:
In[9]:=
Out[9]=
Make a flattened version:
In[10]:=
Out[10]=
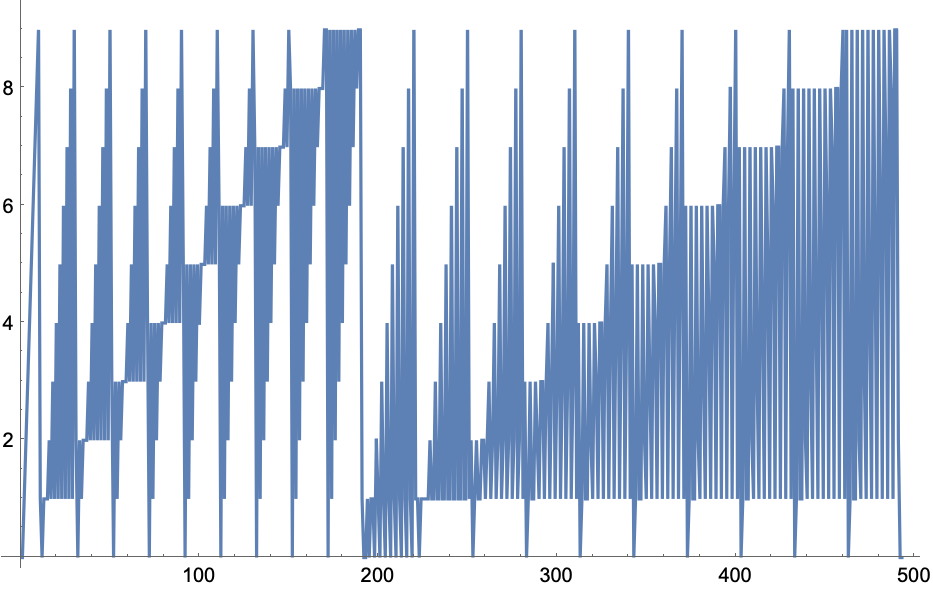
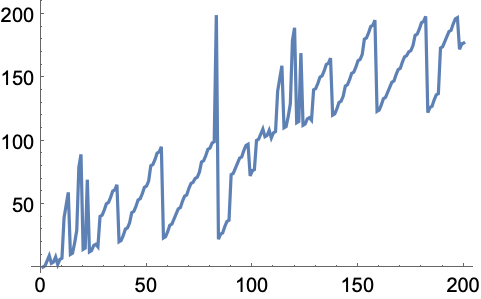
Make a plot from the sequence of digits:
In[11]:=
Out[11]=
Flatten will normally flatten out all levels of lists. But quite often you only want to flatten, say, one level of lists. This makes a 4×4 table in which each element is itself a list.
Make a list of lists of lists:
In[12]:=
Out[12]=
In[13]:=
Out[13]=
Flatten out only one level of list:
In[14]:=
Out[14]=
ArrayFlatten is a generalization of Flatten, which takes arrays of arrays, and flattens them into individual arrays.
This generates a deeply nested structure that’s hard to understand:
In[15]:=
Out[15]=
ArrayFlatten makes a structure that’s a little easier to understand:
In[16]:=
Out[16]=
With ArrayPlot, it’s considerably easier to see what’s going on:
In[17]:=
Out[17]=

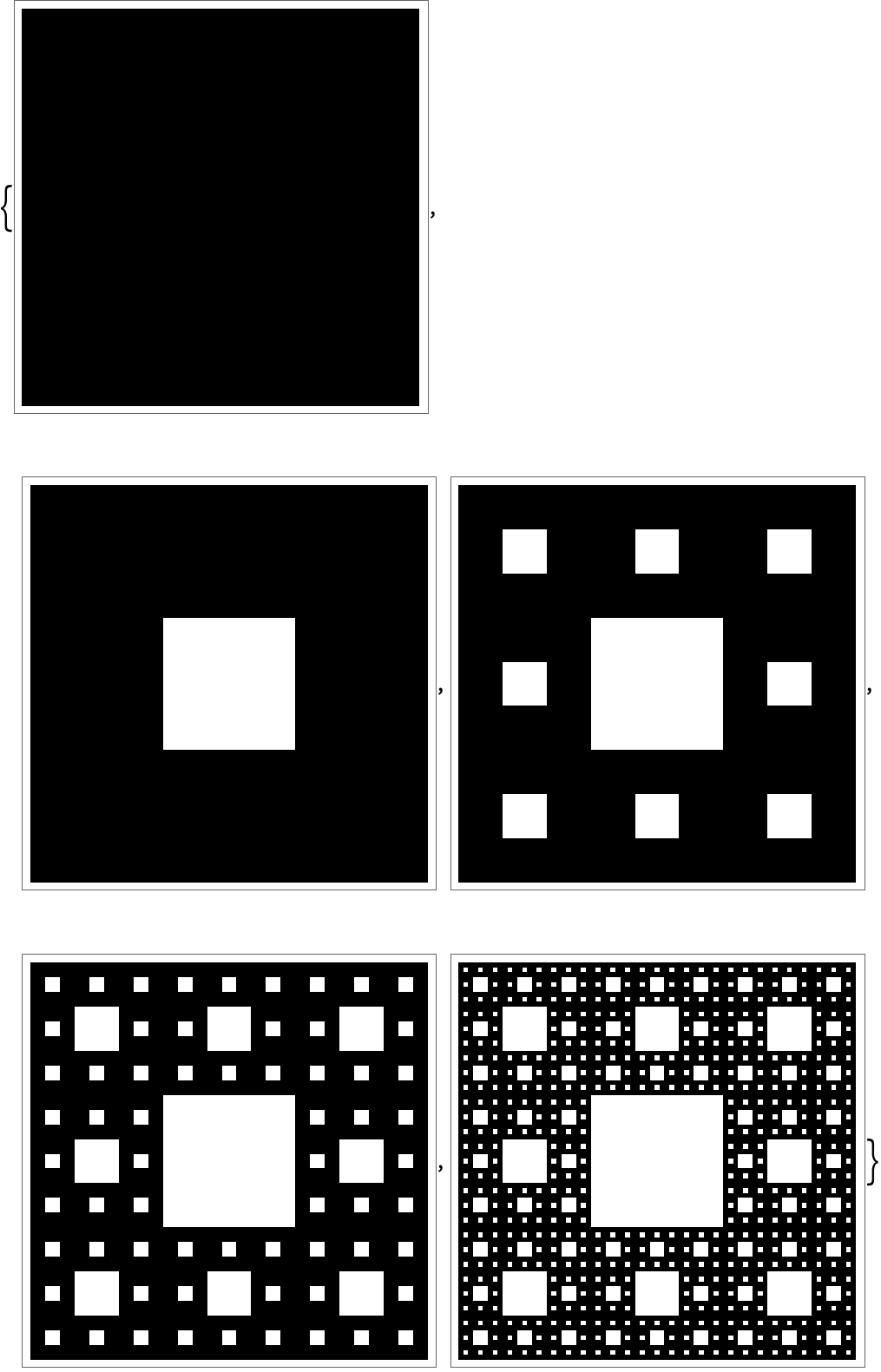
Generate a fractal Sierpinski pattern with 8 levels of nesting:
In[18]:=
Out[18]=
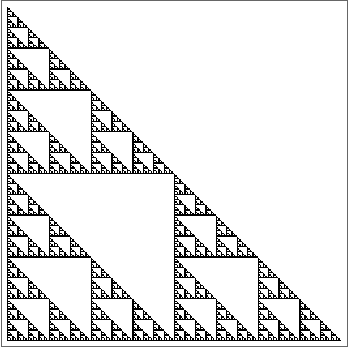
There are many other ways to rearrange lists. For example, Split splits a list into runs of identical elements.
Split a list into sequences of successive identical elements:
In[19]:=
Out[19]=
Gather, on the other hand, gathers identical elements together, wherever they appear.
Gather identical elements together in lists:
In[20]:=
Out[20]=
GatherBy gathers elements according to the result of applying a function to them. Here it’s using LetterQ, so that it gathers separately letters and non-letters.
Gather characters according to whether they are letters or not:
In[21]:=
Out[21]=
SortBy sorts according to the result of applying a function.
Sort normally sorts shorter lists before longer ones:
In[22]:=
Out[22]=
Here SortBy is told to sort by the first element in each list:
In[23]:=
Out[23]=
Find all the distinct elements that appear:
In[24]:=
Out[24]=
You can use Union to find the “union” of elements that appear in any of several lists.
Get a list of all elements that appear in any of the lists:
In[25]:=
Out[25]=
In[26]:=
Out[26]=
Find which elements are in the first list but not the second one:
In[27]:=
Out[27]=
Find letters that appear in any of English, Swedish and Turkish:
In[28]:=
Out[28]=
Letters that appear in Swedish but not English:
In[29]:=
Out[29]=
Another of the many functions you can apply to lists is Riffle, which inserts things between successive elements of a list.
Riffle x in between the elements of a list:
In[30]:=
Out[30]=
Riffle -- into a list of characters:
In[31]:=
Out[31]=
Join everything together in a single string:
In[32]:=
Out[32]=
Functions like Partition let you take a list and break it into sublists. Sometimes you’ll instead just want to start from a collection of possible elements, and form lists from them.
Permutations gives all possible orderings, or permutations, of a list.
Generate a list of the 3!=3×2×1=6 possible orderings of 3 elements:
In[33]:=
Out[33]=
In[34]:=
Out[34]=
Tuples takes a list of elements, and generates all possible combinations of a given number of those elements.
Generate a list of all possible triples of red and green:
In[35]:=
Out[35]=
RandomChoice lets you make a random choice from a list of elements.
Make a single random choice from a list:
In[36]:=
Out[36]=
Make a list of 20 random choices:
In[37]:=
Out[37]=
Make 5 lists of 3 random choices:
In[38]:=
Out[38]=
RandomSample picks a random sample of elements from a list, never picking any particular element more than once.
Pick 20 elements from the range 1 to 100, never picking any number more than once:
In[39]:=
Out[39]=
If you don’t say how many elements to pick you get a random ordering of the whole list:
In[40]:=
Out[40]=
| Transpose[list] | transpose inner and outer lists | |
| Thread[list1list2] | thread across elements of lists | |
| Partition[list,n] | partition into blocks of size n | |
| Flatten[list] | flatten out all sublists | |
| Flatten[list,k] | flatten out k levels of sublists | |
| ArrayFlatten[list] | flatten arrays of arrays | |
| Split[list] | split into runs of identical elements | |
| Gather[list] | gather identical elements into lists | |
| GatherBy[list,f] | gather according to results of applying f | |
| SortBy[list,f] | sort according to results of applying f | |
| Riffle[list,x] | riffle x between elements of list | |
| Union[list] | distinct elements in list | |
| Union[list1,list2, ...] | elements that appear in any of the lists | |
| Intersection[list1,list2, ...] | elements that appear in all the lists | |
| Complement[list1,list2] | elements that appear in list1 but not list2 | |
| Permutations[list] | all possible permutations (orderings) | |
| Subsets[list] | all possible subsets | |
| Tuples[list,n] | all possible combinations of n elements | |
| RandomChoice[list] | random choice from list | |
| RandomChoice[list,n] | n random choices | |
| RandomSample[list,n] | n random non‐repeating samples | |
| RandomSample[list] | random ordering of a list |
30.1Use Thread to make a list of rules with each letter of the alphabet going to its position in the alphabet. »
30.3Make a grid of the digits in 2^1000, with 50 digits per row, and put frames around everything. »
30.4Make a grid of the first 400 characters in the Wikipedia article for “computers”, with 20 characters per row, and frames around everything. »
30.5Make a line plot of the flattened list of the digits from the numbers from 0 to 200 (Champernowne sequence). »
30.6Make 4 steps in the “Menger sponge” analog of the fractal Sierpinski pattern from the text, but with a “kernel” of the form {{#, #, #}, {#, 0, #}, {#, #, #}}. »
30.7Find Pythagorean triples involving only integers by selecting {x, y, Sqrt[x^2+y^2]} with x and y up to 20. »
30.9Take the names of integers up to 100 and gather them into sublists according to their first letters. »
30.11Make a list of the first 20 squares, sorted by their first digits. »
30.12Sort integers up to 20 by the length of their names in English. »
30.14Find letters that appear in Ukrainian but not Russian. »
30.16Find the list of countries that are in both NATO and the G8. »
30.17Make a grid in which all possible permutations of the numbers 1 through 4 appear as successive columns. »
30.18Make a list of all the different strings that can be obtained by permuting the characters in “hello”. »
30.19Make an array plot of the sequence of possible 5-tuples of 0 and 1. »
30.20Generate a list of 10 random sequences of 5 letters. »
+30.1Make an array plot from the numbers of the letters in the first 1000 characters in the Wikipedia article on “computers”, with 30 letters per row. »
+30.2Gather integers up to 30 into lists based on their values modulo 3. »
+30.3Gather the first 50 powers of 2 according to their last digits. »
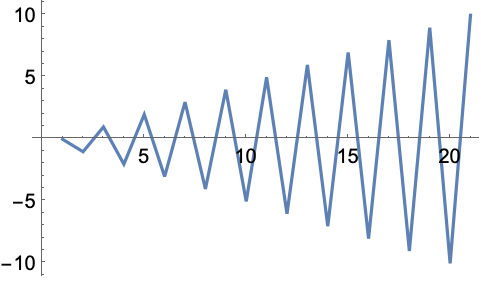
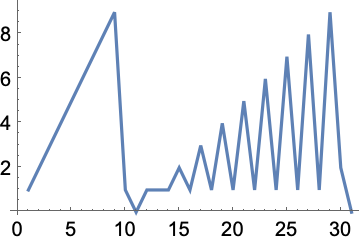
+30.4Make a line plot of the result of sorting the numbers from −10 to +10 by their absolute values. »
+30.5Make a line plot of the list of the first 200 squares, sorted by their first digits. »
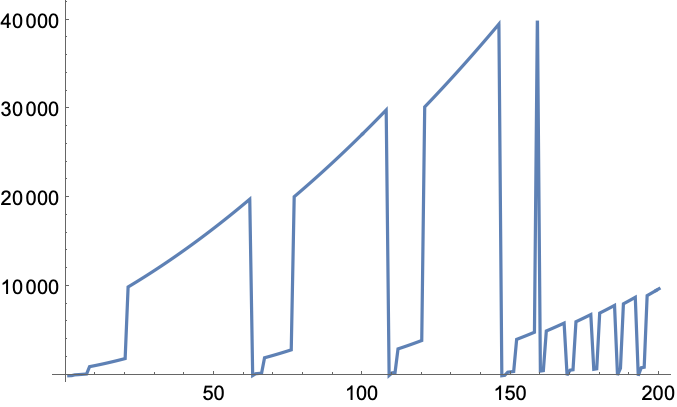
+30.6Make a line plot of integers up to 200 sorted by the lengths of their names in English. »
+30.8Riffle periods into the string “UNCLE” to make “U.N.C.L.E.”. »
+30.9Find letters that appear in Swedish or Polish but not English. »
+30.10Find countries that are in the World Health Organization but not the United Nations. »
+30.11Make a list of all pair-wise blends of red, green and blue. »
+30.12Make a list of array plots, each 50 rows high and with image size 50, of successive possible 8-tuples of 0 and 1. »
+30.13Generate 1000 random sequences of 4 letters, and make a list of ones that appear in WordList[ ]. »
What does Partition do if the blocks don’t fit perfectly?
If it’s not told otherwise, it’ll only include complete blocks, so it’ll just drop elements that appear only in incomplete blocks. However, if you say for example Partition[list, UpTo[4]], it’ll make blocks up to length 4, with the last block being shorter if necessary.
- Transpose can be thought of as transposing rows and columns in a matrix.
- ArrayFlatten flattens an array of arrays into a single array, or alternatively, a matrix of matrices into a single matrix.
- DeleteDuplicates[list] does the same as Union[list], except it doesn’t reorder elements.