| 26 | Pure Anonymous Functions |
After all the examples we’ve seen of the Wolfram Language, we’re now ready to go to a slightly higher level of abstraction, and tackle the very important concept of pure functions (also known as pure anonymous functions).
Using pure functions will let us unlock a new level of power in the Wolfram Language, and also let us redo some of the things we’ve done before in a simpler and more elegant way.
Let’s start with a simple example. Say we’ve got a list of images, and we want to apply Blur to each of them. That’s easy to do with /@.
Apply Blur to each image in the list:
In[1]:=
Out[1]=
But now let’s say we want to include the parameter 5 in Blur. How can we do that? The answer is to use a pure function.
Include a parameter by introducing a pure function:
In[2]:=
Out[2]=
The original blur written as a pure function:
In[3]:=
Out[3]=
The # is a “slot” into which each element is put. The & says that what comes before it is a pure function.
In[4]:=
Out[4]=
Let’s look at some other examples. Every time, the slot indicates where to put each element when the pure function is applied.
In[5]:=
Out[5]=
Take a string and rotate it different amounts:
In[6]:=
Out[6]=
In[7]:=
Out[7]=
In[8]:=
Out[8]=
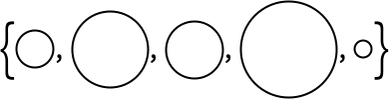
In[9]:=
Out[9]=
In[10]:=
Out[10]=
Pair topics with results:
In[11]:=
Out[11]=
In[12]:=
Out[12]=
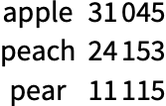
In[13]:=
Out[13]=
Here’s what the pure function would do if mapped over {6, 8, 9}:
In[14]:=
Out[14]=
Now that we’ve seen some examples of pure functions in action, let’s look more abstractly at what’s going on.
This maps an abstract pure function over a list:
In[15]:=
Out[15]=
Here’s the minimal example:
In[16]:=
Out[16]=
It’s equivalent to:
In[17]:=
Out[17]=
We can put slots wherever we want in the pure function, as many times as we want. All the slots will get filled with whatever the pure function is applied to.
Apply a slightly more complicated pure function:
In[18]:=
Out[18]=
In[19]:=
Out[19]=
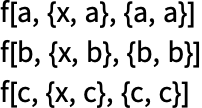
OK, now we’re ready to finally discuss how pure functions really work. When we write f[x], we’re applying the function f to x. Often we’ll use a specific named function instead of f, say Blur, so we have Blur[x], etc.
But the point is that we can also replace f with a pure function. Then whatever we apply this to will be used to fill the slot in the pure function.
In[20]:=
Out[20]=
An equivalent form, written with @ instead of [...]:
In[21]:=
Out[21]=
So now we can see what /@ is doing: it’s just applying the pure function to each element in the list.
In[22]:=
Out[22]=
The same thing, written out more explicitly:
In[23]:=
Out[23]=
Why is this useful? First of all, because it’s the foundation for all the things pure functions do with /@. But it’s actually also often useful on its own, for example as a way to avoid having to repeat things.
Here’s an example of a pure function involving three occurrences of #.
In[24]:=
Out[24]=
In[25]:=
Out[25]=
In the Wolfram Language, a pure function works just like anything else. On its own, though, it doesn’t do anything.
Enter a pure function on its own and it’ll come back unchanged:
In[26]:=
Out[26]=
Map uses the pure function to do a computation:
In[27]:=
Out[27]=
Over the course of the next few sections, we’ll see more and more uses of pure functions.
26.2Make a list of the result of blending yellow, green and blue with red. »
26.3Generate a list of framed columns containing the uppercase and lowercase versions of each letter of the alphabet. »
26.4Make a list of letters of the alphabet, in random colors, with frames having random background colors. »
26.5Make a table of G5 countries, together with their flags, and arrange the result in a fully framed grid. »
26.6Make a list of word clouds for the Wikipedia articles about apple, peach and pear. »
26.7Make a list of histograms of the word lengths in Wikipedia articles on apple, peach and pear. »
26.8Make a list of maps of Central America, highlighting each country in turn. »
Why are they called “pure functions”?
Because all they do is serve as functions that can be applied to arguments. They’re also sometimes called anonymous functions, because, unlike say Blur, they’re not referred to by a name. Here I’m calling them “pure anonymous functions” to communicate both meanings.
Why does one need the &?
The &(ampersand) indicates that what comes before it is the “body” of a pure function, not the name of a function. f/@{1, 2, 3} gives {f[1], f[2], f[3]}but f&/@{1, 2, 3} gives {f, f, f}.
What is f[#, 1]& interpreted as?
- Pure functions are a characteristic feature of functional programming. They’re often called lambda expressions, after their use in mathematical logic in the 1930s. Confusingly, the term “pure function” sometimes just means a function that has no side effects (i.e. assigns no values to variables, etc.)
- Table[f[x], {x, {a, b, c}}] actually does the same as f/@{a, b, c}. It’s sometimes useful, particularly if one doesn’t want to have to explain pure functions.
- Be careful if you have multiple nested &’s in an expression! Sometimes you may have to insert parentheses. And sometimes you may have to use Function with a named variable, as in Function[x, x^2] rather than #^2&, to avoid conflicts between uses of # in different functions.
- It sometimes makes for good-looking code to write Function[x, x^2] as xx^2. The is automatically constructed when you type the three characters |->. A form like x x^2 coincides with the standard mathematical notation for “x is mapped to x^2” or “x becomes x^2”.
- Options can often be pure functions. It’s important to put parentheses around the whole pure function, as in ColorFunction(Hue[#/4]&), or it won’t be interpreted as you expect.
- There are elegant ways to avoid having to explicitly use # and &. Much as f is equivalent to f[#]&, f@*g (discussed in Section 45) is equivalent to f[g[#]]&. OperatorApplied[f][y] is equivalent to f[#, y]& etc.