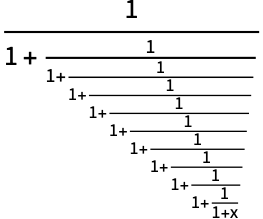
| 47 | Writing Good Code |
Writing good code is in many ways like writing good prose: you need to have your thoughts clear, and express them well. When you first start writing code, you’ll most likely think about what your code does in English or whatever natural language you use. But as you become fluent in the Wolfram Language you’ll start thinking directly in code, and it’ll be faster for you to type a program than to describe what it does.
My goal as a language designer has been to make it as easy as possible to express things in the Wolfram Language. The functions in the Wolfram Language are much like the words in a natural language, and I’ve worked hard to choose them well.
Functions like Table or NestList or FoldList exist in the Wolfram Language because they express common things one wants to do. As in natural language, there are always many ways one can in principle express something. But good code involves finding the most direct and simple way.
To create a table of the first 10 squares in the Wolfram Language, there’s an obvious good piece of code that just uses the function Table.
Simple and good Wolfram Language code for making a table of the first 10 squares:
In[1]:=
Out[1]=
Why would anyone write anything else? A common issue is not thinking about the “whole table”, but instead thinking about the steps in building it. In the early days of computing, computers needed all the help they could get, and there was no choice but to give code that described every step to take.
A much worse piece of code that builds up the table step by step:
In[2]:=
Out[2]=
But the point of the Wolfram Language is to let one express things at a higher level—and to create code that as directly as possible captures the concept of what one wants to do. Once one knows the language, it’s vastly more efficient to operate at this level. And it leads to code that’s easier for both computers and humans to understand.
In writing good code, it’s important to ask frequently, “What’s the big picture of what this code is trying to do?” Often you’ll start off understanding only some part, and writing code just for that. But then you’ll end up extending it, and adding more and more pieces to your code. But if you think about the big picture you may suddenly realize that there’s some more powerful function—like a Fold—that you can use to make your code nice and simple again.
In[3]:=
Run the code:
In[4]:=
Out[4]=
Write a generalization to a list of any length, using Table:
In[5]:=
The new code works:
In[6]:=
Out[6]=
Simplify the code by multiplying the whole list of powers of 10 at the same time:
In[7]:=
Try a different, recursive, approach, after first clearing the earlier definitions:
In[8]:=
In[9]:=
In[10]:=
The new approach works too:
In[11]:=
Out[11]=
But then you realize: it’s actually all just a Fold!
In[12]:=
In[13]:=
In[14]:=
Out[14]=
Of course, there’s a built-in function that does it too:
In[15]:=
Out[15]=
Why is it good for code to be simple? First, because it’s more likely to be correct. It’s much easier for a mistake to hide in a complicated piece of code than a simple one. Code that’s simple is also usually more general, so it’ll tend to cover even cases you didn’t think of, and avoid you having to write more code. And finally, simple code tends to be much easier to read and understand. (Simpler isn’t always the same as shorter, and in fact short “code poetry” can get hard to understand.)
An overly short version of fromdigits, that’s starting to be difficult to understand:
In[16]:=
It still works though:
In[17]:=
Out[17]=
If what you’re trying to do is complicated, then your code may inevitably need to be complicated. Good code, though, is broken up into functions and definitions that are each as simple and self-contained as possible. Even in very large Wolfram Language programs, there may be no individual definitions longer than a handful of lines.
Here’s a single definition that combines several cases:
In[18]:=
It’s much better to break it up into several simpler definitions:
In[19]:=
In[20]:=
A very important aspect of writing good code is choosing good names for your functions. For the built-in functions of the Wolfram Language, I’ve made a tremendous effort over the course of decades to pick names well—and to capture in their short names the essence of what the functions do, and how to think about them.
When you’re writing code, it’s common to first define a new function because you need it in some very specific context. But it’s almost always worth trying to give it a name that you’ll understand even outside that context. And if you can’t find a good name, it’s often a sign that it’s not quite the right function to define in the first place.
A sign of a good function name is that when you read it in a piece of code, you immediately know what the code does. And indeed, it’s an important feature of the Wolfram Language that it’s typically easier to read and understand well-written code directly than from any kind of textual description of it.
In[21]:=
Out[21]=

When you write Wolfram Language code, you’ll sometimes have to choose between using a single rare built-in function that happens to do exactly what you want—and building up the same functionality from several more common functions. In this book, I’ve sometimes chosen to avoid rare functions so as to minimize vocabulary. But the best code tends to use single functions whenever it can—because the name of the function explains the intent of the code in a way that individual pieces cannot.
Use a small piece of code to reverse the digits in an integer:
In[22]:=
Out[22]=
Using a single built-in function explains the intent more clearly:
In[23]:=
Out[23]=
Good code needs to be correct and easy to understand. But it also needs to run efficiently. And in the Wolfram Language, simpler code is typically better here too—because by explaining your intent more clearly, it makes it easier for the Wolfram Language to optimize how the computations you need are done internally.
With every new version, the Wolfram Language does better at automatically figuring out how to make your code run fast. But you can always help by structuring your algorithms well.
Timing gives the timing of a computation (in seconds), together with its result:
In[24]:=
Out[24]=
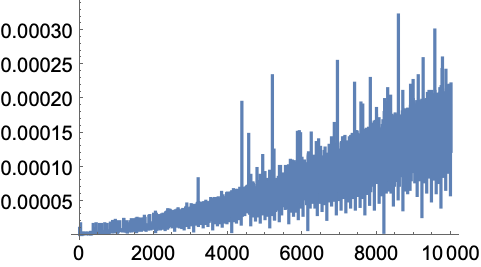
With the definitions of fib above, the time grows very rapidly:
In[25]:=
Out[25]=
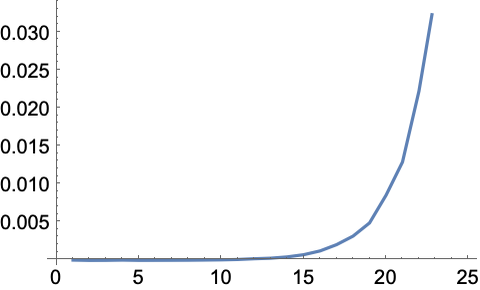
The algorithm we used happens to do an exponential amount of unnecessary work recomputing what it’s already computed before. We can avoid this by making the definition for fib[n_] always do an assignment for fib[n], so it stores the result of each intermediate computation.
Redefine the fib function to remember every value it computes:
In[26]:=
In[27]:=
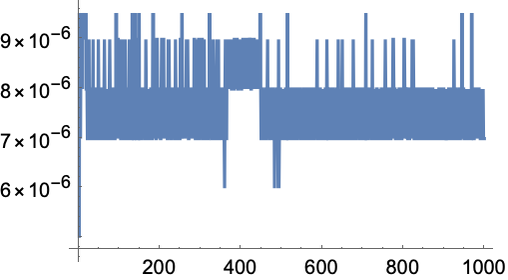
Now even up to 1000 each new value takes only microseconds to compute:
In[28]:=
Out[28]=
Good code should have a structure that’s easy to read. But sometimes there are details that you have to include in the code, but that get in the way of seeing its main point. In Wolfram Notebooks, there’s a convenient way to deal with this: iconize the details.
Make a plot with a long sequence of options specified:
In[29]:=
Out[29]=
In[30]:=
Out[30]=
In a typical Wolfram Notebook interface, you can just select what you want to iconize, and use the right-click menu. You’ll see an iconized form, but it’s the code “underneath” the icon that’ll actually be used.
It’s also often convenient to use iconization when you want to include lots of data in a notebook, but don’t want to show it explicitly.
Create a table of a thousand primes, but show it only in iconized form:
In[31]:=
Out[31]=
You can copy the iconized form, then use it in input:
In[32]:=
Out[32]=
| FromDigits[list] | assemble an integer from its digits | |
| IntegerReverse[n] | reverse the digits in an integer | |
| Timing[expr] | do a computation, timing how long it takes | |
| Iconize[expr] | make an expression display in iconized form |
47.3Find a simpler form for Module[{i, j, a}, a={}; For[i=1, i≤10, i++, For[j=1, j≤10, j++, a=Join[a, {i, j}]]];a]. »
47.5Make a line plot of the timing for Sort to sort Range[n] from a random order, for n up to 200. »
What does i++ mean?
It’s a short notation for i=i+1. It’s the same notation that C and many other low-level computer languages use for this increment operation.
What does the For function do?
It’s a direct analog of the for(...) statement in C. For[start, test, step, body] first executes start, then checks test, then executes step, then body. It does this repeatedly until test no longer gives True.
Why can shortened pieces of code be hard to understand?
The most common issue is that variables and sometimes even functions have been factored out, so there are fewer names to read that might give clues about what the code is supposed to do.
What are examples of good and bad function names?
There’s a function DigitCount that counts the number of times different digits occur in an integer. Worse names for this function might be TotalDigits (confusing with IntegerLength), IntegerTotals (might be about adding up the integer somehow), PopulationCount (weird and whimsical), etc.
What’s the best environment for authoring Wolfram Language code?
For everyday programming, Wolfram Notebooks are best. Be sure to add sections, text and examples right alongside your code. For large multi-developer software projects, there are plug-ins for popular IDEs. (You can also edit Wolfram Language code textually in .wl files using the notebook system.)
What does Timing actually measure?
It measures the CPU time spent in the Wolfram Language actually computing your result. It doesn’t include time to display the result. Nor does it include time spent on external operations, like fetching data from the cloud. If you want the absolute “wall clock” time, use AbsoluteTiming.
How can I get more accurate timings for code that runs fast?
Use RepeatedTiming, which runs code many times and averages the timings it gets. (This won’t work if the code is modifying itself, like in the last definition of fib in this section.)
What are some tricks for speeding up code?
Beyond keeping the code simple, one thing is not to recompute anything you don’t have to. Also, if you’re dealing with lots of numbers, it may make sense to use N to force the numbers to be approximate. For some internal algorithms you can pick your PerformanceGoal, typically trading off speed and accuracy. There are also functions like Compile that force more of the work associated with optimization to be done up front, rather than during a computation.
How do I uniconize an iconized piece of code?
Click it and select uniconize.
- Complicated behavior can arise even from extremely simple code: that’s what my 1280-page book A New Kind of Science is about. A good example is CellularAutomaton[30, {{1}, 0}].
- The fib function is computing Fibonacci[n]. The original definition always recurses down a whole tree of O(ϕn) values, where ϕ≈1.618 is the golden ratio (GoldenRatio).
- Remembering values that a function has computed before is sometimes called memoization, sometimes dynamic programming and sometimes just caching.
- For large programs, the Wolfram Language has a framework for isolating functions into contexts and packages.
- If[#1>2, 2#0[#1-#0[#1-2]], 1]&/@Range[50] is an example of short code that’s seriously challenging to understand...