| 40 | Defining Your Own Functions |
As we’ve seen in this book, there’s a huge amount that can be done with functions that are already built into the Wolfram Language. But you can go even further if you define your own functions too. And the Wolfram Language has a very flexible way of letting you do this.
Let’s start with a typical, simple example of a function definition.
This defines a function pinks that takes any argument:
In[1]:=
This uses the function definition:
In[2]:=
Out[2]=
In[3]:=
Out[3]=
How does this function definition work? The idea is that the := defines a value for the pattern pinks[n_]. When you ask for pinks[5], this matches the pinks[n_] pattern, and the value you’ve defined for this is used.
But this is just the beginning of the story of function definition in the Wolfram Language. Because in the Wolfram Language, you can give a definition for anything.
Here’s a list of expressions:
In[4]:=
Out[4]=
In[5]:=
In[6]:=
Out[6]=
Now let’s add a definition for the pattern f[x_]. The Wolfram Language will use this whenever the special definitions for f[Red] and f[Green] don’t apply.
Define a value for f with any argument:
In[7]:=
In[8]:=
Out[8]=
Clear definitions for f to make sure nothing gets confused later:
In[9]:=
As another example, let’s do the classic computer science exercise of defining the factorial function. Start by saying that factorial[1]=1. Then define how to compute factorial[n_] recursively in terms of another instance of factorial.
Give a recursive definition of factorial:
In[10]:=
Ask for factorial[50]:
In[11]:=
Out[11]=
There’s also a built-in factorial function, which gives the same result:
In[12]:=
Out[12]=
Instead of having definitions for factorial[1] and factorial[n_] we could have had a single definition and used If. But having separate definitions for each case tends to make things much easier to read and understand.
An alternative definition using If:
In[13]:=
It’s nice to be able to break out special cases, but the real power of being able to make definitions for anything comes when one goes beyond simple function[argument] cases.
As a simple example, consider making a definition for plusminus[{x_, y_}].
Define a value for a pattern:
In[14]:=
Use the definition:
In[15]:=
Out[15]=
In[16]:=
It’s very common to want to define a function that applies only to objects with a certain structure. This is easy to do with patterns. Here’s an example.
A list with some Framed objects:
In[17]:=
Out[17]=
Define a function that applies only to framed objects:
In[18]:=
Apply highlight to each element of a list; it knows what to do when it’s given something framed:
In[19]:=
Out[19]=
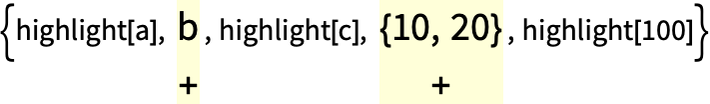
This definition applies to anything with head List:
In[20]:=
Now you no longer have to use /@:
In[21]:=
Out[21]=
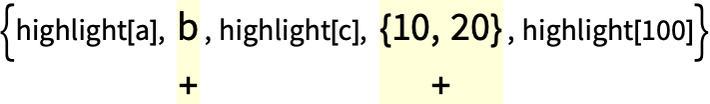
Give a general case, to use if none of the special cases apply:
In[22]:=
This uses the special cases when it can, then the general case when nothing else applies:
In[23]:=
Out[23]=
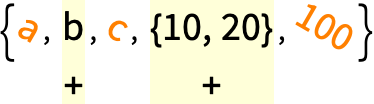
Note: These exercises involve defining functions. Remember to use Clear to get rid of definitions once you’re finished with each exercise.
No expected output
Many possible solutions of the form _:=_ or _=_
40.2Define a function poly that takes an integer, and makes a picture of an orange regular polygon with that number of sides. »
No expected output
Many possible solutions of the form _:=_ or _=_
No expected output
Many possible solutions of the form _:=_ or _=_
40.4Create a function f that takes two arguments and gives the result of multiplying them and dividing by their sum. »
No expected output
Many possible solutions of the form _:=_ or _=_
40.5Define a function f that takes a list of two elements and returns a list of their sum, difference and ratio. »
No expected output
Many possible solutions of the form _:=_ or _=_
40.6Define a function evenodd that gives Black if its argument is even and White otherwise, but gives Red if its argument is 0. »
No expected output
Many possible solutions of the form _:=_ or _=_
40.7Define a function f of three arguments where the second two arguments are added if the first argument is 1, multiplied if it’s 2 and raised to a power if it’s 3. »
No expected output
Many possible solutions of the form _:=_ or _=_
40.8Define a Fibonacci function f with f[0] and f[1] both being 1, and f[n] for integer n being the sum of f[n-1] and f[n-2]. »
No expected output
Many possible solutions of the form _:=_ or _=_
40.9Create a function animal that takes a string, and gives a picture of an animal with that name. »
No expected output
Many possible solutions of the form _:=_ or _=_
40.10Define a function nearwords that takes a string and an integer n, and gives the n words in WordList[ ] that are nearest to a given string. »
No expected output
Many possible solutions of the form _:=_ or _=_
What kind of a pattern can be used in a function definition?
Absolutely any pattern you want. Even one where the head is itself a pattern.
How can I see the definitions made for a particular function?
Use ?f to see the definitions for f.
How do I overwrite an existing function definition?
Just make a new definition for the same pattern. Use Clear to remove all definitions.
How are different definitions for a particular function sorted?
Typically from most specific to least specific. If there are definitions that can’t be ordered by specificity, definitions made later are put later. When definitions are used, the earlier ones are tried first. ?f shows the ordering of definitions for f.
Usually yes. First, though, you often have to say e.g. Unprotect[Max]. Then definitions you add will be used in preference to built-in ones. Some functions, like Plus, are so fundamental that the system locks them in a protected state. Even in this case, though, you can make “upvalue” definitions that are associated with particular structures of arguments.
Can I do object-oriented programming in the Wolfram Language?
A symbolic generalization of object-oriented programming, yes. Given an object “type” t, one wants to make definitions e.g. for f[t[...]] and g[t[...]]. One can associate such definitions with t by saying t/:f[t[...]]= ... In the Wolfram Language, this is called defining an upvalue for t.
Sometimes. f[n_]=n^2 will work fine, because the right-hand side doesn’t evaluate when you make the assignment. f[n_]=Now and f[n_]:=Now will give different results. And in many cases the right-hand side can’t be meaningfully evaluated until specific arguments are given.
How can I share function definitions with other people?
Just send the code! A convenient way to do this through the cloud is to use CloudSave and CloudGet, as discussed in Section 43. You can make things even more streamlined by using the private publishing mechanism of the Wolfram Function Repository.
- Many low-level languages require functions to have particular static types of arguments (e.g. integers, reals, strings). Some languages allow dynamic typing, with arguments allowed to have any of a certain set of types. The Wolfram Language generalizes this by allowing arguments to be defined by arbitrary symbolic structures.
- Having a pattern like {x_, y_} in a function definition allows immediate and convenient destructuring of the function argument.
- Definitions can be associated with the head of a function (“downvalues”), with the heads of its arguments (“upvalues”) or with the head of the head, etc. (“subvalues”). Upvalues are effectively a generalization of methods in object-oriented languages.
- f=(#^2&) and f[n_]:=n^2 are two ways of defining a function, that for example give the same results for f[10]. Pure function definitions tend to be easier to combine with each other, but much coarser in their handling of argument structures.
