Faça a correção de erros de digitação sem dicionário
Modelando a sequência de caracteres digitados como observações e a sequência de caracteres corretos como estados ocultos, este exemplo usa dois modelos diferentes para a evolução de letras corretas para a correção de erros tipográficos. O primeiro modelo usa processos de Markov de primeira ordem para codificar frequências do que segue determinado caractere. O segundo modelo usa os estados de Markov de segunda ordem para codificar frequências do que segue os dois últimos caracteres dados.
Tome A Origem das Espécies de Darwin e converta todos os símbolos que não são letras em espaços.
| In[1]:= |  X |
| In[2]:= | X |
Introduza erros de digitação, a uma taxa de 20%, substituindo aleatoriamente um caractere por um dos seus vizinhos imediatos no teclado QWERTY padrão. O caractere de espaço nunca é digitado incorretamente.
| In[4]:= |  X |
| In[5]:= |  X |
| Out[6]= | 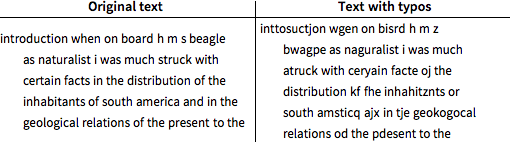 |
Pegue os primeiros 80.000 caracteres para ser uma sequência de teste, e o restante do texto como uma sequência de treino. A sequência de teste tem 16,5% de caracteres digitados erroneamente, menos de 20%, porque o caractere de espaço nunca foi digitado incorretamente.
| In[7]:= |  X |
| Out[7]= |
Modele o fluxo de caracteres digitados usando processo de Markov oculto. Caracteres corretos são estados ocultos, enquanto os caracteres efetivamente digitados são observações.
| In[8]:= |  X |
Estime o processo oculto de Markov usando dados de treinamento.
| In[9]:= |  X |
| Out[9]= |
| In[10]:= |  X |
Use decodificação posterior para corrigir erros na porção de teste do texto digitado incorretamente.
| In[11]:= |  X |
| Out[11]= |
O texto corrigido ainda tem 11% de erros de digitação, 5,5% a menos do que o texto original digitado.
| Out[12]= | 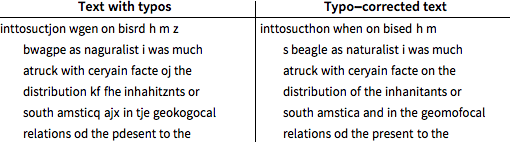 |
| In[13]:= |  X |
| Out[13]= |
Modele a evolução dos estados ocultos usando um processo de Markov de segunda ordem; ou seja, assuma que a probabilidade do caractere depende apenas dos dois caracteres precedentes. O processo de Markov de segunda ordem é modelado como um processo de Markov de primeira ordem com o espaço de estados de pares de caracteres consecutivos aumentado.
| In[14]:= |  X |
| In[15]:= | 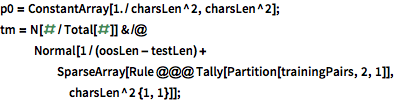 X |
A probabilidade do caractere efetivamente digitado depende somente do caractere real subjacente.
| In[16]:= | X |
Repita a decodificação posterior com o modelo oculto de Markov da mais alta ordem.
| In[17]:= |  X |
| Out[17]= |
A porcentagem de erros agora foi reduzida para menos de 6%.
| In[18]:= |  X |
| Out[18]= |
| Out[19]= | 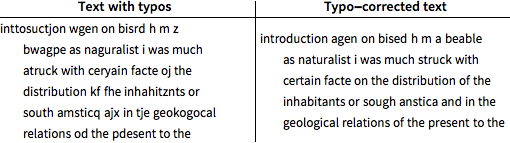 |




























