无需字典更正错字
建立将输入字符序列作为观察值和将正确字符序列作为隐藏状态的模型,该范例对正确字母的演化使用两个不同的模型纠正错字. 第一个模型使用一阶马尔可夫过程对给定字符接下来出现的字符进行编码. 第二个模型使用二阶马尔可夫状态对给定最后两个字符接下来出现的字符进行编码.
使用达尔文的《物种起源》并将所有非字母符号转换为空格.
| In[1]:= |  X |
| In[2]:= | X |
通过随机用标准 QWERTY 键盘中的相邻字符替代,以20%的比率引入错字. 空格从不会错误键入.
| In[4]:= |  X |
| In[5]:= |  X |
| Out[6]= | 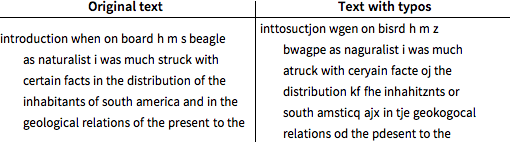 |
使用最初 80,000 个字符作为测试序列,以及剩余文字作为训练序列. 测试序列有 16.5% 的错误拼写字符,少于 20% 的原因在与空格从不会错误键入.
| In[7]:= |  X |
| Out[7]= |
用隐马尔可夫过程对输入字符串流进行建模. 当实际键入字符可观测时,正确字符为隐藏状态.
| In[8]:= |  X |
用训练数据估计隐马尔可夫过程.
| In[9]:= |  X |
| Out[9]= |
| In[10]:= |  X |
使用后验解码,纠正误敲文本测试部分的错字.
| In[11]:= |  X |
| Out[11]= |
纠正后的文本仍然存在 11% 的错字,比原始输入文本减少了 5.5%.
| Out[12]= | 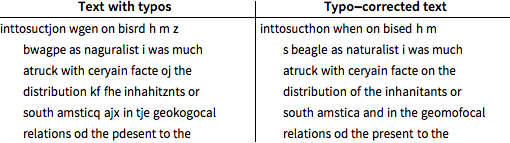 |
| In[13]:= |  X |
| Out[13]= |
使用二阶马尔可夫过程对隐藏状态的变化建模,例:假设字符的概率仅取决于前两个字符. 二阶马尔可夫过程由连续字符组的扩大状态空间的一阶马尔可夫过程进行建模.
| In[14]:= |  X |
| In[15]:= | 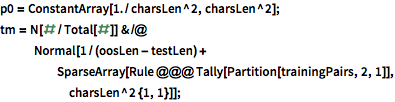 X |
实际输入字符的概率仅取决于根本的正确字符.
| In[16]:= | X |
重复更高阶的隐马尔可夫模型的后验解码.
| In[17]:= |  X |
| Out[17]= |
错字比例此时降低到 6% 以下.
| In[18]:= |  X |
| Out[18]= |
| Out[19]= | 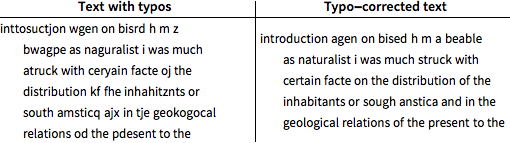 |




























