Nicht schwach stationäre autoregressive Prozesse untersuchen 

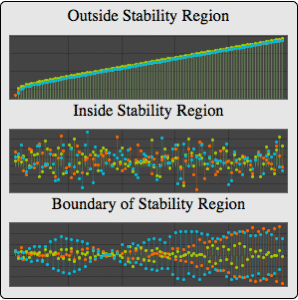
Mathematica 10 unterstützt Zeitreihenprozesse mit gegebenen vergangenen Werten, die sowohl durch vergangene Werte bedingte stationäre Zeitreihen als auch nichtstationäre Zeitreihen mit Anfangsbedingungen umfassen. Erfüllen autoregressive Koeffizienten die Stationaritätsbedingungen nicht, wächst die Varianzfunktion des Zeitreihenabschnitts unbegrenzt.

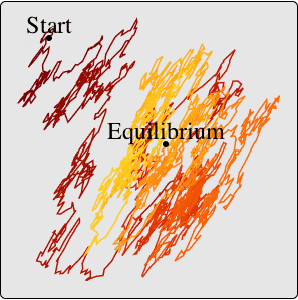
Definieren Sie einen autoregressiven Prozess, dessen autoregressive Koeffizienten die schwach stationäre Bedingung nicht erfüllen.

In[1]:=

X cond = WeakStationarity[ARProcess[{a1, a2}, var]]

Out[1]=

In[2]:=

X cond /. {a1 -> -1/2, a2 -> 1/2}

Out[2]=

In[3]:=

X arProc = ARProcess[{-1/2, 1/2}, 1, {}];

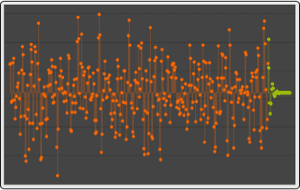
Generieren Sie den Prozess.

In[4]:=

X path = RandomFunction[arProc, {0, 500}];

In[5]:=

X ListPlot[path, Filling -> Axis]

Out[5]=

Berechnen Sie die Mittelwertsfunktion und die Kovarianzfunktion des Prozesses.

In[6]:=

X Mean[arProc[t]]

Out[6]=

In[7]:=

X covF = Refine[ CovarianceFunction[arProc, s, s + h], {s, h} \[Element] Integers && s >= 0 && h >= 0]

Out[7]=

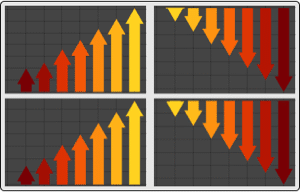
Visualisieren Sie die Kovarianzfunktion als eine Funktion der Zeit 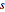für einige Werte des Lags .

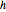In[8]:=

X Table[DiscretePlot[covF, {s, 0, 6}, ExtentSize -> Full, AxesOrigin -> {-1, 0}, ExtentElementFunction -> "ArrowRectangle", ColorFunction -> "Rainbow", AxesLabel -> {s, Cov[x[s], x[s + h]]}], {h, 0, 3}] // Partition[#, 2] & // Grid

Out[8]=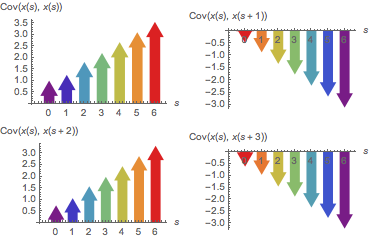