初期状態を持つ時系列過程 

Mathematica 10は指定された過去の値を持つ時系列過程をサポートするようになったため，過去の値で条件付けされた定常時系列や初期条件を含む非定常時系列が扱える．自己回帰係数が定常条件を満足するとき，初期条件を持つ過程は最終的に定常過程へと収束する．

指定された過去の値を持つ自己回帰過程を定義する．

In[1]:=

X ar\[ScriptCapitalP] = ARProcess[\[ScriptC], {r1 + r2, -r1 r2}, \[Sigma]^2, {Subscript[ y, -2], Subscript[y, -1]}]

Out[1]=

過程の平均関数を求める．

In[2]:=

X meanF = FunctionExpand[ar\[ScriptCapitalP][t] // Mean]

Out[2]=

平均関数の長期的安定性に対する条件を作る．

In[3]:=

X cond = Apply[And, Cases[meanF, b_^(t + s_.) :> (Abs[b] < 1), Infinity] // Union]

Out[3]=

これらの条件が弱定常条件と等価であることを確認する．

In[4]:=

X condR = Reduce[ a1 == r1 + r2 && a2 == -r1 r2 && cond && {a1, a2} \[Element] Reals, {a1, a2}, {r1, r2}, Backsubstitution -> True]

Out[4]=

In[5]:=

X Reduce[Equivalent[condR, WeakStationarity[ARProcess[c, {a1, a2}, \[Sigma]^2]]], {a1, a2}, Reals]

Out[5]=

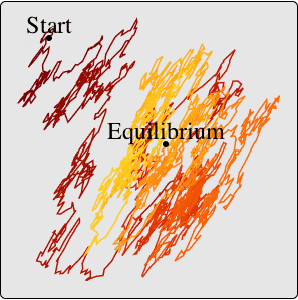
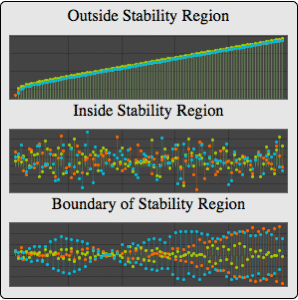
母数領域と3つのサンプル母数点（内側，外側，弱定常領域の境界上）を可視化する．

In[6]:=

X RegionPlot[condR, {a1, -2, 2}, {a2, -2, 2}, Epilog -> {Red, PointSize[Medium], Point[{{0.1, -0.5}, {0.7, 0.6}, {-0.9, 0.1}}]}]

Out[6]=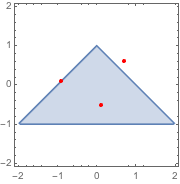

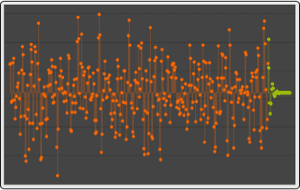
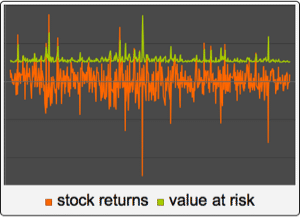
いくつかの選択された母数について，サンプル軌道を可視化する．

In[7]:=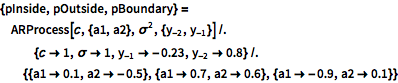

X {pInside, pOutside, pBoundary} = ARProcess[\[ScriptC], {a1, a2}, \[Sigma]^2, {Subscript[y, -2], Subscript[y, -1]}] /. {\[ScriptC] -> 1, \[Sigma] -> 1, Subscript[y, -1] -> -0.23, Subscript[y, -2] -> 0.8} /. {{a1 -> 0.1, a2 -> -0.5}, {a1 -> 0.7, a2 -> 0.6}, {a1 -> -0.9, a2 -> 0.1}}

Out[7]=

In[8]:=

X {Table[ListPlot[RandomFunction[p, {0, 100}, 3], Filling -> Axis], {p, {pInside, pOutside, pBoundary}}], {"Inside", "Outside", "Boundary"}} // Grid

Out[8]=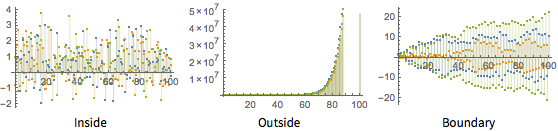

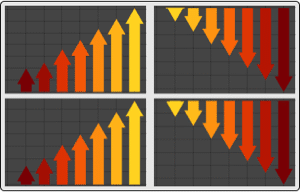
これらの母数選択の平均関数を可視化する．

In[9]:=

X {Table[DiscretePlot[Mean[p[t]], {t, 0, 30}, PlotRange -> All], {p, {pInside, pOutside, pBoundary}}], {"Inside", "Outside", "Boundary"}} // Grid

Out[9]=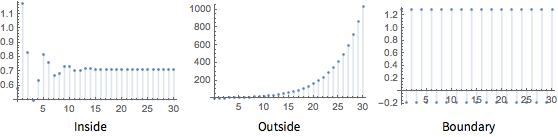