軸対称の偏微分方程式を解く
軸対称領域上で偏微分方程式を解く.
| In[1]:= | X |
内縁におけるノイマン値が値100 W/m2,外縁の温度が10 °C,熱伝導係数 k が10 W/m/Cであると指定する.
| In[2]:= | 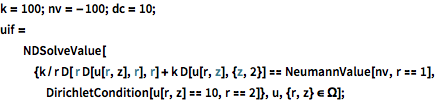 X |
解をプロットする.
| In[3]:= | X |
| Out[3]= | 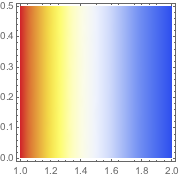 |
解を検証する.
| In[4]:= | X |
| Out[4]= | 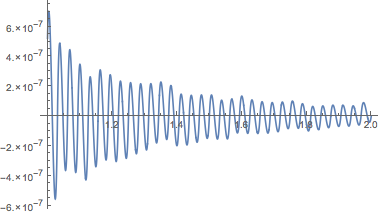 |
解を3Dでプロットする.
| Out[5]= | 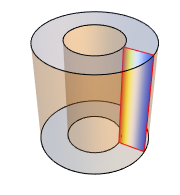 |
軸対称領域上で偏微分方程式を解く.
| In[1]:= | X |
内縁におけるノイマン値が値100 W/m2,外縁の温度が10 °C,熱伝導係数 k が10 W/m/Cであると指定する.
| In[2]:= | 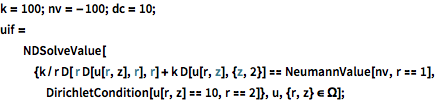 X |
解をプロットする.
| In[3]:= | X |
| Out[3]= |  |
解を検証する.
| In[4]:= | X |
| Out[4]= |  |
解を3Dでプロットする.
| Out[5]= |  |
Questions? Comments? Contact a Wolfram expert »