Compute Nearest Points
For a point and a region, the nearest point in that region to the given point can be computed. The nearest point is given by ArgMin[![]() ,
, ![]() ∈ℛ], where
∈ℛ], where ![]() is the given point and
is the given point and ![]() is the region.
is the region.
Some regions have simple closed-form representation for the nearest point.
| In[1]:= | X |
| Out[1]= | 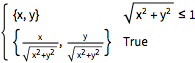 |
| In[2]:= | X |
| Out[2]= |
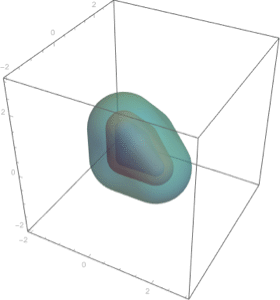
Others are more involved.
| In[3]:= | X |
| Out[3]= | 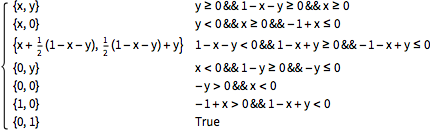 |
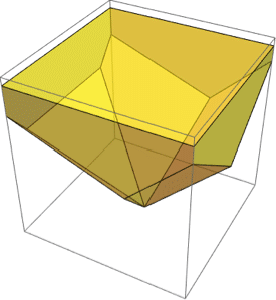
Visualize the different case where there is a different nearest projector function.
| In[4]:= | X |
| In[5]:= | X |
| In[6]:= | X |
| Out[6]= | 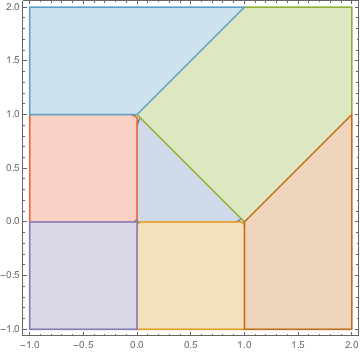 |
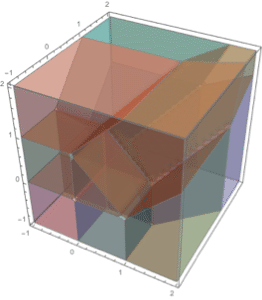
Similarly for a standard tetrahedron.
| In[7]:= | X |
| Out[7]= |  |
| In[8]:= | X |
| In[9]:= |  X |
| Out[9]= |  |