Встроенная поддержка символьных тензоров
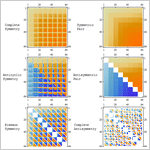
В системе Mathematica 9 введена поддержка символьных массивов, от простых векторов до массивов произвольного ранга, размерности и симметрийных свойств. Новые операции тензорной алгебры позволяют создавать многочлены из символьных массивов, которые могут быть приведены к каноническому виду, используя эффективные алгоритмы и могут быть использованы для получения или доказательства символьных тождеств. Новый тип структурного массива хранит только информацию о симметрийных свойствах и независимых компонентах массива. Это может привести к существенной экономии памяти, наиболее заметной в случае антисимметрии массива. Новые дифференциальные операторы векторного анализа работают на явных массивах произвольного типа и ранга, и могут интерпретировать их в различных ортогональных координатных системах.
- Символьные выражения могут представлять массивы произвольной размерности и любых симметрийных свойств под действием транспозиций. »
- Операции тензорной алгебры включают тензорные произведения, свёртки и др. »
- Приведение тензорных многочленов к каноническому виду с использованием новейших алгоритмических разработок. »
- Новый тип массива, задаваемый симметрийными свойствами и независимыми компонентами. »
- Операторы взятия производной - градиент, дивергент, ротор и лапласиан могут действовать на векторы и массивы произвольного ранга и размерности. »
- Новые курированные данные по ортогональным системам координат, которые могут быть использованы операторами взятия производной. »
Antisymmetric SymmetrizedArrayRules Symmetric TensorContract TensorSymmetry TensorExpand TensorReduce TensorProduct Arrays Matrices Vectors TensorRank TensorDimensions TensorTranspose TensorWedge HodgeDual Symmetrize SymmetrizedReplacePart SymmetrizedIndependentComponents SymmetrizedDependentComponents Grad Div Curl Laplacian CoordinateChartData CoordinateTransformData TransformedField CoordinateTransform
