Mersenne-Primzahlen und vollkommene Zahlen

Eine Mersenne-Primzahl ist eine Primzahl der Form 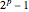, wobei der Mersenne-Primzahlexponent 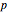selbst auch eine Primzahl ist. Jede Mersenne-Primzahl entspricht einer vollkommenen Zahl.

Generieren Sie eine Liste von Mersenne-Primzahlexponenten.

In[1]:=

mpe = Table[MersennePrimeExponent[n], {n, 1, 10}]

Out[1]=

Bilden Sie die entsprechenden Mersenne-Primzahlen.

In[2]:=

mp = 2^mpe - 1

Out[2]=

Bilden Sie die entsprechenden vollkommenen Zahlen.

In[3]:=

pn = 2^(mpe - 1) (2^mpe - 1)

Out[3]=

In[4]:=

AllTrue[pn, PerfectNumberQ]

Out[4]=

Visualisieren Sie die geringe Dichte der Verteilung von kleinen Mersenne-Primzahlexponenten, indem Sie diese in der Liste der ersten 225 Primzahlen rot markieren.

In[5]:=

primes = Replace[Prime@Range[225], x_?MersennePrimeExponentQ :> Style[x, Red, Bold], 1];

In[6]:=

Multicolumn[primes, Alignment -> {Center, Center}, Spacings -> {1, 1}, Frame -> All, FrameStyle -> Directive[Orange, Dashing[Small]]]

Out[6]=