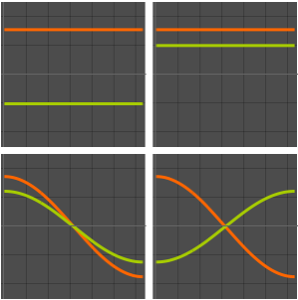
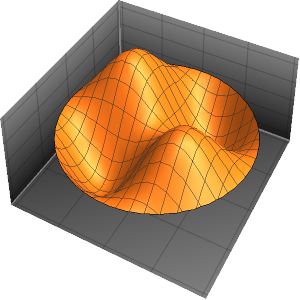
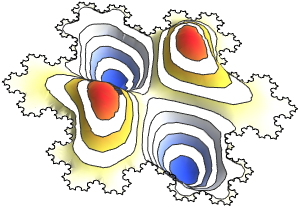
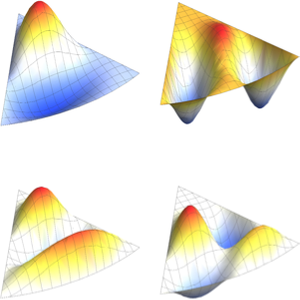
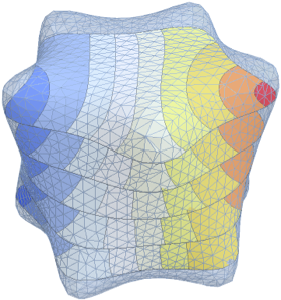
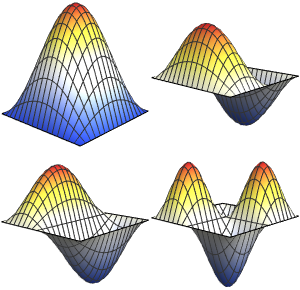
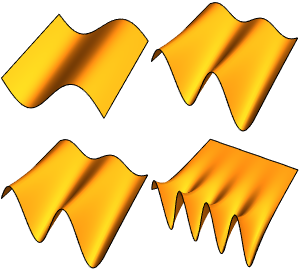
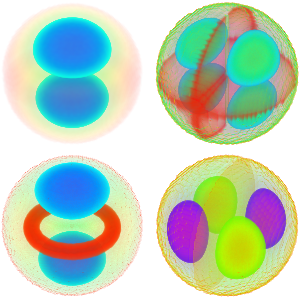
Les valeurs et fonctions propres d'un vilebrequin
Calculez les valeurs et fonctions propres d'un vilebrequin serré.
Précisez un Graphics3D.
In[1]:=

gr = \!\(\*
Graphics3DBox[
{EdgeForm[None], FaceForm[GrayLevel[0.5]],
GraphicsComplex3DBox[CompressedData["
1:eJx0fXVc1973/0CRsMEuJiiCiqKIIgpMVMAGDFBRJ3Z310AxsLDFnIHYHaio
swPsVtRZ2IEFGPCT87x7vTe/n9/rD1+P19PDdnd37+lzbsWIISG9zDmOsxzC
cXk47VNSyP3XjCsi4HcLJfff6u/sjHhss1xcdGY4x3321eFyZnrT3G8lO8cl
9//58z99c3/zS140yf2WcnIcCS+oeuvphWyGa/Q7+KDc32Lixxm53/LsMU1y
v5Uqh0Lo94r7hEsja/vROIZ4EC553iCc95jvT78Pj/Cj+3o3H0Z/33UEXVde
ubGxAe/7qAXhfUYIelzd1a8lXe/0ClyvWFgE4VM6exB9WlgA4YecCRdPqLVo
PPMeE718cHN3+v9TtevQt8ThuUreHUl0xfoGE75sehv6fdduFP1/5SGEq+en
BelxYZdAOLe9tBGfa0G4uGdILZrXoWcnEr56dyjN75hBBlzydwvL/a1GjnDV
41xJK8KFGx6N6Lf2udrejf4uYIpgwHcXcKf5c6/vp8fFt5b0vEI/Ez2tE0ll
9MLLmvR8G+6NoHEHJ9HzSMfKVqbf+wTMT4G3NC9S2D66P98fuOhwj+jVuw0c
9PdVgyV630J0RWc9LhctTjjn7FzJgB8MoXWpfGqoXQfjLDiF6NXssKb6cUr5
3/vQ+EMqNNHj6sh59Jy8wwgDvXLgEs2L1Eim6/FPF0s0L0H1+dzfYgcPrM+T
wLmtC5yIzn4O4eLt44TLvisr0ngOtalK9Iu6zqb7xXvXpuftWdyB/v/8dMKl
hGV16LmOZLrQczvMBv3hcKLnf0fVo/F9dw6l+fT+RPMrhifW0ePK8iIV6XvU
Mx89zmftq0b3qT6Jnlsdf0uk8Wd8wDy3TfbT47LXukY0vvsejfW4cLUuzT/X
L4P2ET/xbF/Cz4ysTuPp3yGQ8J19gLd74kTjyJ8eoMflailEr1x/7W+gv/WH
+JA4d3wpuo/rYtx3mjfxGS7R1orm89oi4Kuv+dA431ciXHjqRbi6Kh30tc81
yP2W4+xn0fNXKpl54n/gilOJTOKLt2c2MuDND+Xk4sLveFonnEtD8DP3Tv50
fY5rpsc5bnPj/4XL42YE6HE1JLUtjd9sNc2n2CO0GP1/yUpd6O8elyG+xq8+
Yk3fvhFd6e9W/PBl16EPH12N6JWUFIaDr3NsX4gu7+zY7xbsW5MXJfX04u+c
woKOXkjL14ruu3PMgFycT9lN+1oRhrfOxZUqXwlXR00CXsCM6NU33wnnOu0h
XGg2voGgGw+/pKcXXX9ZlLcBDyvtSeOZPUGjp49QHfRqWALes7n3ZLrvnG/B
RO/dAPjF+YTz9kEhNL7rnwkXNwBXimwjeqF9Cq03cXwSvRdx6jTaP/LU9pAL
d48A7/WF5IJQFfTae5QaRWO/1TXJ06pElwfzqJTmLPW4tCoqkMZhB1xm8lTD
Ob8ptN6UChZsX5aj6/BOi4x4pd7+RG/720+Pi5e86DrSg/mQM1yvsfT97QXk
pu0FyJ0VCwiXnqxtTb8HHqTnUVeFEy5bBIFu4LGGeN5w4htSlnt7mrcKd7z0
uHL7EuFKWn5vPS7Wvk64tGdUK6Kzvk38W7Bw9qXrVVtCOHe9f3H6fX0X8Sne
9yTJbeHBT5ofwfwe+DP3juSPsPDuGBpn0480D2JgFuRVU0cav7pvD+FKRjW8
tx1emIcj42nfSW3Gk1wVvfJE0ThfLIacW9eHcH5LPsKFll386NsR9HL+h5H0
e+AaoleKt2lH93GJGkzjn76T+Kpg1YRwIb3wEBr3rhrAf+4gXPQrQrhY0ssN
7+lfvoGPcv10gB5XV6Sl5fIrodJFA84Pe2FOv6d6l8i9vrohbAqNr4R94dzf
3OellfW4UDQOfODIEWc9rqZ+oOuoOanN9eMQF+wA33a1baXHpe+qA/vdQo//
/ZSl6/QdiX3kmo/kvtIIcp9/Y0v8U/lahnA1pCqee4gHyQvR2oVwacYPrOOc
Q3QdsfM4wnk5G3pX5yeYtxzwK/63vWfut5zRSBs/02854iNqOKM34Tzo22w3
PC8/c0p9uh7Tezm2f016r10g/b+Y6DeNrjt2VkOiayDRfUSHPoT/XU/Er7h7
VXC9ysDF5/FEL8W+gF78GeOXsp7Q9cUv6ZAv+cCfNb1aWgj6/8aP8UhCT9oX
clxpWk9C6z207vnWPlj/fKEqdN8Ll4hOanoPelyeGHqv4vkaRCda5CM5zN3d
R/tLXeB7Lfc+Sr0WtfW4mJpoTfcruqSOHufEhg9pXKkJGG8Anlet40v6thCU
ivmLiyVcqrCf9Bg1cCfhqiPolYQPwIe0IfnCT+Lq0vXn74OcLleGcClkEp53
3HKaT6H4dpI74q+8RK/c7kB8X05+Qnqy9uGvzSD9WHaM03CaT+XxXML5b3Nq
6XF+wWtNDwZfb/aC5LXcr24jRYcLa2e2p7+vuMuIb51PuFh6L42Td87nT89b
LHIg4XYXiA/LPssg/0e7DKL5eVaNcLHzAthfyyYTvWrhQrgUZlrPhvUphJpw
mh/Zjq1bti8EMyaP8nEN9OM0ybW7e1v8L1zTW2QfywA9Lg46Fqinl8QHND/q
u1LAbxWzYf9PH3FTraYC978+MvTCrxfmn9Ch0oJ2Gr02Xnov/+1z3pPhtF+k
//Z5Az2u0av9uhGf4fw7k9zhqx0hua7OHQg8/CLJKSn/dtiByV1xPZseRM9t
WInxDPYI0D+HOKku/ZZtUw3PJ+wqTddRMsr5G+gFP7qf0nsSrVslk+kDl3Ly
0bgKDm2Zi/99XzQe+fVbOz09nwk7XUkEvWpTgPRzwWYZ7N8P80mPlefIhCst
+sNejoj4QHJk2wrgAsPdG5nR38V44D1nHSA5L9q8pedSD7Sk96nMOUL7WXK5
gnkLa4P33GMf0fOdkwkXhh3X+BV91O2X6hJdtdDGBnzOTNg70xYb6CUnW9hH
jls9cr/Fs9mQQ2XiXen6mcPdaZyM7/Hl1xEfk8UXHnpctc4kvqa6tuuQi0vF
Hven65RaCP4R5UU4vzMD+LGeZN/yLacbcOnOOOKDQuuCBpzPGUa4lGWvrUPi
rzr5oa1D7MfMSOzn/+jd9PRCmR6kHwkFIjoRfqg7vW+uRE/oTcFNOxL+rSfw
oNOkN0muwIVP92j/KrVftFJ08ync40k+Ce4TWutxeW04yUHVN1XDYS/sgNyS
rbbVo/F2PFiK7rNwP95Dg3n19fRq1z8lMd8z6+lx/oEfyR+pk0lek34g5WPy
qyPw/+NfYvtVNufKCcZ51L6r6udTabCzOv0ds9fEsNskR3ilcxU9rk71oeeS
+jaqbcAdzWkexd6PSU9T774kO1RqHkDvk7tSi967OMm5H9G/8KHnUjKOEs71
DSScr5uCdbcvi9a79HbXVLrOnxPw87hUI/nCT95HuDroDelFQvoGwsXEyYQr
qT+DBO6/jzzUYhLhJvsOH6nmPfL/qI9lg/2r0Wv2L7/lHfnrNP+Y4HgE+onl
JwOu+tYhe1PZM6+JHpfdF3rr7ysmOkDP4a4F6HE1uJwBVy8OtxJ0OD/4NOHC
0/HW+r/j1IJtDL+1547rF0Tj+WhtZbh/7V6Ey59Cm+pxudQN4nuK2xs/Ax7e
1Tb3/tIVq8YGXJ5L9PyhdI0e6/agNckN5VI/0if4TdExNA/H9/2h63OdCReU
7YSLbpvy0P/fG0m4+H0q8JCEr8Rvo97SfMoLUqKJLvyiA41n1QPC1SeXCFee
7SZ9UClynt6DnJUGPPN+GZrHQ8vg34r6Brncx5fsXC6pF+T/3AIkf5XUBW2J
zvcF7MRZkdBbBscQLl99Cz5z9wzxc7V7I8iVZy3IjlML5gNfuv8R8snMBnbY
SOBc2bqEy/FOhMuVGpH/lmuRbU/fHs1glyY2h7+3+kF6LrlGCx8DPu4R8Q0l
JM1HP/+y4lqOxu9UVNDjqlM66ROSEmPgP5KVJ/mJNDmofLeC/fBpPvl5VG/g
XNEU+COcP2X4/g96TW6qddzJrhEt8byqeSP4nQf+IlxxuQS9tl5p+C2vVwZ+
+CL8y4/aEj3vXRX63XcL8P/K7UgPFCddgf3dIxH0l/vT86hNnKH3NbtAuDIt
HHpjLNec7u9tPpTGczB/IaIPmxKox//eNz9dP3W0ARcPvyS/Et9wvZ/A6T6t
2kFu5jP5W4g/ctkpsJe/Q3/XcPF7d+z3USn19biUEOpP9+WuEv9XIx4TX+VH
HX1K+2nqNciRBzsI56zynKb39q478JG74WdbbWub+1uLL4g5ObUxP7CDxOUm
uQq7h+m3Ovwfvbe7pqcxf5eIfZWRrulp2O/MzuKaRMBfwfwqsltj+DWOLCVc
8rahfcNd20LrWG2zo6WeXnyWjn31qRTsC5fwMNClQ05MeeCW+y3cCyR5LTZb
DX0iuGotPb0sxxKurF1B82ry3xbO78yes5ke52q0Lfe/cPXXlup6nOtym+yR
v/ZpJaLb9rMd0W0QKR4hDZ+AeMnIyUQnXHdHnKLYOMxXx5qESypwzvkr9GSP
ND+ah4zrkHfju2D+rlUmvU4KfUy4XG4F5vP5auir/XeD/mU2/D/8HLqO5j9X
fVeSH1sIVgmXu30gXKnehPRx4clzwgV3jX50Mfpe/74S3ssC8tvwvYbRfpA/
5FTR40qNQpBHOWeq6XGpvBXoZzcmfUBatSSKruPwG3ZCK+bniTlBOJeZRbia
/zTxV0EALpbyhx7TrwHxX7FQIeJ7Yq35eK5fJ4EnVgX/jMigOAoX09CAS+eX
ET33owG9L6k5D3/I+/Jkt6rpc+FHOZ1D8Qv+UjPMSw87ohc5+FXUj9tp3sWz
+eDX35BI+oNc+T3Ng5K9woCr+dti3ZRk/nAWb1KDedi3/XuBb7L1w8cOKUDX
77mRcPkOWz8NvclOkZ4WCNHTK6f96H1pHzUsMhLPGW+wE8TE/sC5IuDXB89a
0jjfSHiPR2JB3+IijVOLPyqbFmDcg2/46XGx/kjiA2LSN9BPeUC4WqwXnj9w
qeE6QvH30KMK5ye9XVy6KIrud/Qp6c/Sl93gewVOEi6+PkT2kFJ6GPT8K0mE
C97NSC/lLMa118+D5NScriPE+Blw5U8P2FvFF2A/PsF8irdHEi76+bXHOKE3
CnXHOmC8xQhXg8cSzm3fxdN1fM+209OLTwaSPi6L+0n+SNPZuj27hviruKcm
6dvqXLbO/WYgnuh8GfLqDfaFsKEH6J/Hg69o+876PuIC361q6XFx6iPip3z4
fDc9zqXfgD48vKMTvbdWZ7Efv+aHH7vVe8Q3tzQjXJ6XATv4YCT8N9cqwE/7
uFoN+j2zB/P3BIC+sQ/Zd8qRxW3186C0L5mXrtukrmF+5G7TSW+UK1u1M8zn
CV/SZ1SHESSn+CVzsd4uzz2cq2/ItyKB2y9EHNxrHfln+ZovYS/P3oT19qsZ
yTu+ywaKA/JzGvah62RMQHyxdjLhXKUVvTEv4xCPnP6F9B15dn2iF/2uQA+J
EOtgnEMRl5xRDnx4/6FaelzK9xR+7NGTYWe/7Ui4WCqE5kto70brmY/uQfqn
NOwE8XG+1O36elwNNtPsdgPOxW4ieSF4HaP7CGfKYD0s9IYd/ekC5OQdvC9p
VUHoU7O3Y1zL/YG3HE/0atLUagr330fcXJnsVfXXmyoGPMSR7AKuZ4rB7yd/
yiD7Qsq3A37XCsF4X7XKV8jFlV01DLh6oAldV/3dyE+P85Or0/pWfSwQjxg2
G3rLAMhZIXwr8gU69SJcKL4d13Hci/hSJOj55FjCxe4ppenvwjoizjtrTRmi
n2hflsbfxotwcc1W8tvLylz8v5MP4ULn1jyeayjZm0rKBVxn0DzSY6W8FkZ8
divYQa5mhMtJuxF3zr+McHVEUw/QXwP919Gw30aOJvufjx5A8yFduQZ7KTTB
hp4/KQXro+0f8NlbMVZ6etWVI31Y3dmrCq6fQtfnmhVFHNZtniP9XYsTuO+Q
F39ycamwZUX9eMSJl/LSfFXoQPMhKbMIlx/9wPopsyGH7K39CbhO5T7wH38a
npWL8wURZ5cthgCfHge+7R2OuPCR+WSXqhugr8pxvtBXS+9Y4pP7e8wqA65U
fYx4c0J+kkecpj8XjIKe8N+H6cs84hwbzIheNod/W90CeiHdDv7rybZ43pGV
itJzrt4JOy39CdmVvM9LittKVmNBP/cx4Zx9jU+5zyl2e4J4bk4O5Mf3J6R3
CQVuaP5aPP/+n7QPZZ8nWrwY8YqOKtGLMe/Y/LP1kywTf+E6Ny2lx+VPCfDT
nanHcLwvadka8KOx2B+aXipYDaT8BmXmQjc9zketpb/nnyV66HH1XUGs87Qj
9N7F5EOYn5MDSJ8Tjn3BergIXOrYkvi/MEGxM4wnYT/Rc+N7g0/EpkIOrm5F
+orytCnFh5V828Dns82h36j7EGc+dgf0bW4j76VNDZLbJj1Nk+NVn5KclyvD
LpbH1cP6rGqG+EY54LxbS6LnbGU/otvRmPQ37nhDktdcuzaEc3dnA79Sl/RD
VdxhwFUusgL9btQG/PjuL4p7iqPXkv4hLy7UVI9LYZmY37CJfnpcWepG70vO
iKbrCDafCBfmvqJ1LwR+hD08dSDNpxJxguwOIZrh/aPxXnbug/2+25VwZdc0
rJ/qRYvk4vxjCXZd2A7wsdYLaD2oIevgT+0ei+u0qw38qyPxTzFkIdZb5bzE
h8V3w4kvcVocZ91l+DuGTbNiOH3Ek58hN4/MsNLTyz8RR1erMr9ZXBvaR9Lh
2Zofkz4aLg+dRHyTXzbFQK9eCSBcbLUBcapS+6E3RtzG+1AnwW/54SZw5alB
boqxwDW5qS6uRnqx3CQa6+doCPkFlAHWb4iPxUZhvTXeiHj5PpX0EeHtYeDz
8hK9sHovPa+SYoV58zqJuODLfLj++Yrgw0Vdab+o1zMpP0FMYvix60QvbYrF
e7bZi+tMWkbvUZjw3Inm7zF7j9OqZurjN+rOIpgfxk+1j7C+lgGX1neBf6+W
G/jYgjUGem3/ynFx5A/m2zyyFPT45z+l6dsqO8FXh/OO0bSPVDWW/k75jXUr
n0skvUqZ+AV/F8vWc9tJ4F+jWhO9MB7yQvkxEfTx3yH3r2IelFFHEC9K6FYb
4wE/lPp8Jr1U+JLhrsflZXuQB1H2PPFV03rrUR5y+ljeUnpc3W4DefOgiQHn
f4Dfqm055Eftq4nrfMsPvc17ZxXML+L78r0hpOepY1Nr6XGl9jTiy+rjzzX1
OOd6g/iAUCqzuKKbT+5SG9ITlOHOVfS4unUM+fGEkrfKGujjev6k97G6G41X
+ob8NylPNtFJi8YSLlyuivkZfpb0G/H3WIrvcO7VgAdEOtF1md3HeyUiT4/Z
fXLLTOQx3U0GP2x8FXl+afms9LhU7Dv0lKLu9nQ9txgmv16R3Jd7JiBfL7Q/
1vPhJ+aEh26FPvZhOPA6neCn8itAfllRhp7G3T1N41CcRpMflA9pi+u/aE/X
FxZ8xXpbBFwdPxLvb3l5zM/ALhMI3zkXeV+NakF+bhhKuODO7II35+rqcfno
Qdi5dwbQ9bkDS2EvJCKfT9gUhHFa3+9F/59yDnjaAtLf5MH3emH+/xAu3hJt
9O9RXCKSnio/Ty+jx9WgjSSX+RJbDXKWe+xH60OT/yb8PNMPms1xN1znygPo
GYP2uxnoLy6k68s5bkwvxT4Sa/Mk7/g1/1x/aD2SB+qsWchHtViB9yX2Iv1P
WDMNfp6Ildi/469kE79y/wC5agt9WBFeEh9TZt6g8fD3JbzHlstp3cgtzxIu
fYvEfWctp30imD0Cfm4xcBdfWg9a/EWLg2jxFyHOL0CPiwuOQR91dQvU42rB
K4i/PC5DclBdMBrzNseZ5KCwqxb8yEfG4L5rSpFdI88CfxXmdoV++yHuJOnV
x4dALrP5VCP31aB5HLMCcnzbVsybTSjh//I3IeIz8lP/yyeEPsnyCYUyiF9r
+i2/8+2/+Yf19fTchaGaHKcPv+Yc7NnW7f1oPP27IG9kyXN6Xk0v0vJwlAt1
kefE9CJTfs5fvSgXF8uNQzzz9gnQH+lC+W1q+CXyeysTPiFutag04t6JRen/
pVoK3tc55u8udcIV84D1ppxIofvydaBXmtZzWAbsvsU+bgbctxLilFNfUp6z
ZJcIfEUa7MFVjUlua3a0cOvGc4pH+AcYcJ4PIz8/vymlhR6XUvsVoOs3ek72
lNT9YGca9+O98HvbdqR9JiUMoPiynCOBz0Rvc6J5bdWTcLXuF8JV7jjxFeFe
A/iXqlqTv0gYAzuPK9MQccyPPyk/QWh9EvkvaaXgP5n9jfgOP7MG6RvCdcYn
W5an5xfq7ENeQwqzc7slkB6ifdTL0Cel4Gkkx5XeByj/iE9membiQQf6//41
YKdegRznZg4GXvgu/A3bh+A6E2PJfy5vRN6TXLgH5n+nBfkLFIfPWOenmmh8
jOj58FLgn6dxXzVnHK1bdUQ07XexfRL0jYGbaX65BtcIlysCFx4FkP9HyXea
/Lha3Jn73Bl5E7c7VzHgEuLU3HG+ugF/VwpxuJoRNB7O4SjmoXAxur60NITe
Dz9nHdN/qsBvMPgizZ+YD3qa9Ka3BeE/3mC/X7mPuPmr08iLGF8O6zw6D/Sx
rvfhh4lR8f+2ZtBPIi7DH3jLjeL3av8DwO1Doa9PuEX6glA0Cfpz2h/YsfGD
kPdZ4xXwxLtanIk+4oMPJn1bj8u9Ss7W4/KXwBJ0Hws7zPMfxN+46S7IG8x4
O5qeo9/Lr6TvRz6DX6rhB+DyEY7ongYjP+fxSuB7+/wm+m3tkZel+ZMdS8Iu
XjGmsR4XN3sg/6/aPIOfWS24iejl1rsRD6yJOKBU9DnFBcSkW8hf2H0V/lzb
PMCryEQvjLmM51E/Eq5YVoYfuEk/2AsTYxB/2roL+NY+sBcmVEFdTCvQm/xX
92ehLmZREumzwpMI+DEqvCT5yt9aBn/Uvt6QFxM/I49h1hHwk+fRWCeFdhA9
1/gO4vhXsX/V0/HQL/MlQd+5CztCCN5cS/8etf0uOZ+idcWfcgJ/2ucTRXgb
xJGl8rHIR6jQHjiLgyhBjcFn9oNeluuT/JD7DYZeVGAO1mH0ryzSP2cOR/5R
zjzoyV0cfpCfpMVY2G3rjwEfNewj4XVY/JDJL66NyT+i5Z9g/WU2orgs1wD0
ah7EJZUWoBeeZjC9CPYXF30W/oo6get8dTi/6D3yx/0yDfT8Az/4sbmHWDeH
2Xzu+kZyja+xh8kXRl/sBOlLyovl9HfiGWbHHXAiOSXdQN6CUgF5C6pX/zw0
7gueiAuyuiTZ3NmB7rNprwEXywwDf/li10GPK+3NoT+dXI48yOBjFG8SisTC
LnDsDz452hH8KsgedS+RN8mvK1xgeIgl5Ob4xa76eRCrcE709znMj8XqzrS8
WA2Xf7P8ov/yZbW4NvLoMiLh520ajnX6c95Mut7+TFpnQvHf8N9umku4GHkL
cefh7+G/LXuBcC7lMeHCLGMekVDAnPIY+IGBzE9oCX9vrBvhUkwFdz2ucpOF
/4VL2ajPkW+9qWa4/t3yqAMw+VGvGfyoUsxOVz2uOmSTv1T53teIb9tFfE8a
1KYQzcfphchXcamG/e62Hnm+BweDDx/0A16lLtkXyouBkAsHlsJ+u1sddtuQ
SVifNXJofXKrBhLfMukzmzpB7s4MbKbH+Wre8I/FmbU00Ac0J3+Z+LkX+bGE
MuWozkWQMpB/v8sduM0QqosRhuajuBfv5E76tcgPI1z61RX03C/oozz8b9Kz
RbAf36/EfZgfT1xQ2Y/myW8o9rkD6JWlpQgX3N2Jv0kPC9M8KMVXQm/fL9vp
36PQ75UxD8n2OtYPV8SYh8ToNVycao06oBnHcf2U98y/2of2jWyD9yWI0WT/
SN/t6b5q5gK8r1tZoN/xGuN9+oTyuMSCIaRvqYcQN+cquQ+n/w+ZQvqZ9CM/
zYf0ojbhcuWriCPMZ/yO+b3lql4O9F3wJ/hJXsQ7+OIFYd+mcfX09Or+BOQP
5lkKfbvCd8ijvHdoH8mNfyG/ZE828HfDkR94eT5dRzgAnJvS35D/ZvL/DJ2E
9XN2CvN3MbvmWoBBfzD5YZj+oPxC/qzGN9QV8MMrWcA1PqPhXElW78PyGPnf
82kdC0OnQ75veQj/3uv68KvLQxH3OH8W43ceSrj6eSPkfotrWG8N3WGPfLMj
vU5YlY75PPoK8un0Acx3QFGsh7lp8Besr0fzLQjApUoZRK+tTyEL19HWp2nd
HvoJPnPAg9aPGJOf7HKhLtazVBd+JGl3FvLZmD6j5THyJ3O89Tg3sSrhQqWP
qBuq9Qj6z7MgivcL9WAX8J3+gP6mK/Jdbnuy+qbitC9U6zDkxxzrBD/Hbrx3
oSr4oOI3CHyX1fcJEXnJLy9Fv0Wd1+/F3Wic9/egzuvpAx89veh3KlibB+H/
Mz/09//saw2XU7Kwnu+Xo3nj0w9PJfusbyau8+An8XG+yQfSP03xxC/2hEsR
bwL1OF8rk/K75Mozm+pxuWKhf/yfVgY7SPSMJT+YeBTyXfRo6yDo6LnLFY30
o+sh30F7X7s45Es4uCK/7gzqstWEwsgPGRIE/eoD8iKUBCs/GlflvPB/B8Gf
IN90Bj+KWgA/zKRwTQ7CzuqTB/TCVND3rg65v/2nE9Fnv8Q6rJkKf6NVdbKf
hA3J0DPX1YVftNFh+Ett32Jf3CqDdb7VG3672XMo35XL/93AH7iUSGPebPvz
NG/SvCaE/9VvwX/GFYa+XQ/yXc5+/xR+bPBjE3/u+i2a/EItMuCfWHgeekKD
TSRHpSU9WB4y89/eHYb67Vvj3PS4cqkW4vGuQQZ6MakSrRO1Um/CpWI1wM/7
QT+QpoQjPjJwMvzAYVmok62UAr3z+3LIhU6hyCNKvIG8jPfjcZ0nPoTLyTmG
/F4xCXmr/AwfIz7HDn6ToR7+elx+tIb4OB+8FeMq9xrvsccjqnPmdx6CH2+K
ivdu8wN+tOCt9K0G2GA81fPQPAgerZHv1jsDeRrrutFzcdWeoI6wchryATwL
kf4v/uaIXs6wjaLfe5aCT6e+hv677jD8M7tOQ+9t0JTiF5L/GuhLXUfSOpRu
tIBff8sG0K/e5UTXLRJJ8ldd3wf6zMuXsMM+38T1pw+AHOnwEHqhbZYf0S2p
SHkUfPJEyi+RXt0Bv89fE3kX8e0I5/fUoDwL5UZp5LMV2II8s3/krOLihf11
b20dPa5uuAb9L4n1JWD5tJwQQ35p9e6s1npcywuVrpsb6Pkbu/LRdU6eoPnU
8lvEyDrEjyTz1gZcqmgPPvV+sgFXxATk822KgR1nqrNegTjEszv19bjcdxny
826X8NXj6r0w5Bfnad1BP05lVmvMf1BBA879RP2F3HkZ7FxLP9APFxH3vp6M
POli46BPNrSg98TNKwk5xvRM2TI/8ooKVwvS49KtDogX7KzpT+/NHnlK8tHD
mN9JV5A/KGxGHpp6Fnn7/sdYfS6jv9UN+UuvWsJecSvM5GM+5Ac3WEzzyhf7
MJ3wUqsQv7vXBHGMyh8JV06Z477dTHVOqOvLhzoovpux/kvDTfUUJnrYscKZ
PeRPlVi+k9Q/FXxtaC3kJ8SuRBw8vzf6g9TNi/W/cxnh/NG7yHP6HQF9z2cP
3mOf35S3wJXNj/UcuR/8/EM+8P/TBZEHV5jlzwx7Ab9xwCnkJyRD7gj2B6CX
JZxD/bQmvy7vhT+Om2HEj3QiPiBuuA77Sf4Gv/rjdPDbqvWR37TvNPzDCR2I
H3F1FxAu1U2Hv7frCrKX1HKx8Mto/p8BLuh7cmNrbT0uXL2DOoQcO4O+JDyN
8Cf86G0/+nst73T4UMjdT8sa6XGh3GnkHxafZcAl/3KwT78dRL5nw03Io8ve
QPSSst5fPw/8VuQb8PHeAXpcsRwEP97OA00N+Ac/1C0510A8Yg30VbHkEcgb
t/fQdyvCfyLYdUc8Zmck/LodmJ2SCj+SGtylGcbP8qjHnUHdUKJLCz0ufT9B
fgrpzvdAPa7W/AW/Z2Z3rb6E9f8QPP7BqxpxY18a2cOC3od0HXku/G/kw4jp
11l+jqjVd8Lfmol8cXEf6DVcyH8D/Sxy5mp1OZQ/IFwOoDiU5DgfeIIL+TWV
1pvK03MkrDXQS9NqIc8q1YryH018OPYm8klu5DPg0vVmqBuaP93Az6Xo2tC3
h1Rg+erQG8X2fsi7TZoLP/aYGdBD1AGI19QYjfc/vi/eF78b+H7W96UPcKnt
SMRZVuwm+Su3n0D1p7LjLOTz3ZNhZzu/HUC/t/5AnuUO0Cst3hEudogGfaY5
7F3z6B50/TD0ixHEHci/GP+CcC2PRW7fxoBreS9KTlfcZ/BC9FeRetek+3Xb
h31R5wj6tIxpRfqTOOcr8gnXnkB+eN+hqL+q5oq68HIK+O0YCXUCu2vCj/tt
AeHi2Sish9SDtA6UrScIl7KzwK+XPUF8fFM/iptwt/ejj4CLH/jkpVHAx85H
P5+4reSnF6Q2lP8vL9yLfgRXl2P8jytBvyp8CvZSsTV+dL++FQnnw3chLrNk
F/iVpo/N3qbVHdNHSalo8K+KtVkeIId6OlN9BcM5zT/GcI7V1QrMzlUXoL5C
7rMP+giT1/zZD9g/veuhH5GmJ89fCXl6w4fsfs1OF9rI6JvRqSnDWTzxcwLi
AhcHW+npuaIe4GOtpyLvfckz5JPX8QK/SK6I+oU3j5B/ntwRfVWChxIun6tL
/nxh6miil/INNejh0uu9iDddMern3Ila8FPlmVFbj/PeHykuIicjb1mtWxv7
K6cc6u6XVQGf9mdxQy9vxEH+yiO6DpNHysN00Ee/Q738u4+gN7+P+Wl7BOvn
/XYWt1JxnX/y8dSLmM9/8/G0+ZSOnwCfrod8GymuD/FFpcVdvPfjbPxPf5A8
lVeeqWt4XukD8sN33CO9nlvJ8jQm50c+ie0NwtX0dPCTrwUxX3WLUrxAKOqC
8cd0hX043Tifit8HyNkhawkXbWtqfIlwqVEs7IjOsIOE2eVo/0qjaiCPu4IZ
9KLBMvoY2CW563F1sj3ydX4WdNXjYrFSWFf/9HlQP7M+EqyuVGD113/lhpee
XqtXVb8x+qMlUId0pBv481gL6HljOxGuTOoO/pzf25D3pfFtLe9Lw7lH0w04
b9EP/D+jKvqf1JiC/lqvIC8Emz6Em/rzHIxurceFU+PQp4z5W7R6CpO/Zcxl
+GF41F8I7THvwtMbBnrlqTX8MIk7UEd49zjw4/aoEy8/AvLiUwr03jFBGP+c
EoRzpa5DbynoBnn6sBniz38SIAcrMrv6xDHy2ygPoIfwIw7BDrfZxPbRKdg1
/TYRfa7/j+g1//aajg5kp5e+XkuPi05PKN9DvLmqtoF+4dgfJJ9DysNe1uJ3
eYuhLuZ0t5p6nHvc3z8XV2tnoE5Sy4efuAt6hauvix7nzNdCL78puepxIXww
9KGX8BPLG1mfFvkO6qFjXwP/sGgK5hF6mrwQfi1TvtaGXZTXIiz8hbyR8ag7
Ftyfk39JcbtIeRfymL2w1+Zugj3mZYY8Yab/c9tT4Y9a+BbzVvszy7u4Cb5W
7h306IWl4bcfDFxuOQp+6Lygl9OKA3/ZEfqfeTL0zI6D4Cd1WOljmOcmVthX
lS6R/1C2uYT3K6EOWdhxBvkF/S6Tv0W6iXozOXsL9Dwmd8SP/YGXiQMupcA/
U2gg8IU2iOdocdvOcfD7NN1l8I/xPdbA/xg8Dvw5PRX6/NuBRC85X/bR03PD
iiG/9NdD1F3arAf9QDfEuYMjAzF/x4EHpoAPv0edJp+8BvOTugR28bb8sHfP
rmT5ZokUD1XO1ICfuwPyD8We9UlfUkdYsHgTixPt9wR/zK7tYcBfmMFeXr+o
oR6XZw6EHJmwl/khGf+sE4r4a8DGxnpcbNKP7Edl9TI/PS6Xc2D1ySFEz1+4
jXXugfw04dkO8M1u8LuK73chjmzeD3maWddgD3bpDH2F1Sea8qtZfaI83wJ1
iF8KAn/bHH0nfu4gemErcLnTFuJLsq0b+LGmPy9fCL380/ymelxoK8JOb1TF
QC+cKAH9/P/04WH9R+SShv4VXMwU1FOVveyln2d+6unyub/FyOrG/nLHehLO
tZtq9J8cfoe8oKPG/iH8KD+sG9dJhjo5efIE2Hu/dhn6kCiXxvnn4sIQL8q7
EfeyeMpSli81OAn5SywuIy/xQP53eh4H+n0U9FKFcvDz7JvG7DVmt+aZSfJe
2R0DPcsiHnLBrDDhnGM51Dec34g6L9fh6IdoNr8DroP1I/HViE4+2dmI3+oE
/XzCUyN+fx3mZedCwvmab+DPCS2LcVhKhn6kkus65B2KLdrocT7+D7ODzrXS
40LxOcjnix+PfmdMXkulI6H3bhpgwMVqZWk+pR4DUefwtC+uU7EQ4bxFaQM9
bzMTen9fFf6VXZ/IblI+w78kbTuNPjuandguiPq0SEnNCFesmL9rfiLVNws1
0oAXBC6Ov0jxdymwDfohaXHJCB7xhW5WDfS42uoZ1uviJQZ/nWBXFH6krpWp
bkLroyItu0J2Fr/7Z2s9rq74gXySnIut9LhYZDnZa4LnEOZ/swSfKfuE8pGE
d+VD9Lh87CTlaQhHhxro5aLxlAevRhbG82r8p9NB5J+X3oD4VX7Wby3Dm+Zf
vucLu4b1ZxOVM4h3tqlBuDp+Gvq2tV2Hde5SAf4k+54kRxT7kXQdrgn2EV+k
HvIHytnh/b4Z7kB0F+pD7phNAT37iEtbkT0ouN8ku0/d7o18tiVjkY/neJFw
E33vTZ319HzpDrDf++/D+y3tB/2E9btTZy1mfjD0u1NPL4FdVW0n8Fdz/HNx
ueVGP8wbW7eXyiBvSbxJuGg9HutqdQ74lKs96vVWTsD6d3oGudlzOfEtNeIk
/Nie+/C8YaMpH0BovxR1iJlncd36CbALziyBPV5+AMYxcgStC3E0y39+9Qd2
vla3uMGNcK1uUZ2KukVlEOjltGDQx5nBb+PqSnqvNLgx+kRd+IE+qO3SyB6U
q3jDH/rRDnkj96pDT25vSXqa/MSH6eddwE/MUlmfxfWI889uS7h4NRz+fevl
DfT0UuotzNfGq7RfTH1RJoyB//PAYgMu/96YQfkbeeNC9LhSI5LsPbHOWPTb
CBwFP9jkCugH5HuW8mxNeWUu8HuqDkcJV1eMQ73B4Gfwtx1/Aj6t2U1hJ5E/
tDsh/YQef3of63uUeYYBj7eC/7h/EuSS1gdmKZMXrYcRHxVbVIc9e2gRvV/R
4Q3iLF+q4nkLOEE/2G2qRyP/iloa/duEfizfKjuHrV/061PDjHVqSibsLzWh
EM2Hqa7zfRrshemSoMeF0Nngg3alDP55Nf4X0+dKNDbgV8agv5+6muX1xUCu
WexFvtc//Wb/8jv4ecYtJ/+5cAf9abkNttSfmYt7ivqAGuhnq1zPhP/nSDPS
M5UjDalPKbfKjt63MCEP9M9h6F+quor0XqWCU5BP9K4O4fL6zqTfS1vzIW9E
6y9tlQM/15UyhfW4eLMB/EfBLlX0OL/ABXXUw3wdMG/eWP/uUXj+8MrOepx/
BL1XPAq+J45qB3snsjLmn/PEex/oAv2nlAf01HynWf0Ly2v92Blyp7wP/Bhd
GH2yG/SrKQ7+ud98xHFc/0Bj1IFMfgG9+sA22F8ebRH/6hSDuMRARu/QBXrX
2WwWb0UcTbr4An6MV2/J38B/qIL7htdkdRfXqujpc+NwRGd90ZLuV5f1T3NY
jLj5h5/Id7MJBV7+Pu0LebG1lR7nmpijzmv2UD+6X/du4HsbdqPOmeW3a3xP
y28X974lXKgHeun+I8Llwkc4+jvWj1H2W4a8Xsf1DnpcmfIa/dNWz3XU46Jj
IOoKrpkx/YTtd+EH3U9OTod+xeQvX38D7IFzRUL1uHQWeVPCmbVG+qHOhHNn
h8C/VH0A4r83L5C8lqtaIc/FE/EFNbQI6mvcnjO/DfJDxCmz4Be9UdMF8+MJ
e7BYNvwUpvUJem19an1+tLoArS8QP+C9nx4XlO50XylmOtGrIvgYF+9F9W5a
/wo+ugr0loI+8L/32mrA+cQuqMs7+RB4iaLTcd9LyG/r/gt1dayfjDQA/Q2U
3s/q6HElNp70VPVZNvyFdgfJDyVXBz3/8A3xIX71XeiHgVaIF37Oa7BP1Vcf
wG9HzGigx6W5l9GfJbBbQz0u1mf9BD0G07406Qk+ychftZqDPhj2LL9lyXTS
P8XNt2FH9xoIO8LDhvKz+TKjaJ6FspgHudlq9H9IZX0b2DrhGu9FX6SQxoSL
ZUAv1D5B88axfrnyOMcI+l50HHFGhos3O0QwOu2D/nJ3jxDO3/YpSM8z/J/8
zIVupB/8qw9LLZ+hHiSpEvOLMnvZtgnySsecR39HLZ/ty1Oya5TSNQL0uLJn
J+pVmV1lsrPGQI7yZ3HugMmfUHYNyVFpWRX4T/Y+oPosoaE38rVmvkN+WcAS
qvNSze+jLnvab2/cD/VcShDqWMVCr5lflNkv9iNwv6l54Vdm9oXYeTme53JB
dz3OF6tG/EoOfWCg1/IBpK4LoR+x/jb8igj4tUZhHWv2uzo3kPSu3LxuPS6P
FJGvvudeJf08iOvTCJecx7vqcWFRN9TDZv3h9bjyJRh+TvsNLO+d2QVFCkIP
3KUiP1njS06NES+YmM9gV8oTjqJO/+Yqp9z5U8sNgx8meyj8bz5jiE+rthPg
3x5+Ffv5WRWi56qiTpmfsxD60urV7fXPq+WXKpfXIL/6B/wV/KVihKsfJsK/
sZbNpySBH1knw09zID+urzqij5C/P/SmuMbAE++RvBHv90f8vQ36CSjZL6iu
gfcr7qx/Xv4X8h6k9+0pTiu0QZ86aS/4jPh7eUk9vVpwIeqRkjyr6nHu8Xj4
o0fC76KdpyA4t8J6m7HciDedj33+frIhr0PI74O6+qS1xjyQ1w2QP5qSbsDV
ev5Er7hGt9PjfJobzke5ltXWgPObCtLvL+kGXLVUiV6cWL0dnovxt+VZRel3
rwqwswLfj6d57WWFuFu7O1gXma8IF7sFwI+z9xCrt4Uc5//aL7m4Go/9y91t
gTrcj4eRRzLxnaDHJfO98Oc8W2LAVbUs+u2y/EzTvmb5merYBV56nEsLh79r
ZYqHAS85EPi8Gw0M87z2Jd539K+GenoxwIP8sPL2w4bryz5HUS+9sR76j2n9
f0pmw1/n1d2Ai3NDiJ+LI1P89bg0oCfywlN6GPwkQgmR7icFjTXgisdu1AOU
GAM9pHF/vK/YzoRLwWWNfpvjb5Fn623q24/4EOvbLzhxlnrc1J+fN+Fuelwy
32xYJ3LnpfRcslDFUHcj/ugHfjjlHvmfxMQaUUR3eSv0zO7da+lx9Vc/1F0W
3FXfgEeOgL+l/jicGxGwA887vg701OOdaTz8zQ1Y59U/ljTge24a8a226Cs5
AvFxzumCH41rkhn8HrHotyZnQX5zl4oAX45+a9wf+EOUtJuIv2n76KEn4fzw
RQY5wg2HHihHBRtwdVQ87NZ936APbLmKOEhoFdZ3aSjy9786Un9seY4v5EFK
RcJ5r+GUnyAM2gu9MP4dxae4IiVBv30a6S3y/RzoRxr/6cX6dS7wMeBiMeQ9
ig+j/PW4+ieL9olWL6Dpexo/53PmIQ/KsQn0FpYXoUywRZzwYGPIF+ve8Nve
KYc8DY3PzHCBXl1gey0Dnn8C5sVnr0EOKkE4L4krijo8k9zsvxVxqCdpVfS4
2v83/OQnzxbFvLL64sFOxM//rrtKBrznNcQZ4wtU0eNycQH716IH5TNwtq+Q
D7ZrAvLZBvmE6O/LzaxD/h11aCL4TcoRZqcjr5Uf6MPOU0H/Cn4J6LU+UXJD
5GVpfaLEe9vgX7mOOBTXtL6hfxSfUwryi/WP4hqvCdbPJ3/+Mfz8ieeCDPMc
6gb+6f0Q+GjosdwcF+CH7hjopTJX8Jv/TPMj2BRGv829b3+jH4lFWT3Oz4+j
fgJC1zIGeu7EYvR3GIZ9YfKLpjUivVSYl1xLj8vdRKzDkEUGevk95CM3oyX0
taGTYFdur4o+onbTm+hxsYUz9PguYf4G+s+V4P9aPg18q/My1IXFxcVR3ONh
Sehx39YQribHUT9PtZk5+qyz/nWq/YqzpG+csjfYldxpHnGmuq0MuOi1FvU4
3SsBn/YWdn0y9q14975BTxNOjII+7elglAuxf7A+OvE4j0STa2mNoef/g/OR
G5Gn5LnbmF/6FPMvF0V8TUw4hjze/D3hfwn8BLs1EnxSjByJ+q/y42j+hCGs
X2ViF5p/9U8ro55T057p1dON9w2YhT6cs08b9Z+1ZRBPP7q6g/55hTZWoO/k
3Ej/HoUoc/QBH326seH9vgtDHX54ffi/hwGXr9aHf993LvpfNtgKP8+GC6gX
Zf0eNT1WGJSDc0FiQ7C/+jN9dY0t8g+mHQgy0JeQkcdQxJnFWyHXRItaoJtf
tZEeV3NOYJ8e3GvEhVTiS3z9DjgPK5zlcXlexHs8Hgz+/OMN/BLzV4MvvAV/
lta8x/rpBP7M9y+PvouBU7Gva6wi/qbVK2l+Tq1eSatLUlsz/wCrS5Lifevr
6UWHVDxnXuTtcjvAT/hDSzGPDDfxJYYrF+u31OOcy37Q22xlfIzto0bgU8Lq
0YY4CP94FOHqo92Im5x6iX20EfxLvrLecB351HjwMbN36I98ZhD0mc398fe9
xjH7hdmJpWNwnsTJOIOeIysuqF9mfnKpMvJJND85VzKQ6TMs/2T0LPRZ+CKi
H/nyKMQTu3WE/haCPtIme23aAZxPtR99pwXmHxBPsHrhci199PTyb9ZfemYI
7OOzqfCbDXPHeQBrLlOdimR+AOv/DvpmCvtRLym8fot9dMwJ8ZpKXfEeWP62
XDczPz3XIwvIOwnr39QP4Z/9YuqPajHB0H9SaHgM62DzLQOuHiiGfJ5BnsZ+
lUV/IX7JRyMPJyse+dvb5+H9XdqFPmlnkQfIbw5HfHeqJ/zDycDVM/fhX0sQ
gGt9GIolE67lF5n8XYyfa3JBwzW5oOHSiyLwH3YM+0L5Nq8aoL6n6UPkK5o5
Q9+7thd5dGHWVG/I5XGEvpT4CHEf68vwo2bfgb/gwTv4tar0j6DnPHMReajx
j9CP9MtRwrk9Sejjeboa6+caQ7j8Yyv0xS09Kurnk7sYSutQ/BxdyfBeumeh
LjQSfZI0XHrqDD+cexTjY6b+tCSP1Zo4j1KZhj6lyrbG0Hd/l4K9yPqXCkdQ
183HT0L+W+Ou8HOu3Yb88HWhyHdr7YG60ZdZsB89K2M8LUTEJSMOwS+6pkQd
vBe2X5qjLkOuz+pY2X6RFqCOVfqF+k2hPMNZPay4rQD4qsZPys0Df+6ct6Ee
F4o2hz5n29Bbj0tCU7bus1E/x+IjnFoc9Txz3iAvJWcO1eupO9chb/j7aw89
vXwLuFQ7GX0Ja4RjfqrZYRyfrem+PD8LcdiS+xEPKnQD/786DPS1v8OfcGgE
+Nh62E3yqobkjxBcCuKcsz9rwW/3rUX+RMUlJGeFdOTnSJeLII/h5THmB2P5
A01w3hVfb4QBV7YNgZ5zJttTj3NrLsCu8N1fyzDP9f6AD//OcdPjqpsb5F2o
Z109Lv5uQrjcJZri4SZ//shQ2u+qoznlkZrOdSoU4UDXedQEfZw0+XIqE/4x
b8+ielxMr4V8jKLxLnpcnlwV+WzWzeGnHD4O19lQD/60Xq/gv2J+b9mimh/d
N2cX87+Bb0gLoXdxkVmQI6VBr1aXEbf7+t3LMA/BwfCfb7VEPqamJ88+C//h
sXwNDfiIl5Cjdu4GXBmzl+jVD6WQz8vOy+BctyLePeUBs/MFwnmvEMQL21at
paeXZw8AHh8G/fPtOug5DohvciNY3sizjZALtnPBxy4CF7chz1PIMxbx2V82
yE/R9ldKV1pXXO00Fz2ulqyIea6G9yIcuEvyXZmA9yKtKehsuE6+tchP6htS
Dzj6aQgJ0IdFbj726bFhhItj18KO+LjSQM9tbQT8eBzzezN9+2E29I1bNjRe
k15dvwDqEVYvN+RZ8aeYHjIvj4Fe2bMccQ2XNdBz2TrR9EYhCP5p1RXrRIlZ
BHlXrCLoK7M4i2QDuflnCq4/uB/OxShWGH1IVj/E+P8MI5wvLCDu0vEe9Oi3
/eAvOdca+zm9lcGeEir3QnzR7JefHheLJCLuuWG+gV7pjHNkRbPz4Cvf4R/g
a+7Gc22ah/dTsj/29b4q0AcO3Md1ZvXF80Ycgt818aUxr+mEL+UZisfvGexu
Zd0z6numLn5mwOVFDSkuoxTNMuiNXPexiDd9Djbgal8H+IdTLWjdyldewL4e
8Bn259Vsg12mPPgA/1nmUdgv1jjHxHQ+jvV9g99Mab3hG8UBmZ/KpA8zP5Uo
J4cY6B1T6fwLPvUi8vwPjAV+9+gfff9JMSMG+jnrG89vD6Z+d0LXhdDnU9Dv
TuoyBXXfPfsi7+JtNuGcd1vKPzXl60ZegR8n9EtTPS55foTfZ5urAVd6zQOf
6nEQ/d8qzMd1Ui9AToV+hX7hcgPxfafS0D+L/0Z93OkYxPc3svzpgmeRJ9EB
9Fzt6TiH4FM1T8P8zOuAfZHgY/D3Svv/IF55wtpoR68Kp3oraZmXIW4r1+mN
PNL9xrgJ16Ug+f1Fv2MGXBjYmeiFkYcN/ispA3JNLvTRgMs7vaHHmuwgJgeZ
HcSZubXU4/IlZge5VW5lGP/sQIM9JYXA3tGuIx9tTXX/8tZ8eL+bmxBfkG5U
MOTh8GGT4B9ZWaC1Ae89i+jls7zhvEjZ6yT5qeQmB439nl3CUVeZtsxAr3Sp
hn5xt+rRPHE2WfB7j9hEfEPZVwhxpC9PYDcVkcj/z3+uj/psORV65que/oRX
cEPfIJ+8WG9VXkEPnI7+PYpbGfjHVk1FHNzjK8XX1Piv8KfVbIc8Z7ZPTfPP
9qmwfKMx31JAnbnWR0fW/ORZObDfoll+rDk7B+3GE3YOC+j5zJyaenr1p8VN
5Bcx/1v5C/CfD+hN+gk3FvlmXIcf6H+1KQv1GNr+cvFHnN1lmIMe56fPwLqa
+KGaHpeLDQT/3NoGfoCB4MNanZq6px324yTgUpUS8Bflbw9735vx4Z2F4Rda
EoK+6IeQhyDMvO5HdKxfuikP4co1wrW+6KZ+F9XRh0Ge3Blx53G9oHf5+VC9
umJRG3lumj423xx9DoMzEY++HAE+uWwKxSOlj6Ugv+Y5oQ4uHHW5vI814m/z
vOC3b74a/CoG8k4sVB9+/tetkAeyfiDqHvugL6Lwpi/0p2af0K/8FeujGDUS
9nYs+r3w50Evju2DfLvVJdm5RaxObWcz9A3IZx2oxxVrV/h1W7UI0OPilxXQ
m1/dMvIHLwfUL3myOuk+iFcqu3ogbzwaddj8l2Ss/z0c/MzPPI1+j1GLkb9V
tAPOZf1WnvJv5Q/l0L/XMYbei3b+tZKSAv4WVN1bj8s9D6F+yDLM0NdI6DCH
4rPS8LKGPo2izU+c2+k034ALcbcd6D4PN6FvzRvY9fytTugXuicc/uDLB+AH
eHqY/LdStXXwB1dMhH3aZjLOA1ttYcjbV+xaQY5vn9DIMA+vDsPP3xbrV+Pn
or8v+PbFp9CfNHvhcx5Hmv/V1Qy4cH0P7IGI1UZ5PTUQ/kP320Qv1Z2E/b53
CV1HvX/LOD81L1L/KOnPS0E/Tr5xKuqCErwb6HHhCTs/+7CZr+G5trwlvvrf
vkPemnYegbK5FfqO+iFvTXo3DPpbgfpEL2n4wLWEc9NdsM+0/Od5HcHXGofX
1uOqWwri9cOaV9XjfPepNL9yRFxFw3uxLIj80YSF+fU4V/YO/AsjEyoZnqvi
Y+Lbwu5og9xXlzigziLqGeoHNb4xojD05otFaL6VbJzDy2WPBP+ffpzej5yH
ncMrjIe82GqLvl4PFoC+0gXCOcEc/X/OIm/WdM51SHXEY1ndmWlf/N1Helzb
R1KWJV2Pzwd9TI05hvOtXu6Bn+R2z2lsfnF+QMcueL6VczCe/KNI/koPBZx3
c8YiisY172Jeuk+7uex8HBZvPXMf9dknNqNOzcsa+Jjv6Jv834fVm/P/nuNQ
VY8rE1JgJ8yF/1lZ7gk/wIOjqENp8hZypMIY2CGz7JDv0YbhZjaIx524jHxS
7ZzuCYswbubvMuGav2tUhKDH+Vs1DPSc7Q4DvbpqEeqH6rdAPzZf1M1xlZ6j
vtffEeebHUDfCn75W8qP4GZ4ws87LhN2btBzf8wnsyN+og+SWmyUoc8AN6U5
4tnr0oheiED9lGhZCPmT75obriMUiIAfsHwO1uPT18wOqA8/r9ACfThrLiP+
wZV1xzprvQ7nJ2aUgF+ntiv6T5VE/2QTXz3eDPV4XqcCDPhBHvxcuuqvx/nS
HWk9y/1q4NzbR6OhP2zvTteRnxyn92ain+KGfgWRhQIwbuSB82euIP46Y6W/
HpcHvoV/te2Z+vrrqKdQN6rOL2zAZakq4rxfoxsY7nt4KOzDW83QT/ce6iiV
zgLk6053Hu/vIPTwYdtQHyiupDg+tw58WD43FX00QgIM5zaq3i+hTz9Anp4p
btV9D+IZBYznPCp3LkEv/1iVxUkZ37Yyg36e/NaAq8FMTn+6bsClSegnJjdF
nobWt0HKGgL/z5W3Wv4G+hPZDYUeWBh5GuIfRt9zEsZjVslBf32xQD2yf+Xn
E8sa7nt+HuoGDzlS32UT/uUl+l/MZvbL3vnQn6NvwG9j1pvqyOUmvcHHBkK+
SiGDCFcugZ5bNx7z2Bp6pvwa9emyfAhyLhN6qTwGde6mfgvubVl/Qg/Qe7v7
sOfX8lJwjmEvPK/uo50XD7zUEEv9/4t9bBCv78nqs9oUxnONGozzdUceAz/7
khd8eFIYzkc+lkq4qZ+5123EEZj/Xx560hAX4KMLI78gCnySG3CbzotX/Xga
lxrwGu8lqswFqsOdW9eQvycuKOJA43q6yYBL5YohrtFonNE+ff25Ep4jytBv
RJnbAeeF9Ugz4OKSVqDPi34hpnMcZrVCPrk5+qtruFKLR3/17Y1QR356F/oV
WEYgz3ztGtTxa30PitbFuTZv9hr9mYKC/VV+pqce53ztMS/BY6F37MF5B/Kv
LhSn4b3M0adBO9dgAs7HVUoehF6z9Cjh/LDCv6muRMsT+3oV+oyWJ3YV9iaf
Cj2Z7wC/knDGE/JwHOp0pOQUP/r7v3oC/f/qxYh3/9UTcB/UC2jniwm1owjX
+rGb9C7W30O13o6/Y3kaQocDOL9mXijwd2VB/+w09J7dO/F+LWXww9FzYH/W
mQT840aMfyI7lz0T/ny54V4878gV8LuFjIH+WRL1cfLGnYgbvh9jyBuUJrch
vil3K428g0bn0c88dDzZEUJwGOR5s7uI0118jj5vz7ogj2IHcKFCB/SpO4Hz
HZRSSTTvksz8wCHnYa98t0KfxKXo7yNuwLkPGs5XnIB5nJvE+lMx/bzle9Sz
hx4x4qPnk39M/PEaeTFaPMWxGeqs89yBP6HHchZnuY919vAx/FuVgQtW79Ef
4fkbQ5yCGx+AfOt9AXX0uLA+EXZ6fUcDvVC3BPw4+ZfAvvTF9cXe0GPlh47I
03EBzrn8hh++ngX60jw9QrhUHn16uXup6OO04Rj8J2smIc5nG4J57RPP/Cfs
3B/7nuir4DCqJz3frKHIh6k1FnWO7ctSvrQU0xX18tMT0Oc5FfTiJB/0k91c
GXyP5YNJxzo70f9HjjTiqUPQr77tIKxH7VySSUXR/30b67u4qQzpo1xfB9R3
teaAa+cd929AuLhiGfpL7KxH9HzdVODp0YZ+ZeLMRcgvTN+PuFy3ZdgXf5wQ
V2jeF3L7KnBh41r4EfqxcwCnoq5NeB1M8yl1YnV5M1i92/M/0L/vSew8R6bn
lHcB3ymAfg6mvnBZiTiXKK65jx5XWZ4tH3jNW4/zLqWpjkCqfgx+33VXyc8p
WtZAn4hWr1AfdHsW/KItPQiX+EMUz1XHXydcOTkD+bem+hHwH61+RMvLNdUx
sbxcadUo+OUiYffxxQpj/az8Bj7xrhn8J35TyD+oZG9y1OPCtJfkT+RfXHPR
49Lxq/S+lE/MD8/isFrfcu28V1NcTOtz/k9dCTesKekhYsn1JP+lU4vAl9xP
IW67+D7O112QhLh2p0LQJ9/Ho874zQb4BywPQD8x/4m8pGrnwCe3d0M9yLvu
WIctE1mfimd+hA9biff76xnwdrsIF0uPN+73J22oXkYMiDf2XeHNcJ5CqquB
b4j2f3AO42kb1BPEn8N6UH6hr1C/r3QfecY+9Cd0O0bvm09SEfeZdxbPW688
2bfyjzusnw+r22K/1QW/0dfkbjfU3RfYA7r2OfCz3WDnAJY4jDzbBktxrq+W
D3mnjAPdZ5W7Qf9RU4ZUJrzvFKNedP8J5BrLD+cvQt5p+eFSqjXi8vPR/0ct
Ww55RPMWgz+fYPIxTyLsuscP2tD/F1oWRdeJc0acSxhO65H/M4JwddQk+D8f
PwV9JYbHOaE+YvJ0OsdG3TgT+sncQ+SvliecoPkTWo9Fn5+FndBn8s5P+GmG
4Vw2/sYQ5BtPNModIf4u9Pg75gZcPbMM8cGof+TX667wL11tD/9c9hjWtzaL
+CrXexnJQTmtFfJSokvQ/MvHTqLfiA/GKZ0JQh1Et0jUO2rntx5C/pY0bB87
14Xh/CnI2WVNEH/uyvbRqJ7wW6ZaUB2udr6JbBWAuoaqZoSL7qUh33NaAk/f
AHp27gl/uw/JO7XVPNIztXP0uJ5BkI95+gfqcdH8POIR2TgvWsPVDH9a30La
Hdi/p1i8ONyS+u7xc8qAL+4ZgnEyfUbeVhn139q5Qichp3ilQTM9Lue44Rya
eSON9EmQX5qfgy/MzkEYUMiN5NIy9MPWzpdUdqJftvLTXvOXIA+ubos8ZH9Y
X2J5WczuPvaT5IX0SPUy4FXRj0V518lbj4suR+GvKPCD9BrOpSHxRWmigudx
KV9OjwtnIpHPP+9haT3OcbHwL2//iL6GwehbLma8QF3oRfQ/V9vgnCw5qQOd
H8GlWcGP2qAC8PjhVG9p6pdesxxwrV96mGD0A/SYh356FR4Y/QDjzsM/uEqr
CwOuFEJdmNA93eBnEOdHob46aQvW7fc4vPcun0nO8qcuIf7yAn1+pJBuOIes
9DHIgQrwG6v3BprT30Uec2Hviz5KUAOqL+aSmzvrceFpBPnx+Sfl3PS4fPQc
5ZEqLSbCnuqyDeeSh+eg/0l6CtaDVndsXRr9sEZNBn57O+i3jECc6MJz5vdg
/ORcZ+hRZk8a6HE+egfpD3J6bUNeh2QZRPR8qRCDnaWskokPi3/tU3qOP4+p
z4O8uHqQHtf6Pwjup+EPP2VBcpvv/wh9ITbx4F8V7WFHrm6PdTtOgd/qW1n0
vTbrDvnycRb0+JASOH9hicj6ujyEv/jgC+Qfafu9STjk8mtbI157Blt/bljH
RwvjuUo+AP9heYamfAmWlyscmGaIR4gz3OH/HOoOPYftCz62FOktYrFqlfS4
sD4T+ozFHwMuhX2GvGHna3MxyMPXzteW73iy+AKz+6zR11fTk/87rwp8RnTe
ZsDlImnE35Qy8YZ9JFWfT34bblOklf79qtOewe9/66TBb8OPL4q4/8Tur/R9
DPjjodCHFllCH9H4T2JhzLvHY5Zvg/sKz98iTvb7nquenvuB/jNiXCz66mjy
JXAJ/LrDP9bW46pVHzzP6Qe1DPQVL0J/Y+e5a3UBpvPc7fYYcH7vXPJ78M82
Ij/O2xx4/V+Qm0mjaL7lskfhj/W5irgP8wPw1xNh5zI/gGxxAf3tp8+Cvbhq
I+hv7kAd4ZZI2k+CZTzku/UInLfTYDnh6lrId2nJV8Rn3n2Iov/vXZ3GI5fK
i3jZRJwjr/RxIf+q+Pk74m4q6BWLEMI5rb+DFm9asAl9XaemMT7J3mO7WTjf
zQJ+A1N8pJcV6uKdhhno1YRz2J+F16OeSMuDcr+J+H7Fncin8B2O8VzeDHyM
gLzRxsDlV3mR/5bnPb5Zfp3k/pv6gao92gfqcbHeHPLbiOvZOc82Ceg3Uvk7
4UIEO/9k7gOc1/k6DOv2OfzDsk0O8DkD4ceYPBl5W58zUQ/45Srk1jvOie6j
5a8OPYn7jXZx1OP8pm/g14UmFtfjcshE6B+VJ0GvWIM8H/XcWJpf6UoQ8phi
kW8m2+YFv/J8baufZ+4y6z8rRBfW40Iizh/iKrG+vFk56F9v+QXPxfr48pnA
5Z+sH6+9iR7++vygl9TUbF/98367i7zJOtVt9c+lhLlgPId8zAUdzrmfgv4y
vBT6bWxfHkX/X3wX9OoCZrDLd4wknOu0B3k1NdCXXr14tB/hI9CXXq2LfunC
VY7ifcoJ9LHX+tma+ihq/Rx+i/B/VESePP9iA/orDriPeAvD1anZyBt5aA1/
UeJHnNvy116g+1v/pDiwUuEz4UrqZeTV/7UjCC+Jc6XlvImwG2PAZ0xx7T89
4C+3R/9G0e094dzYd8iTyDvOQG8657rfE/TT1fjn5c7QrwYmIG85Ogbr52IP
xIcWrEb9eovZ4Oc7z/nn/uaq2WMeWH9Uuddm6D9zQ2F/M38g/+I08mruLoS8
ZX1TxShnsge1Dx+Nuhst70uIe0t1/5wDcHVMph/dPyGU+uIrVmXxXjr+Jlwp
NgZ9fTX7NKo64i8OS8ie4qZMo3pDPqx9Oul77zrCH9AxHfkAV8s9JT15jkA4
N2gy6hNLZDwh/Fcz9G2aPhfP9cEV56Cxft0m+WiFft3i87OYv4eTIccT0nG+
eYSMc6O0/NXRPK0/PrhqLT0uy7GEi0OGws6qhbxW4boLzlFwNKPnUneADwsl
V74hvbfOOOgFa08RroZY5pA//3A7ohcfnyScexrzkfZhVxn870ESxr/7Pvqz
2IfSOR3K6lg8r9NXre8PfYTVpyFPOQ51zY9/IS65Aeewq3Usif/Lp49Dfyl0
Gvyq8APE5/YXpvOsxAHrwd88cb6F1l9afx4o/Z1pP7J+IKy/tNanmn+APkVa
n2rOoRXy+afAD/ZX8CJ/Pfw4/FpjgUuHB6CPWPxD0DP9gRstoD6h+EQHGqfG
h+1+4Zy2enMQH3/avAeNz44nfVvm+tYx4P26Iq5337WuHuds25H+KnyfBn94
hf3gz0eXkx7F5eMQd94xDeOpm0x1HHIA+g9Id7Ef+Sc9INdfxcLu0/Sx8K7Q
2/+MNuiTsl0s8nBWWxnyN9TP09DPJ+kU+vANi8P1r1VCXkqNJPILcRu/4f1O
fYz69/M90HdK/go/T6IP1k+fUJxPPT4F9DHHiF7eMhx5Chtg/wrDdpDeK49J
Ac78isKbichr/RXZSI+LkxDHFNelGfq18qOqIk4alI5+OV8xb0LXB9if0kjS
a9SvkXjv88KxnpuMR3/RDejXJAj7YD8w/7MyAXETzf8sSGPgl85AXaFSpZvB
/yxsZXEW5n+WPiIvXrrRBPpMr6HwL5y/CT08FTjvNBrx0N77WX8VY18aNdx0
ToShjyU/wMKQryiOvYT6xtbbDbg6Ef0tuZ4jWH4Ry/PcWQL9mlf18Nfjqm8l
nGO3cUpTPc6fvwQ+9X4H9Q/gxKLwl35biXqr4GBav6r6DXrOxBkdiT6/Sn5X
1SmDnVfenHDFdRarF2PrMBl9mfiU5Y30OJ/Rw4/uc3O9wS/BjW5AuOxSrBTu
z/I/79qgXmD+4s8n9LhUAH3kPjil+erxD1sR79iVB+chNFwOP5VHPtg72TfR
H7E//Ffqty3E1+Rn0dhHa5ZjXfl/Q3ziwN1W+nEKi/2Rl+9223C+nrJUgjyY
/RX8h/W9l/oMhb2RYoF8otuo31cXJeBcmaM74Y88ifWmisNxbq6rnaG/sdxv
J+RW20mG/aKkfPPPxTkz1jfIcTTiLHd2kD+Er8j8Kq7A+RyfXzSPrC+Tqc8/
68vE/XfOJn3kTDPkeagt6upxPsETfiHe1tNAHxuKuFXgZapPN9VtdZqKOHSb
Dy56XH3fFPFWT9YPn/W9576lM72U9cP/59xJjV7rB85/Ab1cvpd27gN9xCZ+
ZEfJkzcbzoNQg/xpfjiXF0wesfrWBQ1xLom1V1MDfvEr+pVdq9pEj0t/DiDO
WO0x7qP5vcesMpwjpjs/yIBzWc7AF/xGPuHtGMST/8mXMz3PgPJMXhvPMdTo
TXjvPnQfk/9hXQl/GrdDAS89Lqe1R968p5Gec0mi51RqfMR6/zEL+7f7V8xL
Rk/Ej87dRV70le5aP3fUmV7+BZzZj+qXmuDPSeaYzzaP4G+8PZ2dI4P1IN4+
A7us8ih2DjvkBTf6OeokHQoG6OmlV2uQJ/DUFvnRk5GfJneNpH0l3NgLe/zJ
BOgb5o7IV0xrgDgIy3MT8qAuWj30BN/jbyEOK9ihH0hWG189LvV4RPudiwnw
0+Ni50jEm7/+eXZCN06lXnXYpSHtVL3dJHZL1Pprwa9mjnMiuP/Oa0dfOzMt
Lw64WBP5OQqn0cey/owinvsT9pH4Hee1yJd/4ryndOD/nTcBejkD+8hE75qA
OohFCzDOJltwvphNHPrB2MUCPxcFP+/RPfDfv0Cci2sRh3xUqTr4txaf/e2D
eNWj1a31uNh5P/Kott4w0HOFPeAnbTcdeba2taBnBHSHnuM9FXiVhqh/juwJ
fPlt+LEruoG/LEhC/9DD9dh5DSw/ZDnyReSLDyrqcSVgDvrTBOy1M9DL1XEu
8Ka8yLtegrwjWUT8gi/fE37UZwyfMRR91e0CWX0604dZ/bUwNwPn847ZhX3q
kQk/WOhsxMfOs303vCTWT+QoxJlzpkNOFYC/m0sphP1a+wr086hmiBcfbOFP
1xl8FfrYmD+0DvjJ1YG7bsZ7PFkEfodTk5GvxOLjyjoL9MccdQp9RxqUQL3T
Z/SbExqmauuX+KoctwXyrKK7oR5cefkJcrTfP3XiyejLJw4x1puLlZORP1Yr
ntabqY/iDUs6T5yzi22gx9V6HM7HHb7P24BzkRTXlh89h12fgvNVRWE08RM1
WIX9W3kB4ZJrE9ifb/ODP1UAroZ+hXzs+AV+HffP5PdTrpWzUfD8qAvc4ED5
8+qajn4kf7t/Rb7qIB559dPLkj3GdzXpgbSvxV84R1n6D6c8MCkLOJeFc5Nk
Ju/ECzgnSVna1ZB/pY70g50w5ybObWH1xcrbFogbtTLWDYndPsHPE1YD5ylp
cXbzqYhLpbci/qIGB0EfHjmNcK5duSJ6esXlCPwPhzaDf/RGXYNyugr8QgPM
YD9p8XquNOqeLvYM0OP8zgTiD0LoUX89Ls7rijzPHZmIbxz2hX29dyPRqQfy
Ik8/YjrhYrMdhMvhqIMWuwDnbouQX91mw27V5Pux4dC3Vpk76nGxdU3UJ87a
Y6nH+T79UDcRcJjp26zv1v07oC88IUCPixboEy2OfNVUj6tB25F/8yoR/mxb
dp6dJfr9cTEq9kU92GvCrGHQV7zr+dF9lDvgt73tYV/xIYQrRz5DPq4yR95F
Bvx53L/nef2Hl9Pj/AfoU1Je4Lwf/IC84xsHur7WT9jGCXY7y0PT+JvWt1ar
x9Fw6co1+JWmJYBvF0HeOzfRB3GjSu9gjzsh712Y8gPng9kfxj74BL4quanI
1wwsT/KC67sI+nD0OeTXrWN54tNgXwtPMuBvv5+IeMfBfdBzFmaj3m3Fb+jz
O6eCr5aZCX97ycmo/+OKURxKjRwNvXnVavghWdxK60Ol+ev+7WfO/adXV8K8
oy5Lh1fV4+oLH8SNG8xGH5Shvogvd8pHfnplyljwv99l/pA+e2Aj+UvE+qno
ix19Kg/R3xlAfFEaWAdxqcRkGqdoOQ91lx7IP+fvou5SSqyGvuiBiYjDdcoh
nD9fBnaz1jfJ4xD6i1b0baDHlTMLHhB/7h3gY6D/9pD6b/AF3Zj+zPzGFX4g
v2vrtaZ6XD3bFHpJe3t/Pc6V3of9XMSZ1p2Why+Zd8X5nve7wl45Hw+//eCF
6Osd49pETy8f3Uu41udcsFmGc75YPpIQIdbR49xMdg5g8YGwA2qi/7DYLRT5
WpuCqF5DGsX8nynnsE//zj/hajnkyx1Ohv+0djLqcpLKox/F8HHYFw/f4Hzm
rs9wLm3V2vS+1f7bWD7Ga/Tv7XAEeUpB1Wg8/MXSyIP1j0JfSHYum5SvAMXH
tXPZtHMYxd6vCdfOYdTOa+P3VgSundf2/9g66zivja6Lh8WluGtwXdwXCbBs
cfciQRYorsUhOMXdJRQWd3dS3Gq4EygUt6W4vTDfmV8T3mf/4cNhyCaTycyV
c88dGZf1mbMpvM69Lek/mnRvcS/uPGpA/LPs+ZJeXDt1gjxZT/kdxU5Pf7ql
c+EjNspH3Ds7uD1wGfv/6nfkfWTc2707gzhto7XivTmLb0r+ZyfqJxYeRneu
+g32vWX1xL5gDt1C/WnW19hFXcOJp5TPznpQ/DftCH0NGvjjV3q7lreIM6/0
4facgaJu2uhyJKa4n1oyPrlvMnVP1WqiK9YM3GnWGntidgVx/tqfLzH+/rzo
4nmnPKaf2t617Fex1riiLjv/EpFvVPFG4/wleDB2wRheXHv5ScSLjXT/JPTi
5rNEzMuXfV3cT5DqQ6f6OIJrUbSEXvxbf9x9/xe6VJOv8HuOdWEe8h36V9g5
Ez8Sx67diPdS7p3ArYFJpa5VN95LyYYjxPjtl/A7HfobWiHPxHmsZ1yPH9k3
H/qBPZ/hVx8ZFyae+0QWgZvZXsIP+R99tcT1gndyv0Vuc58X88HjLLi1CvdJ
vMgqe4d62ClZfPwcs95p4gtxs8NPf4FunrHrCDyurV0M73g7eid0q+r2KuHF
nXGZ4H12/1Dai2vHZd/2G1eU/Sx+zAcX4IFljazhxd3+08mrDq7qx51U9GFs
cFysQ20r/WJMqYtu/fMO3Xulk5weXXQnQ2X8oI2Md2qji6h3CK/NffIelW6S
E3MG+Freu5srVKxbbVrbIDFOxfeiJSMuV3uS0D8IxBl+2Y4+xv4KURwPbs0p
Q92x1PPxxDHge49bg1+idAWr9Eev5/Jq+tFLHUIztAT6NcvWsd5G3eO9jy5C
XG7LUdZt1C2swzXv4YG0X0meaI7kN/aqJ3XST6J/qM3Ff1+T4p343o8NkXoy
0n+/+hc825gtxXeivjtrO3wns/l94qX92/CdViX/5N47l9qLm/XG8j3+g469
wvV0lzgv4x+G5zZlFc9V5Xvsk6rf7GO7ZL+k5ZMq+vBK9Fey4sbzjbeujOU6
J6aEOZ7nctqew9/v+dkXb3Ej4M/YuSb74jZWjITwqbaOlPX7cv0kySl4IcY/
Map78YA+4UlLjDciWFd67yARN3HzpfTx95y2EeSvC8T38ffsg2mxY9c09ePn
zqH/2+hzPe/zajN+41x41MeHu6PQpXGWPffjk0dwXiRs7Iv7ueMrwWfIs9kX
PzSvT8kmcPMe7+v6Evrx1WpK/qADfAZ7zBrs/Io54Vtk/wHdrKebsBM+PCee
8no3+cPM7GNKH8BaOIi8cIpIaS/dE/aw8WM+Eb+3J1+V8dXC5KvWVoYHteji
QIHXNuh3ExaOPVIZPT3rYj9hb1hx93COST09K2V39HqmFwn14nZP+lfp5TLi
998n/ma1r02+udkp9sl+xN/s6dGxn8b3JR54iPibnWgk59N4m32oMffjtGr1
WPjdL39Bp+rXaWKerfnnqEPYIvvkDkU/xyg1gjqEXzfIulTG2zNl36igumFi
3lSeYsRU+FGSh/Zl/XAdyUNTuNl2nw83fovLOh9GHtauP4lzIWIu9os6f0/M
hadnyzpdhV+OC0+yXr5cXtxdPop+gedd3rv67jonpg6t80tf/3d7+0T0TC4d
8+PvFuOfPvH3i9dLoO+tH6rB/v/KYr01bs15IePPgfNU6iR89eO8eEBXIVUQ
cfpqUk+jbQrq7s/vw48p9Ab/N6ib6J/ldjiJX9bjOut/+wzhnxi1Tvny7+68
4Hdif7j0xFdP6jTJK+pj3Sab/Pn6H/YJHoxx429xX/Yc6qzdsj+JPJa59p7A
3cz4m+Z3dUT81C1nC9z6XtZf1yoBj/GLP+t9XlVXZZhZc3hx6wq68VqMJ2K8
MxAdRW11VvJz6vvt2xqemPx+NR2+ivbWwm960Synd7zlXvKND9T3jX3kr++T
useuO4e+M1L32Fw4FR25F9QzaiWiift0EsUV71+bRt9ed0x93vvW6OQhM6Rm
n/z3Lefc5d30HxuXgvPufFX2k8xjGX/10TBxn7eegQ8by37+JhnX6dwGXuCq
G/DhK3F958c7xPE0Tdgn+s3P4hzVZHzbqvpQxF31F9ifX+tPxfyGgDvPGO98
AHenHBJ2oFYqFvcTaQq+pMIDcRuFr+td1odvD4d3OewW52aHNPine3aRp+48
gfqtdJJ/ngadKCvaWuzVn9k33KZFqeuM8oh4e7fDYr81K9/HDv8USr+PxezD
2qQU8OEKbiE/vxbcztMR3cnLccnDF3Wom/vxB/zBaX9gL2ycC0+vcz/6KUud
MXXOKp0350Fd8jhlQ9hPom5hP5Q6Y2p8oD/CsVf4769579q7LCIe8cWukfv5
E/G81pAZ1FVV28v+nL4I85CmKXyxBbUaeHEzBnE2o9Rb33gj14+cO1lqNvC+
F+ffNuhWSf/DiIafovwT/bP0S6Lg11hlJd6UflUq32HFII+o+tJrKl79mriq
WRjcfsy6sl+pPvUyHibXpyH71LtjqSu07jUmb5tgophP+yR6bgo3hnXAjixz
tyjzTJ2mNrk/cfCjl8nbq7rascHky5tOKujFjWb0L3aT3iGe170Z8bF9YehB
aS1Y/zKf5Q5FP+o//0jmHRQfeMkUqc8gz5cW5dGVLnCFc1PxN5o3oN5w42vf
eP3Ec+ytX07V8b2vpP0F38sdeKaeD1/4ij5r+37w4UpnLICniOPDnfyxiT/8
vkfgRv4W8ELHdSQOPApeqxt7vjiH3CnjyW9O4tzXj98hrlp+IXHmTmfxdyzW
lXWL/r/W0YrU7WYcTn172B2BG5lfkxd4m0mcI1ZR8gLGc3h9etkY74V92+II
+jwyTm5H2QEv5D56xWo92F1YD/od9IrVeCs2fe6sQ3GoR65KHy4zzWLhJ5ht
btTxzr/xNuF54V8f7VzX+76sD5MFL1OvdKyOF9crX9gj8o5zD/pwa3wNcS7b
M2LLc1/2lQsNwj+PhV9pS73lr36leC8P8SsD+szST1G8Au1CSD/xp+r3JHkI
1oYRAlc8BNUHSo1XfaCMxLXhQR2lv5497HiY+H3P6oj16DynX682aiX8NLMp
+ZfvYnC+9l8Ib/mvxexXEfPR6/ixE3bU3Z78+x/n6APSZA15u0Y70aHpcpu4
4g3J2/x3EvvV4rTDxP/fNhj/ZE4Dn86JUyIJPJ/uQeCfkgvcHX3J10cpkO/Y
3U7479/i7qVH2b7iVt43YV7cPJw+p3e8Uz8r+8yyB/gj7Qr59k877zjyQS1P
+u/z/gX89D9eSn57DIFbWRri70yZ69dvaZud8RW3iftyouEvO8sSU0e2ext5
M9nn2jC6ovd1YKGMh3OO6FFaUU/SBPtcnUfmuFbwqrtKvDzjnXkd0FtQfdnU
/il5g1qaoqy3+3K/TYr9Zv54SYy35Xfn2J/gGdZaU0XOn/hx+1jo1Q6K7sP1
+kX4TpsG+h4qPQf0do0D8O3VeXcuGHugdmXDi+vxyWO6aar5xmvLyXsacxJX
886zc6I2+1rEHuISad5hJ4eUgQ924jL+wX1wveRU+BYtZsl8KPXO9uhz6PA/
Xc3+M20X+ffpA3muA2VK+MYnZ/9xCj4jXrqGejqjbEaxH5qT6gjciEZdnj6i
lNBLMlN9Ergzk/doh6yBl5A+o+9816b18/nXAXvgV/xr50wfH650Yr/2PRfz
J/ueW13PYLe0NmUdq4wXjU7L/nlmGHmzabIuZmYinqvEGZ8doqdZiY7B88F+
XOo2u1oNH24Uol+AXvj7rPxeyaNbEk7cb1ueHF7cWhPMd3GnRLAX1zY+Il6d
OTd6YqoeIRq40nVRuNJ1+VrH7cXNcNnPbnE6+nSq/TmOtEO+2Bvi74pnK+0N
dR6p8eo8clsW8NnD2t2r1Am+/Vzch0s+j7mkXCkvbl4OIX+xfjf+bLHfWD+V
gtjXxmSET1FpJd91ZXQctFiFGN9nGXiU5OS/c22GN6H6JqwLx9+echueg8xX
Oh/Ijytc+yafbr6E52IoXtlxmTePLPXvfs/9OwP7kV8PHk0fKvW8bXOzDs07
173jjQNR+K5nDMMO7NRK2O36xI/EVbbOhH+4ZIfAjW3vwRvIfscS13MMA09z
vbAXNyuvpe9w0WrwuWrK99vjA3Zuh0c+HrX15dwU93OmMnnRvDGE3WDML0F9
VJKk5G+jpCBeczxc5NPNBLHJw1x6S572xEvsw9Dj1IeoeGDFrPT/y+7AHxoN
b8RqdQ3ezagc+Msnvme/mju8vPj3yMnZxfxUrom/nDSjwL/cGfmoSPjwdqzP
5I8mbsUefjkannycJfjJQ7CTlS60WXkB+JJ8wm4J1H1vOUh+d1EmH4/Udhdi
Nzq1fHaONZXxWpqxtR3P8xrnI/SvfzduzqzlxfXIRNS53wjyj8+MHrfWuQz5
KcUHkP109HJzanlx7Vlb6gG67Be4HXaYOMnh+OhFRP+lpne8u6c1etN/JRJ8
NDvIIV4xYgT5x3WviEtUJu6hJ4gKr+XscfDYcvyjGOC1M6NLpu5n2U3srWm5
Enlx93Nf3vvW8xm9uPO0Cv6C0repNsxX12beiMRuW0vdtFv9JvHnBzNkPbjk
T15zsJOz2PQrHJQO/ME19rvb/xAH3Z5S4G4jqatvXhL5QLvbY573yhT4tUPb
kD9V/dqO1+Xcbdw72Is7xd7QL2Z4N994fWce9BdkPYQ9LFUrcT/3l2Xy4tqo
IS3FdTr/lcaLG0e6gCfMLta3MXQJfpJ5ju9o5jOxrsxUsl67SKTMI4SJ+Ll7
LzXvYTS8DjvlCIHbSbqRP50/Q8yDXmEP+/i6Athva8GtpSv4nvd0JS4a7jBv
6bYTH+62z8dXdH4cGiTmJ1XGMC+ut3hL3OzMHh8f0k3xo8g72ruTU/c0Ad0P
/WF8fl+Rx+QT66GfrP9p+/oOGMsYr/oO2G+Gin3b/o/3GOLFjf94jwL/dv/X
JD/Y/Gc6/rHKr61qSf/o1pvFejGux2QfyHWMPtTvFovxRtvY7Kt3Q+D/75K8
Apl/Ma4NQbdcxsmd/WPJ78g4uTPoN76/C+Batcn4lUH017Ykf8Zy4F860cG/
PC/PtUvyMgP5WPW88DJ1+zh27qaow8R1ou/E7m81TNa9ynOqVz389AIfknlx
PVYi9kPXob5T1YPvL0Wc4WDNjF7cuJMJu/H6+1xe3I3sw/e4OpvcD+X1x59g
Hw/OU9uLmyci4Xk3uOMfX3w7cY1j8ZnnGuPpI/y+5EORX5tzC7/70FHw7Y7g
6VlZ0IUyS8Fv1HsNx0/59Lm493nNycuIAzSbWcCLu4v/VDwc8RPIm2t/Mu+z
+ol6NIU7ukO84PSAOF7cznqVPHHNCT5+uNGmCLrou7sKPGDHljxK/dua22E+
PFVt+h03ifq9F9cnTIkhrv+uHvVBL8Ph6Y2qwPldI5HAjVroIRtLWtP3JGMN
dBhThFIH+uKxsAu1zbuze+9Ti0//ArsCvJSA/ZPQZT5rJsjmxfW566mniBel
oBe3q8Vin49ZI6cXtyaUJ59YpwE6lLPJC2grn1LvP7Oc7zrmqmrkWWT8yu4y
Ff9Xxq/0lpvhtRXeRZykb3Xslr5x+J5kHbHqb+um6YRduqUM7+XjBPG8RqEK
1IttBte6bVV1NbxPxSMKy0Jdg6qH+30xfKHBJ0s5/2O8/m9a8vpz11X04tqd
jfBse14Q8x/YP6cM5PkPJinoxfVOxcX5ZHbtltuHfzwv5teOssfHn7Tu9kA/
Mf/K7724vaO3+P5dp7sP13OtF9+PtbAs/lzCN/Brc6cPEv9v+VPB53JH/YUf
0mLrc1G333qIyPO7KXfgzy+/J/hdTvTi9P2clQB9lXsO8dMeP9Jf41Mb9BNK
x8MvrZWLPi81uwncuH+H/FSGdOg9FxuOvRThlBd/niCvaO4YS/7lcXH8teE9
gr24eWmf+K7N2G+pE3neGz/rXEriwAuvo69ltcZfK9sAHdSx/ybnOnJ/GH4K
/d+I+lm8uF20Nnmv/U4uL25VSC367jkPFvnimdril+hKlU7h82et8D7wcuL9
4sejpxD5L3PK87peXPXPci9QNxfwl8vRp9s4P8MXZ3CLpoevtzB6Be/9KN1p
rfxT33X0A5/JV8ofZ4Csmyt0Bn9E/tjfl/DhxqJd8ANfjULva/8x2Z/riOyj
KvkAZe4TV2+7zIfrc9aTf0/xOrcXN3uiz2Ol7M5+XngSvOWjGeGryLyV84H9
MJC3erYBu6bnNPDuHcqLP523sn+KtFeN1Nj/r34q6cXdoET4p+Pp4x3AC8fF
Prt52qen4dyMzfc5rpv4PeYg9MrcJRsErr8/jz3bTepXX1qL39IyKL/3+vaR
bugVxhlVwItrgzahexV3OPoMexdzPwWq+vJZVjb4Ayqf5dzpik5V39NcX29J
PqtxUfY9NQ9OMPzYzW+pW+pzFL9M6VJKPNAXWOLancXwmorN5XtMnhj9ktb7
BK53mcP9z6Yfm53xk4hr6ZMkr2PkwyfCf1Z6LzLfpPKYCrciGa/6l7n5C7Cf
dG4k9Grs7LXxN3o8pa72bhnwbBHU3SfvBk/xxzYCd8d+RJdK6mGq+KGqR1Z5
YWuvrPeUeWEVl1bjlX9tZh0D33vAWaE/oNsr4Z98N5X4UMbc4KPD0PHvUVTg
xo3nArcm9EbPQ/KanNlhzLPkNf2vvmZiHm/39OUxncNdfhXxf7ew4cXtpjcF
H9j50ND3vVv1854W8ctcUfFjpJ6MnY98itPmQXYvbqVNSB1Ktyc+3IkZRl1x
OZ362p39u4h5qrqOfljDFos4jdnXErhWvRd4qYECtxPEQ+dn6gDwaxlkHxAb
HYSrMj/ephZ2o7sRnaq+6ckP1s2CLk6SbczjztHw9gsF+kqL/dv5iF7xt3VS
5qeuvnqrgH/x6TP872vk/QLf4+uXIs+hTTrPc69ZxveYZCf9d5U/+PYd537c
l7m8uLOAOlnnBHaPwq1RmTmv996kPveQCQ9Xvd/vj2G3Z2wR7MXNZNnRQ3jW
lX3pwTP0xgs/wJ6/PBfdkpP7+b1dTPgwLb4T/FJVF6M1riDOI9W3XcUVVd92
q9Qc33h758CUct7Ej/09Ol3f1iHqKde29eJfeeZf/zTaTRW4c+4TccIhediP
q5HHcf+MFPaKUTUG++JL8j5mxyDm8VgQz51gpBhvjIiOHdYS3eVAHWhjTeSr
3FZSj1nG/ewS4PZn3r+qJzVzwiewMueC/9xe5ptaZKHO7C466M6GP7BX5qXh
ulv6MN/55H02agmP8b9+K/TDjq6R75h824+/Ij75bX8WIybjnba9ieNuIW6g
h//FvH1Tl6H8Sqtu4TAxTz8Fi33PWcY+bl5+j7+cPzd6X4+DyacWjiLsVet+
S/Czqem38SO641rjztR/TXzHubugrbIXqJ+9xD7sGldreHFzbXbW33/+bEL+
HZ6x3sUQ8bdAfOZZNHHO2SmipvTi2twx5HHHpPCNN37LDV+3UlyxrpS97YZW
ou6v2zX0EpSd0/6UyNtbHfz5F+v8VbHOta7+fI3x3RbGz6oh9E7+6/9eF33e
mm3ieXH78lXs3p4lMnpxffLhUnJexI97a67ot+icOlXW8eBKH1jhqk5TrRPz
BfuRkdqFHyL3K7sedWJm9gCOv14H3AgvLvskPOKcXXSU/EQvdGWtndnbi+e6
+5E6gUh0Za2kNQRu5KAfunm9e7AXN59Ie/twT8lrmCSey0g7D53V0M7ED+Rz
GbFGoJd7cpsPd2JGR8fkUisf/9kYsBne9eySPj11+xD19c65eT7+s717G/Ug
r7bCK1H823QGfKOj6AN5dDyEXWIV/4c4U8YezcX4HGtln9d1ArdqT+C5vj9C
fv3jc/IUR6eIuISR9Rznq/Usk3ien34TuJOwD3H5JU0E7haaLnB9uBWoh+L3
SP6YrIf6f7w7Wfet6giM1/D0VB2BdrKKiFe45kGuk/y5T9fFKvJc2g8yjll3
O3pTB/HH7b3ow1jfDWE/uBCX76vQFfG8lnu1hBfX3EH4LT/UIk62vjj+b4Ik
8Fnf5YG/OW+CqE+x6lQX+mD6hoLEA9t0FLjR6jvwAm94n03Bv9jP6KCWnIJe
WbVS7cTvHZEIvuKrPuxPCyVeuhv1YnVGCdy8PoNzp3JLdNHutRLnhetEyrh9
OfbDnjmwx1ZLvOQvJeW8sW8V+sy8yTiSU3EK8eebT5nnrcdY/9fC+b6D/sAe
njKNffzX19Shz6lJ/U69Tewjsg9OgIej6vobLhd98ZyT9L/T635U8Qfx43Rs
RTxTnqfG9AfE2aLAN9P23ccufbkAfkgG8rZm9lUi/+P8tFDgVi34WkanDfDO
vytDXLHaMcY/68x6+HBV+KO2S/2gFnoCnneCLQ+8+S/z13Hofp7pjJ6W2g+z
56F/0IVNib24taEceYjn6PparcPw16RerlYvL3mY3j8S75L6usaFgcTDm9Cf
0ehHn0TzURYxn2p96p+PCz/UeRorpRfX+q8TuPXoJbrXJUtyXuz5DF5W6gvN
ljr/+29iz0s7XLswrqecf/qt/ZuGONUvjDcG0F/YTijrKqTukNkRfoweXp18
8nD8QW1eJ6H/q31aiv86VupYTj0p+r/qTXqRr68wRvDtDGOasL/13N/BE19N
PZA9t5m4jnVqGv7v29zivbn9k4rxSnfLHEO/MKW75WT5W+QrzMLod+nb9gpc
6XEZXcmnKD0uLRDvkvnKiYf5nr/B3fcr83hx6zb5UEf/k/zXrOwVveOdYimJ
Az/6xH7/9l5/8Rxb2hOfr9Yb/njXmQK3/0lGHuLPYegPj78vcHNmIuLk311k
/8tCvxv9bk3sc/cO6/fGQfJQUb8T61I7MwE+4bRDxIvi/B7I74j5UHGzs5uq
/i/cvtEc/vGKuj5+jtYiYRXveLdWcvzKl2+po2i0Fn2XJKfJl23Pz3XKlkBX
rNJf1BmtP4s9fH6QymuLH33dXYG7afL4cHNSJuLOPfx6IdbCx2G+/5+yBOv/
ul3GiwfyYqdOsZ/GHSLOzcB33a4CfWrT3f5Q1oMbUztiNxT76KuPNi46nBMD
ZvjtogJj8HNWvMztxa0ZFVjn78fl8uLOogecE6+X0Jfo3Dbiiuk7oiMs+yca
awcLPMCvLkYfI/34CupH4vaGJ9+9CnyJir3Rtd71XtjRxqpW6H0lqkQd5ZzP
mcSfn+7y3T8czvgdT/AXc2YoL64r+5hYLvl4J+FBw4vrt+6R56iVqoIXt6Oi
q2Y1SSnOkYAd+7Y1fQayj2YfiJBx5krPsG/236L/4VLZlyrqCvziBC3FPKh8
jdYyFv1FfhjVgOvrAtdr92feZL9Rhat+o3al73y4dbg7OnhtV8m8tuxHLPXw
nV+vgK8nru7svMI+eyueb7xzsDz8ye9Ghzmax65uHCLyoVriXpW8uNWzKHz6
Nk184807CdU+Q913IF+GP+/B03pxIwp9ipR+gptJ9jdaV1NcP7Av3eyUWF7f
t79peeuK885ot9Q33p6cgL5pyzdRT6DyCLOqJhD3H+9Wch+e2xZxZi1hvOw+
fAY8TK3NUuxoGX8wltakvvdAl6peXK99gvxB+74+3JpG3FvLGyb1KNBRMQq9
oI70m/oF/VpS/Mpv6h1U/b5Ti7oGcxB1DfqmrPAj+/Cd2XNSEX85kJt+zSdn
ivyMm5f+QG7paPCtt6/Dr91F/tcoo7FfR8YgjjMV3L6xTsyvHn+I5LNxjptt
z5PPyHeV+qMGh1uJ6zcwxDrTH0aK/2cfui5wO8Et6v2mN+c7m59F4M4j7Cel
G6M3pV47oBvT9yH1ERXQ6TL7XmYfe2kxPqfU77rVFj90U0X44PdlHKDuZfTk
b1XlzwoOcYNKZ4mn5WsBz+jWLvAOu2Q8Z7Cv/6/RAJ6DEy+R8L/c5ZI/M3IR
cYfW6cW+646txDoJjyVwVc8e8C9i3IRP1n2f0hsQP4rfaL9WOlvSfz8BP0rp
bGnf8B61IcNkvlL2dfrYjjjq9dhVvLgx6Br6cf23+MZrdhV4Sg+lbrfitYY2
xu4/u6ucF9fPnsAvLpRY1l/Dl3bDoqLHFBEi8mP6jDBhD2jx8GfdvjmxO8ou
ELh+LZx6sUIvhD2ubwJ389crL5+T873DCMHfMKoHozelcDd/KzEud8OMXlwr
/bMYb6fdhf8yb63sayZ1PzrRv9jdlTSeF7e3bmZ9PIuFf6f6BF3MRx2d6qtS
ezxxA9lXxbz4d0bveDP6OMY3CqFOWfW7rLYMP9NdF92Lu6EXP4u8nnYypRe3
WqdDjzv/LbE/2s3gn7tvr7OfnMqLPsXT7AI3knSX/LY/sUeV7tnFRfDYWhyh
3kHVvWo7yOMuyV/Yi1t1B7IOFlJPoZ2DR2HHmYhd3mMD9vMU+Kt6nu7PvPp1
yj53H09C727RSvyzXorvWkrsq2bzHPCGjhQTfdzchpnFfm03nUJeMeVteA6x
z6PHbcxi/Y8pIcYbZVaQ94pWQnwv5qy/+O6qdxb7l30qF/7fTpnvHjUePZ/f
7uFHHsB/NC4lxZ8tl4S8n7KvPj8jT19pTW4v7k7Ljn211PLpyVhF4/L9Nzjl
05+x6o4Q86tdC/PhhnGGPFTOa8RXJy/lPhOWQFfiSRLud9F32J/1Y8Ibb/uR
vEp5+mbaxmvyU4/DyavMYLw+nPXsbg0lXif3DSs4QuzDWrcIYd9aw8bxXQ/u
xXe+ezj532TTyLOse0Weo2lWEa9S+Rd1TjkHsrGPyD4+1vwj6rxXdvozVVcG
rnTRiENa2QJ5gqpeXI03j9eAF/EsprAbrRHoT1qxiqPHUCo59cU2um1mwr4y
bil1yKOmVvcjfgL9RzSH773m5SDDg7t33jHPU6OLOtdAvXP6Y/A0Cp5HZ1ry
tPVqM+FBTS5WzotrpXviH705UdqL2/eOER8sfVHapXKdWGexT0+UKOvFjWlP
yCskTVLOiztxQ8uL+030zpcf0VfmF/X85pC1vvXp3A5BX+vFfhmv7okdW/sm
9le+LMRnpP3jDLyNfbjrofg9Afs2xm/E6QN5Q9nf6tQpYV/pk7UqXtzdFpf+
axtbSH1aaV9tiEKdYJqmxFdUPLnMG/pSZJvnw809vdAlv8l5FIhXZxuKffZm
PXyb+PRVNBZGMJ85N6Cv9eo+8Y21tbHX4zDeacp4t8k76ghORZPno5zPfKWp
C0vasLIXt6+/41xdFlnRN35TbdbByt+YT8WD7TYYnkPujBW9uJvlFfv2lCz+
8YmKUgdY5CD6fopnUjox87MyxIe7d/vDYzuar5hvfN1Q7OYZm4K98+++l/1H
Bk0o4MX12h2EH2qeq8k631eK99Knuniv5qCbxNlUnCdHXniW62+yzhcTz7G3
7Cd+9fEx8T9pJzi9lmCv/myW9uJ6a3iQVoS/DsvMdJXvSK9Qyvtc9tRc6FxN
1hmveD6prnCuBWvSXpXrpMNBeGy7Txf34tY0zkEr6j4f7t6iH59errvIawT8
35iliVt+yIHexXDqLKxETajHiSX7gtWQdZ1nO7BfpZN1mirP3stE3zblRnhb
yzuxb487Dz9E5oUV317lhVX+V+Eq/2sMj+Ebr+WexbmQO5nAraSHwIcQ77NT
ZxdxZbvhWuKK888Iu829dVngRnt0LXSrHvonZk4Zj5d8kvkH4Jk1SoFuVe8l
zP+a6UJ/WP3ot1/IOMZ8P95lvg83jlgiv2AeLizOd7P6EvoO7KpH3DFzSYFr
IfDT7HEGvJuo2Al631Hg1Wag96n2vRNDw8T1U9t8Zx3W8/12GRsm7wc96k9r
OX+VPmrpKeTHf4IH7vzQDf5Sk77ENWdupR78+iPiBya4ubmNwK1kW6l30LqC
H94ncDvfadblrjjY9RP38n3tvybGG7F6YS+F/MN3tKMd9UG/o9vsTFrDui3G
OrbuH2FfKll6mPj/65NGenkd+mAZB5D8Db2TJv0CWQd055DYn61O7dBlGf5M
xMn1iL3ZxN9/noydsiESnatNndBfvd2E+EAF4ntGDXQ2zMWviJNFuUJ9dP0h
8FF71pfxBNkvO+MTMd6tPVu8B+so92me7nxJ1AGbWdAZ2Cbvf9Ppy+I8jtcQ
HdS4m7FvMz0h3h6ajfqa81fpN3RIxsuqdmN8u0vYyTWvw/vqd8zHx3PCnwSJ
cSpequKH8sft+oef15ct4rawP6R97dETpp5jslbUi9u5SmYSf57/F7vabsZ9
Vu8h8K/6P9yv1Nmo05b8gnOuvPj7yxzwaGpMZn9rkqusF9f2dMZO+2684cXd
rTIO1raZT79Fr1jprpjnmb/6cHvmYxGntpdmq+HFzZBst4U/WnmBeG8Bu2Xk
CerIfpF2rJuR+XxQlPhdukX4QeOiUQ/Y/Sf2n5OT0JtMn41zqu1L+Af5you4
l9ktKudC1f3YaR8HkQ/aNkzUm7i/Eycyp0UQh99YmjqUzR0Ebvc7i95CsTIC
t65U4rteVzG/9z26peirZEdZU8iHF3hPHGDxhQJe3IiRVOBGj/voUp+n3tM+
Por7zLMXu1X263RarYePFxGX9TlnGv0Eo58iv7BH4l02EOesfwL8dAL4CJlP
iX3bvNsQfvzWdr46LPPJVPyiUaHosvY9zHmxoiJ2hhafeoq67GNGcfoau4mD
fHw892Bv6uMqvKd+8bDk1d/rgV30aDB2rtQntz+25/elqFTCiysdXXPmX9K/
lPp+aU+T9woL9eF6xATOoUTUeyp9QjP+dyJf4FZCjzqgZ9jxEbrAs6v6x4cl
4vyb0y/U974OFeA7ylu2ohc328zj3H+7Psw3Pl5JFa/38YqdjQsreXF7zh72
4Qv/5SPEvD07wPNGaYM9lnoI9mpcDR5I6ytiHzd/WkQ+a3Ex8O/pA20kqY2f
/ShI4MbjZwJ3p9zGvwsqTb3GffLjxrg2+IlBxYjXjfsbnaNk04hjH4dHan5o
RB45UsMfVXbO1rPYMWbWwt7n1c48pv5wPv2WraRT6acTa2Umcb20qQRu93kp
cD1npNj3nNXjwb+n/44Veyr1DPLHSZ9sDH+nH40e+7jIUyidNEfqpKkffTC4
9iqCeMFTv46WFlRJxE/clo0Frp9E104zOjwVfuelh9RZJl7LOXvoOHWw/WXf
wDSHeV81NOp51Pi9iSzveDNxVKn/IO3/kzXJ+1T63Yfrry5Qh9DwJn6Pihu8
6K6J5ztfRffhKToJf037lvcu15Wxxfbz2O9LfZXCf4T58HMOvA6Zh1X9blQe
Vv0o/FtesZUPnRMnb/pGYh4lb9YKayH2E8Wbda8St3GXdMOerDkE/6HtwPJe
3D6Zj/XU9DLxqF0beS9PBvB9bilBXqiG1H9bGM531+6TsLetaFIvNCX2pN2o
hvBf7Wv+/hda0SnEX/9Mz/7WfC5+jtTVdKo9Zz+XuppW/TziPo1DqXmP86JR
Dyn1LgI8XqV3MeE6+gzqvS+qN0+sqzQq/yLPwSVLRf7X+Gehr37N2J9TzKdV
zl/X5sTfgF1Y0F8HZ9WNJcbbf5AP1dbQF+nLOiPun5C8qpPqJ/jMVWuwTw5f
hn31ujf569sryeNcjenzo7VpveElhEzy+dHmr3ngu7dK4cOd/EN5zpez6ROu
+hf8QD2Y/n419RbL0T83QzLwfhcOgle1dQB133k6sg9XLGb4njeiaZi4TpeH
Ply7s1F8X3bGMvhNap0Hc77r7x+W9V2nCnrXX/4fdlBCC12LCk2p+7t5Wj4X
uhaKN66FZoI3VLm7wM2/qXc1drf1+en20wvwb5a19NW1Wdtt6hxadYdvHEH9
mnV8C+M3divjvU83XTtx/5o6Ry6u4hyctUisA2N/Y/ihg0rK9SD5WhX7yfiS
rIusHST2AfvWLh9uZyYeYq+eoHg06Orcmyz8GWvNSc79WjPgE77UBS9Lr72L
8ZJnaOQdTV/LFVdF/FPvMkGcI9qQYfAtHj9CD7nDWeycIbIffdphwq5zQs5w
Tr2dyXn/9h/iAXHjS3tvtahr1Sduxc5/VBD8SIf0/L4l8rxNyffbKFLUy6g6
+kCfFFlHb3e4Ab/7InaLvmgs8QhZXx+IYyu9l+3UcVgx/kVP3s2NXzNfrhNt
Dufd/njUFxTfy7n85CF69VNKs+/XL4jfpuKEZ+jPay3+taQXN5YuIl6RaV4Z
L+6GxqKushXrxLi5i7zDq6noHkawzhWudUW3SvG+7KnTqUuSvC+j3kGRZ7fj
9MWe//EKevLV/hB91c1PNvb89cbwYy79RHxsYB/GjyrFOj50XbxH/SjvV4uL
zp1ZPj56eu14v3q6GejZPU5JHysZF3JrPgfPPBb98Djt0FWQ/SWNOnlK+/AJ
KamjHJkE/QMVpxov7faLf3Iuq/0hdwqB260rlfaOd1YlUDwM8q3HH3F+yfPU
TWURL60VhTzynb9Y563pw+v8ZGNXp7iA3kf5P3z7sz5wEPt5js5ivajfa8bu
LfAv+w7vX+ouamdaZhLzGov4k9P7IPWtYe/ggzUOBp+9g31jz2vxXZkHz2T3
Pq+b+DT77M+5xPXchewPzo7fyMcFR8/kG9/+Gfv102s+PoMdpT11+tLOUbiy
c7SrR6V9LnUPGt/nHAk+XcGLWwWSCr0Gp+PiUC9u35lDPb7UgzKrZxT6wN/q
Qbldu9M3UOpBKV0ps2NyMT6gK/XPXsZHfuQ+d2SQfMHB1A39dIJ5uBOXPGPi
VtitY+D567XQh3fKd5bnheRVtoqGTkr0Hoyvcxo7+dN79GpHPhDfoxXBOrcu
bYTnd7d1mHg+pYOxpgN6lPX6+3AtSyzqLlocxQ9IMBG8Xm725+e3qANS6/ZU
Ftbzmtr0r2hQlH3mFPxD43BxdMsb3ezOeHSxrWZD6CfY6pbArfuSz98oVQ7v
9e3nQdRhVt9M/Yg633e9gV9bvIFvnRtrY4v1pi057Rv/5XuhP/XSBuJ5zfov
0Vu4+Ix9KlZhdPUK0R/WrNRQ2P/6wm3EDw+jA+a0miT4jm6H7fgxw9ALdRbO
RBeoRxXep+K5NRnPdx2vgeHDe08V92E0O+Ibb12JBR7lIjzxaongxbXcSH59
6TL6xSw8KN6LsYc6B/1EJ3RsenyHTsjRP4kDKPu8+wPffmJmuo3dtWQSdu9g
3q/TUfZ7fPcefHpngVsLdsK7Nso2FvezvRB1NZKPreVs2kj8fsnHtttsgRdQ
I1SMNys/Rs8xanHByzLibsS+qpyM/fPBNPB+st9o9Fjw0td/pn5F9U0rthO9
5Ra7fH3T3LDWUv/KULzCb+oHwN2YGvXPn8Gt/tGLeseb+amrN26cFPoE5q8V
6Pcx+7GPb2/lKCVwxbe3OlQhDpZK5ouvdCceKvm6gfyy1EF17hYRuJGa8Wa1
RegLhPn139zYxPmNPvkLe3HbJN9tLm1V3Ivr2Xqig1CoCvn8afhHRtqY7BvH
tkk9Sfwp61YFdEN+RIdcm8t4a0M59pNIC377JPRA7JttsQ+M4Xx/B+CFOlYb
Gcd5iI7CSsZ/5b2I+zr9GTtNfb8lZF7jXiriM+p7D4fHroU8K+7FjT6Hsd+y
nRF5+ED8c/+/nHf5Gsb24tbb7OiMD9mNf6/6TbdJLHiHVunH2by4fayQ6Lug
J70R7MWtD+VeiPNC6qLbURNgb3/j7wd06mR8QP24M+KDqzjAxdf4QSPxg7Ql
+aKJv0+65NOn1SNcwbO37xBHtbt15lw7N439qHApgQfOu6FvwJuhg2J/tthn
7Mrw6rskpq50YVgz8VylO2Avdv2VvIw9RtQvaEO/w77sw3lorM0oxptnqDM0
F52Ap5huMjyZhPHg9Z0Jxf7/JPm0m67DZz6owZf5BV6utaQUOlxzsoj8kXPm
EPW5M7vh/8d4T3+VhAfIb4ZOoO4uTyvqSrM+QZegZEnBg9EGB8n5QR/VvTuY
ONJC178Pn90Gv6t0Fd+8aZNeiHWifd8bfviGaehidYou4or6Hw66j7NnkpeP
spN8zcSo2INKX2vjbHQJlrREbz49+kJOr0LoHA7Zwf4TQf8gvWRBvtNfKtD/
bRI6RW5kdvSy7rSV/dMl//PspjCB/7G/uBd3H5rkUQ5XCfHiZvy9nN+TqEvT
Pn1Gx0HGYTSll5tAU325yZN+fpBE/jt+SdRuanxl77zZ1yrwnY6xK/rms2ts
sU7sy1d8uF2BvLi+vbCIGykdM9uM5j+n1Dn4TXwycP2gk754pv5nI//4VX+F
+caHvGHczkfcVz/iZla5s/gp1Tf54od6pS3oZZXcxLmg9qsdjYk7zS3ui0Ma
rWTdevHoPtxuWIW6gEsLhD1jFUdHTt8Qh31P8idVPbjipdh5/g724uaQn/lO
PwWRFzmcGD7JjlPi+9Jj3hH7lp16tYi7aoUe0/+92DKR59G7rBW4Gb6OesVE
JcS+olUtR5z2Q33yvPducY6Enibe9QwdCivDMfLyx7CXrK0f8WvWdKDf3S76
wX3Z4Jn3Rc/gHSzkHDFH5RfryuqYgn1JfafdxwpcjzbT8OJOwbTk5TsVE36f
NQt9EieYfLR+ZoGoH9aWgusNuqNfd3UJuD2VfftlO/QzP9VHb7j4Kuq4N8cV
36nRZwb8bXXu/PiOuNb48wW9uB4eTlxx73wf7laKQbwrZTzxHrQnq1knT5oJ
XJPfi7Kr1fq0u5QP8+Lu3KL4cd00H25d6cs8PLXx3/+W/dyDGgm71D5yhnhR
7McCN6IMQ6et3RaBq343il9t9h1d1DvPxryWrPNU17ErvtGLsw50KObFjf1F
yB+/7VbG9x7v4u+bDTfCr7h6TtZraMQlM2+GRyHtED3fRoFrffqI88UqXYW+
SItH813H3J9NPHfqDAI3yjTCHlt+XfhzTvog/IWwpYyve0Ncx8yO3/TleiK+
6qQIE36HPpF4rLFtgMDd0X9xHi3owH1uW8Bz/krdvZWlNPe5qAj2YMfExBtW
5GP8Doe8UuXCXGd3RhF30tqPZZ88+QC79+B46pFbliMO9pp+WtrynGK8laMi
/tSB2dgVc2QcO35S1tu7XPT9UfNcaZPAnR/LxfLi2ssTAnfPtYQPWHS24BtY
UYaiT/vqN/CPD+AnbE/MOmiREv/ivMSfLxN/N86HkxeeKu8nYUP09HZLPrB8
v/bS6+hafrETxLi/ihJP+wBvwOj1q7C7rImTiadFlGW9De2SSeDTxoBvH8D4
jRr5PVkvYPaPR1+bNz/X8OLaBgddoPNBvvHuoVl817JfvOq39VWf4evflc6h
wpU+sD76J+L3IfThcsztxOuXToQf/nKo8PeNAg/hc6btQNyryBO+u6Tx0C9t
m5frdB8sxpvDolMX0MGFvx7RRuTN9SrzOCdOfaIPocyzW8dvoy8TNRnxqKbh
5N9LXSVet/Y9PMFRcan3ubwRnsk3ev6qr4TCzaYJRntx7Zt9ye43WtVXc773
vwP+br4vHqUXlbiZln66W6sRdxoP/1zP8XuYmLeGNdE7ac13bzU5KXBrfBHi
Im+34ifEfkAe6p8Ywu5T+Rc36UtfPZJ2pxnxh9cR8K/ilRDjrYfN2Sc7EZ90
WrXADxuPfWVMSCP7dW2hDvoWuOWiB6G3bI3fP0H2f0yUrLZ6XnG9E78SH5tJ
XN5tuAJ+QgZ57jTvw3l09Bb7wHRwc/lQzqNshdAn1LsLu9o5x/wYxf6hX6Gs
F3YGFGR/69oB/m/aTNjn+16L8U78XryfurOHCXx3CHWLiyrA9+vUU+DujLzw
jSqux+77GVx7MdT33gP2Vb5SpR0P7kSvzfd+bBvnSp155BsrEA9xh0alf2Bi
cP2K1A+M/ZH32XY9+cbMcnyupMSL3wRJO7eZyHe7N0J8+jPGuA3wkb7ps6A3
aeTDA37ryi7UWUu/VSvflTjYxq4Ct+9pvviYs5668kB8bFZ2+I9h6FgapUpT
H6j61sWYCr9R9q1TetEB/+4bvWgzOv7gt3rRVjTwgF70vHPMd9BTrj8F3UVV
d2wkAld1x5ri8wy/D19uQgyfbpjxhviw8/Kir44y8F2nvI3uwcNb6AWNyC/W
lX6tntRtHAFvpFwe1lukIeuCR6ET07q/mE/jUDnipzUHwTfTi+LfvWyMrlD/
6PA9x5/HLz7YmrxR4efwiCrI8Yl7ws+M/krwtO3Bv7PvdXpNH+K91N076+BB
6a/oZ2ys2STqBfR0zwSundtRSD5viJwn2W+unKyXpL7E/ECfhf90t2Xdicwr
BfBnKm4v60+Didubia/47Bzrfnrs3kOlfPaq1bNtmJiHnN3947OQL1O8Aivp
DPxfyStQPAQzdC51JZKHoN8sLHAj3gPGT51FXP1DSr6LkU+ob911hTq+YlP4
Xs/M5jqt5orzwz28Fj++P/64UXKkOG+MtUmnCt0Npds5Lwg7uPubDIYHNxtN
wL5Pp6Xx4lbQd5zrktekl6vdRPz7N7wmK7g0cb9veE1GReKHitdkVsoDn3Da
Ffbh823Yt99XxI56jF3x5f2yP9eymGcL3ogxIAX9N6sclv6y1M3e8EnEidzR
XUp5cbvXhrOCZ2j8U9yLa1YNdBc/NscPk+9RLxsDu25IkA93306EL745keSH
Szv5l0Osw6r9yvnGVyfv6fxly7o8Wd/01+/YAVK/KICPGSTqFvQCb3zjnXMz
8Wfkd2f/k0ro56jvzlkRTeDak55txHXNNujT1qUOWo8hx/9NHbSWZYzYl6yk
vws9BGdVWuzA1fuI8w+U+h6NO8Lb7B9BfuY4uB7zGvoJn+b64i1u3Lr43Udi
+HA76yPy459H+/xBK53O/jU9gn1G8uKceFPw06NFY59sNVry5eKTN7xB31jX
lXy5pK/o37o9EftTAbnPHzklrms0PyHGOwPkfjstFX1jQ/4gT3UoknzWxEP0
X4ky2MdXt9eeIp9SeIP4bpzt5H+1qunwgyagG2/Mk/5vwdrYz/2iF/Y+r72b
+IBT5yefX2bnuUCeS/78V/eUsOL/xtEddWPcFfoPCrfHbYbP2u25T5fJTDsS
vncb+n0rXNtNv2/nenfG/zaDvucJp6IDI+MVAR0z2a9K1XsqXPW3MjPdF7gx
vhHzFi8b/JsRI6hvlfuJ3SN6QjFv9w8m9+LumA/ieYxZkdm8uLXrsuAjqTiq
HvGJuhUZR7WWfyav0bkQ8Y1j/VwR7x0ObsWAn2Yu2fW3rO8hvpT0COfpo+Zp
HQ+ur/yVvOoMM54XD/DYjQjhZ7qtr6FH8e8s/LLyG5Iacrz4/9mrD5R/Fz/O
zNvYyYUrsE6mDErsHW8cq8P4VEsC576Yh661sNPGTC3iw7/RVXDydiZvfiaI
PH4v/AU9+q8Ctwc3oJ7oWCHw8UnJv5eKRnwp3mr6UNyMh/6fzHe735VB7zPR
AuKxh1knZqWB8G4roC+orwM3uq+lL/Si9ayrGnXgG0Qdiy7WuCvkkXth51uW
i710ZLrMz+IXGFXvob8zr4gP1+Oh7+mWuI5/ofilj/YTx492An5r64Xgi/aJ
+jF9bkH4vKN/we8Yl1HYJXrDX0O986lNWSj2DXvpYPYDWUfvNnxBvXLRq774
odl5iLADtbtXyYtOicd3EVkWf/uPc2FfcT1nNPaN4CbUO6cfWV78XUvP9xX3
JPZoykHEOfRL4pwya2UQcQX9dQ8R71H1YsaeI2L+nSiZcnpx0yxLHHvQxWxe
3BrYF3+yS2Xsi0Hp4XWcjAOftn5N3stL9HmdY0WFPovT8RJ+dLk9vP/hnwT+
1R4WeAi4daW4iNeovnj6TXQRVV887cfVxB0jRrAeXh6jX8m0u8QvFS8l2Wry
6O9ysc6fjWbddl9DXnhJFBE/MaJo2EOrhvFd/fdDfE7Tv8Xze3FV76x4nqre
WTucQOQV7RtF0GXa055zKxCnlbxQ62f4sXdDpN4I+sN2lByc2zuucf3a1C06
n84b8n7k9yvXz6QglY/04U6bXMFe3KhIPYV54hZ66B/Nit7xdpL86AR+mk4d
g9ofliQT35fVclM+H74yfyHua1gxL26GPKU+v2LRvPL3w8taXwl+RmjKgl5c
m/6OeJ+sz1W4/it+l5azE3HWv038wUyJy4vrv6lMHH34eupQmh4kT1pP9mVT
/ITOaag3rvuvD3eGZSPPGhrJufBqC/vDjfziHNESz//eO9583g1989e3JW+K
H+ufIPg6i1P44hDOUPr7uMP3+eMTI6l/N58ODpHPjf8leeZ2kkolvLjimRvu
D1yvOzxV7W0jdAG++L8Cf7+Degfp/xpZnlBH9v4k3+mtWgI3nc8+Hpc2kH7Q
5pTOBXheaX+Ob4QdOKurD7fH5Sa+3KtnsG986beMT98bHsTAcuTB747gPZXs
jL5jMPlxo/4Gn26Syi8r3SR9uL9+x/zhEvkyWe8T0Cuec9OHqzoge3oe6stk
3ZNVNwPPK/W1zL5NqPufcZZ9Ly597rTZwfjdn/Izn2WqE8+V8TF1rin92EDc
rE5+H27djVHdO171HXYKPsd+8/i54t+r4x8pf1l71Zg8eL/oxJulv+w4rekL
FvVXdPdiPiUvvPk99Znh80R81Zp/Fr7EkeHYN3+u5Xwb6TJ+8Q3iRKM0vjO5
z7s1ewk/SE/g7xPkrF8m+p8arQzDi7uLTor8uFbE3z/IyrNN+NPmkr/I/y5f
xPNef06cRPKZlR+q+Mzax5TwnKXfau28QjyiLbwLp9VF4irlM8i6oBXoCX9P
fzft4wq+R8kr0HdeIM4geQVGsZ3Ef0LxC7Sf4IWa+fsTL1qLX2A+2VSd+WG8
VZa4n14hC/p+Nemno/Imet3F7D/FYpXw4la7pOQJCnwvxttTycs4xc5QF5D7
N/KmUlffmU7djdZmC32yHk+BbxD1Ndf5nffv1Msv4vD2mhHYM0H9OP+TFxW4
M+cZcYMyS8iv2ZPB2zzg/E5ylLhiElP441aT3fCTosRC93bk+h/EdWd0kTp7
0WQdDOOdVV3JyxT5zRcn0VL1FPwA916Rcl7c7Vmf91hwcSkvrofPEeeEGZ5P
nDPmszycL6G9OJ/CN4o6KWdMHPaZtVvheVaujp0/NBbnTsrm5OM7peSc6nuF
PE4Wvmtj2Gn6JbWKgh0VNpg8ffXNxI1yU4dl9pzM9a/GQAexEH1XzRInVf2+
z372/HDODmvJ/STLJ/wCc8hN8tj5ZDxnu0Y+dc14eG0yzmPHnopeVUIbvD/8
B3NfKWEXffWbxDxI+yHgN0m9goAdIv0sc1AUkefS6rGfGO96c92CJ6kfWo2+
mdGjH3n5g4eEv2akn0VcqCl8ej18I3wumXez8tvsC7Hi1fbi+gnqEOxXr2p4
caPIEfLE0SeRb1F22qB0oj+j0b2tr/7O3juY/kftL/rGa5WnoMtUADssoJs0
c7KI77lrn+T24uaolPDVp4YU8OGViUsanaPSt2Eo/A19mU5+qHKQtCfZt/VT
G4S/4+6owHeXwMEeG0H9uZZhJ/VrY7BXrfwucdosDznf96PbYwx5RfzrT/wU
pdenz7hLnZeyk8fUhZ8m7WTlvwT0/e7KvhqZ1vjsNLfrZ1GnbF0Z4+vnpS9v
jz2aK1Z+L25sa824enlk3ha9JnfpKfG9mAsflPDiesRW9ObqHvLh7oHoof9r
3tR5pyeKS5+9EXKepR67vXIt/CZlp506z7rqQB2WnegP8J3nOD+mSN3CaRex
x/59TFxv9jXySbfGwd8es5S+j0WrlHK89/lDCuLv9TaV8eFdsonf5z6L5sfv
PoZfN+2u+HczlPPFWTgT3eYbFwTu1LkC/ikBet3xVwrceDpE4O74HKJexp7a
BB6i1L0xrk+NJv7fmDqFvbger6Hwd5welYr6xjf5m7yx7D+o7ENtTFp4Kqpe
QNmTU/vD670SjN5TCexG494c4njxE9HPIn4m6muGLyIufLB3JnHdseuZ56of
2P9Ldqf/yR1wd+sx8J1hxOH3X8N+7j2K+FWzuuQ9uqFfZ73Y/lbwS/pOoR/Q
no4Cd9e8+/QVt/TR9DW6yngjzgXwAUXwL4tIvYu4hd+Kc2bALvzUpI/hfZ1b
GiR+T9qE9PtKjg6G2bDiK1HPW+C51EtBp87uXhrdz4L/5PTibgrZp6ZMn+xe
3Do2FL7Fvh9EXML8gXhIoH7qx37ESdp1pO7gREHx/50q5wWuZYoLHvozvHGp
N+vsv4u9J/VmtfvtyEO1kfy3WgvQBa1hojul3nutFeBxGsi6IT9PWJ/8jHWh
+Bvr98BfzTaWuGz5/czPS2nf7ogOPpK8sNmpMrzEa7vhA0Qyn8YAm+990xN0
/ZXd+PwFesqy77PKf6m+z6p/tKo/+rZ/tKpjCvSPvrocO+0l351buKx4XqPW
VXjZc7DrrPRb2L8qrcOeXye/0+WP2YcnfiTPqfalcu/+/XrfxoittXy4Fh4k
/rx7Ab7Ah1nEOWV9pdsgD/uzrKczFkaj3k/WO5gJqL9T9Q722TmMP0+9nrZz
rfiu9dpjsdPu5BfntXv8BbqcMbriFxYuRHzgxVTyLDFGwKNO3Bi8ZC/mIdps
9DAs7CX32QvqT8+iW2v0GMh7N3R0u++v8fPJh+cR368+85k/PxXjHnU3f/rz
VnrGaegwX3hY1ovbzanTMX9LJOJkTkfp14wYQV3l8UPCPvHaFQJ/3Bhdprjg
5p6B+ANx0H13l8xsK/790m/EM+uNIp8s9Zbt71uSr1yQCd72Z6nPPGQV+35N
6lb0fAWob1rUn/zWx3DqWTJdh+/RYQC47GNo5ClIna/qY6j6tKv84FF00k2J
2x/Q+Ve49QM66Npnxn/1jMV1pq4if31M5tceLBXnt/54pNQ5wA+y50Wjz+Ih
jfGKBxtRCj9c7gOB/qpyH1B5GYWrvIzW4k0Wcf33qbCvyrzGntjUAzu0XikZ
N7tCfCTzW8bvCwNf1h2+wVDZh2IDfY5cLT771zR4986LufBG8pzlfX0ejn1d
dQF5tD572Ndc4kkBvYUDaeDdpTVzeHFjw1X853UDdC9uZSkLn+HnJOgaFftH
8pfiUNdweTf9IzJJPH0f4ryToovx9uBg/NMHVdA3kP1QtNn0VVf9UKzt9OPT
Fmelz0uHBHy3HWZgF+9+g50QZSf2SYHt8EoSfiS/0HEffujJXNSFufTd0N5y
bmqfkxT1Pe/NVmFinn9CB9r4eRN27xLqbTRVb7CLOI/Sb7Fq92PdDSTOYzzo
BO9lKn3KAvP8wxxZl7re8OJ664X4BTl+K+PFte7wS7WwS+I8t8pG4AdVRu/J
/JCSOM0jcO1QLerpij4T4+0i9OF15tVknuMF+g+Kfd+tHp1+Ot/2JawEbtkz
xDkZ4CcvmUIepV3dXD58UhPyMU3Q6Qno4sZdA39yS3YZXzQ53+/OYL+dTV2C
NW0u/LGfEqBP6xQkH+2AG7keCXvLipxMfF7xLd9OKi/fiy+/4+6py/w+/8E3
3jy3HT5D59K+81qrep99LLxxKS9u9IlOPUbyfiE+fM5Y6m0TZmTemrZgf153
lDqayehRBfKn/Z7CJ1z8O+Pr/4DflH25wN1LO5X/Ln7s5w+IM95cFeLFnda5
qSc9mrqsF9eztTK8f9dKP8eeUX1YZD1LIJ4Z7NeJDtgzqp+LzAvo28kXq7yA
yi8E8s7f5BfMXTLvrPILvZeI+lplnzidstLnK/sB4ktH0Q/UKj9Fl77L0/Jf
/zR35EKfQeoGG223lPPiih9r1xgPfyn/ddFXyO5XjD5CY8vLvvMjBO58bM33
vPpdPS+u1qH+KJJ4z5DN2O1SP9Y+XsWXV3Ln7iO++WKMjydvll+ITsLurmE+
POY+dEMWmNQH3IZPZSVdx3nzUA8T95+wFXH1rimkbpcj1q3SG9GL18SODLep
z5BxWtetyvt9da+IF7czV4a/dSac/LXkhRqr0RmzLzckvpSgAPzMBOlkPsX/
nVo9BvA8sq5W4YG6WsnbDNiZkrep1o/iWblJSvjWT6AuXq4fvclAib/nvJtO
3ZTS2/8yD9iZy9DbN6LuKOcdb9an/sp6PxadgFkDiLevHkyc66cVzH/pFuBx
bhNHmJCNeZqTDjz1bHjC8VZiN0r/Uf/iPwp8USbOnSZrwa8Owv6sVp/xpbCr
3al/06foDvq6huzP4myR+rqTAv2AhJ3t/iv7lbd/Qj/PD4WxS6MR57U3bRfx
k2/zXOahhgK3a8g819W35K16rBH8GuP5WbF+vjgS9CsvnJn6qnT/sA4PrSTu
0/AuuhMztoFXL6ji9uLHLAEP2ihUKJt4/gVnyHvf7FeeeU8t7BVzUwX6S8rx
bnsNPJPF93ieukt7URvirtVG0R84xUyBu3Xz4O+b9Rl/Cb6ik+oXpUcMz3PI
qlbi98SciK6CwovtELi+Oq6IU6k+biofqvq4KZ1Yu8NBcKkTay2ILXjEVrns
wv91Tj2ib1H1KvCLjz6nv0ny+yqPL36sC7nQWeo2iPj4oT3Sr5F9tSqZ+MmR
QT7clfVHbqVdfjwFunwqH2HGl/22ZD5C+4W4llU8Pfjbl+QtCvTFDq+fRuD6
hOZivIpLBPS9ZVzCPqOR74qNvrd9fjr+W+bl+G3Jwc3CFnWUjSLhn/TYTF3n
h5ay//tMoV/tVAF3DsVBD7D1cZ/uojnkOHydjJvKenH7xyP4n6/wgwJ4KfpP
m+MG+/qR6SWfwNeNMdzfp+z7W/AWrHj1vbh1+wD2bc+t4py3atHnxYiRG/6q
7HsY0J//ph+ivvzTUC9uLvfzc4wGMakvLhTdx8+x26YVdrP1qI9vvDWYfsZu
GH1pjemZxPuyk+Snn9Gih7JOWr7f1y+Jl2ZOjV1/97LArRkH0cP6WFrWwQ3B
nsmSgzqGU6upP/40lf1/0iLqKpek8p9TvSf4eS+d0S+ywgrT/+loZermpc6b
df4vwcM3Oi4K9eJGnBTie3dmrPCPvx+G7vwF5scJWYMfMeDCRZGnu1Fd4O7Q
6uzneTdQV5h9MXoRGRZiV2c9TZ6yYV7pR8s+BRFjPok45+s/sYtUn+utdpD4
f3PylvPi1qO8N0Q8qklweYHPzi7sJefX19nE/bfYTD53/h/ESfpUF36ik8gS
480SfwrcPt1S7DNavT5iH7VXr6ReqdJE1s223XzHW1eAN0oBb/bu2Rre+9FL
ZoI/sKsK8cLa6M6Zr6NhP9fPR153BnkxLfgyfMWtr+APnoF3p02qIOwQM01/
OQ/yexncCX5vmsx+PMZN/JQWzYp7cWN/dOJEJ+hjHNBvj7WfPgpra+Gvl0ZX
0i3eT+BW2azlvOPdQx9FXtbdlRu+mYzrmqsm488WzUQe5GIe+F1/z4AHUO45
cb/cudAru1oRu7lhYh8fwIqW7H/yqJ1RDal7aTYwzIvr69qJOLzTeY1Pd8J4
8Tu81qFJfbi2ZgT2wbx4vnyK3hZdd2v+2Kpe3E5SD/v2Sj36D/ySkDqpqOPI
T++7KHlZMv+y+JaIx9qv5vpw62QekY9Qcc4Ar0DGOZUOXqBfWN+f4dVM+gW+
U9ah7OfvmhKnWGXi38xmP3eWNVZ1BOLHrpCTOkTFUz9YPZb3femP7/j6iylc
jf//uOyr3nce/SvsX/h+axUGnzJRvDez4FK+98UTw8TvjRIM33VyfZ739A2B
6x1Kw18IjTNM4PuLYT81qSdwO/V1zqlsDTnX5XkX6N8kdXusM/A8nf2h6GPP
TMS6lvH8wPjRacmjX7iGnrfaT3ZMxO8Ly+jDjWUd4N/Lfk9WOuZZ9XtS/WcD
70vayco+Ubiqb7Kfnxbzrztlmf8/Potxqn+cuk/99z8FrvrHfatX4KavSj24
8iMOf6L+pWOvFF7c6DCJ/Ug/ncyL28NGoddwYCI8zHXw8aw/l1C/L3kdgXiF
5HXoPUeHeHFrwm/4UYVv+MY7Hx8Q33YHcd713Mk6cW6SL34eNZP491DqvKz0
aSuoeRD/LuvC1Dyo/GygXkzmZ7U5N8kPDKJvnfPXG9bToyxy3vx9xIx+1PdZ
tRmvLUlMfajs12aGz0S3QfZrC/jXqr+w9K/VfQb4t7Lfn31tHfP0ZwzmrWpj
/DsrCF6MVpf5OYX94y6KEM9hpI3C+Nip8cMvJIP/FT9bK3G9yU25zysH8YP/
7N2S+4/kO0kSTr70YFEx3iizgrrRU9Oxr6U/5ea7Rz60aDXWs6yLMXt8EPl0
900Q31nqeJyPDdMIP8698LPMI0v751pd0VfM2aP57FvNGIv9sHyUb7wb/SV2
9rZV8nyUeY3smwTuZBlDnER9p2vSwv9ogo6BvXsP33XD/uTt/v4BXs8M9Dq0
0NR8v3L/DNQbyv1T6Y4q3PzQHv2Lc7HQvyrJOnS70jfR+OtVAd99no6BP7Hh
bVEvruxGa34RH25kaFHLN/6MrBOX4/WM6+krI3Ww3Sz78O92py3kxa1DneGh
Wb3glQxNJvZza2JTztNI8oa23YHzdMFrztFL08gPXg3HPin9I3GreloV73tx
5qOr/x//SuJSh99tHuQbb9z+UfVHhvfVBPtH7Q9W0Dsxn8bzBdznmhbs58sb
cS5lecH44vBG7IrUN6k+1HqF9uhC1O0N7+jqY3h12dHTsMNXoNek+lYPOSb8
XqPwMMmzCuh+oPtwbTl5H0+eS1ynjlnWO96tvQJ74+6jbOL68WeLOjUrG3UB
3/Zncf622GecOdm9uB5Rjn2mdSj8hxnE842RZ+Ht3n4DnnsOcf7rx+jD/jEF
egBle1Iv03Ab9bbNXlFfsvx76nQ2wMs0vtyP+H9K50fej7FvTnYvru7nv/OF
51X7qv1l3xP4p9HEYep9FPh/546cH3XuXEu7sYzm4RWoesVD2WQdtIzT1vkX
P7FfN1EHYKfeT/xtyWsf7zcwfsmf6Aoti4YOjDGKuNyeuvDKml8Tz2X8Bg/f
XFuhPPMXTv+PHE3Ir/XIJHDnWAz8vsPxuU4n4nfW2674VbnRN9avjsSPWkW+
y46TBLsxfkn28aWpfM9lrNxGXvtco2xfcefUnyI+oO/S6P98XEvvxY3ULXhP
+wvQZ1bxcA4UJ29a7kJeL66fWwHf8nMK4eeZl+FXGxMPURdQrBB6pDuPw8tI
MA6/IOh74qgxY7CvpBhCndSsD9SbKj96B3Xc5iT//myNLIhfPHOYb3/WduRl
HcaS9akx4fVZ0WZgT85Lht9/VPL3OrUnX6B0/OQ61ILJz9lDLsMLv1hJrGe9
ZB147XVzFfCOt8d15Py9OUD4mbpN3xZtvk28ygUP7M9Pn/GdR/Zi/MLozFuc
hsSjC57MJK6b6Rm6ST2Ib5kjI+Evf0gB/6f87wJ3my5h/J6U8IjeDJB4+jre
eTPuD+S9vOhW24vru5LDq9iYzjfeWVmG83J9Afxi5yZ+YtIeYr05kQ+EX6Dy
JsbqfeSDrrnEGVLfgl+R+x5+/oV0wj5xTq0Y5/27MfgNupxqfdaqSXwsfk2Z
r5d23eyP9F8Ycry6F7c3jUfnNqbl44lZwYvZr2XfPfMjOjZu5v/678g/Jc9f
9ukL6lbNixvpGG+8yCvPfZlH6Pn0kagHPLCGfULxSS7mg1f/62Gha678MrcL
+vJ24ZxCX8XI+jfx9qXx6DM96SdxXn3xN7CTUw4S4/Xl+HHaTxb1G536iryX
XvYn6pKrDQPPuEjEPfQc4EpfQr+9ROD2etdft3UsLrzhTo99cSp7rgNu/OzD
jRYLydd+HFrOex1rPH0DzSRDfLh7bN0WwXPuXbKc9zr6vsVXBO8ibQW/fVIi
NbyfBDmKeK+jPw2nL2TbSUV9118YT9ynNS5dMd9zPW8ixuuPB9HnU9onTsqZ
xJc+nQ324YfjiH5eWuKzBb24cWpkkPi9DU+QF5Y/+vbF5Jdlnl9TdQ2yj53T
K7N/fJHvib9/wzMxktvU3SyISVz2NHVP9p4DrHv7MnbZR/gn9swwWY/vr0dW
ffJU37xv78ccldmXl9Ory/sZBw/EevGHuK5Vjb6cyj5R8WrVd9g+X7ycF1d8
HrPXevIk+3KKuLQWOpc+qpeikNfto4E/K0Sc6g79GJ1m2QXu5MtKnLx8MpH3
D8Sj3ufm+eu/zeLFjWMhxHmuH8rrxZ32/YnHDvxLvHfbZN/W2taUeZSU8Mq/
2ef12rkKeHG1n7tlx/vsaif0HDzD95PRg1X+xQn4oO7yfb7xerMz5PufXvTF
Z8xZR9HhWdrcH88JriRwd91vvvFu3tJi3eqvlQ655Lt2bCbsTHdkA1+drPGg
l8A1uZ/Zah+LSr+xrzpd4j7Ufhg7oNMlxrtS59CKwXijbkJ0nOoM4n1nDGW9
JCtPnihqLOqhat5F3+x5SXiG73nP7umZ8GZvpScfp+cUeqd2rzrUc2ZKQr73
6k10U6Vum96gn2+/ckY+Yx0kSenfr345QBx7/VsfjyLgv0zozn1L+8Rc8jvf
W7pyhb3jzVEXuU8ZJwmsc22oyB+7n0KZ/zPka/QHVdFt2D0SPulUcDN4u3hf
TvDYMt77dEqlwI4Z8E3dRBqXesmNBUv58FGbOJ+mfyzhm4dq+9FtWf0xxIdX
dsX6d6rWLOn9vVbLSPqV9PXX7ZobE8C/GBiCv2LSn93q1Yr4zKYSArca0s9d
vxZOHLXDEvTRM9L/XV/WnrxGv3cNvL/X2JYEe2D7Zh+uhY8mbhm0XuDmGOpG
zUoL6N+XbKhvvL1+KdeJrFnXi7vOZeyZUU98uHnyAedmkR3UheSfIPwju09S
wYswJoKblTujozIkpcDdS92x1+KgB+IUnE7dx7Mk0i6VfY2fPhXxNH17m+pe
3I6zhPzys7y+8VbpOPhdS/+GL7qCfV5PX4v9q+pe/zpv3pTz61Ys8sV7FW/8
J1G/7E67S/xG8cwXzpTfUVzi6PvA3Xdl3gu+Yr1TrPcc1Glqb58RDw3dyror
R95ZPxBG/L9HSp8dbpY4ix/aIi/5tWQ1eV975lP/sPYgfeiG8h6dWk/wGzsP
gWd1Q46PWEX8Ofc2yS+Scb9335Gf+O5JiBd3ra7wLwf08OH2uKqcj/u73hLn
n+pb9PYYuifLjr/04ZnSsb/90F/orwfwNgPJ17YaQhx4VBH4dR0Gkh+/nVjY
j1ZrmX9pMZTvVuoAGMnSEV+VOgBWRCf8NQ3cvteePNn9YuhMB6Nvo3hExosH
6Jwll7rBknfk2DvJn87JgM5J04di/9VDa3H+zIlJ36U0GciPNogd4sX1ejfR
WU1ZhfO7egS8tSZR0Mds0oY4xd32xGFGDuacTc86sWI0Je4xDX9K6T84vfaS
P5X6D0ovwsnLelN6EcabYYx/IPtpjk/ks4fsblMEr1LpnVrLG4r4nNb3EfzM
xh/KG57xbqP3vvFO+CpfXbm+oxnxiEl3BW7tlPXjhU6yHzZDx9J+K/tuR6Jj
adWk/teWPDSn8SB01d5rCue8aSbxP37jXFQ6sfvuUs9Z6lEhL669pX+JM9wq
7htfYFHYV9xtgT6i0Y+6eePKbfREEt4V/26WLMs+kSAedtXwBALX29bm3Gsz
kPNY1tcH+Gyqvj4kv8BtyatxUlzGX+oQXts73uj8mf5zu9uwrwfqIHrdEd/P
4X6+/t3WlnrCb3Ee9ffhTkik2Jes6GuxQ/vOEHxLfa6G7ln+v4V/rfhaqt7Z
ub6AeqUBZeBxbYhTXvx/Wcekxqs6JqvQM+JS+++iO1emFXySVJ94rmnwOd3r
tdiXX6L3qEfA/zQzoveo9CGdY/inSh/STFFJ4KpuTjOqcG4u3CZw4/k1xk9o
JfY3xbMN8NZkHNhuiv6J3kjqEuzsCP4Nb1/F8ezXLYnTBPrFS73p+wHeDusw
jLpH6wm4HYXxVlmJn9nl87Ps9mewZ+bm9NV1Gs8L8J3PyuUbb3zaTzyncCyp
k09eWy86O764XptO0v+V9vnYn8V+qupttVel6POo6mH3R4N3VrQE/lSV5qIO
yKoSJPul0hdS1Qdpk07V8d6PtXWG6Mvm6Ld957sdco987ZVF/vHDrhD3fLqa
OoCB9ahnmS7387vws1T9lLZ7G/GWA2VKeHE7+VV4TXIdqjh/oJ7u++6ZxP8b
STzfXZQV+y9DOvQTzu2RdVKOGG9Mwq40f8jL+W7kxH5+uJP3q/pibEcPVy+W
O8yLa/UfUk/4Hv2NQJ3ChEqsw7GlfLjqs2lEfYcO6hqpszFlL+OfzGPfTl9/
GHhW7nN9PfR/UnAe2XV2s27a1/GNt6YuVf6k4oXiH74uhz5MtIB/yr6oePBB
Ul9L+h1fdbQEvnRfQeZZ2oelR/OdRlQo7MWt3wuTB/y1VX4v7p6cz3MlK+Sz
n82FNYR9buet6qtftvpdE36OXttvP7vNCxL/GVGinnc+VZ8Ou5M/nqa3ayns
D321P25mD77+SsQT3nwTZ9OO3BfxojfEw+wjf1O3G5KU9bG+HXGk2HfYf6r3
4vstuZD4WbSp9A0//AE/ovkqdMWUHteJofC8K24v58WtmhPhc1z6rbwPj0tf
Oif8Njw7Vfc0NAk8k+DmPjvW3dxP8BYC/XBV3F72w3W7naf+cR66/fb3janb
f62V8Y43C85AL7rNAN++5CxqQh1E2znlvbidqxJ22JmCPt6IPX0GOhFp/iFv
+LK4yDO6vd5Sz3bnNnH6Df0Fbh38EX2zo/WY/yQpBW42Kc3+Kr+jAO/06Czh
jztPb2FX/F4IO98uQRy2WHfqvH4Dt2p+EvxM3fnJx/8x+gTTj2njlApe3PnL
FHE87fEZHy9Im30NvuK4E7KOT/JAltwiPzs+Qwkffv0yvLX0jX242esQ59C2
nuz3OdDP1DNmgC9duRbvvTd1RHrvTPAYr8i+iHEGg2fbzP3s3Q8Pqgn6SNa2
8WKftVdV9PGgtPl/4381H+d7LuN3dEQtXep5KPzhKcbPyk6eOVLWKZcsjb7N
Kfjv2nXq/d1py+ETj3uBHdrjMvmgdt2Iv+z6nfNU9h93L2Z9KuyWxH/gXyo7
x437QNQh6nt8uNZ9Df1htxD/1k+hC21meynqDfUm47nfJh3Qi64zQOhBmdfw
R7XeP4Iv3vlCjC91gvxS5O+cd79cTyXGyXyuGVPyk2U+V/sdfqLKg1vJ+bvx
I7wFR/KZnUVj4UlenlHAO5/mswXsD+cPF/Hieg/4FVYsu5hv/vVqrIPYqamT
LsQ5rh1fJOzSL+soteMZb49/yn77z1rer8xv2on4u5t2uuHFjR+2lRe/d4XM
byTpgP21NYrA3XcdfOOdUwZx5NLYOZqsd3FTEU/SRhHvVLr0bm4d+3nW7VDv
eOdNBnSTtm9m/wmS89xgIPn65+fkdyr53inoa2+nuGp4cWtfWfLHFYtTF6L6
R7xIBx8s0zmf/W8cy4du+Q9R5briu7D3ozPsNppV0YsbOahv15JP9uHm7ebg
iQf69j33QTvmaX76EC9utSoEXiMb9RmT45BXytSW97PQ9OUvrM/l8A/lvqeP
zI6+hLQfzJMvsCtSJ6JvQret8MrKdPfh5sQj+A/zp6EDqU2jbq7sMuIU4bPT
ifF5SuDfldgMb+RIMngCnUPom3m6DPm1U7/QH1Ot23Gp2F/2TnxZ1oMbnZ6g
i5H1se4db+WtSD3PxNvw8D/IdRIJv91+Qx8/Fec0Ij+X9OKa6v+i7JtuEeh+
Fe9BPnpwL/bbgH0o89RKh1/6OwpXOvxO7cKcG0oPYfZC9qlRKTJ5cSsG/oA7
c8P/sfXVcVls39cjioWBie2IChYqYoECAyK2Yic6omJhdzJiXrs7xo5rJ4ox
inntwtaxr4HdqLzXvfZ5fjN83+cfP6x77jzznDlzzo611y5ixeW+YeA5l29D
8W15XjjiNquKo86zQBzq+De3R14s0yPUk+yqB52lyRswPs18nIvnBkJ/5iSf
X0cro65ydW6uK+f1KQegDvNoIt4/V/iV6sjr2P/PuMCPD8K+rR9sQfuk2igd
4qUXWMdmnrcT3cez9Bi/D/u5vra/RL+n4H7URzYfRPqTppfJ+rBDYdf8HQVd
ymzj4TcJf0r04WV/Ss3uAx6N6PcdB56z1Aw8Z2k3dIGUuTWQt87bn+x29enA
CLpOD0/iIUjhrtDJOZqXcG36v8RrEv1GHX3flr6HXszBj+nwfLhP2T87wIuN
zYznXhW4aeYHnzWqoy1+KO1QoPN19zzyzzXfgg/2YCr2w0VNwEPfgfpBYynq
lERdtjEKdqOoyxZ13Poa1mnnOm41bT6MPwd/xByDfmHaLOi6K5exHtQ1i7EO
2ty2rQd1VEPk50pCb8HhJyb3o/1R31YJ+dtyz3H/GdLD3tq8AnmHUs6IIxV6
CB3wd4twHk3g+5/WCHa51gR5vb2zcP8zg5hHhboAZTZwrdZHoXtMH/l+G+jb
/WdB/JkvJUtG4gepDd5Bx67CF/Cv+KPP2eppHW9U397C+rs0KRi8zZZySyuu
RMIP0lKMN/uvxfnhdtrjz/XkK0MQ53yXA/u/13bEg0X8c1sxjs/+LmnF1YwN
Ebf5Nhz1lSM3IF9ZtSd4ZupQ8GWmbgT/Ktce2t/kNsD135cRt7//GvWqh+4i
7i72H7/r2Keuh9S24kbD1LSv6Z0LgM9ftTz2pUG9kW9tezHUOl6ObYV+mZNX
4XdvGtOdrv8X6pfUjkNQz9R6IuHaePSvUbLNQnz+6HvU64V2Qvz6xwuM72XQ
ePX2Vdh/HUogzz98MngCeh307WrQGfth/GbgSWehI1SyLe17Zv5p6DPuDv6A
HjAEdYUf8oNvU6wU8mguV+m+1F4G+DaNQ1GPFPgE59LpC+AF9Z6M8fsWoA5r
4t+I/0QGon9QA1FHxvanF/TslCF4r831sYQrzWdCh8VEfZm0Grh2ifv6jNgJ
+0f4XxVbwt69Xi/EimtPjsFulEyKU8rfkmk/UwIGu9E+3AvxS+07cDVNclrr
eP0r4qLKvmXZKG+cJ5PQ9aePMaED/S0nHrLpyOrHq4bS350/2XD5VyR0xmJ/
Q2dY6LmZuVBnZd71teOjUA+Zcxl4jktZ/3ZhLOLjSbe5H3p/8APd3YjXoKxh
vdbXUcDPtblG9vapR5hnL67n+lac9gP1dn6sr7Ucb1/akfYj0Q9FG8TxedEP
5dlh+n2O92VneeIvSv7oS6BkbIn3InoGrX/1REMbLrXbCJ3P3jXoOYv1oE3p
CP6A9yQfK24c2gdeYsdjdA4If0QPy4P81/1+Xtbx6pvDqF/bkoB9PfYNdD49
WsF+MJvWtOJGz7WIG+bi6zEuZf4H9Ta+61Fn/Qb9Fs2CPYPpv7caTPa/4foY
v+vbCcKFfm9KnrN2pVCYdd7kVqOwXjeHoe7vRSHUKZwIpPs0pn3Be/YoHcbH
jMN9s06dvPYK8hGsU2eGPoaO09ZBhMtRraBnUuYX/MLmq+CfXthOz0PWQvDc
RD4r8xjcT9iuUlbcvLKJ7t8o7CxbcandZ8IVrxysN8XPpftW9FEoNgn1uznz
Yx16VcV9hr2n+1c04Er72xj/qo2/9TpqyTjeJ3cHWnHZ+zT4Cbv3BFhxrZs3
eN3l6mG/8VqHuoNld7AectaCrsDofagX65ma7l+tk0j7llHyAManXw5+e8Q3
fr84Dpl/ZGq6fuCaWlZcTeNOfGnp90Ebrtx9/PWPH22uqQI/kT/G8PHkb6rX
Uuex4urvljgHW4/IYMXl5MyIg+32wDnC8Rb1COIq+nvkxx3ncrow1LUVqG+L
V+s/Ed8zM87wsc3bESes85rgCzniABe/It998aafFdeXVEU8s9NMnHfec5GX
rDARdc7phyB+m+s1zvEnK6Hr5dYFdndJ4FppX+SNGpVlPRPEl4ROoJL5AuyZ
B/i9RpIL9oGkH+g3eY3t80dzED9y8YKdJvhONSfDH980zFY/pScfAX6ynp91
vDlzHHjSxVMhf34MdpT8owPiF4GDSN/RfLECduz7IPhfl6LJjlIeboVd92UI
dF3GL/5F8f7rx1Gn8AJ8/T91uH/GO+p2I5DHMG73yv8HN/3HoX701RjYX422
QSe7Feu7DAsAP6ED6pKk4Cq4z2ejUKffg/t2bZqLOGqqN+gv7PEZfm24L3Dm
mehHUC8p1okRjXkw5oMX4bDfBkLPXM42zIYb23memUfnsHs9aiCOvfw381I4
vrfxJvRi5i2y4VLXUlhXjvog+IkOna5pBRF343oHJdt06D+cR19vgUvRPeBH
ZMoGPtuA8ojzjV+B5/JhJnSnRnsBz1kkmO5LLk9xR+3RWPBnSzxH3CahIPGH
U/IzjcD76YCDnynt/0XxK+Xk7WbW36X+XEj9LkW9mMN/53oxgetFzgy04vLZ
s02s4/Xaqyj+JnR+jE0FkE9nnR/t6xDgbUKRf6/W16b/Iw9gnPV/1JXPwHcW
++qgUtjvMh2rYcW1F6hjVJ+jHkrgyrTnqLtIna6mFTdbDYFOB/OFHH4o84VE
nxftBvqwiz4voi+Mo5+76Avzm3XttiJ/pMw+S/xRM2MmjhtzvcnbGaSXKIl+
TDufw15Nbozz4lcLer4izi+fGYT84+gl5ay4+W4g9EmDLttwNTIB+Xs9C/p3
CB3p0cWgL9q6dGkrrrzPAZ2BVzPhD5VDflav2hE63Y2Ogu9d4V+8v9e5v17b
Y4gf8vsreETGk3r0PeqkBeDtxNSE/8P92fWYRYSL/uyijuB/6hoeduB4Pvtr
mXeTDpP2LQ7+mlQH67DyOZzr3fLY/FklYAPxcLSmIytbcdknDHwBL3GO8L6R
H7wdXTpti7uaBR7D/ijTtKIVly44wb/zGV3BiqtnpiOe5vqoshVXQqCPpF+F
/eZ4X651R732o3GIQ1adTvMjF0T/HaHXIeZH6HUY017gHEueSuONntDrEHnt
lPVNSnH075B2sJ/S6R7qEDjfrUxhnPPdctw+xN9eQW/KSHiAfm+vB6O+pxx4
QcbdeagTn3MRdlwS9KakXsMo7mY2qEt2o74TfdP0QbHoV/HqG+GGM3Cz1FDw
Bnt0IdyhxzuzD/V71d4WtMVb1Du1wYd5B31mx/M9WwN1Uksm2PrHydnLIZ+3
Lb1tvNCjdujec/9NoSsi9EkELuouhX8k4kjCP5Ke/XDDfSL+LBe8BZ2u5mco
vmTtI0zzdTZjeut4KcQJ/JNN8U1s918xmHjaeqnOtvdC9j9Hus1m4G5bHkGu
8steFyb8TVFHJvAxOwZacVG/5tB5YD1zI/ge8eyMhe9hR01eC3svIBh8MbGv
JnVHHD7ftlArrr/1BO/qG3QGHPmaOYtoHkU/PiOsDHTPuB+foWA+1Fh3wuWs
Lqhr5XkVuH7wB86p3dF4DldZt2T8RtSFsZ6VmWYz4ULPSurDPCLuC2C0HIX+
FMUd/QWgb9gGuOUD/+O/FU7/ejuhHoLjP1rheHrf5LGrqe7JUT9beCD0PZx6
0XMTuBTahfxGJcLVg37XcvAs5forKA9ljIgh/0499Al1UMvLoe7iYUkaLx0D
blZs8oR4Gh0/gBdZtBriSDeLIB+d3xV98LbnBt+D89fGiAPQK9qSD3muPEtR
7zDbwZOHnlaxK7CLPE1R/404dGPwAbRBD/2t45V3wHX3LtCf5D7XUoNr4Hv7
+lS24nrLHrjPoWsCrbhcIi3sndLraZ60TsOglxJzn84zfa8T+iimX4Q4ks87
9A8z4uh8lMuOxvhtJnQpuy8Hj+5pCPS6e6FuRPD8RT5F8PzVBuDjKaE1kU95
kA/4huK1rPepHWqLOGWGf8AD4j5T5r/vUf82WEf+lnE1vADVjRiDR6PfI+cT
1TxNoMN8Mxr8drGfHASPXBrMfRbEvtFxZDD9f8Vr4/zKsYH4+fqO3JS/kZtA
j057PRZ8/lUXoIsVHsD6VHZemdnNQH1uAufNZ0dgP2V9rZS8NeVNM+IBqlf6
0++Sv9TC+3l8O/XJlAvz73W/hjjYz7K0n0nDe0NX8LgMHbx19ZAv5Holbc0G
5JEH/w37SvDqYx5Bf2nPrGArrvW8hDjq/pH28Rfbwy8pnw/8hdtjEacNuAGe
5NhW4O17v8B7uusY/JCS5xAP6If+FGaTX8D7Fyd72PC4iPX8cBrmp3QN2p/V
ai9wXnR7Db7r3hfI021nfMsHrGf+mP4jHH3kDQtu7S9P98114o56Sa4T1/sm
wr4WceAsaxBnkNr7W3E55xGcZxvmBlhxpWhGnPdXukIv5CTXMf3KjT5Z2Xfh
3M9/G/vbi8rQqaywp671OlrgU4yvs4X2OfPVccRVBgxCfFDeiTz4plOIC7me
Qb1VGOuLhIPvanQ+QHaI4Mc5eEfJ6AsinShclecJ+eJ66Osn356NeIX/U+St
/FjfgHmqZsgs6LQwT9Uo9pj8WeXibOia7j2E8aeGob5Y7Nvj2+KcWg8+iwPf
XwDx0InNq1pxacIZ2FsXztP1HPylVfeIX6Rdu89+Adeb5D+KuE0p7gckeDVv
nr0nf2FAGpwzV0uA18R8vJR+qNCpEP1HHOuE+4/oPR5gvpiHIK+YzHpldeCn
+jvhfPweS/a2soj1ZBg305lk36i37/hbcbXzfeiqsh6F4H8KPQrhBzl4pMIP
Yr9JjS9HeQThNykVZoOn1AD6AOalCujf5qjf59/r4G2+wXyX9kR8MinMrssU
fR/rVtg5rs9Zp/Ek7n8DxivXL9vzKd++Quci2x5b/kUq9ZjuU00Ya8ONB2lQ
l7vnFvzNzcxTjdiH8/T0FNgdFRAPUQ59wT7QrCyuM/YJ7NJFJVCPM7IF8UTl
yt0iCHdbAb2F8FjERR5kIlzZPak1fe+vucgHNMwWgfmpT7j4WPnYVlzpW3+A
Fdf2l6b4nr5KYX85GXn/M2y/fCwIe965dDD9f8wzdPTLYJ6hGl4G+4BUCHZ+
GR08/FIPkTd8Cj15obtoRCEv6YiPtUNeUoq6XdGKK72Rx9TLbUZdw8tj4MmH
boJO7KBPqE+JH4z4baEq0JPKE0m4NnIo7N47l5B/v7IR/M1HHMd7twL9Lkrb
eR1S7UTSM1eOF4B+IZ+P0uU2eyhfM++Tbf2ohe/BvuS+UQ6/TPCoOf6j7G0O
/4vjP6IvlYO/ynp9pssrex6nzCvEzb91FHkf9O+QFMzPt/c1rbheCbqs6hjU
hagHO1MfEHn7OrKb9VqXkfdpj/6eykN32NPvTkLH7iz4gerjjYQbX+Pgx4v9
kP1x+UlPG67cXlgazyHShpvn0ddBPVHPzzrP6lHE96TpVapacXnqLMT9qiy0
4doSxP0k1hNSB79Gn6wGPsIeZX2/94iHOEfQ71SepYV+Kut5ij4R2p7xDa24
cmwY7OSXcwjXT94jXI1y5jpPJ9JhcvhZq/rBz5n1RPBSyE/W0sq0X6mf8Vz0
ZK5rqMrnHONKMvSoBa40h66bI97V74iDL2XFhT6GNKZ5ZStuzusZah1vfMxi
09OQvkuIA3CcQTk/gvITapbM4MnPQT9lOasb5SHkkQ+rW8erTcqhDo3jFQ6/
eLCM5x16B+/1kivo/55zLXRXWXdUjNevrWQ/ujb8R45rSfXGYF4K5bbh2tpM
2K8KzmQeo53/qcVWRF6mxyK818vnU7zOGMS6YzxeiviK+uglJ1iv7DPs2K3r
kd+tAH6ZwI271+EXMd9P4ILvp3oXobiWdkaivg+S2Rz3H6Gg382HPcizT+sA
u2qeH+JYHdd2x/NbK95nrGe3NVjPk1JjPfC6FbxusW7/R4cqRV8JgafsK6FF
gQ/v6CuRrkNZXB92u/wTOn1m/tc+Vlwr2jKY/v2ZYKt7Um/OR117ofN+VlwZ
Fw8+WcPGHvS7GzzEuRzugrzSJSfse4uBG4sfAy84BPwBYcf2u4h6B7aHHTo8
bA8bhesQb0ctD70do0mkTU9JjBd6Sua+x/gdWwuQLqLSJBp1u5UzcfwB+Va5
Beqita8ZiE9iOMcgD+u/G+cEx5NT6tkqDZsTLvRdtXmPiZebss+4iDupK+fX
sf1ez9Tk7+vPoXsqdBHNeatwjr9dZ8ON4KfYX74Xt+koGut2gL/BfV2Fzryj
r2unw+A1LNmBOrU+b5H/fveF+MVG5CPUqVWtBTu40n3uu4G8tvL4JeuK36Rz
zbEvfUHdvXI+ztM6Xv5UVexj9NFr+dL+YJw7h/dwSxw9X7n2OMLl3h+hR5c1
kuKCSsYK6BdzIhk48/ocul7M69PixqK+Y9ZdPPetX/Be+65HXJPz5kqBnmzn
NKP50fZ0h/7228JkRykRrsjXSLmhA8O8Mun3XIrPyH75WPcPdpeeXJ7OTePc
aejBesvQN37HujGeWxGvGFUC+dkZPjhn126BrsvM1LAns/zE+Pg32LeHTgHP
P7wt7cPaeORlpAl58f6IPlYX5xNPXlFS+9vwvYMi/vxrPgoIsuJmztU0XtcO
g8c25Bzmg+18oUOiZb7IPJyHOAe5D6xRzzPEOl7ok5ilfLmP2CKyP831LaDv
wPqZ8tkY8EtZP1NrXiYYz+UV4fqSNLRutJ93KX9ltvkIPyvkH/BIdm12p7/z
f8F9dp+BPNHYjIQ7/FOn2dChK4x5FvuSfigV981cA15HZEms/w57sQ+u5L7b
oq6zYFWKK2mN2tN7odT0w7l2KhPZ50brPXhfmt0HT2ZyOtjt3vugc9bPJFzZ
1gr5jggV/E+RV2L9QBEXUu8iDyXiQubkgtCRug7czDodeffSheHf3/6Beeuy
AXnEsFeIu5x7Cn+z02H0lQwKw/73Cjpyip4G9ufsl7SO5OT34PfOA49LbdGA
7lOfiDpQY5I7zpeLJ8B7mQPcbHQP+vlrAlknDbwatQj42frZGbC/qmB/VmJ6
oB9JzZOVrePNDLHIPzU5hfpmsc/MR/2XcgTzYKzg/IU+DX7HP9CxVDnfoV5s
h3ji/nZ4j9xGsW7/J8S3t9XA9x4Jgg6/XDuY8ANDwUMsVQ+6DfG7MM8XpyGe
ubUr+G/SSdTzzLjma8W1CxLiKme9qtnGuyRhH557EvrM0algD6SPgp0wIjWt
Oy1nQ4wfsAh2z9QNtP+I6xhPUV8vTShZwjpeWpye/BP1APxfh3/6G/6v1O+n
LS4knUH/UHNFX/gTiaUi6H7PXQL/c+sw2AlOhwk3lszB98bfhR1erijh+s7t
4D8szB5P/tDdYFxn7TDwb+fsIV6BfAt+q358ks0/1ZIy4vrnlmK/LQsdNW3k
XMKVJZ/hd6QLh95j4waEa/vOkZ1puNRF3egl+GXKs9pU5yh1rm6vQ19dCeMy
zwy04matbuDbb6yA86dCJMZ3Bw9f8orxt443fgZgPjvjnJHX78G+ZPbCvjmn
Kt6PiYcwfr6GfbPqc8LlPM54L+LBbxM6Fdp02GNCp0LJfYt5g8wfu/wdcRjW
r5BHY7zQr9CnGvBDO73EfnjIDXEErmdRozmeyfUshm9T7kO0AXipnLBf76B/
iui7rYZFQz9lHPiQjv7deWeS/aonq+BDDQZuLF4NXaAlHC+PVJC3bYV1qfSo
wfk4ztdffo84Qmx4mBVX+7zDvlwtzDZev3YGcfMlWVGf6HoA9uT3log/7wuG
3/FwIp7jIfBapYPOqDOImonfW7sF6gIae8Kv37YU8e1FHshzpTqFdT12CfzQ
cttx3h1ag3Ob61+0gq7kB6nxTbkPEesNfrgO3Y1bz9Lbxv/6Dr4d14OL/hQi
ri7qo+VfmVnHD7/fUFCHK2/9in5znPeULhyF3Sj60P0Oha4J1/kKXF/UmPVR
Huai+1mzC31h5t/CefqgAvAtD1H/+x59hVRP04PwYdeRV6rfAvqQiZvAWxH7
SQf02zCi+gXTdU+UgT22yQSfuWhPnDPv3TH+wRucawfHwp5kO03e/gX7PNur
Drtd1JU/aYP7kv/B+dVwFt2fOaC5jRenF3lDuF5mtR0P/kq6H2q9EjZenPko
N+zwOtOgxyX2jdiXeWkem0Y1suJS2/EF6fpf3thwvfBJ5O0OXkNfR2HPbyyN
+whIb/NrtFbbwdcdcAN1h8PScl3JO/APVwy3X+fO+1C6fs/hNfC9zF8N74Lz
xjssxIorxW9D12DBoybW65iDquamf/fMtfM/EzcRP1AputiGa211+FEXwb92
zMPdfbg/b0/oz8yLwjy8v0K4nPUOxu/GvipPaELzoxc9Y9Pllvs9caL/j+tE
xHMXfbKUvbsQr6jEur7NR6IuIrgB4tihwOXXyHupkb1h/0ybi/jGliD6Pcbp
vbg+xzG0RzXwO9vUg70zAePNXanAY7jQ2MY7Va+ehZ3W7Ay/jziX9cGt0O92
R+8GVlwp2p/2T3mAp3183EmKm8i32iNeFN8bdnjv2XhOXosQx+uAelj9r+O4
n95XYL+JfdJ3IH5nrtV2/OAa2P9X1wZZcWnCd/hNK2pg/T97hzjtPOjgmBN9
mbcJvpDZJyvy6FPKBNjwCwPoXFa2XbPlR6QfreD3/dWR7EaHH+GZGfHu8T8q
WsfLFVDPqcYPQB+oc2zXRc0Npuvxx7HOJeh5qi8V8hMd+8/q+FrW8Q6cx0vv
1vH9cP6r7mfET1jXV+QpRN5E+wD9c2mOF55jh9Y4b9jOlM+gb5GwMyVR9yjm
mft8iX5hjvOO+4XJ1+MqWXGjSnkRt0W+RsTrRL+wzrcq2X5v9xnguVaN97bi
RlHwjfQCkytaceXtCPBfeV8VuhbCX5bDV0On4QH6WhpfRwBn3rijP6lPDOrm
OL4tcFE3p91aBrv0BvrfydszYrzbWNY9Y77WuEPgs94dY8OlGjuRH5mwmXXk
OC+mJkO3oO80Gy57Lkbda66sZa24NCcL4oxuKnQkPjqjPqVzW5p/S/ycdTxU
2G0cP0/ZN9Ay3tU6Xm38jPKMjvW/olUy8Tye/FXAiqt1TrvTfZSYT/XNDnuy
30ziwWpSBej5iXNkoxP6HAV/LmXF1V3pLtD1f56oZMXNctWQj+c+jNqrudBH
StGH0ZgEPGUfRjUvnpfgYUqL86AupXt32n/krW6wz08Ppd8h7ehGuLGyOfDe
J8E7TQc7UDo8E3HaNo6+iui3KOp8WX9CSoX5NH6jrlM6vhDrv2cb/N7fu+Dv
/doF3vXxithPykYTb1JZFYj96nBrts+7Ih4SlR11TstDw/F7s8HvHngU/Zf0
SaQbZq4NhP8+ZBHyaFuKhOM6feC/bw2F/xvnQzwKZXYS6q1KoR5EaZ0d/Ipw
BXUlb8ADMU67EC7Llei6emxG8MAf1oW/H+kGvk7sLvAXhH9XoQDOg+FZFCtu
7iqJ+awK3WIHPqsY7IAMAygPrldbSPOorlhA55q5J4TsT9F3Q/NaC33SmgF5
rLj6mscndS8GnO2EzpewTy5cVs6Kqw3Oom7dJx5xx9Ev4BccWcK89sehNA/l
f2E9HMhH+5E81pVwc14w/O60Y6CPtH+Azd6QFh7C/PbNYutjrqx5AL/g4Fqb
HqPqu5vOD3POCtyPsCs2foSf7pKjhhVXlimwk8b8xvd3moD+Ke/A69O3fAP/
aT/rD2ceSHUa+o800GWIwnhjUx/Cjd/9Ud/mynyeOb8Q/6oo6oC4Pj3DQfhv
QsdS5EGEjmXFwoj/rOa+AxsyIb4z3xW83+XANe9a8Mf6XcP3MN9e3ziYdbRW
gN/7qBLhxqveqBN3xnw47L24IfCn1jW24YpWBfEmpzjEJ/j8lfVhyAeE9OJ+
sqgLUyLSoF5oRH3Ee5agLsx4+Iueq3p2r228sLvksbFY1/1Y9zs4K/BXH0Lp
+1P216uzld8X6K7LaxPBy1zI+9xK9COTxkyDP/i4OHh5jZ2wnl8cwnMf8RH9
rNqzP37iDdbHKhf4gyn6DmurysPuYF0gZdca4ulJI8bWto6Xc5R8jHws16XX
KI58kMi7/U7G/sx+mSr6X/xcTPaV3Hgy/LhPxxEXWDbfzzr+v42O46ricxPr
kOPn5nJf4lGaVTkOGZIPOh29Zzey/n9asa+oX2Z+hYOnkbI/wj3wNFL2R1Bm
l+7G1wcf5v90sXA+/3c+Kna8gBVXDrXBevfieGCpF9AzOVzC7tecAB9OqXIU
cesxXYFf9QL+Erxa9W5pxBmm50Jf1fxb+Dmjr6tcNz/qzI/cRf7kIPd7dQ9H
//gAg84v1bkUeBt1p6G+hT/qmkTyw7UhCeQnq7unJ1MdVZrj6B/mHk+8Pt0v
FeKNE2Q6R8w0S5HfLO2G/k4fdrSl7z0wn3A5EH0K9OTdhOtzi8PeXn/S5rdK
53eSnSDfemPD5dZlUf8zZrXNn5Xet8+O6yUi37jnFPzln41JH0yaWg7ra052
sov0oHSIc052w/70YRbqf69Aj9j0cUNfhW+IW6oHj4KX0yeI/BU9FfppKqU+
0nmutyvE/ibsf6l2B9JfUhfH23ChR61nXYW6UtF/89w58Dbr1YSfseYx4VKJ
j/Cnklzw/mZcDP8udSv4mUf+wj69pS2uH3QdunnnsmGfzhQI/NA2xHMGdm2G
eWN/ZGtu8Pq66ViPoj5oWTlab2pbbzyvbK/BJ/HeR/aBvHYZ52cSwWf7WQX1
6bFeqPNINoFveI33/0IY9z81wGPJjji8fK8Mzv+n6AtmPBiGeX54BXYy94WR
HmcAv+LJDsRVes8mXK7VjuoX1BaVgul7jkLvUVo3C/odz9/afq80A3UN2p49
HoRfv4N+Q6da0box/jlKfDl9dQL44VmPIZ8i+qWyLpzWNSfiZZtn4Pw82Bvx
pXy5obPdrA7iuK59EV/y3Y948vDsNn6I6vac7l9zao/+xSKv9PkVxRu1Oelt
uPS5LupMKh1qbsNZV1zr9Au6LwHQMZZaTyI9c6Pa8lD63r63CVdcKpIOhrLl
O+Jba+9gfM/rNF4NceL6XPDPtcgM4KV7xCNfOqMR+Ma/f0I/ce05OveNnu2R
71t/E/e/di59r9B90ip/RF13gmnnyfTKDr3QsNQtrb9LO38cfuaZO7Z5MCcb
4Pm8GW2fN1/ogWgumXhf5bgK8/HMqTry5/WwD+vtIxKJN7RxMXAFuFopKBX9
/XBlqO0+nydCX3f83yFWXM+BejYt/zT7+LX5kSfbcM0WRzL3sK6aPB71+lO5
7+3m6eDh9KpqG29kS8J45xE2XKl+CLpJN3bi+4Wd4xyKPgG9AtAHZmd/zM+8
irDbGHfsA4wrfR/Z4oFy4iHoFJw5a8en1kV+Pc0q8PRY39WIeC76TdNH5BP/
MwgQf85yAvtnHOcd6tYCv6hTQfbTEW/Rtg6GndazewErbh4uC95Po8RiVtxw
9UQ+LOwhxe3k8dChUHvOhn2TKZxwR9+9edC3UY++TW8dry1GX5L/n842zSP3
LzMKHUc8mvuXqTtf0ng1hPul3roHHnyTBMSjhkK/2sw3FPrw06+hb29F6Feb
BuxYpcxSxPcMN+wn//aEXiL3+TLetIZea4o+X2KfdPQ7WwAdMz0C/XOU6v7I
v3KeWqswAnUtIk+9+jLifOkm4/y4/x77P9fdSyHDoXvDdfdK54UUDzYPlyA+
iVF1F+GiHl+aNJLGO+rxue7JwUPjuid95h3Yy824P3W542R/GunmoX7qJXho
ZqkQZ/q39gXaz7VW6Aetd8yVRPGFUvds+7zpV+oD8ZAPt7Wfd6Ku89Ik+/u4
8RXFE3S/WeCDfQiGvTQuG/x3jtM6eEccp01Zj2ZsKgC/d/dNPIdBy4WfDrt9
Zj7o3xTScT8TB+N8fRSO8+Gzgfe6UAvwUI9UD6X7uZWMOOfPm7C3blcDLvhy
Pe7C3to+HHG1SNh7xsp5ZK+q2e9g3oQdPrUc6ho+zoedMHg08iad45CXGVAS
592cebDDi2pYnwWW1LTOm7poO+ph3TPXsuLa8+XgRY/9Qvfp2J+zdiNc9Yst
YL0fKfaxO13vcfrcVlwp0wxxhsU3Stjuf8BjxDVY38kYiLy80HfS2wVARyvF
ejP7vA224qJ/ujQ8AXbyG+Z7rOychv7Nu8pWR6AurRZM/7a9bMP1XdvBHzMW
KVbcGBSDOvr3TeFvdnyGdc79MtTP32l+9IyPgHN/DW39jJq2eeP+yMatdYgb
XfDGuhqZl/I1qvMErrvn5xLjhzjT4VfIc+0YDDzHANiBXA9lvpjWm+6b66GU
038jbxCeC/N2ZT3OF6630o5lBc71VlJwCj4M64iaLey8GqFHqmtbbbha8uwn
ek+/Z7XFydVRAdBr6v3IFleX09QB/9aI87HiRm8ZvEz3e5WsuPQD/GpjxDnU
1++CTqmxsCp41H9tx/m2OBN0JJ4PxXnxn59LuFg/7OcqF3PXss6DcWIW7Vd/
/GjreOFH68N8bHaa3PEdeJuBJ2z7kvogCnzY/tmu0vwJ3VSXvqQzbPptumDF
5dHn6PwzgvF7RZ5UO4Hfq6QuYcP1ipHI13z+5mPF5cboq2J2zIZ5E+9XuZOo
F35ah+t5ue9hTFfwOF/usOsASxLZpWZYRRuuud6h8YpT84ZW3DiZGv28Gl2r
Z8Xlf8YAnxFvx39dJjtDK3DN23o/8oY0iP8Hb/O2jjefZ8R9H3vnZRvfYxrG
F2kIP/XrC+SDoi7S+yvsfAfPX9j5aYbZcKGPIXg7gpeSkrdjrkXeRPB2tMYZ
OA/C9en7H5Augbp9SUUrrlV2hY5EhoVVrc9L6D8oa2ZUtj1H1nnQi5S1jRe6
EKp8lO+Tn+/5XqizbFIW6znLghj6XtYF1RNGwh/6yDjriErv5sNf+DWAcKVo
dXqvjcevmc/J+a9E1C+r8W1rW3GzFtcpN5fqWnF55lXwXSfFox+aeC8mhMDO
SgAvQ/Q9Nw4wb2PyoUpW/D/7EOfTxek2+1xWVmP/dO1g21elH+groI4pFmob
vySRcKmX3a83TPADlQDFhpulyuA6X/s2ts3DEeYH+tVFvsm/N+LkSVNoX1NX
HyW7XZ/RE/WM/+ZBHHicry0+oHfeh7zsi5Y8n3zuGAbyjK0MG65NSEBctEka
8GJFnea+u/CnavnbcPlHPsSF295rYcXVxzehQ5m+IuJOqdBXxSjbHXGgs3gO
+mbYsUL33lgzCvVfQn/1fBvoLV++6m/DEwbieVfbbtNZlQfcAB+g10jk2Q4c
h05M3/bUH0H/2wv5qGvxOA+7ucOvTNF3W6kyjMYbnTOS/SaPfY33fQb48H94
9YSL95159epQHs+44M/rDXdj35jhj/exQz70u8maEfic1eC5dT2Nvm7/JGDf
8FhPuOy2FzqlSzHezN8NfPjlncFb6vzA5pcp310T6P06MNfuDzZ3I/vEiJ4K
HoJYbwsDnQj3aYV4/ofp+N57U1F3n84P9SgbkvC9b+bguT5MxP5zaiHhZovd
oTQ+knUOOd4r6p60O2FYL+PR10BZOwf+Q4rxynr0n1I/jLHp3+pO0C81Z3B/
sGTUP2qfWQd1m10vV24NfXa9zFl+v9i+Gj8TPJAD1UVfPPoYE7pSPEKvMd3d
Om/qndnEMzfHFMX5mGYn4hiz9pIuihF7j94/sz9wTc9Fz10e7VzXen1zE/Sv
lXFH61lxY88i2BtPbtr7c4o6prhC2PcMLYr+7r4LdiDzl4zOfQlXfOLt+LkC
vaz4nzpuwrk+QtRxS/2qIq90CjqixuQ5iCdk+YR8wmHgkpYR12n5IAzzWgzx
5AeDMI9fUadi7sqAeGm199AJvbSC9iW15EXEw99dhX5N+oqoCz6Hfovy3L6Y
F1GH3hm8MlGHLvi9ZkPoIQh+r+AJC95+Sp6w0E8QPGHZeybsqH/zYD1M6U1x
P2Ua4n5y7YyIt1duAruofWWKF8mtUAdtdJ3P+pop+wVgvRq/sR6N38noezTb
sS7F+PLW8Za8OepTOf5vHkyy4fqKnMjrbL9S24or75NQt5P9vu1916LLkR+u
RU207Q9q5ziKM+jZBqGP3MMD4PMsxb4nBw0LsuKyn1N9/tuGmx5j0E/qrif2
3dfpKW9rFL6F9TwqHP6dyOdGn8c+0uFUqBXXXszHPvLcz4YrdbJjvEdW/I5f
i8BH8nqIffZRJsSpeL91+GXVyuOcHZ+HcPX1cYrnmzdfYF7ZHtaLNiH9Ee3A
q2D6dyRwJe151J+VK2arqzJGPkEftNf9oZ/B+gbqjqyIU7HOksCFzpLa0rem
FZfCG0DnvLcP+Bh541Dnt8UP537yVPSRObAQdooOP07/Xgn4F5xr8voI2BvZ
D9ryQcrNvrSPad1uIS/KfHJ5+W/w7N1H2PpVmd8PE9/PWNbHxgfWlgZTHFJt
GxRkxfXuoxFHK5cffMZCqaAPPzme7kd5kxxoxfUSFYDz/uPokyJ1caL7ulOQ
nyPsT8n7GNWD6wF9GltxxeW+M93Pwb42XH++hvxHZfZY7PNsrxrtt6X587fQ
sXHk71ifSp9yB+t/L9vbmgmc+brafuCCryuJepA53SPovtOEol76dX1ap7rf
EYprmct/giezphrqa75+J1xy+YV5/Osy9JN6ZSdcz7gO+Y9Zx239a+QPKuwa
xvUiv2y44bmtjPW5GPmuI/4+cngRKy6Pvof6o4KfC9nwbH9DL/Hye+SXhb1a
cDyeV9lTyKPx+2i8bUz7uXTwBOz5/a9pHpS/X0OP9Oc77EsV7hKufYggnQvz
GvIYjn3gEvdNn/ewlhVXnh4gv0tf1NGG6x1jsQ+Uuoo86Wcn1HcMrU/vj958
COy6PueQvx5QCfyHEHfEUUcCVx/vQR9NnxjUYYg4P/crNzvdgz6w7zr06wve
jv1E1AelHtGc/8ZnwROc11WaEq5OHUX5RK1nDcqLOvymtQngtwUUdLbiZvr1
6HM2v1QRK24sOgK+TsZ0ZG/LBfcg/6WA32WG9FWs47XZqVEXv3dnkO36yl2c
49dHY30Jf//6AfAYtw4KtI6X93WBPsB/643wyjWA83pz4GI845LPYpt+l7Ye
OktymYyIi4t65H3ofy30Bxz7DOsPmLsWeVtxNeI7/KPg5VWsuOHfKsx6Hb13
P9t15J3hwfTf146CXV3oC/L7R1EvLo90g30b1Re8u4K9abzqmwf53NAnGM/X
d9StiOt3Ooz64leTYM8sdMY8PF0JPPtU+PW5s9v0FiTXoO7W60i8rrSOuSPo
+1fuxTjR173sVsINzyPAb70Cv7T6DVpvyvEzza24uuxXUyuuXb2A3+vcm8br
N58jbtsP8U99J/MPq7f58Wf/FDoVgq/o0Kl4/JxwZe5LjHcfS/UqehOV+0um
4CFPHgq+lPsd+JtZx6PuvsUQ5Ff4PdX7VwK/99Q9nD98Xhg7shA/Qk8og/5H
RRFnlkL80I/yXlH0rRDrfIwP7BnXW9DvHzYG6/xwNPJT512gA5OzP/HZ9JY7
Q//8Ldc/yfXL/QhX1FyI34Wuxjm4jXXk3L4g3nGjOXSVmj8ED6pOZuj4BT1G
veTvO8C/RiEfORz9iRznWnX0X9H3lgqx4lrR2Xhf4jxtuDQKcQBtuTP2Z7E/
5GiA8bc82A9lHvWNbIi3t64MvobgyxleeL8qHvG1jjemFkKcNqoKdHS/jiA/
wnjUF/E0t9qoX5/tTn6EsQhxSHn5XuQfa/fH+IgZ8IsDb9H5q9bTaJ0b7Y7j
HNmWHnbpspl474oXBP7tGI1XFPYrp6OPrTlVx3UqBuN98dmN+LPbXsRvmG8s
98v6k+LAPV7bznfHum08FHbRaZzjelJ4Tvp7Sx3oDXBfbPmv5dDrK/d3ZSuu
DNkCffEZsytace2njr5IX5bY4rSKXBQ6DOveN7PiQp9WHdrenn8fzrqsbqPp
/RT9C0SfGr3UWLy33O9A+vQd+IcV/D5z/zWNdWcbfUFcVtirWaKw7p/NqGrF
lZb1kFdaElLZistX3kLnLvoh8rGlF0TSdfdJ4PO46rAnj/rTPKuHq9P7qEVx
/ja6Ouyr3StyYJ4v2/n8qdPR+Wsc2V3Hikvmeeh7zutR24prQRrV+1n8I/Kb
JO4naMFLWXGhFyHGC70Is44TngPXEzn0AZifJnChayHVGgTemksQ4lqsayGf
2VLLdp9RxWAnmOPtv+vKYYobaD2K2XD1TS16j8yjw2394PSGGtnbmv8BXysu
5xmEuviBJWy4mf8unZd6Qk+qV1M931E+S4k9G0x/j/9A9po+Owh5wOALhMsV
zrrT/38fdax6/2GEaxUS4E8IPcl5iHPqIw/gvRS89LU38Ld/n8ZWXOxjZsxB
23j1X+77w/wBvXgA9gHmD5gdToInUD0D7KXY36g75vFSPbce1vHySugJizpf
NSPHATqc5PXcGXZjqliOq4ejXnlGIK1PrSnig8q/rYE/XkzrXD0IXIo/Dp5C
hiWEy+3SIf/H+4nZ7iD9bsd+IvQwU+T9Rd8Wx37OfVu0Hj+rWXHzL/TpU+v8
8rXixuUCNF7u+Bh1nSK/eXc59DRrvsG69SlKeSo5ySCem9YnDnbpxudkD0iR
FUhfwkzqDn5B2argp7VAfYe8vQLq9Hl9yoNWw56cWLy8Fdc3sX/37E1ZG958
iE23Ta91C/5Oin64aosZNJ8p++HKebZEWsfro1BH67h+1uF4ryekr2nFjZdN
YUeO3mXDlYeLkR93j6ltu06NONSdLUa+zoFXzkb7mHw43j5+Tnvidf3n58De
9tiKvntB1xDPuv0KfnTLUdATEPbYpZIcx36M96J8AcpDSQsGIm7ggTpKofsq
CXuP9SiUbZvF/gV/8wrOB3VMu9pWXD0+hnBzFvQ4lIdXsH4F34D5b9rWytif
F9ZA3r+NRvEu4Rc7xrNfnLIuUo18Rvl16V1artvi/NHoDNBpPJq1gXW85tIZ
PM+zdj06ZZXQ/WG9H9avE3pAen3nytbx0lPs46ZHWuieifqyOugvYxZrj7zQ
j3LYPyt/I39T9AV28I05jy8HJtTD/XNdwMEcdK5L2Zfa6tG0flOgK9Rqnw03
K0/m8+sc6hNd8B4Z5+7gfphX4+jzyzoq8oQS7nR/7YJxPi4d66gbso4XdUNG
aGboh66eBn5UnZ/kHxrOFbAvCj9rKepf9KKt7TzM956XKO8WgjoLhz5zpc+k
t6nv3Odtu0+hozVqAMUrzaXgLcsNsgbT/9d/GuJ5A4Eb4zsgHrHoGudPOZ4w
6xzymxkf2ep0jGU9BL/Z14oLvrfgqRo9qyG/KXiqsyfAP+g0HPb5OPB+9YXQ
QzPeDCJcmrQG/FfWU1KvziS7XegpKVVmwf+9VIj4mXLEYvTNPLEFeh5FaxGu
+I2nuIQ8YB/q/3b0wfemz0Q8BilkOOKOn8YBV3bR+lC+7US95DN34jMrESbV
XaijUtF+YwzEfqj8QLzVPOOK+s65BbFP/h4IfFN24kGZTkWAFzuN+FTbSOSx
RPxkEvg9ql7YVi+j5JuE9+tKv0pW3HSpgffIPT/np3j/DA9BvduzL8FWXDn7
GH1VFgUF2fBpB8VzrGO9vpx0B7rZ2xfa4jzqwLmoG3zRvqYV186swfP+rCGf
cyM/4maPInEdrl+QSg4mPpioX1DC7gKXoEckF94N/ZH634ifpcZOBi+3BvLy
5rO06a24lvMz4vOs5yz4b+rPbuAhx2eH3mYi+HLqa+h0iL6W8kvgoq/ln/ed
7kvo6jCP7o/OEn2v0FlqHIn3wv0F5ZWkaPDz9UweNazzKbltwPnyycW+/zvs
9hqCJ0n2pL4zk8b/P32M08x7V8viPsObkD0gdMkc/WpZl0xZ9g79Ae5vwLlT
dCvq8SvsBp8t/0bC9TI9abw07ifm/+QR6FGHTbE9F33RzHHW56KeB2/SqDYL
+Zo56yta7994uB51cyW+hFhx2W8NztOwqUFW3OHXdM4u5oH7RLGOn6PfoSzO
HeIzWfTmqllxx3jWmxL7odCbMkevINy8r6DutVYtshMEz9NRDyv0rMLKYN44
vi3y7+r8VNhPOkF3WnvggnzT+xzIA/gyHvIT/cgaFUokv1acp/M6kF2iLwl2
Uyy4fOY7eCnfHuS14Rkl5JeZl6hvzoO8A/MSpRddsQ8kA9fCliE+w3xFoesu
4jnyykXIt7oPhN1eoxnOY/G5PmU8/428/KsytO6kE/OQB/mIdanPhh6CGs7z
+XoN4sDxEuz0bAE4j1ZXRzw9oWqQbZ4ztAKPq0si4vwX58fQ33u7QJ98SiPg
BvpeyWtzgT/09xfUhXOfLMmnDXRjE6JxXngGY73lH4l99rE7+hlNXkm46pET
+bVxq9DHb0oFrNsvD3BOx22En3h6LOIVbuGIZ82GTqbmdAn50CJFoKsQg/6W
Ut5o2A8/n6NPXtpaiMeLfTLwHvmZaseR9n11zCfM5/1OKfbVdtg3uB+6g4ew
KQh5xxR6pI48uwTdIbnES+TLhq6ALvTjeazjh/dYW/AK/crbrPGz4Utr4jyY
Xa+aFdfnjqJ1aDyvBH3m5+1RB11/BXjILugL4NBRacJ8qh51oaPwDOO1O/2w
Tz5Bv3gtqSvFCeUpX9Bn5CXyyFox7mv8Mpz8ayOqPOFG4W7IQxWpDjzLSOYH
Mh+gTjSeU84LHH9GHs34mAs6cdf3elvHq3o++CdjXfG+BzI/5IczdF3ClrA+
Xlqc16c9YPf81T2UxmfPiHPTzxP1CHUKEu44310agA8R70X7iujDqzqPBV/w
zOriVtyYXx7rxFP3sOFtNXofpRTntRIQZtM/dNifrH+oX5Wg/9Qa9p6eMBf7
VFH0qZSnA1cratjXerjb1qeu+kLHNvmsPe8zNwbxDq+rmL/evyLov//uAj3z
rGtt69kYcht5dd6XHPk73pe0QOhaSAs5vneEdS02meCh/TwKXYj18ag3+Gsm
8Nef8P6mm+dO/0adhl/l5YHx9+uj75JrM+6PHIn65cLZsJ/f6gCe6aJGqHe+
85bihEalvuWtuDxhJ+WnhO6ifArxCqG7KPpfyNc4jsH9L4xBj1DHJPQ82+zD
uTzCKRjzg/z7f3YM8tylagZbx8sDPiJ+WmEU8wNZ7zQ91rk8uh33Z2G9wQPf
oNPYcb+3bXy3AtxXbz7y/EJH98JGxJdLzwN+uQfFueQr27B+YoIaWsernu9g
L3nepTi5w78OlMBr2rMwjxWXN7ihDnfPFbzfmz4jnrZ3H/zezadzWMeb23wR
R20KvoDWFH6Tfn4x/LTN9VAPV34P6krSdUD9gnNT+AGNtkGHs8xx1BW/u876
KlzP6zYfeTqf2dB31dh+u1gB++oK+3rQRr6D3kuuWfDP3bmv9PWBnB8JJlz0
UzB+dcK6XV4L47kPtTFhCK4bc5nyvNqFONh7GdbhXDyWy4PwsccIV64EBNP/
z3pBSq45qO9gvSBteCXE2S4mxtC4Ez9Rxxmzkp6X0hj1I1KDgeAR9VpLcR7J
vzHZ4Vr0QJsekTqpT2fr9R26GazXJ/SIlLQSrXNJ2GOduW9ImVeIi7C+gZrc
BzyiVw/IX1c9q1B8Us79A/7JwpdkV6ibZiLOOeybvW6o7yybjrfaax72+cBD
4EuU2ol8aGwvOu+00Qb2EaMC+POB4+FPfN+D/a8J9F6k8Sb6KnxOD/5hZnf6
XWqHBdVs+ET0X5ePBfja8NzQ91OzrOU4TYr9LflbiBXXC06HLq2ygPPdB+G3
7p8KHVI1BryU0nGEGzOOIh5eIwk6FSewn8iv+uN86nQG9gzHRdVo6PEKPXkj
cjz8RNaTN88PAN9T2NsVrkG/N/PI6lZcbdsY+c4dUTbcaJaB+7rO97I+H+Ub
9LmMFf/4WHFtbGGKyyhFN3nb8DRe8AfunRZ+Eq5T1xu8unfoXyYJ+//ILeRT
93yz6afKcxTwnDeuovixI49zfiDrmkGfR+BCn0fo8DjyREKHZ8xu2M8doXug
12gEvYj2a+DfpfWbRPPwfEQw/X+sD2MUykW46Csq3heBi/dFKtYN+ZNS1cCr
1EOQ//oM3qxDt7ZnOHicXhlQT3HuX+SRpv0DvldR6CDJT6pA373ufOTzMuF9
FHraWuf/6ePjir+5j8/SEcwTQ99zOf1G8JKbXwS/okd16OF4lqM4lFwwL+p2
QxZDL8XrA/GVlR8jnlM9hLBjg9MSr0xLey3BihtXH+O5O/ulN6x4NQ/weL9E
Yr75o29d5ETft6NDQyturM5/6s915TRfGtjwhy9Ix1/JHQt7fzfqyo1cPrCj
DpXAeu5WDLooyX1hb69sjvnlvuRqQj306clRD/m40eC1qkfRL01elwZ20JsB
6POudoZ+QcHOiG+6oy+8PrEv+lBwfwpH3z3Rn+JiLvC7s3lEED6rHelGmlMn
0Xkl5xwLuyVHX8L1GO6fGI8+70Y09HhT8vekq86wE0LsfD/T/wTwXvM4Lw97
XiqfD/2JxkrFrLi2/S/EL3Kvz2fF1aE/YHdO2YBzp2MI8mH1d5J+mjx6g3iO
sCuahaL/RXYd9X01q9F49fXFbPS7ityHX1+yHa1/bfkhxKeiJlW24saMM+Bv
VNyGejjxvlS5iX2pyWDbeG3AffBarnD/sqs1Sc9fy90RdnyTU7S/KnNDCZcq
+obguv9W4utQXEUvin5z8pevyD+wPaDH7KD5UnJ4V7LiZp/CiBsk3wSPLoLj
q+/Xkh2pjffEeTsAuDm4NfrhDSnJdf/rkU+52wVxTBW8S7kd8izynVn4vV0K
wZ9uXxN2fpf0dn1jYWcu/af2/xcPtecjZH0j7OdB0Bk04qfYeJL6tzF4j+4/
RNz0xFv4R6wbqR2Gjo5sMN+A+4BI92/TeLVXNOGi34fS4iLizaueUtxPcy+H
+r4CeYMJb74Sv7fkB+Llqkux76ozbqPO9L/9iv77KUffLo4XIb8gjy+qME4f
o14t/r2Ofl7oeyHyFNwvRm8EXrHoF6PfSA9dNOYba32j4UfPv4x9UsxPgSvo
I+DK9Shinp3ag1cx2SvENj5uJ8b7V8HvzXcE8fPIwlj/A2MwP8dRNyrnnIF+
c/f/wbnZB/Wh2uYpqD9shHofh06+6Nt7JBHvSzN/4BvQf9mokt7XOl7UN+nN
t+F94foLdcdz7L95O4AXM7Y68pXhCXTf5vIw8GKE3uaIEcj3ZatEuLlZQT50
wGic33XSkb8gvduD9+U+87y/LAMP9s1feL82XoHdvi8f1kXvnfDLDn2A/rJX
eVudi5n5AuyiWcVsevJqsyvIJ7ZAH1nzBef9bw15SnxU31SoU3kKXK7WlPoQ
ac/Rb9GhU1p4MfUhMjvxuZoMnTStsET6KY5zle1eKfT1x8NW3NGvxPFBXE34
78MmCd6DDTdu70R+q2rXUCsufW1exzpe9RwZQfefOx/ed86zqzL3t+I8u9Zt
C97T9Y/A++1SFXZSzwCbTqYYr35dgzyDWM+TIrNZv9fRt4I/Wswd1INwvELy
v0rvv745xMeK639FwZ6pmc6mh2lEHsL+02S6Tc/K+DgP39eiDPyDkOm0PyjL
06D+N308eH99n9P+oIb+IH9fv7YI9tLU5chH79+CfP279Ijzsx6mNHwrrVd1
1Cyyg7QF0FfRS10Dzn6T+W849gH2m0T/Gkd/Ac67GbH3oCsei/HG7wScq7Gt
bPETuUhWYd/Y8y/X8Ny16ZNs4xXlFfq6Ld4HP3jqVNJjV2NXUR5NlVciv18Z
/QXU8usIlzbfhR3Xexr02z2cof/G/Cvt0ynwIAX/inUzBP9B6GYIXpbABS9L
Xh7ZiH8H9tUbjcGz7PEUv691L8QTpv5AH6s8A3EubK0Ce6AX8sTacGfU/4p4
SJVvyNP3aGfDlWnpwJMb29fbisv7y+B8NN9jP2O+kLbtB3Tgrk+Gfsl46BeY
ZSTsh5zfkfdBj0bkd0Q+SIwX+SCz323bfi7HPRf5Cdt7ofacDPsgW3Pbe6QU
mAK/qFc2xM1EHcGrDcwTHWyrL5ArdoaeTJGbNay46uUB3sOdMTY+sOijqt1R
FBvOfVSlPnVsuKPvsIjTLiqFvDnHaUX/EUfcXswbx4HNxRgv4sBiHqSnbFes
TRR5Gtv86KNfoZ6iaBT4rw3jEdd96gxexefi4Gc3NBBvCduGeGL+xrDbd7wG
nvEQ6m6yoo5G5+cuN+V+Qx3QN09yQl2PnJn5CozL37iuh3G97ADYx6F16PfK
G2ugzvxZV/Bg54MvZzZaVol/F32M+SUQ1/qyFuuH85WiLljkK8XHoWMvucLv
vReHOrVaB5C/qRGNei2jAeWXzdfv6T6VVSNhT2c8RPa5WjoteHRu0DU2xpVB
PSjHQ9R/PmCfrYX1JuInxoFvyC9edkJcsA78nP/eQ9v5In3Nhv4gh4qUt+La
95yEm159i9vwY2ewbz9u5kF4Q/TtFL/X8C6PPmfMbxH7ifEwA3gP16va8D95
IrrPIdBjl/0Ocv3wTOAPYQdq3/Ecpafon6hWhL2npGKeYSN+3iG+yCOpzhSP
NM/kIDtPHcN+edg8+DUVHov6Lnve9qEf7A0vXF8XvMTlnJe8ccfmf6nuabDf
sT6zORV6y0bPDI2sv9fhJ3JeTI/bijoIX+TNTbU/4odc7+DooyG50rpW4z4U
USzfax4sCrvRy9ndhnd7h37x0aXzWHH1NvqsiN9rrCyKeKNxtpIV17VfqE9P
8rP1YZHOF0Ne4/578Gouz8B7pEPX3fh3Id2fXus89tnxL/H+em6CztsSNxvv
Syt2A/yB6FC8N8F7EGduqGD+L/uFWMfLtVXkNf7BvuWIJ08ehf2n8yfUv7I/
KydHIg87s1zoH9yhF3oDdSNmj3q1rLh0+Br0Igq2hc6tiHs08aQ4hhSemN+K
637QqTez9/ew4saGnKjL02NEfSj8D1/Yk+pY/3pW3Bh99CWdvzVn1LHi2sK3
OfB76mCfFP3cZ9egeJDePK6ZFVcGX4dd9LIZ8nldOkBnci765Qn/VGsKXPin
SsUY8Im4jkCsN/Gx1N2g70P6M/Q7zMqso8V5EPGRz3TH+K9ruU7pM+0HxrJT
qJsbsAo8RtbD1NIWiKD7ZD1M6V1a9CuZfZnsGf1Lb9RBBPeCbnEKfU7l4e0A
K64Gg6cun0kMtv2OeNSf65Futn1aWZeDxilvu6HOSMRbGqA+WtrRN8CKmwVh
r8tJrwKtuFb3AOonvwWjzkzYCRu4z9qLG1Vt+C7Ed8wBztWsuHLkBOzg71pl
G17zFPYLT7Oy9XvVNy+BnyvI+yWvzyJZUL+XGXW1Dn7R2OGwz2eXLm7Fpfsf
MP9OpQNseLFW4K/UPFzDiht565C9qgTIQbbrHxyL94U/+oNPqPMV/NLY0hno
33Fu4DO0Sab5V9NNJ1z1eQM//cZvPJdUiYp1HnRtL/jcBfPa9mGla06Oh8g4
97jv+X/+Wo4jFlwXfdKrrclDdYiLYkQcBbrUF5LT0v+XmC6P9Xu13IuQR8/9
KL8Nf1IB9vDBepmsuHxqE/bV71URnxsMvT4lYAP9zv/2aehffSxOuNmyKOVX
jJfVwItYMJriKmaGBBpvHN1l01tQ8x7D/USFgyfF+QvTYwf0QXJMCLGNr1cC
dtGBOhTfctSnZAuD3vjBa15WXC2/CXne1UG28Xr/ZbCzOu5CHC5tJsR5hjaA
TqOrhvqOwMzgxV3t6E7f09oL/sXPOIw/+JV4NZI4X0pMgt0XP9t2HhlPN6BP
da+KZay4MuI+8nJdbgmcPkKPzlx9CfUR57OSHevAH60D7j7Vvk5PFEZ+/3ec
Lf4sXz4LfuTxVI2suLlxCuy49f+gjkPo5B++ibxRtTBb/bL09K9Qwuc72fLF
Sq4n4AnMfAdevFjP2w5iPznSGtfxWoj11nQc+LtTR+H8bQBcngc7RO+yEPxx
odvmuwv7CefppD3FwMfjPJ3SejCdGw49t6/Yf2Q/J+ioCPt2BPQhjZ9Zbbi0
07UB+R3ct9Fht3DfRm3QaJofR/+vvE2wbqbZ6wKUbNPxnnuvR3xL7DOFciGu
8foD+FPH70fQv+K8SOlfJ45HPLNDV+gCcdxYOjEW/ZuGDLDjbunR/87liqcV
l0eHIW7fJh/562bjAuDFtRuC+Kw2v6EVl3IPhE5C7ZO28apfLOqKq5WHzrDK
eSi9FXgCkbkoHqlMA242yM71XRL6YIvzjvuZOvjJGR8j35mCnyzsasFPFjxn
gQues9rmEPe7zIv9cMli9Is8d7CyFVfX7COetrE3sZJt/JTDlI8y2leBToaP
D8753RfBE2p9Erwy3n/ME2fwvPYkFLPique/qBsR8epWIyLoevnyYL+euxa8
VC9/iucbmWaBzx/L8X+O50smdM7/e6/Ac6wZSOP1b0WgzzL+Dt6nMNRpmose
gU8wvBjqCJNcsH6qfkWfgK67YR/2AP9H6nsCfuSEH/CvBG8qYyTiOdkn2HCj
bFpaH4ZXTX8rLnVQoWNjFMS+UhTvrxpyBnxp7j/riF9x/1l14gy8X5V5fMVW
0Llge0xPzTrtbI+JeIijjyf3FZVOVOH8Mp+n9Z2RB/nugnUo7JnxLxEn8qtS
zTb+7AOst6iFgYYFN8tBj0Ny7W6zo1T3KDyvaF+bvSQ1yInndaoq15FDX1Tv
vgS6H1IC+W/GufrIY+VNI9F/P/+jmBXXPTOQfpqc4wrF/6TAHOAXnux2mXS3
fsfTe22s3wjdWm/oL8klnfC9/uPQ11IuD/3woDPglS/AeONnLcQBsx8he17k
p7TDb7EPD8tgw9U3P6CjtywX+ped/Qfxj7cm4fLauaG267BerlTwcDDdT55Z
0M+fmB71412mwQ8qMg544mvosHGdnIhXS1/ec36d4xw/OV/MeibKqdKoK2xs
ghf65Sv2Yd6fHborvD+L/dyh0yL68HI9gsDltA9FPgZ8H++t9Hu1G4hzCtzx
exmX+x4HD/PVPq6PvEHzYHhG431sPBT5/YRDqEcLdyZ7Ux/dB/n9NiVQ38Q6
Y2K80BnT3MbzecQ8h8droH93zvC24rIxguwHPesoW32lUmgvxcn1Sl2gLyXe
95uo71Z8RjS04ubydsjTVHjSwIorN2X4p3fcwJ/aEkp+sXl2EfUXFHWOgl8k
8hHGwnHkJ8oPgxE3W7RoEeXHv6RDnDia54HzGkr6iuhrnfwKvNDaLVEXfHUZ
zpmSI6E7NHYD/PHft6nOy8ywDOddnrXgiR1LRfat+oR55gXaIv7CcXVH/vRm
OTz3pXNIH1fqdhd2RcC6YPqdzHeSg7xQT8F8J8PtAvb1+jtRJ3V/I82X6sn2
+dGjWA+HzsCemXkEeQNeP/owvHdy00EhVtzov7AR5v2XjXdh9iiNvhqsU53y
vZObdcd9iXqu9n7gLZR0teF6viPQdfrdnnBhJ5gdwItIqScp6lJNLx3+SPNM
0HkrG428al3wa1L2bVfXxKCvxN4YnPtd7yIfn8oV9fsRE+Hnxk+EX1F2OPRb
dvhzPftr6EM1dYXO67tn4N8+3gY+Fa8rve9RwoXelHzEDfyI/bfAn2x+nfJd
om+jqMsQfRtFn0c5Zwz4Ttzn0bg41zZem/cc6/D+Kvj1S7FulbL18f6n4OEr
0/IgHve8LuLHuzDedJ0NP2FdS9SN9UnE/tPmp41Xpr064vA3/+AOHtok4IKH
JnQ51NiyMXSfrMshR3D/mCzQs1JjauO9TdGfXR+ogi+dog+7OQ3j1WFOwXQf
wp78NR3rp6dbkBU3+00mXKo1zIZLIdBx+t88OOKfcmbOd6dlnl4rjoOnyIPL
7QQuo17yWzLsm4DBbtQHZGGMDTdi2f/9v/Fk96je7QrSvtS8oU3vxYyZjDrN
NB9s+SwzZGhJvg+bfS7lvUr149rxneDzCJ2iasdFHxCRT4AdKvoq/R/ua8W1
AyUQj2e+nPIA/TWk0C40/8YR5tfdGQad9pGIT2o3gOsNEWcW9SU664NpafF9
Fry8FdeWzkbdYQPsq0Ybruv/sJ1wI9KT/Hr1333gM2Z1ofNBm9qPxktxD3Ee
Tx0Ku+htNNlperbx4K80LIL1efUicL/G4Ec2PQf7qsoW9GHf40zxHbHfqsun
4/kIfunaauC3Dj6KeczEfXx43zZ86+H84X1bHZFg44eYtz4h7r/6NXhW5aZR
3kd60wn5R6Fn4tkjgr6X62r13+3Ap2iC/rbGAfS3NTfHkj+vfppF+48UPBHx
8Iz7CNfKgf+vtRrB+gEclz4+HNfvOtdRf0R/C78vD+KN0lS736esy4g8Qa8V
hIv9XG6VF/2Dn7z1tOLSfSdbnFzakQRd+pGFEY+7cAP9sudORj+ap8jPmR2+
0PwrYQr61/T8Dn82qTt0n3YD1z7NQf7D2Qn+4+onsMf2zUc+9nAU/KQd71Bv
klAPeZIO92FXpu2B+vRCUfDzvlcS80Qf43pv8A3Cela04uoB9DnQm9hxs7I7
zterLtxH5i14vMv8vpP9vPAJ4jbLgKuD6lEdvVz0hTtdR9THZfQQcWD7+84f
Zehp275hdHnjRP+2v2jD1eTnxN9Imb8zP7FuZIo8oMj/pswDmh94fEOJ9bp5
n+5RDfb2yiTFen9ygZBguk6TIfgdT/cg7uSG/qCmy1XkhfPXpjoVuXEoeBWb
47AuLsFe0pIewf64ewLx3ivA9TyfwBv2OwS7cFN26KvO9ocfOPMOeMvhQ/A+
PuoEv/rtaZz7Z5qir8nSzMjjee3nfD3bM8U6IZ9Y5LANlxYryE+x3qk4Z4Xe
qekRhD5C2/hc/p1IfB15fTPkG0v+g7rvkKG0b8v7gUtLocuqbhiE/dxjMOLN
F4754feuobih6ow+QurkL9C9qKijv1Kq1zjX+D1V67ygeVYnvFOsuJLvX9Q/
nqxuw6Vmc6AL+XKzYv298tgy0HN5cIOep5HVQH3N76xUdypl2Ui41B79Zcyp
JWgfVOZAN0mfhP4yxvL50E0q/5j2DcETEH0hVWfUX//nP4MvMhd6ccI/cvAK
2D/SfA7CPxNxj2hvxNW7I2+oXOT1s93e11XY20Y650bW8TKPV/ojz6i3P4O4
3JLq8Avy7rDpPEgOnpJCdpgZdBD7m9AtaVkb+enDjcGDnQDerDZjGfJprPsq
hQA3N6IeTa+BPm/CfzdTrUW9dJ3pnAfm97rcGeShe/ez4dLlMcgLdg+pYsX1
VYVxDm3eBD5Yt1ERNK59KNmZeswL7AOL2gJ3M8DPmroA/inrBqvNsmO9Th5J
uLH9Iuo6yuREXPEg+sWL/LiSLxZ+hPNstkuhO60lbcJ79RR1xgJX0t/Fuqww
v5oVN+5e5/hIfTz/a3heaoZZqEOvdAHr6Crq0bTb/RDP8FmF630eDjthUT/Y
6110+N9n4d/JT/rA/uS6OfnWQ9ilXDenFkGdnR4AO1ZyagU7nOvy9JkYL+ry
5Jroe+/wl8vnxXt1LhY8kdg34NcNXI96n596kBU3szyCvknmklhHPj7Q93p+
GXrukuTJOM6fEq+QZxyxuIgV184HYr+p7w7+zME2uN9LAVh/y3Pidws+88Op
wfTf43wJd/R/PFkFdqGB+gMHz/n5Kfye5HKIV4q4zYwP8HPHueD+hH0++R7s
s64TK1txPQa8ZXW0s318q694P1+NK2KdT6XSfY8/uOTTy8uKa0VKU38Hs0e3
UlZcvtQZ/R+lw8hzzc3O/cgyUFxHaT8b6+RqNvSz8J4BfkDX3cw3gF8p9atJ
49UmEvpjsP685LYB+sgPphe24kYmb8S7fmUrYMNPV0aeKwl2glzyMNa5fpj4
Y3qqTGw/YP/Ur28hXC159tERyzwrd96TvqvmWu2DFVe/3KM+I1pVrxzW56LU
TnD9gxsvV8Cv5f1Nut6MeFDKhR+iXzF4GkngCesXHbiPFTdTm/7W8fI8UW++
HfFI0f+LdbClSf9Cl4L7fxnz8wTT9ZYus41XZxUP5uvCXv6mIT91JZ2Dj02/
4+sd6Cg7z6HvVScsZD4Mn+NN68OOiXaCXyvW1Xf4j5LbpCAb3ljG+Eg3G250
hl9pZvpKfXzkEkUpnqn8ewb9fpxP0Xuq/g6EDvb3tx40/lVrnBvvasI+/zgG
cYO94wkXcSoR3xB8WoGLOIbQsdE+XsTfQseGeZvCnhG8TXPkCozPfQ9xkFq1
ZJ5PfPol2HgIIr4t+Akivm1WvMj6CXzOtnAOpfndJOaHdel3FkM+YEudQCsu
R5VA/m5Earz3ZaAfYnqpqH/JHA1eds58qDdZ1ZbimeoBXEdr7Eu4tDQH4vyn
47BvXMb+b7o8hp7+VdTR6jv4HP/7PvIyX/5FXixFnYKedAJ5WrYnpZKwJ/U4
9Ht12AmZuA7CLR30AUR8bEcA+PMFG9vtpX3ISxqP7faV0jqScOkw+rQan/h7
03Gf1oEDvKzjTf/vNC/ygj7eVlyfUhr75KDVwYrle82DyLNqn5YGK5bxxtWx
sM9zH7ThagXYP4p5xxYn0Ytz3rO7XQdeWrgMfv318zZ9XWW2C/S8wtfb7DHN
5y7yLu2/2/PmU1Hfp+7BeeQYH+RP824OLYl+a2mLIA52rwvswfa3wLvImB91
f7dn4bx6cRK8/ULhxH/Q4/Zivz4c4GvFlVywK9QZ6M9uTmmK8T/a4bn6pUOe
dF4w4iAutaiuyniUHjwL/ybwq6IHS3Sdl6wj6lkdcYDWH79R/MfXCfxT5g+o
wzMgX97/ijuNE3p3Q6AnbJSZUMaKm8+r0Djt7RNPK24snAZeKfOKhT0seMX6
ln+x3gN2gt+ZuQnsbT5HZA/G+RzRnyWin9mlGPSpnHsG/UfSOIH/L9WBvj37
0ebwPLCbGlYlXLp+Ev516sLAd+cEXgz6nNrwPdjPO9SF/kOlE3S/RmRj1Dtk
Xwrdy+AhsB82/US+biL6QajL02J9RMfQviLm0/jVtRDuZ7cNl/S6pD8sZV8K
f12st/d9iZ8oud4KsY7Xo6C/oP4eAn7303Lg9/76Dvuc60cd/I3t+amfq7y/
QBUrrg2fRLpSapbzflZc+vnwJtV/d9iGfGll6JwYPvBX9bitOAe7i751V+HH
5jqB9bb9I96vdYuRR5Cb0PzJWT+yPrkT9l/mIWhRUeA3Mw/B8Rn8FvMo4rdb
wd8ztnEdetx+nE8tEpDnDz4OfuAj6N1JoYds+kj6tQ7Q+1raEfvzo8K0P8tJ
buDfXIaujtCJMlz/Bl7rLvyVjTjHtYaV0O/7n1nQ7W5VDef7fB/U8T7Pb9Pf
UGLAPzSHtg604trSCahLvT+rug3PeBy6Fh9m0nukfW9GfBIlRxH8nkLlS2G+
8qHvm+dzzGeWbGRPKnubQy9u7Ar4ob8uUT2OsN/k7XVb0++vOoDivHrD1bAD
b+QgXN9/153Gf18FPLoJ4XJSAurFNdH3cAt4wty/NSW/15zSN5j+/5fxrDe5
Hbr0naDfoku+2K96jMTzGHIScdDFAdiXQn7QvGh3M2Df/VECeYz8BTCPneuy
HhXnZXwiwFuqnGQ71/Tq0A0xrsb5W3GtG/pgKRFh3J+d40JPCkF/b/nTRtbn
YnhL4GWzbqSDx8s6QmJ/E7ijbmLiYNS1M+/FUPdR3EyasBHzF78R/vLH1KzL
hroP0xwN/O8viG89WYV60nyrCVezfwSvbVRTel6Sa0nK1xj1k1DHOrIN4cZH
CXVVN74Dv/4UfSSXpEZ91r6fiK+zPq22Igt4vKxPKydvQ35O6Kyy/oy2bJkN
d+jVXL1XxzpvWtkg2M+LjXo2fN5ErKe/J9jyqsYof+xj2ipatw596aynwTdb
/a/N75NW1cJ1mneqY8X18nUR3++Szeb3mWt84P99vYx8/W/kO0R+RfCxlWic
Ow4+9pSPwDup4N137Yv4wjln+PUHm0I3fc56xBEKM982BV/dyAdcxCfV+8xj
PwZdODM1cKMe4pjm8jKoS2jmjP1gSiLiF+OiaF3LZ1JDx3/0KPg9C47e5zo0
7EfOPVGnv96F69iYb/xxFPKtP/Mg/pC1AOyNA9zHjfX3tMrvkV9Lob8nTc6L
8ay/J+JdYv2LeJeor3HoSzDvSDlRFf0M3YYR38w4d87BX7KOF/wlZQ10m+WB
0MHQ0mXCehsMf02tAVz9OwrxqIDnXEfM9U0zhxMuudX2teKiXlv9h+2r9qg7
UC+2Q7w1Bn3BjEKzkPfcuRd6OpUX2nDD/xni05fQv8XY+J7eL7VDS9Q1le2A
ONUj1H2oPQ+E0rheA5HHy54R+Y8pqwmXd9YEH/CFM/hXzW7Dbhh7E/XdIq67
sivFV+UZ+wtZceXv9jZdBtX3Ln6Pjw90zMZtgZ8u7A2PG+ClvVXt+LPN0M86
NDvEhtfqBj2xjhrZI8otjltmLof9PKkU+k6IOO3gMJxz8QuhY3CO4+Htz0C/
b16QrY+SvBP6StpupY4VN6dCd0MbHi5w5DfLLRP+DuJjGuovtD254K9Fudnr
NYZyvnVMJehCcL2GPnoO+MxvDfBzxL40ehh0rgqEhVhx83AC7OnyATWtuLwR
fWFVb+jQiL7D8m3WG3ka6GvFtQzQG5FezIA/kYg6Nb13DxG/sPFnLB/oZ/Q6
B77EiHJUtyBw8byM7DNoXWo/kbcVuLTsOOK0jWbacGNCV+jovsf9OuKZbohv
Ch0Sc2orxM9ZhyTlfer3oH+ojLtX04rL3gu5zjMj3icdfSuM6/Ohp3xlPeKF
gyNg31bJgPWTn/uiFvuNvFje99A5eVGD7FnH83r6DfyBGrvTW3F5fVXwyIo+
z23FzXmB9r5i7VHfrg1JcLbiWl7EQRzjQk3inenzIjH+twfVcUibp+L39asE
HlqG2eR/Cp12pVZl5HFYp12rDT6dXg/5bNVrdC7Mp4JzW9SvfYB+ujz6CfaN
NN3JfzErNSV7Q/vOdfkinn/qNtW1Kk1yh1lxqYIHxWEN59c2XDm9Hv5q8Xz0
fOXMVaAfsjAe50abu6yfM5dwMzwt8jwNWW9nnT/GtwyH3TZwJOZB9BX1Ko/9
sMpR+LsNMlH+Wrrqhf3qMOrrxXjpBPL46rS9wfS34JE+Rh86/VIFwuXQT4Qr
+YrBHi0zPMg6XtnuxTzNhEDb9b/Og/4d64jKmZk/KXREG3Bcn8crZRmXJFG/
I+pkoGfKekiij9gfvaQU48tbxxtfDcQbOE6utElHOieaft7Gp5UapME6TsGz
VfZcRD7L7zji3pvzo+9qnc14j7b8Df/jYCH0vR0cCF6IC/M3Gr5FnCR7XvCz
b7tgXaWdTeP17m25fwZ0Y4Seg0M3JnE88JhlVH+tL0kDnXHWkxE6Dw49meYm
5i/WCboPu9ZTvbmcMxB1YD9+o17t3II75Lcm+iNPtTWGzi3524MnhPu5w85/
dQj5iCd5EOd/lBt+Z9gBwvXIr456VbpvEXdK2mirI3DsS9NPkF9gvC1r26/0
5oHQcWb7QehvC/tB/jIEeZ/80OuW/PuCB8y6tWK8/qsb8KNfES86Nh73+bYR
6mqav4O+fdxywrVfJxCfTOWF9yZpJXQMrjwI/fO3djOceDrm97/A+wpHPlUL
Qt8HrYSJ/mJhvujDwvrhIl4qdFPVn9WgLyfion9JdH1jyQPYmyJekTcH4frG
TRWtuJ4wEPHSvxeDD8Z6vIZPEMXnzYyZ8HxYv9dMnEFxJ32qjjrjDzw+IiIR
dTom4qb8fsm3dhShc74H7FZhPxuLBE8J4+Ws4AtJPbOUJ55SJMY7+APrUoxP
wWuy6M5C1zUt82iZ/6OkEjj4P4bM9aFOEvrfLAHPVr4Gf0L+yPzbZPByBa5/
Tyb/Rkv9AXXsIn57w4XzLxy/FXFgxkUcWLpzHzrSw/ygv53+tbhvfMQ+ufoS
4itr8oIHLvbDjXsJN4572HCzySfUS75eQveT0r9TyyzAfX7hes8qncAL/7sQ
3Y/wH7VzU9D35GwbYb+At5Z5LfKrFyIo7iVfZj0wl0rFbPc/ZlQwjfvPXrXi
xtNMNa24sbllmGL572q+atAljOhB+Q6xr0qfN0GPb95YTysuJ3pBV/D/0fXV
8Vkj39ehSHF3DcW1UGgpUhraUtzdgxXXxRfY4FLcneDuumhwK+4eXFso7n3h
njvZTL+/t//w6WGaJ89kMnPl3HO9Cudx41YzjXS+1DT1pPvXc22m90irN6W0
9L023sR+Pm6jNF4p1YLOZcWjp7AvkG/KAR09q4Oj4wW+2Q5en0+2YF+N7Aq9
vuDmdP9Wkxbw17olQV1Vkr7Q8XiNfhdGZeiQa74H6P7/9Cunvxe8Yu5Xrl1a
g3nMzbqFbxfT/WpHs+JcyA5cudh0B33vPrmFfgm+94cC4LPddvq2QC91LfJt
Tp208EPzId+mdr6LuArXgSr5R+D8XNsaeO8zhBsLuoGHPfMSeCvf4+Hca3UK
+0GBIOjwHfyJOHzrNqgPfRoXvMDCvM4rvUN96Id5uI/TyCPbA9CX3WxwUOLJ
2PHQL01/tqyiGzfjlEQcvmTCUAlPkxH2ilcA54M47lp2E86D9ac1CX8N/0Sp
FVjOjRvTK8P/taohXiXs0uvDwBedfrKEGzenBCJukHqbn4TvTQBe+JW4Gd24
/qsR4lxJv+d042q8IPCK1+SFLorIm98bBh7R1nhSHxxtFuIq1udCldy4Oawo
9vGri0LduPo6DP3PWNdF8J2ErouIMyhhyAOKOIM6JoEURzUr9aL92m69RY6j
5j4o6vdEHT/zQp0+xAL3c+N/+lzQvx7A7SX/9SGm6/skRDx86krwab7vQZ58
bxf4HZ9H0Pe08gUijlgwDsb3AL9O+S++BLvd4e9CL+j3OULnhdrpYTKq+w5z
9gHUtdzCPmC3B/77b5GHfwpc9NPRdvyC/ROrn46V/SPsCu6nYy+BHoPAtQbQ
a7DWvqb6GIfnOa4B5eUtvz7kRzp1i0V86Hmpeo5j7vHGSiU/33cG/l6on42r
oL7j58s0/P+ITyXqKZ4XjTcZF+PtpofR/030Oe2O+KfWJmVRN26Vroa8aeTg
3G5crxeGfTQwXSh/Dv1o47YgTtW+sVSnroUmJ71fXfks4ebDl9AdOovnZr1F
fY35nXVn0uDcN+LhuVhz+NyPxce2ZjKeCHE72+se6uVfX8L7Fx4FnlhMMeJV
GqOAG7X7om6lVnHopj5Oh/dg3UTka/g9NZ9PQd+KW9UkfW9zaRrUpbyuGeAe
r2SJgt1zqiLi8VvGoh5qeMxPsqtjltA5o7+dDnyFGYeey8NPsOsLoE5K3fgS
dkOm9zT/dsnxOGc6tCZ/2J5aDnrX65LD7nl0n/wac8ArxDlnVEX+Y8At5Olv
5EM8pDbirvqjFfD3ud+E8qUy4qui38TwJqH4f2GX/gVdpJvHK7pxfV4l6F8F
ReGcEvErz0nwcxPuC3aPVyv0ojyCtv0vxHtYz0rLrGE9N7tQwY1byR8jvsS6
TwIXuk9ariL0Pjj77Slf8P2WNyvuxrW4z7Fv3ylfzI2bz3ejbmTPUEmPQU/0
MIiut2ugxPtVN7VBHu7I1+Ju3A7JjXXLcVFhhwv9cOsJ9OSN59wvo1dn+BGL
0L9b4GZi1Odal7ch78b1HWruash33I2QcKNDty/w1zwqSjjXEduhexHX5Diq
naReCpof1sVVqrFeH+c1RdxJe18Qdbgcd9LfDIV9yvVooj+IXfENeCTMAzSV
ZPC3g9+Dz8I8QL3gO9Rv9xiE8cwDNJNDn9wqkBk8U1/kf62OS6Av02kx6nTn
BAPPnQb5K647MKrw/XPdgahT0Hd7oQ6F6xSsJPsk3MqEdWgN6QQ7Jec94nEZ
cR/Qfmt/PwQ+suB3MY9Xtd6DP5sP4+1mwaiz5R9n35i7Bjzd7SHIzwtdlCIr
JJ1WZx3O7QQ+6pxXNK9K6CvE/5c1g65snB/ghc2MItzuHA57lfsfOf2muf+R
sb0ceIGs/6bfAq/i9/cs7cbtN6yLtU+VxpsTLiA/s2M5/FeOb9ujDself1cl
QHyi6wDogP+dgvY3ZckY8JQv7sJ62bk1LuYHcTbtDfw1/SP3KSyBfI0ZDVzo
T4rx5mf4cWK80BsXcVGhN67t3Ia+Lc/wHhkNBqOvR+6xzC/F+2itzQp+j3Ie
cc2IdvCz7k7bTv7v8jsSb19ZkgN2c5nP0vuud5lGuJ23gLwPnEL/IyvsobgO
/JqpK2Bn1z1Bz1c9tw92eL2RqE8ocgHPve1u8M5bD8e5M+cH+lAMYftqSgbw
cxpcgP80KzP62xZEXbb1qy70IKf+C3x5CdQvv2oDnbc5ScBjbb0KdcT84+zz
SsqKEv5tP/I7rDPzR49Lc423034EP4p1Vu1Br1HXwDqrIh9t/At9cicfzXln
a3cU4SLv/PsvwOt8AHtA+4K+1/9Tn8X2n7AfzEi2Hz5dFHkOxHPY39S9a1B8
Q/lqlXDjWnNP6ITYr7zduB32lOqgRX7NqcNl/TqlcT/SDTP3dkQd3BfwWMxG
qxAnPwPcqP8TuH974o2qh//B749nIm7RdDPqr78ahKtfoj3ofrt1B880VTL4
kQuGYnzr1PTcjUqbKU+t/jsBz7ukQutHD0qJ/cqKRL0x65SKfUzo6pvb85Vx
4/azmYhPJmiKeObSo6gbiz6Ic/c5cMd/iTkA3vC3ZojvlboBf/PdItyv50nY
I6PH4fPmL8f+tsgP9bC/4rO9ujz2fsj9Inj/rBOI9Sb8tdQtWbftG+IBzOP6
0yeFr4P8+P/RN9CNi7yJ4VFVqiNWP1SH7uTMx3I9cs2U6NN073RVN65HzYPO
6qziiOsua0j1LNrzJahDPzwJvHr1EPzoC8vovRa6TGabtOBds86GeqUgvl/Z
9OAnHVChN/T7nKXPX5mZcC1OMlrHduh78PIq982N+XmHOCrzRgQfTPBGRP8g
R7+RdeFEvZ7+lfNiol6vfX7E+zh/YSTMiPhP8xiab7UPdPOMXTZ0VA+9BW+0
+nDE6zpsw3yVvQeehifr7JU8hPzg2HLMW4B9YnzIqAL/UN2Nq4Mf0Lli7bFr
uHGzswflZc0Z+yX+g7ayKT5/b6hUP67rGniw7yZjnrf+wrkUWJz0XLSdf8GP
z49+B3reHDj3b/eFv554KOKFBbfh3D+gSJ9rDxuB9dtzhbROrFGX4TflfSmt
K6Ud+PHK+i0UvzG00dBrWl9Niu+YY03oW7K/LHBlw1AJt5Wa2O+FLmWJHKg3
SDsVvLvc2amuwfqeBPyqKsmk8fqIibATWA9W1EkJPVjtfPlQ+nyRx+yaDv7V
h30Srl3qC/5ibl3i3RkH9kDXZd5d1CH4tiKdf330c7G/x/rRYefvl3nmxmuh
w6Dj/RR6Ux9wXmgHZb66EcV+5dC2yKOVGgJ/thl0nIwtXlIe04oZDR3DqEQS
rvu0B89tnxz/MX4hTmp3GsPxAbbHGueHf5JpY0k3brZ9R/UA5t2a/hLuPRnv
8car8Ne65oG/MLgD9tWyBaAf0jI3/KZzNWGnMU8+dn8royt4hspk1LMY+dKD
p8E8/Nh9r5T/4jlSPzgzkuM5ceCP63MQf7Q/cb/FeBgveP6iX6o5qOdw+n+u
fxf1+I7OtqjH5/ECd+rlQzjvKZ5LAS/EucobsBOEvutM6O7p9beWd+N297xB
dN/DozmuxedF9zWiDlrWzfAuB/3Df9fL+anMnpL+hmGMh47WVeYVx69e032f
Rv6JtM/oa7AunPXzbxnsn/UqSLgV6OVF/196FfEFtDWH8VyzMZ+33RyKt+sz
ByOv4L+NcLv0PYlXoL8+SPE9o8xp8Kg8Lbx3ifZRHEbZ6YP6obEXYL/dzQHd
JMEzFH3uuE+u3beTxAdTRxUCr7tWmxrS90odDHu6pqc0D9bnEZx3LI51u1Bv
SvjpOORHCb0m/VkwdIRYr8muXR08OI82NF5bGQQ9bj0J6reawU5Q+ingBebc
S7jW/yzsje4PsT5Gr0IcW/g7AeNwHtffXdSNq50nhtL1OU/n+EGcpzOjzov1
Qj9GvPjwN0tHBbtxZfo42OUD8ki4Fh0X+cje0E0VOmbqmmDEhb1u1nbjWmBz
8Jx8p9SSxkcmg74r11fqlSZgnXB9pajH1Ft3wDrhekwrFexLY05y6G9eag2/
MmNa+I8RFyjuZC8qR/kb8w36NVgRJ4Ev4H4Ny1v5uHGtDfo6mQ25bx73adKH
7ZD0HER+ROg56MW4b2y2CvTc9aityEfm/MXxklr03JXU9RHP3PEJ8f8d0KdS
JgdDPyRW/kWbkR37zFTEBYVfqX9HnbLyHueAs18dY11rcT7w/ibODy1OSdRH
PjiMc9++Cfv4VD7oMKSCPWMffQy/48qLVHTdHiMw/2pt8MdYN8zhr3K/G6Eb
5vD62L/Qjvqjjpf5e8aZCMLNDiOkfIT+6m88z/lHS7tx68cj2OfJ9FJuXHt3
EPyq3I+grxiaC3mBnfvxuSUQb9RaDgIfuFh9wvXR+bFeWA/NmjeCcLVze/C4
xb7dLQa8myJTZf3PFktJ90y5kCfUjev2T4pf62XaVnTjv89Bymubk5nf8Qt9
sZX0U8A72hECXWgRdy26AnnKiuUzunE9cjbhf+Jdf3B9I+xb43lv5Mvao++T
4IlZg9EXSsQZ1JJvYF+Ivmb//cAu5jy3viwO9ME436E3HCLpGyrCXuPxyn/n
LOxFob/RIyd01UR9bpwQ+BF/VfJ143ZIR/BO17XG8xB5vUXdoJs06xLOVc7r
mS1P0fusdkHdl8gPqnlHEO7kbTjeYnyNgX84Be+R9YVxka/n8ULPRIy3lmyl
/JcauAV+/7URqPt4vx38ncXTwc/YNgfP60MC6B3dn4U4YMAckW8WfDfY8f/b
xxY8fbY3LG1tEP8d8qzD/ia/QC32QuD0YzZvSXFUu9RaCVevYrx5v7e0bs1k
4JWp3kWQfxN2u4J6QiPXGYmXaHT+AX3tE6UlHqN6t7lkP6ghueu7P8da8B77
h5oVfTs1m/xevWEN8JB7BYJnPdYL/MtpLxHPKRKM923mZeDV+2J8ZQ28uKfp
EIeZ9QP5eFcc6c+/9vLJWAffPGEnD56C+sM0lyRdZZF3Vv5eXMmNO3lqn5Oh
btxcnBbnfSfWi+D3V710H/G41KwvIfKD6xHHccYLnXker53ch3ieqF/71ZD8
lj99i9y4Wfg6dPxy2tJ4ve4zwrVjvbG+hr2g9axcrkHxTdWaSLiuxSP/2vTt
jD5EH8Kxf/zIjbzhNB06Bp3AN1ZCm9F4qwD4xsakrsCbn6LxRpL1hCsRLfG9
ErfF9ZdyP9QJ24gnqYg4oc9CzPf75PnduBJ/F/zDro9zSuN9S+K5DPEADzzm
DvKeIXiPzKgj2A+rfQc/Jx/vh/NM5AeGcH4wKfZP+7PfWaoX7vJ9GO4jCnzO
KcfRf+LKScKV49XoHNf+3reZ3rd3x+G/azdpvO7DunlxhB+BuK62HjxBEccw
O3nBjowujX1WxDFmZsH502kw7HqOhxi9WuL6r3OIvCj9aKm84LdPyi1wmh8j
GfQ6lIhcXtL4mtB/ELwObW9L+I3M6xD93axrwdAJ4f5u1udw2JtWA7wHXxei
7jHOWeR3LiZG3ceIRi9pXpaGQD+z+h2K11kNqtM5GNs+EfuqcmUw7Atvf+pP
p2kq1lGmObDbB3+Brk8O6NTrJU8F0XhRz56vP+UTrU8LJJ0BM3Qe8QD1W+ug
l9C5Evj2IaVxrrw5iffvWnY8x0XJCNfLcpy8pQp80lF8n/9+OD/GetDZo3Be
dWRe/b60iFP1GoT4VYpRiJt8tdHX4/kAxK8+sj1/7gXwds0lfrj2YjPiiyvn
Sfut+ekazusRLaT91ry5GX710taw/+9zn7L1hWkfMP6+iHNXrwz7c9si7Cf1
CiKeL+qCzSnQX/q9Mui+YsUZBC7y8n/yFDRPgbz+Y8Uf7JAx+D7bs6IfRKlD
QfT/F8uCR1DoJPo+NM9KuJnhFccxzsMfqVIe9ahBYyQ7Su1cCX0BBjaXeP5G
fejLmZ/F/YofDfHxFzek8bb3K8Jd44WeCX3P2PksYXeZ3xVh/+D5LofemVEN
9pvg6dmesN+sFsAFT89KAlwPLAH7TMQPE4ZL+tEK2wMuO0r8FHTj1lfwOLRf
bLe0hT3m0iGXeCCKMgV54xiMt71eCV7F//CK//yrPkEfAVPUGa0HD8N4kwm/
f84ynMaHlEHcuMFaxIX+8SDc2n0W/KR6a5CPapiIcP3RVVo3wh4U68r6FgNd
/+5vgujzRZ/cI0G0n2gtyoe4cXVKD+hQNM4APzQLdAbsggPQJzj6I+oLQtEX
RnkSjX3nWRD4hrnQV8Lyn4F9cX/dzNJ8l7PEvGRgXPTn4j7F8nj1IOwXNUdX
SbdZ2f4N+3vDIlXduFk+xKnTJHxTTsRF0+ak728l5X6Oyb2Aj1qMOjWnfyji
GE6/3RnJK7jvx57eA/H/m5EBblyb2Ah25uGU4nnjnFUPQRcu0w4pr6e9QX7F
ODmzuBu3A04hH3M1H3jizLswH69AXc+AV9CtcvE06Ht9XI3nH38T7NCfq2PH
5bBvfamAONov+LVOnZ2jQ+iML+ger3ZvK9UBa2v8EP/ueUDit9prT8OuWpJB
wtWx/yAuGVxduo6dpATi5EPviHlG3dDVoeArRTcLkvBTDXDO1xoCvyz5TeJV
6h+bQI+S+TbOfS5Jg/qPx8PLunEzwWXotzKfzfmp3KuG9L2Zh6x5Yl5cOPTE
4wN36aEB/8T6Zv/th7wuEHdWvjn5RtirJ2Anu8aXcI83EnA/ndjx0tLtkGfm
vjlWtVaw02dcRfy7zyGaL60W+qGaCS9LfcH0A/XxXLh+2XiIfn2iflnUO1tD
i0DPl+ud9TU7pHNBzZoQfBK/DpI/rl3Ljz6kq+XxynBP4pkrFXifF3zvb6jT
MAbGwbyvbU5+jTLnKOIVZ/fwOctxy5yo+9TeHizixg2Ob9rrdkq4WXo56sat
7F70vUT89rEP7RfGpVe53bjV06L7swPAa3K+V6o8iAclziDlve3XzYMIH1mx
khtXszXG+TsuZ343rqVMR+Ot62W9JLwu4m5W7+f5GKf1b41PT7ixS5V42VqF
euBnBcr+qXVlEPQNAhx/Fu/RtpbE8zYCZP9X//F3dvffKy5dMrr/SY0V9/2Y
m38gXrK14NdA93XCSyGv5dWM/CShS68tRN9JpZ8h4frkd4g3/XpXyI0b0/3R
R6zIASmOqpwrAH+w4GYZL7QLvAeuj3PiM7Hq40R8xunTzX29xXjR11vt8prm
J3bfPeXXctRN1I0APu0M2cnWwXKh9Hdqf+QLftxAf716JQk3oyYSbq38iu+1
5CnG3+6L8Z7JYV9x/ZCoJ9JblcL46OPJpPnJsQx4owrZpPmMfxn25Ro/CbdX
+UHfz3yVEzj652rHTOSZ0pXN58bVH6ehq5CzlYQbpUohn5YfeqKiz6k++Cp4
/WHPkCfaXJ5w45AfzpW3Q2EvZ/clXFPLoz5hzjPkNQ7dhU5I8zyo953tRbh6
eC7h2oFWwK8MQx7lR3vYIazXatXtiPr3kpMR1w2ogrqBsPhSPZd5eDf83o+v
vN243uoxrW+7VjfU+5yeDN7X4kHg/Z8/hjz/T+gV27Xugkc+Pgp8sa0Y/4cv
SvN/8CfV1RqTRiK/UAk8LvtdAtThcvxKKz8HeeKRdzH+8RjER+ox76si+seJ
vo3KAfSPU9fcx3nPfrFa5xvO8Vj93G3rJvLsA1KLeBL92MP4udwbLp2DZq5M
eC4BTeX8agnUiahWWYlXox29iO/XvGgx93warYdDd+YLdOYc/Cz3ybgwrqAb
VwoEAI+Enez4R5dhJ2vvHBx2/nPgsfX2HR3mCyGU/3d4O5cX0/XtAVUKu3E1
RWXKO1uf00j1JmqjBvlxPY4jij6zHGd06pIcHP64q16J90/gWvYDcv+aejto
3Zj75f411uVw9NlZ0l/CjRGbKI9i17Hlvp9FeoKfdDEIeh/Z66DeJ9NY1BcX
ySLhysdktP7Naw/l8QUbpOXryvnc/+XtM59K4Kq/Gxd9DfTTyaFLs2HmcPr/
tiryIlNTEm68PEi4miIj8B3bwatsbxFuFZ2Kc9w4D5240HDEQ8r1gN927yX2
wdkTCTd+HkYdT+RVvO9Ft0OvI7oZ7NlUo7JJ85zpYih93rrI5NI8V56MuNPF
7p5u3JzxEfUVE95J9q02v8Evin9dTCjx1a3C46CPFJxE4DjHy0yKCnSNUz6i
X5wVsYB0XZQkHRC38i1NuNq3DPrjTN+BvEdp6DSbR8c24fuXPld58iAv3Wf+
frIdPskXdSbaWskOV3/bCX9+txPtRhyaz0GzIvSwRL2twJ1627EfEBcazTqr
ZS7CDxH8fI7/O7p/zM83Y/EBtMxOv0inXo9+71xNjidwH0B9cXLUnR5+gDxY
rkvg382/S/u5NTEH8U6s6eBlmikSwy/4nhD1EhkmJSb8PPevSZaQxttfm6en
f/3k+bGuwC4yVu2S/BFFa0rfw4y+X0Rzz+dB6KgYXZYVlPDH6CNrriqz/aAL
N6PbSHak63+gNzHZW8Rt8H5xn0Tjopxf1j/Ep/y78sG3gnu8XrEB/L9xeC+N
r5x/yYH3Vh/j4LDD8zF+l/Oe3MfTqM86KQ3vgY965/Vw+n2aH+zz/nfAs016
iHDrr/uID7xDvESPiaE8uTGP4zwfgYt6HIFr9Wypn5E5oz3qXl7skPofqWpG
soesfZulfknKgSmo0x+L/gNG7vHEFzJK+lN/gt92Fup6w5sBP1Wf+nTYq/N6
SfPG9VZGSPmMEv56Ns7xnmUETj/qRtRzWZN+gocSq75PufgY/mhWru/beukW
7Rs9/RFHL8J58EvdbtL+usZL8heUX2lRv32tpGT/W3dqwB9sVamgGzcq2ODf
JnklrS+9y3jkd46ckdfdsQzQP/zSWvJffl8Bdo5nblonjj5ww1/o+/LmvBQn
0eJiHWoJG1J/B+e5ZPmFPEW+71nduPmxDPJCnf+RxuutliPP8xz1QE5erOxn
zO+ydISLuKIaXhZ5wxWI8zt5t6CciDeedfhd0HPlfUn7T3dUyg8KvrD+g+0K
X6x/oVMk+vgI3H6QGvFYwbvIifmy91YNdOP2ej/U3yzoJ4/vsRrn3dhI9Hfg
ej1lUWOcTxVe4f0YuBv9fAtkIP1V7fGGSu7xdqnsdI6ryRTwQIU982QV9Rk3
31ZLyM8L+1hl8I3VtaUyunH16jnCrV4jxXj8HH5LuJ7naSLNBWsLisPurB+M
PpVxwRvUZqDeQbuDeK/Y55VliKta0zgOzOeCtdiJt4qfrPgc7kNzvrun+3P1
WR/FOSFw2EViPymZNZ17vNHgCfafclPpudvvgqADMDwV8in1R8POYb19s1Jr
8JHmXEXcjPX27an7kNeYFpTOPW/2ivnggTydSueM0qAsxTHN3szrXpsa59Py
FrjvvCcJV9fXwbn0qD2eZwTGC/1/a21W8FpZ/98Mf4U8VGgo8m4P5kG/sRz3
kW8KXC/45jOfN3I9prBrb+UQ9hvW8X91wnKdJo83zkIPR4sCL0L5h+uSVsj6
OboX7AYjbiy9nXjQ+9CWn2edt6rQiZ3eH7ymeHPrunGr6DDkL8fOwHx/gQ6b
WXkz5rffBeTRsg8nXNHLnaB9lfvdxfajzSuJiLfr+NFdryNvVXOptP/Yp+Bf
a9fPyftVTuiBmp1GgxfWOi78Vj0MdScF0G9IG1gaOjDrVhFudirK/YZisN7W
t8Y53Gc8PTfLHhhE1/leiPZ3fWswxZ+cOpqOCuHm9mfEdzauox7f7nSCzkfd
azL86MaHEK95uZK+pxqDPLXYJ7WzlRAXWrVYwo2RxaF7OaYn7d8Oj3FKD+hd
31zg7cb1YjUy/cFVv+o4T99iPei9f4APxbp8Dm9cGUafq33xgH7kskjENxtn
oTiwwn1tzFj6Etps7tccW1+ifi26rr67M/LL5/xwHeYlOjjzEhXBw+yYrh7/
Ln5kXaarfyXC94kAn/F7J+KVGdMN1KFP3YF1ExDWFJ8TCjsjgQb+sk9V8BL3
ThLnYqw6aObtlHLOHej4VL+P++gbUdqN65W6Yh976Q9dNe6LZC7s6EH38XMU
+G+jM1J+UEt+GvHG2ndgV8+rgvxi9u3wv98ZiIdz/ab5IAx5osobkbdl3Vdr
VSTiIuGrwXNIvAf51Iu7PpN9MnS1tH7s2qEU19WHAxf1IMqrrPCDarzGeTdI
wXk86bPMIxW6cOJ58fN1cH6+2sVUqDsuoIHfMnIk4tUbPyGPMz0E+2eKuLCX
rpwCPpvHv06AfDzrA+vH+oHPxvrA+uz7iKev5OeeIxf2sQJBxM+1TvcFH/VO
N/Bn5qwlv0EzatFzN1blg7+0kePDqwrg/HkWQXEY7eQbvC97cyIO77Udeaz/
+C3wd5k/47LHpDyCC5fyBRbzE5UYzp9+v8jnKecfHH4F/t464YyX4iex+fBq
jHwdEZ8R11EPyfaVezz9P9dnibq82HosVhTGx67vVt/x/fzkfgLM47VLbkJ/
z6F9CBf9ULSJB8Ej/29+/MT80OelxzzbrOuorcTnGVVGIA7EvHrlTE7KjxtD
oAOn3uR+uDlyQOepL+r1RX8rszDq+dXEXN/PuFIR9f/a0wSo82b+vOgnaOf+
xflq2EvKV/PNn/dF8NvFeNFnUBsJv8ROOwx9A9ufjiE7rt0M+B+b3sDuanqC
6tH0qcdQ//f0La6T8ts7Gn85AHU8gsebOg/q8WfkKSzhCwMQ13u0gNa/1moU
/PCNf1E8xbpWCe/lx0/Ix9etSvunlbId8nvPxmD/aXdIxFOk/TZ2P0o1EDr8
Srus3I8wG/Qj514eiudwAPob70PAb4oXDnz2YsQ/kyUjXK92iXBjI3hURq2i
6APJvFMjb1XEOb9/Q/31TsSrLc/2wB+OwfpejLpUJWhrXLr+rw/Q9RVx42fz
KV5v5k0o5X+1cycQVzcqSPlfJcE28EESVCjlxtWmSWF//T436fu4zs0/1xd9
cJTojdifuQ+O2CfFeLFP2hVM+l3rvx3ja5dW/3/Xp/+/fRN+f4YQ+K1dz8N/
mfUe59Nm4EbRCqjvSxCKuMm2nLRO9O2TwEvzWgd+kgVcy3gDfMj2l2D3RiTE
uip5ELqZ2ToQb0nEIe0yAbA/GiSXcO3ALPgNJdY0cONKygLQLTnRDONP9Yb+
xpW24EEcYb428zTUd3IdkOOPfBL5V95fPThOxbioF7DnDUSciusFLO0Y+G7e
2Je0ghfhX/vALxRxMP0D531j1S/rH9mfjFUvYzaCPWDm7Yfz1NW/if6d+Jd0
/uoe+ei5myN6cz0k27HRabB/9w4W8fmS7t/tY0phN24HB6IO9MMl4u2oViD8
1nMxsOfSHiR/1F62m+wNq9lb6BGM6v/0oAvXM8yG/9k/MrV7vL67POLeGfqA
b8x5Da0X+9Gx+cNfRT5d5hub8TgvH9NT9IGC35EcdftajzIUB9APsp8yC+te
aXQJ+iKFkAdUfuUjXMsDfQstzzDw1trehd/X6DTsItZJMOciP2hvRB8hgdsP
kWdU6zGf9jbyQfoj5tMyL1f5jPyR4OUqsfjJdjM8d4cPybjF68eFYx95z+vn
TA5xHdme/M/+BK+NeQxCb0fE95Ra4DFY3E/KTFUE+pNc5yV0xoxRwIXOmPhx
6xLQv7PlOlwre0vgdXWsV9G/uPZqxPsa9kdetnML8Hl6++J8Ljlck8YrKYHP
nYb7vFEU+pl54wXR32f5LOt47J2F+g7uS2JlT0dxP7uwgnjswA7EC7Jfx8M8
jNHAdwgfjLyeqy8V/Z2VCTyiwxHQqdgZhPewVWrwTO0tyN+Ff0TdbCRwpW8f
jN/4Afgsf+hDct2oEVYaOiETBoJPx/xGdcNOun9zXTfyc83qM8HXPeKDOFiO
PoTrxbmuJLw49FC5n7uj58D93I1ShTzduFomPXQrjhxLJuGbr6G+eOgPOb+Q
4Tvew0Z7pLifWlyFzuCiMDk/dbMOdLevL4SfIPil1gWqe9eepwpy49p96DWr
nWaUd+OWz2PKzynXHJ0ovC+LHkv6UWI9C/0o7eXITxQPEHmuogmRd2w19nug
G3/blepn7DkHqM5F4NbdtFSfY8Xtjf3JowN0pA+tpuvaL6CLplQEbo3t+I38
oLfYH5y4RwbEQcyMcj5FPYi4idCjMO5yvQnrUajZTiFOJuqFzy9CnWYFRcKV
GcfAnx++VKojVv7NBB3pJgcqunFtS2madzP6dIg0fnJ2vBd611A3bhU5jHkO
7+JF99WlC/oRjx0JnlvbSPCFuncGHpAEdSJVl4A3PzocvAK/ctgHmT/5f+my
8r8OfzIWLum7mmnAb3Le6wHjwAdj/RmBC/0ZZWVR6B1x/wW9yjDq22H0v4l9
qP8a9BX9GkX4H3+Ixv3keqJT/8PXcvwL+rzPe1E3MCzecHzfCOzThzzRHyRl
DM6X4IQlpfE1Tg1zjzcf3oLd2zP+EPr8oMPQzWv6Ge+FXZ5w5cUy1FOl2wv+
ufCDMk+B/7B5Kfxg9pu0hSbqgNqAj2MvK0bvuzImK/ZvoUckcNZp1w6y7lDX
FoQb5kQe7/AHsY6X4xyyv+OcUZw6JuTNBV9Oj+H6jmR8/s0Ygvo40Td2VDVv
/nupb6nRtw725U0jkIfn52g/bUx+uBX1r+bG9Qpjoc92GX12RBxVW1wGvKUJ
r4Lod1ccla4XAH1UEUfV8r+huIddD/FqhfXEBE/Y9cN8AIdvLPwe5O8Er/hB
Yn5/Wccg4BLdh50pE/oHcP8+6/IR6Ar+WA2d+IcXYPeObgKeg9eoXO7xujIG
130SKPiQ+Nw7SVfRftW6tObGlUI+eyieU+KSxOswMjSk+L7QdxW8ay04JgH9
nga6cWIf1k++RLwypYPDrraBm+3WY1/eiLiK3mc5+vScuo7+Hrt6Em7/FZ/e
E/1jJ9ilpapQXEXtir4+asHRFHdU1I/ggyqzwJ9pP4finU69c+ltWPe8nkU8
UOhr2QvioL/AKzxfY2MY8AvDcf4W5nqHWakwXz24Xk/wadcgT6GF8r7lIfpT
Y1+LzW8UuN5tOvkvmq+J57viCK1btVl++C9N5gDfNY6etz6wJOGmfgDPPWtv
2mft8fHF/kg/+qTDqLueEr+wG7dfpqK8o+6ZXNIdMk9vhL5hWei5ib5OypIO
WDf9RqDvuNDh9OJ+NMMnSXFg8+xx4ifY9y7kd+Na3H3A405EHvzXc/Tlae4J
ngPHYxSHT4L9VMRHTd7nf/sBZdy47Yn9VnsH/M9+wt8LcTPm36rRy8AT9XlO
fVHN8A/0Xim5yqFezvsZ4equGYjzxAlDvfv63lQ/a3f9G7yGWH00jAQPsO9x
/1mBK8Y4xA+7oj+LNmMe+n7W3Qv7deNm+K29gSvqcNpXRT8Xm/vUi/6G2oNL
iGumPdeBxnNcVBt5Fn0TduajfJ+RaQrWwVV/afwfnRb63Ia+QfRv6X70vZSV
U7GuXnsSLvRp7VIHoGP2KZxwLXEO6NZ+WUjzY9VuhvrWT7ehM9Y7E/hwr9Ff
PrYujdIc9qxdiPm350vjPe0eBD6D0Dee5we9lfVPSOdSORmF+7v3ic4NI3AH
3o+c78k+sz6byDMlDqG4hfrmI423Tnjh/HmVjXWWVcz//kNkpylBxyTcjmmw
i+IuPtllPE36h7TPD0sBfavraXCdpjvRN5P7mgnc6Wu2qll1N2583SL3Qft6
Q+6DFiveq9aDXyd0uYUeuPJmMvjVzEcVuOCjGuNHQ6euWWeMX1GG8sJ2c+e9
YB4a8g324oTQO028Cn3idiaBP/88gYSbVzqhH0Pdc2RfCF1cNftm+lxtaURd
N26lHQSdyUBTws1Ppyj+Y4fkhz6Z0PEb3Rz1JMsMxEVF/deQX9BxCChI4506
rzz1abwx+bGoI4aOK9sP6hQHR16N6+PUMaFsb3Jc7ibOIW14bz83ru4+Bj/F
SlxMGn/oGOK9S+MJnH60zCcRZ97uKfV10frvQP/EVF/BTxL2yYIlqO9o5QHe
yPVqhBvTxxKuFa+UyD3efF4ZPJuh4BX/p0cEf95q11Sy59UD25Cftl5p7uvo
twqQv6f+OB3kxtVal6juz6i5ItCNG6lykN6WcSqtpFOkJHqJfEnzPNgnhP7A
XfBSlNLIcyohg2if0bJ2cfoHuceL/kF2061yPnFtMezfh05L+Ue94TfUM3Yo
RvwER7+lzyzE5Wb65HHj2qVzqBfrczmzG7f6R+FcaR+J98+3E/g2w+ODV7fu
E+FqUtQ96QtaA/edDn2iGR0RF/2SB7pGuU4jr7QHfWqUffAjRBxDq1iL5iF2
HMM5LziOIeIhDs7xELVreeifOno1JdHv03NabTdufH0Dnat138AXFLwj1mfT
lkaBX7gnBfQ0WqxA/GtVNI/3ZB2MBIgbj2/ZwI2bhVLAX95UH/l31gUS55qS
pAH4+yPRF9vocwB+0NpawKthvDjvzDFtOa7LeZY+X1B/MrKljG96i/2A909z
23zMA++f5ow4sGuajsLzrZ8T9emFq1P8QCn0rA39nuwT8UrtEYuQV281jHCj
ThzYmU3WkL6pEW8u4UqLLeCpT44PHvsE9Fu0P3/ifhx76XrWXfRbtCYvwn7y
bQPwYIzXM5TBvlUI/RqMtDWhy22kxvmXeTjisE4/xD7QEymBPg5ivFYOuHL7
E61nJy9TeSP4ukVnAd+7k3CrawuKq5t719DzNHqVQXx+vj/xRuyH7aEztBrx
efvlvwn+jNcmaHSOmksYHzOVzh3Deg5dwcSNcL4cmUHxArXTvnxu3JzhC7x6
GPyyExPI77YmDUd+ObQe/L99J+Gn550FnkKqhtCHiMZ4/Vlj5G9O3srp/r5W
lQlChxE6gXs2gQ+cbj7WWVRe8PqfXwDeJRF4IdnmED/C8N5KuGbsQl3GjvjS
9bWur2A3J36NPgACz3wButMJtkm4ObQs+Gc+GameUr+8i3AlRyrC7YvzcrjH
q50n0rmkzTsCu3R3VfhrQ7ZAPyHFMQlXU+yD7kaHdvXcuJHIBo9w1FPwFUR+
JC50f8xyXSl/Z97di/svkJ/2eW3cA+hI1xiHevMbAeiXl2gcdJrfjUE9yM/B
sIPD8kHP79pmxHMWVQM/9DP2e6vsEXzutGDUR2RNDH8rxRr4L69rAuf9Vo//
mOwiZ7/lfVU9/BB2F++rauOpyI+LvsD9k6EfxLxVIW7c3pUCcafv8yq6cfVC
CM7jPh2Rf8k/E+s/4dZfdJ4viINz/sQW1tOeBN7L6e5++J3xf1dRfMD+FZ3F
/RyN/g1hj01NhrhgxGo8d/6xr2dL6Mbta9mgm+DgBnD+XT+Yn+09vEfayX+g
d+d/CHmLYR3w3l0uAj9kf9Mg+rcI7D3d+wX855YNodfwYBTuP0Fr8IX+9gb+
chHWQ5yJwH0jsW8NBK70fkvviXprGr1HWk8NfXPKXKDPM9pM5Tg86yH/ykzP
15r8oLwbNyuhTtCY9hi8zDMV8RwbbCY7XEu7n/PpwJWJ22kejV7f6f1W3m7A
PCdZTvdpncmJcyp/GOqUzzTB+b5oJ/pGFAJuTWyD+ucVr+CHtOA6oLJP5H51
WbrJz4ufz/88l9/P142LH+taHvp/wds0x8j1jQJXFPR5MazuHu7xVpsM4KFM
fIr3Za4n9quwq4gXtB0KftcuXzyvJm0T0Lw87Uvnmr27OvafR8Wp7kAdcw32
z7/eeO7rY7A+AwrQfSoR9bB/LurmRfdRMxP0JG4D15t8xT4evh7253mcF4rH
DhqvDIEunW3Pxfwk9qb7UTtvgE7Dgjm4/rMT4AGkzQm9hUcl4OcaiZGnKACd
V+HnaulN6HXXnoP6po8Yb42fjnzNB/AeDe+s5IcaXufpe9mngNu1UP9rWw3p
XNOfoP7CKpudcHN5b+I/aAEjUdcp9HbCIylOYoacl3DdawPWyeLFBdy42Wgj
8jQps/M64XPh3GiaHyNBT/AKuT7ObjcR8//v+lJuXLm+LB79niq+NF4Lrw7+
X5tp8DNaNcTzrVoE+lkjCiJ+HLQQ8/z1C9kr1vGNeC/Sz4d/eioQcanEu1Af
8uUB/NDGf+PvBwUTbswEbjfIT/uGWfsG+F0cPzTfzEY96p0UmH/h930vhHNi
Y4cQN26s+oz+PQP1im7cPJuZ6pXMsvlxnnypj/WzaxP283xlYeeMz4h1u30F
rW9zVkHwJUT/uzmnwDcIu1lUwssXgx3VNE5xN64/3If3MeIX+CxzA6F7fPox
9KaX8XnOuHljMepEJsYlv8bI1x54yqngjXK9oTL9LtYz1xsq3/4B7jkX8/yv
hXzNTRPxHBu4PmAx4msDeoHXtmEznuPZiXh/M9xsIN3/jrn0vhm7cjd04+a7
YNhnqZg/wOtHn1Ad8epBC0q5cXXkHexj3xQJ1wusRL/4ej+Rz6qFPsX6jTvw
VzMUgH9+JQzred8A1L+seAz/rCNwo9t3vD/vEiHf0GMo1vnA02T3iL5sIo8g
8jKx8wsiHqvOKom6/NmIc5rxjsFuyH8CPIi0V8APSdwX63XMYMQv7ZOwl+Lk
A/+1K3Rd7GU98bl5odeqeY4NduPKAQ39wjbtquDGTQN1T9ahbciDifxppsPw
0yv3o7ifY5duD6D32hhV18eNm2vaU12JuTpVcTeurfgYj6536xXizcyL0I6i
nlbgpm87GR9wupx7vPGwLeLhdQqCT8F5IjMcfrdyICX89WU3aLziWQm6o1+z
o45wAXCtdlLYcyM3wQ/j99cu9H4r5QGW7PN14+adN9Dj3jzE241r48LgF0f/
Bd70y3e0HsySaz5Q/G10AczrkUist+vzKN5nNzsMHY6xh3C+r+wIXc5X0IFU
zkBXxPRvjX24FuwivforjL/aAXn3Z2UR50ltUL9IM05+rleDnazsmIn3a9Ap
4oVb7dfCr0/cAfyBXhXJzlPGIz4scOPEbMQ/ub7Y8ChGcWOnvrj5HMR7DX/C
9ee74NekaMM8pSmIMz98i/qRYolht+adiH1vQmfoJw4PQt2nGo7107ox8euM
lbWhi3IHvBEl4jh4/0+nIn++g+uR//qJuArnNZxzZ/wC6A6vvuLrxrU9CWBP
THiOenFfb+Dt19P+r3f5RuvEKLUF11nmhfj+rfGIg/VvBfsh0UDi44ofYfcK
++k/3JDw/7G7hJ3s1xk6oktaA4+3PS/dz5ZC5F9rgb2G0/x8z4a4xMjS8LuZ
12e228X1PejHIXCnH0fGiuBxH7Kwb4xKE0R/17w8nWt2ncbkvws9HDX/oopu
3Fbae9D4WiOhh7lvKa6z/QF0r+ueYL1N6AZrs3aC35w0J65zYhT6A9bYgDhX
ppyhhIu4XKuvaTH+EHiq70YgfpjpO3h1E8cyz4btxrdfEZcoPI3sbev7YfjR
bVvReyvsJf1WeeRP2F5SuwPXapeEHmDXDt+IJ6Elhh1VtRT0UEbO/Unx46+3
vfC5OfC5Q8Hft7pH4P0Q+171q8SPURLOkHDteFZ6jlbb7nQdpcFu4MMPE243
8ISewophiPM0CUG87mlu+Mcc79J3doZdHQ92lNCVNcbVAM9s8GK8H+Uqkr2t
V6pE56l5ZS7ej9QfqH5H+XcD4iAf1yB+8KMozrW03ePTfBVay/pg6M9lGZ1Q
R8X8XoE7/F7mAzt9vpgPLPppGgfRF0z009RDPCq6xxthibjOKqWEayn75qDn
lfwf8Ed4n9dK3EZfmSEPyrlxva438C6D8NzZL1NatIcdMkasc+gm6RPSIJ9S
vHaIe7yW5xb4NMwTEDwKZWxW6Bv0nos4yntfxHm6bce5Jfq883hxvusRR+E3
PfBH/OdBDObrSgjq++22WLePnhOu5m3pRf+uRn23luYr1nPgErz3K7eh3mfv
AehnPVqN9z4P6sSVfPuQV9m2lp6z+vog+y8R9HyNhdARNSOjYO+FJ4GOqogv
1booxZeMm+2J12R7bUS++NMjnFONslC+W/13M/LLkzPAPqmyH/qpa7agPn3Q
CorT2hdDEUdSz6H+9PZzxMlvRiHPz3a42qQo8bHsYcsquXElGvot5oxI5P+T
38Y6+VGHzlP1yiDEaUN8sG/3vAXe/bYyyHdfSwm7LncM/MCf7dFHrMpy2E2d
/4adwDoY+oZyyKezDoblGYn+z1UxXn0FvQuh6+vow7OurxleC7wV3yjC1RXp
4PeN3FFbGs/+oF7F4VNgXZ7xoPyFtcfpU4c837E3WDdH51aTxv9cDr+P86fO
uhV1JaHtsQ9swvto3BgIP4j78DrjmUetx5SCvy54Ykfvgs/82KjsxpUaI6E3
0ba9hGsPD0BvhfXgzReroTu0Ix2+T7WB4NGx7qhdwwP9y/jc1xPBzxXnvpHA
yZuDV/OV9QMtp98N66z+x3Om++U+vHYM85ZKRiP/VZ91tFL/BXu0aAh44MMK
4L27uR287ifNwXfvDlw9HIa8XsazyM/zuaCeP0J2iz2jInT6RF+DVwVgpzVa
nc6NK+lXYX6TncR8Rz3Cum2xAe9vZ7ZrBG9QD0FdSbeNwW7cCD0KHa5s6NMr
cL3LYdTp5S9C9r6xM3I4Xf9uOPziTsmkOKqZ4zjVS1oJ5XiscmcR9XtS2t+X
465fU14jHmHRlxnc86CVLAienr8feMGnoIPh+OPVGiFO3qg34cJ/N2a+J79J
rwrc7pEYfhf3FRL5faH7LeJ1dmgp8AQ4XufobzcPIlzob//JU9C4qMLwK5uu
Qb3UWKd+B+vnIOtPch2Q4L9ZrEuplJbr19RlrCMwuyb2K64XU82L6MNl+ocS
3h19rJR9V2HfdK5G/+/w2PddQV3S/Tu4D9bVVOwh0AfZ8AV1dNUrgheUrA/s
wvPcr/ky47fR30pX+2I+eP80Gj0Gn7zfgApuXFufHv7C+GjpfDfSZgffj881
Mf9On77Xv3DeHSxPuLa9o8Qjsp4EEu7wiI7kRv0K17dq66AfpKe8IOFWv5qw
1ws/gj3F/cr1f8aB/3GwBe3P5owQwo16g8H/uLkQfYYTA1c3Iy6vZvpKfo0a
sQB9LmbsRBw1xxLEvyLAS9ErN0K+Z1Md+MXHOC73721a33ZIfqxP7hulXawA
eyVW3yijQ1rks5q0lOIYxpwo1F+/+ibFPbSElWA/7w+Gjm3BeNTvXvetg7rN
Vrek8UY8xIHF+WWGhMEP4vPrT96Z7pN540I/X924CnFl8f6+moi4mW+LnG7c
nt4B8Y2r6X3cuFlqJsWV1IxLoAfcLRLnmvdmnF+ZfKArlfgN3b9yoi2dg/qI
pMXcuPGqIMU5tcKo11Zn+8AuepX7C+rIYZ+b90viPPp2lOx2ZQDsAeX6d7qO
daQNeCALeqMvvbj+vlJUN2RM6iqN1ye1JD3qP3366HdRXzzyMNU3qed20PN3
+AOTYZ+b89qkcuPmwHyIO2f/kEvCPQyKYxt9V6IPS9R4qsOyW38kO8BudZz7
XdY26Hsp0J2xU9+D3bp7KPyv4eCBGwea0futV1gBvHAUeL9HVX6+zHusVBvn
YAU9vxs3dV4naZNLuHX7K+LO9c6AxyXs4WYPsB89WYk+Re0+4nMft8U8Bj6i
+KuyNBvdvzZuA/i7aQ7Bj9+UgXB160/wGzfMpPNTK5SYcL1dWeLFKS9Rf23H
SQF7LxPnAdvwPrgnhPkJlXE+RsXB893eg+5Hu/d4DPHmliaBTozwT4XeiKgf
Fnaj6Pf0l6+/G9cz9EBerR/31ezP/NJlg0L/4Opv+42umxe8CC1tUtJR+bP+
adxH3KfRty31X/hj19H/Cx4C+8uif66oixH9c7W08RFHSTYF85+sHXgCmcdo
7uelBkKP1Wp2A3bUhlt4Tz0GIt7F/DfBjxL8N7PEcM2NC96F8SEL9ssA5NGM
lcE4ZwfHgJeVAtdX82Z+THz+IXFoPVqfEG/RvvWFXfKtPuI8IxEf1kcHw87K
WRNxoZOIAyvvIxFXfT2/lHt+RN8l/dwK1NdMx3xaL38hb75qckU8L9ghtn/F
GIorpqiLfbdoBaxz76P03PXSNvS0VgTh/CrTaCTtJ82zS/aM9mIw8sVbskm4
taY86l9OBUh2juIHHVCj5TQ8t52oA1LntaG4nBa2HXE8jpupu1tAz9OD9Rsz
oE5HrdAePLlf+yS/RrvziOwue9827j/Lfvd15F3UvQclXOk68A54y+i7YTX5
iXngvhtO/44tbOfH6t/hXJ/7d+jD+mAdNWgCf7ZJRvBIBhzBumo5Dv5awFro
VEb3xrnqB96C0bQYjdefQf/Dmjsa+/bP2vBbd6OOSu03DfnTkd7Q0XjZDnxj
n+Swe1vNge5Pyq+Iyx14AP8xT0va74QdKPwU47cdSOMmfqB90djF/cfndUD+
JnbdUxEF9TynoJ+mroAfraY5An72uyw49+twn9w1wYjHcb8/oxZwp98f9wcU
56zoD6i0Ad9V+ZQM9zO8vcR3VfYBF3xXgeu7C0q4duUJ7IERL8HzOT0OOu8t
lkp8IbN7JN6Hutdwv23A61Z/uzt0X5ej0A95TXrEAQb/QD3WvO3Iv619gbj0
PK5LOB8Xzz/3c8RFN7VGvcay+JxPYX9H9QcP0auErxs398cB/+rnctSrhLE/
1WIn+kj9PtcIf9YP+wyfa4Yv6hSMA+jHYpdO8J3ei0fPgujvejxAPtVrBPRp
542W+gNq8wNQlxoUIPWp1N9e5TrGWeAnCj32c2sQn8np9IVHPU0p+NvqqTie
blytB//c3rgf56fYn0+NQl4zbg4Jt468w3vYe3llN26+YR7O2EGIsyU7gXVS
IwnsgamFpesYu1LiPPBGnxTn/EpUHPHc660k3J6Jvm5a/7HchwX7mDqhM/I+
c0ZWc+N62FM6p/WZkVXcuBX6k/R91IdvUJcp9s+1LeAXZ5qOvBY/d71KN7zP
acbinOI4rTbtO/Iuz5rCH/0G3VczZkpe+tz433GOd5mEOOevYOLrqGUOy/vk
ThV8jpDKoW7c6tkT/uMCX8wn99u1ku+DHrr5GnHCibvw/kUhf6RvTY688/vL
WOfXGkOv6Rx4a5qyDu/FnOqIn3R6j3qtafcx/tVq/P55Jn0Po+4mxGN/9gZ/
/3VL+nwRpzVDoB+rRBSleIn5Jh/2t7S98D4+ulrMPZ9qsdzg65zLgjok0c/o
VBroXP84Ab7HdN5nlpaBbvy8AMKtTy9gt3RrSc9b2Yz8jmJivFYY/cVEHwft
QRnEGTiPZgaMgL79shuIkwxrJ+mMW4dbYJ9XUsJeH30UeQyOcxoPYyQ9QSW1
rzRe64n+7UIvwridDf5nfcSFnHqoOuiDYvZcWME9XvVIgPe+W1x87w8a1vlK
FfZlk3/4vWNe2aX9sM/qbKA8uBPXmtYfugY742Z141aRZOD7+l9P48b1Opex
DhdV57gx25mtVqM+c12Rim7caj8J9sy7xdANzpAWfYe5blcpNAL4pvDudP2u
VfDevjpe0f25Zodq0GOJjuA4G/Z/PVEm6N1cv1tNwndPgl5TmYHSeGPHE/jn
u7eAD5LmLL13ytpDNF65mhD9Fm5D98Pu8Q/tG2Zi6Fc5+h6fZ0JP5xzXhYvn
mB6/K3vmwT8QvLX+X8hP0Q+hT4h1shn4UdNzQR8gIFgar3vUQ/3bzX/k+Vcf
5KVxSx8mluYncRj24ZGZfrrrXtVLgYgzvI2P/tcdoL9qX48DPc3mixGfOABc
f9mC/ED1SmLUsc5E/EoN/wSdgU/z2G7k/flMYfKf9SN/kV6UouRHfUrXGUE0
nuMYTj0L18sY9SPAy+mcELpqW+NDJ7JjqvyYB/Di9KKJad60Jk+LuHH77nzw
Qzpjn3N4qrOwDxqXDuBzOa5i5FhM41Xf54jDrWZ+7KJViFsWqg2/IRy4YSjg
gXn2BZ93A+taFMgDeyJbO5yXLe6DBzumJ3TGV8aDX3PkHnAdfo06EPaDahWn
72tZbUW/BvxcP+Pwx2g+w3tjPxF9HlPtRDztbTXKU4jx6gScE2oO1BcLXK/O
9cXrDuA8DN8NPYcmXcBXmdQtyH19a/JL5N0LNK/gxo3GShBdb98MCbf2p4F9
sawIvUf/6R+ir60W70cNN24/aIT6jqIZpT6V1rs+yDf1L8b8H8QrTH0w69wd
93PjQq/W2joNPFbhv+zdjftpMo51AHh/WzATdvmzVVL9r3mjFfLlQ0qVdeP6
6/t4X1pNLieNP9uZ9gerTl3EXXdin9fGXcQ8jgYPxOHrptuBfirsn4o4nmMn
J+vNvEo+38+WQb/SahfLuvHf5yTsEu4nZWW/STwH0U/KqGCiP8PHkYRrtUsT
j/BP/RfN307gytqpeen71tSRL7heFjjXHYg6dMUjBeGiDt0KqgE/Og1w9TXi
BWbGCTjnRf735U3aN5Stz4q6cS3XCOSv5y8qKeFN/NDfdsJL6GIehj1sXfWD
/VTiIfQWhF3XNBx1wiXiQr9IxGmzo/+TrQwtIOFxH0j7g+M/8v4g3kfzaSY6
32O/jxbzJ438h/Fc99wme1hl3K5wBeus1QrCzYiuPA83sC73fOV4V1bmzR6E
ntkWBbydb89QR1D9Ec7rbTy+91PCjZ8YL/QujMXJcf98buoJMuO8nQvcHtYP
52bjnOBri3O56Ebob3A8xKnvVlKCd8vr0+Fr8frUpp3xds+/HlAJ9sSd9ODx
DT6F9Zm6NHRL83ZBnK/OAMSpfKbjc819tSW8no486eee8viD6WGf5Ngo6fxY
lwthfznFdaTFh+H7Tv2nqvt5CftNK3GZ6jvEj9F2JnQkiman+Jv290Hwzarv
xXt3dAu918b0Z1Xd82alWwd7r1wO6FPVP4x15bGH7APlSFbY7bugH2Xv3ou4
bvgMxJG2A1cTJUJc5e8RXPcNXop2eCDGe52r5f6++udu4L+VSchxPPjF1s+2
eE9LRYdi3rCu7FMjcO7uGyLh+p4qqBsqfYZwh7+9cDLFMezUulRfYH3dTfli
rZlcd6BVP/WD4kh3v6Cf6tun4F/VGHGceGJPrleT5u1JIO0/atNyNd24nXZh
UroP5aA03ij5iOoH//B53N9X8HnMmn2Y74q4lvYrEnZpeM+gP/8qGYZDh2fZ
ZvQ7jqUPaZ30o3i1vvUlxntgvHHzLuHW2c1S3lafGoX5DzkWKuFVk4NP1gi6
lPZG7Ff2lGjUJXWtKV3HWlEUOvsRHGfi+bfT8O/FZ5V14+ot9C8x26yX9M0M
j51UV6ll/x7gfi72iR+om+X393/iMCFeqMPo1YL1iHbgveb8uBhvPUhE86Yt
aJIP14fOpH3Sgr307HAeN274d4e+ShvuRyH6p2cZTHkEJcmOSm5cD3tEdpSR
dhbiT3HWIp6zODXyD1ZxnFNNtoA3VSYP7MNd+eFXxR0Pf7lzCpyXnkvx/vL1
leEB8H/2Nq7sxo0pd/D8jIn13M9Fua7Hpc/ZkC2jNL72NORD53snwnjwuIy1
hwkX/H8x3uH/d71V0v1ctO41EUd6Esj6JHweJYKeoFYtdYAbV6dBB9icMaqM
G9f+AQ/VSOhbDtfn9+VRFuzz93qhvi8T3gs75TT4C98P8fuL98ieiDyCFvcb
8ERBvM73Y95EvTzzKkW9vDl7Beq3y+N80QomonNcm3df1mdbug7nbMMJEq43
8IM+1ciphNtfOmJ8Hei9GqsaSOOVFf0wn8zDdPYBpw/4NfDVdl7HvEWmw+9N
4lZ1z79xuwrqOVeNlPxfY5MPzl/9sRTnUS5URJ5jqiJdx55yGXmON0MbunGr
yiroHZ2JlnC78TLUY0++Js9D+8nQV+inS/uDHTCX6vjsb7fkfSZeIPyLfx+H
StfPFoL66/FHpM/VBjdC/KRRdkm/SLs8PoiuW+nodrc/aPnpsEsLF0rnHq9/
ugD7vPVWiS9q7FgC3bWYYhJuhanQDzyE/u8O3mAr9KdSxQcfaQf8HSNJO/gh
Rn/EBev7wA/K1wr6Ajnawb4W/tS4njhnKw6Cbtaj44hjL+sJ3lL6ovT99KHg
PWo9o/ISPtSEfgPH35QlntD5ul+K6/6gQ6hGJiP+tpK7Pfl/umcO2KUdRlJd
vNWvGuLAo7MAn3UAvH3/fc+hH8XxBM8AnAdxy4H3yLiaLSmtZ6G7KOxtobuo
pCtRzv0c9UU1obPJfQntOj2RT+Q6a5HXFriopzZGHyBcWziDcEsbhPiV4vA0
SJfmv/40Dg6dLoGfYR5IrD681sgs1fG9uN68VFXoL3S5UcWN6wProX6h1jnU
B6WFXrdxvTfqlFlfLnac32zfGHpQot78Y2fY66uvhLpxc1pmnFMnS1Vy404d
ONebi36OIu//J2/ixgV/RnuKOKTIO1vr/Ak3zvn7uHEjqg/q9K49kcab25Ii
zpB6kMQTU5NfxP5zJwDx4xobca4sGIr3qGxC9LXomRj7b9VSWDclxuI5XhqP
OFHJ3jifysHPFXXZ+ratmO+v+9jPxXqzU1/Fuq88XsaHFcK8tiyMushM6Ddh
5jcxr3Wnl5Cu3zM/5qdnHQlXw1ZgvtPVQv4iN/f9PHoLOtUL40vxditNDeyf
4y/T9Zz9qiB09pR7wyu4xyvzN0O/7vfzBf7f86X7DBlFnyt0KozMNvzly/0l
3D6wFXnJs9H13Li+6zTGV07W0P29jGO9fPD9RteUvu+K/bQ/W1nGS7hdchPV
QWjHoachcOXJUewb/p7QCeEfo9FI1AWMrCBw6N7kf4u4w4urrJPPOgZxriKu
urgm7T9OX8KFtaCf45UM/IfR7xHPv9oY+jz77mZyj9d39yPcSve3rxu3QxTy
g8wZfYGPv0DXMbfHoC5e3eIjjb/QmcYbDQoH0biCkcgDzo9H76kxOi/ieLk5
Hz34OOKwKYORT/QCrn47gPnvtIjeY8fumvQAdsL5Y9DpnTiD+X7VKS5sT90H
fc4He8Dry1cS/aWOL4B/NpZ1GNbvBk+MdXucvq6xdHsELuKQ9pC/EM826mN/
qJGCvqc6dDX0bMQ+yTrnZs42Aqcfo2MN8Gx9Okm4mTp7JNUd1y0M/RVR/zgx
I/bNESlhB75mvaBn8VCH+HYe+mR5Q09AWVeF7kd5MZtwcz/rDySF/6PdnSzt
D8aN1og3KkNhvwv7fEJl+POVJqJ/LO8PlvGM+MBKlSJBblzvuPEZ1e0Wq1RB
Gl/gOtnz5nozWMInR1O9uT7qHfatWRWhoxWEfiKqzxkvut992cCX7o2+B+a1
LqTvY9isz7b7DO5jWH7p/q1mBj1va1qnSm5cbT6Z7Ax1A/rQCV0FTVuHOOqG
HMjTNo3Xib6ninipMqY26jDanEL/lEVJkZ9rdKWqNA9j/8J59sUDdpPHKOiB
N8pC544RMQP8aY7/297PYWf4Vcf8XEUe4U9/BMKXsG7rHs47LEiD/EEnm+Jg
xijm27COt7IkGN/3MnCh4212h76oyOeaf0F3VP+eAtdhHQnjToEaxBvx9ZBw
5Uxi8AN6b8b3Gl+IcLVwr7dk59xOhHzC5CjwXrJkhZ7ypBmEqwczwg+Ktxt8
L86/q6eAi/y7keo47N5H8ek6RrOb0INe0J/7tHjCb70zluxGvWRCrF+xD/vN
IT/XfPitvPu5aONToM6Zf+zQWsgvKClRvxd9ib6f+dSXcPU86g4EL8LRy2I9
WL1LZ/CIRT+dG3mwzpf3k3B1VFnUadtHq0n4sDnEr1OayP2h7A2NEN+L1WfK
ujcMdYsXc3lJ42tWAN/G/xPqq8Zvw7lw9gj86grRsI8qT8B7cacieNE9cqKP
4YJdwF93h39exulPDh5iXNbfzDSO+VHIN5nGJ+Rfc2YPduNqtkR56fume4J9
oEovxIEPhyKPewN9g7WZ6H9qN+2N+MIw2K16islY56lDELe/9RJ4w37Yn7M1
Rrx3fn2KP6gb52J/qw/erPalJXRqOU5oeD9Hv+K1R+q6ca01eHRKal0ab107
DT/xWQLOR2AfFjr8evI4hFuHFkPXKyAp4VpfuX+onW43PVfjbKAv49DNHjQP
9hvreepvVoM3KPQ/iyVqhOe2EXhYZtQ/J+F+PXwe2ZGTcb5wHx/1EN4j0ccn
9nihDyb0f5zvxfo/doqlEm5FRICfyrpAaoriOHeELtAlf8QPmEf62z7B80iU
sZIbN6ILox45OEzC1Wj0ybB7LEYcTvB1R3hDtzO+j48b1yd7IP5WYF5uN24W
CgTfvepWzv9CJ1MvaWIfXpqVeXHQ39YmeqKeQTsu4UqhSuADHfpM556RLRu+
15taHFfqQP6y1uQx+Gld0edF/TCBeYBJKU9tKjtIF073ekF2lyr4Zknzoq44
Fi9L+Bf6rNaIv3EdsTEe75WZYprmxvWxJVCXdXYdnpvodx86CH7AkcsST9UI
W4h4i/+R4m7cysX9NMduQP5WxN/KH4S9kTRjejduRSSC/7Gu2U3EB9hvPWtB
7z6gB/wYYVfkgv6UdjtbXTeulANv0N7bUxqvDEE8X2s0Py/Nf5YkqBfekRJx
/majJTtcrTMIeZboobJ97s/9gsOPSLg9E3EP9WS0hGvZQ5EXGX1b4okZIfvA
J/myl/sFHMU5xe+pwB29KaHHG98bdnD5ZTjvIooivzku1v3My4w8lkdNCbfy
5UA9xRV/qe+qPnARnUNa1FnoUl6+jOsPfEZ2v5bQu577/pX1CyjOry1PgfFt
LuJc8B0K/3p1Ddqf9CUFce6/6kXrTd/b24v+vgfOd2VYHuwjQd04D5gEdakJ
R7I+7a3ybtwOSQieWb43qPPjfhxKphKE64r8ffUwxD+FToK5MxjzzzoJxsKF
rDMm82CFfoKZKwTXYf0Eo/Nr5Fc57mFYrdHHfPxo+h7Gtybgky8vA11e3ifF
eLGvWrsKyLzBI+vBD+9VFvuQsPfKByJOu7gyx8Ph72th7RDHO7sjoxs3Dp+m
986cHhbgvr4+eBr8w+qx1vnfzGPcOaqmex7UNAUekZ9ROQh/twS6bdqmtO/o
/TwYwflf3+F0H55DwQfcmy9Ewvm9U4r4gN/N/U2U3guRj1mWvqT7fkQ/bjWi
D96P9IgPiP7dRnR8L/p+Yh8rPhtx1RU7Ec/IeZBwqyP367KhB+6MTxkKe5f5
6k7+a0Z25L1eTic+l728O/TTusbHfnLBQ8obWlvmAL8+rqYbd3hN9fpiHxX9
KXrPobpNLc7PYAl/VJj+Xp0ason4lUL/8Cf8Yb1zbvLnnLrsyCGwi/Yf4nwo
P/fG73G+j85Qwo2bn9OBT782RVE3bu+sjHM/e32prtn2zoK8daXH5Jcp9Vfg
nPo0muN1XPcYty/qSpjPb74PreK+jv7rCPyRbmekPIjieR/6X5lQl+TkL1h3
ThnWwM+N2zO7IM+uLSvhxq1rPnQemeOKQVc5ZiSur/XD+i9ToTieC+cle0xC
XHRwK283rvYPQnzgQaYSbtzceRx1312HM4+C37u1d5FfqdkB+pdiPr8vAp8w
X5/i7vHW0dGFMN/QkdBsC+s5AetIzH4P/6IucKs6+jQqJz+h/qAF607k47xS
zVTYr8pAr0xb1pbriz2Bf4f/Lur1zErj+D1F/shs9QR5O+bPOPPJ/Bl7cK0K
0vgUTXHffmW4Dp3zUH1zIj7OuiXOeNYtscNEHTrjZ7zxvI/WhH5mi3q4TpO2
sFvuP8vp/lx7zXTo/Ff/kkHCg9EPSJsbCR3WZOCv2r9qg2e6IA37axy/SlCc
zjlj81c/Ny74DOaYFqj/E3ZLnHd4fpNTV5PwedsQryw+AHnwkOvwOya2xHvC
P/a9KdAb6TnET8LfdZVwvUZt8KmiewA3KwPvcxQ6iuJcmPCGnrtx6ijlmZXm
b7Fum3tifu8thF6QfyY8x82JCf9Tl0f4EOBa3cGof9i6KwjzIOyWWh/Jv766
19c9P1apYugbF1jPX5q3xh2lfcB5r0VdT6z4tqgLUAdE0ueaoagvM+NkhU4C
5yOcugDuMyV0hgUudIa1hPvY78B6UCv0Aq/Obs78T+6D8/dm1Be1GMnjYbfb
WyvTe6sZY4Ld47W4Gs79zrWxL/rdQ96oyn7wIo75UzxTv98B6yEC559TvzMS
61n7G/U7gt/i+Edc7yPy446fxfVB2vEJiCcJ+/DiLcQDH6aneIwx/B2eS6f4
OPd/zz/N3/YtiFdPWQm7boQf/N+CR6GzNVSleTQeVgL/N2Aw7DgzGdYD66uL
OmWhr67frZrLjWuJEe/VjyWBvpC4z64LaB3YW0IQtxZ214Qw8Ntu28jTlLmG
79sjB/z5dQ2R9ylyBefF2/ZYV74rkG/PVpn8fWtHadSnzCjP58Mo6PV1aIZ6
72bT+HzJDV5lte7wi+quwX5/7gPiCXE7UJxEyX4OdsGdXKh7Tfga+gsW3kfB
2zSmHUGca7EX/D/mbZr2IuTREoZkdI83GwHX5p9le4/9owW98Vy3TJL0LswS
01D/MyQS8YeK/F6czAwdrVW/8N4sbAx80WbiAWhH/Sk+qeUZDV7cmYgg+rfF
P/T/hvcYwq2XvwgX/Xxtr9vYr7ifr5b4BN2PGZyC9MDNpudQr7SuAdstzIfM
lQHnRY2/irjv3364GHGPl6gPVZtHwr5t9B765GU9wa84AlxJXMmD/p/7Sgg/
/X/6SrTcBrsiVl8JMV70lTBLq9CzfVUFeUaf6ugPkfaotxs3cjyiema1fias
CxGnjdbxvBbFQR6wLvZJY30Yzl2nnwu/p/3GIT+6vwX2/+S8r5bqR7gWXQ92
0JmesLtmhUI/MNl57D+bUC+pVx4MHeFYOj9Cp0L7WgD8UPF+LVkAHkudspob
VyYtpfPyT9z1z79O/9O/PuL9bwlc9IGyxwPX95Su5h6vHCuF5+eZh3SG7FXr
wMd78pHyF+rtamR/WkFXoUv2ZQX44rnHMv+H+2Gtz0r5EuMx1rsRbzvs1TPx
wH/L1Bb89GmoP1X9z9B1lALIpxiLdsHvq9kL9aq7tqG/TA3UedkNB0NHPfoq
9+1i/lgG9DszM9yRdEGNA4Hg0Vll2M7n/X/mO8R31o6TcesadEdvD+M6F5wL
eqsOqF/uXBW6dIHIyxi3eyFOe2U89xfjdcLxW+uZL+GahvF69cWIa/OP0WjP
MP6d4p92nFs0/9rT/chHNHiDOOqq9tlwfc6fTjwJu2jPq0xu3IrIFET/n683
dEQG/Yu6szLo76JuQn9je8Js2GOJXuJca4A+kFpH4KoXdBj/t6+QBr7FY6Hn
wf24q7OO5H/jS7jHK6mH5cdzYXs441a8R7HqvJQTk4U+Kur7ub+G+jUGPJgY
jBf6D+pnjNe2N6Y8lPKW6wVWT2A+mNAL4vOX+wrpY18hb/AKeQTb4ybqpLiv
uuLxBjj3VdfKnmO9XPCE9WJTvWhcq+N0P/ZZ6C1ry/4mP9Pqc8yT/v8AcL1K
cxpvbEyPPkciPpwEfq7VZ3oJN249Lws75FIOHzeujsiPeTpyFHWZLjvwz++G
zxna30wv4Fpv1CNbJ3dKcRXjYTD6nTfejb6BddGf1HqfrpZ7vH7v4lD3eCvD
TsQ32uroy9YrxQ+KA4t4CPN1hZ32+76x7w1Bnybzewvwi1aEs54/x1EvloRu
QJFeNd24Vr/HE7JLgx5I+WszvBn0aEYvq+HGjfpXqd+E2aiqNN4e6knnkfbm
JOpNykVjf1iUDP51d+iHiz5o5kzwsbXouF40L/Xjwx7JnhX8tzv9Jb16vR3y
+8r1EcwDZ95I+XWIM5RY6u3GjR/wN9Upmo8b1+fuhX/nvR96/oKn5x8VSvf9
RvhHzNO7AP3z2HxyoX/+X78h7M9CJ0TrdB91SFw/ay0eDzvkCfKWdk3eb3t1
xjq4mo/Gq3lg95qPVyBf2/uGtJ7VnK2wj7zx93PjytTy2I98s5Vy41bL5ui7
cLoCnoPYHzp+g275MPSlVoudZbu6HZ5r15mwzwP3g59YYCutWzN3JP5O2FeN
OiDPt2Nofjeu/KiPfSarh4SbRZKA53FWJ3tYv/ce99OkpNiX/qfvG91XZqfP
FPS/1jv72v/0j6PxldiuT/II+3yAAZ5MDfDotcyew+lzP9VH/rQh+nY687mz
F/KwYZXKu+dN+XCbzg/TqKm5cS3UoP6Col+PpXJfUe7X8x//Vu5Tb8bo4G3l
xHhr3jLoe5+ogvvJHUZ2o+75CXbq93XwU15kB142B9Zhg4Pg0+XsBDsz+C/C
1USnaJ80eb1ZXjNwnkZ+o3lyzvdsN3HezUiU0I0rrFsnfhycdevEj5UB11c+
rXDyI3Rd7ufu5EeYJ6CdOIh+sMwTcK7TpY24PvhX4wfQOaK9+Qc6nylGQZ+U
68i0UhvAr+M6MqcfRznkK0U/DuPhZMSThn7A8zp6KvTP/FhXwxGPEet2yR66
HzVXF/ht6xMCvx+F39t4Yvw8zmv39Ia98fds5IO8P4KfM2wI+XFawRfoj828
GuPwRPB2roVgXzmYBeuqTBlaV8oz1Ffap8rBvvX7ksQ9D/rRdiOleci7FPU1
wl71eAV/OH2M5D+aU3qgT1/7kUXcuDrmOOL+CdHfVWO7UQmA3WgljYYdkXwH
6qS2tUG9YlFP1LVNzAg781MW2JPRW7Gvjv6rHeEPE0p8RX11X8IFX9FOnZr2
VSXgCfIXTevBHttXEfVMPsc64nPXgqfxOMYL89mdeB1253Dgm+sgzvYuG+nz
KG/A+zKyTYEemuirzrxiZUde1JV6oA+7Pgn8Jb0f7EFH77pINPQmkqIvp74l
FfRyx2ej99DMc1TSwdbioG5KbX8R+0Cp3N3o82r3AZ8y33XsA/3+pv4pujUA
/aT936MetuAerM8Tk7zwvX0w32lfY52kq438RL9m0AO+sx3rZF8LqptQt94N
xXPYB3t4WSbs418bYb7f34ddnSgt4pk/N6KfQs8jiHt42YhD+RWm88Iej/6e
xucG4P1mhx2qbkJ/T6VjNegTzs+N8yXBRIxvuRZ80YdJOV8P/8s6EkS8IxEv
FXWLIl4q4qIOznFRxedaoBs3qqGOwqiZE+f65fOogwuoAx3OvRuxf+bDeWrr
vRFfjoiP96PsVODTV+H9adMKdfPRX2EX3c4OnkauGNhBXAeh3bqA/l537yNe
uvkb7KtCs9GnQ8Q/u8+V4p+6GQLe/tXj5F9rA3zIr9Db5EA9cs89iP9neIv8
zqEj4MkIXamjl8GjK9kEfIYduI7e7C3WVXLUJTn1kgNegBdyHPaLwJVx4CkJ
Po/x+Nkgui7zedSXk1Afd+0ldI+bfsK+N/Ag9NaiZhNu/5gZRONWFUQc7oSC
fcBsAr2jpzhfhO6T+vt8ofnKUQU8mSfI31l1w2C/NsA5pT0Hrv8+p+j+0x2D
PZgkGu/FynnQD0+7iD5ff+bJ9vkm8EbyTGQeKexba4IX1bcbFa9XduNGhmGU
F7dz75HG2wkygDd9fAPs0UEvaH5s/1GUT1F+n+P0O9vhoo5G6KLErqezklSF
7nQW5Ne0p5XR/+JBUs6nIw/ovBccZ7P6JsL5wnE2S0EdnlPnFXQP6/U859mm
YLy5/wHhaqJI9BVhnTT99SXENS6+xXP+MLIl3c86P9hVrdqjf8eV7C0IL9UJ
uh8lk0t8P7XLdpxzHaFLr/6CjpMSlAN2bNt/kAeeAt0ko/Ngwq2YllhHV/n8
MsJgr5te9BztgX9j/M0hsLNbbYO+0PwJ8LP614A+xqoL0jyoDYOxntpXg/6g
8BfmecIP94UOj5aZ+c83gynebGfrijpfxvVlDxD3n1optfv72vcM1KW3mPXL
zZewdyxH3uv7hUTu8dbKNfDTg8ORh3mcfTh9/tzToTTeryr84Bkq4WaH6YRb
j/3zYR4fYz9JVAfnYORRL5qXjT+BN/uK96jzInq/1LsvsJ79LuPcelkW+ZaM
6L9jxy+A+OHmN6iDKfAI+Sy7DXTqalSFfZZ3AXSr7mfGPvbuLdaXyMtUQ12D
qNMXdqCo0zeL5fJy40o/xP3sjR85P8h29emtQfR37cJlv/tDSfApV8n+u6i7
MTPGQ33cw6mI1yX9gfhydMKPqMtgPYRkqMtQd7dHv1C2z/Vb3Zlndo/fg9nI
J15sS3FP9dSx8u77t6cWht3SdITmxo1s+ZGH+Lop0D0/6s3jOLd8ECdz7Oo7
6AuuzMlG86ZewPmoxfsB3k+WH6jjbL8bdTQjmgEvWBr5vogA7D+rGtJ+4vCx
907Bvs18bPNKAfZnmT8fkAi8wf/H1llAaW2Eazg4FHcpEhZZ3GXRDQss7u7B
3Yp70FLcKRQJpbgWKU6Ds1hxKRbc3XUvnWfmvwn37jk9nH07mz//ZDLzyfu9
X9V2Pn/ZnvMncd1pUudB5ZGbzCGOHD66pBfXIxOTvzlOnytjHnFmc9Qo9se1
b/Hvbu4iDpwgmrg/91wE79NiOf5JTIGbHS+Jf61n9D137K/iPTWT7KS+SsYH
tDM94D/J/kfWYsar/kfqRx8UhX1F+h0BfHTnMH7Hj1B+kPFAfq70gzSZ3zHL
bJJ+NPm1AK78Polbe9vyXseczPosdiZc4M1uyj7O0h9s8wT99aELuf8UV9E/
qFABHqnkqwT0MSSvTzu2APwm/V7tK3lFf3ltN7pBRq6qjbif6iLe6zofxDlv
v+1Gn+XF9eAdvj5Gve8n+i/baWMK3C68C369eh9fNIYn3fo8uqq74WM4z+JT
z9+muW+8uyaBsDOdPZeFXafsbaUXaq2Gn6mvfYf9XDNM6ATaJQfDvyhanPmZ
Ngj/r3d0+EdFirEPxP6TeH4ZHd2qG8n53Cpra8jnBY9169VW8nf1I3DrS73/
F3fabRG4+8hRfQqoa1b9NS5sgNe7ZEa4Dy/yinxHdQ1/Qcbzrc4l4OvsjSn1
5eR7F9ITXunj6qW8480fn7Lf9kVvMKCPEbOb4P+YxxKL+be2zYJnsmsd+3bv
9uhhKp3MtSmwPz8l9uHaHof7GZEL/1vph8z/lfc0oqfhxZ1c7C/ujgphPnyX
K353FvSmDrRbKHGGwug5O8uLc15EJiXOUHs5fKpjcdH5fjAdP7TR2MuC1yr7
XQZ0MGotp6/83fbgv5YFrzEf/+HzRXR8pb3t7J9NfdmSzPW9uLYsTOSxtB+n
+cZr4cnJb8m6+0DeR9bdm28+hAt8c3fpN+1FF/E7XU3FU3IrjocvXwc9N/OO
Q71K7ofokiodsHw52Pe3XKUuYyv11/qX89il5e+RH/gJvS832hR45iWv+PJK
9pwVxC+++TX/4VpH4mV28VrE2Rs145ypGYs8QNw+8FzrHMPfGfMWvv/mGPTz
mH1T+l8yn9gnRNi9Zs65NX34nT+o32j8mutEXy1518mwz9+V4H4enOM8XTSU
c2FYauLf706BP+1EnKrXFuy+2ujBGrHjEfcOblCGz5X7z+9PT4l1cnC8jI/J
/fN07TkC3yD18R7hpxhhv9GnT/ZNDtjbku9n3OhUw3sd51U69sf2wWHi8+SP
uzMa8yPrAgJ19FIv8b88r/i3TQfO/QfkiZ18qX38czc6vH0ngePnpTdnXTmn
8tX23o9VthA8va7pfeMdF31O5QepeJ3yg5Q/FdANUP7UkCWSByj9nWfwEq3N
S8K9uHnSpW7x354y/tNM1gvshp98cEewF7dehhCfupzNx98wa9KvUM+w04e7
Azivzao18A/qojvkNGtN3lPWsap9INAXWPKoFa54LOazocK/D+hgf+5A3dfU
5vSDGNsKvbXbN1k3STLBix7UHD52SCwZh33tqwsw4r/Ff/5xMPvG0RvMf+Zl
xD/fV+L8fHOC59V0H/5PWHziYb8y3jyEH2iNC5Pno4xvSL0Ou/oE6tX+5jy1
BxQlXhd9gG+8lbUy+SlZR2O/Z50HdCzTnISX0eASdc1u7rOirufICfCXkeDj
990UfIB29fHTLzDeuvuRvM+SGfTjVu9Xn9z4A3VH+niV1uECsi7+cw0vbvaM
h18xoqfPPtea6+xPR1v48mu2vQ5edKerhX3X2ToR3uCaNmKejd0ruZ/RA6iX
nNavgfc+zXGDyH+P/VTJd52ubdFv/Poq3IvrWmvyYg2HVfTdz9U69LGKG1fw
FIyNUqelTxA80q9zb4s8m+p7NawV8e1H18nXH0THVU/xkbiV/DHfjQvEq//D
ncdD0ZuU+VC1bs2VpvjX/kqe2lnaCP26LEvQkxwveXqtr5LX71W9nHceHK0o
eg1vioV7cev+c/j29xf5cHtaIs7vaMECdx5KPe3hqcCHzvLrHq2sgJ9Tc2Ep
L25bB6nDPD6I5654SqPWcI7Hz1DEh78/Lb6/0a9riBfXU9CPxOz7N/139j0X
86+dMekPEF6KvvPrZwvc3BiMnfM4M31yZF8Ad94LzpUC++mXLnV4nIdViJdl
GifnX/KNC57hnPxaF52/XZIXne0Vdl54tKzMm4zvTa6BPZxocmIf/mcu4Zdp
3ctk9uL2JRs9rOz/+vZ5I6VNHO/TefJOcZT+zBp0WmQcKaBXI+NIVshu7NjO
j8T19a0ruE782KznNfSz0D+2AO8ylvF5ZV6+2mLs5+ex5b4aV+qe5eX5XryV
0YubMcaDTxyIvtngEPgho0rh3y4pgX/67kNb8f3jfSEuU/CVmAc9//J2Yh7z
1Q0T/7+1KftZS79G8gHca8nqeudNH9QQvYE5pdCBn0J9q3F7IXr0c8PAV8rv
W/ygwFUeOcAHk3lk89m9jF78v7yt+P8v4JNbpaKir3hhXUxx30ct9EQPXxX1
PnqfqGL/1OKMq+4b36Su2De0nmc5T7o63M/dIcLfcxvvBc/4TOB2lKfgNTgv
AvtVR/Y949RwH66/sdkPE9RHR/CQ7KOacxg870ut8PPmRxXX1yqX530Z01Xg
1tLznL8b56ArdKA04x9p3GfuwtSxpcsAf+OXLzIf+ivx5CyFeC6Dr3G+J+6N
Hb80vRivF3W5fq052P/Fkoo8VqBua/B06tkP9fbh7pNzxNcuNfPhlvs3fK/5
73x2u7GBulyjwT38x6Gn2d+qFWB/DhkmdbRkvcN6h31vzr+VvLiTKozza15L
4i4tigj7U/+UUuwvZv8R2DWSt2bsKkA/8vGryvrwiRewN1LelzxD4thm6iD2
8xjD6njvX2v0jHxxuWliPt3z9K3TI97ADz6hNfDep/nbWHgmBxbW9+L2Y8lL
yb+8uhfXl+bi/E07zoe7q5kH91Dsar7rN77E/BxO6cP1JGU596+kpP9Ijdfk
xY5tYD9Zdlj22xkq8lN6/zH4R9/xHLQpA9GN6RSCX6V0C9MegednUPcfwBu0
Ip8f1N3ffzbPb9iT3TaW8N1niXbUXcaM7bNvtQm94PNvnin8HrstfpnjVEHP
v2Xiwt7nYuY9iF7x19sFffgv69Drfv+ykG/+92QmX99Kq+Edb8V8jh0zMn0V
33V+XU3f2yddannvUz9UmLx19fi+56tHojthDR7cwHsdrUJq4nPtu/twY8s/
2JnhaX24nqAoca+Uv/r8Yn1NCfLdref4PtfoWZn5yUpfDmPQHoG7KZsSr4iV
GzzxPq7Toihx4B/jV/J/r8bkjdxyPn6RXS8Uu2VZE3hMO16K6zgb2gsdOaPB
dPzNTuS7HXu7eF/0FHnE52q/sH/qczURT9cnPBTz+r994Z+g//NpfFEv7uyh
3tNdclnGaWUdaF8D/k1TdFDNJJKPsa0z/nulCbJeQ/KCsjchD1r6ueHFrS6H
2BdWP+JzRhC/NVe68BurJUNPY8h28M9NRD24vWKlzMvLuOv53sQPU8+XdVjE
Oc2+/dDb+e16fu94LXXScHHft5pJP1fqlG7txns7bF4ZL+5Wqy2ek5Elim+8
FucIeYH+su/Nnbf4rWdTUM8V+VDoymuqf8hn+H7u7D3XvH1FtI8zqNN537KC
d7wm+425n9AN0j/CG7SP05/sf/mrkvci+asqLqRwFRfSG5djvnKMZF01GEid
75jsMu8gn+/c2PCKB0XL48XdXnPEeWoGHZO6oHJ9LnjG+Xt8R7B3vP46BJ5/
XfiBgfdU6uFo3Wv5cPcn9HCMAb/m9+JG6xdSb+QydWCKX3d7Urjhma/APibr
CLSSF4p4cev6hXLe8eaf63zjjRzFyD8UGMTzWFof/YuWG8E3xiFP07+a6Fvk
NMpNPGZCBHG6ne9EfMyqXLkk8yB1/7bGYh/Y3r+493s5jeLQv+NPo7h3vPb8
Hno7RkHOyZUnsGOPZiDfWfOKeO+stdghVrU21A3JekYVH1b1jIG6xXjwMVTd
otFxi4wL8bycKvRb1YLgWZipea81/Sb7c8S+MO992o8KvRX8xktLfXWU1si8
ok+x0e1gLHG9EsQrtN1TiGv88FHE9wK6yrX/4Rx6lbuI9/pW2lbEf2KcpI+r
2ienNmN+opeFj3YvK3nwKWfJW6XfGSnivuWzY2+8/UgeN9tL+jRKO8Q9IHVD
hlKf5I7aSl5mYARxWFmP5qwvR15S1aPtOkz/4jJTGf+cfqaWkRG/Y0xynuMf
7agzTPsIPfy/ZX+x7mfY/540on9F6ZdCt83cSX2TqntS/chU3ZPSS3F6NeR7
fa+XIu2o7/VSbJX3l3opWoo28PO3h4o+p/rrNsTh22wibjwQ3Kz0BHuoXFfi
p6pfqqxrtmavKuudT60ddp3dfJcPt8+XpD4/1+XyvvlPF0z984iB6CvVX0P8
dsAv7NM7ugrcSL6CeR66iLjVb7Lf2ddZ8KK3yPq1hIPQdWp1lPjAiDYy3zWT
eE40jX6dg9qJehK7P/EfLTyY8yXtnwdFHjoD+TL1XliDe1CfJftBBN4X2Q/C
GgJv35V8VCNDBngyIfTXdl7lwK47k5t6j0VzuB8zBvm5ATlU/oX6AsVLfz9c
1akpvJgXN4PdUt7x7gJ059wfm6KzlzY/PJCar4TdrM0dK76HczIf78uC3fR7
Dl5IPe7V1Iw/NxT7ps9XES/VL8MDd0NPwXtotAke+7UF8MZPo3dhRT9AXUal
g8xPs1XUd51M4uNFm3WjEq8oMFz2lZZ+x61gkc9Sea7AfqLyXM9a+MbrozaL
ug77ly7wtbqsxG7ZtUXqycYR19H6yD6zPeqj/3BvmbiOXuEQ+8mF3fQjeTdK
9aPg/H35Vp4vsg5A4e9ln9CB8LW07/o8qj7CKq6i+gg77ZLTL/G3ciLP6FZL
InCt3jr4Vrnpt+hqB4mr1tsq48bSjtp3Wcyv/c+CTF7cmXhQ2Cfm6wBvF3s0
juw7E3nKZ8ca14Oph6hyzm/Hlm9MvXrU6j7cHIL+gPthO3pZJyKYtwErwuTn
qR9ZZ6FXdPx4MS+u54sSy/GMN5aOYHxV2ddsgdSzuiP7msn6JvcRfYhUfZM+
RYNPZTLe7N8ev2n6YenPynM/WXr4hE9yYcfl5rm7RVaih9khqJx3fvSek2OI
v78V3acD4Ew5F12Mn16ssm8+F9WBR3Tljs9/sY11Yh92G4/zjXcjFqPz89dH
/PTJe3lfWrfGjqmdB3/k6Enm+XYm5il5f/CV0fjcH4knOrUPis9Xdqnx7GJW
8T2LRuT14nb4QPh2d6aQh89eUtgNbpwpxF37umFe3B4Ar9F4n6SsF/9mr8B/
nr9d5HH0t2PoSzj3LXGthV/E83UWHhe4qRNXtI2Vsq5W5nO15mJfsAt0jOPF
zeyD2C8iQ3zjtQc16BNZcABxiyUlBF/OyXkCf+o9eiDa2GICt27mhG8/erjU
TblDX7mkhxmfJw7xQ2056yRm1TDx/7fWF//aB5di/6z6wv2OHIreTrqdxAvu
0tczUKcj+dgqLmdd3EFeaWMqYY85vwbjX6d5h863jIdrZ04SL/pIX3ctkexr
v6YR8QrrLH0m1XNsOom+DnOX46f/ofpLFoC/f62n1PmXeaWnu+FpZJR9GCRu
j0gi9jf95vow3/WT5Ioqfh/3pYwX1wd2RD/xzPTyXtypsJ986wu/voSKB6q4
XwCXcT/nn54PRL4xGH6IWXsxvOJaD4T/F6hXupzsqeAh9e7F95V8fvce8VLr
peX7Xka27JzfNdeJ5+jkoA+dFVFI1MHZx9cKXC9TUODOm4oC1+LW41w6O3OE
GN97N8/xQw3i6rFmCdzuRHzGWQmux6S/sKaPoN7vEbxoq00q4pBbZoj4qdVk
Gf+/Z3HBA9Q2LoYXUaIE+9mk0YI3aE16TL3n7VXkuZ7t5HN/Q8fbWbqGfTgK
8VvrwRv8o6PTiSteBXd22uJ7ah8zE0dUfZ83HBPzpUeZFurFjX7x4d+cS4e+
St4F5E1mt+M9CbuM//EX/Fv95m36COTLB//20nrqXOIP4r0bmxn7eekGrrN0
POv8/6mzE9e5KPskRwN3GsGD/P/q+MT/77RF1IG7negL6ew2seN395XxE3k+
NqqHzmzYXR+u3Xss1pn9LNLX3+2b/ynsuv/614vv+fMY+o6lySfmR/1YTXoI
3F18sqh3vJOnp6/fvdo3jHSsW7Vv2JE28Qnlz8Z+LPxhK1l4uBe3pl/EPit/
UIwP2J+JiM+oPsX6admnT/YpVn2CVBxA9TvWcrciHyTrI5y9UckHZW5O/whZ
H+HejImf2HUYOkNyv3L6XqCvQftQ8lz9fxa4frzhLeEPPlmJv6LqPlrQz9Lp
0jNM4DPjk+9bSV292j8DcQy5f6p6B30KfX9UvYNnPQTiJGL8d3Wd2ib0l53Z
I8nbq3rqLzHEPqINfOnzR6zKA9nfJX8p4Kd0qEl+Lk5L8XwDecMTucirJt2X
zIsby3YTf5laWvgLAR5gsqSc7+/wgwI8wGhJqFu/FOkbb7RFP8gsgJ357T/B
t9be4rcq/NuP4N2ab8D/i+j/hxuRkUJfXm96Hb2y4evpo6T86ITRwsX83t9X
3Itbblridb3JG7u5N7PfhhQmDjWwmO865ufDxP0l3yPAG5F1xIqHoPBAv3Wp
o+Lo1FcqHRU9ntRdU+dLgrTw1XegXxewc8bnMrzPKxCXC6+H3XJ+AOfA2Ndc
56dswq62xhcW13EaRXJuHotBfjHsLnWTK7Phz+4shv9Q/o64X7O5zjx8DKIO
VPIP3U4VwCX/0D4zR+DG+fS8p1vXCNxJNzyf9z7d/H3QRTRzozuRkn52ur0H
fznqcvzIyUUEbi6nvkLfEkK86lUQ91m+GzoSP5xm/c+OR3zgHfoVRo6W+K3X
E4OffkP+aGUSYQ+6vf7mOpkPM293p/4g8OpSD6HXF+zCr3/A68xM/NCYdpRz
X+qgBuKHUgfVTnTJ5y+bnYn7WA3v4++s/WGEuG8zM+dR63D84vNpBW4W2Cz2
bdc5JeudZTxhXUXWSanKZby4MzkBz+NJZvbXYQWIe8QpIHDn7erS3vHuD0UF
ro9/Sny4TSqRh7VGSz7/8QPkTyZdErhe6yr2QN1q5GH7gFu/BLGPXRiM31nt
LjzwAf3hHRk/kOeqMRNe8ag5X4T911P2Jd9wX+BascbwUcPvMN/PfxO49SFI
7C9uHvqMq/vXp+SDh1z3l9w+PGIzflbYuZxe3Hx+IFzMv6xPsRtyXqj6FGte
EHWyvcCdQSvpcxnIT8n9Wean9Lf9yCs1ZrxWqgf74fULxCFlf17zS0L49Mki
8aPr/Mn5WLcMvCXJIzUX5WEd/u8P+Xd1/yM6iHVpai3EOWY/6SLq3dzh7dCb
TnYH3QizhsCN3eHwaRcGMZ/DD1E3d2WI8KvdBbcreq/vZh8l6gHtHenx11rD
l7A7bvTl76wT2IEqf6fyfXqF3oyX+T4zFfURdib0up2Om+kb8tct7O3n6C9p
dYaJ/cSqeJ046uQi4rmbuYcKvXs3gnVilQF3nfqif707NzU67Y1OU0+dqR91
zcsK0fen2jnqrxNW4L0yfscei7EPvcSb5agznBpf1M04x6zx3vl3L6SL7cXd
8+nQl2lcAf/9QlL8qWJn0b+o8KPmxfWK68V7bRxqndGL2+9r0cdC08R+oN+I
JI6jadRr5Xkk8ib2E3Dna/eqhme88YxzzYjCeOPvZsSZlsn4QEhf7ufCEvyk
jG3pf3oKHp5d6Cv6C7Xaw+MaUz5I4KtrifVlNJfr9hj7nhHtfrj4N+1e9u0t
sejzmjQj/q7SuytWXPRdspz78CxkPFbbR52YnumB+BxjAvFb+4es8PfmrsXO
lfp+9tF+5EevPiQe2xPcLSXziGuSTQv1fK7zW1Ts557vMxge3Gw4ke/f7hD2
VeIsrPMc9BtWfeSd3tQXqD7yan+zp7D/q/1Nr/QMe2Q4uDOiN37QldzUPRzv
jh7g0lyi/txqLHVxmk2B710jMTrVS1OHM2/wwO1GE8X+pkde4joXQwXulthH
/XzZprJ/hIyf5DuGXVGjq9QfkPGr8FfgO2/58kfa2N5h4r4XpfDlo4361L9o
H7r6dXoLnBH5U7P3bfJmI9GXMLUK5FFmjEHHL3IC/Nv9ZdjfG96TPGv6TGkt
KhJXCktA/D/ajBbi+6SbSXwtSqTII+l5p+L3fXpJnG7AJ/RTTwwWuJ2KPPR/
eQTxuROom9O7nYH/3L24qAexZd2fNgs9MsXnUetQ8XnsWcfRW1P76sHi1MW1
XpfRi7uXf6Xep3W7IC9u5W5G/VHmeyIOaa0l/2K9oT+uE75GfI6zfo30E/OR
n0oRE7tl+ih4ellzUqc3dT9xlAlDGf/SBE94AH9T9pvQE+5kX833N3EopXs8
QPLMnUT06Vt8kfVzMwi+zpNU4nxU+Qu3xgvixUknsU7XM16/1Jfx+Zf58hdO
+uQirqE/fkn+8zbnlJ3wJvyn02vZt0OJJ1i5K1Kf23Qd+3ww8QcjT0Hw+DUZ
/ygfdt3eXOJc152cYj3rqf7kPO1QWZzvqv+C4n3pMW9g9yZILL6XdqalwK2R
C4nXSLtO+/Ffzhdp17kRicgLtLkI/rU3eOMXGZhnqVvebk+Q+P+hwx6GenAr
RiXi0ZO+oLvzQ3sx/4rPb495wfcwxsA/6RUd/kwtV+xnmur7kLsHOuBF93Be
T2Q//C8/Ir7/UPquWg9Yz3rGDNT1qX6LUodW9VvU88t6yfeR6F68wg8yLmfA
/o2iCTtAqy39oLyB8fARX0p/6lwL6tJUPqvZEuLIqfP7+Et24nPh4nOLDC7v
xa2W2yt6n5fyd1S/DJUHVO+vygMGdA5bgqt8nz1kNvEiWT9ib1hGHlnqQwbq
UJQ+5OyhYWLcHxLfAx/I+Evjeup8SQjP1vpaJtSLayXekw+etcfw4nrZx/A2
rl/B35b8RifeVOahdjvsjs7FiRN2aoZdeuw1+5iat18MMd5s3qOwFzf+aA/v
oVki4lHqPA3tCv9vZBVfP1ln7EPFE/b7fT27lPLi+mCHczAl74V16QD8cKnf
a92cznmRbCpx+J2S7/opLnGBi4mJpw7ZQl7pZFN4EQd+xf7PFou4xLtHPh6C
YR1B30/pGc5rKvWNZdzm1Xzxfa3rhYO8uDGxhcCN0ckEHqibbtFc8kLoM2B8
jRT7rpn9UVIvbn/GLvpfPKDfklneH/bTi2jkK57K9ysD/rXS5wnUlUt9HmPi
a+rxH8o88tz22C1vr4v8g+KluJNvs+8PLEs/o6/tyZvXy0ZfkH6GwO0VMp/+
MQb4wbXYsbvB7YhQdIAX4o8H1sPIYfgnfTpx3sq4pbW+EfzwrXfK+/CTdYgX
/XsZPteFKthvodGpl8nyW5gXN3f2FnFAfUNl8qm5nuG3rrzIdQ72QPdjCnxR
o96U//e90Nwh9M1J3Aw/dwn63u6BB+QdEwwr4R1vFLxcRz4nX9zJnlMMvkTh
S744lVEyBvt21Bu+uJbZDn1Gc8hUdAI3lCCen+MseaN9Z0RcU31f50Yt+rdm
OkJ96z74ydrO4fApa89iv1X2ZFgYeeTpHwzvdWzrGnzNcxV8uLvxF/iaSx6F
enGtO/Pg1CzL/h8NXoptF5P9I1dJvSmld/dTuJjPTVtyeXHzwFvel2epcjue
+VTnu3NlJv0+Jkve9aoc1J/UypHfO9626R9vRd8V7v2+2phL4eq5eHH3xDDi
tmd2FPbeT0BvVta3BvhIsr5VX9IsxItb2dALNW5sL+ObnzMxiM82rkIcaEWI
nM8o8GzLDfCNd0sdIG4787SM98p6xg1Xs4rrX88b7MXdKAdE3M181DmpD4+P
7oGm1uGCxK3E/Zz4Jb8XNx7q4OMis3txPd1mgTtdNwm+vXm+s9Cb1TbPEjx2
a9tR/Kl1JVkvqRMJfrhz/1f45+1WUrc1cJTAtZ7lxX5m/8J4hVuHZmOnth5S
TX7+c8mnE36pYayqKnHxY2zpB9+oQn3e0yqlhL3kXh7MuVVyBPzuNxKfQH27
PaY3+/kuef8XW0qdzF7YbxN+FP6J9pj+u06lQqznHeh+OR3Gke9YU7OM9z7d
kAHwva8SHwu8v91msC/02u+3P2fPI84+vr0Pd/+eS9x4xA3JV8EudRfXJD4z
fzt5nJs10CeJoL+I3vgP7HrVl6f+FV1cZ+q/PtzUpvM9hk2o4MWdguVFHFrf
y3g3YhfXaT5ejDeSdyHfcVD2aWpBXaI9/CO8CMVXDxvF+jj/zoe7hfLCL5T9
X/SQwuQXVF+JkUl5j7ulFLgZfxF+7LVS8QT+MJi60Uro7bi5HvvqSfVUOXje
9VKIfiVaPXjObtsojJ/QH72NCugw2olHw38LL4ue08PW1GUlzUd+p8Nz7I7n
mZn/8+gbm29eqP2A8+zQR9nvSfWNBNffc456cPgb8nz9z677Dw/s/yci4ZH8
c8DPq282h3Uyrr0PV+tES6yR95I/ZvbfBN/F2NWY9XyL893I8YB+M7uz+fj5
2oFh+NXbJb64B/1WHoObn9FbM/sSz9dvL6a/ZD+p29Yb/Nu5mc/x3IfHnvfp
DJgxpvhwpVMa6EMh8wvaqM/MRwsZl6gJj9k8LvkE53Yzfvoy4UdYs4PJ519/
Is/TUvgX/8u/9el/ep4jzyWEvIt5Jpfve5gJe6B3U7OzL09o71gU/v/hVkgQ
fkqK2PBu7hOnslckRwfzruS3zAmlDvGvZeRRNv8heH9msSvYy6P2Cn1dM9jI
+t+/TvLxss9HScEbMBsVg5eq/JqwDPDOWzYP9uEPGih7kf084T7OzYevsSsi
Vvr8CKfSfuqmDu8v7cW1p4+4vuwnpep9VD8pM3VlgdtJr4n93H0xD78m0S32
/8zgqr+hMWKDei+Yt7Pt4KENy4k+jbLf/m2CnlipcrG9uPs8OniubWHid2VP
Zm5Nf8G9O8N812lTQuB2xT994/UUYcTlZtIn0Gx+CP7AmLrEQY64jI87Eb3r
QtnFfmin6yVwPWQC8YGtucV4Vaem9OGVbqGR/Dg80mPEE+wt4fRfKFtOXMd5
jc62Vfs4/nZEW3Hu2z0OEMfIOlLYde6WdcL+CfTpSN+TPpVHUhMnlHay+Tkk
P8+jhzo3yZ+e/D86kDLfig6kNjcb8U9Vh9jjsIh/Oq2G+eoTv/mJIs+uf6pS
2otbXZZlFfM5NyXrqFoEfa8SbEJvLdUQ4u2X9qHHVTMDfoysgwvsG2PTYicp
v1v1+ZVxEqvPUOpRlP+Sujb+4IA4nF9yfsynH/EL6vYp58VV3xOtw2kx/0bJ
GbwX6WdhzycsGcZ4aTfOfS9w40A2X72ANaGZwO1I01dfYA/tzHXWViYP+PhP
+k+fpG+LUwJ/TsU3VL85TcXPJe58jqR+oQjjnff4iYH+dG/uk39Rdm+mSpL3
9rWoF3fitcS+TXmQeoI12J9WXvYBo/51pScKT+OBjLM0CODohT4B197J+Eok
uolaYeIvrjMn2Pu5+pIy+ClN4geJ34+24f0KG83553I9O6rMd9e+ruahhPxc
gdvvy5C/SapR7x8p56HNEJ/erqby6d9Wnvi3a2lZZyp5gDMLwROQuBaT+r4A
/l1+yvl3QxUvbsdNwXprUqyiFze7JSNeJHVRrCuricdGlOS5vJ+JnkzfrfDA
pxBXMZfnJz5ZT+moyPXWHx0VLdrfFX249hxed/M4PtzM/ol9rOwPArfirgMv
94H1vw+/OLA+O+7mOkc6+fG7pXx2tqb68M5ZQdxvk9yHlX2eZ0lNQ/u/P/ac
jvRnPFRJ+HeqP6BxuIL43W6aJ58XdxuPgHe9ZEIOL67HLibOTWtvK/IUOdEr
MFtewS6qOR38NPuz9ZS8p5EoCfpmX8eTf+94Cr1O6Vd+Hzd2u+0Q8xDwfxO/
gd/WRPI3esckz7/FxV+KeA5vf1sE73XrjeiBT09MPPzCfvof3jlFPOtQNvJg
PwxF721TDez+xdk4D8NC0B2eKM+PWB+43qv84Hmm8XlfsR+dr+wP1jTiM/oe
2ZdcIy6qP5e8mR+LYDeGdBJxLTdpMXRCi/TJ7f2+ZpX38PYz1Pfhxpo49F19
XJV9OMo97K4Fn9mH+2WnXjBmRvzlK23xC/4oIe5P+/MN+3lceIfauYrEPS6M
JT6U44Pwc1Uc3j47g3iSjMNrkvfy7fsS15XfV+Fq/1G4vfgmvNp40ehfU6kJ
+anUC6gL2EtdgPV5ILq9sy7RR7jWHeqX12ZDV/PmV/zTxtHoxxGaOUx8ziTq
E7V9Z4kH/niGfT+0t8+eMZoVk3mXReFe3IlVGVz7XTynQJ1sd1eMszM18vEw
rU8/BPhLXtwpdov36vrCcC+u6aep+4q1m3ik8iO2lhDnuJGmYbgXt6/Wgcfb
IKycF9eXHBfrwdlX3BcPt483pg5qzBRxnUA8R1vLdbr9VMGLWw1jUwd1a4iP
F6cPvYLuwdqurDf5Y6VbLsbZuxbl8OLOmAvEJ6cOyOfFzUImcc60xYXfZy0f
j99X7bSw543fkuPHjYGHr3fpQJ/awTfgiUs+v54tD+fOB620FzcLzET/Ikps
4gcV/mXfmNmNOoulEfidXy9TX5NvO3GQpvHhWVWkntpc2YU4m3wfzZ+lfsXl
EPhFsVv7nrt2TtYVt0vJ+yTtQKcNvHPj9Ab8zFQRgv+gRc1EnuhGEvyZ6XEF
j8VuPpz39MK0MPF5sr+APiIb6zDPEIEb4Q51LkmmBIm/y5lB4Lb9GrzNcvJE
T18QD2yxtpX4+8ktue50+ge592KC/8Tfm0Oecv8rVgpcH4tOtF1rIfwBmdcz
+/4jzkGtpQWfaB64tvgjdftSn0Ht29rAtcQL2uaGN3sfPQTtzFj2vQed0Qe+
KnUSJseCB7amGHzaCfQNdyaFw3O6epM4cLMjnBfBk/GrXy8V+Vx70RSBu83w
l/TDLwRutDqKPb/zd/Kdo4oRH1W6WLKP+bd9BnwX+jZG1BD8xMOd0RPYLvv6
bfiZ8SOzi3oF40ZlEW+x0yxED+7kz4m8uHYigjzm6FVZxTwM+Jn1WeQleeRp
s4LE9ZQ+TMP51E9KXX09ekL0wKWuvtJjVPq3So/RuUPfEoUbscnnOV1fS545
drWe4ZhYt0biE+W8uNEgKXbs7gZlfeO79BC4puyrHvAZ9OsPBA/NKDSC5yB1
jQL5wSI6++7c7QLXo/el3jj6fs55pQOc+1/uo1fhEC9upuwucKewJvNu8n4y
jmR9nLss/V/pf60vwnq6G7eUFzcLnEInosuukl7c+lCQc6VGHuk3yTin0i9K
eZe+NK0TC9zccxj+c4zTwY7nOtqiC5y/a/3+oP0xXiAvBi77SEr7U+mWqPfF
uWVJ/cM5wV5c2edG2s7BfI7Ms1ebRr7gArx6J+bP2F0tKsCrX0QfJ2chfaDM
nH+h/zXws8DN4HHY+acMdIQKHArzzrPz5yzsgQ7PfPPvjhyKLvnz0YYXt0LQ
81c8NCehw7mpeGiZlsm6oRbErwpZnEdnNLEPW+Hg9vkZ6Agd3hnifV7O1/rw
NDK6PtysfQ+exsF4JXz44pbkI04cK+a9T+3eeuKbPUODxO8XSqCzXWAE31/q
/Ctc8WbdefN9Oleq36tdfT/r6C/2Bz1fVXjbH+6xTnfI/aR9Vfyl8xUlDzkR
7520r9w/zpLHa+UQzwkvL/yfb3Y28cLDzdCHP0I9sht3pDwfVxIHzl8FfEt3
zsdrXcR4I0NLeB1ProrxAT8iSgfmR/qnar3ZZxexXx/cgQ7SXNab5Z4lX9t5
HOd/j0lCL9HVmqcT17mBrqrx+xbw+wmeC12vaUHhYnxTOX5CeZEvMJ9u952b
Ro7h+FPv73A+qLh0/2LEGTIkqeTFjRwR2DlOvHAvbpeMh/+8Qn6u6k/dvRQ6
HoUcgbvlfiNemmo7vKtuSQSu/zwb3teNgdijku/hLquBvST5Hna+W+jDfcfz
N5tmyebF9av0j3eOVRX7g9HxE/b8sDsiLmTl74ce88Rl2I1904t+Cm7fKMRD
y01Anz96OZ5TnWrYBbIuQH/SjLjrorvEKVQf8z454FG8iJ/Ji2s9y8ETCKsG
D+IV+QLr0Q2uL/thuQPbgMt+WG70rWW8uFObfp3GP29954jdvIzwT80x6E4E
nm+a+8RnDpb04Vrd6ei0PlxteK+jj8xFH7HAe8r58n/fU3D1nip9BlUX5qxM
Sz9Hqb+ncPtLB3izbhPyIHn2U0f2oSHvdce7kvci9cmjl8b/Ob7Sh1vXf8Pv
K3qxtBc3Irbg71QaIOO3fF+VNzSfbffhxinyj3qGNr7z2qwC39gpmso3z1qS
uuHi94d9qMuQ61+/dkf3PS/pv6jnpZ679py43P957nK8eu5G/ZHEj7vOhPd1
qZ/or2SdigrPRfHETlN3Zt6aKZ+j5MM0SsE5UiWijBd3lk4lP5FrN89Tfa84
xHu1A4t9uDGDeIiWgrjx/57vMdD1k/r29hrq95W+vb6miBivdFmdJlZWcR0Z
B1brR+mVOQlXlfV+rlkujrR/AnFaEVcxsz0ScVqnHflQxZv99m9MMX//T55U
fJ7MbxhRVNxM5j9yD2SeZL2nsT4372eefr76UG0iPCSn718+XP88Hf789/u5
jDcareyCXtx1q+DnTKafsvGbtOc7wPMxj/ah3+C0Mewn8adwHkzbQpyp0M/0
ZXiki+tqI6+ii1IF3qblziB+Z+/jfrfTF0y3L7HOl6yR+7/kO9Xh+RmxZxhe
3OjyV5i43qdOPtw5ZrC+W1Yi/3twOft254RivHuA89P+Y6c4H41XkegySF0j
lVdVukbf9k/O27sb6NuSET0b4/UGsZ+reijnVmzuR+qEG7kKCB0JpRNu1e4q
4od63vwC1xYN5D4T/i77f8n+CMeOiXiJkbw7dXyyX7n9JC1xGWk3Gq3isx8W
qCp46VpAL7o5z+thSDIvbgZXGyz/XvzoZeORR1X76rAfM/K9b/L+PaRvi/s+
i4jDWA2XM8+pBgrczlgyo/d+Any2AT8Tv0gRJ9x7ffdQKvwHZ0V5L24uzh6o
G/Li9tWy8HzSxOL/L5L2xubk4n0zMnXy7YfGjNLU10fcEevOGCB1ilK+E/kO
4yL90fSE4MY/4Tnk5yo9B3SD3g33xam+j9dpqTOhsyTXszv9EPHt+tXQgamM
DrCeLg7x54F3fTpdWu5pIl9oNxhYyotbSwbjV1fwnwtauaicmwOihnlx/csk
9p/fuxE3yN2bPhcDQuBfZVjE9ymdU9S36l0M3t95WwRu/tpfjNebyj6+UWKj
11FiL/bYJod4aNFUUteOegHtRD3qtRZVZnweR4y3rqDTYfW5ofwb9DGiM2/G
DXSStK9SNyk+9X5a1F7YWeq9fjSc64eP9uPZj3HO5khKvcCyvay3zavgXX3t
CD9E+YlVo1P3+t1+HuhHJvuYBPS6Vd/kyIvECYbinzovlsAXkP1EzMWT4ZnL
fiKBOuKopeCZf1dH7EYwXtUR2/9e4DpSF87stxge4/sNzI9elOu3ctFnXEv/
RH0k8Si3QznyodLOVLxWzfqFPKW0MwN818vJwgSeIR15qUUt2VeXOGFcDx1o
p1E21tucUtgBqz+znmfWAH81kfu+VRg/b3QG3scKxIvclnvoB6jsyZ/oH2r2
LWr48HWSJ7ByuA/XRyclfj7qM/yFueS57DkH8MuWzCRPKPsma5XR4TT7U1+r
cCvbA/ylMcuoh9p+XeDmkNLo4djoB6o8uDvlDDp9v46q4sXtOTdUfoS8krNx
kPxd/Oj9t8m8IXaLmfkKvKMCa8r68LczqTOSfcYVT0P1GXc6X8IPkDwNd+RX
sT84tcdw/2NnUI9WqSV5EVnnZd9HP1nVeel1CqOvq96XUvnEfRiltxbz4vqA
H3gfk38u5r0f7ac3vL+yr5P9fph4Lqqvk7F0kk+3xP09F3Gw36/4dfnO7oBf
0a6eD3fO94O3lHUyeZvBMQVud8kBz2l9kNStfCj5bwtV303OF6s+63BzEepv
/5wk3gOVr9E+3hb+phs0GV2+hnuIHzxYCr7zk0/PzWn2iDxE78w+3P7hvJhf
ff3pil7cvPdJvIfWrSbYLa2IS2jl0kh+obST5XxaFbGT7QLnQ724XpU4nfNx
mIiXmjH+xm5Zeaai7/v2e+dbb9arcthR/X9i3569kHN98SSBGz2CxD5vVf6I
fZAevqjZZAf7+bK7gsdl1bhGvuPCRIE7gwqI+JHz6gv5pnD8caN9OfKq3/WB
+n7/9PaBEn8n90+tCvOj9k87R/Eg8a/kz+hTNHg79VIIXmGA99UyCvXSrTT2
ue5/k6c48pg+BVMt7LTKUjfmxUX0Q1Jckn4Q82yf/EA+vnjU8l7cGhQHneU4
xXmvVR/2u83oR17/cRUvbhxMC/81Yg168lt6in3b+OO6Wjc+u8VYt5q8y+WQ
cB+eifiI04Z+NFpddCrcye8Eb8R4ZlNP3EXqV0RtiD3WZSz1oSreNTkCOyx2
3EI+PPllzommNQr5PrdBNPIIA2P4xtv13uGPHb5CXzvFx8vWHH9D5jv0PrIe
XOY7vv++6kd/+zP79Gt0dK1tFclnO1HhEWjgxugbnO9tHsp4pox/pk1EHVOT
IkHe52Xkob+SmS9HNh8egv6f0/fHVN7r6PXhNzh3S9AHs/s08mjRsvE+yL4V
Tq3xxKtl3wr31doU8vvgx1nz2Q9kvW2AFyTrbd1x6fDXNn8V68FNOIk6jaPE
5xVujOiEPmrNK8Sf51BnqmfY5OPFadeoA1K8OHdVeniNaj9PY8Mbiyr7oKnv
u/8p/Z6CZ/tw82rMIPH7xQnghZcxz+1vBsnvSb4iRjvO8RSXyEu2/1nWP8p1
MoL1Zg6NUciLuw1ZP/rEvr7x1rhrxLs6VXng1dUxj54X92/emizq+QJxqqcd
4ZGWnEp85m/Zp29EYuLs7/oRd1HnXYke5CWvLeI9izkDe69IIp5Xg5foJUi7
wgp5Snx5VW4f7rSdhL70SfRp7EMd6LeVLy08q9m9OSfDy+N/9dmKTl3TqfCE
QztSNxHnvNChcHenIE8xf4KoK7TfdoOn+GdBmb/oLvZt7QF8dbPIE3gGf4Hb
uaqQx+08j3NV3X/lI1nFPB+4Fu7FtR8XiP3cqNnFN17LXVvwzJQ+v/HDbPY3
Gdeyy36ij31eeAXW/Z+Y93dbw8Tfqzq+Kwnwr7pXwM5dj1+shU+Dj97wIjwL
6S9b/w4n3hr1EefvonsCtyt+oQ+1jNepurnv43WBejrVP7dCTzHe7pGTOPbC
LNgzTXLgN9ybTry3cULq3coE87xk3Mn4OwX227PJ5X14HRN7T8b91Pml+heo
OGHgvJM6rtZPL3nvnVzEtRLlFevZ6UM/G1V/p7ViP3fLr+O9GzCfOut/0t4Q
8Z5BIyX/x6QuO2l20RfJzfdPfu99WiXJI+iDaxX04k6qMOyP6j3RA+yFrpc7
+BnnivxxBuF3OMeO+XA9wzkfbhZKJ3U8pB2YOTb7Xamw8sy/rHfe3Jt4wQL6
9gbWW4vl8LRvpsAvLkFcyG73Dl2Ib8e++PyeE3lPb6cCv/yAflJnHOz/irF5
ftEWpxP3J/vcGXP7XxR1jzP/zeHFzTw7oot5Olg+rxd3p/x2XdTjD6b/lLP1
ANfPmub2f9fRd0i8CfuGWyz0qri+9Q57Lwzeo1P1t+ji+8g+VoH3UaOPlXPj
DnmPGDc47waOFetc9TVzx8k+9bKvmT56EHG1NuBO8rZin/m+373ltKQv48Ij
nNvp6H/nJIgHj79ZaanjkYP56RpJP6zsC8r78BQ2dtHm0VLvsd4Igcv+UPrJ
2+SlZf2dE/cz+KQvNXzjZT2pmcjmPu2T/L67pLAHrNuBuk7ilr8FePOKByh4
fV79TIln9uJm1yXsWxPSs78O640/uPUqfRWtH/Hrvp7Hzj65QfDQ3I9f2A+i
ZcJvD12KTkLyzOI813/w89z0xQ3FvAd4cVW/Cp0Ea85ddEznxpP1z4leiT4J
J4aLug3r8HHOoTk5BY/YGtJF4GbtgSXl9TlPl/WEBxV/mqr7o871XQX0sZzz
QtfAGUEfs8B7NHwa73WVkVV8eOE4YeLvbheo7MUNrRJ5i3a14dvJ+KGxDJ0L
s0Uu+AKpiR9qvapShyLXiRrvam2jir+Tfdu/7/dquYXI38Z7SD3sxNlZ//vd
7pQEv6NBCuyEufV4bjuXSR4a54h24Bn+bKfNWby43msu+rdzcuXz4taiAegW
yXPHzCDrtuS5o2lj6ZvQ5wDvXeKi8PDWPYd3lnsNebfjbzinJrwWeWY7NnwJ
cx51O6ovfIAvIfvCB/rIR2O86p+oF4nnsx/0+lHgzWb7O6P3/p2/R8r3cK2M
PxDfNiqgI6pnJW9rrSVOaH1qDr9o7Gv245R8rl38FHZ/dVPW65F3DuiHy7ps
PSbjVV22Nme41AOR+dDpzz6LvExon9Re3GzzCb+vcmLW90+b0C1paKHjE1OT
vBGpKzJpqax7jELcstA74SfqB+Izb0WJ4wXsq1XdmYcP8wp551l/3YZz5Rr9
tRRubc+m6k18cTxVr+fcQa/92z4Df2oteu7GDanjLnXqjDlS5/3bOe6dN3WO
6+m2cf/lRjGfuV1hh/9fHTyp9/6dDp6xlDjm/9XBY7z+JtEjYfdm3oddkTwy
4Ndz37+J/cFdlIr6f1XHd7uB2B+cKz+hAyV1ulReMqDTJfuLKVzZUQH9rgfb
qT+X+l3q+oH8SJLJvs8N4MaS1F7cbLGf8yg592PXmOLzR5wx7QVvz04zGf/4
TTbixLEOUe+wYDD1nusvoM+9/pzAtZw/Z/eON4slE3ltZ+Ak8T3sTAt57u2C
iVfnLSbtOhnXjZOf+GOyfmFeXLvHPuXOuFnGh+82lP2jzh1hR6g4v321F/dz
DF10o/0M4omN0bc0l4Obt+DBmmFrZZxB5jEnpoRvsD2irA/vMam0ms///jXG
poNPu7Gzj/+j/wwv3dmzpYwXD/A5q+4mTlr0Lvv9U/YNZ1ABdKW+7SdifuV+
4pw7ES7+/naY2H+sXSmlzmcb4v7P24LnhUdnHcyC/9X6C/1wr0g+3uyS1IMP
6Uj9tOSrWNHoH+1+2iP7zUnei7R7decV9dOSL+c2oQ+1PcF/3jl1WyrdId86
VD/OqX2+9ebOvXtX6NhnjvDhes/bUfne0p9T+/Cw9+yz0q+0V6cSvM2AXyn7
cuqR4Kovp+rXoPqaqf3W/p06UuPjKvIdQ9oI+0pf1eSSsBOUztJxh/PoD+xG
c4XUUT/W+KywG4dQf2fGYN/Wqk7huUT9It4TvW0f9KmsyuhKL5kjcDfXAOzb
QhvQ2T+Y42uoZz7Nzh2p2/rOH3EnVqR/QmhrYafol/GbFF9RO7PL51c6V0Zj
/yfK4MPNIy+JZxaaRJ2J1OfUY1aiLmjSZx9uPJsC3zVxtyJe3JwaH32uI7cF
bzNQT3fsq+BlahcXFvLi7uKT9MG60wl/ub7sg9Nlishn2HZsVQ8tfvQhW7GH
Dx0p6MWdRrqwq/Q+p311f+7yvoyPaxGvCqWeyO1/h/k/1Jd4Us378OrX/yrW
s/P4Gv7dX+fg54ypTj+DUgHdS86xF5/g9/8eV+lsS914Wf9i+PuS2Ll6iPXz
vS631pjxTqkgdPir18YO7JCQ8zTCZv2cHs5z7FomTOC1Wovx9tD6+DtZ5gvc
nFxcnPsBnsa0tvD015YTeMBOyx2f9XnnNjrru1fBb9/XUdh5+lCDebs8hbqh
+cyb9l3fYS1PHWHv2VnKh3tx+8JF0cdQn73Qh+t7YxLvm5rLtw6tLYnYD3tn
Ke/FnUYz2YcvtPCdF+7MDeSlpN+k3gt9SnfR79BOWJvn9Y73ws67/7Xwx4Ou
Y/ftBXdzlIshfk+4HDtW8S7cdPA/Ki9P48WN63+Tj+/dK7MXN5+PZn9/m5P6
k67kGc0Jc/FrMqm6Hn9e29qQ2I//vh9e7tfmAg/E5VrEFOPdGVJ3JKq0Zx50
x54+8jv84aH4oeY/TeE51KbfSCC+Ousv8ollu/K5Ax3s8MJ3xH1aj+aSL6q4
BLx9TPRrBvzjqyPQTrYUOrTOu405wOX+sHsudTWbZmfx4u6sffg/su+eFUp9
SqDv3rzpoo7WqPaU87H0Uu5P9e9TdSuqf1/H9rz3UsfVWbZN6CjZo7f5cLNf
YupDpa5RQD9c8pbt/Rp2x9VT9B1cUpI85ZlyxOOdK+hL/nkNPnOl9D4/znld
F3v3762+eJ3R/Af0hrYWYv7ul4UHsmAW+pLpprDPSn9N6S04GRaxn84pJ3Cz
YgP8kOqDxXx8u390vvLnQx9ndDB5mc376BvXtxH2bMctZbzjrcqHqMsaWwJ7
StWHvqSOMqBDoupVpQ6JqdUo48X125K/9+wwdalJXsOHWRAfPsS/qwRulCzP
+i9XDP2ODJXQHfmSAP+rdjv4o1KXOGDPq36LMg4f4MPLOLyZKDr1Byr+vOVf
5uUY+coA/qYZ+0L6IJ638pvyRAr/SO9S2qdvpuoNjd8XwquV9p6+5HhG7/gA
Lsc7Q6mLCdQH9WxC/Hb1B+oxF04TOvn2jknkuZ7exw7PflPgqi+88+sodL4H
zhC4UXAf8c9+hWReT/pZIe/gu0YZzPwF7Ofs8F02Ny/rHW82GyxwM9jFPtkx
Bf23UvCUzL4LWefRpvMeVVgt5tMseFnULwd0mF8sDRLfbyD9Xs0/sZ/1WFex
U+PGK+t7js8mvxd84BVzyT/Gl3564TJRxO8yPhbgYzstOS+aBupNJY+O/it6
pxiqLkH82D8Xxv6vttqH6yMt6tCXHOZ9jHYbndgU764L/63zWOb/QCH6GvSZ
IPp3a/02wdfIVFzg2o1xQg/f/HMf89TiF/jzn5dhP385wfsbdoD80f5P1MsH
w8M0Lx+Eh989HfUqMt8UmB+Vb2qATlTAX95UC//TuZ/Ri9v76T9k3VV9neR6
SC/1Ta5fCBN/N6aIeB+drwnRk0psCdzqklPg9umWfF4C+oqYQZepQ5yQTey/
+s3YrKsbBcV4Y1hfkddRPH91fcXzd6ffg8/VDz6GtWCWiMOp9zoQb1f145u2
5Pfiqn7c7ij7PnSV+hX3a7HvzItCPq12auqz1raDd3sSHqM2HdyclZh81t6i
vriT/k9V8hDWrzJfg12kDQzDjvlhNTyLmzLvIOuArJdT0G2oBA/cSJoR/3H1
J+wCvRj+0bbx+0UcOGZHeD0Vi/O+vD9OXqBuDTHPgTzjiSLYGVmzvwj13ueo
QeiKjZwgn6/kwx9cgz2zNj9xaPljNTyMXzqrtsLF++LcoY7GbRqoE/e9R9rt
ZnW882NWfCD8HaftSrm/kb9QukDG5rmcH7V+4z2KMgJ7aH4o8dCL5E2scp/p
az6qGHWk0h6z22wRuFVgP5+bOzfjr8cl73n7gtTxY191C+Wkf8edfYW8uHE7
I/ukOke2ROd8k+eIOfmh7Ecj+xUePyLy/nrlzoYXNzoWRe9xaOdQL269jkb+
bv96oU/sqvkJOsv6LLE6yDdvt+5Qp1FhnbADjYvyfEl+hXVyJ3lN73jjdG2x
v5lb4/vOI6tDLcFj0Q8F+8a7B6aI99H9IR7xHhUnfDL5vbBzJtjkN1PJeGar
Vk9EfqQt8eFvLybrKq/NeboiTwHf/X+6QN1KzuzwWmXfYXdJXDE/bvWS4vsq
voRZQurmPcyfzYvr8WNLvgS8SqUD4E4lX+DRz+eclH0WtTfRmc/sTeEbNvqF
+FLyXKm8uFFhA/Gl9i8zenE74VfGr07Dcx6ZXugn204W9B8d7EajdGX6ZwUt
oG/ptPJy/mX8c3o04m19sK8C+20uaV/JvmMqHvt93zG3Wjz2c9l3zFgzJKP3
+k7XsyKfoT8rn9mL6297i7ot693HRF7c+OsV9SFSb9b8ir2k9GbtyB65vfdp
JpB91KQObeD+pQ6tcfGWmjfqZ2W/bGfnFPH+Gbmqijpca9kz/K/dc4K94+0R
cYhfHWzpt3+K3IOfGnqOOOYS+Z52DaLeb0g99oHSyYirlLlInnphUZHHM9vd
wV6a+xbeyO4Ogu9sxL5Kve3DXMSl131hP9RiEE+LgAeiP+vFOjgeh3kYjI66
6dCfzp3XFD+xGn1p9ZNn4W9szyq+n5kkWtb/fjeXxyD+kU1Ht/rJTvHe2TPu
sJ7npIYnOnoxdRadtlDXUvKB0NNT9vz/Vxcp7l/a584Y/EFln9vOsTDmU2ed
XEx5U+zTG7b4cHdmjTfivd4WXM6L2/f+eCDiU0/jiu8RqD8tdxN9n0P9qU9M
eLeVGJ9pD3b7kkfEo+vmw84scYc4da6zUtdO8vrmrmL/DSnvw7/tG+hG9I+O
btbMG9xnzc+cm2eIU9lTwO19Mk51bBpxWRUPTNkBnbcGq7Bftl0kHjhA5zlu
aca6SL4Qf/btG3RxkmwirzJP9g8aMR1+0ZJY1H3mhmfldCxD3OHuNPqrqDhD
oh/hfac46PPj9JdtiDs9GUwdXzH6s1jHxqOv0q+Bf//8uQT50vx5fM/FejgN
PZltu+CVq32myTr6ac3Yii5r9JaNBV6OPkNG3UPEwWaEi/fRPLYCPMdY6o0C
fXYM6tsT9MZejXeP/aRhPeyJoynoNyX7drm1Y4k+nVZwTOItsj+X0fYIuPRD
A+d1b1PMi9LVd+U5onT1rTFZOS+lvWQPZh6tl6Y4D92Xh9hPWzRifZRZ7uv7
YzVOSl1cDsn7VjyxMvDCjX9K+3CnS3L282bLfLwFq+AV9p9b98LE74fwN/Wg
kejy9IzLvN2hDkgv2fij6JvT+XEYz0XWl0m/w562Ev+omQGP5eEf6GAWuB0u
/u0t85Ktq+F3rNwjzjf9yGHwUjfZP+c8RIey6kfiJMeKYJeq/Vies3Y/+lpq
4W3F/di54O3olwdQlxSXfV2Nd1LDKw7wVFOO4PqKp3pgHH0bVN3BbXgGdul3
wn53T8YVuH30AnXWGzsQb16bXOBmjGhSn24K9qQ6j9IeJV+c+VkFL+4cfose
qNSJCti30s5XelD6FvhyAT2oielY54pHl3gS4zMWlHXHcj+884z4bceqPtw+
eoS+7N0rGV7czHJUjDfbrcXvljx87f2fYt/Qb+es4MXtIdc5x9uWrOQbfyQ9
dd+Zb6FfEfWp8Hf0v3aJ52SOyYbu6yfWmzN3JLhWvb7vftrRz/F/4wzy3Fe6
Rkl7++wQ67ehIn+nl+lJ/ETu59a8m8SnTk+m7lzWY2oXVvG81t0K9eEl1uM3
Na5OnXIK9kM7/gn22XFh1M1LHojVPhnxVlmXpB8qyDzLuiRlzyu/QNnzxqc9
dby4yhOpOIbTius4jRq+FOdXxTDi4lfysa7WJRO4fTYCe+dv+rw4j2NiP699
S5x4dxqB6wlZn+bn2PCLZP7dTdIY3mr4Ynhx08CdlOjW6lUPwvuWeTTDTE5e
o0jBYt75N7VQcd/ah/iFvbh99w/4GdnhrQXsnzE/w6tpki2OF3cGHhTf0w1+
Kfg+VpcweNppS1JfF5Eyi3e8cft39tuxj6RO+DOx3tyol+ij8PgrPMxcsk/x
Xx3QQUhaUd6/rHPp+wt8Fam/avzEvqf0Vw03mlhfzqCK4n7Mfhn4XtFCRPxW
X99L4Hbl5LwP1ZhP58gA4pmtzrF+zvzu00XX+pYIE7+fSSB14VbAP69/Bx7O
/YP4I8oPOjEMO2pW/YJe3LwyRuS5rfaFi/rGvy4g4kXu5rrkVRUv8Sn9hq1O
vcN9+Lo18NZ216/gxY3pc9l38hxiH+pcQtbpd6Ef4oirMj8in3uvK/BAni31
4XrB++TD5n/2j+92WvILvudHoZNmpa3prx+ZK/uCz4ou5s+Yk47nolH/6dTo
66tDcbNGELdNOibMixt5lsHDC60T4sWthh2IG85OXdJ3nf6cW85P6zkfbxA3
1nP1FPX7bskXe0UcQfHuViQgjnTnb8EXCPD0SkRm/e93VU+tL8G+VfXUxvpz
5Mdk/3H7xix4mRN2oRO2cyf4k+vc99FMhXzzWWzWHeHnvr1bwItbqx4KPoMb
JXlRHx7aR6yT/3iw4vfbUnf90U/0pf2jG/H7nvQNcbLnQEci2jne9+rR0adK
H0v4r/aamZwPI3PQz3rrK/yDWu/Y1+uAO7+0CxJ/P44+e06sj+hw/tKTfeyP
reRtq6drBp6a+uUod6p671/bGUPsd1btdAV9zyt6MuIVfdEjMa6noI5jkxUu
xst+cIF9IDd1X4Gf//VHqAdLXhC+k5WYfFPHWOiHrn5EPCPLfa4f0QR91B4v
hL0dqKsKpp+23nIj59LJHMT/+1cTcc5A36iyMq4o+0ap/lDGxNicp7I/lH75
kvCztHf4U9or+NPOoCSyjue+wK1tDjotfXej39K9p6hXNceUJQ89ZjfPYZGs
CzMGhonvsT8ktfj7hjeITx6VflfjI7J+RPZ9MAuJ9eHUvBXuwz+mpa/Porvg
Nb7w/sZKQB/PuaXEOaj/fAd/qmtz7OG+C8gLxppOnLkh+V+l26Z3GsU+L3Xb
jG/nshgveZ7qXNaOBxEnU30hm5vwJa9lyuTDP8cV38sK3Zzfi+uFD/Gel7/K
36n4WJqExM2axPHjb9PDVzemhHtxLe589o3l1YinpuN9tx71RO8rXjH4mekl
3mUh15d6wt+vT+f1bXnOyn1+z2jyH4cairxZYB+LLIUdKPvXuL26w09T/Wsk
rm9I4MPN0bfxI/9twr46piZ4IeKgdlTZz33Rd3WsMq/qJqCO1YiNLppuS90w
PTv8j2GXyLfUQH/MOZcVvG5t4qw7CzN+7jrquYaupe5N2c/58uInxc5bx4tr
q+cRtyq0wGc3amszo7s4KSH++5FNxFVOD6V/nyn7EW0NE3oUrjZc9MH5r95H
jKuRC52KZMV0gcu4tBqv4tJmp/xBYlxT+LDmOvo6u1feozcWh77oZoI24O1S
ET90psKTqNcaHv6MS/BzdoxDl69xAvzkx0vIj3RtRL+bWJv5PSV2hZO+GHWa
BfdyXh5fVtc7D+6yWfAoWo6Wdqn0uxu66L0ni1HPi7t/oBtvXennG2+22YC9
F+cj+8li9OedK8fFulF9+uzIksIfVH36jFfw/gL1ZTtiLxa8grbHKnhxd3I+
+gxWPu7D9Ybb3grepqzHDKxzWY+p1nPA3pDr2djeLdSL27PaEo/L+6NvvDVu
X03vdYz5h33vhVU5Kjydtf3EvupmmCv6Y6o6WTdnOuJa0m63HhyUdYepBK7s
dud4Fu7nHXWIRoZ23E+9eH57acVI+D9tIyt7v68dLRie6h540QF84CoRf9Oe
x+Q8Wheou5F8tRTUEcp6HP1RAvwc9wr6JTeKizx1oD9IqkfEz4MGCX0kq0tR
eCMfKhFfOpdI4PrPRYhf5EOvyY0zED2lmiXhm019kND7vYzIY+SPci4R76sd
bQ/7zOAcxNMCeW15/qq8tupvvoj8qepTrPwmPfIK15f5X233cz5nN3EeM/k6
X77YKFjQny+O3cRvL9WIII5w4GR+L+6G5goT12teswDzL/3rA+uIJ4+pybmk
/NDdKWsx/29LenHzWmqR99Ki9irrxbVSwfC2x5FfNp9JPe3Xy7m/ONupa+yF
/rYbOzP6AYqnoeIJMo6qvTyI/TMnFJ20mMWwbyudwg7cPULgxg8VqB+bmgq7
8kd48uYfc4kvZb+K/TY61hjmuye61ZF1qQfOJHU5Bi8lnv/jFnj3ncewz9fd
g/5DTalz8if3Yzy7yPvT4zz8+YngdoVG4n1zQ6+QHyxFfFRfG0zcZuLOmt75
N6s+/ir4kCHda3lx98fr6A/u6OHD7cRLRBxY7f+Bc/bb/i/mfcNDgVud5Ll8
6arg5aj9P6CHc7gI+hWSl670rBRPUu0PTpse6ITMmTNH7G/f1qd4jrdHgz+q
eci7nzjH0nb1jtfPUidr/zxAjNfHv+XceR6DfNwpXYx3L0QRdo/eVK6fnEEC
Nx82E/kMo+N16tyljq6zcBzn7okI9ORk3MxKwe9KRzEQT5M6im73hcTbpF9j
jcxL/4Vg9B213f3FeaRXNNFTer0ffcefB9CvKkZUeETR3lXn+vRx089+hPdy
a4bUJZB5tH3T4Wmlu+TjdTifqVvQi1SFLyF5L+ZPn4Uf6Ryb4Rtv56X/pVbU
FetNU7zE38m7uVlP4ReGLcEfv3IA/6f7FmGH69tGcC4casx+ev0Z+7Hie1+L
Co/iyPCcXtyY1kTa3wtze3G9YWoxz9bLHrX4vvgLWt99Yn3qY7IFiXEybqbN
G4k/W/iVyIuZd97jR+Sty/1t7CT9X/leOI0OC17sbfzfgF2UL704j8wV8+hP
q+Izn3qFi/urMyS7F3eOvRa4sXQS8YxDxMPNjcHoXv3YiTqse+S79SXJwdvl
YV+MAZ9E/6utsEutHo1Pe3nC9qeJnDfJ4yXx3qdVAB0rY/9C+sXI/cd8VEL4
xda4+8JusdOw/7grmhDnl/WM6j1V9Z76v9NEvETb9BfnRHHqCIzmR7BLpz5H
j2h6as6vJV2o++gAbt/vgD7g4IXEeXTiS9aDcOpww07A09i5rZWYt270ZXP+
XEv8Pt5+gRtTr6P/sHcM782tPAK3nnWEzy338+/1Qq2Xy4kLjZuBbuTn5ehd
l76HXST7C9jTBsK3vxgMj3a3HH8LHpIm173VeLlYz6quRIv6CDv+x+ecy2FP
w8X1Jf9EnS+Kf6L66Vh/yni16qeT61Zu73il+2dXSCyuZ4Xu4nnseI9dqE/2
nbPak/HkH0tOkzwHuZ43biAfIvWj7P30xVb6UebxxAI3/iAuao4aRf1ObX/c
Wx+1mf69sg+XXmuGsH9UHy6lu6J1AA/orsj+XMpeUv25jPcDxd+5U1uxv4Wg
i+V2dMm//DEP+6TxIeq9Lw33vadWzbAofH5pWU8heXFOGH3fPtXx473GcE6E
VSOeHBFEHLLUb/hf7U/V5e9rg7dDn8Q62ZW6vnnVsD/f3cS/OPCL5CfL+Mm1
1GKfNLOtquDF7UR3hb9ivx6a4L/PVzw3a/9e+sRcmk+/tkGlqV9ejx6NYWYh
TqPqmqXeo1onCg+skzGv6UdUmXPKKHWKeIWsR1Z13Eq30L1A/0QjDf1ZVP9E
a/VkdDqzgJtpUvA88vTi+XSvxL63oiz8+C+pWEdbwa1tlwUPwfxyj/yJzHe4
J0LDxN+1fFXZi1uZj+IXv2/uy6c4U/qI8Xa9frw35ekD7vYqjD7XmnSpvPNs
1ZzGPpAjvojDqHiglfA39pNcP8bx4rqzF/xzQt5jiWsbElUT9oasw9V2S/tZ
1uG6cX4t4R1vXTlLPH3Ei1AvbnZbgb+0O1EpL+4mvyq+l+V2Scb9SDu/4lLx
HprB0bJ4cTdvf97zYW2DvLizcQF27Ht4LuZnqRMo+3HoM2UdbSS4/pk6W8WX
0QJ8LR1+TkQb4opdko4Q/664/UnYV4uvkbdNl0Lg2qNh8Iqrj0b/UuYB7a8h
gl9iJF0k8k7KDnFS9g0Xn/fwFby4f8jXaIvHEfdplI4+EGq/Gk/+TzewnwP4
yInk2YNKSD00+R6d/nRRnPt55xfx4mbeFPCxV9QmD6D0aTPmYT/65248L27N
+x09juiF+JzSU7AXrl6iTuNpFe4rLfUbdsmz5CnXhojxZvkS4vP0DecYL/W1
1HkUeE9lX5uAvqjiJXabK/MX8hwPvyDiMGaOsOJe3Pk9JnlnPTZxsvRr2T8b
VSPO/7WsmG9r9nriqHmlfssd/Ay35Wfsxtut4Vm1b0Cf5ckrGT9uF7ys1Z3I
tyb4E/tKP811C41H3+DBVdZt1w3wHHLEIJ4x8yb3fzgf582C1tiNd36Vdks6
+Fnu0ZjifveUFf6LqR0V54E++7rg5+gnxwpcO7dJ4MaclSnE54eH4e9M28D5
0f0ZeQyZZ3T2hbHfNi1dzoureg23g4MuzVbq1o2SpdDVzLoX3URpV2tvu6Ar
dEbquUrc7QBf0/mrvNArDfRZ7l2I5x6nYhrvePPn9+x3D/qk8uJ651PwD1Rf
wvfodKm+hPaCaOK9+HbegmdrSz7uQT78eGO3iBtoW7KGCXzNF/b5/Q/Qc76m
wYPJZrM/36tEnPYA+rBakNRrUnpoG+uwPlOhz6C/Zp0Y6bPCy8p8C95oIfoI
WJt3kXf4EEk9nIwDK7vIfWTn9+LGoM7w9GJNEvuwqcl89wX0xK2tOQVu/26w
rzaOFLi2egLP9w1xMzvONPjK8waRp538L3nb2Cuoa5W6B06sicTZpO6BHUk/
O3vFVplPX4wO1fjL+AfLwC3LJW/aYhZ+RuM72APv86O//0st4gkvwfWQOfAk
ZX2HkZhzXNV32Dk0eLyJbqELeiUhvJ19adD5SxdMXGjdQfSD87Yg/zOnBjqT
BYrC4+rwKKMX107Z5LFiFQsSn3ejE+OPTOa9XVhc2GnG+Kd87syz1NX0riP8
LH3DVOJUneKhW7GoLHZLqNQbSfTxpTgf0oZFFddV67n/EXhFD7ILPkvgvVic
jz4Kd4Yl8OJ2SAT1IAsfiXPT3Sz7lb97g18t+zA6t+hvrvowqvp0s5jkq8j6
dLP3YOwjxSPNnQ/+d5ytZby4XV7qEqfqwzqNSV9a427FxOJ66wsIu175j9bQ
GsSrs68u5sXdaXcF7tZfXcI3/tjP2B890xT3fl8r6WpRz+CMSVnQNw/vknOe
tTxVwHsd/a/45N0b/FvIizu/SF5HgaPi+WqZ57L+fxoQJr7HgJCsvvnP+hR9
2Cladi+up/sFfvmfI8R6t1Sdxdcw7PUUVfFfakyDZ/6mEzpfjfaKeKr7bCr6
85EZ+Z55/hb3r/xxq/Lix2L9ZxlVwou7V2uIOIPzuFuIF9dfzH8n+BjS/1J5
gYD/JX8C9VyLT8L7TdF5bKgHN2dJ/eSClcW+EeCtLfyo6jqIu3/XL9uD5/Di
dvHE+Isqrr4sBedj8rToprRnP3R7VRO4ue+MON8DupHt5qNflDaqj7ds546L
nXDCz3+2loFbC3aJ9W5NH4S+1aB24l/3+KoC3uto4QOxPzpNhCfaKJJ1cjEF
PNVFku9UlPfF/IE6JsWbUva/ig+r+Q/gsk7E0zdTzo/JdeKgZ2hEAXc20XfK
Mz6zd7zzxqLefCs6xu7NduhnVlrLOXWD/Km+5Al8Walv5hxjvNI3s4xl9fh+
l6m//ryDPKtDXMrcGkReaR9xK7NFMP79X7GJR+V6QTxF6ogG+AxSR1TpegXi
NlLXy7kyxFePr1c00VN6Sh8nfZu0M7ub3P9vx33nqTXvJ/F99U9xyUPKeXDs
3dQrrbnPPibnwY5fm3rLclGlTgjrxGwbh3znqfUVvLjTuTT1L7GP+XAtxQBh
t2vdIyp478e4ukr4yx7dCfm8pG74HeqO1fO1q8KnN+KWZp87+ZPgkRrn1wi7
y15QTNhZeuW/m4j7LLeNern2+VL55q33LM6VmQWy+Ob/9Al0bXqfSeOb/35P
4QU+ui7sNcuk34ee4iPz1agv9lW9WdRpvjvAuf7rOdbPoplin3Sn7hTPxd6w
k+f+KKuwo9zBoexfjZpxXtT8h/Mobh/0Gtrl4Tn+M2uE+F4jYoh5VvZ84H2R
erluyi7kNaQemm42wL5qcFrsx9qw9oz/GhwmrnOwiTzf0Ut0R5YW542eBn9X
Pyl5cZXmo3fQbpOMe0i9r63N8KulTq+6H6XTq/j8Vn7uR/H5nZbX/XnDxevh
VXZv6c8brtjIubCA8ebCzKzDWMTj7PlNw73jnb7N6ecneQWBOlPF98sWAb4j
IXmQ5ZeJM/QeSv5U5k2MZAPQFbpDXigQx75zEl2wu7IuTe2HK1uiN7F0gm+8
XTw//nnrjcRH62cEz3GYfaG4On/l/X++jj7MoNrh4t9G7PPOojf488N+KOId
bxduK8bpXcai63DxA3ZyGvqiWZMyi7iNJv1rK77sS9siFfxDmb+264E7oz7z
HAovE7hbriS6tDf+9fUjc8vFpi47qAT3lWIF5++C+fC+Yh6h72LuMejwVH0r
vqeKe+v5l4v3QsW9rQ6L/Dy3mqk5v+LsreLFzVR/sU9+OKV0aDh/ZP9rbWUt
7H+pE2IPuse896xKHHgYuBvUi3xnuWzko8pKXtypMuj8TK0c2ztvZqUvxOe/
FEnlxfVLJ7D7k6+L6sXduW/JsyT7Qp9qaf84cRuiH3h1f34vbvd+Qnyv8WIf
7kZuhlda+zz8vRRXyROl6Q+PqgX9sp1XWQRufGrJexq7EOdFyHWBO3nQ09Ay
bMP/fbGW9ZvPxa/L/IjzsW1t+PXD3tJPaKvU32rZnvjUqLzER8rYYeLvt/QV
cTCnJvwKd1E+eb6z/xv1qC+y9ibPKuapawnqK0+XFri9KZhzSeXl783Ebq/S
AF3oaY8FbkeEortbe7rkick4TI9s4jpGj1o+XG+3BDuhOXVhxnG5j2WjLsy4
29xXl2G8OMP7GGu6j4dvR6nKc5R5xoA+sMwzGuEHpd3Iua/sfqdtevKoL9Jg
J7SNzfOTfSrNLq/EeNWn0hi/k3jwrL4895ybWa9nYtAfQK2TX0zW66+PKnrx
b/uDygsoHqbUvYaHaR8N9LclrlPj//S3LeYdb7apCZ/F/RP7o2968mF1MsOz
SPqXjP//zH67H92MgI5KyfTUY8QqXMGLa24R7MajITIvLPe9gtPvivcpdwzh
Nxs3tlOnX3mcqHezq/bBD1g1B7/jbnLyK/OiUSc75leBG1nawnN4OwK/swT9
LKzxibHfD2XDb1L8sfeF4IcMNkt5cStqGPnmBVfY93ZmAa/RBh2CDJXEPmBW
gV/k1GrHvi95iQE+kuwj79SPEPondnXGm1KHzThZVsR7lJ6GFZ5WPG97zhx0
eFTfk9tn4HuHnIztHW9MA/9m3xFX63JZ2pnDw8Tn71yIPoDKS/7E+6KNSd3A
iztlhshzXfPhVlh0dEPWpiTupfzuwUtk3OcH7JMus3kuo+Z8Ec+xG3amvYY4
idWl/Ud0Mz6JOjL7F+KBxsSz8MMT/i54K2ofMAqeYd0k7w4P8zX8HC3nMHja
i54K3BkFP0dLmI7zQB8ozk872hH429Zs/OeK67DHC4E7t5JRzy/1rwL6FVL/
Sv0Y9Y5hj2mJlP6Y+HFLDfLhVv4fxfcK6DBkSyzeE6NmLnSlFg8WuL2Zvtv6
y22+8daBUugkzHxb24trGwdJnfD9ZbzzH+ABHl0h1o9Z+bbYZ4x6IcTfNw4V
fr9W4D514nP/oT7nBfzkQH+rlPADzL4NfOvEHtINu7zKrnpe3KlOPNytEd83
3uxIPNz6Mr+u9z7NyFXinLJ/gW9ofZB9xq9fJw8xtjdxlwmFqB+4gB3l1hgi
979SxCvfNOK5FHqBrsv90uBJerFvZ/kjr/dzrUP9uX953gXq9NV5t+ce+q9Z
Q9AtnF6RPEQH+Ld2RvjSWs8u+D9uNBHnc+IR73VujSU+nD1MxPP1S+OJD/ef
TBzY+QDfJPM44smL6zE+29DyvnmeeEv0w9UzFCrnvX8nU9qY4rlMri14BWa5
pCL/pY8qKeq0nYcLseMWJRe4dq4u+cdRmwWu+jwqPUyVX3O2Sd0zmV/TlJ6b
5C8Z+1coHjX2WGjfVuLzujb16bm5IweCD4Ef6146XNP7vbQ6f4vvZe/f6cPd
kPKRgrczb7jUcZVxkigLX4j9odIoH251qix0wcwCHWv68ETpRd23cypfbe+8
WWULiffLHjrZz8foNhK+UfitCt7xdtks7PO1LoZ7xzvXYgjcCR5W0Xed87uU
/qrqsyPyTOrc9OC+Ogg7D/pFqn+Wpk2BH1tJE+eCEZ3rWPNGcK7nl+NfRKJH
EI3x2vP6gq/ifiS+am0oJuwexTvS4qYUzz3Ao+tLPDLgj7fEHgvovcv4jNKZ
cfpKnl4JGbdJVRs+5bH/Yeus46w2vjYe3LW4hsUdFvfsAou7e3CKu0twdylQ
JLS4FfdCgOLuTkNxd7e3zHfmNtnfe//hw8OQmzuZzBx5znMisr8eHC7y1faI
KyJ+Z365HOqb/3kjRTzt32kp45u30fEFj8taOxidv0QDOovrnO/L/nbzA7+v
SS+B67fh+xkj0FfTNkYjL3x1PfWn+bsKu0PFn50xG9DbfVBI+HGWM5d8UI3q
+HHXYhB/zZoKXYuUqfAXJA9Wvw6ueLB2qvbcv0MdmZEotnjvzEb5k3h/r5u1
iZgHLWwQ60Tu2/adl6yrhsEVvbj+B3Xj9qqc4PUrs/9/ATdKZoF/FW+k1B9u
TB4rcieun7Ic58vLV1zn5wXox+Z+Cn/1rz9EPMJssxJcnqdK18Ke0Fj5TeLj
/nRR5BHMuGMreHG9WC3l5/jret6HKN0Nhcf34kYEeFnGd9atLvU4rCb86cjr
aFI3QZe4FoHrKNy+UVr6uTIunT6pmGc39yriQHL+jT5ryPelvFHIO147fI26
vCGzC3txc3084oidSvrO2YCu0fvb1b2402oH/vnw7DW8uNvjLfpcLbN8FXm3
nDXFunO+JaT+uexu9C2uVCGucBz9cK1lB3FeOLdjE494dEuMM781q+W9TyvH
FvgtR+iPZ29axL40BP0p1e/PafUAPW3Z788+N0fg9t+zwbetId88eKHAtRjo
HrvlygncWFcYXWhp/7tr3/IeZgvEp6m3+9cSEH8Pp++nn51Mf5dNzTgnFW92
2RP+X5tCZby4NjQb/WrivuGcykkeRLNisl+1Wgzf9idwe1oL7MM61ciLSX6U
4m0GdJ4VLnWe3ca/B4n7mwCPXf8wQPx+49fErK+Y9KXSK9PXwDgRC77YY+ol
7XobwgQu+2gH7FLZR9vuYwjcLSX90/uR4T//6yf+wL31CGK+ZP8RVY/g/lRE
zL/6XWq8+l36KYc8/pBQeCkRtrMfyn4BTqYQ6ohlvwA30XzyIZeWo0M7ext2
89cD1BOdBXdrVIZPk20K9uDa9+wnD5pir56hn52djfl32oRQ7xl1al7veKPN
Yvy5LjXyeXG3+5L/F7c0dP7d3D3QFX6cEt2tVaXF+WXMvKp0JsXHyhUFu/qP
EmW8uNMvLvEZed6p6zvHj8cT972GfliB7418QOT/9MgNffaD8Xm20FO3li2U
9gn8ZGtEXvrHvGvjtzfWzIko/pRxfifNW+qmZZxf6fM4kken9Hm0e/Bb1XjF
f7WuEbexElUlrlUd/Wg7KFjEB+ymvZqL/3f3GHovVSZRL6vquFtWJ460d7+/
7vuvc9jbch/QJywg7yz3Aa3sXYG7qxcTl/4UlOgHbn5Jht+n/JFJ/Th3Kvb2
4UbYSeoqMzXx4e7bpewH338mHp+gB+uqXhrOifXxw37gAT5DlzPEw6/+xHNe
Ul78XjPuZeLXj2cTn1t7TOB2lNzsGxeeiXPQXtWV69x9CS//Z+pK1Xw6ldB/
1KqQn1V4ID/rpmT86szEG0+XVvqqRXz3qXiV02OU8uJGiwfwNq5tL+DFnQ4r
4L10qY4ud9y2nF8727IPyr5p6n5U3zTzC3wAazv3o9/5Xexj9r1Bsk4HXpBT
e4Hob+5Grp3fi1t3f8c/mVYafaqmBai/a5tVnJvGykGi/3mApzSdPkzOjm1B
XlxbvVrYVVaTIXxP+YP4bQ+/hcr5ER97Vxv5XlJfadWa4eNX2D8f5b0pf8q3
b1gHMoaK+2qwGX2F7eRrtHHRWDcyDxjoXyzzsKqvuvmQul3VV926llPkGc3K
4MaDOfAt8vYlntVH5u8mNmXdxokb7L1PfXtx9C8Pjc3pw9t/hecca0QWH/4p
H/Z/M+rHA/ix1ex7dSf5eSYvx1MvcUDGp6VdpL2R+a0E7wp4x2v7F4v93zwX
u6hvPguspC/UmjG+OJVxe5h47urcUTxMVQen9AYVrvpxqP4d1kzWm+rfEb4O
Qqu+nHrF2heJr2anvt5sVo5406QZPK+k4EakbfAngv8ivxpPniOPKpEXzp0a
PoU6d5o9V/k/8TH6BfG9cl1pS+vh70ZPKXC94Rf4N2/OijiYu7oM9Ronv/M7
64/JJP5fjGnoHnyoKtaVVjsf+QfFuztVgP5omRb53iPz3C6ex7JlBb24tbag
jHMu9Old6DL+bB976ceL/I6992KwDzfqLiPuN/YKum1v0KW049wVfD3r81Xq
KQuvQ2c7KCn1iFmHC9x9jl6lu2qZT5c4UJdUZT95oGqJynlxK0kMgavxzuw/
Woh/3/ITfIIbpbErlM7tFvSp9dPyfJN6qvrM+2K9qf50Cg/0pxuxjP3+ei+R
F9AGlkT/SvJ1nREVeI6Sr2v+foZ4cVGeu3nzJfk+yePVVjA+wONNd4u4supr
nC2TiPPqw9EFUri2tCr8wn53y/rGT9oszhezy114lZ9P0ddp4E/0V6uCLoGb
YZPgI9mt4de6czfD82iyBZ5b/COsc8lnVu+L4jMbsbagA7SuHOsz8h30o6yF
5O1vhDEPT8Lg823qKOw1U9/L/YSlSC2uN/Emulby/u2FtX8V/JZj6D7ZM56i
85B7tOj7o/opqPfdzjeM96X6M/AsOZmHDRnJG+lj4HvOiSbyv2abz9SFdSyG
3oDSy+3WFX3AedOJK7a7Ds+t1FLeu4OJqVsKySlw62xJ8uAts8i+ecngd7m7
8JuUXxE6hPmcQj8Ot3wj6t5KFOT8XVQPHtL27OI8slcVYn+rL993GW8P7Huy
zlr1mwjseydPS/9hNueJyjMmicE6rnmPuM105tMtcxo7Le9W8gn13kr7QSPe
pd0SvFDnFnVS5izeZzOzm0nc5/hdnPuV6/LeZqohcC0D9QXWL03Bf5f272+t
BJ9B6xRMP9EKESUvnbp4Va+qjYgDPioW9p7U4VR1kWbjeNiHqk4tWh/iCasP
814M3Uc9/sOnQo/B+FM+lxkziKtcb+rTSTbrfhV2thFJl/wQ8jJG948ifuE8
e+mLp5lzM2P3T9lGPmtIXOxDZztx3nkx0P9W513Wxthbfy2if9OhmJwLFZqw
/z5Mh1/cKz3nYLxP9P2ckNcfPy8xjnrUnRfJL0zJzfeWGoH+S6M7/vFbrqMH
q3j103Zhb0hevbOyWm3veOd6CHpqI25x/fT9OH8ja/hlH1YSH8jUWd7PFeL8
9df74gZ6osvgk2744gzaw0zYNVq4+EPSw+ThbmInKj1z89luzpcqkXN5cTve
XPTOTuzM7MX1N4Wp79pPPihw/srzyzr00ocb9Ti/jIPx63lxezf2m155If5i
gqjk3+eNoM/Xhkngso+t+fmO2Mfsa4x3b+2Dr/k5ghjvfv6IHXeoBvH/0/vI
8/39jf21VUTm63Ew/YM6J2T9SH/N7vEWHYRe+8B3/CX2U/P1Beyx8c3E/TqZ
d7LvpX1D/cbKdMQ1E2xjH0hZgP1k3d5Q7/ybRXpmEvP4+UiI73l1nyjigO6S
lqV9z2tbJ/SzCqep6Z03pXNo7RvEPGdaJt4780p38qZ3Kwnczlec7x2Xj3M6
7yDsLqVD/ja+qBM3gycW9uJ2jQns7zUqGN7v1eNKfbC7hg/XkrhiPbuXhoZ4
cTNkA7q4s+Kj19WN+ikrbzny2m/biffMnQvuGHOZz+fJqI9Tdeg50ZVznvXz
8TrMI5OErqMRe4dPp0jLk4Y4pHsf/1rZGyumk5ep+iGpF9dCT/l0Ocx4+8T7
E9DlaDoRPcM8zjDx7/3vhYrrpcaPs8ezP5ij8OOsLGuoA608VeimuteTCV6c
Nv2IsPPtggsErrtTRP8pZ8dy1slI8o9O0qv0s8g6Tti3bobdLcR1GsYlL3bn
rKzTxx6zJ7YljrESfnEgPrYnA7yXYroPt+Ofoc4rxhhhrwV0KUfE59zd17ug
FzeGtRBxTj1JTeppFqBLqZfehR91bAV5sD3g2rc71HX8Uxbdx7vEz7W+j6kz
vxkTHsK0OuwPebaSH4kSkfrfP9qz3rbOAp/9mb7Dyn/JsQ3dt3VPRJ1L4LmX
e4jOycjxGb24c172TZh2Db5VvJfw7u60xK+ftxM+dvA9gbtDS4t50UPSsc6H
7xC41a6G2E/0UgdL+67fYKTwT7TfE4Z5cf1KXPwuZ1oZL24/fy+eh6byYp0z
txDXOXJD8M7dlkekHQgPxBwi67GT5UHfplhB4Y+bk/qrOJcv72bufUD9ad+5
YV7cyhkCv6pTUx/uVklYRN4f+aIa8JqsJqNEX0jjFHxhNz28JufAVNEHRH8z
gfxLIfS6bW2z2Jfs32JJnUDZb1H2SXTLpoXHvX0ddsjui+gy1ZzOPpuwBOuh
jkMdVO5u2L3ti3L+3l9J3ekfLcX9B/bJ99PhRX0Klzc5+Fi8b8apm+W8uLGq
KnZF+odB4ntbjeS9iJkJvZ2F14p6n5d1B/19u22tEl7c+ESdiJP5Vxnfw99x
atG3Qqs93Re3VHXKZpMc2CMa/qzbH31GrVhX8kqRJS7rl9VH2Z8B/sBHDT7J
pVj4m8EzfTr+AV0aFVcpEezL+1tFdnMetq4CL2MF/WS1XzuiY7+hM+ds9YP4
ieUqERfZ+Bf5qNOHwQ+cgJ+X9yr42hXwBJ6go2IkisI+sexP6o7jtKLf4rA+
2O3vwbXszdBBS92K+NwA6pTt0V2JH35MW1j+PnGOWY3+lvoh8Hn1L9+xE14q
Ph/5H/MruMof2fGvSL1Zaf90kP0Avi3GThnQHB7XtGMJfuB2gYhlveO1YzGF
n2C/rEkfm5czRX7NHbWC9/FtRfK0+yfAQ97eD36Y2Zh8dxzsHLMf/SaN3keE
P6LH6Szyj/r3ELk+0gm/yZ7TCf20MrPRQ5hVPZPAbxRiXS3C/jeLLYS3kKYN
53K1rbxfByvJ9SztsRlR0Vt+vgo/ciLP3ZoxEDtIxs0C603y51VfHj2E8aov
j9L51E7KuIrU+dQ7x/L1i3fKbKZ+83Rt9jMD3Sd35gby10PLkK+vPlPEKYx8
t/GXpe6HpniSUvfD3HILfp8RG52ZNJmoA5L8KOMh+vaKH2VWrkYeMr6MUzXB
3jI6HxTjzeuZWP+7p7C/f9pP3mzWSHSPR0ZCf+qwLu5Py5pK9pOS/c4K6sQZ
5jE/euTe6KH9QR8ZFae1Lep3VJ89LVCvKvP9i5L68hSqH4f1Ev83sC+FbcJ+
+pjNF6+wV0TMJH7XjWXkISSv0s1finhO3T7w19YmYV12L4Cf3OQ4cYkF77En
pkehD1npIH5XSu7LvL0ZO13GK9Q6UfEKu1pjeKElKlDH/b4G9bRShyEQT5A6
DErP0LyZm/uXeoZK/zAwb1L/0Fp2zfDiRi+D+OzGXeQ3F+8QcQPDKkV8ZuFR
qStI3ZwWPzbrJmtR4hYrZdy+5Cn6tawuzH1Je9iYfpZ+K+H4z24cdLrspwOF
vWefzCXWhXutDfveikxB3vHOTXTArGb78vqeV/Vk+FnalZxeXHu3iLjSwNj5
vLjbuCn14Hl30J+qp9T/OZIeHtLi3OyvAxuhz2BXgNe4lToCM0sBdITaU0fg
dC0fxHxKfzbLGu7DzurTwbNXnBV2oHHoQx4vrt1PRFxX9hXVR3YIFX+XfUWd
UcvQf4u5nvUzqCT7kew3qvjDqt+o0tsxi8l9SertKJ1ba/VU6k2kzq1xJgF+
6wKJjxhBHlfmB7Uw1qHKDyo9Dc95Cu/lhOQPjUkj1o87fRnx3EtjJb9U8gfO
wtsxt32TdjV+ihO7OXy5F0v4fcOljsSDdGFiHpIehD8wSfpBud/IeFEu6q46
DRF6Ptai7a+FfzePfLRTGXvV2RNb2Dla9rTwx2Wc0269XKw/Pfcg4i1/P+Wc
TThFrT/x8eZZxP+rt4x+y7uOk5ep/ZXnpj69n4f5xg+rQRxG2jnujWzo826t
XsGHZ3yNf1W7mw+3eo6KJq/POVh5LnpyObtmdDy48/4M/Af9tDjP3F3D6UPa
ZCj9fNe9w9+WOhKqr4eqE1H9svXC3cFlv2xVVxJ+/H/17LKvkKx/UXUuTiXZ
n0LWuaj+ngE+jNRtto/R39OKKPkGV2R/z7HFfeNVnzLtSDnJc45A/cjCJSJ/
asf6LcyL24UfwrtYnN833poMv9nZFoe4h3p/897H3pvXC93Q+fI8ShQPP/PD
JPa/nuB2CvRG3ZSrZV25fA++9MEerpQl1Isbn5YQj22LXllgfM1J8PrWOzI+
IM+piMGcswfn+fqLaV+78t6N2e+LF+m/1COuE7GqP740iLpRZ/1SHz/EbUf/
dWtmBx8/xFizHX/vW3b2vbpbW4g/T1fhPRjUn/Nl+0bwbh3hV2dNyrmWJbnA
7XL077ZLDOf82bcHv2xoK/Geq3pAe/IU+BiyHtA485Lz9nws6prXW+RHr17D
Dle89LAy6GGd3eOLi2rd5tFvfmlt8oS9LdZT67744zNyYJ/P7Yf9+VtkzuVN
NTiXGkVhn179WIy3fkH3VV3fzf83+0W39sV899PtM897YdEiXlxPd5+4leQ5
aPJcM0bmxW8Nmgy+LKs4B52qSwUfSfX1+J/99lwZ8CP0CzA33GR/ln1mA+NV
3vD6Mta5x54R42We0e1/p6V3vOvkZZ+s3BN9m6IZscMeN2f/z4t+l9H4n1Dx
/6QOgNKrVzoAdurx2OlyXTlJe5O/zpQFnruKb3/ZRh1Z5UC/HvQPYp3FH5F6
cep8VPwc90NE/K/fn/J+1UspcCtya1+9klVsibBTrSsnxLoIvO81YmT48Xcz
4d++eK8x7KxYb/atJGI/NZ5PIY9/ajZxwCFJ4Tf2IL9vHliAXzVuFPZv6vHM
5+Ki8Ellfzo1z6qPksoLK1zlhd25SYiXqHx94ZLoDwdH9vN8ZvK+26UrBXtx
I00YduCA1748u/ZmKuO/6yIeYNaNwfXf3ed9qDIIv7I29oD2rgF+5aufyXO9
rIsuwZ4+8rlK3pdaP7djUE8edTnvZcKY4j1yy739Iuy+nOBa4yPivXP2DhN1
qUZbcPch7539tuxHwU9WfPsT59iHJd/e7pwQflkcA954ifbsn132ivPcmjQF
3vjQOLLeZw75hzNSR/fcaqkLiV2t6iWVXa307RWu9O2tHfQrV/09jaGN6Ffe
Z7ysr2mCX59yoOhL66bZ6cONBUMFP0q/kUjyvmS869V66iA2VvTFu4wt1EPp
IR9947W6uXgPXfqTm3dl35CJv2QS35t+HPESFUeSdRyq35yRQfLWZL85o2aO
Er7xil9X1RX2sJHiAXnGek3wb8P1cXC+tuTcidzPh1uZKuLXjH/NuRZ1Gjoh
bbsK+9hps5vvnz9B8IuMpa8Eb8wsHRN/reJQ+EhlPor3Vou0R+Bq3/h3G6W/
S+fGpb248dPP6F4+mOPfZ1pVwk66jr5IYPzSfeQBv8s6NnU+xjqHDkbLpNhN
cj83O4yjPuufmYYXd92UxBOTjPGNd2vosm6orK/vm7HlNDpXVfcS/z82Cj72
+DeCP2wnuy/ux24Er8YqllDEmZ1T1L0G+qvOJF5v7j+X2fe9Cc/iV9ze48P1
85/QZfj7Ous8nG6tHndIMS9u5LtGvq3ZSN6D1LOx2w/HZHynB+W982Zf0QUv
xHx8yIc71xLTXy3uCh8vwtk9BJ0k+yTPfcXjFuJ7ph8jr7ByIOdA/CpiPViz
MhMfijUL3t3sdwJ3I6UNEn9+L4HujhkmcO0p4+3JrB+nWCb2sbBq8KlDSnGf
9XKTh63fCHs3QxXy5odWCdy50U/Mo3k6MeftYakDPbWx4AdaYeXE/mVcesO5
UWebwI2RCagTb7VAjHeGPBC4/vhVmHgORzvBr4v3T3UvHsgrSdy8+pg6mxNP
ibP9dYR9ufgX8rr3z9OfKFNTdNwiNMF/LPyFfkY7jmMX9mpheK+vn89Vx3v9
wHshr2/sOVHChw+YLnBt7jq/3VXtd87RnNt9+WsrA3XNRuyK8L2l7oqqZ9f/
ie3jybtxSgr8P73EEmL/tKLeIk4R0EUEV36Hfvd+Cu5Hxu3HrSUu1uI7OuWn
88Ab/HCV/TTNOvocfjbwT0eeg2eoPvGlfrj0r6zK8zVxf+3qgp/8KPZre/9u
1u/WX6hniSf5Q40M3vNpjLc/zRM8ZPfpIPzGlha404k45vx3oeLvc+AzGE8m
oGv0VPJ9FE91P/k4N6HSP5R9PWJnJN867w1/qv4XRbYxb59vCL6ENZL8vpNH
8iVyjBPXN5dLvujyAmGO53erOkd3Vy328TuNynpx/R38DOeP9L71YK0Nrcn8
J/XZ7U6eoTW91w/sA7HPFPDi7ubOLQSeZgn5vDD6ZCrdGLNIhmDv+ICezKQD
8McSfkP/4ZEND7/+WOLpN7+ha/L9mcD1h8HU6X76SFxoIbx99+w+9JTkx7kr
6wXy5SPfNymr4OvpVUazn62ImsE7Xqs4r5x3vDPlADzuc2XRWZ2ZS/LtZxDf
GgnuvNhO/nfSV8ZL/QSVD7JnxhBx9EDfJakPoj72h7Hg75eQfzlBfwHzO/F8
5xVxfnWOqPi8Okfcb2WI+zZqBm/hUSVRV67OI6sEeOA8iluG+nhVd1yjNX5d
9Qdpfc+l1CT6WvbIFmOPB7fmRST/sC0BfYRSlqaO5eBx8hk9p0sdHlkX9qCY
1JGJQzz43i10KVtV4rkOq+Ebr90KIQ5fcan4vQG7q3ouvu9yXx8/zYg0mzqM
NdtLe3Fr8Trybb2X8f5uP8T469mpV0pfwX8O7nwozgt9QDrfeacfs5m3WvOJ
I6k4QKEs2C0Fr0b04trxNuiFKd5gh27YRS8S5/HiAbso+7Ic4jo1CvA8Zx5s
IfDRNvf3OSyZ936MMHlO10kT5MWtujNYJwmS+MY7Py3EnpT8LmX/6ydPh4r/
J/lgAX9H1V/Lem390DiuI+u1VT2s4uerelgjeJqYV6fBV/Kep4PJa8g8rxqv
8rzmuwf4u6p/6PlFnF8y3qXseaWbatY+K+JdSo/F+ZIZvENR4qVSL8WeAa/X
WNyMOOu2cfAka+6BnzaMOkHr43d0BZ50Ec9L7xrA6e/4XOKy/iBQ/yv1t9V7
rPCAzo/MF6j5VPmCQF1tHXieqq5W65aHuNmOmcN4rn3Qt9o8l/O3F/V0eqbe
9K3Q8zO+I7jbuivvc5THYn/TpO6TFbWruH+nHXqixrTU6AaHpsWuvVeMvp0v
Oor7MSJlgQfeIQbrUdkPy9bi/+3/LYsXd97UjGh45/8I60TN/4/+s755iyt5
/O3pZ6hwe0YB4nEd8sKbU3WCmurzPcun22A0WCrsAye5puKsxOtbDUKvQw/g
+LMtwfVso9CV1d+K32NFmCX2cWd+QXia32QcKeZi/OuYf1IXmJ08pp2UfV9P
XUTMv7YJnoD7rg3Pa/YS6movg+shreENfv1OvbnUd3XnDvPVE2r/1fdhB8v9
X9Wxmm/Z/62o9KMxZN2r0TDQtxu/4OV9/E3JCzUvPOH9Cn6HHXJ8LLyaxHdl
XBk9Xn1fGHydi4Wl/yX3gRj12a9unfXhql7MDO4l+UvSfqgVXdjJP/waL+7c
qoG9HYIfGeBD/pEDHm3MWPm9uJP4Guff3eI+f81o0CbsB+4uof9dYPyz7eRD
a15Et17y7fXm5dinZV4ywLuWeUmVxzSikOdXeUy3DfW+gfHHcov4jnblHf37
lJ2fbEYDR/vvE3gvjs/7f3EjX2kf7nRv2Nw7Xu+6nDx1+mnYD3uf4v/nq4Ud
FA/cLkH/S+v6auH3GAfncT8fZlJH/zQZ/ov0B91q8BTt3tvQJ66NP2guz0s9
UvTD4nus+uBWnK3CT7R3fivkvY7mJsZ/aVpE9p2UfmvKVtgzHwv7/BSjUPMw
8bsmXfD5KWbClMS11/Fe6J+kndNmkIgPuK/k+/L9e7AXN5P2Kej9Xn3fTVVf
7+OP2O/3CnvE/udpCS9uNusYvg5XxHVVHa75ZxPsiGXwzI1CvbETtj+Ch6L0
RuathGdTrEAe3/c+6YIOV4jsuy0/7j34Es6rBpm8uHW8FO9j4R4i3hXg+10Y
TZ1D5lNZvbgRPQd1XFWK+MY7i+rAJ/6YNZl3fsz7jdDX6mxE9+Lui8iy/ou+
GMZleb6rvhiy/0Vg35b9L5y7k+FzXWC82609ceqGO8MYL/3T4afF3wN+j/Ir
E9Fn0Yx7gnxin9wiX2AM0h8JvsPwc7L+qGtTcf1MQ9HFSPyFddi9m8DtxUmI
W+2PR769id5EXP9VfNbnmnbU0SQYj92VlTop/UYrvvdgwRbiPssvp84l67wi
3vu0x+4if+P48wXm7PK8Ryf8+QLt+Fn455o/76C9rStw9bHKt6S+Q/GUVL1Y
9gHYA7Je7H/sMcnPN2d28u2f7oT68KJy0kcgMM8FO/C+HcoizlM75mDiyJuq
ST3ELPASQwtL3WjiwmYM+Onm67wC13JOg+cd+hx+x7GfxfMyX5zFb3pWVb1f
6H2lfEYcoLpmeHGrQzH4tBXL+N5H+xO6W+Z7zjfj23dRn6Mf4vxzOo4p6P29
zuQj5LkP9/bh1i/sA/qw1+m8uN31qzh3tEyOP5629hDxnI2Hg7zzZhx+j25S
lshBvutLPSVN6mIaUl/RfIvunkc/U34M+Nhle/v9vFNlqceJ8tiHu7kfozex
e468T9lnYVgM/PDLt9N5cTPKePbZsdnEfWrdZHxv2wnq3IsOg1/T5Qz+6KTW
si7uG3Z3+hnYQ//61+LvTehb5/aTejLN6Kf1PzobLbCjwutsOF+7oKsWTl80
kB/auVnmeaUebPmo5CE+yb7tyg99FcJ6LrtW7J+qPtfUvsNrvRglnxfXF3Zm
vZWt6as7Nif/Rpw/XQsfrrevIuL54euXVV7Pudgf/ZU5ybH3en6lPndzjNRe
3HpYhLzLbEPkDfQp8cVzc7OXV3X/Ss+EuOP/6pzk8eL68yjUOZ6cKs5380VZ
cR6peK/yj5zYU8PE/N4qRX/UhyGi/7v7uw0vXMaB1XizzUW1LonPqP3h0gZ0
CVKiK2Itm8g++eRSVe94s8285t7xzvpJwi8I9P2JR39PJ03rlD78lyJxxO+7
WS+1FzcqtWaeegwK896Pk3i8mAcjhV3Wi9unOik/Wun9SjtZ6SzQJ1PZ1WbW
xz+FGx/fO14fn6aw/Dv28gtpP3fFP1K4lUHmMa+mVeOJN9WQehzrc6HX8TEM
/t6nt9gt+/Li50qepFEc3AorE+L9XfqSibXkfYbTvRmKfxpniDx3/PF880kh
zofyfxInryZ1wZ78yvkYs63oj6mtDCEfkC0CduO56QLX81TmvOzfnfrT6+BG
28rU153Z6dMzsU+NE+tUvzC8shfX7brUR6d6TN1urivsM53PYc+rOLCsRw70
zZF97hSu+r/bJYeEgUvd6RcjfOs2sK4iHivvxc3hg+CJR2mEXfS6Inaf5KOa
O/qJ+QzEyYtfIs4v4+Ru/a3YR6XXwMNZ2J1z/MVfxb3fq7dvzbn/fTR8mayN
iYOlJk9kjp4t/QsZH6tVmTis0V3EBa2WYdjz6YsL3rg5qmeouI7kOWjj9uD3
Tq8Y6pvnirHgzc867NNRM4fk5Zw+HMz+kvspv6tfffIX89cFe+9HX9AePYS1
0o6Tfo37j4zbZJT9kZpSz2W1vIH9VO9oCe94ew5xGye0E/x6uc8Y0UeQ17t6
gPoaqZuhN5S6GdKPUOOVH+FECZwXzMOO/9Gjlu875665eBj98EJqoGPc9jp5
llyS35KzhNgPzfdPBK7WYaD/Trh1GOBdyHWo1rN2txTj5Xp2Ln3O6p1/t1VO
9CL+ruqz543M3Xje1ZrC0x+QW9il7qHY2Jmrr6Pbn3agtG+jCNzUF6HLVDK7
GG/mWYrd+P0255YzEn5j49XYeZEjo/P5vKWYB3NjXOzkT+i/qfnRhizAjyt5
n3NY8r6UPoC1AD0rXfaPs2NO8s1PgCcm50ef9QK7Tq3/qA+IQ6Ue438vChdk
X/ow0zfeaVQYXb+RdX3vi/GoJ/vb97+Jj335TwdJ4I23YW/k2CbyccamMcJf
dkv0o94oSgj4z42w394GYVf/+p6+T6vx0400F+ErqXjCh6PEG/tJf2H3TnSH
8uMvuCViE+/cmww+QJbn7wUvIiZ4IJ/1fLK4D6tALPLa2ZPDKygS9bPQCZ+S
O0zMt7I3Lt7Av5uflPxI/b3ogr45LnUp+4v5cBZcJb4UI4uIpyj9JX3APeJL
Un/JvUl9vF2Y/rdWxZjM85/PQsV95rOE/pg2eTj44vPwvF6WAw8rK65rTiM/
ZZV6Sb1Y/IkCD+hXBfSmOLfs8zXIB8lz0D27krqAlGHYO5IfpT0fQt4i3m+y
ry462IrnoE84h/7GefRmle6Bqo82F0zCr5b10cbYM6KvgVM1PfZ3zKX0PVlc
DF2r3vj/Wqyv+DVzC8l9TOahOkXhnF2XrpQPnzsZPyJvX8OHD40Mr0+uH7We
9XTv8afcWMW8uDnkCHysz7FKeHFr5COuc6qgr8/Cv1dgfOSL+DcyzvCvPcZ7
N7B5iBe3F6fBL7vyGH2gcPlfhRv1BjX34rp+ubh3vDvvZ/LL4+Pwe8qfZp0X
mk/e7Br2T8Ce/zXQd0rFT8Cl3aKflXq5Ku66gPFGxgjU+yZy4H9+akZf2h21
qZcqM0PgWrHKjDto4YfMlPZwld+rye/z5TcdY0ly5//DL/QgPztzUzkvbtyN
Gdc3PjZ95MyZpqiv02JNJV6o/JQj6N3Yl0ezD4/sIP89o0/XMXDu5y7O8252
uIwX1zZfRE+10jd4Ny3bCj/ayXxC8MfMpU/vi/rOqltEvaQZ0h995G6FRd2n
eWK7wK0OPZSdKj7O8dPgWfbRZ2JkHxE3ULjRrSx+f4UVPlyb7YhzxFz4B+dw
0lnDxP00yEg+LsI87KONe8C3JYYPur0W+ntKR90uF6jLM7y/N1ct4Rc5JUL5
d5WP3tyTerf8qfH7VF1qhujEY8ejn6TGa0NLCH/EvPGIfFM2eZ0SOdE7qzm7
oHe8eb8lPFKZfwn0q1X1GpJvGegvKfmTKr/sBFckbizzy/pVf/xQm1RP1auE
izdGgO9/sYNYj1ZH/Ghr+zHe61GviMsd2oNeQCj651bwMcFb1LOF4ld370c+
q3IHGQeZJs59M0mXUPF9B56L81xzk8MHuBKR79nUEx6q5Eubt2fSR/vkFfKZ
M6ei3/++tLiOuWs9dQ8DPtIvfVcc6r7KZRP+nJnxE/vxmJ7sA38GYUcNaCru
x6kSjbh58RvELQo0E7hx4AH228FG6LF/miRw++IH3p8Kz3leg9GhdYb1pH5j
ikZdbbfixIP6tmVf+60j8dgeBZmfh+2Ix24I7EP4x5PYd/Q2X8k/prkneJ62
8Z5zpH8U7Bm5D9t13sv+Uk/FfbpB6F3rj88SV8lZHx59pYbUj8z7jbru3Jew
c57l4fdWvy7yJvr5tMzr2Lr83qp2Znl/Pr/bOZw81f+H/7u/C7/aSr08zItr
u6KQV+uRBF1HpYdQHd059/NDn26S8yEydYkpd4V6f6+eLAq6FRHm+3Dr9HDs
9p6/w4NW/teunfiz7rUQ73gnODLXKbQd+78v9qfWW4fvNwrcbFVa2OF66Qzg
Wp783uubk1+R30oQhbqcOPDJrVit4KUsj4ze0cw29BUywfWYFnHCWJWxIxKe
Rf+i5WB4ZaGH2QeS/hfHEOMnfRT7vIpjuM33wpdX+m/dk4eK/5eQ+mtt3n7q
ov4Cd9uDO1npm2UUlnjQTuKofU7Aw+70D7ydj5tFXkblu91PL9HHz/cbPNYX
5Hm1Od2IaxU4yTy3I59rXe1GnjfzJepi4rM/mw79C8z4FvtEkdPY5+eaB4nx
DXLyfGdnpt/crvfwXppvJP4wjz4pVt8qYn+wqkUQ8T07ouwTtIy8ZPg8uBNv
CvzSC9ngvUi9CGurTjxsm+Ttq3lb28vH2w/Mj+Tta3tOY/8/fYF9/nY+/mGy
Q9ixDSuj/5S/Pfp+XeMQty/TWOjtGLMfiniOeVdDD29OKYFrW5bBV5iiFfTi
TtaiYp91v8r+9lUXtRD464nsM2H0KwnUlUc5R53e4+llvLidsRXnU/eJ6P1s
gefpjGyG3SzrRq1qUm9N1o1qsn9TIO4h+zcZdTTi6o+rYodcTos9e2IHfqiy
Z3QT+7fUyPxe3M12nPxRyDrfeGMWfQSMcqHk/xVfpfr2BOK5VO5d1YvrrSPT
B2jwcl9c1K0eJnjv2kapS5/lOHZYiV8F39vqeJ/zbdYx8E0LVfwN/dqzjphn
s8k8ER/U4xWr4v1eo29H6gPPE+/XIhIv1b/TD1XlwfUP8DTcz+Bu+bXkwWXf
JWfZU7F+rFcWdrXs02TfaoM+QzFw86bs0/R7W3jjsj+jFv8ldRCyP6NWuZd4
XvZv4PbdxNRv9DlIPLCT5NuX+STiJqpexkkDruplzJifqANIQx9t68oJ8m57
mpA/2kKe2ircm+s0vYKuWMyk6GJcxR5VOszmpyycg1KHWeW7nek8F5Xv/pFX
Ev/e4h/m5xH8afP8OMFPCfDkJc/HzTmF/g5f8nPefalL/4ong5lP2c9a8e1V
/aPCA/pdr26HyHmAb9OlL3GZ32T/SsnDsXpGJJ5z4KY49+xhc5qJ62/5jX3K
rSTOT3PMLwK3DkXw2dsB+/C/D35zu8S1vLh9Y7/P/tf/qX9P2NOynvG/uDr1
jHqmjcQHthC/sjtnCxPXda8X8Y8nDm//5Mo6Qcn7+hIZ/lvwHd86d87o8Oty
DPC9d8ZfjbFL49EPQm/1nHPwS1Kh324V5L1T8QS9VFT6gkl+qapTUHlWvfUZ
/NcQ9Fu06j2J2054HCq+5+hR/Ktbc6lbSRiIv+GvrZbvYRviLuH7Dhg/B3D0
Vi/LfgQlO2EffB5NPUKnydjHbnbsj+AJnIOXv2JvFymBnRGxI+O/JidOXSE1
fOk550Tdh/uxDTpuL8qg3xiZ/gLuXPo9aAls6lM77+J97nta7G9argXi9yr/
wqyykf+f+rjAA/vnx5LwpGueDvHi5ux5xAUW9UNf895k6u5/34pfGLEb/QhC
xrQQ46NswQ4dugR/N/pN/O7ZeanHSYJeijXQIZ+Sc6D4vfZ38mYq3qXyF8av
kg+l9Hxi78rMePRODYM4bfj+p2ZRGb+V/U819b70eiLeC2diVNWnw/ce2cnu
iHXvZpgV5sXNm4tY98VP4QdV7cj+M/kveV53UTwrPrPfhsuDBvpTE5+PHstn
hyuej7H4b8kbl+9R8p/EfbjaJOqqpN+txxvAvDsr83vH66d7qnyqv4+PjFs5
Uchj6wOzC7vC+vCN+PgZA97E1IX4RxfCBK71dvN4r+/m6cDvvjcpnxd3LryS
eREDvQh5ThmfZT+2t/BYnG/gVkt4LJ4PegSay35RrLM4D9X8aGUa8j4M7JHT
i7slPpInXdfFN96Ylh2/5ldb7PPuINnnK/YS6rhe7Be8UKvSZ+plM/9CHZfS
E4uF7rHSE/tRtyhwWbforL/J739j+uwlt+ganz9s3K/D/M9ZwfXjnCTPvIt+
zeaFnuwDoffwp68faCH+3FUEvuP4AsLvtO+lE7h5PArve5kU6PqqPGaNkeL9
/PccAn88grxY3VHEbx9PKeodr538Sh6nw1IfP8cs+gX79mpkX5xfe94D/3Fe
AfzOo9h1bhzORffDUfJ9Kj/y4LDYT+xzGnawxXj74gz2STdOph9/BvpoHDyM
vb2yGv5vd/SjzLojeQ9i1SGvl5h+3M7aePjLHWJwnkj9ST3kFudW0to8hz8P
c15Xnsnvr1W9pHe8Fi0t59/JTORvxyQeJvDN1KmpejpVv+n2HYt9IvVSFK7y
COZaO5R5kP7juInY69FelPHizsKVxMG2P0YHUb2/qQ5zvVPB7OMqz/6istAV
NPdkKS2/l3PzMLrf1qvlrLMofxB/+bIcP1HqqSodBqWnquJCgbpUabeousLA
71J6HavSoLOr7OoU8MC1w4WoE1R5tJnBxE2Wnw/z4sbMFOzP7wP7APFpyf90
9MIqvy0+VqJJgt9sZkVPRn2cJ03R2ZZ2V0BnWOpOWMWnkjeR57s9LAF6/TLe
pfwOt8ZydHXkPAT8EXkds9F56icejiWvfWsZcdpl+HfK/3UN6rK1eVPE77ZO
DxHzpq9PEkXcZ9VG1LcVuY79d3Et+n5dU6NTdxJ+pVG2nIiH2INWor8in7tT
+xZ6VisHFfDi9uiMYn7sxVLfQq2TI+fp051xE+f2s+YiLmG51ckPDpX4I+IS
dulq1G01b0kc4tcy4AkS0zdI6icE8oaSf269om+80cCkfvOndPg/9V+K52hV
e0M91LE5+4UOStR/FB8bPZ8NK/GrGo6K7sW1r1/EfFjZO2GfmfAqzHPoZzkh
I9HbrjkI/7ndb8RRr1xDj+dTNOZtaVbOa/mxp6/NzPcYRQ0Prt9smMKLu3MK
+HWiHu/kd0bbVdqHh3ZT+6Zan9nk34U/7ozZAA9FvqfmivvEt+9fI85Wo7ol
7rdjIvzW1LPJwz6uIHBrBnUdZpul+b3jrSE9ffXLgXUr65dVP4gAfrIgOhWX
f+G5SX/WebQMnvy5VfDvZBzDqH9P2AlWlgulveO1F4fAI+4W9qFdMi68I8nr
Vh9ndTsRr/1x3gm8xELq84ZKHvj5LviH9Say3xWM3UL8WX9XqPh/Pe8yX0/Q
lzZjdBK4e+oxcdY+qwTulu8MDzv6fv5f1/uCz2+HfRJ1dGa1aOJ5We2vwvOf
mVfUpWh57rH/panB/cfpiC6rrLNQ+15AVyToIfX0OZ4Tz4qdScZNusFH3Yre
lLF1Ovd5KyF++4NoxC+aDiWPfHYDfsWnr+QBIqYnn/KxF+urzh/oRpbMg57v
lNfgMdGTtKvEoH5/Za8gvn8y+QuDPoU/dLB/XM+JNg5/+dpL7KEekeGFzUPv
16jYFB3gSmPJu6r+FN2KoW++O5dv3RojTqDTIvNogTy14o28+l7Mi5vr05JH
k/m1wDko82ua5DcqPrOKazhpBvm+16nbQegyGZPo+6a/lvy6eDp6lFPAnRey
jiAauH2iqIw/SP5bUH3iipqqu5H2as4jrOcBZXy4Md7Evs33a3kvrr86Tp7o
7J2KXtz94yPz/LGrD7cqd6eeJP906ggfDRA6P+ayobwvsp7FjEHfJVXPonek
/sVO1l+M15tS/+J0+wyPS/JknDzJqVPV9sE7GE4fGXNYee5D1sU4t8FVXUx4
XRq7pwl+sE9p7/3bfWagI7czaqhvHoYfJu7UqrEP16r0xK+R/rvbXMZ5pP/u
FN/vn89rWcmbn33p40Pam/pgv67J6MOtrQbjja34YzJebbR6QH1S/hPEweue
lnHsbeQB5zb0jbdL1+J9aVYI/ny+fNRbbD7Fvn3mBfot6pwt+Ys4r41Vuwt6
cetmbdEPw1p9rIhv/IIeP8nrZhLXO17Ztz8aW6Zn+IFrz95R9xZ/pdCt1Y6v
xc96tIJ63pCp1HFszzt/j2cezDXR4HVFQk/XjCZ1BZMOEd9jFczHubD9CH5Y
3PHgEWOSP+8px6ckjxToiyT70qrzwt18Xvjddvle1J8njyS+1z39D/GVdtQH
aYff4y80Hiz11fOhe3N6DnEMp63gkxrTE8Jv399E4Prt78z3aMY7n2OBfz/D
OooA38nY8z88KMm7kPzjcHEYMzP7QPi4jZUW3H03PlT8WSO/WJ/Gh/nCDrMq
/i1wbT9xSzvnYPgaY3r64lT2lUjiebmRB2JPSX64NbiLOPesN+PhW33JAO9x
min2MSc+eqHae+wW/e0X8pQ7svDcZT5av9VB6F1ru7vid1Y4TJ4l+Tbs2ToL
83rnXz8u+4RKnlJAz0TylEwTnqbSyXRfwSsKb/8H7N5w9r/5BT6QW2Iv+Z2r
n8TvNCJd5vp5rmLvLb4o4uZGxjXg+eNjzz+fA/78A/ztixnRh6w8DF7ixVqc
0+MywfvbmY569Cs1sbf6JlD5K/GxZ6FTZx4d5vMX9Dlb2RfbbPaNN0v/g1+3
BP/Szf8z/MMk7/8W+i0707BfHgG3Vn/ZJ3hNr1ISv00bhfp82W9C6RoF5k2L
j65NaBXOlbZRpN7QLeq4D8VG/2m8jIdUH0a+8ulAEWexL+eCj2pZ8Bqj9IO/
KPmreq1FzM/8+T7cnIqOujZJ1s99k3VD9reoP75PxXvcaMR/9DjwlNypq5Xu
LzpgTeOQ13mepbgPv5KP82BEDup7BjvEKY6+oh549BV4znJ/c4IrivfIvn4q
vRe36kcXz9/q34T3UdqTeu75xJk/N4I3Uugy9ufrBZwv9xuW9443tT1hYh5/
L+Lntyc6TP3P94n+Plwnygm9Av2X7/jlEUYS19o6lrzGVPKM5u2l8Nz2ToR3
trUbeYnTDYmP5Swu9iV3YQzs9KWnRJzZuZ2BdX5hdAbv/RiXT7OOb1GX45a5
LPqnW98+EseJFA/+Ue6hQi/FapCW/FTV7eiRxLlKf/Y+Fv52qojwKJZ1GCjG
tx8If0+rgM5fELgRsx71dM+mk7efMVecd9bILaHifgdVwS+obFOn/Cu8BafZ
Rtb36Wzsh32qUO+666divt+Vqy2/K8W6El7c2b8B3v61K+Svux/Dvi6Whnx3
3d2FvM/FHpxe4ObQ/MRfVfw5ck/Zv7NECS9uzv4i3nO321Uf78ucu4x9pNhZ
4h/d6LfuDBhF3GxeMOeW7MOu14go/FljfXZ4HndniziSdb8k53CZaQLXExF3
0t9EJ78+ooifpyf1hbTsEcT60J2ZvI+yft969pz1tBbcbdmA/fT7H77311hW
mnV4eWgQuNRnTpxQ7BNKJ9lsAh9A6SSrulTFt1R1qe7BNcTtx0m+ZeGRPMei
ncQ5a6SqBR84iDpTM3UvkTdx61YWuPNtGHy7EOLuAb2FT7KeJVw/RyMCdQWq
LsPuGkXo+v5PXYZbEr3fcHUZaryqyzAbTcWuuEJ+342Slb6NJX8h/j9lr8Ct
f7Kjx9uM/nf6OvI7xmfqp4zjfdCfy5ePPGjHZfB//qsv4H7/0+FVeEEv7gRL
u15+zNpBxNvPDcvnxd2gc7xXj15jt0odb2dUH+LqhaLL/RZ7W+lNmYNy+eKB
+uPuxL1r9/LHCbvPhseV+ZTi+3M/uceKc9hcP8SP12hJvevky/AJTfx0x8hK
/ErqcoTXadcetqPe2r5KH5Cdc7ADV2fFX4ubjH1m9Ap4EBGjYk/8vk3g5qFR
Qq9Sb3Q4uxe3U+QWfrJZo26wD985S6xPPeQ2dlPzLaKPm/m+I3W4CRtgly3r
IOJX9j3i2/b4VcQdq8h+N5WqwBs/OrGQfC7oE07LDu9Ir5Lfi+unF4v3RU89
oqgXd/M/Jy5TJRRd33s3evK9iXlf0i0X/TrMZncF7j522I8GoCehqXUV8yJ1
BCVelvXi5v3P+Lm/3CnjxS1Vx76yP3GuZPSndM91iyquf+G6LsZfiYXOxx03
FfPpr3c3M9M319Nfl/uReSDrSE94hevIO9hRsoeK/yd16c2N4G4OG3/r5QR0
UJWfe6WIeN+tzn/k8eLOs6XYVS8f5PXiesfT1BHLPHsgfq70NBqP8MfhCkcT
dpu9ZqLvudgPpoCf3lLIO946/Sv6vFNiF/J9b3v4IXbczkW8uLU6FB7G5LsF
fb8r+mfm8UZa7LIaNuv6ynHs8rw38nvHm3YQ79G99MRB/myLv1kjEs87Q0Pi
IBWH4282TwSPZ1AVyT9rR9wptU0c/9pLla8jz1CLOkGPvyPr6Az0hT4onXv8
ILewHP++eTkvrsZ7eCPivVW8kR/+k8Q5b17xfWaly9hdywvAn3/TA/5b/7nU
XUp/2TqBDqcRNWuQxNlvH56hLjfntmRe3Ogh6xVb1hP2oJY0A/Ud77fVk79T
fPSR1H0Y+c6Rt9r4kd93KjV6j1/3kNed3IM4fI9N4nruskz0//jXDpTzQL2t
tAPt8+gOKV0pK+Vb8tPzSyT34o4xF7974VHmZ2sc4mlxY/v0mv7jXSxHD3fp
Q5nHkf0g8n/Bz9pfs5oX10tFgHf+YnUVL270+IidlfkC9n64uKt9cmKouJ5a
t7kSifdRj3nEF7cxd+Zl/CnZL1LlVV9L3aRP0bjOwj0inmxO/VPE9/UxgfHs
J3nOynMFPzvgR3xnnbjSLw/0WZB+u3k1F37vp1P0eR9NXY87Ooy4Q5s/4aX0
H0Vd+VnqB7Vh29EnekGdoKqnDsxDymcCV/tDwJ5U+8P5Fdkd7zwMPS/GG01T
ZPLi/9q1jJ/RWpw/5pMY9F9YkEbmlWR9SSv0e535p6hfrtnBp6elb0Wn3UjR
En/j4Shhz+hbm/O+nGtDfmOu7HcQp3P4fDf7m8wLB677e336aErcapUui+EZ
b5xJgJ7Mob/9ugonR0tekF7YO96dCj/YLhCo6+R7P7AP6K+3FfBex6lUDjun
V0J0vNS+urw49SdGb947GV8y3i8Qz1tvmEjyiOR7ce5P4of1UhTx4lavGvTJ
+G+/knkTub9VXOOPl515CQ9nx6wq3vvXTq4oKeeN61/aSL2n1HsxXvaA/yl5
mPbjPdir+/f46qyNgSPwy4adEevBiJQLPluMpfhFc9776g3dyA2Iw7c6yf5Y
aq+wB6zQyKK+yWxSGD+z8yHshyYlI4rvC37JudNb8uIS9ijp+52fJsrfF99f
37itZEUvbi2rJ+KOxpsk7EsNyJdpvz0m3/0wH/f/8S3nv9Q5V/3Nld6g8WaD
WFduIvqtOLeji+tYEdqIc9+4OV3gbscBIfJ+/Dz/DxFYV+F0Rewp9cLXxcj1
Rl2MUe0tulAVVhDvOlKWOOz2bgK3Z4yg7iN+efJ9rW1xjujfhpMHGbaIvO0X
9KvMTq+GievN6grPI+gn6opWPhe4W2aieJ+cL5lVHwfmNWZr5vXcxJxeXLv4
HX/wSKQ8XtwpdlSsH3ctunSBOpdMKegX/nWUD9eGPEJvIsV7X/2LmbQU/qy5
JlTcl/LjZJ939zY6dVrSFPDcgoYLf0zv8MQ33nCai7iqvvM7/Zia74VXVqQU
fTzbU1endwfXcu/n3L0ux89YjH0SVPWCiM+rPLjkMap4oNZ8Cv7rV/iQzuG6
6CfEfsF+3eosvLt9ufHLZb8V58kOeFmy34rS8Qjk36WOh+rD4o5gfKAPy/hn
+F/HL8DTHnkWO6665KOmuihw4w58VD3GU/jRz4cJ3HzCeOOnRap/EPb/3xP4
/6cyFvPiVsv5/H/VH+HwQHRIwvVHMPpEIZ8Y7j316pmI32309/GN3RurOT//
9b/E7+0/Quj+uSGfRF8ta/PIql5c/ynrbYEPTER+Pu8dgVtF640QPJAoxRQP
FL2RC6WU/g48/+EZyRcf76o7XjwoosCNkEsJfPj8TOwDtReI+LY+uCd+reQ5
2JPYP7VvEzh/lM58/j/oG9ppZHbHOx9Hs5BXXUz/bvVxo87Gfk78Gb3rXyKR
N4nQCv360SM5f9OMI567kr4q2gXZH7Bpf3Tvd4WiP5avHfaOjLfbr2rhP1fs
Sdy7syb8Kr3yMPyqY6uw92Uc3n5WivPgUKC/tsgnau+U/4b9owX0kaTOSb2j
Chcfeyf2gDbnHXnK5Db72+nMxH9z/BTqHW/8np58RN8Gpby4XmIp52q9z7JP
H33V7aIRRN2Nea5xDi9u7UvMfvh3JOzzOVVFPEeLOAC/dWFL/LNMu7Az+30Q
drJz6zrxraG76SdS/InoQ+F+bsH4tpfo63EkUiZxnfaded9TNyU+v/YX4uy1
hvjmwRkRW9hRVsUhvnkzK8QRuLm5psjPq48V4rBPVu7l61tiJuyADsaf/vHa
gVJKP0TFo1QfJeKTUTXFw0SnZd4wX3xEC/hHkod5eStx4KsHqSufosPDXnyS
+Qs5IHA30Vd05+Pb5O0lf8w+GAs931/X6t7faxR+Sz3F3JSJvfNj7UtBPWfc
zOm9uH2IPJ2+pWYKL+4aDnZLC/JZKg/+I4/z4+/u7+SJtHgjeS9SkSdy2swk
f7S2EM8r+wbiPrc3+95HveQN9s99vX3nnR6lBf7pznIFvbibO1/oD9yIFN3H
r9EKFwnYCV5c1QPaoe998TStwzTiU+9kXW04HT9nYUX4LDKv6iYcJt4HO9MY
H26fb4B/uCh3Ri+uF+yYX94HPArpt5pZH5Ov2X3bXz/aqSd8ucF3fHay8ZvE
H5Qu4sXtX0fAA9S++s4BJ/NzeOed9RAv7mbYzX4d726oFzc3joNneIz9x1E6
D+/w12zNVfYV61n2s9PkeE3VoSvdqN4dM3vv09GISzuvtuf04vr9tvCxp+bN
5MWNUsfhY8u8cKBuVPat0Ko84X3ZVkHgxsT3Ir6n+EiB8VIX0frQiOckn4u2
Ixvxt+6l0RuXz0XvXJo4dmn6dync/ksT76N2EZ5jgB+yg/iv0SdPfi9umwPh
OfUaTPw1Nvk4M3lN8o+//cU6UuuqzGzBr7NS983jxZ1icfn7lmH5vLi5fjLv
T2gp6lPC3afKwwbyg0rXRepvKFzpb9j3bsAfkHkKI0JreF/v0aUzbx4kL796
E7zOlYb/eW06TH3gs6m+52vk6Ek+r9Zm/Fr5Mayk8DPar/K970aDd9hpSbYX
8OJufvxBZ+GOko5nno2lwfD9hrvUKSp/KnYQdsP6wcW9uBaWGPt4W2p1fdbn
qKSyX1i0PF7crHSYeTw0LtiH385IPnp6IXQq5HMxZkcV9eH2b+l9uB63XKQf
fzpNBvjmQUt3K1Tc16WNyo/kfhIPRg/1a4EQ73graR1Zx19c1M2ruJY+MIR6
rNMbWC8Z11KHGCk9PDnpV+qnz4JLv9Jatox6vTXUlZsfKov7Ma82Io8wEdzY
/Yn4YYEm8Fu3PGV8OfYdvWd2n76NvSIJem7Jb+b34maFNcTJL6IvGqj/fXeS
+FvKguxjHySfLVERcZ4ZLRwfH9WsuBh//dd5Pj6qMf44fmaaVWqfFB89cgNZ
79TUt98a8wqL3+u42Fm21EkIxD//iw9Iu5b4wI9+fBL39eOzrFXEbS89bSGu
ezWNyKdaEQaTV1Z1i2uOUy+/ukw+Hz62I3nDZyPlc5sv+P/OL5Hp61pkGbyH
FfvIl6fqQP1Jg97ivDa2HyOu//4A+8+yQpkcz30614+SR36sw3u5eFro75qv
5hJvyybrIup/gCdwh3pR80tf4rblT4r7sL415PcGb/PFvd0F84iHt/bHq93V
QcLfsOvuJj4bLg/rlrSpu389mziOM4R+B2Xbo4/94LiwH6zV1Ec4yzThr1mR
JT/HpI7D6Y0+cWC/TVYTfuY43nf7KevKjTeJfSL8PinrQJ31u0vIeRMfu9wk
8hrjB/jsCiNXK+KA99oSf3t9Cnui2nx0fLqVCjI817fzDeM8qxqZuj8Vx15w
wmffBM4pjXpavX8J9NsU72vcN7Ffm4eiCr6T2ge0jw77S5XI0Z3/5/r/6eRI
/1rq5LjZwM3ZwdiZdbILXB9ei7jshgL0w3nySsSpjap1xO9RfTytmbfhH9hB
Ald9PK0rg2TdPfaD0oWzpgXyT4W892nuOzFjt+d+Fa5+j335u4//ptV9tVfs
x0/R/w6cy6nps2vPiBHdi//QBxd/T70Ifpo6L25F9PUzUvEBxTtS9ReBuIGs
vzDvRRH7k/7lKPpuDeeSr0zfRvCn1HMx46ymvrtG1oxeXL8Yyj7y8UGYuJ/X
gwQfw6xX9p2wj2RfbLOvBU9D9sXWV/2dnPuR+22q/oJ3oR+cJfYBt2FkeAF5
+wrcvFExvXe8EbMaek1PqDd3IxGfd1fD43FnSN0+Wf9rJKXe3KjemHqHSd/g
gX2owbmp6lLDzVugLjVcXYObg/yY9i02PLEpO4h7FPgKf3ZYKPGiLK/R1wrX
j8k5fpx6x0vbiKvKfkzO8zjsk7Jfm9EHe0X1a/PoEUp/Db1CK1+qxBIXH2sl
/pH2sYnPH7Sm2/hHv2TGbmpRhj4LRUv44vIB/pvUlTVWfRLngFujPvpR92fC
C21bmHMnx2XRR9so20XlHZVeojrHxPrWnk5W+VbOsdOPfgo3vqB3vLV6p/i7
e5r6We3+efTf6pzCfs4g+cKZc6ODlho+r/2iKb8/5yve33av8KeVrsWKwvzu
scRBFW4uHUscpmhOsQ4DOsmPduH/dk4S5MXd8k3hdS3/J70XN2/Lfupnh/vy
pPb3ruR9gv8AV/yEQvAAtXH07w3U3138Ez9oYu+CXtwahz6t0jcL6NxKfTPj
YORS3u81t90T8VPLHFzci1stsSfdpF98eV6761v0oJJK/f/v+MtGJPT/zbjg
1ne+V/UF0P6rWxTn7Q89W4FnIG8SqP99QJ7L+vg3dXj6TeJ4exPRH+q/uLfU
O5Vxb+kfqXpz5R9pd9cTTyh9Dd2V0jK+U7cAdsRD6vS1lVMziflMAA/cmUBc
wfgrueKf8DylHpE77k/s5l2Dwry4uaMC+i3zXqCHE68XfOO8fYmnn8cvcwv2
py7vfHPmU5ui1j92eBbm0fzMe6H8d/MncF3WddlPOXf+/VPUfRmlsHPVx4mY
j7qp0ADO/pAN3AneJNaJm3IF66rrFvqdLXwh+0fzfpmj8sBDizyL8yag05JK
rCt7dTp4iiqflcVkfWyK6OPtG9frfBT2WpSivvFGvsmiD6C+/bqvv7kZfzbP
Zd0r4g3jt4m8oRXWVJxPTs2C8C62gJvT8sYW81HgqXh/jS1dhP6hftpGf+ri
PZ/uqLNpBfbU8kSVfPjdCczX/Ad+fG45/IsGxAnUOnffSD0yyQ+xI2K/mV+/
w3tsIuMKMp7gfOP9tCTuyLiE8wU8PA/BPqLyx5J3oK7/Ttnx4IbSt1T462Eq
viH5HsnQL3ra25cHNKvUoo/7f/ut+qQMh6t4IDq37bFPVdxMH/Y96o+/Ow3L
ivfVOX6YvNLzZfTRvlhC4lJPLMSmLut1p+he3MhYgLhrCplXlee1G/dVWfV7
xXXlPmB84ffqqeR4yde14zDeTd1d8MQD/S6/JQ8S4yVvMMA/lLxBPWUN+IAH
C6LvNKGU8L+cfQvYJ/Vp9PfMVVPYP3ZPl/q2jRL/NSXn/nvsZLs157nWhX7l
xo2dAjfK7YAHWHoIcfj8Q4T9Y5Vcz34Zm74hWppn6G6ouoA9icTvdm7/hf6V
qvP99AH/8kSxbF5cT9iW9+zTRN94Y14/8BwjsP8v/cQ8LD2FXZK5qx/Pfxa+
g8yHupsv43fLfKjqO2OWGUFeSfadUXWy9mhwVSdrVWC+ndtXyTclyYO9H6g/
DYWfqfqeS3tM4coeU/3Q7fhtwWU/dC0s0DeWPqxPpD98sZWKc4uPlaIy/Uml
Tr7+bSb5HamTbxwoDI+lH/i/dhp1HarPkcz/WidPc14MOsE5/BG/TKs8Bf+7
IfGzgD0/g/iaircF4j83ZDxOntuB/iyfpW6p1PO237P/2JE5FxVuPGf8v/uE
Oi/ZZ/bvF/aYk7Qq8Xlp/yv9VWX//9CxEfexSj6vRW2Zz8uZ4dWtAzdvo+fr
zB6BfVQzD/zbfPuJk6/5LPYZY2kWgVtX14PL8e7aR72948PXHau6aSdOeepk
U4+FN9L3GXGTDxHEe2kdGQVeIA/zlmUwvNTS7cC/tpF9RaU/Leva9L3sVwE7
JSr7rR5P6lKlzuOrg9A+phbXdTcv9q0frWJh1d9N1asG9MPF+Bhc35Z1N+5X
7Ftr2d/k85emII9Q/ZN4TuZV6kbNYknIb9SlblRdR8UHrPePxH06ldCZNxLI
/kG/jhD5a+06uFtyCnG3qxEEbm6cRB2N1K+2798RvF6r4GfZX17GFSveF3Xx
7u6Cvnyr0faY0GtS/Nvw/V7tTZmLenHlF+jl4Z+q/JoWIX6o+DMruLt4GX5E
UEKBm0Oq+McngNfnTsjg65ftBI8Q8UHrEH3rzG1BYh8wxj6gDjzNFR/u7pJ9
taT+khX5BfpvSn+p3dBC3utrs5ugE3S3qy+eqYesF3F7c3kv4szJvon92105
jf0ic35xXgT6qSXOA89k3UX0BlXfkwQacYOTdYt7cbt1euphX42OLr9XfOy/
XrAvVYqSyotbDVdhzztF+R39fiOPWT2i6LdnX2kDf2bnWMErsNeX5z3qlkDW
3dC/2Gy/AZ7Gyv7Fvbi9HzvJHJNP6buwHyyrFyauP03q+kjcOfpS8p1ulfDi
5rfbrHvZv1vxLlQexNzwSOBWu9oCt67cELiRuCN1tBvYV81m9bDvZd/PQF3V
kLHEQXrJ+hbpX2st3mP3NuPcMdPjX7uNSlMv1bkjumtB4FakW2LfsWOT9zSk
v6PynuH7I9uttqJTO+oN35sUvWujxBn47wFdUKl3LXVB9V4Jyc/81gF/f8wG
eM7XW0r9JeqpzaM1iSudmSrWo7OB8frZv+GhXtlEH1mpz6kn68/+WzO4jg+v
WQW+8dlsPtxIMgi7XO6TgXPnOv6FG/oYe2viBvRAKqakn9f7gL2K/3IUe1Xv
EEXxpfmMLEA8seha7KY5adHNa3CB9+3OhTw+PDgD9v2BjOgwVzLRw6xNny0t
VhPslAqF4IttpY+tVf4cenahD0W+zB04RPiD9qirUrf3Efqrj/8hPtCxJDoa
XQ3BK1N61+rjzozL85J9M93yu4l7t6UfijYuaZh4LpN3yfdd9n8ZnAE+cPOu
Jb24/Tf9xeycleBVKd2Y4DD0VTbGS+a7Tuqx5GXmp4/uxbVn2dlnS5Tx4arv
klnzEHGMWIbgSWr5i7A/nEWXTL9WSuBWEqlLJvsLG1EmoMsq+wsb0f1xAKPP
W+Ktf6Qs6sWtVQsFT0Mvb/p54//sgTcSoRnnSrYJ6MY8Hy3iL+7iaoyr0AAe
VOKd5JGTnUAXSNrt1rwg9oHxHUv58IbDsWtfRgr68XfzGX2jrDSp2G8nvGG/
vwluzmvr5x3+Xh+7SPZHc/qvFzxAhdsvpwncPp2RuHD5k9jbqeZijz3NdE/w
iaTfqj9diX81PSH+W79rjE+/mf3zWX9xrik73Ezemfn77QD5j/EDGL9hgth3
3JZfqRN5sYnxOy6JOKpbd6B4XoE6rxjtxLq1PkxCX0rqRtopmrFPbtiKHRSu
X8b/6EbKvKrTOg3jf3pOXLR1dPJ2celbbfbIQ75k+ELiUcdLwE9V/oKVE3/n
Wmru73dd4Frxkvy/nAd8uHVhB/ojhdP4x0cbjN1YcxR2fsK8xPEqNMePmBck
zl/jlxOMG7CSfTzGJ/hp2dBJdq6fAFcfpc+s+J/XY8Ajy5oKfk7KVKwzqcdo
DH8Kz1PqMSrdRf0645Xuoup/pPoLh+9/5LydQR9h2f9I9VEyZjxgvOyj5CQo
4usDaMYtQDxcxskD/WtknNyscIK4lJx/91wb8kLTR2fy4SuisY4/5s7rxfWS
0k56Ao9d61ZA8F3dQrvp/1f3FLzdBb+gPxCUW/hNZpQe9PGKL/s7zJB6+Hml
jsulz33F/49OX07FN1C48n/s+s/Ic8o6JqdVNubxcFgWL+7OS4D9MaGtGG93
PUD91NKY2BlxDrBf7Z0sdB214FEiTm0nkOfFlxkCdw88RA8iyXnikDOLsg/c
uoKuyujJ6EwMBTfz1xfnixH2nPhbgXotxPWb3hNxJ/PSa97TTtcEbt9fTJ7m
QWP209Lo0jtX1zNOxiHNIr3hN8o4pPN+PPZdzLTwIT/OF3aAFWITt9zKeKN6
EfiH9c7CK55Qn/X5LXOouL7UFwr4p1J3xb5cTVxPizZdzINeFB0zq/4Y8f3W
uEkibmZ8qIr9XbmjGG/0GQleiHox7dmvYl0rXqWqm3YKPcDvTviPwLWcG8nD
7fsu86fS3tBikPeLKvvISNy5Ews+/Dj6xhrvr6BDdSsqcZ6Oh1lv+SMPE3+u
L8d83u5Lvu1GRIHr2d+ih1z5BPp7MesRV8yz8p3IDy7Z6MPdgg3pz2VELOvF
9Xix4NcG7/LFgY0k6+ArpMAvM6S+pb5W+mUDOsGjVPZzi1bkfUpdkHq+4Ean
IPz0g81resfrBe8Tb5l9g309rBt1yn12E6eqdQLemupbnegUeeJn/ap6r2OM
ncH4XDGq+O5nWpB4XkpvLaC/KvXWjKytiW/IPvKWM426g3/9OzGP0u5V/p12
vCn7XN5Bwn5zb9XED1Wf1X8Kf9zuOgh7+JctxHGVPkPbqeLvVt3zKb24Xd8U
fqiuHaQ+Mlon4oeyv69ztSF5/Qsd4bdfbSTytnqP0eRVpL6TPbeSyF86UXb4
cKtXZvx+1X9Z4qr/snUqHnlaaZe6/yyl7m/5+SS++9xZRPB+rS1mTC9uzDeF
P6jXvJzCN/5Vb5Gfc7f+hd17MjX3P+QjvMcTB4gjmgU5F2rAJ9SmPZL87Vno
b884h/1Qm3pMszbjrbFB5G1yyX4O+7twPzn7Cj6PE/pW1st2435KoK9iFo+Z
znufzqQ4Qm/N2kxftUB/hwoJ6EcTwI/7cLvZSPzHXnJfPRwT3ojsA2tPA1d9
YJ126LAF5ufys7g/rqM9LCTWtbV+Ijoni5sJv0ObmQBdkn1F+V0j1ojn7uYv
TJzlT3AtaTuR77RSdqLeoflqGWdeQn2ONY/487GVfG+NcsxXtD+kX5ae66Tt
LHi8RvpH8KlOlQD/aBM/b96V96A2/HDzQXH0OU8+oJ/4CYvrZ7sMr2BpA/Fe
G2NZt0bxJtz/ofzU00v7UJsQA3vtzRTiOW574reFQ8hL70IvRY13Cpejji9J
A/h4B9dw/Q8R4ePt7iJ1UYjPu0M3ond38bz4fuMev9f9fR088s292M8/5OQ9
7b30lXgusl9zwJ+VOmk/zjXxfVtk/HDpVF//Kuf4Vl8/Ebv/KmHnWmcXMD+t
L7Puq5rC/grU10h/WeXB9VvU16g8uNLrtv6UdTcBvW4TnexvxBOMZg3Iv/Qn
fumOr8V+G+0Gcfq3sh+Z1D3+obcp8K6PyP/Gb8/8bOjF984fLew0a8lY5jl3
aeyJXRmFnaavm8B7/egX/P0kweQBU/Dcray5RF2A80cY/PRH03jv/sxMP8gJ
iTgf1T7pFBPPRV9TUMyzM5s+wk4jK5P4/d3Qc9aCS9J3rEhDsX8qfXX39+Lg
Ul/dbRjEOq++i3q9yHXFunRLJUK3UO57xp4mYpzxdajknVUkTjKhagTxe/qg
e6xwrXwz0YdOK9vCN17fuPG44FH2bM5+flq+v3+doT786zb4OUfTMT9LnvB7
V6yDP3o8OvOwc4R4H52x03P68KdxIovfX7xPZi9uRcsv8lmqb7XS2VZ9q9XH
MMaxDuU5pT76klY+3C5bF/2BUtjt7pWB2KVjeuKPfJB2/qXm4PMioeNxfabA
jYyt6Rd4Hd1RpVuuVRuCTvHK/eibpSkwTOClN6DP8OIf8uObqCs3gvcQ54ld
ER1ridsV5sOHH6fqsqUu36dxxPfiTgv24trrOuDnNxTw4vb3eMSLwu0b1oiN
wu7UH7fI4cXtVN2Jwx8qyviRG3gundNzTl8mH2uU6sbv2vkOP2XefPK0Mm6s
7Elj4hvyjTVykN+Z25b1nTIu/K/VXYgbR17CObi5DnGjJeBOWa6jd55OvKFG
X4GbPbMI3HyxhPjKssLwVR6kC/vxd+v3yGJft+dUw26ZEpO4RvuyPlx7vox9
4PSQ6F5cPy3PkVYd4QFWb8y81RpB3evO3uz/M2YwPwszUn8YjldjdR8QxnP8
Slzqt0mcg6sWULcypiX5vo07uZ/+BTkv3/fBrkwg+ykU64q/GW2t0MvUjxfn
fl6rOuPm4r1xzpfkOTar71v/ZpSSvvXvXr0k/B4tVWvu/xP9jKzdjcT9a7vP
okuZ4xk6KYubYZ+q9dP2BXyQvkW533WsE21sfRFHdXq3wd95c431Of8J8adU
HciPSN0599eRxBsndQr14tqUR+TZkk8N8eLW8PfwNJ+jb6/yAvrpGfBJXkYS
z8uow3rT06bi+za+5zlrk4h/bmsVJK5X8wR5y58nErccnOGhiM/EOA1PbmEb
gZvXfhb1gObimdQBnGqFPXmnq7AXrTE3uf6mWeyHtb6KukIz7gvyJ/Fbc516
t4iHJh5PXlT6TW6mkdQrdKnBuZnjkTi/tE7zRb5GLzWLuhb3IedapbycO9PG
YCcqnedrH6XdsI08uNz/zbmFqHtpk4s8TAF0vfQtremnlLI9vLRMZcGXJGa/
upYSPnVscC1fQ/pJLVxPPv+l1Ds9uwy/5Z9z5Lmvb+I96nFJ2MP2pW34i2vv
C9yNnEjYLcbnvaLuXR+ZmXmYiE6jNmB4eS+u6v7sCTOIV6dMQB+rV4/+EfXF
+ekTox9fQBx+CfVv7svJgnfo7B/GuoqemXqQfPnQ5ft5Nc/9LvV4CncyjwbP
nJZ5W/4WHvu7Ecxn/G3Ua5R3mO9jcdhnPjXm9w6j/6pbIxV58LYFyfPG21HF
i1vHp6CP1K0D+fqIjYUfZxYcBC8h/9/wauX6d74+4nkMPi772rBfuY0iPYEn
0teHWx+TUx8TtWtBH55yolhX5skl2FnOXNlX8RtxuZR/inUb+N4vz3ku91fn
996POWZ/mLhuugU+3GrZmvh5m7aFfOMXJRHj9dfL03M/rFvnW3viJjs2oisb
sFueottVv1BO73ht8q/wxto9Tuf9Xc4ZeClarCj+33u9stg31fM1EkzmexMT
BzG7rEMnMPdy1kn6u2LfNq+2Jo6XqAh9T+J8h4/Y5Ka4XiDfkb0p8bXUJeHJ
NMnK/nAoD3HGnsXiif8n61msXy7St3TN8xhe3CiwBT899berezy42+MpPMD9
VaJ751N/etevc6T2T6XH8T+44+u/YLU76Bsf4AMoHSTFBxgKj9PcsYn6vk5F
g8S/z49PXusU699KvY36w05tsJcq3Gd+6m/Cv+64DN2TUuOZn72po4rfm2Ox
5DXK9Va4KzoS/z4v8X3Vzviel8LNtBfY9zKdy+vF7WPLWT/pH/nxHX/4r3Oi
D30vkkl+78FT2EtXcnJOvs4sxltrZ5FHlnxsxacN6EB+uEvfhJeF4asPPxng
mYjry/iM4pkYcx7F+fGnvvOSiBO6fT6EinEZbgs71+wwTdRZ6Fv+FLi9uKTw
Y/Tzf3Gdeb1YV7uKse4e5ZHXr0Q8IqCHxvf+0EMT48y0Uhdd1mnuHYTd9XOe
8t75ty5+Y/6XjaoKjv3vRnkr7HZ9hca6UHZmk7LUye68F+q7fuhR6vSLvhe4
O/0QcSpzveyzSfxejTff5E0r9qU45318V6twI+GPu1H7hnpx40h9+i/0KBni
w++lwx6+kor6WrWufmuATqMx3bdf2Vo7+EWDj+X14kbhKOwDxU75+BV25+7k
X7qM9fUpMBt1o2/ydMff92cROiTWpe7kQdS+ceG76Edj5CiDzuhQ9g3j6iYR
n7JSnijqG39qv4iD2X9tK+u9T+1bfurx7qET6JxjndhWb+yM0E7kJ+fS90E/
35+8RYJZRbzXt6bHp/66ebp8XlyLnxe+Rcaj6NdU3SXi/5ZdAn9c6gkbMZ8L
XOkJ6/Yc3jOlV983m6ivMeqwbyi9ejOoDPjiydi5Uq/eGoiOjXXnH/Gn0XMv
vJdI0TgXyxSp6r2+e+Qn6cdlKOi9f7dUGeZ9mP93uY/pO+iGzKZOXX7sRn8S
t2+epLwX11ueFOeQ25j6Cn1nIfJZ05OTV7YWUq9R+Dy8vydhxCXuN+ac6czz
1fe3Qcft331GXE/uM+aGWcLvdYf2wJ9ue5j1OXEA63l/FJE3CKzPWJPQE7u5
CL5GQXQtzILx0TnJ1YP3Zz31EUqv9d/znvzaqMVcZ8B+1tPNofA9c43jfdlz
XdaBFwvzfq/V/jr6aOuzC3/BzPMA3ezPqbH/Ew9gvaXpIewy68MG3o8X6Jo4
TaoI3LxaLlT8WWkM/nST5fABshzFTo2dlziz6luafS37wrPe2by4XqIq9m7E
dVl945PH5f07WpF9ZsVH/M0rx9EhKrwBfG5MYY85GY7RB6VLEmGfqP6MWqQy
8HKdB+m8uP3XDFU3JD5eXRoxL9EmifPdKpCePOYFyUu8N1XoaWh1imGn9viK
v3Qgo7ArlG6PFbE7db/lumTy4s6dZOznNRYl8eJG9eTCvzA/RYd/pOr4zkv+
wPQcxCHn9kOP6rfI/0fYW0ZpjTzv38Hd3cMs7jC4hmEYHAZ3CO7uLAtBF3fX
YIu7exZddHGXYIs7LA4P25/u+5vw+5/z3G84FE2k011dctVV2LE7alHHJvHz
5vJexBuflJZ2IPrfyd8T/bDsX59cOzEC/Fi95/64RMslyP9Imt87Xi9Skr4q
7a6EiPfc8o3r29+oV99T2s9LU6EVuMnisbN65Vrb/tQdFJyf3it3bq9QdhG4
pYnneJ5Jf2CXFpwEHrwH/YyMJrPFvrZq5xDPo4WOF3J7TmSxDxWPqPNnKRF/
UzyiVpqJ2Kcyj2YdmUFfk+yZWM/bbsNbsjAndYRjU5Kff4/cXrJW4JtVXlWt
q5/ruAPrTdZxO3WOUidVsD15saCp4CKOx6TOTua/7JCI1L398ymZV65LXJ1e
sxfxDMkbY96F19Fd1lDyQfEdrc21hL2i5etGHbaKH7pzhdyqlgt7RPlrip95
QQVwSifgc3b3PgYnEaktdbv10W+ucwb9ExSbeK86l/+pTZ11reo+P8L+vp58
z5TMxIH3TmPeGurgHCbtBd868A/027qe4NaKadjvD0eyHiJ2IC5zrgr9KILp
T6ff2S7mxWmcSPw/vdEs9OrVhvS3GpEbO3rwIZ4/bBO8JA+CkR9ewX2HzUO+
O3+YuH6qlYyP8QE9uPwEdoQF/6H1R7DQX/qubfAjZRnGe128RT1QZerR7fgD
ec5K68Bz9Ia/KKCftc7CX3b2kfcMzFu2y8Lvs3bcCxHv/2gJ+Ie8TXn/zs3L
+75v02PYdbW0il65MzeWsN/sEj3gcdmea4j497XZsa+iOE/2eeTu7u7UOSaI
RX+JdwbPP/zJc5HPUrjierJurn49kadw3qYnDqPOu7C94JHGPSLe/scZ0e/P
6VCB77uoM/UG3egDaPQrjB6+Mwwc+VvG62lKE4dsVNoXLzXSReP9J80r6H1f
u281eHNiFCjglbu/fxLvaxdKU8g3P1VfCPnP/pQ9a9Ys8V2SnsPekPyK2pZM
8PSlo59OgI9xQFf00lz67wT4GOOSPzVLVsrlfX4reQrijcMm5/HJXy/Bfl7b
q5RXroWfI254UPJeK3u+eFGBi3I6mD65XjOiyAtbz7tShzghhHxH+FDsvUkH
/eNfm9iFC3v47qvvb1PDN35Xb//4sql813GGHwB3NKUr+rM6foQ7rjLfNVN/
cFIufDXumm5iXtypd2T+QtrJew34ZveWCeH66FW9TCP66OXPW9orN583h+/y
1tOM3ucxHm8mT9AxUn6v3M2/jzqf3Pt986/NHknf6/j+uJw1oTDz1usO9urg
o9jnWQbCK1H0DvGlxsew52tP4Hmio/81eW7+p//F3+UvUE+t6j27ZDslvqfy
p0pMxq5ORX444NeMmklfh+UZyCPlQr/p2/4EPzHjOf2A/jwk9XMBztmPGn3J
lP7JcgO9o2P/2UtDscdWngZ/+LAQduEU5Eb1cPTD1xHUqVfsxbzlz0v9Qt85
8IoM5bwwwvODA9gc6uuTZeWkj6F5y1ByOR+tkG+fLuJvAf7M0yuoY+meh/ko
tYe429wifKchpat6x9tZXlJfIfsiBfB4qv/XlXnMz+/nsLfXx6RupPFi9stR
+iA773+l7n7SePp0VT4q42Pjw8R1H8/hO5fvwrrquC5EPO/MnMK/0zdO4LuU
rIJekPaM1romfN8/2TPGyoT0NfnJnjEWST5sac/YE8754jBumsxi/eiThpXy
ys3dB8Fp185Xwit3zu0i7nF6COfnvlChr8zpCahPLvmAfLTE7ym8ijs3An5i
ScZba1uD16/TmbrPRe0l/qST8M+t8k2xW490oH5w4UXW38Ld8EMouzRi+e8i
3/2ha3WvXNcOPxL508hdfHI3+LjYD/ajgcSFvl/nffUI4FUqwXsR6OcYb7b4
Xlq+i9TNq37c7zTieHmzZfGONwrFYN0m60i99Qb2r27WhV/jpt8OtHaSX1Q4
Mb3+V+nvZ+a7Zizr48u1nYfgjt5nrOSVm48OiPy+vu22b7xrvQDP/fafYN+8
hayUPEEfqVdT+s3sj3yD3553zGX4UT/hkbSJ/eHzVDhVJZe8FvbKsrJ+IRr5
hbl3ySPciEH+R+VHum4VcjflvWTe57H7zYCP9e5UX1zdPDAFezH+aV8c3uld
lXrLrnF9440lt+hjovrHqb7Vsh450D9OyWW9g9X2Cvte6mF9/jd45EpPpz4x
exnmR28k7eai9DtIQ7zRuPdI9nO6zvvKdWKVL0VcJt/FUl65Xnk6dXSRIxKX
+zZO6ufp4H+jv8nCfWR8eOQf9CE6ejS1V263+EC90g/7RMxDmvv479I+0TJE
Z94evRNyvURs0R/NfZQi3Df/eaNyX/kzo0wE7yHPHcVvqXAgit9SD4tc1Xsd
58B+MW/2xSVVvHItVyb48zfm9ccbIw0DX1EiTh3ei3Vobh/HfE4t6pPbj59i
jy0/Ud07D24/6uXsP+P45MbtfOjH4NZVfePrEx9wWq2U/bNkfUq3srKePrrE
f8q+FYliCn58rVtPwyt35jwQ9rNZ/iP74gL+iLtpQ5iQ550u+7VJ++TqBeIV
2QaU8sqtSEfRGwnBCQa+72z0vp16o8Ajadk1cJKNmsOTkDKcfKnCVXa4Sjyo
QgKffessOkwf4I43fHKtUTf017WcQm61k/ich7MCep7nLCHxiuh5/Rfi//pv
jDfzW9QdZbzuwzm4MaITx3F6+OxwPUYnEfex9NiFvXLLChf2mXZmpk/uronL
+N/YX8bWb9LOTwc/maz3cfdKuaz3cdZFyu59Hkcrw/lfapVPrjfsgH25/pov
7qEfOot/XYc6x4DdOGwlPDDPbsUW8/H2mvC7ncSfxPfS6vUWvI72jd/BX304
JORGy5livWsfbzC+8CYh169d4bttkHiMN8/wZ3rvFXJ9whQhN0eAazK6vqrl
nR8z9XDq3itGqe2VO4nhNbXSVyIPW13midK/w95ptE/2uZb+RfHDwl6yKq4s
6pVreW6yPoOH4OcqvJkWnzxEkH9dme3k/k37FXzv4RYinmzWyAzf3blx8PQ6
s4Vci3lK2FVOsfH0bfyjGXHp/ofII57r43tfd+9G8V7GyVc1fffddow+66HD
feOtlC71ICfj1/XKtXKl0Rsd09bwyvU2zcBNPR9PPNhoy7nWazf9eLJFoY5h
IHLrrzzgv+8vApdbZzL2cImpjI8VW+jLAI5O8iPpq9L47msPvClw0UakPLIv
m+TVT5Ua3onTPX32gJblVpC4z7Ai4Dclbkf18VFxG3tWXDlvxG1UHy6l91Sc
R/2cZOAuVL2V+imcxo/vDj67wXt4QB+Vhpf10WKhp5yi9Cc1szrkx2OVE/1J
3bgxyXu3fEG9p5b8m7DrysIb6R58TX3opyBwnvsaC3vQ+o2+P1bNAeSLH9ZH
XoO6UXM3civ4JedYoif4KSWbYy/fGIqejDAbPZZjCn5BHeoQrVPBIm9uDt4i
9pGehT5dqq+NkdTm/JhJ/Mne+FzItVsp6ePTqGSob3yn75x/sv5RxdMC9Y+T
yxAfvzMJvH2brPB+lmldju8iz/1XISJubh5rwLmn/NlzpeHDLTvDJ7eavKHv
nowLKrmqt9WvzkKfKfz5xFvkbxZUL+uVa50Kwv8g4x6B83pWdXDzgXhIxf8f
+W3w97vhXw/g4T9mhcc+we3SXrleaiBxm8/xZNwS/Kd1PWsVEUfqvp71M4Bz
R8/R7aXYRwtWsN46yXrVqcUFHtKum8tnl1pLR4p+nUahUfBZ9h9KvqZhAvjN
VhcXfp+xaTD5nfIWOIT0Z+FvVzi0/KN8/VoCcoVXnDbIN946Aw7NWhsMr9fY
gei3bqvQd1O7Uaf2fSh6stZj6lt7NqNO/VQ66nRu3yZOLnH3Af6x6cSVrOLf
sMdqDYB3vXsToffM5D18vHna64HwwjReQBwhA/rKedKZ8+Kc7DP3uY2Q2wck
nid4ttTr2PPWsq983xwxy/nmeVts+MzWVC3vHW9mzsX+lHXHii8o0JeztC3k
VhYXHqFweBoVn7wa/x+fvLheVexGdV+nNeeO3XUN/muVwqI+0RiWBPt+gCP2
tX0wtpC7aaphz72YyL+3mNdOjP+UEb8+jPM0cP0zqdmPs7Rwr9wsMpW6/oYq
ny7raG5XEHrM2hBSxTcP+Q1hTzrdfy3rvY7xOpqwJ62Nz8K8ci1JC+pihkby
zbObf3JUcd/3633fxQ29LHAaRulkhX3Xb5EXPqKaAwp65XpwOPZV9Jm+8ebh
eEJujHka7HueVnPod9U2eQHf9Usux8407tN3R9WzV8ef1xP088/n+tHEkU+C
Ww68VxzqDfVdmUN9z/NbUnjUW4Hrc5ttYp92K3pc4A2GLGT9b3vEOpS8dq75
mn7ro+NgFx2aJHjpjZIDxHhrXmz0lbZFnPtW/Fglfd+r6iDiK2Mvg++V9T5a
8pjUy4xuAq/gPfwVu+5r6iuSPxDvZZfLLsZbxRKS/5PrX/WdV+tf4fkDconn
d0I7if1o3C4q6g2N5pHFOeuWaYj/nY06aKvHN+oQ8ifFTg5Hbg7aw7lc/wL1
aKreOWiP4FO1h4zP7ZXbJw8Ludvgan7//FcF/x92n/21eonIr1kfg+hTNGAB
8puGeH6zXDn2b+cX4n0D9UpxShLfar25tFeub28MjvprT+YnreQHeDWX/dPg
uuTrmy7u6zaOCs4t4Tf41hatFXKnHvrZSH2APtFndNF30nxZlvzH3T+pO/y9
n+hDrfSb8WsZ8uCTkLvhX8AZrmss/WW5Hq5+po/Ak4g+PaCPmxRVzH+i9PT5
zEm/POP0gPcC//ljPYv/t/a90D92gqXEr9o6ws6yE8nxxUvAJ1bzTk3vfa3M
/4KLzT+/hleurc0AvlnW0Qfy6aqO3mpX3St3Ezz/RVwnekffe1l568Ln23Em
+FVZf+3mfiHmRS/1L/G8S5XAaRfPCY684kfOQ1V33LeY4HcxRtfL7pVr3cAd
ajG6pPfJZz4Df1XdJa/XlDpfK2eoqM+yb9zFHw/eS12P0Zu6A+kvWFHB+yl/
wYwbBx6bSmfJE8VLJr63Vfgf6n+fjxZyK8sa5HH2wbOo+uxEiwefpHk1t1fu
FNpOfmHs6pxeuZ26PzikBWPKeufNqNqJeLXerrxXrh1ILXAy2t74vjoXN8mN
EPFcry3xnNbwS9Tz3m7NOl9bkDj09+TYOQ0soU/s87OYt+KvsM93rGHfyf1o
nMF+VvtRf/YVf6TOXuzAjKGsk5ZfiHdmXcH4Tdmwk7aSDzX6LMfumj8fHpAB
M8LEnwUnI6/VDvy0PK8Vvk71f1H8rkbZavQfkfyuSh+q8QEekpn3OIcj4i+Y
vSqJ726PecL7rmYejNuzOR/PUV9jJGC8Pq+oqK/RLhSW8cCf+oq6qZAPo/7I
Oi37IPeBP0r/HblRe6IYb06ax3fOk4W+SGsPi/e3Oi4T8Wx7SSb6Jx5tQf74
RC7We/bu9EuKeZPxUTXJ2yP1yXj6OrkD4oFzG38BPpaBjcV5r8k+UJZ5HPtc
9oGy5nBeOJVfsS/2x8aPyJ5OzKdeNIi+GC2XZxbjU9wXcQnLOcH18z5DH5aZ
4dMzTodJ4MaHF/LJ9TRfOJdLjRDXt8MWChyOce4wvCRTS2K3v9kBX1CbhpyD
LSaSJ638J7idfL9jN/TdK+wN610rrr94CXbsryqOJO97fBi4qaqzfHaL1q8S
vH7jC/nsFn3sJOzbQn57xppDn0RjznDiIYWXEz9f2Jt+Fa/OgkMcg9w+vl74
Teat0dKOlfH5PrHgy94zhP7Lkh/J6XYQXFce8kWBPiZLogt7z07f2/DKzXhv
wU+q81T6v+o81a7XBUdRq8QQcd/GS8lbyH6spqwzUv1Y7bjwFzlJwdVr2QcR
N75aF56QnfGQx0sDH6/kv1X+qRF8Dvsy2hQfj425fT91y7OyCvtNe/aQfXR0
kDiv3Vbj6S8cm3oHK88J6hGOtfbxGmkJe4LDzFqzpFduh6+mbqHpYfBogTjD
dvz6+fBsu1WJS9gxx4NvaXC2gG8+K6xh39ZLkcs3/09Kk7ftO5u6Lik3mvQn
LlB0C3WsUu4WzU79s6z/1b/uQ5/I+l9V56u9R67qfI3EVcp538tIv0ics9pf
4yt45Xr0rPB9tcjqqwc3+n2gXkv60QE7+cQJgTvXDzTAHjc2wIuyLCFxue7X
Wb9ThsOT0HwO9dGzNvr4hcwq6cBndIkd5LtvL/SMcywvOByZT7HXn0fPnG1S
yit3su/36SVtzUC/XuqYObZ3/o0ZU/G776S9t88j12Pmpd9rnpypfOMzfxXx
op/5qQJ+4rdQcEn9ZRzgcSVxrtmzIhBXP4qdb3UuQ1z0cKwg7/X1Fmk5X3dE
iKbeQ8hr/6b68KmfrL9ykTeoI/NoEif8KJIaT55npO2bB3PkXXjgC69E3za7
CB77IvVrAf9owQFwP2O6R/fKjQTUEah6gcD6kfUCdt2f6mRnHcXuaTqjmE/+
+wXWf7TOKR3v80c5B79hq+hpvXLrTjTBp6C3n0a+bGIP9nuEHexnWeelnseZ
8NhXF6bkqi7MHniXPNKTCtQFZ42JH94qeZhXrie9Q9zta19x7rinO/O+NYeA
P596kbyaun7k6pp4vuGfiANv5jmNASnEd7Ui96NPvcL1ZaoIT2zVg/SpjwO/
sZ6nMvwy62Kjtwec474deor16RxLIJ7/x3xx32fRRdzJSgpfQWCeT38En5fr
CHHK2/HF9Y02HYk/fyMOrI9PAK/yzXDqQ7u8CPE+p/KP9CONZRxA6s/ZD+Ef
/y0e/v4F4pnmoPTkaza68pyScZ7eJvVZ+TtX8sqdx4kErsDMN6mCb/zKDeTH
Jc+PtvsF/RYlz49+5bm0Y+GjcBrkEv0DrCvPkB/9Dt9XkVRxhfxuQ/T8QPap
FprSnw+V86byodbcAvB39WO8Gwe+USNadrlupb9TLI+I01kf42X0yo1FdeHL
aGtn98qdeZJnp/s46vh+38nzD2+K/jw0NdT7PGalhz4cqj6QvJKKhyv8gLu4
K/3Ef8IPqHqfn/EDarzCD+g7wAWo+2ovJG7gStwwr9zK+oq+w9F2+8abIfD7
qHx3gK9Vxg3sX1aAx7h9Vfi/2pnqIeJ6sj+L+yg9frHsz6L6sOhxGK/6sKj8
mlWP8zeQX1Px3kpT8Y8k3s9MfRG8vPQTzeuy/06ki+jTmfBO2Oev4PfmOuLH
h1ddEOBNFc9zTCfvfOoSvGk3Tkg8JPXaTr/28GF+iVfWK9c2xq8i4j+JG2NH
SD2jjf5C3OG3tdgLC9PBT9JvNfibrHNDvOOtoxvE/nDLLRPnl/74JHqv+Vri
q9FfU5fWbibfK2Vx7Od0uTjv2sxCP/RfR3yjYVyBGw+cs9kekg/TDsfwyrUY
+3nPjVFTeuVGkoPsN8l/q85H/dRp8R31q5OF3OyQjHVVFLk5Igt5tjz033Rm
DxVyO7iJOM8D9Yw2do8Wqyr5iKvPsecTpiBfPO5omHe8OwGeJiPOLxJPLu3h
GvhxRsTb2bxy+/6pgyK/dnBXAa9cf/ivqL/WZkpcq/T73B9+n/j3H/6duI/0
74wFRQWfufkYubUfe0yr/0asByP6ap+/rNfdIs45fdIseG3lerNHJwYHO6Vk
ca/cvDMYf2mu5LffdAD7Z19seAu3DWZdFcTvdt3sQt/q6ddhVyY4MERcv8dL
eAbvpMU//fVP5D1riPi+W3gP+jvbM/zcSSXAG19NhZ9+9JmIC5lzyQdo3R3m
ITXxMa1dc+KY9fz8D447gLrz3vTxds+Ao3Zj3iPvNbcB83Na9lftRZ9uvcVW
6lAu5RZ+q3H9L85NmUfT5pbFn5V5NOfIlpMijqV4/ArNhEdFrynObSU3E/4i
1oMbebsPn+nUwO536g0I8cmny7qe16lknFDic2T9i+l8lfyyMl9fpld6/szh
y+9bB5+JOIlxv3Emr1xbO4a6i4TwogV4ay9LvK7EBWnVZB26xAVpMwuE+saH
k49xn69+KuwCyYtoZ7ss7Aer1xn66fWnHl9rORbce4Y68KVtXsl+SdYa+cue
sn4N3LXxawvut3xLLq/czG9g710oV8grt4PPwpv3KFfYf3/qNQ7yfYfGJd83
Y6CYZ2VHGX92gScw6BR+fOg1cK0NelA/8jf8BGanq9SvHS0h9IhV4hhxIMnn
4AzPAi9HvAa+/p7Wt2/gqufuwu7M9w/6fFAZ+HoaNoZ/Iv9O9G30XjKPkJ71
OBS53q46euavVfAnjy6O3pB1687yyLIebQX4DLMleJV0LcH5Bq1FPqor9WXJ
ysMfInlrFf+2NXor9Qfy5z49T5ziraX4G+FHzJSVc22ufN5oB8FVJI6HHXn1
CfHSPQnE8xsHj2J3Dn/C9ykBP4kR8Qo4vMVn4NtctkDInWuc+85fvSXekvPU
TnlJ8KW4sabIc591aDcBn2lsfol/rPR57t3gNk5J/0COt5Ly9wAeUuGHpT3j
FtzJ+pT9N7W55+g30GwT+nDOWK7Ttwp8CAuCsGP7/cp+uf6biDsZP/x6w/uc
Edj/qg5X2S3217bgdtt+AKd6opDYR/rr22IdunXh97MzRkff7stAPbDkldXn
d0TP/8Qra3aYgVzGwxU/rX2+A3am4qd9VlnsOzfCA+wB+wv+0L2Ekg+VdWg0
HYwd3XwQOPGsMl7dHlyX+fQDvJ9/z4HXsVld7Plz84jP376DvE43+gRNO+6L
G9gP+5LP2L6vvFdu7t4s/FQj8nqfX+DM+UT9fz2D+i+FC+2znrqt/9OPnr6/
xscAbzDn81/wBtutHso6FHlef3oMrq5CTvzO+3+w7+K+h+eqR1L/+OdZkRfK
jn8t8bR60aQi3q7wFYpfReErtNnL+T4DJN/mhHzgi5YMxO4biPzHOoCfYq8l
9q9bJV8zcZ0t++D1+G4Lv8HtPgh7LNNF8og9fhfywLyNOwkeJmFLzuvIUp/M
T8jzSH/NmV6MuJD01+yHX6p73/fH84g4s7OyA3k5qQ+tYx8EDlnTs/nG6/dM
7Lxlh8v7nufkRsFvpfwpPXkf1qf0p4wh2Sp6r6M1uYefEvFX3/xbv20Wcif8
OfbeXRkn2ZgR++Ow5O1TeYcnhTnXO5WE1yjCep5T7hdHzwO/TcnI2JNZHvj6
v+rFdg+Vf4cPocPV/N55MHKnE/EQu3Yf9FL7xuzfHgWo45W4soD/osUHjzH/
FnbpkBjYRdHWwsvX7JbPXnUXr4dXotwk4l7TZb+5i7XRJ9kqw/euFYC/+iK8
eM6yhvRtenKK93ofARxUpPr0P6u6nvPxUnpZdzoP/EmSi+Cxe38nH7RK4lm6
0YfabjSfeoem+YmHbbsAjqvgAOqi13cOEc/zGn5gPeQQ/tqNVfAZJ6e+1Sqf
ju8S62pJ7/tq3VZjz51tX9wrt6pPIh4RMtwnd6IkBMeVtzt50TeROX8PLYUH
+Z8VxOnbrCPf9/o9PKupn+AH3Kde0upCXYH2tSv++/BI6PnyXbl+NfAk7hfq
cK322N/ahJrw9a26jV+Wf6Hwa5zp4ZnE/GWLMkTM58Im+DU3HXiVHsQXcmPR
Zvygq8VYj+MSCrneYiDxsbzFqCP7ZRfr8AH3/fF94KFtvY91eLke+Z458ah3
KHaeef5Yl3lbEOinTd3PZI36HG0i6/r7d+yVHLLf2+LAeOymjYxXeSUz4270
oMwrWcct8MhTD/OcKaZQz36TOmmn/SWeZ/UY+s5mGEl/qMV5iCfIfhzu5xXU
jal4aYkMwn5zB2/K45W7dT9jFx1Arwf6JX0+I5+bc8CW/YzsD7IvWCbZ50HW
F9u3ntPX5HWPEHE9VV/8dJ/AI5qdd4tzPnC+TwOPZL54kN4r/4/fSTyv5AlX
/E4BnvDN57HPyvfC3kgRiT4fV1aB7/L04xDycIkHy01fHjPhXeQ3+8vzBf2j
bztD3euESOV88rProoq/hy325WvMlqnw/2PBvxeYZ/M+fkKXPMW9cuv0Kuyr
aC/kfaVeKpUfuaaLuIr9RfZpkn1llFz1rwzIL0THDg1nftwug4jHSXtV6Ull
r9q3Sko5cQ87AjhpN8bMYl65dR0+DqPQn+yDN9nQJ+dy0r954HX0s/J30sOb
ZB/cHe6dN7dwWVGPY73u6jvvtN4HBJ5B2UXaRJkfkXaR3eQKdXBd8XOdq5NY
f9LuMtruYP1Iu0uTcXm323euL+PqzkPZ/0jpwxKrOMfvzQPXWS8C99WtUO91
jMUbfNfRgmQeXF1nU03s/kPV8LcWvWM9fPtFyN2tE/FHGkwRfXOsqM0qyfeT
8yzXyayKwp50b0705fusaW/IO2thpb1y8+qvwl+2byxG/tvL5uI9kw0BbzTl
Afrg8S0htw92FXaUGbIXv0bxAxy/Jb6HtaNHuO+9Zu7hPI1RA1xxsYes/3o7
4OlLj763kkUdIubVykyebnoE/BSHOLZ1S/JC941JPkjGqxWu1f70ET1z9g28
5Wf3wzci8Tlumi9CrvA5bvXT6JvR27B7U7UgrnpkJDwHUU9jt7SfSJ/TWPfk
Opd9ZAZ84VzeU9qXt9ITZ0deuVVx73j9eRriJvsa4+9M4FwzagzAntlcjnWn
8C1nRsGjZ5H3UHEMa6kOP+DZx6W8crP1KeTD/5D86pLXfWBHzvH6nXJ65Xbw
IvLHPZdl8MnT3yTvsmxyLK9cS3WResLjK8AH5bpKfKZ2YeKevQuSt1R1Chup
91Z+q6o7/tlvtecQD1d+q+pfoOLkqn+B8+Yrdk2ZNeyja3noN9CyuG/924sL
4F+tyAd/aWXiG3a71tTPvUjNupZ6w079XuDe7UZpfXLFX2rqvULE/5O8NFbd
e2I9OVXx55XcSXVG9un74BtvlM5NfCGW7Dsk58Gs8Td4g7P08w3UZad8h7zg
KnleSH3e9r6IQ9rmABl/ln70526C/8HUfvfZ88bOBpy3u8HPBPJ3y7uI/WIs
2Cn8V71Uc8Hr7uz7Cx74yg8E35S9pxP9E51VyHPsoZ/Vk2GCN95pvg4e+BjH
6DMi8Ujuw1fEl3dHog+nlJvrU/0l4uRFVtXxfi8rYhrwwR3G1fF9l3uHiPd+
reKTG50lDnCmqmenj4BdRdoBCVX9O3LtXFfWfaU9tb3XUfX1Vv8CvutbFSOC
w0j6yBdH0lI84X4rL4DTU7wEMYqBD1zYCnmNZEJuJQGfb+6BH8sdK3mw35QG
l3V8q+wHFIt9fafM/1PuRIsCXkv2udVSPGZ+MmXEjtS60D9r2kXkuc/ih0yZ
Wss3n2eD4RE718cnN+dXFfkP7dSrmr556HdDfG/Vb0j//lB8R9VvyEhig/d8
HJv4SuUTgodKH7oc/b/oIHm7F6nhn9xFPzKn0GXs/VjpRN7COZAQPVRT8rs+
pW7RyboT/bAE/ab/lgd/fFXOIt7ndBsWoz/lhvVFvN/LLTGR/FDQ00Jeud2g
PnUWsZ+GiHGS79388hC7Z9zJMl65lrO70DtWlsbo+bXwxJrTu7E/Y0QX55jK
1xh1z3GupDhXxCvX8uXCPoy2Lr9X7i6dgx0r6yjN1nuHiOdUdZR7X8Lbt3om
8ifhRwROuMVX/JUhxPO1+iOvCfnbYpJnTNbtPjwaJJ7rZMNyXrk9cbCQuwMW
+ORGm4/Ua8TRxfvqGzdyndn7wI9WzF7cd/3Guzlfnrzgew/dKs4FZ19u8uXr
P5J36x0Kbu3rPnD4JY6H8V2kHhs0Qfihxj97hTyQb9qYh35+OYfI+KHM73wp
Cc5/08eCXrm6vl7qsC8fZ2Ypx/p5WC/MK7c2dMffav6grPe99L5r4U369Y3U
A+x37e0kyZtf0ie3eg8nTzHxFjy3krfZ6X8F/7AJcQklN1ujx8wFx4N98mZv
Of+6LgfX6hagT+Kfz9g3r87Cz5OI/Jr+9/cQMU7+zA5piCcoXjw7uqxTlvtl
4jlwtzciyD5NMk9xZBTn6Ihw/LPFBYkrji4t9Kp7JH417zy7iW8Qf7ycrrJX
bgwJYf+O7F/JK9evpSAPfn2xOGfNFBlEntca8QZe9Xq1iavPlvb2AZnflfvC
yJCS/Sv3hVE7PjwMoxNz/SpDDwv+0niLfPzJqq+6ET2U/gO5iafp63Kx3mT9
mhqv+ri5DybLOlzOcTPPbOLRQb2IK8jzxap5D975EvQX1VRfvFiR4eP4X/xT
9j2X/XoLdQMHvgkcnTX3sHhfe1RxcOOyns7uaYKbMufRT2P0UM6FNhdVnlr9
iR/9fjD2wxnZh+2L4nemH5+5SfUTls9zH7kW0eU8+cp4d9I94hLXZd9U2YdX
rwkvqjvhHn72d3n9OPiT7njkmhov5dboEeTb40TF3l1SFL7i0IjgbmQ9kdkK
e8gdaxP/nBgFnEST5s+EfmvQELncL0b15sQfDoG/U3wURtHh8BJU7SrtDblP
Rz2Dx6B9q+reedYndoHPulgesT5tiXs0nx4U8U93MPFVYyvfSy87IaL4DvPK
0S9I4iG1xaPBWUkeb3V9xeNtLnyOnSCvr/CQWsRb4NmjH0YvVTyGfb/pz2re
59fWtwVPHyViVa9c1e87M3cxflkCIXdjwluh9f/DN968lRv9mTCorm9+zlKn
bAQn88vz5iCuNzRlXe/8W7EP4PeWTybmz03yjvxUwn/xX2r0DBL3nxIZnFTj
L+zDKIXoXz5iDnirgn/Aw990eVXv9d0hM6hjWh8n3Pf8Y+uI/WCUnOl/r9s3
4BeVfClGHdkfQfKluG4nEV91f4Ffy46xTPIwZg713lfVR6h+v4HnSZSUOp2K
t0LE/Z5eaSXG5xxI/eMq+oc776gTsWJMJg416LaQa9lnCLmxVRPjje47fPEf
58B+6h9rJPX76UV6Sp6yU75zykgyC3ztgU+hXrlWMh1+SqBvMn11Fd+sVf4F
+/gBcRJzcE/8/BapxPcK2L1xS/OelwfBMyjxV3qM0vg/z3NX8MrtgzI+q814
Wsr7nE+Ogpe+v0G8l915MnnVMo0Ezt8NTgQP00fy1FbHRtjnOdP78s5GisTw
eBzJUswrdz7kx94YYJbwyq2IIeSPFo4o7v2O9opM5FNe5fPJzZYbZVylYz7v
fDr9U6CH2+qFfPOf4i31iTk3FvTJy+bD/q+TppD3+kbHhuRrQzg/A/voEHwI
xspO4F4O9id/tOeu7AN+mHi+wh++p95S//yE+IrMc1kNeuAHHp2Wxyef9hl7
8Q78SEpu3i9PXXfPHtRhjKTuwH3wlTzpzW7kPRTu6/le4qEHeggeRXuWrF/o
ODVE/HkpYrj3vVSdoD7/rE9upxsBf/GRpP7x0Qyxr+0yx3373X6wRIxXfatV
XDqQN5f4PbdeU+QKv9fcZn6kP6X11oWece4OIy4u+dzcSxmF3P73D6E37DH0
G3KS9gFv/bQF+f/bW7GfF50LE8/f+pisg5Z2davyAhdqTD/lkzu5br0Q9nzH
hNl5PkPc1y6XgDxI2Xh8H4XLqpYDPzffxVLe+bcqTZf9uffCe9RXfq/6Hag3
SEccNfC9KpeCxzW2wj1KPtL309B7aW4bPvngLfz9xNESXrmbiL+72SIQRzn5
kH73RY4LXJAd9TPnz85pQu6GjgNfVJR4e4DfaUt1MS9Gc1PyJ6OXVN9J7R/2
fSCu0m8RfByF75X3yq1r8TmnOoG/Ml+CZzDbtqFfWJR2xOdVfrNYVeL8naaE
+OQrJD9d12ARl7NvXcPf/FoDOyriSeITxyNgD9/ZRT1JW/rxBvLIy2Q/++1x
fH1JzJaV4INdUYM6zSWyX0mL+vCz1D+J3Xv4I37H/OfEqcv2xw5cuAh5vOzC
D1d5Uns3doLKkxpjvgi5Pj3xEHH95+RljDbLidcq++FCPepJb76t4ZXb2bLh
F1R46pc3HgWOa2Rknz3g3jwv5tEwv7KfVJ+a1VmJv8S46rO7nOCenBd1B/ni
D26rpwKHoL/2xx/MVvBp6K8uiPsE4kiZ9ol+amaBCmW9crv6U4H7d+7tCvXJ
Qx6LfLS5IBX5/6nXmLcT8amfHBqfeE+zuM3F84xKQR+ruO/wa6Wdb8aoT7x6
ouK9keuz8RzyKAcW+ObB7Ep/GSNWSfrFpBzzm5DredmfRlrffJpjs1OHlWaB
b97clhp43KffqOP/SL8hY2tbeLFkH3OzC/3gAn3Mzw0h/j32EfLp9Pm2D8eS
/r7E21xuShyjfJ0wr9za/4w4+N5k5b1yw6gkxunb6MOpHwd/Yhw+QfwlaDfr
fJ3sp5Ma/L1tXSR+K+PbeuL3xIFnwDOj5G7+W/hXeneJE5B6NRn81U6x7Gm9
cmd5BuyS6KHgTlUesO588vTT7hTxzqdzugn1GlsTFvbJ85Ygj7B5WxHvd3Qm
H6VuUeJGAjwnEjdinFlB3m2PrIdqXVrsFzMlfUsDcaEd9K900x/L7ZWbb7aA
v5H9l+0IiUSfR9V/2V0azPwviEz/x1TzsO/Lz6IONansW9fvHvGEm2cyif/X
hDy7HlQX/+KZ6ncj4yEHprCO3Ybi3DTTDUEPf6wHL408Z5V+dnuPArfwRwx4
ZqIz3jw3Fr9R8mb8L98Hb4bix9CiMV7xY1hFIvrGm/2l31e8k8RlyX3RfyVx
G6t1Ua/cKDdBxCXs1Gdlf2oZj5oeARzj0fii/kmfEUwdwbee4E1HZAkS446V
433nDkXerVSQ933t4CHkI/KWE98l8L2ipRX+hnupH/W/eQvzfdfdww+J8saH
h3R2XwZnlbeNb72ZjzZRJ3h9SwHf+PLELe3UK/N7v5cR0hOcx5oYMl4k7czH
sk6qfDXwILIPgtFaJ8914SjrcPUkMQ/ms6gh4r2PxRf5gcD8yLp3xRugR5Hf
S/IG6AV18AMpkeuRe4OfkX0iAutE1rf+F7cU10vYATxzknXsC4nPV/3KFT7f
2X6DOtaL3eCn+naRfJjk/fvZTlC8YXoknkfxhunpu5D3kXUQdpuh4MaWnCru
leu5o4SJ66SJXtQ3vvhTITfcSGK/GLOqCn4h5+5I8h2SJ0HxgSh+P2fASfgT
CsOnbVeVdbvTE8g6TbluLzcU8QRNlzzeyu59XlQTf1brJPwd9/MF5mEBvLTW
2n/hM/8Iz7YeL5Ksr04gxjsd6PvpDBtGHrkt+s152l3kcbRuHcFVl3qHPvwy
lv7IoYvE+5qJjrDvOowQ55TVYJc4L7Xa67BTNtAv3tUOY5e03oB+Cksknt/K
W0jYf8bjg+DNVr5nnaw5SXwmjPiJ0xv7RMv8FntD5uutK/QxUfl6rf9h8fyG
If3r0E/0E70WA/vq0hT86FSpiZM0Whwk/i79ff3DryHi+jfn0U/wrIwDrI8p
5PZBN5N4P8UbcP4+9naJORm8crfKRvhEcmuJvHJnLP3grHTZyYNc/ST2k500
tYgnG1Vvk7c50564wJZ28GPGzSjGW0suinyeFToAPGGBxuK5tKpxxPzozYvS
f3pRR4kfS8M6f9SWeai6Q9S9uqnpK63dGEPflttJqbtcuY/6o79nct8amcU5
b2XoIa5vT/z4Rvgjc3fJvO4Q8uaDy2B/JrhAvETml/V/6+K3JwJvFchHl27L
+f7LIx//gPm+JXGNct3EdzHjsU/dBRmx1xuNFHpF9Zs2rz/nOSp3hF9K9Ztu
MgRc8ZVq8DbIvtVWPYvxZ9MRd5e4KbPaLeqsj0m5ikNWQW7likI+QsrNV+BQ
rSbUlSu9arV/Ck9u2k6Cz8YtmUTMmzkhJfFS+bOjFxL6wQg+h36oc0TgTm27
HvJyx7Dz3i8Bvx8xjbiOEd5TXkf39RnQ25y7XdIjd6NRB2p0HpFd8LPtGeIb
b0yMJHBfRvAbsW7N+x/4jnlqiffR5k5JJ66jTRFyveQfQu4uLSb8d+Ovhej/
2Pj79sqEIh6vpboKz16mv8R4+7cIYn1rsr+w/ZG8uDpHtJaXGS/PEaO6y78f
Jr7k5AgV++B/PKg/1dUOSibru+ElMw/Nh4f9RVcRJwzgE261+1f4dz1GRfTK
jSUjRF8b7fNy+kep8cO3ijpBd+007K/P4N+cpdPYL9tnw6+r8j6vwrEzG/+V
0Su3+tPfyC3aSVzfylkGez4oB/UzCetzXoSPEnL7O+vTzpSxuPc62oQZ4Mya
TfTJnT1fxHxZqS747Bm3egTww/32kEdKsRk7p+8M6qByq/7pcnyEfvjPK04F
e+VmvIXE8SWvZuA8lfy6Ci+n8p4KL2fXMEv5xss+vO5d7ARrPXaUHjRU6Edj
/Thxf/vfpYy/uR97ILhiZr6X5DlZnJJxrWaK7+Y2/5P63CKbsP+LLBPryjg4
DfsqdQfsscNJ0BtD9+OPny0JH4d8zkBcqPpyeMAbhJJXGNmM871uf/Iy0m4J
8MrK/lbungbivZy79bH3cj8iTzR5BHrk+1j6AgwjXmT2+4z+nj2OeE7ymUKu
P7rD+vq9KP0F3s8B55QGHJfiHVL9PqySFdh/6SXv0J+JwWHcayH6CKt4nXZ9
nbAztb7XqMvYuYC4Vssl8Gd2o+7DfLkH+eCv9Fca+xbe48fyvea2IT4S46jQ
V8ZD5I7sA2JM4ftqL1qzf+dP5/yLu0LIzYMtwaWMzSL0izUrqY+nQu9wkP46
KR6HeeXWjifwsk7u6ZNrKTaR79/1TfL5yHidm4S8yJK78GpGg/dYTxsOjmrV
p1re+VT96I1D4fBMBsOfbNopqQ/M7wq9rs4FY5HMc/XeCG+E4ulNDR7MPHoi
3Ct3EsRiHSebKP1B6e9Xfir4JFU9b8CvkfW85qRZ8BgVkTj/Bi/JC04IJh4y
ibykmScr+ifKdMYXJu/p1PvC+FSdqT/TWzUQfw/NRtxhb2T4BubGYn6ibyBu
I3HxRtMg6b/sFee7kgf802F72Bfz71I304Q+U1Zu/EpbKxwknqOj7C+WtAD1
Dtno42fPKiX7EUjeAonPCfSdkfgc68hUn9wY9ZD8yNg3xB27c+64bbvC0z4j
M/iZ15w7RvES+EWyzkVLJfuNyjoXN6gH3+VADuIzJ8ftEN/l/GDsk0sFwAsV
XSh4UfTc8Bk465oIufu5AnnWyY+pf8oHz6c1Ffy5PasE9m/PwZ3F89xbwPO/
myfiZtb6oUJuZl4pzlGzaHTOdclzYrVJjB8X5xT+WRB8Kc7nWEKu79kGb+ul
edQHDP0b/FtOub/ak5fXhv8Fb97tvtgvCmfS3RJ4PuOoxXll5aee6MxFoU/N
86Ppd6/6+kk+bac2euD/9IOoSn7ZyToKe29IC7576pTgUhXfVKFH1EHsqe+z
G938L8AJxMvntxsr0h/aLtcPu7LrIRHfMEMP4Sdsj4N/dP2CkOudwZeak9qx
XyLDV2Yuvk3d+5hztbgPcuf5I4H7smY0oe5N8p4FeAWHRqWvluKFuLCfeH21
35N65ZZ7grhzvr+Te+VGkrkqrw8+WuLwVf5di9InyDteGzaR6/T/Dp+3lplz
Z8wFvtPor3xnpT+vZMKPi/gkxCu3P7zCH3R7lvHJ++QQfq/efg/1hTKe5kTL
KNa9ceu7T26lIy6nLVwXJq43ZY04H80yEYkjbfibfdR7C/5yky7CntY+OyGG
573sX+qDf5gq+60kO0pc91xRxkWsSB4h5A567HuImB/3uk2csYfEs0VbJcYb
HedE5zmln1W4UYT//m42KnymlEduTW8j4oBaMfS5G4n5t5aAP3Cq0XfS6TAN
3Nr5OPA3/j/OffGe0n/XHnEOKv9d+ftqvPL3jU/txH6yooyBZ3VsBfy1QavA
IXZoBy/rUfpluiXpr67wctZ5ydOyU/IknIH3T19bU8yD/fdS4kgPnsD3+ypM
yN1X93z73X1ZCJxuvD0+uZU5i8DjmvlWlPN9r+29hB3uJjrGumufj+tUfIid
ofX15a2Mcun0/57DHteDPKTsk2JHyiz8GeNkOPIXs4Q/62yIK+bHahbuH38r
LfMWCZyJJuv+3Ib4Ze7/5PRtlHLtf/gWMd5+X5p86/Oqary4vpbqOfWhpW8T
3yieifOuxi7wFu/aCTyIsdkQ9rne8Qt1RntnEUfsGgX50tL4cTFzvRH8bYp/
rzK4dDvzG+6n7NjNg8BZZU8n6vUDffcyHw4R15uoUT94RPJO92tDXfDEyyI+
YH3i3Dc2LRH+uJFxCzzlb5LwXHU/Ycfaj9CXs1Jgb9ZKJM5BI1kO4vKx/8Ku
+HycfGHc4uSnAvXvpcDxxooMb5KKw2e6Bf71czv49gpVEH6r9Zb6Xrfpv5nE
/1tWjjhYh4/UaTizyEdlbVRPPOeQGPBZpOkHz8oF6fdtBzep+E7t89nIy0i+
U+M65559a77oa6A1fsY58tllf8ycSx+E9l/Qp4lLggtOOoxzp7WNv/TliDiX
jYfx4NWJn5u4ZeG/JZ6K81q72Z06fFkvbCVagb8j64XtyrWRRx7Dvph8V5yn
TuwV+CVNJG7hh90r/l3xjrbHD1I8h4pXzWyiY/dKXjXrzgOur/ym9EPhV2+3
4qvgMUidlXU76zP7M/oDwTMR2Nf7qEPWl9nE9Rf2xE7+9Df8DH2iBYl/v7tG
5AW0zbPpUyD7BVimgx5T/QLUb9J2zimJG1Rx1wBvvOy3osd4Bh/MzSk859Oz
rL9/yTc5j5FbYxKoOhqfnWn23Q8+dlMsycv0QNh1Wok5oo5V74xc5XOtjm0+
ibhH7CGCzyDA8xCrivxeSXJ45fb6g+J7WeOnomfvcX0jkuTPrOqKP42UD0Vc
0azTGPxo4+sSTyL5XZtGBSeT+Js4XxS/q15vlNhXWqua+728E+5iQ+xPa1wa
+llIf8pIIPniYmRhX26Q+OHnI8iz3p1G3lvuR613YXhBR/TmOxQjnqw12wYP
SQdwyyr+bDnNBI7afp7I5385gx6Kulm9wUGfn2XufER9eov51POp+aw7T+wv
/Z8yRb1y9+77CN7nMaT/qJ7H+OFm+cY/mBwm5nks9XoB/RMtF3nHWuD/AuNT
PWU9/Fgn4v2KJmWdjGxIHVSxffAqKf7S0QuI189pKetK5Lxdqsl3Hfc2p+++
I7LAM7DoPnFHxW9/gT6wVscToV65lq+beG79RhTfeKd4JuL7Y/14fn1aZPR4
jU74iy33MD8L+2MPSR4/Zzp5UsXjp495LuRmZcZbw9lH2lq+l8o7u1OiUc81
JHM5r9wcCZ+JOe2nOog+1Ffb1nQf/txpnYR8duOTfrz6rQfgupeOA78p4z9O
DckHsixpCe/868dfyrr00z4+XvdjUvCl9/HnAvbnyCDq4S935b1ryb57SyuR
x1pfl/rio8id+knAS30G16FnhXfXWbhX1BFoEWKzL3ZPxZ65uAb5gd0h3ucx
2hUDV5FygU/urPtM/D3nDp+fYmVoAd7o6rXS3vFWWCjx/Z9wRK5bCT2VcCg8
q6vZ186Cx9xPrmc3dKdcJ0vAmUk8nupjongnVH2lkqt8q13ms8zXxBVy62F3
YffobyP74/P3xlBfsOWb7/nNd4OFXC/dzyfXi0aEZ8/eIL6b4jNxyzwS+Vnj
A/3X7OhDue9Y+D0Uz4k9EbniObF7/0VccNEQ6o82W2FinktMw59Ivhi8TbRx
Qu5kGEmcZs8w8Es5C4NDmD2ispw/8XPnlsBPkP3Q1c+0fyde1um55GmIJOxt
d24CoffsNzHxBzpkE3ItdDb9ditGlP3WyeO76WYf8varstf0FHLVr0rhz+3+
XYVc4c+tPofh7ZP5KS30Ezi06zHEuaPyU26q1NTLyH5/qn5W9fuzX22k78Ov
xNn0O/R/0v7IJfXzdvziCoPBifVhPpXcbvcJPO7H05w7O9qAE2j/EntP8pca
hWReUvKXqj566hxR/ZWc+xMKece73dpTh9y0jdCryk/XDg0VPO1arLOZvXJ9
YLiQW3Ucn9wudxRe95uns3if34i0W8idcfDMBK6THp4Zbd8jeF4lvtR4fI+6
shFrfHhU+/f74BS7dyVOmxc738hWhPzU/svwtQzOSb5h2hLln4ifk5Y6bnvW
CvKShR74zil74jrqA/NOwE9U++h0DvKkV6KFeOXazF5ivNEpmW+8kW0w+K3H
w/CDH94j/lliF3m3w3PAgzSA58E93R27YgM8ItrcpxKfcEfof/3p6zDfc0rc
iJOqV6hXrs2eWc03fu9S33jz7rus3vFW4rj1xfjWz3L7rjP4T777pbu+8frp
9Xz3S5MlP2dq7I0hWciLjKtLHGNYBezeewdEvkr1R9DX5sDPkv0RnK3DwdfE
bIP/niir6EesSXvyh/3YXDxPrNr0d2y0XcSnrW6pWVebR4rnN1pUF/2OnIXf
RBzDytuQ55c/q0UaMd45MVeMN4vMFftdl30W9Jt/kWcr26eyT16bvlNu6krE
RZQ/eCgpOPhl/4JTUOfvsbxh4u/OzlJeudVjLfbx6QMlvHL9bCGhD+12e8l3
q/0yDhyJ5sbxyfWvhzlfoo0L9sqtHb9y3kS+C49UL+wWLUU1ERdzNr4GHyrx
D1rrB+jHDL8W8srt5Nhp7ru9xbxyJ/4D8V72kDP4rZ0Sog9j/IG99GM9iOeT
60H/sR7Ev0uePXsOcsWzZ9xuWpPxsq9HnM0i/+esPFDDK9fzh4hz6r9+UOL/
S7vFiN8rneA9lH3LldyOG4u+OAN6+PSYW+Ij/vimMz595U65RL1PW/ZvID6Z
j/2r9pF9uYMfrzUmCXGY1ybznxQcgB0BPh8zqA1xgAtrxLpU/bkCvArPJtBf
+ye56tvl9O+c1/s8zrncYj2bffzvpSWLzn7cuU7yhbIenLTdGF99A/UuCleZ
MTrx6GULfHEbY3he+jXXOkHeqtiRlmLcxiic3/c2MD/POgq5Xq4RdTdlgsDJ
mPDtm3e3ELdY38X3/Mbk7OTxZdzblPFeFffWXiyTPBvJeX4jJvpW2leBdavB
M/iz3N1dE/xASHxZXy/jh9WaiLy5dXxuCa9cn/MilZifPzv6xhtncpHHqVOF
/IPMg/+wb+FZOPCG+EMkGZeW/bwCdV4RkKs6r//4M7k+fWytU6d9dqOWqqo8
TxuV98kvITfGxCauezqHiNup7+tmSi/0mNbmdXrvPNvxvtFvpV3c5F65u1gX
490kOXxyo9xGzuWHB4O819fP/4v+fBc5yDveqT9KyPXc6B/nLv0v3Dqh+AsS
N6iFgs8P4AYvxsrve85/T1HPXKNMDN991xetL+dB/ALrWeptp++GWN7x9qvJ
Qm51TObLL1g52b/OrxFDvPIfdjn7Os5I33i3fEG+6zxX5jvUPGzlfB8H34Xq
72xGzAyO9ENp7O545MPc19/pa7i+RRnvc1qlWbfmlkxhXrnWcjP+2vte1Gts
sJqJf1/6HTxJeXDB6mcV7CDsH33bmcze5zcHY4+ZmR2fXF97BPn901m87xWw
x1pHoR9FcDD9NvdvF+vDiPk+p1duDJ9EvbAdo7z3Os4fH7E3JK7VSN3JpyeN
txvBXYzoIfSDc5c+bZrym9Q8RDzO+g+vVdYrN7LFoM75N/plKNydVnmi0DN6
gwGyfpP+pM7UPMSndmYp45UbN+A91qRdEdAnTS8LP0Lr+ybMK9czTRG4GXfL
1SDxPrIPuzHsGXqs3EpwYBKH6T5oz3MkKJLTK9ebzSHf09308Tw4jaMLvak7
T8K8cq3COOIvveApDZxrOXgvPeb20l65VhbeQ9W31JJ5DdW31Jj3knNv/mXm
85e1rP/G8Xw83nbnydglV+CrUfNgtJkLnmyo2l9S307KAN/E+v0hXrkZmgK7
rcoA6bfCR+3mlDyrkrfK7dIYO031Q2m3rbR3vFPpCLgHxc9cvQbrPMXG4j75
+HDpR6wr7ZUH9l3u4sSFXg3HTu7fUvDYOBcygTu8LvmiJL+N+Q1cr5HTKOsb
H/Ib+zP+KMmrxE8vXhP9rmk+v/XHjz6/4dfhWZxdAXs/3WbiisO+cB41Kw4+
OHwM/rbCt6i8lcS3BHi6VJx2dWr4nrZtAtfzgO/u1hlAfGd3GfwJyRNrnqNv
oz07RYj4U9l10zXi17/dhhdd9v8ya+Tm/B16g/tOmQAez52KXn2vlfSON07+
inx5FfTH4yZ83yfdWE+JTso+S3Hoi3e9K3Z/3T4Xhf/9W3yeM8NB/MBpNYRe
VfrWud8FPSn9d7Vu3TvfsAfeE18NnGtJUsOndvVJKa/cjrcTXhU7nex/IXnv
D8LvZA3zn1Pu6BvEc4v57TEttAH4mxQbhTyw3twBQq7wDwF7VeIfFF4isK8l
XkILK5Db+13c/lOph4/+Pb9PnmYBfbijh/rHH0qPP/hlne98sdzEvrhrQK+u
Ww1OeNov1PctOsj+7ZsPu3ZbHnik9h7CL8izjHxhp83gCdPG4Dovs5DvnjeR
vH/Bftw3fyThn2tB6G3nW13mf/VU+kz1+Roi7mfRN9aOXk7gOqw08OcZ5RuI
OKGVbjF+6Vr6JTpxhxM//FIXnEnNluilVKOE3CxRCB4AI5g8ebTuQ8T4x03J
J57LSZwm5nQht881Yv+ta0H8f4/sj/yuJPZl2SfkbWR9vRUVnj43TSn0YrU6
nIP9K8Dbp+zSPu+lvRr4gUt1NvnkzlyZ5+lM/t0q7Qr/Re/fDj4G2S/PWdkF
HuR0PI/2HT43Tesq/FXn83fB16T436wWv8GbUOkjfVFkP3Gt0W3ws6XKyv47
/4g6Pm1GceoV/zks/DKnlpR/yiDyaNqmI9Rvl5gs5HbrHPBdX28BP6jyL45R
L6e3qxzNK9d/v4je7lhU+vuyrmr/r+SrFmyAd+3X3JJ/Br5l+0Fl9PMn5O6d
qNTDZp0PvkbGDQL9cyPGA5d9ZZvIizkZFtM//fJd8Zwq/2tGGYO+SL+B+pH9
nI9unKS+vKcar/KeRrvcxOF2HhPz6T7NDx911+Hw9nx7izzbI/iojx0Dd1R/
Nfq2625hx5u/jRf1fD/3QzTmrc/nlevz2+PfZZH1AlJuxuiFHd6tlMjnKDyk
kW9IiPheUeFltXOYrLdV4LFV/DmAn1T1PjJereQqXv3Dv4VPtAXXMZrWJy49
9pgvLqEtvkPcuNBD6qO3Uf+o5dxE3rzJDnAOh7qCD9EbUc+ypayPt8c4c0bE
i6z+S6k7G4idoEe7QV3QliD8can3rNIl4DdxjsO78Ns89Fiy39GbSSUOrYMN
T9eYL3zfPOhJ510Wgb/SbiaUeSvsBCV3b9rs87I1y3rldtmo2B/7ykn+TOmX
DYhHPkWPBc+qss/fPcL+P7GnuFeuJwe340bPD2/CrFDiHlO70k+l/TYhtx+W
AT+21wT/l/4m57/yd+bvQc/W8MdXrR430Y+/TyN+r+y0KCEh4r0vwbOhH7/A
PFdejP3xOSvxvflH+e49c+Ln12zg99fS56beT/7+56/FJn83IGN07/u6kUPp
N1Ypj6yLkfnK4/QBsSJP8+GjjGLUhVpPPvrwUW4L+kxbH6uxfmr8Sp/N9uCc
nWppWSej5vD8n6r4+ykrf/DECfhR25T2P+ehZ8TTJD7QPJFG1rWBD1S8tVYO
8vuKt9YqCG+r8wEeVOdLl8ryvgJPbr9HbkTU4B8Y9EXov4A+rH4Wu+TAys8i
T15vEHXQleiz7I7egz07jvodbfFK4tVptmGPyLoebfd9eBp7XORcG0ddj7V/
FvzLjS2J/8GO0nv8zvnd6yTn+QdwYu7aJEJfWbEGkedUfbqLpice+xHctZI7
14OIn7zY66vvtkv2FH0LtDs7fHLjj5jkoa7s9uU99Rb16a+Rf4i8PjjG/3ib
xfUK/4n/1OAr+dxzObHDZi2izvFBGYFjMZ/T51rZ1YHrSHy7ffmE5BmQ+Zda
Z8m3Bk317Wtz1RL6P0Z7Rv3aiyHUZz05yzmyeRu8RzKvp0e9jZ4JAufg3L1F
nuVTyc8CJyXxaYE84E+4dPsTeUCFSzd3tyR/p+K0x24Sz23yMdQrN8eOp44k
zT+CdyeAx3iZQMbTJir/RcT9zCzYE+bVYmGO57tY7a+jx8Pv+uT2p9TExRb+
g7zJMfLU0eJKHtftZb3jtW/5g+X9/H63J44nrtfyvtRL1Ksqudv3Ae/briC4
oxZp4c8v/xS8Ryv8aPt7uMzbyvhehmvw4y0dm9krt7ZER//OvABevj34E3fS
bvTIia9ivq1eRYX9YLQJFTwP9g89IK5zgvpra9o54o0P64tz2Yo1A16C3QOw
E/Y1Rt6MumyrJnL7g+RnUjzPBahTUnLn2/fcfnkzZb9jT2sGdujr5dR3NOxF
3PXLcvyO8YlLeOdZn3adeOOICv56yapZZF2SQTw/X0WxX+zo36lrGL8F/7FE
a4E/N2IuBkdXulBK+TziZ+4eBo9PyuZBXrn2cj58YXNSJfHKnQMpwe/p2/3X
KQFPppHzchrf+ArnOddPyrr0BPmpe5qyDH49iRvXM00WcoUbV/61nZF6WOVf
qz4ddrZh5LVln46f8/WKP+f/5OslD4l+dZbMu8m85MRbrJ9gySuo+HOGdgVf
dCq3xG/A/2ldgj9N8V/ZyePxPJL/6r98B/eVeI/Lz9OKeihp76nnUfaeWWSZ
sGPtXSN4zjT0G7FGP6cfZcvk1F0OR1+p+LbVi7y2im/rQ7Oj55WdUzsdfTHj
9S7plTuZ4W/UimkSF/cL+z1iB/jTGyfCDqoein642pD9OUXW0a+thJ7fsZt9
smW4WEf62j4ifq7ygPr4r9W8crf0J5E3NL+YxJ1WbGee7y0GdzpsHnZW/BHw
EBbMTtzpyXJxX/1tLs6dU+/J61ttxPcxUtoCT6bnnEWfo8y94dXYlR4e8keL
xb/bpZBblYeAv0+zQPz5X18VMS9XP1F/ffMV+qLgJPJjUd+yPpvMpu/Pr2fI
Qw8kf21umk99R81sMs4g/Q57IvJFzahjSct4bXUO6pJOpBH7yTkQW5wv5ghD
5FkVb5jlXhH+SIA37LcqxCmDa2BvzInG852cQJ2rxLNpg8ADGGXXkd/sJuNF
Fb4QBx8Djlr1GTGGLhd1EG69ZNj7si+Jm60v/vPddCIOHPglDIKXo/0eFbcT
P3PBKuyVCGtKeuVarIzo/6EPQ7xyY90J7Mh9u4WeDJxT2S6DF8r/TNhTSq6X
+UJdTZVI0g5Zht96SfK0L5tQ1itXPORmERc9dH86uN+idYeJ/PXmlbKuUPY3
n9YC3EPyPRm9cnPTe/ggJkwMEfOg9nXrBegpydsT4LOVvD1a1euGV27kgufH
7Tgl2Puc+r1inHdd4T0I4Mqe0i9WG1w5ue/6fw2lTlLy9gTsT8nbo1X/JuIJ
AV6yQzfx31tvE3gALdsI+CiO7xPnq9mhCDj5VJ3Aox7IgP/cIj31KE0Y7xZM
ibzPZhWPF3aIfnArvJd9ZB+Gm5LvtFhl6puOriJf+Yp4UQC/NGyLrNuSdWFa
q4jiObb48XVmkWjYUTPvKfuCuslH1A975OQvnyF3by7x8xGl2Y7fm3piAd+8
dchKPE31vVK4u1PfZfx0BvH1UnvgTy14Hb7OmOnxPxWuYNlk+F4GR8GeUvHG
nRVF3MG+AR+XETwY/6jNVPSvrIvXjh4HZyHr4hXfhfMuOnX76rxolDGLV25d
S8xzP6tPvd3d2QLX9J89I667V/ZnUXEkS9Z9SJ4Bayn8WopnQAvKKeMrh1iH
y+JxLr6MDH5Tzpv74Bl+X8WVkjdGzkOem+Q5MvyTzyu3IpzBvj8keb8uS9x+
9DPsl+wzsPeVndMsqnh/q3Drcj55j40Cv20+gDfbztiK/TVsHnxw325RzyLt
MdU3QcmV/abk1tKe2EFRZF749eM7oh7twyh5rlGXZM1cR//BiKvAeypcbvN9
4ruad6dxXuc6KvwU/dojzpUUr8C7HZ4ErrLwBfg49B2c20Wz0xe+Gv107X8y
wJ8n7RBza3v2+z9RRd1NgGcsMTzkztZD1JeHwzPm7JyIHu9Ef6uAPT8SHir7
0UARlzBmHWd/6RHgj5b9sIzaQ9G3krfKHTsyu3f+3bBIwj60p6cM8n2Xh/mJ
Yze/lccr14+WhWehTkniMs22874jcoJneFBI7iPJY1/xK35QpS3wh71qQR2l
+w5el1Rj8cviH8J/3JQdvE6aD+CRayM3uhehn9N47AptP3yS1l768lgRWsMn
Jv1Bt+OvxElk3lNrDH4ykPd89kDiZiUP/P4p2IW1LsLD0/I+fR/qpyOO/yAE
HrjbyJ3CU8kjZc8Jj8e5SfCw9cGfN6LWKs715T46F1/E1Y0RC318WU6qZdg3
E6b6zjs9yUVwcZmzh3rl7thJ8HtMS4hfK+OQxqz2Yn6c3lWLe+Vu+bTY2dIv
VnXlyi+2GkgewvToMfMudXFWx9XyXJPn9aYS5AW6zcFunXSJfgS11on5NJs+
kP6dPB+bfxHzZiWOC95S6edrH4n3jdyY0zveqjiBOFHZwwW9cjeG7B8n61Xd
pQXwO2S9qtliEPEDT1823rOoqEfWz1OPZtx7xH1LTxdy49UM5l/GP1Vds4pj
K/5Yq2JR1nnbSDznPnjq9DM94HNMxr7TS6UV8+AsP1HdO29uP4v10XAWdt8B
nsdc2DKyuN7t2DW893UOhFC3srsC8lWMdyZsF3EEo/BX8HHKXgpLo/N8LvrG
boheSlVK+HvOoCrUjzScj53cIBnrSg/UZWM310B/6uc/4Z9+JD5mPaF/kNFk
MuttmaybzjsB/oKnEYS+ciMpvmKZ78g0WpzbTtqJ8Ba+q8I67ryzrHd+nEUx
sZNX0UcgEI+avxo+6mjT8Tclf5FdlXoNu3gt+JbTzWT9rxvgw3+q8QH8Z7uX
9Ok7XAh+78/N2I/3FlO3PngselWn/5Zz4lUd7zy7hcKwT3Yv8Mmdh9h72sn4
db1yrVxp7MCU/4rxar8boXOYl+iHavjGX5+/WeDQVh3wyfVa4dhX86iPCOiN
RFWwtxrQT9PsFEv4j0Z82eej7jLRF8JsNZ19UYs8nzu7N/p16TnwQj2W4rdk
lLxBCvc7LCX284pb1bxyq3Ef/KKY89J5n0f/eznn428nffxLTorx2I1Zrxf3
yt3BN8kTNYzgkzuFf+G91jwUz6uvJT5gxpH9c7fd5T1eXsLvrjGI/fKv5KXc
gNzO+LfwO+x2xTgft+Zkv8h1q3ARgb54EhdhnY1axTv/1pkK7OdSkat431fr
U4b1dPKx8JvtjQZ5rp3bqafVtGjyT2FXW3PhkbGCU/viMGYd6uHNJblreq9v
NQD34ryITh5f5ve1/mvBmevbJH8IvFLW8CHIP+yS603G3wqeoL5Tyt22+3r6
5Nuz05ckbVni5w38/PZGvyDw0qpOTf7cyJV8ciN8KvkZVfd6dAZ9rJ2FEm9D
nt0t2l7E3xUfqcLDq3o3s1o07hOROJI2LW9EMT9GTHCJQ18KuT1slqjf08re
F89r/PKec+FTkODp88Tr1JvAK7swEuv8lDwXbt77Xfg9hyV/55ld2FHd8sML
J/lzAn3Z/pJ9rs01PrmrDRb10arvTICPQvadcR4UgG/vijxnKy/A3pb9aAL9
zWU/GrtIBPqItpL11MVqvhLv++C85OuQfJtP3mbkO6yX/Vb8/KjmoI/kQ/d0
Jt83sLJP7u5Grue2Vf0gs9W1cg/+zvc1uxisr3arqR9/UwN7L1lH+HBkvYxu
1iUO3J64V6D/8uZ0L0Ue5e6DCt7n11+Xxe8ZPUT6d+w7e2g+zsvX5ct7xxv5
c7EfjUTkQ98WhAdm87Yw8V3at6IfheR/UDzz+p3Y5GdkHyt1zpopvon8jD4+
gZDbxVYLPeN02sv9nVHkWWad5tzM2l/2/flAPCf5a/RA6pTUsxxPAf6tjezT
tyotvFiXc7GvT4wBF37/CefACeRatW3Ek6tRhxKwQzJV5P83PYGeb0k8xzm4
TsR5jNabZd2Eib3drazAHbidX4R45ep97cjLwYUqu3f1Lvbvg6+FvHLj4yTy
eg/AtSm5tmsrfqjMo+kf8MucL9+ph1L5NeXXS7mdY3lt5qkv/cR7Fievutmt
zXPqPH/jOPSnDdnjkyseb2v7ZvC8Kq6bJofAFbhB2Xx+lt7hvOjPovct4Muv
WT0KEp9qX4k6fYUj3X0e/fWwQXmfXNsXJuRTLJknQq+auY/Cm13+Y4hXbg/8
VfDlumuel/GNT5Q58n9yp1miUN/7pioWRcxb76H4fdKvt2J1pO/dmMqFvNfR
47nsnwwjic8pXkTZL1L9zJGZ0Z8/9u9/48ygR8K/cyrF5nyMnYnvXrWbOGf0
r+xfYxt8zdqjNsJO0GaW4dwPnwf/Y9xhp6nDlfnlv/4AjxdUhTzMLOLAPzYc
cvmcP/e1VHzaej1wBYpPW/2M2sPgo5M8b0brltSnX1hJv5sKw4hrnNOIV/WT
/csuTsWulXyqCu+t8gVOrBzkgZU+aZNf+Ef6rJqVvHJ97TL4cPZ+EvpNfS97
dl/iTWOeBnvlWqs54PP3Vyc/pL57vPqcO1PP5vWNTxos5lmvGQe84gWHONK4
I+iTNS/FvnHn/sO53Pqo7C+6C3zEetlftdk39NSCnT4+c6dxJfzhMasyMT+/
E6+uVAU9nrC+sB8C/Gn/DEf+dpfw4yxnjZhns+8Q4Yc7mf8WOH098k4h12LE
JH+QuBfnu9x32qCK9Jd8X17McyAe66YWcRNzycWqXrk+7Tx82pVK+uRG8/Xi
OYzDY2U8SuYNz1wl3l2rG/wztf8G51NtODxOaf8U55o1d6WMt78DbxaxZpj3
Od1hk8EtF93ve35jq06caWkJn9yK3gk+q7uH0B/h8ZifZa/EPP/4iXPfVv1k
f+i9n+TwH0q5XlTix+R4XeIT7Kom+06tW4U7PREu4jGK90NfF5f86MM77Kdf
thIPfLmWfFXEJ/CCXJkh4l32xcji/a3IS8H1SDyqdu4GdkzlgcTDdj5tLq6b
7ju8P0eH+ubBiREFO8cp4pObIyMJu8jOsbi8bz5Lvxd8JspeCryXtJdUnZrb
pYLMH1GnZqSrK/iCtAv5sFczvcF+XtpR7FejjeT3eNgW/yHKZ/R3t1x8l29l
RD7V/nsccchXOYhTlT8FTutBA643/it64/vETOLvfeIQ77mzD/63QePAj2XY
HJvnl/b5mqrinDD/1PH/FH9OPfpiGLOekd/e/Jn3/RYu5E6tT+D3pB5wgtcJ
vkR74Cuf3Lp4Xawb61Eu8d3cErOJJwyNS732iNzES+fMRR62if5Ysn7WTXNf
xD+N4AP4XxFnYocOik5+6lM98XyuNYFzvkRFzpEc3ZAnbVbWKzezPSDfUaam
b7yR9DTrL1aM8z5845vD8DCvnS7yFEquT8kB/nLLAPpXDmou5I5xh/0SmpLz
v0MTIbenpgAvuyWy4CVQ9YDG8snE2R4fzOiTr4wA78/wzqm8cv1YX/Zd+R5Z
vM+jbZlN3GlrRPqcqnqWPuBZjVFHfXUo2jf6BNsn94d45WaFLRL39S94UZWP
HhiXOOG1HTm9cv3vtuI5zdaHfXK3yyLyJYMHCvvHmv8UvNmz7vg/74Ilfkbq
yUgjyf9WilHEJ+++grj8kbZindq/0A/O3jgW3NIvvxBfKRbC/qrcGpzY2KmM
/zuY80vGz80ig+BHUetTxs+t2LHA7Z5gvPbRfiHi7eOGCv4QI+Zm4sllitG3
KcWdt6KurvUlcCab9sOHU7utGK+9A2difqsLL9Bd2Ye9c3fsovvfhP+iT14a
X7yHwjtd/PSPqO+LWo84mHWG97Xpc6O1usV+VvVlH+MLvLuxrx1+p+SdsIdk
w86efLu0V64Vgn/VNBb5x69dQny+axoRJ9c3Lkf/PO0C30rhf4kPrMHuNU4e
wC9t3UbyBUn9uTBpmJA/WJ3fJx95QMj17xv88pvdwCHdakLfogdDed+DGvHf
asTJ7anNOa+rESfXZpvERXtlIC+foYE41+ywqCL+qZ2KwPPP7sK8bcoOTuRv
ea7dhQ/cefpc5A3c6jY8zvFHYY9Jf1kfjv+n+GbNl4fEelR6Q7evkOd7MoA6
0FO5yO9fb805p7/GLpD1IE54B/rmrNsm7XD8EdsiXuy2pk4nID+eW8yXHjRc
xDED8yb7tppVivjkzsLaMk6x/TU8VNJ+O28I/WWVOy7OsYAdEj6W/z92D/HC
bEOpE392C32YYy72cIEh8BM+7IC/M3MK8fNB10Q/PvNwC+TfEsLLnXMO+/E1
fBn6wLnUx0TvhPzJfuyuAfGo19m6m+87qLHQM+bIu6yTGK0Z3/wice/aSXJ7
50cLHRIm3mdExiDD817OyNf4S1bxZF6523Q6dTgx5mT1yrWUfdBX80fU9MkX
rRL2nJb7p/PuzyfkEdakruUdb0VcAx/oXewTbdIN6tz/fkq8XdaXqX4Tqr7M
eivrmKrL/vJ/lCFvEWl7ae94szZ+rB55ejGv3IpAvl/xfmiV5HUk74d9HH4G
typyY0h79O+wARm4jszLNwQXYk2YJuyygN0bOQl8jBczBfnk3T7Ddyd/evId
fJf3S8lvZb/EefI0D/UU3a/Do1i/t/D7nfh3iZu9P4S+q7sspni/vMj1ml9Z
P/J9Vf2del/93RH0fNP94HiPtxXXtUaWxK6JepA80aXW8Lm3qkIcaCF+ljan
o+ChNY5InMUV4iHm9pLUDy7hHAzYD7PLETexL6j4gfg5x6hL0sKSwIdxcTl4
p3/Tgo+U9URa1kbE12U9kXuxcVTxZ5XO5BOrHaeO1T0u5E6H2uBONeQB3KnM
syvcqXl5FbxESW9gJ5Utgn8Xayvfv8tt4t+R74Fvn/Vd2BXa6IXkg05dFuef
aU8G56ns6ov053LeLErslVvl18F/lKWpz693ejcR86WnzQPv3uTHIu/vZH7A
+l6xlTovlVf6soM44ZUlhldu1VjId/q+zCd3F3cBNyN56bVDL4R9qHjpzXRp
xL424+fBXlrqiOc3UneQPKLSPpkznPmKGyz59+R5Wr81da1j+5J/C7oGz0mC
4ax/6deoeEWALzrNDvz1PhKXm9MFv3dV8giuRH86E+Zz/izYmY/rYL85+wdS
//tsQB6v3By1hXm/Nzm/b3zvjSJvoSdeIOMS0q6rM574/7V6Jb1yvXoDeE5+
/WR45W5YGeIbYa3EPOmSv1q/1o/8+o0DErf1knhFw8vEXaMt8sWvtCElsJ+6
W+jL1sk5x89Vxx9+91cmcZ36G8EnjK4J3rrVURn/kfW2A+gXZjSXfuJPPJBW
9cHsv7PjyK+VPwH+vdx+/KDcR5Cn2yLs8v/q47zXN8Ilz9WU6SKOoecGF2Gs
eSTrdHbgjw44gb569yf6S9b/WomrinVlPh0EriLkKzxLqp/m0jjinFP+S6Af
q+rL3DuP7M+C3taacd7blwfl9cr13VmIa/093TfevN+XPG89/l/gHJku8z6y
/7vSV6r/u5N9EfE8VcdXezd+8qS0qbxyfeA5/Li/t2T1yfNUiiKeR+LnA/kO
iZ9X9cJmEeqpVb2w4gO0Ep9qI/4u+7AYaypgDyh/ahR5Xa3tIBnPlH7ZlVtp
xb8Xm17eK3cvpgwS4+cG+8a7J2Sf+qg2eRCrFOu2Ul1hZ1iF0xOPfXSKfFnD
KcTR8tOvMHC+xJD94C8URm/1vyfsN8X7auxpwLm0f7SQG9ngxzMKsV6stsOF
/L86AjHPke6BM/plDfb2IPxo49JT4n4HB8GfPJj+106zY36/tSe4d+NJvTDD
85zuNMnzU+VwWa9c/xoGn0voRF89uxv5PPutXH9fPbt+tBW4i2FP4ZlU9x1B
f3OtCv0BA/sol8TrdkmP33rWYp6fdqY+bWHOEPF35dcka42e6bqUOFOJ6vB+
DOzJfO0ait4e2UXIrbX/su/qNwaneTobceBYvYQ9rZdOD+6jY3Yht9pWZ/1L
/hMVp1X8J2bfmNRvKtzvuPK+Ok09y2P4cmWdphGeo4R3vDEuOf57lUU5vPNj
pQ8mjh1/RSavXN/dgTje9jh5fPJkJX39mlUeJ9Cv+fOfPrl6Tv0sPCF6lpvk
fdrBE2LnuIteV/aANUryp8Ab9jMeT0vYEjxSaCL4TucnpC7y/6PrreOstr7v
7zDI4K7FgnRwdw8DzODuGrxQ3J2gpbgMFCgSoLgUdwkOZbBSXBrc3f0p533O
/SR8f8/9h9fsprm5J0f2XnvttZuWLu/9XqPzV/LHmzdwjpxinlv1BoFvKzxc
rguFh9sFpoJPt2P+2yfzgyu51eAPB91gvWdFnyjQD1F+rzUVP8B5UIe69vwJ
GYeoG9lfemYV81x79ob7FF8o4n33US70YGPvxX5sMnVhzcb75rNboDa468/d
Dd97rFGM/NO6uuhTRMzGn8+SnD6MmR+Leauutxu0J883cGuoz75rCvy5Lwt9
djfHYvrLbllc1mff8B6cVIcfEsCvIjeyvxyc7rfL/r5ajflS3y4Lz99xFf7z
0srgDBIvslIf5/y+Fh7qtWs747GvDR9b1mffTn8pbdWP4notMfXRVtqG4Ng/
teH501MfrQ0ozHo8UF3gWmb8LHxvI/RKVH2B2v+/ryfVQ3LxvbKe1Ln3sIT3
92qlqKPXbs2Fh1YlKb9Xt7DLfjbm4IRcP1nqY3/6R+I8Er89Do7nFl0Pb/RE
COOZ+Zh4v9arjaG+cS7yO+Ob7DbzYlAk63dfmMD/na/NyQ+Xk/6h1Q4eo6zD
CviH8rwwgycKHNjUnlA/cvYL70vqvdgSV9djSd38s+N8711bsJ1xa7y7tM++
KY+wO1eH+a63xmfjuUN14tFsN+AvDf/hiPCThy/AT4sl+YHNRt8SflaUOawX
6ee709LLeDU3dWqz+oFnPr+PLvrdNgJPCMznIzr7ZN+KSbx2Y9Zt1suxOim9
dmtgXPj0Ua5yvkicxBhIfsj+4WRxr93MfzDs29968b9Lee3ugDngCS/mC93Z
QP5xZGL2k+630nnt7rIujFuaUqIuMmDXewq7+XSIxMP99TtqPtjdm+Gnyfmg
zdaEv6p4uU6fuGLfdQ+uru4dT8ugf7qVC32FgJ7G7Kjkv55EQQcl2g32Ycnr
sJ9Ogg9eKgi8N6iiqCPQJkUN99r1v6k7MJKs4xxU9eDtfyefkiM81Gs3Cn0R
42ntbiLiFCv5NeLlnE9E/lsbeg6eWtKow8VzPh4t6oLcafCnAvHIgoXU+3cs
Rz3apcf4yfmygFfOLoguY1hTcb0R5xfO2VkP0JHdQT7UDD+SUdgjwsCtx10D
F/rpK/H5wzH483+sI76oNQl99hzXqLdV/UQGzoHXUXkcfSvq0H/EvOv48rPq
enfRKa5fV5c6uBTdqDtI2Fz4ve556oW1aUfh120KA//a+Qp8ZuYh4tOkbanL
6/K39LueynqBXszvD4PFeDu5p1KvsekMvM+mK4gTVRyRYorYr8zZfcv57rOs
kNS1p55LH/UzejuynstePhu8tFh0cN9CZcV6cIwZ6EPL+WYHT2P9B38UvBHt
ynWB4zm76sIPm51Z2O17j4TdbVqGOC44F9f3yyPseosi+A+HqrA+5Dw06gfj
hzdoIuKMAP65Jym6WMYI6qSzSL0aqw18Dtm/z51dGv9G9u/T5lRBvyp/a+Zb
CDoASg9fT4s/o/Twnb/KFmLc5Pz86QN55O/6PSn8RNOz1/Jer98yxX5t3Klf
02t345UWfd3MTxfqecfTOfCb4K86KzL57HqyavDb3s/w2c2CNUU+211co77v
/nOnkA86pNX3jqe18RS6HgUC+VZ4sFGlfsipoJre6511M4l/pB8b8DPbbKF/
QkhZ6g5fXGfcvjymfmPdEHB3qZukhSWjnn+EW9prN+JmZB/ZXbqYz56MOEHr
OiXU+zz6uNycF0mMsr7n/GUauNQW9JYC4zAuUtiNe6lCxHg7twR/0BpxElyl
6FrZD0XiA93mwg9fL/UAJT/cikGfcu37fqCSp/ff+eKLl7XoKR4IXkjM/aHi
+gTP4QGGfRA4kdmYuMbMfwd9zr1vxfM5iSxh10ds5/q/W8JTkbxH1e9A8R71
dL2ZF/WrCnxPuzsSfK9BdupZ9vBezCm7wOUSFyjpHTd393rihXlVfevOTDOK
61cwLwJ9XqoWEnkmfd416l9mX4AfUqY++YXPo6nLzPUJHlfBfPjPsd6L9agP
+oz9bEp0wEtOQbejaknh19nDE4nrrLd9xf6kz8OulaBe9ZtuofhX6k3pJ06J
8VIfo+80VY/Pfjd/gdCn125Px//sLvvZFJnJ88hz1s5BXx5nSbbSXrvC591r
FnUVyp8Zm4h9bF8I7/84+T6lr2hdR5fVrA//3GzSEj9jaX3yIS/GU0fTqSH2
gqFif1K6T/aM7OAGiUv69CEtA36g1jWt5JPA4zK3tRU8T/2XxtW9dqfrTjG/
jU0RPrv+3ICnvumTbz+x3s6m39yfbj3vOBhR4KHZVXf57G7qpvBDRmiVvXaz
yUXqKIsOrei1a2sdWa8x3GfXE+PPGLlP+p7H3RJJ3JrnqohD9Z7RwHUbhqv+
LOIT0B+T7119zHWyblTmEfSiXWv5vjfnVPaTBtt9fpe75jz1tBN3+uzmreZc
L/WrA30kZR9Da05G6s4upqReaeAKzh1Zr62uV/o2Wru74vc6L9Oiz7m3MH77
oyG+fdsxl8p447zPbpyR+nFFP/v2f3tyDq6PE0fyEKn/0ntT36pwxQAuIXkR
Sp88UO8cuRZ7nVfkMWQfQGd4CH5SpqPhXrve/VaQuL51WnCD7Y/pq5krI3rI
Uy+T1+i9H7/3Vmv2gReT4Qn8mQH99iQZOBdKxfP9Xq1pd3hHCWvin0SdD589
2CGP03g8/QmDRgjdFaN/P+opeqQkb3trlLCrftDGuULo7LZZ1Ur8XaEy8eDo
Duxbl9ILu5mvODjaxQnw+W8nFXYn+C/GecN7fodaR5/3wFuL2ASPwNTZZ2Lm
EONkdazq22cC/Ja18fz+/Pj6gldplJ7p8//N61fFetfW+eMFrWcE/eNU3z3p
L+nPtsX6f9mtibcEnqun3BXuu/6PT/HE35KnpOJuxVPSqt0q4n0ed9AZX5/x
wHPKPuOqD7Wyqz7U1hzwT6fYdPze3u/ZT236/JrZ5uInZ+1GvioyMtT7e90k
yUUfH63ZcZ/d3rX3jeA/rBlS1nf913pbvl3vHt3vi0/thwXF9W7iv8PE80g9
ATP0jdRtNIQ9gGdWfEWdfD94y+aj/NTX97sEbvUTOhnudNnfPDQ9+EzC784X
yXdy/vyTfhHZZf+4Z/OFP+J0fiT8Ujcxdu10402Cp9G4NPW08rxwKhCnmCF7
qnrtehMTXZoZ8annmrcbfHjqdIH/6sWWwH/otZ6+JK1nk19+VfVH3/sKBd+2
5xxJ4bVbn/fCU/qlW0qv3f1d4gKv57JfjHpAvXmG7sQjU+IJ/9eJXEZ8JD/m
4NL5fffvM4p654O75L4keU0NLuMPvDjPOXKrTAdhrxmXeuZTA8mbpCgp7M7t
r+y/Rh/qOLcdRT/9/Tzy64v/Bg+8vYl836k2Yh47m+KDhxfAbjV+iY5usSbg
TGM2y+v/gAeVgr5RARysWkH8jBXh5b12a99rdLL20jfVSfhW2J2tg4lLPwzG
D908HJ7q0HkirtNSbMVPm3YZ3aTLOYn3spjUx8t92Fq9nbj6367kT3ZOEONg
H3wr+Qk2OmQf8jLOG6gHNBcWF/6CyuPrTasSj6eO/aCMx24sLiD2azPt9DS+
63/blFH89yhHQn2/d+wo1nUS14cTWrmGEUc13uG3p/+DuLPtGXDWB7sYT4O+
G/rnNyV813dd6sPxAuMvcTz3xV3qDvu5vK8+u+HtyX7H6nrV71gbOb6k124U
/hLK//+U/l9qXZTYSRxd45cSXrt2Q+okyDyFMz4d71/mKVSdu+IFqX4ceqal
4AfT4BWYBS3yx//mp37x5T+c+88vwysNSwJ/TfVd6ntC6io89umV6RXLwWOY
f6y07/ol5AXsVbVEfZx9sy28mUj4EkqPKKCTL/WIlN9uhNHXXvnteob0vry5
0d8B77jSgHUzMiV59maMi/HmA/vk9QL47Rt+5nztWlHyDGXfh+514Uc121TO
a3fjLQGvO9GAOvf8RZnny9ejN7c8tq9vghk9Kv079i8TfpeRriL7//vX6Im5
Bvbw4uzPIcdEXapTd4LPL7UPXEzG+1tU12ffVkDcx+6fwm+fP4R6VXNUXZ5H
nvvd8opz3/llHPl8yYfR0j2lH0GRSvQNGd5V9JFxqpSn/uRsC3Fu6JOn0f8x
b150mbZ2RG/n0FTiiwxd8aM6lBc4qua2Jh65LfVKfhoOvno6Av3S2/SH+17v
V+EbKm/r8bfhxYXmwT/s117ohDsn6sJz7dsMvDBbCPb3M5kfoed8OK1zhL+t
OhMEbycQ79jx2L+UTleDxK3E3z/18Ol36ekHiPvb6+PCD3/Leaq9Lsz+PzA/
13cujc604sFKHQBrbe+aXruWcBt6LDvL1/DazSy2yGdb54P88ULBqTHE30PA
LcxP0dinMqQXcbEz8C+Jq0i8euwXsf6t3o1q++z92pLnHrXZZ3evJYTvNDaU
em1VDyX7+eqFZ/p+l1PqDnqzw9P57Ob6zeSlRlbw/V6jTUW+d1Na6jLeZWNe
xZuE3sH4roKXa5zLRZ+joG3ogfadTp/bkXHpcxRrhbDrC+hDp0dDP8qMPRH8
5D56Pspud4E/pn3nl9ozVot5bIys5vNLtTyzwY2dKT673SaL4B/YE1qjD6r2
4bFd4V3V6+Tbn80288iTjNwCvy8+57jxgy3mg5kuHzxldS5kXAmfvMdWv31A
BPPnZXiY1+4MPs64ybqbgP8s625UXkDZA3mBTdHxO/4cR7/IV+/xf6ZPheee
Iil5W2sk50usH8T1moZdOzoff7SF1AV5hh6v9f5f/KItJjoD8uPEXM75uOZ1
Pq/dmJSJPOiqmoqfRj+OIv3Rx6ipGV6727FENe//r+zfErbi9ybrGuz77z/F
Ru+iDP0lAvmd88/F/HNep6zitTv7+oDH5d3uu96cV1mcI/rB9WJ9WA9XEv9O
iUr+KFUa3nPSNsTRlxpxvl2DN61FVhbjr9/Pz/75oC6/a2YO8R7tCKV3d5q8
01d0jN2i0ck7n6Hvtl1qxnDx36XelNWpCHn2fNidG92os5Y6eUpvU/vQEv2T
Mv19dfpmJfpQu//eFbqVii/kLkeXw51+A5xB4canmgvc2N6c2Bd/OflKUQ/b
LJcP79LuPQP3bT8o1Ht/40Qe9PkXpqngtZvjgtHzl/oY+hbys0ofQ+n//Beo
cR+p/+MM7JHLex/94m6JAyeUeoyKN1KI8Sw/W5zzgX2v5XXmvdQfU/3vlP6Y
MeEV+aVr8ArM2e3BBZ4ybkonXz8VQd3Www8pfPa08K7t5kc5pxYkg8+Qah16
zlnn4V8oPoPUc9akn6m5vcAlpJ/pXKnAfJF9GZy82chPdK1UBDv9F+xjeYiH
13YOFeM6KCf+QIl96E4v7ca+3uUlcU2st0L3ymjcmHmSzOQ9zpgs/ApnqibW
lx1FSyPu32IwvIsr2I0o4PxaM2n/4xcfD82ZWwYe8Num5b12N9da4hTZ99hW
/ZHff0X3eBf9KLVq6E44L8ty7rrbffNZOxOdfI9mGvI+1At+pC7dWF2MeK3n
RupyLxQh/t9eTPUvYD85iF35J4F9VfInlX8S4In955+I3zPqAXzDTxFCH8BJ
lY197Pv9WeJyhttE/GutZR/Q3jckfohCv2W3YxHW17ajxAP2VdZlavoFGM2r
iXyiVbM3/TFipEKP4lYyfv/WhdRxy4/1kr6xzpK95G3LrRDv3dKoZ9SPdQsT
v88oC265Owlx9ew/MnL/4vh7twbiv7Voy/ikph7cKNIBXa+L3Tlvs40Vdid/
hLAbm1zxfgO82eTvqTc48UNVr137KSP+c5s9lbx2O8rO7I7m+6Th97H/u5/R
gTc/yfNI6sC7u7InZ/zleb0zHnh272NZvXa9YU7ikLfsl5paf3I/1Rv/I/ws
7f6vwi+3biwFN/mppuQzXkPXpdIu9JpuFoOPc3wOukCZq8OXWoT+a4APUOYW
9TWHP+BHT1vUSth/rwB/MecnGY/8IexagdjwksfFVfXf4uM0OgvvtGiXql67
3aG5wFm0rrO+uz6ZwCWcZVfQ6foQLNadu+ZH6nPX0JcksG8Plf1W3O/W78C1
Uk/Sv96NqAb+R6185M2l32KvLIWezp0bIk5xHk1kHg7u9VjgaTK/bxw/w34u
8/tW7yWMZ4Yeok7ZbfmaPGi3+tSN692FXbezsQ/Y+8HLa01ogf2isAf8FqlT
bcXQpX9D3eh/+xj1cJ+pG3UKB/KY5G9k3ajVfjX1xwrnXHqXPHeCM0V89o6d
WG9T71UxvOO/IpxzrckdX57BfL0cPHFI9Mpeu16nEPjP5EmFGU95zqr6/fpp
i3jtqn7ffLyE+G/pNjFv3cMz8cuf/Cn8Bf3DCjFvrRsj6JM4JEjkAd2vV4Td
LT9T8Zt9OgN2NE39Hp8ugR0Vuzu3u8DvA/zwiem+oOs9O4XX7iacI/Qi7EJB
nG9SH0Y7FlvouuhbEoF3fkLP1jgUST3q5nLUV40uDK9yRB74eRkfUn9xB1zU
tt5w/fOoIs9pPuEc19OnYV0tdxOJ50t1rpW4f/buxOFxerwWfmfF0cJuD09F
Xn8t71fLVBac84fk4Hpfj9FnYWFf4sQZl9hn8lZGJ/LsWWE3QvuB/xS9JfK0
dsmNxK3Hu5OPm1WWPNuxOuhMNj9KX6Wyi0Qcbf4l7c+qUMe19g/sR9Ftts/S
N1ytX+d1TPi7av2WQTfA+rSD/MGe6+hgyLoeJ/NO8mQDqetxH6ckLlN6OLlW
MD/n74Pncpj9TQtqTT3a//ZP/IH/zuPv7Gm8dqPaQV9cY1a6yj42bjr+cGB9
BWUU/9boHu616z9sE36pEWUxdcSqT0STddRH/N28gtduLIxGPUOyfmJc7EK/
cx5VX44/n62AwLGtOb3Ry3JjkR/M2UfkgcxLfdAfO3SbPKzkA+u7fgPvk3xg
7fgo+PkKx/u1bD6+NzP6e0pnOEp59sfPD3z16dabSfByo/v3H+sddi1yHufI
VHQL7St5Pgh+QfGW4BVqPCfUBq+3f63gteufilAP26R7uNeuNd0reeoPqKuQ
fqYZmRbcIW1vMc/1QWUFPux8Gc58ehZT4PMB/d4LeeBXLDiMf/6wEPhP5/Hg
bo/ewRNR35tvbZD43qPbfPGvvaCo8D+1vNmlrojsm/AoQYi47/VS8NdGPKQO
N3UW+qw8l7hlCni5VvlP7JPP4I8bzxNgP/SjGG8j01j6gCi9mshI9E+i7uZ8
k36me+MafCk3Tgmv3Rx6VOnzBsv35dOh0m2pyyTjAqN7D/bNpC18drtpafim
Mm4I2HcSV2iJd5bz3edCN8b3p4vEQ2fl/jbvC+e+rCsJXC/rStzFD+E3vd05
XNx/1Uixb2gpKuKnnN8j7M6sZ/A/jl7GnuYx9jYP0Ll4XBVd+sLZhN67bX9S
cTv9gPbnljhe4MP8vRfXZ3fGvcBf/SEB+rFVHglc0hx7E79X6StuqlvM8dwn
0C8m/YFCXrs2p7/YV7UVwzgv08SkXlv1N6l1inko45j/znv2wQnEM/pHznn9
A3azNP0trDTdVF8L+hAseiDsRtz9Zb3PY8b/zPm0zwz12rVqr3zPGejDovoA
KnuJTq3E85xfL+ITc25P9sMlQeBUz94Iv81uHqui73uzfRT+Z6A/svpe2R/Z
rRfh2ye1fi/xzy+88l3vvCwl/Ehn0Fm/PRK/0465X9YdzyQvGfaBOslGubAf
G865vPOtmCdmQgscQNZBaGdaZhTjO744/C6Fd5UsS/6oc/IiXrux62/0DHPW
pY90mqYSdw0V68ds1455ePGasOtvurKu1txGZ0D1DawBf0tPepL4WOmn2VlZ
1x2odw7oxFY+DB5enTomZXfyyXrYUVng2fapK3kXjcCrVR+HwLztBR6RKX+Y
166X68T6HNbzR6/d+PMV8+16piQ+e+wG4jpz18yMXrs5KYh1vYhzW5sk9Wc6
54ffMDGCuu3pkgcVbStxxIpSIm+vT+9HXWec1+SR5cecUU3Y/9sPsdc7DA5g
NxR8MGvQM3j7t7IxP3cuEeenXWEJOPydW+zbY6+AK+/rgD/z22L4tinQ4zKy
x6IObtIZ8Tv0Wodaif9/TTjnxFm5L8Y4LOzWVHQT3KeG4HWbXQtjv72CPNQ/
Y+HTyroSN6fm09ML1KFIvTWlF2dE3SfsSi9On7GSc2BRN/LbozaJ32PvCBPz
2mj4E3XVx5vz+zsQX2hB+MlWbl3xeCUflvPdfjeM+pbUlTKK7/s3r8C3jb6f
2R9KLIaPN1zak0QR68G+8KefF30khVjXRm3iV6XDpuqAnN7oaim7qtOxfroO
nhF3Bf06zx4Xz2Ev7AnPbtsgYdeM9uQRrxcMFc9522jP+P8mfr+VLzxM3Efx
3oPTwY/5fv73m1XRa9fOLxf7s7uzDnox9wxwu6+j2Ld3VgPfvPiG8y5XzFbi
/pPO0cdn6W3hbxjPi8K7G31CPJ+1p53gp+iPyUO5DR4JuzaqrZjnbtJiXB8v
oLtIXmDjipbyb/ExR70r7/3b2W5w3ciyCp+jj0yWZ/gTMc9gb9QZXYWdnFNO
j7zobq4pQj7PLgY/si3njhZFE/6N+wL84hue8e1fO0j6yWGPooq6sAWfhV9h
3h4k4lk7zV/oR11p/oP3Oa2j9CUxzmzL7Ps9iS+r96I+BXzfV38I66lFaCvx
PSXOgwtsa+PrU6DlrAHfZkouXz8C+0RuzuPxP/nsZsdc+MkOfSCVH6LtBy91
azvgeJ0qC71MZ0kl+AYFS4aKvxVPZtg7MR+c7jXKeu3OzGnoUt1fZXjt+gh4
C07SHqy/rgOZb0d7EsdpNXz5X/0W99EnTyavUmCsGAc7w3D6wozvSD5c7ds3
UoLznB9XwWt3gzqTh7vxFv/qXTLyDnUPqPXPqP/vPPX1EVP+pLIbpxPF9N7f
jqhAHmfVDrGfm7Pp32d9vEE8kO4cfDDVZy3DW+KNKwepY/2d6+2Ur9h/3sIL
MBLNpB55ajlwidhL0B25NAP8rcMS/MsmF/DrX8s6gqD+vG9Zf+rt6ySeO884
/lW6PX8XFXwwZ+vgol67vmXjW6FjU+5YIa/d3ZSZ/X3UC7Efmi3u0G8olPWu
5z+WUTzfSvoT2T36C7t97meRJ9df0efI2HoM+xb0ZvVRweyTfWIJPoozcyS6
IKpvRbs7wu72rFCI93GKvkjPe4tzwq3ZXZyDTn7Wo/4L69FZvQOd+dENwKnG
HoVHPei6WPcqjtaz5mYffK+V9trN/NOFf2VmTAOP4sos/LQWz4gj8mUGj0lF
P0EryjZ0FO6OF/ioWl/ux+th4u+uZfJ67cahNtLewqf3op0fiP3aBnGeuZkk
n6pJG86rNOHYwxz0kaLXFvGt0h9TfDClP6Z0zAL8MaljpodMi8n3yrgpfq7/
n/lPfzrrxTP08VSerkpczt+8mYQ/oPI7Wh/4SY75S6h4TrlerBs5wP20FsIe
0LUuvR/8MMpcn90dEA377/FlnQ7xr3V3SQl+71/Ed+lfi/3cabQY3Oz9B2F3
HsRAf6fSYoWbiY+z6qdM3G85PLyUwdSjPfgLnHT8LOHXOXnIB5pfiTucF+QF
nfKdJa4OP99oxXOaxzb77NaNcvDPQl5Tp3V9mnhfdi+p59xiNjzaf6aiB3hn
MP1rOi4CJxqzl+ujPPGdK+Yfj1k3fc+Bf9unBT/EOpqZ8yNd2rTi7/LNxTlm
lb2FvW9D8b3WrhLk5VX+uskR8mVnY8Brbf0zfk7X7PSbe0p+J6BDkn0YeP4i
Wd+h9uGq9Eezxx3A7yvfv5W4fn1+8qi90Lm1ek4Udm3jJvEe9AQlybOoOGhs
HrFOnCOb8XO/G0+7QGXwjw3opRhpgsX4O6Gdfder96LFXx4q/l7ZSdSJu+Oz
Cv0WVX9hlYkn8jWB+gs7o7Brww5TV35xMHWsJ++Idf0/vuI+eFE/v03vtdu9
ZF3lgINi/wjUFeaNlPV9ufC/hrYgnxjjLXmfcYnoE5E9XMRN7rAZjMvCVVL/
5CQ4Uprdwm79/MzwvhetDf2H3AMlfXarZ7sw8RzRHpXx2vXisg912lr+83rL
r+J681HmmIZnPPWv7J9OO6l/LPV1ld6y/eh3n11bIXXgP7dFB0z1p+g4kLiv
xb8Kb0cH8h19TbRsc2R9EP6A/etOce7bGU6U8Nq1FbnwB9bnkn3TqqATEtmQ
vlQN1sG3PDcX/0TX8GfCk6FbJfV29IeF8Q9+vcj+OaIAdYLxbuM/vjwt4qQA
3hVrAePzumQ+r13bPoD6U6k/r/SIlP68dXYs+62q85VxkNHXAgf49yI83h2J
2Rek7pnat5XumX6qLrox7f9sIv6/6evxh2PSZ94Y3krEiVa06Zxr2ysTX6+q
Iezm22jUAxSyRV7XCT8BL7j4B+ote0SX+Wv2W3t1UXgA96cW9drdLQk451Lv
xO+Q88o5wzp13ctlvXarTnnW7y9n4adkAYe0lu4Ex1d5BlWfGEoewoqXB91x
VeebaAj9Gvv9Ah6g9qXfW+KH7+uIXpGcz8aeQszbl4PReyvXnPzpmJWsk9Nn
xftxCn9Cd/DGNOKdt+ipBPzbn5vh995OBL9PPU/cG8RXsVrG9dqdhHtYX6/p
q6hJ3Ng88gG+3ZRAvyfw5PfMfztKANcSdi2D7P/dXsYpKm7dS5yi76C/iXWe
eW7/cQ2+xOpK8H9uL5M4Gzrm+tU28MdbtBF+hF5xGX74wf3gbpXvgA8secG4
vW5IXl3pFQxOD6+g5IQiXrtzvw555eyNfNfra3aQP5P9pAL7lewnZT6J7bMb
f5zEvq5rPp997lr0kNPNqO69v7mmG/zDRidqeO1a7svo9dix0BdR73HJe/C3
Ut2pbw2S/ZL2fBH6SGaJYPgIj8hzabHDg8T4taU+3jiyS+QfnJGriFPyLiC/
eTuxsFurBjJ/phyAF7juDHz7FyZ9U+oOCON3wd/WMseEz/poCHwwpde9OC58
1oeJySP37gUv80/qh42aTdEbKfoEf/tdraLyPr4+2oE+kvJjJz4dqJsT97tv
i3PeukXdnN7rYai435kK5LP0E6zTf+8Ju3m3qJh/ZraLxOnH0xKft9gKPrMl
bysxPoPBZ6yxzal7SldouPj791DwkGRd2Y/XlhZ2LcdQ7DOKwgfLuok+ZW2L
gTvIvlGqblT1jQp8bqOnrb1ZzLqV/aS0YOyqn5Q1IDr4TcGy8MP2t6ZOI18/
dJmehqnnFnGCp58C+43kIWhBBVjXBceJdWT2CYZ/2bs4++HJAbz3nffIt6YM
FfiNfaA28UurZ9RVjp0vebNyPmx4ib7luQh0NT/Ct7RSp+S8qVsWPYlbV8Q+
bOy+Bn7QbC7xxRbszt8J4HdWRP8sMP9H7hR+ibMolc9u9p4g+DhuwZNh4j7K
HzvrUE919DL1VyP2gF9Fon9qzg5lPSQkHtEu1CV+K3qS66/f5/o12cC71nbP
4f1e/WNq+GpfLmXx2rWdFaSub2Rmr93OGVW8PyP9dvqgVTrC+1h4hn1pZDH2
te/wN2NdDvDQxfQxt+6i2+OWnwqeWKo8fvirmOCcUodE4ZN2geHE3TXRIbHS
oVeur/+ROsRpicCVzx/geW6f5lw+kkWMp5Eohlg32v5b8BqTDgGXUufUxpRi
33RmdCvss5fsDF4w8nN+r918/V7E56ZeLMxrd5eOZv5Inp4VKfPIkqf3vf6P
OfRX6hSmdPbtt+54qQf3nx8o7X4/sBX4quqX5NyGd2rE/RscMUiedxvoq+Qu
HOn389/fE+vczp4k1Gt3FlD/o32pKtad2g/dZ1fgtbwC5wnUt66V70XPWtF3
fY5d5D/ke1S6Q0pPRs+wlf2jwR9inbq584r157Y6yL6QaB72fZ/x2zMORUfr
h37CbpyWftroF+gzz6CPzDc8RHxf4uHkQQbEAecpRP87u/QWkQ+3cmUQdkPl
WWTfQLUPqL6B9ua/6EO1+K2sJ9xL/UKMyfirU8/x3Mfni+uduAvKecfB/kA9
hR013Ddu5sEnzNcKWcp77cbAj2Hi+RoG/HPq/5/JPpVvZRz85St6qLJPtPY/
u69/tBEm9UelX/etr5n43j3N2G/jpyK/U7QPumHf189KHrU1oBn62bI/hZ5n
rqz3KSP17+Xv/QherOIUtQ8onSi3YfuS3nF248GzNUpvLea16/1jU8dTp5Dv
eqNUXnQmB9Rmf4i2gv0801j0ZwvkFriacQS7U+U3sU6t1P58pbsMnoHTKODX
wXMrFgVco/xf1DeoOpFCr0Vc4dZ6RX5WPf+YLOAjBYaDE/4vnwI/aPjpnMJe
PRO8j1hL0GO6lVjsN/q9YHgcLYhb9Xqnffe39qcWeJ+e5Tef3bzK/HT7Hhd2
u8IXnqdwMjE/jaLtfHVqqt+l+njzPt+ew45bjN+RlLyP1Wk+OOq0u6HCLnUy
nXkzhF+i2+uYz83g8ap+rNrdquDZjZOjX1H4XRzx/N/xewN9WmW+3pJ1Cipf
r3SZ/g+O+iK11GuS1y8vx749iH7EZnRZ71Ad/Nrp1Iz5qPalkHXoPcq8mNKX
cHNp/N6LU+F9RWM/0UqcYj/p1Sel93rrBHZt/wGxn9h7KoALNQ0GR5Z94e0s
2FVfeLNnJsULEB+3IPuCnfpMGa/dXMF7cVvMY3+V/CX31Hriz+xjynntThMD
v3PxZcNr1/oY8BgTXJZxolxfnVJSjy3zPuZPNvXjmwqDQxV8S97tNvUp5tiP
Yh9x6p727ZNaZ+anY7zAnuIH/PBmBakvut6Fequ57albabFJ1BGYR2cQR50d
hX+VqAU6g0+qgJemmSn8Drsk/XHst8Rbat8L8FqzNgrxjptdoXSY+P07rlDP
pNbpPKnvOX6hwF/t4kV5X/sffBX8lLa3E4j/npx+Ps6JoKjf/jVaddaE/Up0
8bv0iT8Kf9pt8BK8Jc4kgXu7IamE3XxzjzhB4tj2Pwvg0TkfVD6Z/eejHEfJ
/9IT4N86T/B3rRjY1fXma+z2vZjFveOvN34kfq/1vmsZ33uZMwI/J90goSPy
P14EeQjr1EsxPwO831t1iGfixeQcf3ARvaAPLcDVI9GJt9bmQncoxwl0hGS/
ZndVdmFX/Zr1UxvF9drQz8zPsw+pd8i+V9jNAxt4/gubqI892Yzfl3Ev+3yM
w8J/tl6XwZ9T+/N7+HN2jIElfPYXb+DPGfI8VPZXz+H3b1N4glwXT4dStxu8
02c3Q7vD8+t0V+ZB5Lk24yD4S51gn76HeWEEOE6Slz7cQ7vS4L3I46S6XNBr
d3JuFni3EynzfpKPYechL6gXrsp+LPuwmz0+ifyn8S6I9d6zobBbDVOjPzyi
GHlV1Rfg9nShC+doG6p47e78IPKuXxr77Fb0JvcF3/9Dw4S+5x9TN0S8P+kP
BPRUlT9wLDa8gnSvxX208kH4M+d2VfONz4JD1DU7qcS4mvsiqcvZHAo+f9oS
cYeRnL7Y5kF0+O2Jv8DffAsuos/Dbt7dIc4fdX8tsrqIz81FUVT9BfFxffYH
J9E96ktO7BT3N9o8pg9alxrYB7Pu3Kkb0ANZE8777XGM+rbWZ+U8M9W+Dd9J
xaWyD6BWvRP6NbIPoNIjcpr1pZ5D6hEpP+H7ugl9bkb44L8dZ70NXUH92v46
+KvdZR/kF2dFnOvs+oM+YLI/spU2IbhHyzjUWzSJDp+vjyaewxq6Ezw2kroM
q2I58Jcbk9BZmvGBeucDR8OEPf0RcMjsn8HPN33m/d5ah/9ScwL+WXhTUX/h
fAgW32O0Jv9kTtmVlfdQCPvQ9fj7S6aI/Vq3/hG4fSCf23Qi+8CZWVx/tA7z
aOtqsV7s6uQ7nCWlyHvWbwaPp9BL6quaD0DfP09d9A9fNBR4oLmrN/v8+dEi
TlAf534m8jIXTXF//c0qzqNZqRi3cxWoZ4gXDD6v5nOqxCI+sn57WcZnH7MS
nGhteFmv3X56V9bVrJV6Pui9KH9YGyb7IUrdGK0nfRK13iPEev1v/8QPmVeT
/agE/Dv9HeegKfl5zpNKId7fZzQqQ1yzfba/XiTFBfxnrQV1DfI9usPa0U9v
fkbGb95b9s0rg+FD5i+MH6L0jiLHk2da8ZPPrjeA52AMX+iLg5zk1akjGLhP
1V/AQxyyV+h3GUuGV/TaA364ZsADkvwQTfKnA3WBSk9Mxj+B6wN2rg/o8HyW
eryNGop+G4G+RUpvTep+62+CwWnyouul+mC6Uw7Ivg9T4ddJXNHqtEXs50b/
ycJuFieedUbvzijuW2wt+vvGgFDxnH8lJA/6sAZ++udewh7oG74RnQXVN9zO
acNLWRNX7LfOu+PXBS8/6Y9lveOsuZ+Zbx26EE+eXCbx81gCd7WlXZd2Y7Ws
I4u2CF0KeS44p2+y/jfY4V67W9oC9+nzFp6nPL+cumXxP2rBE1TnqfXbZp7v
QqjCMcBPIh+XkO+Jj8pfyHy3OTeT73rtSQ76bnY+76tjMvpUEvGF88PfYn91
ImOKuE9Puof+XznrZvHareCC9FH4t3AGr93MooWI7307UuG1zMMvkeAgX3qg
F1tV6jRO+wzfUerAq/ha6cA7WZ6yX8n9VktVAB6pzJMq/9CIORLe6fVLPv6D
Wz6muN7qCE85kJeJgMds/lxcnAvmHurf7Qj0g+yv8KDV9U58eNJ6l3LooBco
QJ2c/NtNVkPgb47qL3/gEvMsZnlw1YM54SVu/0CcefWNWAf/08/vJfLjerXY
1J0pe9T1Ane1j5Up5P1ebeBsePOS1x14zk/0r9WGHffhTlaGn0U/ZS3seLhv
nIcUeY/OarDUWQWXsPdchG+d6bQPV7FKtgRvTLIEfFHxNPrXDBX2NC/DfPZp
N8HnzcXoFzaNRz1+/qUxxHNIXMvcGko/OIlPmrE/4F+E0ifOungc/KLuaHjy
iWT/uPCWzGd57isdM3Xu24MSsE8XOyLwf/v2+uvUeQc+4Jmy7s+p1It6hy6a
8AvdasOJKyW/0lZ9Ud9RT+qx++pM3XG36O8hcUU7BbxN++0wcJqn1GXbQfA4
9XHpFK8Tvyga/7/7sZCqZxcfPWU9dJWjjwB3kToY+i3wBeufMsJuTh7M+6gZ
Bd5e9SYZGIcrvN+za8T3G/VOwcuTfp3zb0viqjJXZH5K9lFdnYX4qU0T9CWk
v2fbk8HFyjcTfkEAH4iYBx6T6Heh36a9HYw/+fqT0IWxO85Db0+N893K8JOn
paQefBP5FCNpf/Kn0c6Cl6u+b4fPk4fOeaCA1+70vSH2JeP09eJeu2nUF/UO
ztORIv60o4bTX2l6J+px+i3Br1J9RSPqwwu/DM8r0Le91xn8gCHkdQP2wWkF
PhWop5D7uaqncBtKHq98v1YMl/xxx0dSZ5r5bzgt8UdXo3fiZmrPPI9XW4yP
/bhvRkP738eqOJ/9beDOHF67/cuP8PlX11R8S58eglXmRx8P0z3Ieef8tc7H
19aC9+AHX/hN8TCpa76/lDqCFd/xM+vnIu/lLAz79m+Ar7WiCPFHF/Q8lb+t
ne8J/m4mLeK1u5l3s39dvi5+r3VS1qN9+BQivu/aaBHPmcepX9M//Uk+I3pW
sd6M+9i1jGnhvTxbJea/6stgv6jDvP6lZHSvXf/lDedVzSJRvXbjRmH80zk7
2DfHH2UfHFqO/tnPZoHTvrkv8zU14He1SMk+JvsAms+XsM7DbjNuMt6x3mek
X8mZvj69HacveqfOkuc+u7l3JPP28Qfy66qv5e4g6n9rJfbpHBo/JgvUiXjt
VuFj/0+7M7oBeZRYDzj3lX9eOxN81ImZiafk/mDFa028magt77EteXmjNHl5
41wy9GlOjCKvNblpQ/H/j82HrlKBAozf9GbCL1EffWAU9j+ph6niZXV+qXjZ
qXdU+LnGfc5xM2ME18t6Ke2rrONOr5FPLWEJ/0gPIZ6yF7Unrp1aLsz7e63K
HfFT3db+/MK77OCDM+v48hHulpPggUOH+85fPd9PAi8zUz2o5LU7ug2/sUap
al67vRsdq//zXhJPEnoy39u1Fhey++zdOpPPvAn+oB+r6ZsP1qUF6NWslfwL
WZdkzITfZr4K1A9St/mKOkF1fimczX3xFT9vNOeV9oX76H+TRzOf3gWPUf7G
qQh/vlvuJ05kXOopLmbMaHjHbUhJ8Iox7BuawvHCO1EfMdehTl76S1oiqXP+
0938PvvCQ+ASA9Zk9dr1bkXhv1X4k/eZU45zpU/UNY/YWs5r10ITYJ/XTvI0
mP/u+VoijjIORKFeSs2fVePw235oWNlrN4PjC7ve8lgVr92o0IC80e1JvvNC
5Vn0rxN8/aGs4+Ho+8u+PNYi5r/qy6Ptpn9TYL0cxM9W/Xqc4k+xq34912sJ
fEkregD/JpOMa2rAJ7E6XhI8Q3dqviBxXeom4ArD+8O3z7YCvlzL9cLPD+TH
l+fFbzq7Ev7Cdu5vNLoDPznEljyy4+Ba/z5hvHb9Q/y29iR1c4mjoquY5D48
p1FXOMfXDQEfamyI59DHHxJ2oxX5Ni33vFDDO/7VNpDnDR5TzmvXdhv+eKpx
HPwXmd+xtuWgvqniVvS7G34N5DX4vbLvjMxrfNsnxd9qnvy3T4p/b96grrTX
XuZvtGDm9bIr4GlSP8Fa9yP+4AN0Ye3X4FHaifvwnGQdlv3sGP9d1mEpnp7S
61N5GfUJ9PdU/eU/mZxHY6j/1W8tEvPn/9Q9yfvoxeW+q+LTgbHE91ljn9Av
I0cJ+Cej/gaXr9MbHuCGUsTBN5NhP6rwCekXrWT/cYo0FPMnkHfoOjRM3D/9
z7714uScRV63RjXfvqp1vgPu+dtdXz7dyliGfjZZm7GfTIkAz59B3bLzqIPE
Y+X+k/YAOLnKx6r7fzI4/yflEfFO4Bw8fxX85FlwBa89EE/t+CL1HIhPnbgt
yefVLheLcZbrZW1xoT+sXXzjs9spI4Tdqp6B39MzLjotpWoRFw59wL6k9JTS
tSE/efYf9Pw7dMW+Ngfvs/Fo+KdKF67Ur+Bd439Dv2jJD/BH6yZm32s3HZxT
1h852dbzfUu68f0JRqH/kHYrcULtdvTRjo3ejt6R/IQef2gJ7ziY7c4x/v9e
KeYfnylhYhyezeA9ZnmJ/nOmkkJH1621jLr/3/qK/cBOFAU9xJyZ4XH/sht/
/+mf8LQuPUSvce5neD0HjnJ9zU/k8RPMJu9Wqrm0X5H8B+odrPpJGZ+u3cV8
DtQ7nB5G/50rSwp6r7db9QL/i3mUOuB/pO6T9E/0aDN8/TG1akXBkyvBRzYi
MvJ+k+dl3oztB79a8sDtBKM4b4vWFviNdfkRvMcC08Q8MRPTV90uPUv2GZd9
1Rv85cuf2gUy0lf3rw8qfwru9+5/+TW/XeL26wqQV1e6pt2nwRdtTb11QDfg
y03ukzaE/ntRppOvHFmC+PHNUvAfVZ/7Kj08lR6xCnvttn6WfSXz0vxeu9a6
n0+fSPPE9eI+IZraZ6ijbA1fwZqQyF/H+e8VeMwT7VDf+CzejF80c47Pf7GO
H1M6FCnkv+zjGrolqh9TAA+R/ZjMffBQ3Kjyef7Af7JW3FR5N+4/tRc49udy
Uj9IxnG/jqTP+7pbhb12tx/XK104eyh1xAFdONVHVenAS51M1QfZmFKP62Uf
ZLtSf1/dhFsKnbf/4t9Qn/3uEJFPMd4299mNCtTF6KUqC3sgLzbpJfUmGZP6
dOCNT9Hpn/JyoxhPc/40/ISN6MaYWYibDamrY/8O//h7vTvtKPPYvPJG6fGI
j6vlxu8ZPLew93udclnZ5/af8fVntKa2Ev6xhz8pdQLBx+13AV40dZcST3d/
TOzrt2O2lDhD1Rn0e/lfv2b0XBK9Kuy12xEH2XdKty3htVsD6rHvRHf+Fji6
rCNwtk6I+//6XmNCA/KjpR76/HmV77CPk0+3HxMfqd/j1Py5oHfc9C3UC3xv
V/vG/8kXyPFycufO671e06eyH3Xogl592ubkU//8DX/oQD50Np5PRy+o+Gvy
TjuCfbiEVaM389J9XMprNyY34JzW4Fm4F6cRF9+YBg4o9Xbsf7ErvR2rRm50
OaROqV6HPrxO8r4+nSUzVgf0XnIvwy9sepTzbvdw0U9L/1naw5rwu/5IJfLX
joVd8TGMbHkEHqv3Qw/EGXlVvF990R88/+WLPM+RWfTv7nQS+0D5foOx27Ha
4U+XauznveRfzPxcGCfc+7uMiHT4iaeSS10UcGn9QgbsD/v69h+zILoW+vNm
Bb12vVNKzq2X8AKMaP75r71sy3N2LiR028zIueQ9u3YkrniMzpu1+22YuL7y
YslHkv2OB91ivz10soTPnuJH4UfpLy/4+inrfRfyO0uWreB9Tm3kK/QB/qcX
JD8GfIJOZ312O8N1eDVji/jOBftqAXRj210W56upZ6UvVZRDgg9m7xxN/UmX
uOjOPb+CLuCNTfm897HK0O9N73gVf2ZwBNfn2S+u1z+ik22tqUf9bKe8Yh4Z
K0f7dNicwaWIVyugV6Ol6AjulO+hOHeN4FzwfftOp/6u5zN4aauG8btVf5xu
x8O+3cfMu89XB+Q8SSXsnn1P1n+zzr+vB1Hv3RydFZ7q4Qciv+zMHhEqxu3F
ZHC4Q++F3UqaQdjNvfHg9Spdvuv5ycOkX0UcFXKE92sPwY9ydkgdIfLL+sVK
+A/TIwT+od9Ljt+fZBHzuB36Fup6d+tH6nRur/PlbfVyTYVfZFz/m/ku4yPn
eizi6PIZwUtTpyD/eHMT+9qiqQqXYN9LPEvgsOailiW8dvcgvHY9QYlSPnuu
vOJ73Rf/+nRurd2/wHP7NDOX93rz5gTsoROJsyReqi/dSl42VmCdck6dSCXm
iVumqg+ndb7kRx8k6Vwfrmt1KkIdabbs7Fd5JP9hYA7+bX0avsH1sfhhS98K
/MEtVwb9Opmfcg9q9Kf79TS6kid2wM+JvQTe7N/ruV//5cKuBWUCZ7ueGP3b
lLKfVPNhPL/iecVgn9EPy3Mr4J/y/Mr+/UfhS66LLpmRbhj8w1PwHt03tYnP
Lu0BZxi6nHOwfEd4jPciiXdW/UafnfKlU3rH2XyMXfVJD8TX0r9yQtFJc9qT
99QfoZNmrE4l6lzV/LQrnOP6lJV/9NqtrOhsG0Xq++zaZ+az0q92H0n8U+pX
f+v7Y3ifR/b9cf46DQ4kcVerb7aM4v8v2JM6l3IlRD24Hv8U50vcQ+I5Vd26
02gT/nrb+Yl9dr0muE/oLl+9jDnuKfXUG0+i1yfnidO8CM+3JgX1UrIvgzmI
88B8MsBvT0XeXeG3ZkaZH5H4raobCuQTP//EeVOvjPJbeF/LWL/O9oZFvHar
5xv2tywJ8bMGf6b/WuvH5H0lr1XbuBl+keS1aksaiPjLeJUcf6XxJ/LIsu+S
Gn976gDy079TP6hnyAvfacpOyfN+yPzdkpu4Jegi6/l+e2G3Xp6kv1HNucyT
qWPASxQesqWS+B6rKH2ZrDw/UQ+yfQznvazncmou8tVzWRUbcM7uLs95MWwJ
72tEQur5lkv73Wjw18e/Eu/RTiTz+HPao29zdaM671iPWa+xfj+s9+lVWEGM
gzOxsS/edNrht5g9etH3KVjWmzT6gJ/VbAL7Ui/s5tL5ok+682e40lHh/g0f
in3HXFnVF68Zp86I89pM/YO43qpNXtLuMxOcYmMO3t9JyX+7JfvlJV0F//hj
NHgZZ+uLdeSeqcV7uxREvXlQXfKYc/z+kv1rSt5PsoG+cXA3yf6PiwcoO/t2
UWlvVqGY93orHXGfqu/WG68WPG1V3630K/TsofCylH7F4CgiL+Z2KgNO+r63
sBtLalKXv7sU9Y2Rh4Rdi2iLDtGzYeCBw5eyvuwm1B/1GUNdw8u35D0WLKN+
S8Ypxu+xyHsX3YtfNwG+5TecWfw7sxB5cKm3YFfbKc5ts8NF8f1OkY7w5O0v
Yr+zDkf4rjd+hedppDryg/d7nUQPRX2BGTteNq/dmhdxRZy32esK/yTwCf6Z
eq7Po8D95D5mp93Pc24IFvuY3fQRfLPc1LkYKz/IfJzkofUYCA540R+PqLjv
WwQm7Zz7TalL0UdlMrzXGwsHUQeS977vvNamNBd5YXeR6z+vo/Shr9Zv7/x8
1Hr087a/tKnstdtBReEDx3CV/j14ReEqUeGHtIWHNpNzxLrQH93JODt9eQQr
JfxexaMJ8Gp6yvf4QxfiTL2tqNd2yxelLiDq1rLe68161NUo/9H6Cl9Cnff/
h5+mzvvOM7J5x8fOWYI8tcRXlW6kwlftJHNZT3PQq9HmpA4T9o/wkV2pe6Nl
Q8dGneOB+g7VT0Tib2b4ePKGEn+zIkr65pXTxJL6iYfQoZU4ub4mHH/jync8
6hrkZdzZqeEryo9R8ja43JPtvjp04zT65PYN4i/7uzo1T7wjcbD/o5ua3Ws3
H32VOvDST07edrOIZ8flLu61m3pZ+Eh9q8K/HQt+7gZNgX8VtZt4DyoeNJOA
O9j10I93thv0/cx1Cf6i7E+qeNGB/qQZJt4U33Ponjj37dJxOCdV3cp1qUup
6lYaoqencFdnRl7O+4Oyj7DSE4t1mnGQ57L63sC5/G44/9+1HuhmjE/E+FyD
Z+TUXNdKfO+0ksS959qK6+11kh+YsIHAs5wJfQp735eegT6Ibplo8JQV3j77
B95fg0sFvXYnS3rw5AXJfXajPn0VzdgfZF8z2e+g9knm7T8yDyPtVurX8ClH
xmO89WLo/FxaR/7q2rtKvMek+Hs36TOo+JxG5h+EXfVb1Oqh56FHS8nzf5R6
H5vv8V5+aAU/YdEa8IvjqYlbgwfAw0m5mXrNvNnpt6jynkVjMS+rRcvttdsJ
ZrOv1k4r9pMADhAtqYhLjb9X5PfajZPnyKfc/Yu6W5nnNWtnTyt+55oB8LuT
H+Z5WmQR56bdfFQdxieE8yj2oRBhH15Lfu9SgZO4vRfzXK1ySv1ycCRnCHzj
b/Xd4necPyb6YblJXyt9BD7SrvpYu4Pmw0O4Sl8q634Y+fT/4lDuQ92WikOt
pZcN7/2N3gb5wazRMmJHP8SqPBZ+Rfq8Wb12+80+YXcntfJdb797z/UL97L/
Kh2zHU+FXY+WLNRrd241hIdwUtYvquur/Cv65Gl5+pT32deuJw6/cQl8Wu7P
ip+pFajMuTKNfdiIGEJdUopO8GtuUcehmw3AB2S/Y9XXKdDv+L/zS/z9Pj51
bZf7k8eM3hNedt2cxAUR9AEx83GOmVszwr+KyTmnnRuaz2t3tpNHd67NJZ97
/h74xtrY4vvMgzLuSA9fyIl5Gv+7Z/ZY4LToj1lzgvDbT2svBf/z0kTqance
hy9U8x7xtdIxKwOf3+gXDT7Il/bUodf8RF7hYX7yVpV7DBfXTazJvvQneoHu
/enCrqcAP9FaNKRO/Sh2K9crsZ7trX3B22WcZV3IInj/2rRsz/Z47Mamluiy
PkS/Rz2nkbmL6EdpL11Y1mvXs/yFjnnGCrxHWediJ37Mvhf6pxxnyYu+G5v8
y8WD5LHSJkIfLBg8Uc8Qh3PzJnWU+tfSAnfVohDfm9ew2+dWC3zV+juWzOdK
ndUf/HoLxh7y3UpvwXpP3aG7uJDQzXDH7qKPb57B1GGHTEWfNvFk9EPTj5d6
dwXRhy/zu/i92sWHzPNCbRgfmWe0ujylT1++poxPSOv6vuuPPx7ovd7OXQ2e
aMqJ1P3d6YwfMuE+cejrTvRZqzCHPGDaWPANjy6lnndPsxBx/w2p8Ze6T8Ne
6Bp4XIMSYr81ckTAozs8AJ1n+QnwvbPuo29Iha2yj7zU0zvYWZxn2lwn1Gs3
23ykXvfEgVJeu3EkXNj1fWeYR4pn/tMo4cfaOZLBa5V+uF6xGzjVyRKpvXbr
Tgr4z0XD0fNXukaz+hL3yP4vWqDvhgYeVzJQD47f2xW/3Cm3l75Mt7bg/1/4
mvmb3WyOXoWbc7u4v151CPnNgjp4wJRSPM/tEPbDbDvpx5WvPvzDKLeE3Tnb
R+CTplaG3/VqPHmfa2fIO8lzynmVFL+4wQLiyCOjwFV+rgSuWXoh9sOdsP9e
WdjdWaFi/MyD8vrRh+HxzNzl74e+Yx7xa6rl4T77haHoD/80pbLX7uSvxbrd
Wgq8RL2XOj+K92heaZfLa9dSxAwR43LuNnW0tdKI/dMsWpV4Z+Lqsl67W8vG
vjZ/Sez92H+G1KDOesFS3/c6I+eL3+mkWiftzB+3IHUKVrT+1AHVaog/I/M4
mlWa+ll5H3NlZuqthiTN77W7sUuK8bQ3FYEvKu+vlY0fTdz/3Q7BL3J/3Qx+
UjgSv7hISfBME96pOa4H9aLrHuF/z5J81A4xhB9iNigm9rcAH7Vcqozi/8sZ
Ls4p94jsy9Clh5iHVgH8c32IrCOOsxd9/PEOuISqN6nbEv7lXw998aBx/CP8
y3YravvGZ2sz8tGpKqP7srWLsLvP54CD3Ijru96NV5rv63ULfTKFy9Wfwr69
uIbP7s6dQl7mwkyfXc+fmTj6ZRfwsX1rGLfPI0Q9gnV9A7hMjRnYo6WHJ7q/
H++r4hz2sbXLRJzv/gX+bC/syXo8XIl46GBpdByWd2bezs/F+0oeVaxru21Z
7j//Z7Fe3Jyf0GGaG8r4D2nCvndjPnV1s2ow/s1PofMy+HZ+r93q/UXMKzdm
QfhsHSJEPYi2+77ASY2Yq2R8jb+nN9iEjuXjzujEZu7C91a6L/wo+5/78P3r
sN7tyT3E/HEb3xD7uTu9K8+/bBM83f37hF0v0ojfm2cX/u3jR6Je0Ik/k35S
Q9+BOww4h1+zpivvcUGbaOL5uz4N9b53Z3+oyE+ZDQbg1w3fIt9jJ8HnMKIu
Yz02zcE8r1JMnCtu26SyPkjuD+3Oi/3cSvdV99r1yTrXN/6K3pXqBz3jAnpc
nQYW9Nqti7fxf4re5VyLw/lo3WpFfjbzr8SVap/ZeSxM2KM4+bx257qsB5f1
pAo3DvQJ/ak2fWBUPzWpE6g9+d1nVzqBgbotpfeu6rYmDQaf7L+ddZrwF/Jl
bVdSJ3t2FLhNSG10c07TR8jccJS6lb0j4akWKCD4h07u7ugjJeM5zJAyQq9C
276G/hoL3rCuUtWHB9u1H/nKVKHUme+fjh/xvDP5x7vjxfjoSbeIfUNfz/No
/XbQ72bcX+Q304Viz7WB+S3xEK35VPI1Eg9xP74X793cnw9cdE88dEirLOPc
i1mQOqAuK8kDpMjNuhi4j9/b9ImYr255Gx6X6kO3IxbrNHZcyduU+iqPJ5FP
/xl9bmW3nJZi3dnmXvyy7Hnwl/KmYpyzX4vJ/ctw/75z6BPwcCp95Dw6geK/
/1Wa/siqXqD1xBBx/bSdmb12c2dS8ituOzEv3CPjqdN5MQzew4WfsQc1pY9J
5CDssp+duXWs1NOgn51WbVCo3w6+4fZzxe91FzZBD61VCfyJWAvwVwfJPsWv
s8Mz1+5wn2LoFhoRb6gD7zYbvF2eF1rRkYK3YD3RfPihE6UBcVbhXeTBt1Zm
HFaQ3zEqPBW8P/Of/fB2osQT545d7iW8aMnj1XK9oL6mywCul/pXTlx05K08
B9EVecz70u7yXszb6Eq5HTgv9Lc7hM6zceC6j/9pj90InvUdX91JQL2VebOZ
r65Wf72BfGbDbuCrzQ4zblkbKr49/qI8v1T/RKN9QngrKn+9ZiR5k1RP4YHs
3Ie9VDf4DLNToHd06TLjFn8jOFyKvOB8avx3VeJc67g/zGd/kJI6n4Z9RJ2m
se0Y8cy7g6Hi+YM6s+7Uc7Y5D1/xycqcXrt+7DRxe85H5HHkPNeTZxd+m/Mp
gY/fq61PWE3gr9FcVZdAnnY6/CujQB323Y7o7mqTkqAz++i1uL+19Ddwwp1f
yef9ETujsHeUvNB4/wi7+6xqGO+FOFH/XJ88+8yD/nHY8FHc3x5SBb3Aesx/
e1lL+hYc/sD6Vn26z//Mvp2xFH1IR2F3QqaRT9EdH05oH58N3teoXgWv3W2c
mPqlP03ZF+Aq+22a5uiYpOws7MbAxezPQ5uhU1krhDrHa/RHMJeTRzJqXoHH
GDGY/b98J/jG3aROmtxPnI2tmFe3J1EHt+kL8XL3juDUt8sU846bEZO+zipP
ZCUhz67yRG6ChdSlbs3O9QXOUA/uXia/E8Q+b+SuSr3q1io+fQxt/29iv9MP
9fDZ3QfRfPi1R5+B9XZ2NDpgqi7v7AHhzxu5kuT13sfusIY461NW6nyNRPRX
StSY/FXM38Fxu9CPyf2nI30B0k4m36jq0HuZ9I/L05PrS6Iz6aykr4kx/QF+
nNrPS49Cp/3uVLnf8jxm3tnoBUUZVM5nj0W/VHP7UZ/d6DYRPcZa2+W+yj7p
lmoaX9x/ZfNyvnHrNwj859mTUMPzHvUhq8ALcvQJ9V1/qAd8gy7bK3jtzsLY
5IcPxDN8vyvWJt7TZPpIqudx2ryAB/tbl+g8P3GoPfBPWZdaA7z27u/k9ZLG
FXluc+Ub9MDXYTfntKQ+JVZKX5279Twn5/iDdb66+P8+8EJeRQ33/l7nRjfi
3PlrQr3Pqec4/krs8xMziHPHnT2fcY6YKuIXd+AR8k2jbuJvPGiD/nnvVuz7
7crhP+9uG0X8zmhBYjwCcdyWGfyePmuqe8fNngVP3piWHr74y6EyXosD3yis
eU3v9WbFNMJvV/0ptPMf8a9kfwq9U+navvci+7kbDVILnEmdI+and2Hf/tbe
a7m9divrVfy3ahl911vRKnCuLC4V7rU7wZ2F/+eu2VTBZ38cCu9Y1mkGeHSy
TtMMXSP9EDmfJ6QgPi98g3Vc9ArvMbI6eZMPg8V9rMoO47PpDHU8SVx+R4fp
zNtrOfD3MmvgftdGgRdVz4z/vL88z3u3Drhowx7kFQoOl/NZ8paVLtyQHPiH
pWMwDk5sgZ9qcSpwLj3Ny3gW68V8GIO+tdWB53eCqXtSPHnr7/08p+TJa1/+
yecdB7NaVMarw78+u3G8CfuVzNOpfhkqT6d0pJVd6Ui7gxPirywsjh545zfU
t7zVOK9k/2jVx0F73ZF8gcKZfzlDXdWyVdz/a2eep/l6eAn/5uRckvXIVt1I
eKT6TPAe2a/KiuhHnvLUoILe680B4MbGH+fzea83YlAH4YxUOLysdz6eGvuw
fpyrcp67A+rir0gdRbXelY6i+zkKehivFku/eojKm1D/tnEd823Kkgpeu3Z1
tM9u32mGnrPS4/oIn8a8bUh9D4lr1chCPvHomKre5zTX7QEXrVfXtw+4OUah
81U7iu96bWdbcPYiu6kHOr2LOt86ayIFn0X1AYmcDH9G6qI4mceU4j7J8ENW
pAHf3p8YftY2znf7aRnyOzKvp/x/lddTH7chfDZVJ6s+6nqVb3Lyk6eyPhCP
OJ0z41dPoO5Kk32mnHFfYnyz6z23kKeS8bI+Ja44X5wnUcK8dsuKSpw+a2E5
r11L6sKflv1c1O/9pkMo7jP4OO9f+jNa1ckyX62eX50XDvylXTEFPhFYj6uj
EZ+03Xd3j8duxf4Hvdw/81EXlETyoJL24LxM0o36wSDsbvl74P9lKgheh7to
eBfx/xlv0fFIu5I+wrLPoz6CeMGZW4a+QLIvpFEvmD6YWxNxbh97zLo4FMk8
bkp/DiNZWt7LtFTwEkqeZP4314XdmHSAep91qQp5f687PS7nzchP8EkO7SGf
VXccvNbxUvd6FToYxvXZIv7Vjt1Ah2vxG3CeL0nQ4T/7nj6k8pw1Pz4E37uc
Bj0TdQ6eh//kLtJ8/oxxNQ76wXXuUP8Z2V7hG8QdU9M18N7H3JWN/aSeWd9r
d9tEB48bv8Rn13fc4pySuGvALnFXd04cn92KOkT4FVqOKMJuJMGPNdtUoS4+
SuLC3uu1jUG3Rf7I3FjA95wpikfl365FfM95+CZ9TxpPyucdB2tkF/yq/+YJ
7ykedtkP1PxvXom/Q+mDo/1WEp5wn6++fjdujC43xf6weZjPP7SvvpF4S6iM
u/Hbnc+tyfuUucZ5nX4356OeH9yvTXNfnK7tQLdc2+P67HbpctiPfvHh0vqN
8xW9428W7OQbfy1ndN/7tY7fpV689uj6vvvHGcC5XimIOhipZ6tHroWHcO8Q
eYAFCRif0TmInweOqOi93tjXX1xvZIxf0js+xi9HWddp+lM/2JV152xvJq5T
+XTVt0K7GYs4umkHvid0POMZWRXefJKKxfheWT/b51f4gedjsq6D4T1a3ahj
NPOF+Ofn1a2cB3fPwxfOV47xNzo+FfzTJrNYN8nk/JS4q7ErUH/HvA9Ch1p/
Q1+FQP9Q2Xfc2N5F1nOhr2vPaIv+4l69hNfuNCwI/2heCPWoUc4yTzK3wx8N
fgyfvHw79vmH1O2agwaRd1N1r0kj2d9yRU3qtTsLK6AL3KVUHK/dzJ5JvG+l
g6TWhdJBUjrngThU6py7BaL752e7NOSDjB2+fcmI2CXyiObNTeIcC+A5oQvg
0QUf9/cjCEOPUp2ngfpleZ4qXk1Ax1LyavQXxYgfK/aGhzo9teAnWB2lHm2J
5NRpdGsu+AyuNQmcXOHMObszX/tQ/x7ApYffYF/aNshvP9mc97d5VHXv+OhJ
son9QUtdmHP+HTw9N0kx6vDr1QD3U/ULRwrTd8Rc7bO72jCRd3AaNeP8LQjf
XovTm/xls0j4XRI3sCOig0ccfu+vZ2w7CD2Fa+jeKp0TO4VNPCv1hwP141J/
WPuckucewHlibbtMnqPSanDr5fSRcXv2Boep1An+2PWjfG/z7fAY6owi/t54
mHzB3/M5FyP+lnkE+rJpyQuI363nKyp5CLIv2+ie7LPNa+b3Xm8f/JO84YOX
8AN/gIegLRqLf9sobRHv9YrfrhtXC/nsIyYQ905pTd2j5KOa2UPR6TRT++zG
P4+ZJx2i+exWKhf/Ye8KqYMq+YSnZH1xRbOIz35jD/WkRj7f9Ub+gWIcnJ06
/oLStR5/Cpx08WrJM5S6uHVWw++urfJBcn5+aMR+Gj62vNeuPWzD/d8O9Nnt
Z5NYf7kO1vaOj3V2Ozq3q/b77GbZ9egghLSp43+PLnq5qk7xO/12Y08z4aeb
F8+Dg9Rhfeq1l4NjzX4OnzBqe/DwOOilqXzNt/Uu7tdjAvNE9uF1RrVgHAqP
Yd9Q592rrVynhcQ1PHYt4TZ4O8d3SP0c7q+/Kso4S924QJ5oXEsxTxSvKaAj
IXlNgT4OMv5V+v9aDPo46Dd5Tm3lj/B5lC6k0l2X8ZH5dIg8F7iP6quizrvv
9eo9fFFZ9wpf1Ll1wVdvbf489nt+qfy4XJ/Lv17c1E1FXtYOXwd/RuKrVshs
zpPab8CB5D5jD4kPPnk9dgHffRKHMP9bXSrotRsF4E+qc01bBZ9TnWvW2veF
veNjfd7Dub86ptThkX1eoh0Er8v8BV7rBtnn5b39VPCd3v1a3Xf9zD9FPtRO
MaKs73lG7qK+8sN7dCLizGsnnv/vfTx3nmbosMl6dv2fxgLHsK2Qal67dnsB
/JyvSQp7x8e43ipMXL/0r/xeu7b7AvHbnLk+3VRzyo+h4vudYlIPUPbnGhMV
vk3Pej6/1M7wJOTb3+akheTHjmahHv9DU+pS7h+Cvy15p/YO8p7u7tLFvHYj
Gbi0tilMrFunj4Pubu68+Jm/HGJebZhL/7jku9FF/Bm+m+VIvdCrez9IHT/8
oJr7BE7i5iGuUevay48Vf0s+mLIrPpgzc1pF7zhbV2ahXx0zrs+urawIH2DU
ZsmLkPvhtYT0v+rdyGe3+lG3Zbe/S1x56BP59JpV8Ie/WPAE40g8vNR8zs0B
IySvFbv78B77SVCaAl67sbQP/qfi6x4YJ+JWxdc1e0WDlx03JnFrzHVSh/wL
uHr7mfhRSfKBk6QaTl1kvlnYP6ymH7HURwrk5Vujp2/fu1faa7cupuWcuLE5
lXcczIIzwS0n/yP5sZxreuXfyedJPVi9chT8T1WXtK2n79xxmvdEP6eQzMOf
KEAd9MVy1FUvuokuQtTFPM+Amvi3a5+yvg8T7xtuK/pV5D5Z3/s81tEo5AGn
zfXZ3Wqx2J+/2vgbQxMKfSEr5JziE5J/WVFb2AP5wQvdhO6HcVjq192vllH8
m6WTsJt/Sf06Hbt+7JjEh6U/X3Gh2H/s3U3qeu16zicpvHar8OVRXrtW4yQ6
Bu3viPdu2j8wn86ikxAYz3dvxfX6nd98dm3Ya/Ll6U7g72WIJfmxjwTvyDw3
Itx3n3+jUQdaIhdx95wH7D9r4HcZ7TcQV47GbjxLAy4m8R/tPvxehf9Yr6jT
tB5it5aQr9EbD5LzQerlRuRFj+bkTHjBC3lOO8E+7hu9P7wF1T8lpDK89IXz
pb8h5/Pi4+L3WkcPwO+t9ULwOb/1oRB/Vx8S6r3e6As+63b4qZzX7kadSV6/
8YNQ3pc837M9YV6mnlPT973HG6IP0Oq2z24srUf9eIKF4Evp6g0X94uMhB/W
MI/Yz7VdnEf2oCXgJ+POUJe0Bbvz5D58iYprQsS4SR6mFtZW5CnMHT0yiu8b
uR1e+jD6QJlNf5S88XHCrl+lr7OeIT3+1tmd8M/7O+wDJSPAX1dTL+Ce/SNI
XPf+Xpj4/9YmB3dqUOGNwDdKzBN24+Rj8ZxGnIKC96U1aYZf+ft49s+YveFv
/RePiPv2H8h+Mi06fpchdZDuc73eoZaquyOOfNEIvP38evo0yT7Obhj6saqP
s/F0JXib2YLzKGIQcbKsn1V96FT9rNKzcmvkgw8s9axU/YhT4hp9M2X9iNEM
fMKNkgD/8Gxd0efFSdSG86djfOK7kSVF/Gx3kXriIx7iv214Jer6tY376NOU
chLzZ98J8qlx/2J/btsHe7TR8BiqHJX1VlKHc8kU8gTNL8K/CJ9CPvTSFOL1
SxIXVPM5x4/4SVIXS/WtU7pYWsvEgoes6tCds9OE3YjbLKX3enc6erDuxl74
9Wr+h/QRfo5hGz7dYC35K/ClutOo71F1xA9LcN41ywl/Svpj7gCp914Cfoix
UdqXN+E8LRAkdRpZj3ak0pEcSBw9FB64k6wtOinTFoR7r7c+9BH7pFG9O3yz
2+xLxpZpoeJ+0m9X60X57fZJdI+1XPDztedh4nqzRRb6mU4cyPfmfE78/yya
7zx17z7GXrhySZ+9SQriU9lXQvHWFE6lnbXg1SgeptmHPO7OQTW9dqdoOOdi
hnnieq3qGvgh5XuS9/wjju96bX4s4vgMb0VdpjqPjKlB7PMd/uV53oNLOPPH
Eo/nn0HeSulUXzkreQvwGdzHEsdQfIb86ANaiv8v9zFr9wd/nD67H3yzqt3R
8a9CfYexeRrz//5dMc8D/lhEA/Ldd8B5VH2Hnu4icdn+2Bm91+t/SN17967U
j5Vx3PJp1Fv9UQK+6JEFYh/Q4si6kvDuGcX1vYnL3PnEZcYN9KsDdUkv5pIP
+LMW8UJy+Xu3XcZ/vTjMF0dYNUPFvqFvXxYqvm8HeKn56EB88T1nj4LHxHLY
Jx/HENeZxxMJ3podJO0jR4JfrnnD9ZUmMz7xo3J9saEVfd8r4xorLv0S7VQS
D5FxkN64PPig0o9qMIB1+P/I236z64V1zmurrtyv+rDOhz7mvH55iuvjdKff
wYM4Yp1a+8h3uA1evhN1NSOGsN8GHwdHHYv+uJG9mHgPxob9+ANL6pNvevAS
P1T57WN30b9yf+bKXruxEh1Dbefi6j57zo30I0x+VPhXbrdsgs+jRW8VXfz3
bk/Qrzax69GvuuI5y0+WfBLmmxvtH9bFlbc+Prwx16B+M/a5Mt7rtbfT6V8f
hF69nrCIyKNZ6ZNw/katCv5zZyy8oxf7qKNYFlHad/9MscFltOalvHY96R7O
94m7DK/dOlWAfP+EN9zn4nv2AfexsOvPz1L/J+uynRSscyP/VLEPGVZ7+kSf
yk89QOujpbzXm0OP+vWbVD2OzGO6OxdRnyHXnTZpEc9ZNIHhtVvRpjOOI4Zw
ro3gPvYd1pWxtqiot9IULlIjNvpXn2dSn6SNChXXVU8k8G69ehN4dN/ppTvX
0cEK8N5Pb+T8St/Vj4u2yE29WeGqrPtnUpejx6c04j3Kena1H6p6dnvnDfEc
2iH4h87trfiBkfHhu9Yib2ukT/hQ5BESR8U/UvFLsQGCH2y1hx/tXNrdUtjd
wuQBz5b3+//Vo+LvNjkZ5rXrWxuSH1mAzp79tQB83cm/ExdL3mMgP6V4j7JO
TuWdzUfUNVuvNob6vrfI7/zugVt9dnvXFPyY23/68HDz9inOxS8Lfde7ORYz
jx/lEv6VtfW85DdOBjcuVoc8Q89jnIPZkwpcSZu2BL6pyo8ENxb5Y33JeN/3
2sXzMZ/7yjhDrkfbJA6xJkjdlery3Ek0EXyjSgX0I9N0Y71kfQlPolQ86oBl
nYvWtDv87IcaunUKd90Xgk575SC5L8l6DZkvM66ja20Ph7ev/xOvJnb0ixTv
LqBfJPPvyq5weKMv8ZexGTzHqEe/P21nWR++545JSx3u4H4+fM9OsBhcZQR5
TKtwP3CkRdtFnsKtMYH+S8rfqNQUvkHGTkW9dqvGCa77dCHUZ58zSvB79fQF
y/vukylNDPH7JW75fV+tb/ow4vdk6iNwP21Be+pqL9DHwM2F3by5mPqx4MF5
GB/JG3kXTjzV4C90+hWuNYv9yviR/884wrhZra/C315hin/dabnAl5Y04vpJ
S2VeQOJpY7vBl7iS0ofX2Z1jUHdzvKjgZQfWS2q5nhMGh3if0zkQRjw45VNe
r93Il5o6lFy90C9QOMY1g7qhvH1qeu32jONiX9KXL5J9QGTf8+WdxLqyq0YP
89rNMR/x94o899ndoyPE+egUk/UW6lyYO0nMQ2NYF+FfWdPGCP03rdl0zhtz
dai4n8zPqvyUUb2esJtdI4mnpt8U9VBa3Rq+61Wey9xJH/PA+ZVuI35y490+
u7YpD/ed/sq3H5rprwpcRqt83Idv6A23ifpWI9Emn13LflPE0Xqx1ORtUrSl
b5G+mnWxaZTEdcFdVf5a6Q8E8tFKl+n1MnDUAdSxap+X+fScA/h8To28lcT9
tDgpfH2XjDsxqJ9WfULTzz4o6qpWfaTeekMwdSvbxh0Q58iY1sSFq8uL+MUM
LY2OU+4n4L2//IjOdkv6emtrbXjC7+Jg39tD7Kv2dPKqCp9R+vzqE7BLPpK9
PCX8ctm/wPyxLPMy1c+1vHY9fwS43/x3PrsxYRP5w2r5Q8X4VXnGvrE4M+f+
u8rkaX9+OFzcX/KyzGltxfWqPl3blBwd7fplynntVoya6La1Zd0H6sEH4cfY
BdB/M15m51w4mR/8Z01v9BfbLoWXmG8VfBiJExpRe8MLlTihspvbt/rsZvIv
AucOxHGFB+CX3omJP/CgAHXHi3to4r4Plvnqsu0uDxjn81vpS3ND6hU8jYfO
YZdO8BquSp3MqNeFP2CPe0k/L3XOvj1H3dmL8377G+ICZ0E1n59sJU+FXfXt
iopOl+rbpfAlFbdal5MK+7c8l9ce6HPdKj7jJPm0ZoL37KdJa5T32rUUNnqa
J14Je6Au410jcAzJuwvoKkjencqLKbvSDdNiFa/k/V32nWbUV9d/5BsH41Aa
zg+pz6BwD6XPoPR1nTEthV3p67r9Ogh/yUi1hHPt9TLiR4nL6bXAo77H5RQe
9T0u5yzg/gqXU58AfqUlZN4kvCnyFOZO6j31D7vhUZ/IwnlY9x3+SbNdAR6m
eM4k/2L38DDF90cDtw/kGc+Uhz/y5T740rprIr6zKrYHv5Xz0wn+jL7hoGv0
t1S6Ad3TC3xB/zS8iNdulnoK76vx+jw++wr6C+iPXrDOMidh/ie4gW55Yf4/
2/xbnDvO9ob4GXO2gDePHy/setNw6tDqPxfjYa0OA2eIXM++Pc6AN16wAzh8
v9HwIVN1x5/5Obno32qUqkR+fVgh8mOriqKzMWQa/Q5SBBO/LMFubUqGftE/
F9EpV3U6dbMJ3rs27f9j66vjsti+r0dERcXCREVHDDBRwK4BCVux9RpjXrs7
xwA7rt2OrdfEbsfu7kDHREUFWzF4vXvtM98Zf+/zDx82wzwzZ+acs2PttWIa
2u1qjSV3Ka40pzvs5u0UwJ8f+st5Hq4LmN97cv2U82xbpyC/0elkcbvd7LUC
uIU5pRnHwvqqg6CjZqQ9UM1u/33/mBePH9Swf6+yMBR5J96nhF1fEIH69tAT
Ne12reR5HP+rDd2X1Q9ebBf0Wz5qjLvjPrhChZEX+DoNfnTGMehnzwldRnVl
qUDH8d7DUG/m/VHk1a39cXV/6CZx/lB9/+ox4UrfDg21X4957Ar87WIfw+x2
qQvyY2qd5OGO46PnY59Kq0U4npf7ZJxnZr/G9uOV5wuBax3c2mGXhjJ+L7CG
Yrfryc8Bn+lRAfv4esQFSsA59HfPBQ+oug126eQl4KAypXCMv5o+HfW/aGOb
OuxyTAf0G0d8Rb0u8Bb25XmjyK8zZ50Cv8L277DrNbBP7Vvo7Acf9BXxQ+Vq
zv5xl4bAlU0/C1y88MfSJoNO9aFljrhJfoo8sPHlO3h7Bl/C/U69jn68wxPp
/ZfSrMb7E3QDfnWZBNRhR1/A9z5KBn3UjnmAFxoeTv6P3tEN8VK9EsjzcPwl
6kdW/y/bRf+vcvI+/IhN3E/t3wq47u4THPGL9GY53odmRnX7/WpRN4Evd/cE
3r+4K/aXZPmBu42tiHzXjQ7Yj5L5Is+8fiHmQUPEoWrpIOpzMafoyNM0Z96b
1u3eoG4O/8uKZ2+/zUN+Y+hD5gFm3O/0buno+15vxrwRvOj1LsK/qTwW9eu4
0tCTHd0BeJLBcbjvvbdoP1UH38W+8onr3ZGwm4874fiY9o68nFZ/DvblI6Zj
fCRtL/bR7M+B/5oCnlL1CPePlnUrb38uAh+rBkrIBzCvqWS8QT20yjpHX6SU
axbhDOWO33zsdi0g7Af1P7asQs9RrBtKjyTUkWNzg19B6A1NDEE+Ylqgo34h
Ne6GeIr5voRd8H392Xcv+BbMhXOAZ+F8hVn5DI2/Wah8A8d5Qj3BK3Sgd4Td
rseuekn9vOXyOI+/nZ10NIw9MQ7eD214Rrp/7XsDB3+Isq8QxWXanO/VHcfP
SV4I9of17eNgrrxM8Z6SObqxfTzlbVOB76kQ5VjfjD7jse9vTXT4k+bx49Aj
KHYuwm43Imcgn/64Evw+gcu6mQh/pvv3Cna7Xrkp9vWaLuH265THjELfJtcv
5F3oRxD1C7PpLKzTV96g3nFgH/pDomJDHOO5eg/68orMCLXb1RfoE9NqLixn
t8t9b4GnJuMdR9+33p11PG9tD7fbZe+alMdTH4x22M1ifxMPqnxvdJDj/IGo
F6je6KsV96tse484yyV5dbvdqOaD+Mpzcpj9PNKjH1yfTh5ut5vHwXss9NY1
7uP4U29dU37iubDeutBtt/igWLdd2bkQ8eD9EIxzsjHA//h5lXWMZxvgLTXf
mNKO8e8EvKU+8xXtP0aHhYSz0uZcA+5rKPwxY8Qg1FsbhtK+pk8+p9jHQQu7
Dr9t0uZgh91kfzuPzjxIHCeu9QFPH/fvSGWBD7f6d9xvVsX4sQ7Xlznor/R9
jvERfVg1ayKuiO3qZ7cbJT2hr9dzpsOuBIBfT42OL2O3q6laUz3PHOkH/Gc7
1CP0+HD42y4B6M/jvm/pWTLw5SWElrHfr5zyK/gEtnctZ7cb5UukIvuEOODV
ma/YdLmDuvgDrYr9eHNSJtR9897nceb8cG2Mj7LhEI73QB+T2bwbdBOrgjdb
8YRdPwzebM0MxHMoFYN86NR5hej+f3TBeyHGYf4U5PHGpKhutxuej9B/cQW8
yMqNsmQ3vR8gvmi8P8xxnmmtKZ8mdyyEukbrzVj3Gq6Hf3wmY366/vmHkN/4
1R91mXfbqF5jZpkN/rrHbrBnigTfvNAfOVYEPJsZWvjb7dov8Jlq926Xchx/
/iPiU86DCR48kQfT71bjuhvWZ3kk+Ki1+9FVHHa/0oh3pg1xHK9tLYW8cPAs
9CXFbcf639gXfZXDOA8ncFyrDcormmn3I+4cqBEey5BnwO9fBrsxBfym8v7p
0Ant7hNm2L5XuhWA96zNPNSLOI7Wx6NeLPKrWnsVeAPOr1q4xJGtcDzjEqVe
E7kewe/hxfE4b4J7mN0u/ZsM9bXL10Ltdu1jNeBaK20Fr6dY954HIZ/IuErh
Dwg/UI/yw32On4j41G0ovTdas9vY18Q43x2NuouJeMda3wrCn9dn/gv8RoZ7
eM9frQJ/mtdOxO/CbxkzhHRvzY1RDrvZDHw7QvfHyq9GrIP/tns7dDRKg2/Z
bDIcflVwHe6XgF2LY16OtO7ASzDOQfCuCB1bC//AvCvqsXPIJ4v1rdIQ7NPn
r4fY7bL7KvjPpZ8j3/CpHNa3iN5YJ/dWchyvtPFEHa9RNPzKm0vAizt5Cu1P
0nLgK6z3fHDPYBonodvD/TXSR9T35d7g+bD8nKyNcJ6U3z0d57k8G33CFVrn
ttvVOvuFDgF9zMcLiWdJCbgGvot9noF4Lrz/XtiO9aV4RGm7XY3Ojnw058Ot
eo00mvZ381cI+hTHFgVO+FUt8Jnvj0Repx3savHdVDfUft4ArxSv83qOAljf
rXicv7fTc4r71F5STbvdXN45m/146/3k40V+W7z/oj9Fnvaznt1uBiV+JD+z
x2vsS4xPk6602En2Vuf8HN+rnnTw92le17E+CFxll92op4p+2JrgXdIifYCX
4DyAObA5+sRZD0vx5PwA62GpHWpBP1zw7o6Crq4SUA34HJc8lLeXeu9EH1Ou
7uiDd4Vd+TkVuhHc52LNC66vmSld8V63G098p1KnXvT+6LkbYF8T63zf5+hr
qFvS3z7OZugl5qfO5ogXtHJVsD++jcT9TvtAeWBjnit4DCe/88f1cH2nkjv8
znWLA+125dV15BF2IV4TdumQDLzOvLXsp/H6XOsd/KjHsYhTWu/GeJ78ALzl
sEHANQ/dCbs6EfWSpT+YN4nXvVwd0Y/hvquk3a48rwv/reQT4BZ5X1NHTUR9
n3E+Fv6KcT6C31V925z7lYDDMTf3wXMXPAn7yqHu/+ahO13vzgId6fuzJAbT
/7s/S3DwtQ7IhLpSriKv7XYlrjP9v+n9EPX9LEHoDy0SAhxIqyrkF1h9WzN6
UX+IlhiF6xT+1YF14MGse7K03W56VwHepncJzifDz1SG3Kbnokd9hD/5nseh
8hX0Awj/8w2PA/ufIu9t+Qmc99aTevM4c79/euT1jHg38Isy/4B+2w/5yg2J
0HVmPSkzdg7ql5NdCbcjvYWelBVfc7+qOF7E41pp8LiqJ8CDZ5ZPSTyu/6sL
dMV78n/qArCLuoDZCbzfVtx0zg/+ZzngWJTjObE+/1MZOAbu31RTZYBuAvdv
CtyC4FUWuAWJ+wusfaf32wL/P7t2dSn4TsuCt8Pa13zzUHyh+sH/N+o/bEf2
HI1pv1dG+nA+ZBvZpZCzlJ/SVrSCPyj0ffxuIE5QRwJHzH6R1j4rcDJdHlay
H6+9T4C/19CV4m/BO6G3nkh8zmoN6N9Z9a9n4EWXu44AbznzQqs9TsD/WX+1
nN2uTwRvg5p9kON4+egD2EvepXEw5ufH+AwIQx/E2L7F7dev3mEe4RGYv1Jn
1DvkOhmC6fflzCMv/LRpy2Dfv5zqXdZ8qQ7+aJGfFOOvdwxAv16BiohTNoJf
Wp43iPwk/esc5M94fIy/oL9p/p2K8s1K8m6Y7+1mkJ6mZiblxPXzOpBmENnV
wBnAAwoc7PIUwIEFgVfKei65liAPVWJumN2uH1yOvAPrhCovMH+FTqjU1kQ+
ScQjIS8Rh6fw97ePj7bYBf2eVzKBN2Yx90GPGxfE5yW7/Br8A+oB9Mfpl6A3
aMzF8WY96JRJ8zY54iDzRUrwtx1C3G9ufAzcUcUEicY1B+c1x4IXSBvQHjhn
1inTTj3DviN0yp5GYx/PqIGvO7wldFteA3dvVr6LPGHZQ6h7tVzpTeP1MJby
jfJX9DPqxZ6g/iB0BLSJiL937C5lt9t5wmkcnnB/AetciHXA4jOJAQ+4wHnK
c8LoewXO0yz9geIcedsS6Jr5NcK+uHhWXvq/C2VxnVXXwD+OZJ105tnQSsjY
x/dUCrGPs/BvtSVXHc/diFTRvxCXDPlAv/J4HwrnQv3yYimKU7QGR7CuPq1C
eTYjhQv5aVb+TfAdCXv8Ooddydm5tv14s2g0cMITK3FdBvlJwa8lX/2A9ewg
6olGF/hLRqM+yM8fgl0ffhJ9H0fqhRm2+9JXjUTelnW0rbow62hLf6y35smP
xCdj9mkQ7jjP0Irkx0vGC+D3RH77OOvO30iAv8PrnjriEP2/Mv0AcNNiHRtZ
AHxJTWsF2483H6dEv1wL9CtZ+3KlC8DN53aT6Xv3tgUP7Z2ftF+ontvwHgq/
whxO/qXU5iv9XS41jnkYviDO8QX/txqVA/16w2+gntg+e5D9OtVuk6CHPmes
wy6PzELjJfjS9UOcf2C+dMGTKfwB5Xe8RtfHvJrCLsVPJ5ytFXd/PIX3RsTd
nmOw71W8RvVTMzYRdZrAeMQdXG+VUqMOJPI5OuPtRT5H3ryb85bAcyqjwBMk
HS+HPE2pYnjPg0tgXBYtAt57YhY898wFEGd1mIb6YGQ23NfkHfS9epvzWGee
Ia9oHN9C67jSaQfjq9EfJPUJJRyedgZ+o9U3Uaw88CRrWjDfAuPAx74Gzr3T
IeDldu7A+7DmvdDXAa9FsAfWGe5DUZf0A57rPvJOUsJn1B2bjASO9Fwq3G/F
W8APPU8OviN+vkqJh6ifebJep3gfUkBnRJl/qJzdLp1vgnGI7l3FbjduzES/
kOtnh12LKI7+oltaKfv9Gl6F8X4IvXvBs8rzVJ58JiPs3AddFngM7ZE7+BQE
bwnzCRtp6wfTcW9KgqcxthjyFYnX0Xc57yruN7iQ0FfGOmAcG8W/i49jfZDT
XQZuM8/A6na7kmkvrddqC/QZaWOLUNykZESfkb79AJ573jGwa6xrmBl9yvK9
/rj+oMLgOYlbh3Vi0zT0S178grqX5z7MO7HvF6qJdWZ+J+BwhuM9VAdmQD/p
mlrIEzNPkbZqHfi5DH/sA7M4H17kNfpAQ5ugn7+3K3RPckRhPz7hxfl5zqsP
Ok/5dmV2Ia4XMF/K6UCy67UHOI5XykeTzp88/BFwlOz/y74lUNf3zo28SqOK
GP82Ceg/OhkY9t9Py5+sNQR5nC/L0Xes74V/XvEd9MIXpmfeXeQltJdrkH/b
GuHvOE//KzcovzQpCn12XpOxv6+uQO+ZtY7x/i7WMW1QYXqeSt+viIvvd4Sf
8zUI6+XXJPq79i0JuE3mU/ltR705JfiXJbMV6o9tP8LvjWxViJ5bi+L0vfKU
M+AZOfKlEH1vUG/uA+J5uqUY9ptm9dDfIvRQ1s9CHTrHr0x0vrtY3+T2PaET
wXk2S7eR12Hp5RbHfiT18qR8ihz3nsZf7/ID18m4F2V2a+QzW0jwH16/irAf
rz4todmPF+u/iLOs782YLNB+X9oZro8sHeFYf6TRHC+UTeE83usr5w3qBdrH
wRjnivHxAM+Nkgx6VVqjFKxDrGB/YP5eM4n5BVhvUW0yneo7Qm9Rnv8qHf2+
/xbF9cqQr/AfCjyhdV3tNhP1oJ0HcXxPzleL9TDPp7r4HXx91rrq7Yq81a0j
hej+crmBd+bOWuiNjYlg/G0C+t52T0e8c2kO8khiXVo7GPnzgOTBdruUUAI8
M+tnUb1d6G0pyX6SXyS1da7b+sNOYXRc3frAIZQDP6pcoS94qHKHIX+2tjDl
ofX4UfArXibJGFd8jA+rsd9ke+blsNe6DvyPyjp1P8A7JKeThZ66c709mhJ9
Jaeqoy7dJTf8tNj3mP9jDdTHz5fC8T2b0vuvl/biOinzCHm74bkPLRNutyuN
Ffi9qy457Pr+9OAx78F+zqa59HzVzn8TbvJ3XIM+6E2Mv1JrI1//6QVdp5Xf
uI51ytzYzvk+FN4HvM6o0Y55ZzxRUF/PW4P2QZGPMiJYj5vxusKPEnhdo8n/
je/oZ6AX1/eZZ6mAWxnD9jys7z3vDj9sXirECxvXYj2Zd47jWUuv2anvlmou
ziven7qIc6Un4INVLlSCf1ugLtn1So0QLw+swOvYcJxfvcO8BNmBp7mHfg3z
dW2us91E3+3SH4gfuT4l+EwsPiLX1+ir4bhbrrAPedGieXF8qknQP+2wDv0a
05qSXYv+Bb6wx8cQd/U6Dj+qAfR0pPu3wHewJQvqSOlPg0eqWxT5h8bHq+AV
92f9s4tJeK5eE+j8VlzgXxjr5OZ2wfZxMwvgfTBzLXPY5c3faf2UzH0OP1y6
xjp9rIOpdY7E/sU6mObBFnQe+Sj07FS/l/B3D0MfUOjZKadHMf9mNPKy70Oh
o+eJ+r2WbhTwV4VbNqP/73QTcUrHbxQXW3mDCQHAszbL7uOw1/mO/mjBAyP4
mrif1FiTGvXGgceAb7s2hfWo+iOuaYH68u/5id8b9kdddOh1le6v5jB67iKv
qDyqQHaRVxR6i1YfK9enlICG4PO8eHgMHf9mI+b9rxDk8ZYjn2NuboV1Yewt
Gk+LN3LfK/SVjHjE8R3zqTbwQ7zarjfiMEsfDf6wsc8X/DdaWYpf9OdTMS9W
TUM/iAvsctAZmhdSk7fIPwhca4ci6GvLtTQ17q873vMWs5Ev4rq5Vnk25QdE
3Vwv0Q/3xzzVQt9Qe/434o4O0B0z6y1B3Sgoiuc18M+KlgFxqd89R95bL7Yf
+du5s4PsxxvP4tFv2AV9c8Ya7gN6EYF80W0N/Vvc/yJ7AW8pB5UKtNuVAOAq
BY7a0lVkHLWI7yzdOo7vlL+HBzvsF4FX0L7ldeAHtNXDwbsxF/hYvcgD8G26
lEN/F+uxin4HocdqNKqBeHHgExxffi/2tfCs2E9ZD1SOK4P1MOwO4qQcLcHH
UuMCztNtI+X7jU++0HNs0QHjUvFo9GG73as58mgNl3y327XdJubbPfALaZVd
UMdfnJb4PUR9zbKfP5+BrsPtO+LKymuQD385Jonwe+2SsG9vO4Q83pEyz6nf
ajYff341jm+39yfVLUZ/QJ+jyAP3/kl5YOnlcfQ7C9z19c/QB2zSEbrX3Nej
X1oCfF5uT4ddLnMcdc92T6n+LE0vQ/NCnbsc6+3ds5TfMP5VyK6UaA+e/wO/
sD6IPOrB91a+3W43v68HD3OuMthXy6EerWQpT36MXjAZ9tNk2O+UNeiLU3uh
/0+fnB240OiXwIVPaIR6H+MGpa0bRF8GfeTr8/vz78C99QOvuf5wLdmNR49w
v2sagq9C9Kf06oz55vIz2H792tCpWJ83lwH+gXV/tBYaxRHS3+0dcaJ+8h78
5HolUPdbqSKPyrhTeSvq2Opc8HXIwSdov5CTtjjqLNrMVfCnLiwFL19kcVzn
WdRTpCaFCW9l9dFM/ghcS/5JqJOIuPVbPHD+tZr72e1ms1FhdD8V3wbY7Xqm
Afw+tMR4MK+Xcfg14ivG51v9KRx3aC77Aux2ySMEfuTxbxSnSgUmoX4a9Qh1
nYTz2CefTSC7NktD/ujADBpXrU8Q7Gvj4Yec2QDe3GF+qFtVe0l5af3hL1pn
9CReb+P8wT84AzrLVj6/XVP4CQVuKo77PXcL5+f3xRz8E/FO7g7edrvWLBn8
3i+3PRz2b5vg1+U+mJvtFfkn4eeEjp2cZTzy0mJeFHiL/drjQDAdJ+Z1TDUa
T6PY3mD7eGoF2mOcxXvI+4h4D/XrC3C/D+cjv713E80vc/gyrM+pXwHfGx5O
dkMJdtSP1FavoRtStnN5u90YdRr7oOescna7PqQpdMoObMZ7smsc6nFt+yL+
Z/yDiEMF/kG/fRp11Zl7EJ9+O4395ttj+NGV7mF+navNvJrsR3G9SYqHHyXm
kdye6008j/T9I4gfxvBPxTrR57C/XFqYjc5ftDj2d/+D6M9iHRN9EfxkoWOi
HpmBfGd24M+VWfmBP2vrgf7LP/hS1Mf7KJ4V81FPHI73sNRTb7tdWzsefbtq
QeDKuK9H1Em1q1XYj+J6Gftn+oaDQXa7UWIz49R11PefBOC+ypbDOpA7Dvtb
sXDgXnoCP6nXBu+NvBT1I/05eG8E3lI978V4YByvfs8Qah9/7X7hOrQv9t2K
da81j3+xPlR3l5etR54nSPDwVKJ5Kr2dhfMdC0MdP3IX3a/xCjogRuEEzOvu
W/BcuQ4up0OdV9TBtY/gY9QyX0Sf8uAxiFvrBMNe6Hmk4756e2G8p5zD8a97
wf/hdcwo+hX84iJ/8uwUzVtp4SGsk+0O0nMXdW0rX8rPS+j/6tU8YWf9X7lL
bdrXLD7h8Tfhjyb/GzivNl1g7451z/QCPtqcE4r5HqMh3nCrDJxTr6JYN4JQ
BxH4Geu5MH5Gqot6urAbpdD3bjaW4d8wH4h8APxrytyczP/MffTdT6A+Xcvb
YZfqXEe8F+9TyLAf781x/bfU7g574b/xvDzCctvt+hQ/8CBXjQIP3pp7tM6r
K4NQJy2XDPcxAX6IdKwRcNXFsiN/9PgudIebtcFzTxiO9+rGa+yD8YPp/vX9
2VDfSH8F825wCho3435W8ObNvIF5Ov4y/G+xngcd532hKvro2W7tp2XOwW+X
etHz1NJC/0K5WBX1nXmvwUPWpy3m4+C68Ne/N6O6knJyCp5jv3+Be4/aQ/03
8vDz4APJchTPfXY87T/qwAvg2887CPeVJqy643pqvUV8nX0G/JSUqzAfGy71
puvakCfcfrySUy+E8fu7kt1uppuF+pr/zSqO459vgt82fAbsXU7jeJczWK9T
doVeh1jf7rlhXn06AByQOM/VAagL+6jhdru2aR/qE1MLId8sQQ/CzDmf3hPt
PeIXq67ki/qFmm8ddH4ev0S/W5wB/+GTL/r3hR/SKx/yFfXmU11R0TDOZq7u
2BffVkPestJyjFvXjOifFbzHNr0DOu/06qhLn2f9qTxZkTectwxxX4I/2dUj
6xCPsf8p5cf6I/xP81A24CinXkF8+rkn/LToANR9Ck/C+/9yFPK/Zd6gbt8I
dr1YLbz//QcyTxf3k168HEzff32Sm91u5a9u3UMd7NE+it+VxtAxkSy/neuh
XXZzf2hGrP8ij5FxQF7qo9+wEPtyLPIeRkAQ/LEpOtmlX2xv1+4N1R/9UyAf
lgx4EOkL8xjWZ96v2Cia18qaYMTjG2sQzsRYhvhOKuyO51v1JuNq4C+ZgV+A
zxA6cY+SCPchsR8m/BBrHNgPsXDXoq/2YhnyU7U9jeBnMs5Z3zSA4hKj7i/0
AXsUpPmmbaiJPG/Lt8Cvnk6DOvV38FVaeIY/8G9qo6vAdUxphnzjDx/0ZS14
ReeTxpcDTnHQV1zfxsqEs9AnT6Hx0fOfIf9EanKK8PvatBCMW/hZsusnnwAX
mXEU1qVR/aDjd/gn7UfatHHoGwhfXZ/HiT5KbGPo7S1Yj/6Xu9nhlwl/1Ssc
dRZJ8Omx/7+oAPIpkx5x3QTrgNS+O12/XrIW5xvXIn6puRJ+g9+lUna7ebQg
HS/3nRVgt0t9fcmuToW/YK1XT2bB72S+PsWDeUyYr0/rij5Xq698LvpgRV3G
eh8Y/yzVdsW6JfK3i/eg3jy3fjW7XV4JuzGrcYjdbhZXMP83NEZ9QOg05c8O
vqTeUfjeuNPI87woj/6ThFWoG5Tahr74SgHYf6vPDbKfR8n6Gnh45gO0zi/4
AHOOV+x2uWp65GuYN8aOa6XzjWPdlrV7gPf2BG+n7gYciDzABf1ZpfcA/8p8
KcaIVoxbA1+KuTQ38k+rEKfLUkPgRubD35Myvx1D93WyPfSMbz+h/VHkOY0n
Gr23WoJbDrtdGroZ9uoPkZd6fYfqQWrxkVnpe4sDlyX4dtQmwGWJvKL+eh35
LyKvqDzPg7w786uoGX2hD7rtR5DD/s8b8Ho8v4nnmCcvxr9lKqp3C34ewTMg
dCjMedDfEXVJc01SSvr7y+nAF0uoi5kHX0Fn7bEb3of8/6A/dNRA4K++gydN
nw4+N0M/RPU7ZfVg9FcJfcPQMogH04Cv1MrvxaCuZ6YNUOz3ZequqLey3qOU
lASerK95gSP9Ohp2Xp+NX0nIF89fTeuxMtsD9amgjoS/VbpURL7tGtetFrbD
8xX61JzHs/SpPYBLFXwy0jXgVgXOR9gFzkfZnA55V57v6g9XysNrLjXhP+a9
iTxbUjDW/biaYTgPzxf3dsCv6AnhdrsZeInyUWaWAQ67NKom/AyhL9b9LOuv
QV/sP3+b7pfznEatU9jPhjJ/1/QT2H97gldTSThM92f5OeUfIE68kYXmvTow
Na6z4DO8x0IPS6yfzMNgytuD6f931sO8ruCB+P8ZdK6s+sv1RMTvH514UcP/
I/y8xOXw7zoVAP9PbEXwnrTrg7rVE9i1MzvA9735M+LTxweR98iAeqdZrwf4
+TvAbiwbinFZlhe81PxRdt4HzqH7TIddLf8F637hwnXtdv3rGewTEaY4nvjq
zeK9gf+fdB15JMGTdq823pM+kSXtdn0r+naVqV+gRzGhN/htynDf+ugBqGPO
z4t8oLuC51L7Pr2/1vszSCF/XX8ZWMdul8JSFKLxKTEi+L/fzYesD+Uxw5u+
f4cP9ts/8NV66Z+I75bOxfNlPjG5KfoPrHV77hLgapIloV9t20zy97Tv7ykf
IV8rG+44vt9u5Pt8CwTb7ebnBuBb+XaQ6pjWe3VFA347MchVsdvrHcc6H5+A
/Lbg0Tq6Bvf76qyv/fzGmgW47qvexR3jU2YE8IGrF6P/SNTHl6OuoQ8cHOQY
543ZcJzfH3WNQwnod0r5sKr9Os279VPSeXLE0v3qvZFH1Sp6IK5ZUJr5ZBgH
Hrcf+MlLsx12bQ74QCUr7psGPqSD+RD3vfwbeZi5lal/R6u/BHXqRTfAZ7h8
DtWpzX8OsC4CdOr0cNgVlzvQBSjfBH9vOJN05M1yZ+AvuJRCv/v509B/95eR
H2O8q9hfBN7VdN3jHJ8GzNffdmg1u11PLIb8Y+xG+EVCj3LCsTC6vk0vgJvY
jHydnq4B8ZQpubtVsx9vLorEOlV0WrDDnm4N+hCYB9Li82EeSGX2Q8w/8Z5M
H03vp3a0ssMuTaqK+j2Pv/rrKfyxuBzAjQ2ogHWubCq85wde/CK9BtbHsfZf
9ttNCXqD5pl7yHt8X4l6IX/kpf2wHp5fTPU7pXEC/PBMWFe1nydQHwmpHma/
X6N3b1pf5ApHHfuFsktGH0jwUtQt++7D8VoH+FdbUiBP7hKEekRRH+S5lswL
xrjxepXbG/dz7Ditt9on5N/+4y2n53X9DNmllYwDf50Sz2NsEX6fOf//Kgvz
cGZknhPme2FeCNPrVLjdLteZ5ErXo7g4jpczpMV6UacReP5qGGPoe894gcds
8UzkfcPmwt5iHPyPJYWJt0Z6eRD60dHQtxB5QiMr+rasPOHH81SPsOov0+4A
z+k2BXiP2zzf50Shf2DZfuzDV8ogHilqIv68nwN4XZEX5XqqtrhjXrtdq8/x
Q8h7xI8PM+A5xvuBr9FvRi37eKpNr8AvSXfUYVcS32Bf7HoOcX+6w3/R30fX
wf548Rblc7TdvVuQ/Rn6+aUOG5E/2NyF7PLTani+C3Jz3H0b9dPb9ZGvaPsu
zG5Xp4+hPhQlS51wx/H5VlBeQ+8NHib90hrMx3cTmc90Je7vFHS75BGdofMl
bXX0vSprWY9h9DfUW4VOSj/E52bCDrwPy8GLYvRVkY9gnQLpAngyhU6Berlv
Y8e4/VwM3uGaKbjOhfjOyHIYPDZLfzVyHN8F/DbaN8wDY9lh4HAmHcT4pz0I
3bF/BtD8Uqf1hO5hmWVYxxM3YX932YA+3POdkOetsIfsZu1XwL2fftcE4ymj
ryFPGPKZ349AL5j3cakd+LL1uv2hg3ZiDq7z1xvki8YDJ2bFIymCg+n/OJ8m
7CKfZs4YpNjv1zwugYcqOlugY3zUtYiXK7g64mJlXU7wkLTv7G8/j+zPOpjc
V2i2QD1I9BUqTS7B3rUS6kfefhS/aHdHBznO3zYa/lmYi0NHQ13oh3rWX32d
+hrndNStqwK/IfU4ibpJ1u5YLyTUM/WeO9FHUFcC/iBXBN63WtAdUHdD31H1
7g48V2zCGLq+ZKOhw/6pINn1WOgOyMVKAKfHfpfAJwv8gOr+Bs9zEOuhM35A
6BKK52vpEk4+C52LG3i+UvHtGM8lSxz1WdEnLi38QPV8Cy/daBLyZRHgpbTy
FRN8wFcf4gX/3BO682ZkSqyTW7aAh+Mx9FCMTkHQv+rxGtd1E3Zzz368J9N+
Av/E9WVldh4cNw58ipY9m47nOIb5GK/hPFLfJeBBq7uA8zl4/6UhteDXsX9i
zYsan7HuBK/DvBf9p897oj4yqgvr4XK9Y/088ElEXHbYJfkq/PtnwBGrn97S
fqFtXAS8UFD2co7vbV8KeTm3+Q67ejID5eX0jhPw3kWD/1Ae4EJ8X0aqSIdf
LflVQP69z8Gadrt+XC70n13ouVt+Duu5q0va8/1ifhnFiiBvuWo68C88X9T+
rL9ZyLe03W4me4N8d1noZ1nzui74T/R1A1lnmfGQiT/A9zj1Sw3HONRyoXy3
0CMWdoEzUcdINe12oXtldDnj2C/UA5soT6u1W+jYd7QOKxF3uK9HvsX7HvAh
U3zRB8X5TAvPLPqz9Prs/4IXRfU4hnpkBtazE/mx94dh3/aqvP14vWki6nHb
65a1X48SdAk8IBmn0zpslDexnv8YBR6/hTMa4rlwPHh2OPSS1oY2cti/NsR7
zv2JyiLGXYj+RO6PsOJ67o+QVoxqbD+PEvov4sPmo8lufn9F16PPX4195HE5
B0+vPmA28PG9RyCe+oa8kHoCuszmJOi6iuelF8X7rK5918huV2anBN9O0BDH
8dKLBMJPSk3yVLePm/oyF94/1uMQdqHHYfTeEOoY576HoJtb9rpit2svbyLf
/vyDw64GH0Jeb9g+5MmPxCGuYb0Yc0EB6KIGLSK7Mbc3rXtGsXbAHT57Q3ap
QgXqp7bpzSH/wXhXOcvV6na7siYRePWdEeDR+SsFcOYb44qQfVYx4OUHXcD9
r3BF/F83nWN/F/xCypgKDrtUFvNUrXPQMc6Cp0gd0tix3xljB4F3onaU4zzy
sIk4//Np2PcyT4EONetpGq1yIW8neJ6j91I9WB7pDl0Ssc6MU5A3jL/lb7dr
E3qAp33gfuRD1oBXVT6Qj8ZfzTGI4lptw3hc98zOwM1/gt6i+hM4cLMc6jHm
Us4H8jjrt/MCd8t6E+bSf6CPw3oTcqnO2PdY70w7vIHeH6s+zrhTwWsqeACE
XdRBBN+p+Rp8kYLvVM7xCX5Nh6o0D+TYWKwj08ujj7JHDM17fWo37PdN99V3
PK+B07HuMd5VGYT5LvCuSouzHLcyXnEhx7GLZ1G8oG+HvoZcZU0w/b3DfOLN
Vc/MQj62HPJxxoMldL/y+GvYj7emIbteBfU6MV+M7FHgBV7ZNsRul2foGOcs
vuD9Vc9jfYtKwvOo+zW7/TqlYOjY2nQzaT2RT2Fe2HDjwAvwPBL8gaIeJ/gD
Fe1SmON6PJsDj9XNC3m1UOhLS7UOIv87dTee5/pgxMuu0MWR7yVD/9SFjoh/
W+UCzvMA+onky7CbqdHXrYTGgnduRAn44clngO+0KnB2RsZOyNetPE1+knH3
Ffoswn5hXfJqhvWHdXOsugbzxos+R2Pufow/9zkar0dWtB8vdDPVGosd+TSl
yAzaB6W0fbEuifrRlwjKzxhJrR39zrrWCbwnX2/Tevy/+qkfxsc3D/h4IlTg
OqaNQ52uS0/UT6q2Qh3tegrYM3UET9oo4JeUKuuAR/oxn98H9rfTzYRfV283
+HFZ31CttoKeo+L+2GE393QlXIva5U4w3ccNrs/qv7COzGeeWK7z6nUOUN5M
5O2FXeTtTXcfx/5oDOyKOG7kX6i7TrkPvyi4CuE/VOkS8Bj+97C+xczcQf0d
tx/Gkv8cXYV41/X3a8Dvl/cG4TPF9RvHOyFuzdQ7pf2+tKTKqDeNLMk4Md7X
KtaH/8988gLvavHJt0uF+uGl3LD39kOcNTkOcfz7YJzn0UL0o/3BjyT61NSV
V7A/5tqIvpUH74C7qsu6ZimLog+xMnTN9Pvx6KeM29CWfubk/J4XeLyVS/DP
1ZXg8RY6Svp1jgtYR0lPEyd4x+mjFo4DrmvuYsQ1t9PT+dVa68AjFB1cx/68
1ECF/Ek5KIjyzFr7aPLD5cPcL9+yEHAo3QOwT70KAQ/kitkOHjN99HvUY6ZM
wn0z/lltVQB4oW1p+blUojyqErwIz5X7/gQ/kuCbEv1rFm8S12eNPEvQdxm4
vx39TF8EfsytwhjP9wfILqV4gn2iPnghpIVNsP6krYV6G/e9Ch4tqz+d9eUt
/gGu6+l1faAbI/gnpcbYV89aOu9Up9AZz/D7DJXtdrMl9195DQGuMgT7qbGn
FfBD1cH7p3ThfXZ0f+QL5nuBF3EZ6rPm5qnwixi3b+1fjNsX+q3CLvRbpewl
gTcR8+JQDfRdS+Od9n0t8tP3HAgIt9vldb1ofVDzeoGffAn0oeTVBj0/0+0Y
/ZQj54PHPiyR+vqFfod0YDbn/6HfIfCH+op3OJ5xetqswehzKeCL9d94guuo
4+1rvx7NNRQ4J657ivsVdU99zCT4+00ek5+pXx+M/XnDQ8QHX16RXa7oA91q
xl3rmYo7cNdKstLgPRM4+bpn4f/sblvNbpem+2PdiOpP/pNaNIHuS7vdFnFd
fdZ3bov9SN5WUNT78Kn8Dnhd5nXX311F39mUp8AzX0qi8VVv+KAut5Xz9k9X
o3/mDXhGLR5vL+igGbl4HNgvMgPB86+cdKtjt0vPjkOftDbyu8b52cR7Jt85
BN2ak9AP1/MDR2qWA++hcbMp+FtubEF+ozLyMmoFN+BkOP8g+IJ+73c8H4Hn
UTYFAee8/nYJ+3NUho/Hur2xGNbPzQWRl07L4xMwhnmzmd9Ayoj6YONBeI9c
JyNP2K801fmkEG/gJdLCrj7Zibqw4BXh88gpgUsXetPKg1mws9600k4NdHzv
hNz4vqce4Aeey33obUYjrv0Dj6Qkk/C+Dj2JfGkPzHc9JBF1ilRtJlCfx4YJ
4Hm7/o3OK/he9CrQMxV8L8rxcoRzVh9Cl0E7dz6Yfn7LwDx1zMs9ogrqqsUK
lHLY94wGXwrzQVn6qpw3k5r7oe8uP+vE+bIuG/cTWXy23E8k+o/M3OD5tPqP
6mZCnvnu0O70fbOzABeY2Aj5vV59yC6vXBWCcbPiQeDEfvux/Ds+fW5i3vF8
ER9Lh4XtSuYuyDcI3rNj45EHZD13Cy/Beu5KzFr0c/ma4FEMRH1KGZ4Z+1cX
4MDVOr1pvzSubOV+fNYT6VYlM8b/IfnL8n7wpZhHslCeS+iIGWXR/yJ0xOSY
VTTPLF7QfeUontX3p6ztsP/4m+oRAu8n+uwE3s/YhfytVuYd8CQPiiLfW+Eg
3scib3D8zMrQXd0zAH7OgUeE0zCm7wHu48lxx3uiJ37FuneqQhG7Xd7REc+l
zmvg2jLkBj5z6hfUKRgnI/DSQsfKHFyY/GXR1y/HdMT6wnqm5tDX2B9Zz1Ru
n4euR/C6Kx3dUAf9JtG8sPYF3xjgXP1Gwd8ROkedgDtSFj5MZ7fLyU8i//W9
C+eBud5XfzLqaNMfYB5UHA37q4asaxniWP8192rI47k9Uex2fXMpzBfWT7Tq
lbxeaVuTFbaPpxo1DHVq37nedrv5tSvhEFXvjeDVmD8WetOrY/Ae72yMOvAp
fo6hwNEZ2wcSHtvi2/GoQO+TGXPAaQ9Li7747cj7GVHHCL8qn8xAeT/lOfiT
9eTjya5/DgGPZeXjyNfUe0Xrg3lmMO7rGXgI9QXQw/0dn4AX7/MF4F2jX4M3
Q+T5OS+hJyWR/6GeFn4V4lclHjgl5RvWBWXcnLoYZ/YzRz/KQscVCULfMM8X
ddQ3wokpyve6dru2ujYdr3skg851ZtQFTNfV2PcXBIfbn6P6z0HEcVu31bef
x/yxBPVBt43wH+dXw/7edCfxq0szgQfTvoGPQnVNSkl2SUZd4AvuV9m9JBPx
YyyFv6cw/7aeZhrzLex2+tVXstB+IVdPcNiVU3owfd/Fck7+4bf9sW8eR3+u
uRH4eamVJ/ri2X8Q/CHCf9Bnp3az2//TgaL7fpET+ca1h+D/5xhXBPeFj3Fj
E+oaKy8DDy8+f2tOu+t2wnfJ2Uah7zhuPuyHUJeXeq8G/1LhK+QPydtiaN82
3qyFDnu1utnJXiYE69gHf8bPX8Q8aXwK+0+dFuCl6TyG1h+jp851Lsab7XLB
ONeOxTp9YyL6go0NFHcrvmcQ52YshfzeunvYDzrGwm88yfr1KYoGY3zagW8t
1xcaH/l9EPha1+0U+Rn6mCNTQf90pRbqsJeLxPvJPCfiPRE8J//xntF1zoce
pXxvCPQBp2VHvzevh3qqtLhPbSTi67tD8P5cWws83mLwrimPyqA+6Lbem76n
5kOcfzrsevGRtP6YnyfDnucOrWPK1yUCPyM+zFcgO3h0f38K2O3K1hOoo/5i
3u5SzakeYa4ohvHb/AT5+50u0P+o4478kog373WjPJ3mG8rrAOapMTgZ+jxH
rhO4Zoq/pEZhNM56EnRbxHyR6l8j/IN00RN9u5yP1ZN0zB/m/xR+kdCJMDsb
iE/zwC/SZ7aDn90zPth+vNB9EDq/ega8P0Ln13h/hvnnuX+28X3wOG1pp9jt
2mbwZZmTe9N5pOngBzZXboUe346twIUG/ot858Ox6GNavo3sctVorl/BLnlc
L/TfT4uvo5Y7dEC5z8v45EZ1atHnJfDqatF4HC/w6g/Br2npQTPvnnwZugBW
XDYnFutk1pbhdrv593Da57RsdxzH65e/0bw2i/agfUlRUyD+vFEMddLgSLJr
DUZQ/l/tuAL7y9174NlKTAX7+sKIQwq0Bt9Di2zQ0XucEjz2zdaLfmX66DN8
yB/QwloCDyz6uF+EX6b4/uRkxl3jPVSuNiCdPnlCe8yzFbdRl6pWBbxEG6G7
Lc6jr2tN+SI5y6UG9vPI7j9oHTQ6QCdIHG9uSo9+6NvzmziO9y+Auk4Y9HSs
fWFIEvLm+gHH9yoNVeTHJ71g3jN+7v+OQnw9h5+rsNdfGYbn8tKxj0iecZgP
W8f428+vtfNGP+eEhgGOcVuzGP2V3aCTYl2PH3RStAETGzrsJddC96fsywaO
83SZijp4vslUv7Wuc1xtPO9NZYLp7x8uIc7/Syv0n11/8SPCfv1m0w/fSD+l
a030vycdAZ/lvT6IFwK+17CfXyniTsdLoy84+GoMz55YtyMuw9/cpKEOmKs9
/O00g5BXGT4YuK+Nw2n9E/hqhfvcjUTGV4vPaOBJlYAA9D+7riZcnuEZhfv7
9wX2gd2nHX6I9u4qdE2q3HY8d/PBOYdelTUOrFcl9Kes95P1pwwf8ElY4196
HdaH8yMq2+1agyXQYb/nVsV+fmnlQ6x7/XY78yf/uAOv8C0P8Kp3gc9X6rsj
f3V5LPomd8OPlfPUR15gRVrqW5GE7nMK8AMoT/p/J79JrNtjRgO/vdyFxs2y
a52Aq5tXK43drsVFYF/+pwvqrTmxngs+cLnQIuQzYuOIv9F49Qv1ppXgexc4
fC1vLezfYQPK2u1S0d14P5YmB24laj54q3w7Is/i/w59jo24r8GjH/BXtQcg
T7xhAR2vP8uKPEifReA9E/nwHaXRH5stuLrdrkSWQZ6hTznk/yPAc25MmoX5
IXiTuM9C8CYZu9Ph/b5/A3oHCRfAF78jEu+pwDUFPwij+9LdStvtRp5W4M9c
d7isw/5lpagv0rou/PnfH5x/mwf6XZhnRlqOeEfb+8KxPxp76lC+VL78FPt+
Wr6vtD+AewkPhv+fB3ybUlRR9DExX7GFB2a+Yi1HH+SNXUqiTn0qH/cHHUf/
Jr8nUsYFqCM3jHPYze3lkc/MNAT8WMw/L994S/NdOfyukd2uLkyFOstQ9G+K
90T2zAZe3AIPwu12tetz5Pmv7w2z26XLfYrx+CEf+L4l1U1Ev4CRshf1nRhv
P1H+X3kZhHxa35aJtJ5d20R2eUJTxAXpvyWj64z80BbXVxT5GcGz90c/nbDb
niPqapUuARd8/D3yD9OPQ/eEdQwtPDnrGAq78bqmw67nPck6UOgXluM/AdfS
tjnqqm2eQ/dW6RpP+7JW18HDr4RptC5Ik+Ir2+3avc7Eo6LH32KeFo7Tt28F
T/vSOg5/UhqWE/qnPQo46h3S9wnAy/Vb49B/UZKWg8/kYRU8F6E3new+/LnU
8yva7dp99FNLjWbRvmm9P73R76achB9l8fPUYn2lRaUddtkddTqhA2XpSrMO
lNCNsvAGrBulPoh22M1JGYAT/VmmtN2uLXwPv5d5m00PjnOZt1mp0gx9aXVi
KK40fKpCt3hhVF37fWlvDyKuYX4qixdC6H2/nQb/NSf4qKUBB9AnUv8M9EOy
LET8deYT7Qu6hj4j2asavf9K+Uj0Jb0q19h+/fqSzi70Pd+PoK+NdZzNqdXx
XgUGcx2BdXBiiwKfxvVlS2+FebREHt54An1nKw//CnUuuSVw2lLzD6hbMZ+V
hUNjPistfo8Db6beH4j4jnXErPeHdcSMEe8a2sdTP3cWOoPMXyf/TA89XMFf
9/JbPhyPfUGu3Bp1q4elve3nV6a2AT5MeuBjP15KnhH4q2a+pe3fK3AyQvfE
6ptj3ROh52XpcTDexij5zfmeM05G6KpY7yfrqigD/oVOQXhyjNug2fA3FvcF
v6d4z0+VAu5u+Gbym9TzpXA9P+cB/8c8G1adkXkbDPdM0NG61hb2yGXIn5qB
jr45veWjn/Qc0+nAQQse6aLoAxK6BpbucMAY4FjyvyT77/gK9jSFkCffGEF+
iOqRH/v++Z/IH/FHGZSC7P/lsck+bwf2ebG/u7FuFvNX6A9/OvhC9XPjg+3H
y49fIJ/Z5zril1cFSN9Wfj4CPPj7e3PegOtBI7Jh3/zLv6r9PPrGd8i7/nBe
j/l6I/LwI13oe0VfufltGvQI+2BeSP5VaJzlSi1oH9KL7ABu6dRGmr+Gvyvl
hU3zHvyxpYyvLlEb+bKLXfHeVc8EfXbPMchTxwxAPDQ4K/bBtJ9QNw0tjvf9
/E6MW+9DiFtOlUe+iP0N4256xBtTuoTa7fL+JxH8XFC3zXID80Lss1GpwO8i
cBcJHcPo963v4V+NMvl7B5JdUbphXr8Po+uU82ZBnPl+Av3dyFMe9qO7aD2V
W15y+ANyBt/n1Ac6NS/6YsV+Wt4bcXunIcCPHC+H9/9fN3pO+sThjuONLJlR
D6j9E3FlzmDYT7rQOMpTHjSxH68ti8b8zb6N7FIbHK/9mIZ142JRx/5uPJoB
/z/HP87zVPRGnj20jcNuTK6JPNDk2cD/pIBfJ6dODTw06xWKdUPoFWpDh4D/
b0xPPPfi/uiHDB1KdnXfJrz/GYqiDzwX7xcCN7JyFfpD+pek+EarehA4iwXl
sR+VSQ28brOO0NdrXITWWW3YYvDFLqhKdqPIA8pPCt0laz8VukuDXWrar18Z
mJrs4mOcv4x85oIF4I96WTbMfp3y1Hzgx9jjxfpNrFdV7zD2G9ddeK8Ff/7E
deBPyw68mDVPXzUH/u3wiFCHPcQXfX9u7siTsC6nfBZ86Xp9CfFH5TSoj3Wr
CBzJ27qV7XY111v0X6Qf4ND9lCYtpny4MWoP5sUvFf0vFfzB6zL4LPS88kdT
H425sQJwbivAm6is6EDHm+99sH6uyM/8VMw/oCP+VAPBN6y/gb8qcHKS4B9m
P1b9BJycsvUGrlvozjyaC9031hUyT85EXU/oCh3IjXiW902pKM9//zzwm5hX
x8ycjfRYpeATTntS492EB6k3Ndw+/uqsrMBHRVV32JXkX6mvRytTyx923jfL
M39C/jvI/4t51LAOXae5YCb9FLyF6uhi9FwFn5jFZyj4xN4vJvvveBDx+BD0
Wcseuz3t1yNdm4NxSzic2nH9nuB9lb5JOR3HFwavoNXvz7ydot/fvHjLEbdq
czIDb8Z4SLV9DOqGjIcU9XprH+e+SOOxG/Lxtj56+r4I1hMT/vY84GG0e8XR
/1q1KPNkLgB/0K4FwFNNegQc2oZNlB/WTsBPMfbtw309WIH3eFdO4GFEX0Mu
8IyZ6S6Cz7kA1jH1Rn98Xyp3qo9Z884rL+rHv46VstuN6Z5hNM5lvOGnLZsK
3qonc8D78xP4KPkn+rn0ihsp761mD6DnqI7chb6biUfIv1HMm8D1Cp3QTvOI
z1FKjHbwfivHmwNnOPwP3u+aNVEHWXPW3/68pEO3kZcflC7AbteHZMd99ViN
vHG3C6iTjuqP9YT7CKx6/R86LxYui5+v1gL64HLWb6iHhjC/cNZ64BE9CN4J
LWozeBTLXYK+yVDYpQd90Rc82ZXeC8tfZX1NM8sl6NKLeXT0L+wDE+dz3yvX
E+fmQx10l3eI3a7MTgm843DoVgmdVuVtOHDPP9D3oL94TX6XwMObLqnBi5np
BeHuzNpzoXsR3h066sx/q3fK8IzyjdemOexy207U96GcZf4G1qNRVgDPLXiq
5evMS8w81Xo4+J4tnpPpudCX/fEk8wIxv0TMMaoXq+MvoZ/vWSLe20+9gHuf
h35Wfdtd8LRXqAyd2nE/gLeNvk12vdFk5L/Op8D3TshDdnPWWvS5/Y1+F2OU
Ad6cxPPYX9d7h9H4iLxTr8qwH5OAv72BOFRbWQnz5z76HLU7ZSifo336G/HR
lmqMK4Bfp++OvvrfOqw+uRFotyup+1D8bjT1Am5LrJPtKwNXF1UY619j4PkF
fswc3Q35VXf2W0Knu5C9+AtHnkd51Qr1VPf1Dr/OODSK8l3ShI/Iu35nnHaF
K/jeAhOgXy1wiRtzM3+7s39T4NYkz/y0H5qzprfBOJ+CHmSTOuDvmtGrNV2n
V2ryJ5TeTbCvbwavlKyDN1vr2hL7csHzwKl63Aym652aDfHvh7XII43a6sDn
aHGHse8LHM5J8PBYOtdx5bDvNxlB+Adr3Tv/MQzjAtyIuF8LNzLlIPKjE9Ev
8Hufxns/8y7uV+QPV24BH0vIbfTv/2hJ12mWhL64/jRHPnxfbeiLBzcALrp7
CuA8y/iB76F2F9J1kNvXRd+68MPngNdU7oK8i4WXno28jNA3lE/hOQp9Q8Hz
r44Gb63g+ZeYd8vKJ1eYBv0jtquBRjs6zuxB67bg21TLD+xAxzPfprRxsZ99
POXv/Wg85Rj0wVh+RTzjlhjXbdX3BR8L9+Nb17OzsYMfVeoznK7HuBZHfrK5
MiGf/Xjday7itZH3fBznWVED/cj7JG+7XZLbYT35HRfTfXFcLJ8HD6/+rwfi
VJd8iIsLnSa71O42/RT6PtqlfuCd6F8RfA4Cv3HND/25Gwo6cR1H/sK+kBl9
jvqCeliHe+eFDvvnLwEO+/ho4PtdD2A9PxmDcSgTj76ePVND7PeldkVfn3b4
El2nUqIZ9pE5U8Gz9L9+DfBNsp8q/Fb9B/Kremn4tYK3yspHCVz0sq7Ic3Lc
LXctiPX/fgpeNzAv1BHQKde1mxUcx2cBf5o2ZUEF+/WbU8CvpHqAV17woWkn
POl+1H3la/H1U51dPVmW3ie1/Sj4O3eg36F1HQ6+xQVjBC4A93+E+ZGkGTXY
DvxAvjj4Mzfqgf9jy2Ksz4PqIO+85RHw5gPmYz3fcVicF/No0j/o01VWol4g
T6HrNSrCPzSrLqL5r3+OcuSBpVzZ6Dj5TWR1u92YVgfXoQQAP1NP1IPaoJ99
U0KYfdyUmZNpXTPmD3PY9YB24F8+OSsMzwXrhtomHDwUu6BXa2QwKI7TxqJ/
RBlX3oHP1DvsRp/g8iheJzlf8TgH+IsPbECeRzzf4aPBr5FqrmK3a365wWv5
+C54QJnPXw0+ijhw+0fkwyKPoo7Q1Af+lsc3Gid1wvp2dP5zw+GfRZcAHmXk
JLL/3ufA5+63Hzjc7K/IrnVuTnYla3fwIz5lHY02TXHdjCuw8MxCz+/wUejP
3rkPfOnAHlhPZkjol/FhPPmQv1GPzL0h2H6/avZUyEcPSOPYf82druCprjc1
1G6Xn/bDPFz1GXW8SoOAbywxivw29Vc/ztNynnB2IPwX5qXRujXCusS8NBbv
90jYBV+x+bMy1kufUPQXFvCFvlW6f3B/n7/QuEmZJnnT70IflnkXBS+u0JMV
/oPQkzXPzHL4IdrQEnQepW4fZ34p517yf+Th+Zz2c+ALNT6p1RzjVmET8gZi
XjNvmPke81rYDV7fzOewmyc2wd/cFAI8Z4VIqmcp+ecAn7+3K3DI+yvi96Xh
mM/cF2NEQZ9Yitawvk1agD6Xk8Ho87k1E/tt73jgpcf4gjefcUEiXyFwQdq8
LuhjZX9Ynez/F+FePDs67Fq3apTnMS6cgO7HLOC35YgY/L1RHdRtx8OuTfRG
nu3eLJ5fvN/NCQqm/wvZg3yy8B8u+ZPdti+A14r3BeNskGO+q1HV8f6Fgf9W
2E2PbXjv3a+C50roy99uijpOk2LAeb6NA159qSv8mCkFGD+A8ZH9xwFHs+ws
40JwvJTRHXrBvZH3MAZmQx9fWc4HTu5c1z5uypkFtG8YuZzjaXSrQv6wWhh8
leboM8CdLh+B9/sQz3vRd3YC64Laf3iw3W4WLwm8e0hUVfs4y83uAH+ck/uz
+Hijxn300czqXtVuV/2fYXxfF+C+7RRUz5KTwLdp/HyC8YjeDb6mufkoryV4
FOUKB4AnYR5FefZNrAergMczXSMo/jT3T+N+Ve4PXbQW+g65wAMv1ivjGnjg
tUrRwYrt+SpLFOiyC354tot8jnEedUPrvfJD3VAuU5vGU/T9/Yc/p/OFviJc
jfjoe9agjylkKPKgzMtqbu4IvM7iFeCNU6uCdzS+PtmNElX4eznOmqhQHVB+
s9ph1+4MwPWve4o8gFifa/miTrHyqo/dLj27gniy+QDH8UbZr/D7bw3Bfv0t
Oda9LcAHGD2GY126Ub0dXU/ifegztrtfxT7OipYX636WOeBnLNQF/t7ldsCh
BtcDzu1HBvC+fsR+ZpweWMZ+PXpO1m1sZzrsxpP6eH/SVyprHwfVoyp4XNPO
Qf2uRU/U30ePIH4q84xMeTalYA/YN0J3Rsq0g/xh8ZFbX0L/Ql6fAna7froh
7D365rDbzXUng+k+qqYQ+lTkT8gJ74DX+tG5lP06tZdNEDfu31XKcb+NR2H8
E1wdcbQacgdxV5kBxe3jrNbC89LvOvmHzaqsy3Z5G+KUHGcorpGS5wfP6p4Y
4PSG1ie78esm1unYivjehO5k15P5ol9gYR7sq+L6aySHzpTPePBUjGR/qXoC
nnfTWYGO4+OT0fjKOeYQflzgEFTvSBo3KSX6uSRP6KhKGwqi3uoSlMN+HiPr
IuCZ3tfB869fHPmlu43BY/IyxvG9hvsm1G/epQm0j4+y6hLsFSeUsduNNW0d
+TrLr+N8ndr/KepgfWdQHkCVwjEPm8Uirm86kPIAUhvsI+rCVNB3qDMNxxft
BL6ACPQvSn/wA+hf0e/4J5+AEZmgOK4/5wvwhEY3C7LfrzJxAOo3LpsUu13e
Wwy4EO6v19PATxD99Wq/jfS9hpINdR+XXFi/9s2tw9cJ3O/l9Zjnle7Xttv1
Bevx/pS8iz7jVTepX0QvgOvQe3o4j+/3CXVPwQ8g9KCZH0CqlUnwjiN/3gU6
feqcEegzFc9l6VTghWKGOfxSPd9A5Oc7NQBu6gDyuoKPS9gFr5Gwa/fAuyJ9
5uNXgw9Z9UX8ZI3D7/iKxrfDT/iT3cujL7LxdOBV39TG+tZ1HPxn/QeeB/Nm
W/zngjebdXxM7lMQOj5/9vuI/ln1LngRRX1BzyDqBazbxXb5Z6cw+v+3Z6o6
xpNx0VLh+47j9f1lgIsu1Md5nuvQ/zIr9CDchJK7YXOcZyvqoA3Bj2qdp/VE
0ktSfQwfx3k2n4KOEusuWcf/obtk6Uax7pK8+4rjPOro+mTXr0cgPv0WlhXH
/4v6VPb5qF+tXED1L/nqeOjCxMwCr8mUQuRfaSndkA+aDr5r/Rrwk1Jn8CPI
iUUEfzJ4j6tvw/U/8kBfTvtLwCG0Hu3Q+zPLFIYeGev9KROvgHf08lXGLaxB
XHbSHTgZcV8r29J+Z1w8z3pzGAcpdiv2wbAPqO9zfsb0GoR4byZ0Vyw94hI9
Uec7eaCc/fqVSw8YF9G7Nn5ynqFwHOE7/6djmAt9iKxjaHTMg/uaVB11vY5u
iDeOzqd8uHIe42akz9KMz4sP4yGVgGuod9wOdrPfr/LhLJ5jl/Q57HZzpUz7
svFjOvwdURf75zn83JHXgU8/gDqm1r0q8jN9wWsrFQ3H+1mkPPAemdvTeyv8
dqVQefA8ykPxvpS+j3mnzQPOrPoWrDd1YDeeZIF/VjAn+kpjkZ+X5x/D+h2W
s5z9eWkRkdifmE/4f/OI+YRTXHXYpeW34I99dM4jwTOsxc4inLJRZwv6ODbW
xvgM7VnKPm7GNT/Ml3m9HHZdxzyVxmXB+be7kz+mN4CuqDYNOBbZdRzl4U1j
IHBfa0KpX0189Ot9wI8R0w34E8G/F/4K73kn4OyEXc6SHXHF3AY1+Tz0vhnP
e4EXY3N55Bf77QA/yB3ku/T9sEt/5MGModhnlC7AW+p1JeTrWb/Aen9Yv8CU
01a229VPLxFvN3DOOznoDOLby8D5WvNOgt6VmeVgOfvxygfMI6VNavA8CX2W
5Iuh11AkI+JBPo+e8zBwO426OOxKa/QPyj9bY16K66mKPlVp6MUQ+/FGuwx0
Hknwu5ZIIN4eoZ+uTekTRueLTDWGvjc6M55P857IG7x3I7t07z3iKubfELhB
wb9hVN6Fn8+i0C82Ngn6LI22FaLxCNk/GePxg95jc8Ab1CtEXensCtxX8Z3U
H2r1vYZzPb3rOaqDK8Py0XmUtWnB15R0l/SezNRLcL95vLCPvBso/Af6yJUa
ol+338o6druZ5Sb3N/d2+Bti/1ZaNXGzj6fUpxjys7WCc9jtpt9k+BXbMjjW
f9lrIvCEPh/QpyXmV3g+1Cvdc3gr9vO38QU+9ff5lf/f+af4Of3khqhXyTMS
FPv3KlsOoL5QOLnDL5JbPEUfxTfWQRbvfyz2ay3/duA/d2F9lv2ise9vWAee
L6Fz+qA0+h9++yf0d8bdCf9E+eqCPHdO4O60ZrnAn8b911K9YpQHFv3XKvc7
ij5u7Xsi4ZDFx0g8CD//82rM6/6Zaf3T20bQ+ywvbgK+hWFHEfcsHAp7+npY
H5JlxPqhgvdU9zgC3ExK9B2rn7aCz2rlPPTF/bGeSCfK4n7GZxF2+phZpmId
+MNfNX/7q/Rc5mRnnaiJdH5zh0Hfq5+fif2E338pe2foJazf5FgnpfM38Zy8
0wH/vr0V5q+yCf3OmSKRj+kHPlQpXxfug96P/u803ciu7ffBfdYAb6tU4hzZ
jdngp9OmfAS+tSL3xS/+G/5l0ROcRw9oR+e/ifPIwXWwrmaGLpgW9wj9GNsM
9NOf+4h89Z60wJHm7gYdloLv8Vx+FsJ+d6gq9Aq4nq5k+Ay+x3jwgov8yX/9
bGQXPBsij8TvjdTpC/znnyOhH1fdRJ1xRjx4qIZNgb3QB9Svq+4pbx9neUga
9Nvme+Cwm/EdUHfc+Xclu119i+enbgqBLmvVlngui0OBX9n/Fv39Im95KAP8
kqF7S9vtyoKFtO4Z3acCd7Y3G51HXVYR+OmsjxB/Cz/hTAjmO+u7SfWAnxH6
btq2PoinRR6yY9QRip9qX8zvsB89Av+ttAuuV/CbnUtD653Q17P6R1hfTxmb
0ttul4rOQxw4MJfjeLkJ4lJlyztat/XLIRif12fw/ry6iHk25zP508bRRRL9
vqAZ86szj+7uUuB3KnoTePOZ0Ac06xWHP3kvvz/uC/bf+wvWu4ZFmE+Sdckn
d8M8DXABzoH7K/XzacAHGzkM8/vrflpnjKwdwSPh5YY6u1iHIy5jXp/KWdFu
1yIKI15qVbGy3S6laoM850jOd95B3k/Olxf8QfcHIc7OU3oMnSdVffQvnIP+
i8n8z/qdao5+FnG86GcxRiD/qfG6KtVG/lPUbcS6qsQwr9TveJy+/494XDvu
RXVvOW8H8AwU7I/9/sKjYPp/UXcY6or73H2imt2ulpyEfSp4F9YPq762G/tg
gRHeZGf8trbYHzrcqd/geW3sS3kk9fVVxL8hnaEbWGYM1T/0uSOQ3/+Dz1Dg
lyx+pDfAJwh+JGPjPOq/Vg82AI9pHej+mjG5o6v89//ifeb6pZHyM8UpapaG
OH40eISVw63oPVTv3EK/U4PhqLf5pgyj4wfPw3PJfBr9eid+UZ1K4FTls0+h
Q/H5Zkm73fx2E3ntL8eRf3NtBf6ZFy+Qxz5eF/OrEesENYferfkwlnF93M+7
HvpxxvZpwKuK99OlK8W32qDCzH86EH2G9ztiHlX7jn6QzdzPHtcX+2vVbuhz
4r4Maeta1AnuDvZ32Pf0RZ9RwNNSdrvx7zL06/27Nq/9emS/Vsgnxm+jvKel
c3pkPHj6mJdM8NwKP1ObFIX9PF1KrBOrK2QU109/5zqm9qIv9tnbVel8mh/w
HqpxHP5DWcxrM6IZcGt/Z0GcvMYV99FgPfYDtYPAhwg9WeARuI/UrO3FcTTX
rY6nAp/GAjncbjd19GHJzdajfvpjG/Cw5cuiHpMD6674KP6o0yiJPahPwZjQ
Fn0Ytd7hva2uv6b3OTv69JVizdCHkDKS8AhKRhyvef3A8dtQ79CPTUFdM/ap
F33vvWWog1SZQXbtXjIPPCfoBlrxGusG6gu6iL5+XOebkSmI57nHOMzLBZ7Y
f1zOAN+Yq2FZu12/lBX+x6sZFfA9vE5eBA7eeIt+QCPtPfLT5Kv9yE+QW4Jn
UwkIwPmGxfyg++S+JKVyCPrURF/S0vZ4/quroV7/3Qt93Ndq0PqmXgYvmmaW
o31RvdmN9inVh3nD9p5DPifqPXRmZwYx7+5FxGMVp6HO434efHiRhYBXiU8B
vr3SpSm/pyaEAp+wKBnt7/rXVsDl+ynJ6Xfm0bL4nJmXRllfCPusiEcejBb6
gPQxXWuN5uMdPGYiLhN27T14OFXm4VTaAH+uBr/FvOgcBn9jE/iI9ecx4PMU
zz1ZR8yLQvnp/Vf6xmDfbJqE+VFX5Twh1mEzYh3y2rw+/8lTLfhphd3S2w2d
7shvKyfiaf8V81GfMRZ5MJ6PaqppqMtcmAnejBu/HP07WuUyFp+b3a4X1B12
/dIJ4JmvVkUfWr0Y4JD31EX9vW0I5Qn1MVcQN3UaIeJHvE8XUU+XI2YiXhbz
vXpr1O0EblDwlTFu0NJDZPt/cRN9b4m++XEe9Bdok1hnoviMyo77i4vAeYcn
VbXbpenJEVcW+gf5XeG/nfLPxcehv35va+xrr1vTe6k9joV/1OsR+PjyjQWP
h9hnOf8snqPy6BTZtbjSyEt3moK6gmsg4QTFfNfaTMJ+d1xCn2ZAAOLXalWx
f3B/n3gfRH+f4IkVdv1nZ5pnWtk+dN0S94lr9X4h33TsA95j0T8+m/2lVfsZ
/8/4tBEf6f1Tmqf05fPDD5+dHs+7753idrsZp4fReLE+i8DpCX0Wff1CvF/7
kIdXSwclwzhndBwv9F/kz9kL2sdH79kX6+aY5f52u1oyEfiiqWPwd84zq/4R
0J9qVoPX1VTAOT/0Qz+YS0/gpheehv+WeyjWR8FT9/kg+quZp05KOc0R72h3
dqJ/Jmog9sm0KbDPtt1N+TY12IXzycwbnz4t8xPdCbHbzQPcL7nMwptBJ2Cw
BDz0SeC8RNwnPWyC9Sf3WfCntgDeUp+Mfcgcmx713Oa+ZFf1Xogr61VG3juS
dWB/zYTO2v/wG8xnzv0n90Q/CuxyU+D6zO+wy4moo6klYRd9vlbfeix468zH
n8Ps9t9xCnjDr4QyrzX7RfdvvT6M7wOP+LZfwPnX7QPc7SYZ+7zoS50yCPHs
pErIFzB/o95fhQ5LFX7/LzI/7bST4FU7cg/x6gnWlYhHX6p6oAPul5+vfhbx
rd76W4jdrk6Zhr6dHO5Y5wQ+JIr7UmNbMB6P+4ySDsHfiM/uWPf0NLXQT5rf
DXzAR5bhelpEg/eAdROMv+aBVz/gGPDbNVxq2u9XPr8VdbH/PUf+mKgvDzgK
XHzFbKjjJNyA/ehIirOlNTlhX837sVdF9CHy+6ZeN6DXs+hjWfv5tX+LIo8j
e5Sz29U23UU+uqLdrn85gvs85Iq/X/NF3OqG+xV9psYX6OaIPlM9PpV4D5Ev
Mu4ABzjDL8xuV27GoN8k/5UQ+/ealdsin/tjML1HZvWL8Ct/tYCfcOMrvadG
6qWoA6TvIPwHpx/7JYiuW/v+L+JZ8RxfoH/NGBZcxW5XnzzD+7GnoKN/QV6b
IPCj4sP85+CbUltfBq+ywL+daYn5JsVVttvVDmPRfxVTmXQJ5Fc+iJuqm+Bp
P78c+xKve3oH4PzEx+qvkWYE2e3KoFnYvxgPb7gXRhxfpC/NJ6VgCTqPkrU/
eI24D1EbyvX0Ry8JtyK134P8TY+ndD3Gr77gHX/L+MlZP/G9gX1Ydxj4SS01
cN76bSeuUj7gizgu8jP6m0Q/yJDdGO8B8c44Yklx4ML6VAWfrYiP/MfQT9U/
Bvgp7vtTGkGHXXMZWs1hH/8I48A86lr9qfDnmEddy/oM95EL+Uv5aBjqoGsf
os51/RjyXvUTUU+9Gcp8ztxHv+wY1osBdR12Pc00er7mvqLeDvsm6KbrrS3/
Cn7wNuwXalIvrGdJSfAbiqH+qN3tI/IA8HNeH0K95sww7P8Ph7TF87qD/EbB
vsBHFt8BvGLgFIy/VyDlUeS2l9CnsLIW8ns9/+gvmMO6htXBi2nNl+m5kKd7
LAU77Evv0e9SpFnFYU/nTXa9ySHEm7yuKlp+rIfbOuZxHB+UBH2TVetlu11L
FgacX0gP4ClF/dRtHPgfdoaIuBJ57BLQm9YGPBL+JOL+1w+x/oxpHmbYzi95
9oO+2tGDjn1BT14WuJadI31x/Yzf/tEI9fF2OdHfcToR/Vl5OmF9ZL0nSxeJ
9Z7Ud9yvoC4FT/KAEdgvxvaA33P3CPid1n+D/9lkGPII8wzojiXWxvwYMATH
3+gOPKR2GPfBvDfyV/BASskl5PFZ99byZ1j31szeHXnFbZwPUZuiP67nK6xn
sZ+gh1upM+pHPWOQ5xQ6s9+mw5+cee4K+AU537U9C/W5ybnast4T7PoiV9Rt
R2UPcNg3jEA+jfcR0/sexUH/h6+g8XnBa4p83/xitezPy+z3DHoQGV8Af33x
ANa39m+AI6oSC/5S7uuUZgyFP6nAD5L4PTG/X0G/6OQ85ex26/3ZWB/riXif
yw6hffrP/mWza0XwBL16yv4D91M/iAAOLvJ7mN2uNYC+2+/4guwiX6E+uIN1
Y1M5squhFbHvb7uB9eeeG+ZBxGDK8xiL0xLPtrZ/LPKEwzqi3rT5M/KnJ7Oi
H+XlbNivVsE4l19L+6hepDPWz9zIJ6sxwOvpLhKe58ZEjsdmiHjWgZeQKjlx
XNI09A0a963z4Pn/y/yrFyx+e9zvJ86rX+mZCt+Dj94ljdDxFXb6Xrkj1lMj
Yz9er5jPp0UB9JE+86tkt0s3JsD/rrEI/7fkFNb5UvOB4yoYQ+uwnHkX8h4p
1on5hbyp/zP4rR4Nggyb3aqnHGgIv2HY6lC7XbrB/P9PSgk/C5/Mp4Hra1or
NZ3/r5TQKduwEPk01xaOvIj6Yz719etHb0O3enRxrOtzVoGHi3lCRDwreEK0
MbyfsD6UnhnPT/CHyM1/Mh8s+ENEf5kRzfgr7i/T5qNuYuwZCV6CY2mYf1UW
/iT8vX/QHyrwesJu6cr0zy/6vfDfe4fDv+reN4fdbq49CX9ycEZHvkg7NRrX
0zcv3rtWLcBXfO8b1u3oEuhXYhyUkvgJ+owbgI+zruflDPAyHGrgwLtKxzlf
YtYiP1Orfh36yKeSIZ/8wA/j3B48ycqVf4APz1GR7PqL9eBbaDwdOCoX6DUI
/mExPkbfkrReqZvLAr++ojx4fvbMrWO/ToEz/O//6DxvBF8Wxl3wwP/Jl6X8
lYfjQ56nUfPpepQel8rY7fqFoeCpG1IN+c0h76k+L19fiOOzdAy0j4/Rtxdw
/jH3HXZ5PvS5jc8dwu121XsH7jc3+lAse+GVmBfvTyJ+PRdCOCU5ZXn0HbgM
Fe8JcDLj8sKvL5jP13795o1Mwf/9rmV8UNxuV/+Jgp93LAv3r7EfPuEe4yNR
57L8nxyzwS8aCJ5d69OmIMZ35XfMu403kX/uPR3xYNN34E0XuPQAb+xH0cA7
WX2jtz4A/3DWZN6seejT8RiL9/P/069Hx5epKPZDjENJz0J0/me3HTy4Qp/F
GJGipt1ubjyL/MKi0pSP0oO/oN40JJTy5HK6ko48ojKnL+q7d6KQlz48j3Cw
pk8E6qE9djjm9e/3CnnLwhsC7XZzV0bkL8zqPor9+LkRwGlz/k3sy0K3S/+a
Cf1cQkfG4x50rluEwI8Zz/25TfHempmjmH+PdYt2lUP9OF3G/Ha78RQ881Lo
W+wzAV/In5FcjqRTbPcv8lS/P1jf6rq64Xjk9zT9AvIJXG81V/am84h6qzJ7
IPqsjfHoX1BX03zW8/0Cnr3NGPBjezQCLqiEhZ/H+Ky5EEy/72mQzrBdj+G3
Gt97Oh51yf350Nedfwf0Jn1uVLOfR0o4hfz8htLIlwt8Sy8JfPoCj/3tCq1v
Ao8t75/iWDekVtmAO+/Y36FHY/qlw3X7+Cp2u7J1jyv9Pmwh+nZ53PRz0Dsw
S39APaZqPvg/fo1Qj8hTEvWyW6XIbvjEot79+hfetwXXUZfc0Rl4XM6vWvl5
5nnTQ5sg73ryIuKNO8NhZ14Iq44geCEsXR2+L963/szrSsFVgS/9S3PkgaVc
PZHfPG6iP3pqWuqzU+egn9xoNwp1A6k88hFdhyNv07QI7mMl9I7Vf6Abai6t
Dd0u9uvU3JFkV9s3JX47uXtZel7Sg5zI50+BfqLSXkU+q3Nv4GYucBx1oCHs
s9ZiPY8G35WSU6fnYJS4GEbHc/1C9MWL+oXU9Crqwh0i0Sf1y4fsSq8KiI/O
oO4vzUXeX/hlYjwl9tv+88Pp/7i/WJ85FHXbqV60/iusW6FkYl76C9PL2u3S
qK7wP82X8Ac5X6F1fwo/M+YOHW/0PQe/rjL0arWsP47TPufmRu+/UmIQcMvd
n32i+ZaQA/bErKjHlUJcYCQwz893+K/aJ/izUkr0IRpzeD8uncK5n35559DN
sngVOD8jpz6Tin4yb4bBvBnio3+diOMZDyb6C0R8IfAMEusXCP52KVHomrC+
JceDOtuNu6xvKfQCUr1nfIzG9XTOM7A+qZZtL3ho+KPtGw5/98xf5K9afNHr
AjHe6eCPiDyzOR3jI+2rGUZ2od86/SjWsxsnuY7A+bdN4bS/q6Occbrs3Q84
gVKdnfzJiXVondJS1nfEg0oG8Cwp75IDP58ROC45b27Ej90qUH1E/QU+Q302
cH5aV/BICD0+wbcgLc/uyE9KAzWsJy/2BNntZup1yJv1eFrHcXzr64TjlHqt
r2236y4acNijFtR12DNmo/3fyBrnzEt0BI5ff9e3kP14dWFVGi8lU5kSjvPs
2ob1PG6MI69rXr4q+uqd+d6vR6AHoDrzxmZsEeC4lsRTPlZ7PRo42LbbkIcd
wPuR0DXO0Rl4KtbxEfuj0PExPVTkJYVO8bc94McpwfOI40Q5ieMFP9h/v8/k
j4h6hsBLyL54vgIvoaRa7kLjxfkKtc1h9Ov59PK0281yN8S4o7+J6+9a5jT5
uK5Rlu1OP3dy6oL282g/06G/7HiNYvbzSKfC6XehpyPymUJPR03fH3l77keW
mzV+R/tP6BbsRwmhqO9fyv2I4p7VDzFPxXzJkRl1iiYrS/D5MV+uwi8131by
t9vNGAn+6iboIGj1fIjfzNwIHQTz4FvY+12EXzR9LPoxTfTTWfj8OiHggfRA
P6mF+41BP+l/OKL/fsrZoeelNWQ9qfgc3F8JHgCz3jv0cTAvgTwQfGiCl0D2
2os8Xnwn8CoUN9Hf6B2H+KYQ+BZ07TPq+qwTJK2vAfw26wRpWzdznyDz4fTV
MQ6jn/o47J7p8DxquvI+yH3B6dJjXc0+g3ntmG+59utf1Mc9erbTzvqwmlEk
xG43cz1MQdfPPAAWH2mH0jj+Y0vmPf2IdTXyHPohI5phPhUzwK9+5gnwoNyn
ryjYH0WfvlQXfMBCf0QpAbvp6Ym+w//H1lnHaW01bz8sboViS4FCsMXdWViy
CyzuDgUCBYoUt0KRsLg7BYqkuLsVDe7uHty1UBx+9HzPud+E97n/4bPTNHJk
zsg118h8sXOaOLZ7Vo/nlWvB8AppP5vwLal6K9mPzKh1kzyd6n+d5V+hZ+1/
qeM0DuwnX1k7BfvnYA7yJRL3aHZoTJ+X4HfEwaUeMEx40Ox6lwp65VZ6yedf
8LAvrmhWoR+SdqCHj2fM+uMa8a5P6+HT6L1K1D05H8uxbmWfGucH+ABVnxon
0zDwI7LvlbMkjTjv9fSSdzczfdD0L2EfBC6oamdxjjv5+8CD1Adee7d5RurC
eg6mzrFdduJCVfNgL79uLuoi7T15Gc8PO8ENS/4NrfkboV+sXclD/vvvenGX
fiinwiLE844c8eE2VT2U+/KLD7dprk4HD2adChKXK/tLlr4MjqilzbzIuLrW
QxfXmztM+kX8TR26nXg19U7blgj9GugTfbAXdSbbq2f2yo3D0YmbznmblPeN
Q5ykTmnxXKvDM/gp64Qjz70Dnnf5c47M4nzJuiu/Xz7YJzdOcp4YzaZEib/d
5sQlkm4Hf3BuBNfXjyP0kVVmGXw37zcRL6p/Ed6GEZNyed/TzKKJcXdjtszi
k/8QhN0wvorwC9xJ1HFbu3rDIz3rIutkMPyxduWW2PetgiXPVkZxH/f2FWE/
Wk+fgdePJ/tD/dxA2C1uw3Uiv2C5dRn/NcuIL/U4jn2yZRnyP5NR1xbtuuSb
gufTeTwG/3ntftZVTYdzpFVO/P4YnbBvjxygbqXdGPpNLOyKvOsk7pPw7SvB
ozutM3VRuVbz3LOJ34j1X6mnGIcAP0nZH9N750sb+4S6qk59ib9vvSb0j9M9
A+MwvQd1NHkui32kHWN+zapnGM/jv4Hrm7aCurPG5fHznpml5X053+8uw95L
uzaOb77KDskg7ltiVAHv+LgO864XOPFFnPOpWsh5aYWdUTgNdQF9enKfRvlE
nw67ckH8RZWH7V8cXq/LXUJ98t++CF4v9+Fg//UV9gWJccxXDr+7Xpco8V5F
TovvMTcvFuebtXCykOsrakWI//5xP3XMuSSvV+I8Yh61yMn4f//uENfbTVqC
lxiD3a3/QzzQfXkdPNW9QByeOv7NMp7vjiZulEjicqO+w69beIW6ztVXwOEs
KAd/0oaF4AYlvte+i53kzHkg6tmVHtCWXSFekJ/+GAG9saEEvMFzJG5d5rv1
TrOFH6N4//SQCfCHSN4/fTB1vop3xQi66OMDtDPLfpeSD9BaVonz6O0o8uMZ
MnMeHW+CfxmC3Jk6jPXRaamvntTosl3GG9v46kmNaBd89qD2Lis457EfxXlh
RnzHuR2dPqfm2ObEN/KMhi/l9XjOi7r0+TO+7yH56sFvWFeS06fm/N8+Xk0j
zSOxPuy+u9N75ealRiquLX4BPrFv+qNZYQV8cqNmTniuvuF9Uj9nV2MfrsDq
11rm8TlH3OTNRL26OxF8nbLTrFlT0PsJ6Pdn7mnBuTkqK/3+ZkxDz/wDvk6r
At+3OzAt73USXIQ2ajv41aZ/yHNN1jUMPUsd1MHJwn8P8CfcrCP9bvp52pLf
xv1AXFX/kBv7Ll8s5K2fC7k9J1Fp73dZMVrCw/zxml8eukvgWo0iF4X/FOAx
LnEIff0IHqyAfH9N9HJEFeqht5JP0R/fIG7xCl5McxNya0Fp/N9LjYSeD8xv
X/o9aOd3k+9oc5R1e/YueN1Fg5J4r3f3t8be3rFN6Dnz0CbmfdkS4nBbIslL
yHWiHfgg9rszs2l+r9yynpNPln1Uvv5UnEPYN3rjudh9W1NiT7753Ycrtj4G
wysrccVmowbwVHdj/M3svxA/STRH9jGhb8JX+4Y81fk49G3ZIMenU3/qUTfs
FfEk51IIvI6bxxE/GRI3kvEHf+Lmic/3zBko5IH4Z/uY9AeNelnWKzcy9ub6
paO/F3LFf746hHy57OOp9qnq46kPWsj5s0T2oe4TRv45/lb4cCRO0krZWeJK
ec8AL2KWddStnJvnkzsjFuI/vqta0it3564iXlF0Q3Gv3Bw2F9zvyHYiPhHQ
Jwtj+/DA+hj6ASk8sO5gR+s7Bot1ZVZYTvyw8DvJs8T6Nyu9hZeyU5FKXrkR
rT38kHGz+793xHfESeKFRHjl9py52EVVrhhe+X9+ipi/2fSPNjdV5Hs3kNd2
1xckj1MnSthX1vaOwr9S9R1WHvwgVd9hPuvHvMh4o/mxNXwpl84K+1PZA1rW
omK+tbXkT4zU4EudCtc5vzLdIq92DB4Aa/026qDdSpyrCeV6vgQ/uXEyH+fR
JexauzD5R8PoyvP3x+T6uVPIP86QONIvko+xGPFSfdUj6mTVeI4eQP3jlJSy
P6/k6b0PL5ZmV43J9ehDe9sN6hBaLBG8/gE9GdKUfGQc+nercdbObaP+4WpM
cJPTc4vz2n36Hr7EvtGoLxj3RMZL6e9rlv+bOmJpdzl1d2K/ZUwFP2JC+Eys
ybvF/Jp/3c3me//u2cFJvEiY0SvXOpcR+tk6Ep9+epJXRGsw7LLQ+xJvaRQo
AN/ItGnT4FNJiR+w/R740kfV94u4yqw05DlVPWa0PsQB2pct4pXrDdaBI154
mTiL5JU1uhvks0YcEu9v/P4z/UpylMMPrZeQ8+19e3h4kl8Gr/Y+A+uwDH1s
nbGzyBtk/si6fQm/ivvmX/RMzJRifQb4aqK+CB5m88oG9keZC/A8H5+KfZY1
F3jyhJfaM38jJY9YHvKbbdMjjxiK/HEm8lQyDqP4x2wzk9BvVhpw5qrvldUo
ulhfimfe3kF/BOOkXA8V8df0DLuFPW0sDRP1MebY/sjrvhD+svV3DuFXWoM4
F9z6X3w4H90ew7wrHP+kzuCPCvyN/qkNPknbW03EkZyNwfQtzh/O+4z+g7or
iY91aydhPXfuI+R2+e7wq+ZKBk4sPC88W0qP9YFH3cneI0L8reKZ+7pw/+Rp
sEM2H2a+ZkST9ZZTffrWbET9lJXncTGffC/8qHqlLLIeXO67HrsfiP15OK5P
brW8E0N8T+pZ/cS6Xn9GnO+We4S6DtnfJ3B/2d/HOsb9A+fC6nTEC2qHl/bK
9TVHyVM/LY4f9iEGft6pKSKeaV//zHkh8TB2TtlvstRr/AWFn+k+p5p3HgPx
Imk32ltWEOfYMIg6epP8srY+FvjTedQhGiM6Y1+2iEdet/QA6rgfgIe3fwqT
8TTsBH1cR3C0WWeV9cpdrWWQuL/KDyp+IVl/oecuJvwU+wL5d+N9HfRIIk34
oYpvKqCXu+DHqXkxkzngn7fNruuTd4Pvwz6SuJ5Xrh/ILOTO7i91GX9pP3f6
TtY5cz67x6jrcSfkE+9vdXmJnzQR/RDw+4wgob/dyVK+Mjf9wmRdg74ReylQ
15CkHLi/jb05f3sXwY7+qs/F+3TDHrDfdRfvqS38QeVzxc9Nshl7JsEZH+5Y
+7EuPAOr85fwfq87ZA34w32Vivvk4waJPKYe7zH1Oeo8OvwE/S7rIlX8zXKa
iXo948byOt5xs3JvJo65sh+4yib3iZu1b3FL5PN6N4TP5GlO4o3BxX361u6X
i3NN6ltjYwahD63T8G9YvX7NwPtY4DxWnmPcLq4Cd3LsoKx7kvjnFPzt7Kff
pxa8hfXQfi84M/0McYv5i9Azm/fRH+10L/4tuo3v2s+60l8GVfeN2+qp1DGW
3+yXB59DLxUoIOxzMzZ2iBHEPrePZyYv9vdB8qvXapGnmQiu3K7THb67r/7a
f9cZGUdwXsi6UWWHq76Z2l/kqVXfTCPzn2JerIllGP8XkeK+1syZ1DdKv9Ic
z/rXYvbyyfVaf6G/+h7z4c+NE20lHjNc4ViYtyCNOIvqG5gIf8RJhNxYrcl+
PpxTZu8E4EQ6JPHXg0u+NePoUnBnb+jzaz8rhT9Qqg785A8TcP+z9GPS4peE
537NZ+poho0kL3hkFvs3xwD4oK7keS/sk+AN6PupUfBHdU70UZyDM3KxD2Sc
wS4STt4m2yz4ESUPm9Jj9pz45Xzy8PevRF49PvrDHd0IP3py5AuvXRToKy3r
UJTcup2Yc3xSTupzrw4gPyT9VmtUNnCup2V9Vk7yOPaU72Xd+qDy3nF2suRh
3afo75O7yxzWZ6yhwo8J9DEZmZr1uf5RJp+8AzyHZjx4IqwHy6lr68F57Ryf
JM814jDWZMmjMa2QT24+2iLitubxyvW89zfiLOT+6Qty/1Ny3QbV5z7r6R/t
dv8Z/XTsCHHvZN0j/5NbuWziqZFvsevluWY9oE9f4Fy7spA8e1YXecFSrJem
9Jc2jso6pq6V0e+da0hcNP3R3LvhyGtO9Mntx6HEh0/3rO0dZ21LNYGb1/bH
lueL1KsfUzK+vZbU8cqNv4qAd+z4hf144Qr++6ffOA+SLiUer/oVphrA9QeG
+OrfzQ5h9BlPfE/472alVOiH/cc4x9vB52AUKIG86Vz4WCrAL6gFFyaOlyKv
iPu44XF8cTbtc236H7WswrnWoSl5yT9/Je7020UxX+am3FHi/1tJn0ur4s2y
XrnrXsaeSBIE/i7tcHB3X+LCv11nh7DfnN1L2Y+l4d02LujE0T+fx17tnUn2
LT6EXTfd4T7F25J3zLYjv3ectb9qgtdas5G+KxJ3pMe6gb9Q+xxxx+aR4MOb
4ke459/hL3+8zL5YH4l/LvueK39E9T3/jy9R/Jse/WNdLir4KlW/G2WPBZ7b
sYa0eyUvhwavtarfUXlDVb+jpYmiPr7OROKW76YQX5L91tV8qX7rdpPBIl6t
l45HfjbevhAxbrIfq14xGvEx2Y9Vu0d+Q+lDc9juSHF9+GDqQN+tx4+tmZt+
7aN/4e9RmzkvsoOfsGZSH6r9LHme5v0BvvbpZjk/kj8q+wD4au6GEl+Sfb6M
OgZ4mlnFhN3kFr0mcHpmmb/hO/25npAr/JX5ZhN+U78XMn/HfrTOXSE+1m+w
b5+6w/PD7zNtBPWdR8+Cc2s+G36hcZfBi3Xfzfjc/Jn1sy4LdrbU5+69yfTL
GZ+Q71Vx9XQDiVstay15sCUP27rioj7a+lCzmlduh0cXddlWs135vONvV0+J
vV3gVF6v3PkYBG5sWjrqbSWPmdlY8p71ri3jPKwH22oFXuVqaLhPvqUD6/D0
/HDv/bUh78ifriC+G1hXN6eQ759Z8gev3DGmo68zhGbw3kfpcTvzjQze662E
9ZB3OBXhvd4s1o08yq3JhlduNEjBe9/fL+0K5HrlwmJ/GU9WET8I+H3pJe/V
T77vsupTN2Wn6s/9isLz7/wseYqT1mDdLf6N5z55Lq433jZXOGfxc6/TD8Ia
eRQ7fF5r9PnARX78eqAu2CWOljy2iGMFePNWh2HPTC3v419yBg1Cv7QLE30M
A3HsyQXpK5HhKvtN5uXNNvRdNRqWIx6rzp1iZ/CH+0tenebwThgbNPgGkhp5
vdc7pXeTRxsWPb9Xrpfeit2QrTh5kkG1GM+w49TFyz62gXUl+9iqvsaBfI3s
a2z2KOKf35Ua58qSnnz/zO3UYd0aQHysFfVWgXrnj6Oof25xHPyC5Fe3D6am
niLDYPJXal1pQ4lryfi/WRf+IhX/N6feJv/1Zxr0f/dKAt9p/rpSnMtmX+wT
u+YW7MO6yN2SzLszZjvxqRWrsMN/lfaMHkU+pXBdMf4Bu6h2c/bjqFqlvXJt
7ilZH3vF8Mqt8sRjFQ/etzy91p+nWL9r0VfmrgQ5mF9X+ENWDHDsdh1ZP1Wu
l08Pm2X2grvYlFDyR8FzqHe4Tn+Q7WmJH862ec+nS8lrzqfuJcAn8CYGuLt0
vajDn0OfPyPNUuyHn0oR9+mYTsitH4uK640Jj/w4+Vr0/dEbZY3rnUen9z7i
t0u3M3774NFyG7Qj3zfgHfbVD8TN3N7YdUaCdK9FXCfrPM6HZLvrep9n1Bkk
cCBf/SzsihTvwP0q/up199HLZb/8wLzI/fI4rYgLOXfySPtH8l/NWynGxRh+
EpyUxA9r1md4tPpPLeqVm6sTMV6yPk7ZCQqXa6faj14aeV3sC6PBBfSMnh9c
aPrdA/le8haKP1PdR/nvzhXZ72agxDlf7Cn6zRm/DwR/JP1NPWk24b8bAz6T
v33VVPDZms+TC744u94h/G6Ft5+G36143dQ42JLHQTuygvrOrEe4fzi8IXrX
8+A3Or4XcisWeUAjeRr0T6vXfFfXKpwXyzeJcz+Adz27jzq/hNSHBuR7N2NP
SN4k9Z4B3qRL+3xyfRp4V6NglIwzB/hthH1mXwD/buzRqPds2IW/Exzi/Gzx
GX6GGEM4zyo+kuMv6wq7RKHfG00t45UbQ77HD3ou86hy3PRgiZvdsJY6hSro
K6tOH7HOjX/xB/UaMs87UvqDJcPh19xF/2Jjexhx8gU1qI9QddkWdbVamell
vHK32Q3wfgMTl/W9z8FC1K202eizH5xK+4njN/2DfKDS/0Ppt2pVf1jCKzdP
P4oQf0u+uID8MfauM+YTdbrf+NfWwOvwu8yJLvKh5tAE8P6kLER/nnvgeeyS
azXxd5IC9CuT+8vdThzMzQMOIbDvNkr+invtsIfTXWd9zoiivjjbP+L8dWI8
F3I7zXtZV5yXfMh7cCCOkY34fJNA3aXYz1YscNjGu0BdA3UVsq7BOHfUn79e
abC+LxT199UdOO+u2I9me9/1bq/PD0Wc4U5heFCU/ZB9u8A564uTntjhkbuH
s4KnVH66zOMH/PS9VSPF+Ml5135aTH5+rhHpfa5Z/hVxvLldBD7HntqAeswq
uYgDFqriq7u0suYi/5h0Jv7AeclnPiO1uK/99rUvj2m+KiT8KafkrIpeud3p
E3wmhy0f/4Aelpnzsl1nwyu3qtHX2JnTnP2h6p035BZ6zHz/SPaRkf2zwh+A
s5X91wJ64NlYgcuyj1YU+yLQd+ZRTfyFZ/fpQ3cjOesqKtUBMS/NDqFn1Lh1
KwjupNs8vqNiFvgBnFHE9Z9shRdhcB8h187/gr2RcJzUD9j5brnW1LluXBnu
k488QtzyMniPwPpPX4g8y6yYpb3XO0mrEMe8166IbzzfN6Q+9vNt/HjVR3X4
SnDMffBbA+daw/ngPAJ1PcSNVV2PUyIKHrT99PF0R7Xke6v9BM6zXQV4b97U
oF/GXNnnR/H01qIPkH77dFHv++uvwgQvltHrQhGv3Oz7vchvabF3hIj5cWKh
98LqU1f/41LhD5p7iUtb+zITd4y3AXtpf1nZx+c29w09Tr474xt428bsoQ/Z
hQjZP2iv8FvNI0/wj3IOknacjPMsOC6+X69/sYBXbh6MBd+rqmtuvBHcrOTN
dlt2Ix6v7J/m8vyb9BC755ed2CG52xDfPpJTrGt9w0LmPfw3+l5+2AnPpzzf
3dHlqUf76s/yPnWixHO7/E5c6Jv1r/oP6l9W+uLGqj+F0fCQmMeAnT/9IPO6
cT58XUpfrcWvtH6fGWF45tdtuIa4fQc73Cu3NwQR16sh338/fX6dZBWpwzoz
gr5Scr25OfEj7JZpiBOodb45M/7CO70e4yDr9JMMJf51LYlPbrQbCj9wMYnn
VdenJD7j5rKxo8oX51zI3R/9f2q75GOR+ifdbOJvO+vl9Mr16fmZ75VrqddU
/X/zbCHffS+WxF1wDiqeIiddZeK4EUVFPsA56Yj6N61xwire7zWSlibe3uYc
cb9Ji9gv1Qv/K/RYNNlfcil5QPvscvqjhaSt4xu33APQyy85v1Q9kX1U1i9d
lv3YVd+xudfFe1uf5pf0jpv5YCV1aMsSGL5xnrFJrG87TU3Dex+ry10hdzfO
zue7/moO4uHhNnXDPcEHGNWLiTiA5t7A/tl2g+t/SQeOP2Q6fPx3ev0q3uPz
bfRPnZVCro3vLeTOikTE34aX8O0Xa/8fxKUlD6o6NxUPql35bbBPXpo+TVbF
LjX4LuKfesuXzN/b/DW9cityOnmlR5N819vRBxA/OlSIOEDB5EJupCXvb7eZ
5dN7Wuqq6JeTZgGv3J0egv8YJ0EZ73jaj17hv2SpF+6VO8PmsJ4/1QEHm+Cp
eK7W/jP7OtvIWt73NIfOY746Bvt5hr/fyLxXGlDLK9c2rAXPtHkRfnftkkLu
BF+Ct7JZaZlHln1sczmM5+UL+bzf5Rx5Rfxx5mapf2Q+994S7C6ZR1P5aKPA
afA5U2/U9L3nz1MkD1i0yP/kWqss4MeabgJPW+ExcZoSoeBtssUR55RVuADy
7BnIP97uT362PvwnATx2mmB4FxvmihD3m7qJuoadb0LE96/Zin83bzN4sD7U
t5rB/ct739MtuDK+mKfxezj3X10m/vzSJI98pgK8lxWbCbyE08hAT8WbSr5C
+TtXz4DfzXhRjqeM29eiD4J9pjPjv6qFONesatfEulQ4MZVvVTgxO965Ul65
9mYy+ctSv7Ifuy0krjI1jqhztw/HRs9MXYMflGfoVVmfSnxiXlXxXP0U/GVW
yQz1vONgfI6GvdejRz3v+xvzzsP/FT9M4LLsVCOp+z5Hvy31s7KWQC77v6h6
2AB/puSlMapf4dwvsJ35TbuO/EiG+OQTZR2K+z7sg7DPTy6v7n0fvVAhzulj
qX1y50sM9PPy++AHt4FXtBPWJP8r4zzf8nYG+MNTkl8I8Id/0y9D+fuq3i2Q
75D1boqf5KudJdZDgNerXGfkNcjvuLPJA9rrJkp9JfVM/hYyb16CdbhQxhN6
HyTefnmAT5/otatHE/9OJ04TiPsNl7wtmlnYK7f6vyKem/dSBu+4mUuGpxDX
pZ/NufZiCeOwaRs8KQ0K+fSqlnXTPyK+MWGgT686TVYKvWfqw4l7qf1VvTPy
XnOJe0xuCa7+dGbiqiVW1eU9ZX5B5mvUzxky2ldnoX72nHb++ovyG6W+knGA
G6nA09QdBM4x9ALf1aU162x4WvyAC9vI/0aT9bMtDxP3e3BO5q3GUm9lTSUe
pnBNvSMY5+9YR9pz8inGhj9k3iQH/19NcCmWE0/k9bSt89P4xi39mwzi34wd
iWMrv6zy9wLvaH7oRp62YTZw8vOO87fkHf+Wh9yumkHEJfXaW/neRg48S9fg
j1f5L2sz+S/7C33Lldz8Dr47Y95Qaa+Sj3NmlhL6x14a0xdvcWPsIV9Y0PXJ
nQN3iU/m6YtdEengryUZJ9afW4N+O9o++t1bucoI3JKebhRxHtlv2i71J/bB
xRAR59PC0M/moBOMf8ed7Avph359H+oinvE+Af6uMQU5r5P+VcY7/razGPvh
RmRtr9zaVQP8ah7dLx++APxl/YzIV31kvQ0dj18RVgc72ogBTq/3r+CTZN2K
pniiXl5nvUochf1Z9jVWOIpv4o2KR/3r/pc4aPIF9ofGIq5uXwj26/OEc7D7
iy0UOEbFf+X+KOt0h8Yi3iLx4daYbsSvGjXGHlwbFzsvTndwMr0L0b9isibO
Qb1WWeFvm5fg63Oj1jHv+R9gh8t6QDvjUJFPVPWATvPb4I3HFhZy3a7A+fc7
PHDWGdlf7MYn9Puzzb76XONkTM7NpsN88UBj4j1wY1qPcK/cjZGPfT7Qln49
69n6I4i4ZMHW1IV/zCS+w3hRC9xLq1LUBQx4IPIe1vY85KGfxg/xjptW5qbQ
j1acogl88rF50IM/rcvolbsNg3j/qT/Cm5GGc8ddMRp75fBY6tNln1kjqi28
CGX3kedXfXvjbmKeak3y2Rt2G/oN681uhXrlxpVZ4hyxThTw1bW5LfOdFfp8
w8SCXrn9cNx5UTc3ysDuOibrEFO8uS5wRnss4R9ZeajPcrqPOinkdnX0zfsZ
zRm3UuQlYiQv4n0frUBF+FV7dCjplbtT/qHuOEn04l65tWAifJQynhzoHyHj
yaofh6pHVv04FP9DQI9J/gctx3Wf3LaSyLwwdSQBXHSJbtRN7SLuayWrKuxn
OwX5JBWnDchlnNa5rvxx7mPGWIOd/1s8adf54wbOx9ziPHdGPxXxE3uPTlzs
aW1hnxphb+Cn/Zc+pObZLNiJ26Wdc3s+cQ+JCw3YORIX+vWHnv50gvjbeHBf
5twx4ByDyPtbFd9T57NzPX7058t9+f7tYj+oPhqq/l310VB8R9/yz+j7b/Lv
rpvgahYOoN/c/tOs3xp/gsMJoe+XWw9eOv3iDeRNetJn6MJSyT/Ic7WyxcjX
/o/8grjv2wk+3gb7g0s+dPe1cK9c+62jmCf3u3jkDT+Rr7S1lGId/meviuul
vaqnWyfWsXF1IXyuNxj//3BQDuMs9J/a787rYYz7z8QtlNxu0wF+s7Y1y/mu
fxcK7rzyJJ/cHjk11X9yZ8c4IQ/4BRka009N9jk1zj4gT7eYOJKaF8XTonio
zJhdiXc8Rs/Ykz6Rf5F2ciBOJe1kha9zFa+1rEdwbiXbK/SEPGe1p6nJ60d0
BOdQcwT6/76GPiywnvymqm9NEgofdMZVqbxyI955sQ71pZwvSq4PnAquceJO
Gd+QdtTHLKJO23ycxyd348QQdd3u3r3hPvkvM0QdghFtJv6yjDe6vWOgn4O6
Cn0f0Ocls8D/0OY6dsQDeIOd2SOIy5TfDl5luuxnNCI4Ujxv+sJI732cwTr8
MTk+lfHdf2w/7PU+N+g/IPsfmTXzUB/bYZ+wl42HFut8+zjer9YRvjd0v8C7
WutjUuel4q6ryslzkLirPvG20AeBurAfqVOzyp8v5pVrszTkE6v7r/8T/8Vd
dgn7uv5C8qejlwueE2fWCIlXlOdv7WTwF313pqxXrl1spHhIffvF8/PJzbhT
xPnqdDru2xdu/oW3d/yP692wvj+K90s3SYy/2i9OsdKKRwY9p9at/DnfvQIP
k1n2IzjR543AXbeYRx/FtFJeoqSIk5t1C+FXZsFv1ZaMDxHjLuNpVjnkKp5m
LJ1OvWlCeF2cAuHReH5i8juSn8dI3D2diCsmLQ9eWOlzyQOmPdkh6ymIc7p7
21Pv2m9PWa/cmPRvcfl9wfJfxX+GPr/xEDtkcX/8sv5/ZRD/ZnyHX5UWPky9
ciqRp3ebzST/oHjm3wXjV6afUdort3tK/pfZwcx7/Z3ElV4doZ/ywaTwkKrx
D7bhc6idC3y75Lsw79Snb0K/RdRnSJ4orXakiK+aiW3sxA7w4ho9TwicmLl1
D7i7Hf+yDvduixTj9vuOIt7nuuszEcc4S58BJTeqzyAOsjeM/n3Kbon6QfjL
ZsHqBb1yY50p7A1D68U5JvEz7rSL2K+JclT3yq0z9D20164S/o1RcAnjc20g
100cKnBn+pvdvNesVsQtT1pCbqSA59zei9x1piGXdU92VFz8T8kjZL1HXyke
Ia1aHurcpX2ux1iB/7B8i8i/6OUHCbk7gvqpr348dXtdj3L90ENcv/k+/XTU
vq6bFtym/NmxfgS3e2RGA/G865x7gf5W6+9QT3h/UyGv3LY3fdsPQvIWwv9l
DsWfCvC+XoAHQFu+iLyE6vsw5S/yXG230ddX9X+PnZk4WOP+4GE+T0Y/PPwc
8d+/htWTc7vxOOKKWZqC17lcBr9G1RG/Wwje6Zu6M3fGC/ylwZfxb6po1HUO
zkCe4B9wDc6RIPgnt+ZAX4Rs+Szy8wv7sC/uXmBd74oLv4jy155OjWQ8ZD3Z
ruS8/2f0sln5V9bVnrFivowi9Ck2ssq+w2p/dXxOXn9gP+Kji7Jgx96tgf84
N5/0C7Bv9fS/R/BvOuoEiwzEDuzl8P4z8BftVLIuIFkiztc4PcnblnxCHuH2
X5Lf7ITQQyoubbXuJuJ+ZmKLeRu4mXV7ulkGvncc9QuqnjQT/V5VPazSk6oe
1ur5Sbyvqve045TDf+/wTMiNeL9QL5MwDBxU47AyXrnR/gvx88I6du4vxPH0
GD3I15oV4aNS+uT5KOLXDeeX8c6Xsa4+9XSb78u4BLhcu/RI7PgmbXzxCvPj
VGHPBOodvlzx2V1Wj4f0u8h1B3mbteSz6r6AT+8VfOz2kTVCrv26DT9A8Qjd
LED/d207/MZSrr2uK/Stbd6Gz1LFpVdmAu8i88iB+iCZR3adbCW997He7Rf3
N9KeK+6VG28P8dzxW0t45WaWgvTN/DU43Cf/bYTwz/+Lu8rnw0t2DN5p6+yI
OF65m0sjblW5GvotfWMhdxr/LOXlIrzzZad/Ch6vVK9w7/iYFcDvGb2KFvTK
jV8OcC6EHs/llet9+greRePD6jze+5u1m9P3vHF33/VW/Tj073Zm5fPdf082
+iCHJBJ+gN4ylOtz3SA/aHXyXe/Gpd+3cbGayKfpWU/jx9W3qEu8cCs910t7
MuZI8IgZm8rzl3Vobp3H/k/YXNQdBvpcbFwNDnnSduoGlR07dSl1R58G4q9t
GS/qlPXi++CL6LUT/+5iYSG3hvwj7HurzBH0SuyJQm78it2vhWolfeNQ7xbx
ltVWCe94Gt+nIH9dMYh10XtQR/Hf003fK/bFqxkR//2t7Hnn9ED4CmUfZyVX
fZytD9lTeuVaj+rge2vFyOCV6+noz67NSq3zXIljjFOC+tuNn33rxwqKAn8Z
Dj+5+UXWXcZCf1lvs6X0zWPblWLenS+X/fIP6cW5qaeYnMo3DgVSC7kVy4BH
4aUh/HR7yxj8uM95ySvLc8popZMvW1yC92jTGtzX3j+FnWwOA7ejD8b/dYMu
ovfv/kI8Yyp1HG61mfi5lYb74q7a3nTkmUYO9O1f20yGfMmD9F65NhceaeNd
tpReuXmvEeO/uyt9kAvIuo9fJ0WI7wgbBn+tmt8FzbBPEl4r6pVrM+5hTzpt
weGoOogdhcT11o/jZN7Nn482c4TA16fqAf/KJfxP81ov8pyK/2fIYvqNbSQv
o59Iy/i4OYR/YcxRcTnZD33AS9b3+M/ZvfKv5w52e8M+Ph4JZ1Je+H8CuD7J
IyH7wGr9K4Z6v0tr/ZB4+gjqoQPya5dYDzUTUF+o1nP4Qc7lr/cx/td9ZL+P
AF5C4lftOtXQ9zKe4BwoLM4pVadjnSee4CbF39F/HBbufa5VtLDwZ+15HTg/
c3UDJ5wtO/xsh1L58gja7tjw/X3jp1sn2NeuCw9BYD3kjyHqaPREGvsxVwS8
gg+Si7iD++it0Ov2Ovip3Oy/CfvBrVKRc+A6crv7JsEbaK5+xjkgedisvGno
b5j3L/JU+lrOo2W/k7+fMID40oYl1HMlHi3iw8abJhHecTDK7ibOUL1ShHf8
nZqRyt5V/KXEP2S/J+0GuPRAf8ZbcQUu3dSa+sbHDuP+VsmKzJea37H/KDn1
YYrn82Bt/MBXQ8p430e/Og9ccdACv51zTSP+n9tN6r3eLXcIPpP0rxN75Vb3
GmKd2LdbZvDKjft/h4jxkf3+Av6R7Pdnfpgn14+MCz3sQ9xy8ZW03u+yh3fi
PkmW6165lQ4+STP/+qy+6//dQB+NWM0ye+VO7qrwUJXOgJ9boTN9W26tV7zp
vriBse4APPbTquLvxqOe3LFPir+dWyUM77wYDVpF/ve31uJKmE9upSPe+yJp
Ke/7uLnKY0++6+S7Xv/Efdxd0UT8z5x9gfukaUTcbXdT+O1VnPNaW54b+zL4
qddxOPfXRxDvPo1cGwtOwOpZGD7476cQb/wtLs/tNpE8o8TnKPyDwudoCROS
h5k4VtTTWSuaEK/buII4eY3RQm6EaeAG+96Q/cUkX0fW3JwXks/HNiVvgOTz
sUY8hQfjyFn61w8+hVzagQG+dIlbU3xKRtRm+oNLPiU35JiIp2r564LruPjU
178k8F1zTxBvetM2ju97U+8p97+uV3EcJ3QFddzSr9H7RAsRfx+Sfank9caT
oozb6uciL6M3PyzqUKzzczhfMy1A/tc46lM6LyGOmWMDdtnGJKyTsFXEcyvK
eG/XjALvanc5Cl4922byeH0k70rfvNRnfkxU1vtd2prEVYT/Jeub9DyTxfir
+iZrfHXyIVuWkgesH0K/2Zz0/QjwSuVxRL7b/nKFvMovh4j3Hi0Gzj5OHfZH
8pnUO9x7lY/7Buf13sfaXE3oEz2X5EmWvH/OU/oZuVmQ2+/gCbceyT5HZzZH
esff1GaDHygZWs4r10JPCD1gjXnsw0e5N6cIuevGJ++t8Kj9OTeNfVt99oZx
/Br69+rE8t776DcvgOefcoPnjvqLcVgqeTlD76Lvg07jpzSoD4/Wzabwczw/
w/Xtigt+DDvO79j1L/Ywbt3pB+r0PwhO/Hoy8gXT4wt70WxMfNgYHQf+wEnE
h9V5qvKqKu5tfHdI8ITof/wh1on5Qyr45CVOL7D+JU7PalCNvrBKn9eLTnxG
xg0C+CgZN7C7TYMPpdwS6tF6dAJf3ayJwA/bPW8KuTUpC/i3Nq3ZryqeFh3c
lXN2CPxYKi9wtQTxzHnXfbzc2g9JI4Vc4X+UnyjrvFT9ndYRP1HV31luH1kn
jr3n5n4MHjis+NEdnu91ctSEX273VDFu9jT0sN3kIDjORhr+t+rTcaOCyNdr
wyZRr6TsZ3e04BVyTuqhXrn9/iN1y3F+CvPKnX/6hoj7SB5j7XwoPOGSx1jV
ZSu5qo+2uvejjjs28WfzB/o92V+q/+h45/FUFHqq9XOxLvRVTpT4u15G+A8f
hiK/iF3kxj1Hn6dx18S5r/+6g3Wb7wE411mZRXwswE9e6xX1G+Xq0s+11H30
/OU+xCnWNqL+Up5f1vfx8APfgosO1EndP0Ceo0917BdlJxiVsG/mfZfXN54j
L8ODNm1Jdp/8bl/wjckf5/HKjT0DsKdf7sjlvb9e7Br6S/Y7VvWDKu6knY1D
XE3y+7kd+2PPfcvbI+P5+uft0n9knRjZF+OPzz8Y5pXb9S6RR78TB3t74wXw
xvO6aOJ+kq/SLAMOWfFVKnydtUryFEl8nXnVpQ+9Qd2lneO+GHe96kAh1/rJ
OtyCxeHPun4ZnH/dCeDky33k+inl4V2+Ghwlrnv3hf53dfpLnJ7EUV97xLkb
DN+/cfwM+eVTQ8X+tQqOxB/K2orntl8j4oxuxhHg/SVOXvG3GMl/xY6rRD2X
2RTcreIHUDh2tf6N5mZBr1ztF+v1H3K/sN+dho/hCZJ9wNU+UrzZ5qKz6LkW
D4krFoon8gJGoQ4y3iX5wMMOi33kFKmfzyu3tZTCbnfeaORpO8WkHj//ZGE3
OK9Oif3ijrrNvjgGn5hxcQLxgZJ36IceShzMXRFXxNndoCrk4/LNxX5dlIk+
p2/+5LzeuBPczx9PsYdTzyQ/frcQ56nkc9My3BXxGcXn5pbcgx1RBLl78Df4
PJffj+A715CPSlgT/6hwAs6X1D8JO8TNuxH+sZcPxfpx+5RhfpfSj1gf2gM/
V+olx9wIrmlS3DjMC3kxrUyQsD+sbJ3ZF/L8sjL9EimuL3ATHn7Fb9ZwJH7L
iJl5vHLtZhX0T+3oBbxyI4h+IsaOm+L+yl4yoi/Cz2rRiHiCxOE41XZIvPpM
znH5nvq9MqKuRGvfyid365YSeSK9Zedyvvd821WcR0ZUcfEd+sb9vOeSG+Th
Njrwr8j1o0fGoZ6uRhbs8xH0U3Cnhfj4cALrsNVdke+2Xi6Cp6UcesD8uEjy
eP9SxPs+5l8pxHtok4vAU9ZlD7jHlNfBz9Q+B6/vHfAGVoN0jPPsSWJ+VB29
9sdPwn6zm8MPY2YMJ77Rjzri/+qehFziKlU9iDHtKvmBiW+F3eOG3BO803Y/
2TdAzVfRmNiX35x31tf9Lu7XFByE5U7kHG9Ef3nbfkH/wmF32I+XyM9plRfV
9I6bW6M++eB6/9TyjefwN9STfG7q6/dhRz9MvuDsO5/c/PCIOo7xb8G5D0lL
fWD6vOCUrhwX8kDfpeYZRTzKaNTCdx+j8sGPAncx6ibxPBVf6ruAvMWSSz65
U504gVUyO7w/xWzG7eg5/MAlHYmnTW9LPiv6DVGXZORKCt+Wws+0WUE9dv3l
1Ks56zmXN1K3aR5Nz7n8W2PWT/7u4OhkvtmqlY71LHFHhplZ8maPpM73ajLi
X7LvfICnbrQm/Dfr5tgK3vvZcx/CF9x7H/nEYviJdpn3wk5QdXMBu0jikcx7
qfM4nnm0u8wX46MVqAiOaC34Q2MS/cgV36/Z9K64v+L7VXyPZkf0sOJ7tJJN
AZ/5Z0uhh53ZScAthdRE36jzZfZm7OOX9B+2Skp+18WlC8jvZH/XTI49mTxl
Rq9ct1Nip20Az6fkzp2D+BHVcwh70mgwnX1wAPyVc7MT6yrj9GLe97HDkgm5
cywn9dBq/xZ8AS5yTuXiXvlXv4t6/LTvw7330Qc/Yj6GLMRvGir1TN8w8nGS
F9peSp7R+B1eaL1wH7EeAvqnXh1wAk1jiX1tpWP9WGlvkwdfFIN6wd3X6A9i
tkCPVeqSxvDeZ9UbxuUX/z6y4rrgdVvKOnupn50+1NnZBSYQ76+SAPvqeH7q
116+8N3Hje2Cq0hUrI5vHCZ0DRJ/n8gBf8VGcLN27Ddi/5pDTtf2XR/8gr4D
N2pEiu/a8jJKvE/WW/QDG5KNc7u85KEKzYJfkQ1esoCeaQRe0N43kvu0xG43
Q16/E/WGV8FrB/CfmYZQ730kJvbR9wWFn/hfPzVxX1mv4RzJT52mrNcwpu+u
6Xtu39XUnUne3cD6kby77lz46wJ67Gp8EY8xSo4U9oL6OUkb0dfuCjzJ6np9
3GnqIx73q+u7T/wwcEQtr/v0tvEu8TlR/9LjN7/e7lJD4G2M7n0ixH1V/+ic
xNutvhLX+ZH+0Ua6dPDEFSWf5RR/hl14Ohf9ioz04Jan0kdHb1ODuP2k4r73
tB8+Fv/dLpnQJzc3wTOjFd5Wx/e9S+gfb9pDJQ+S5Gk5mvtfMY/ZT9EvUK5z
fe4meLZT4TcFvjdxUaFP9C1ZZFwXvjWzb4rq3nHXMi0kDnDNFvsowD+s3n/a
Dc7BlGXJJ6SZyHMHJxXj6EaGSr4s2ddsTRL+zZPc39fsXGfGsfDPZb3fZVyv
JvpBuvcq+ut5Zw8B53njEvtb5TEjdhE/f6f55MbR36lDu7QXPfYn/rjesDL1
Uf/eJy8m7W37zF/knZdtwT6ZzvXavTPU/UbFoU5iR2d49YYXYv5bViruG8/p
sYU+NN8XlXED8Cd2uRrEy4Kq1vVe72Sh74/e8Vxd7zg4g8dxjg/f7bvenZ6K
8VpQT/AQuGXG9+a7PhJ3mne3pvc+1uFxxFVC0HvqPloKqfeW7a7pe//wNciP
SH6eTYXI2+5fJs/F6azPCeR57V2VI8T7vuV6YwNyYxZ1605UbfTe/N7EeSou
F/kUJ8Y1/M0Sss/7TwtfiHqHvJ+J/xxNRfxn3Ze/Ba/1whTkIUsGiTyOUwGe
Q9e4ovpm0y97BXhoK06hHN5xMLL0haf11mQfv5929wK450YbS/rG7Sb1lU74
6Bq+eWk3iPrQnxbX8cr1kALCjtN2Yx9ax+A/NCZhZyo+w8D4Sz5DJ2mBEl65
0xM+DXtbLJ/c7XoHnMeMLdRPyDpHd0BpcJ6Sx0zFxwI8ZvVGCrmWLTN2SJdg
eDYmxs7qvd7YlAi91GZWDq/cGnODuM3HmsL+0W+3p8/ChwXg0d7fIZ8b/KuQ
61/+Qk+W+iB4zOy646jPCh4GPkrGA9W+UPFA46f8ws+z9DRifdt59oo4rhPt
eqh3HPTBy6lfkP6L1fu65L3Hf3HuhnJelb1MX7DoWeGRkfExxZOv/H1t6t5I
R/P4g2s/iHiQ8ed8X/7U+uNzfikv7ZVru9NgH/4axj7KtFyMs+IT015cQL+q
uM3V09xnzOF83u+ym5rw0lwd65NbF5rh3yYuX953n2xn4IM7m7+iV2703wAf
3JIZ+INyHrWmv9GHNPoUiY+SuI4Y1Jc6Vck/qnlxx/chz7SzfGmv3B7+3Mej
peSKR8u+rvp4yOujXVF1GvRPULyanfbgRw+mD7c9stgv4u+vdrV4r65DZfxT
rufRR9GHN2Q/n8/4Bc4NGf8fuAB/Ydgn1vPtxSL/54y9WN57H32+Cy92Cer0
3dTwZpjZn2F3fVcwUtz/TjPmMd9b4vaXkpb13sfNkZk8RNfZZbzfq/U8Tn1j
UO+yPnmuCeQ71lwV93f7jBT3N+f+QNx8PvjAwPU9DPDl1Y+U8z33z1yCd1cv
/Az/8AH5NWdzfeJCR+OLOh07LJvgw7frjCUOcGreux3e+xTaDE56R+lo3vtb
08LAjfWOKfcpeAynyFviY8f/imF45tE9WZe8WK2TYt4C50hkKXhRjh7xyd2E
/bBXj2aQOHDJI5r8lrBXrR4r4c3Je43x12tj772N5TvXnHar0MPnjvnkevwI
7BMVR4ofEztDxZEkv4LC4ag+mwpP6Hymb6yWE7yOGzeGf/0PWIJfOfAd6/Hu
b+AKynzKIOSyziLQj0PWWbiVO9MPIq/s/7thIvFZWX+hl5b9DWX9hTlNq+4b
z2KTRN2f3mpIVa9cn78NPr3icYrxXPCKzqefsZdWNvbpH/PSB4H71R8F+e6v
jx4fS8iPFGM+S1bk/YdFB3+olSvvk0dcA5d89w+fXBvwmvOgY7iwv+y1HYj3
Zv9H5APsNfElPpx9Z0T8KfwR7eS7cN5HrsMZEdTRvxlAXE2T/VLjSh7s7Ol9
+9H4/l/wSMGPqe9ZmAW7YkRjcEiy7kl3jov5UvEHJTfS9PbJnfiTyYcPoY7D
bCXzeqqfoLQzXbcSeuRDBfJ6C3Oybp/kIr/S7iLxzyWb2HcDP4vxNOLQNydw
DoZ3ht8nseurS3VexQA/E6uN2NdGnQQC5+a8PSr6pWpz++NvNNyHn3trLvuu
Nc+1nuG/6LN4rpaE5yp/x7jQied2kzxAqo9qLvCdKk+t3lPlqd3zks9M5U+P
dYb35tykUJ/852HomVuNiOe93I09VSYVdlrCD8SjFk3G35E4Ky32B/KQS54x
DttqC3vM3jJf+i8Sf/JbMfT+/tw+uRVSM1LIO66S57XMr8U9xD7PNl3yAEj8
6nJ4LuwSg0p75fr88uClUvr5GfQd9Bs1shdjv7a6L/gl7AV10cuRLVkvOdnX
1oVe9C+Q/ZIC9deyX5Lqw6zkdlc57lXp82UOKSbWp5nxPu9Z6G6EeP7w9UJu
9W7MfN5eDU6mNPaPXu4neI0ljsXtc4T9K3Esindd1XMFeOGufCQvoXh0g+fR
t/1GPOqWlT5PEoL/MitFQa9cr4h9rvShiu8F6gFvFBTvb5WCD8qa8IeI72rn
wLUF4uoS92b0xC9XcttkvQb4PXLuIU4k+T30vc3AU0ieNGf1NeyZJn8Tty9/
l32k/0Sc2sJvcL672ZFxfEA+ou1VcD3S71B+ujWmG3EYpQ+3dtTle5Xzze+H
ziKP7JyeKPPO0h6bdJY4acM1vvPdarSdfhB7q+N/aVPx3+1UxP2r++MG2vvO
9HdI84h4+I4y6JMOpxkXmf8KxFcVP/aSF6He97eqVhTjZ/w5uJhX7uRIAp/M
Tfxfaxv1j0b/HvAB9npH3Fr+7KXzqfvd8OhHr9yafDpSjO+Z6MS/f5b7vWFW
zqc8EWJdGeeWkxdu2pw63o0fyWuPv0Aev+57/PG2M/N558UZm4r46edw6oLk
vGuhb4kzdk9peOXWzV/A2be5XsInf/kcvelMF/FLa35D4uS/7yZeHb01eI/K
c8jXOCeRy745eqLFyGXfHH3MNsM3zicKYJeEVo3wyt3elfn73cpSXrl+cR/n
13biDYE6giYvwZ8djxTnr7M5E3pj2w1xLps/pAMHEv1f1u2VSOHX2HHogxbI
7/foF13c99UjHz7QznNR+F9atATwaGagfs0+t1zkBbT4l8inqHO/8zLOs0+d
wA/PT8n7l+/E/h1+EnxywTHcJ94CyR+d2rfe9NwXyUdI3tdAf2fJ+6qfSSXH
k3nX0+cW+W7n4c/ElctMIE+VPBQ/8gS4Na3Hr/jfBccKvefEruLbv1aTufAj
LJ1fwSs3vgwSPB3GumE+uTa1Mee41P+aNg1cjdT/9rky1EXmm9BBXF+8eALm
IRbnizZMyM1ih0Xc0+j5Cfv9z6Tg2GU/MrfGOM4FyYuojY0u1p/++CXxvdUd
wHcluiny63rwXfJKst+WE/MmerCIRtx+CXJzSDX02O0FrKvefcR42uveECd8
XChCjO/kfti3QeCcrTy6rDfKjN67EokdcP0AOI19ch1ehUfAHZ+J56jx/L4w
vFfVckseFYkrln1SjHNHyLsqHpLx7UV9n358rU/utq0k7GHn1NBYYnw2lBfv
aYwuAi403nsfLtGseRyc0Jm4Pvyelfo14xt+3v+enZ6K/aIt4BwJrJONNviQ
La3KeuX2s/PYkW0U7kjapUcbsc5W3PXJ7Q5JIsX1L2ZTB1OlD/xpxWKIcbfP
DCAeOaqzkLvD6rAPn+8Fj6b2b5GQxyKP0H40623xULGujNTgpqwYy/m+ejeE
P+j+VBj/oWoF+PI3ZmL9FC9IXODDQREvUvlH+3gu4iYra9M/QsZv3YOXqZuL
P6mYV+5sWi6+Sy9vFvHKrZs7sGslH28gPy75eLXIztQ357wm1r9W6TP858de
wBsq97vV6yr9BX7cyHme1BT8ydrWO9SVN2+KfzcVuTE6NfxEVXYT/8hVtoF4
z6cXkTeFt9t5K3GD7+BjUfzP1uU/WP+S/9mdH5+4t+RDtjr/Tj3h3v6yLzP9
pt1j5eChlf01rMk78Udkfw2n2CPqomYOYN91f029jOQRVfdXPKL6z2k531+k
ggemZRzsufHz6nrHx3hxGPtM8vEG7BbJx2v3yhLqlduJ2yOvCq+d890V8CdP
86PPWyyjP8KpYeBzbpfG7pL8lqruRvFbGgluShy+rOvv1o36x5DLEV65nT0l
9fJNZ8lzR+IJT8BXacaMTvy+cUvecwj+vnOjLHizhb/gr30OEv6E2eNeDe+4
mZvIN5kfU1IX0rkx1+8Bt2oMKiZ5QuCvC/QFHgVftfVuuazf+Q67ISd9zK34
9DF3ymaOEPIWHyt4x1PXWsEnsC9xPe4PD4kTHs463zu7rleu+t3YJVb55Ko/
jnEA/mQ7DfvCXDMUO+2XdeHe8dc3NabeOElx6n0v3sCOLXCYeM6Dwvi/Co+a
LiV+Y8s2Bb1y4/BA6sbfgv+yUoDrsEOTkY8rPgucRSH6rbt7P6Jn+n/Ezi+0
kP4hZUtg13X4ET7paguxJ2YQn/nP7/COvzEpLXGqfmfI908eKtab9Wsp9Eaq
DszLCuRumaLsk0zDydcpO2rr4UgxLh+oxwmsf5mXdBqHCPyIqtvS5takHuHv
qrt3eOR6h1r0bzhbV+TPbcV/vlDWG07+h3jnT4/px9dR+kUJPxfzzeO8HcTz
X+Qv4ZWbLSRvdp/rYd7xd4cvJ26fuxH6X/HwHIzNPrUL+uRm1XLwiBobanvl
1id4VPTwXnV8z805gnhxZEyf3M3HexrVc8o+vHWixN+jU7LeqqbH7uqaAD+3
eA3wc3Obce6oviHjOB/NvKmIoyge8juJwV1Hli3jletrPnH9ePR8YF98RM87
ud/75FaFJQnFv22tWt7vdZ59L/K5im8wwAuk+AafLYVv8h7xB2tSH/ipF1Sn
HrE7/V61I/sihPzueJGncqsit7tQP+z8vrm693208DEC16TyyAF+XZlHNnfA
rxboX3BA+repK4f57rMQ/Wy5H0N931vfRV6xYgnv97qbYoMvut013DcOezvs
FP57vv35fNdnHoz+qXY8n+/+1dBLttkXPlHJo27/pgm8jfmlo3j+t3FRZwP1
TVqrWuTnr+WgLj3Ej7d3M7fH7k/mX29OzNTwJGQ5W1o+l751z/ZTLzH1oZhn
LYPsw9vrLefEwY71vN9l6QdkvCO1T67Vr4n8m75C6pxyLrUt67vPqgHwbb2z
Snvl9uFq8A/YcWS+mPPr6/oFV/z2hY/H28kGnsdI28M3/la6gaIe0JpRiP6c
ozYTD0wIbtgt2l3mGRZzDsZ9S31c2SH0SVB449KtxbmotW6OXx+5GnnIQrH/
tQx903mf6xZ4RJz6s+aXn14R8d+/5so373d45HrYGiHXfz4m+xNJHr9zW4iH
zGol6uoU/4Z7sQY4wjZZDO/9zRV50fP9Dof5xif+aM6Re+9DffP1OD24kPN+
+1/b2kb4m9Zci/XeWvaV7vsZ3HCTS/L8kvqtVVUxT3r9F6IuWS/XLUo87/C0
3eI+xVup+h7w5p/mCf9R2xRV3ic/HCRw/EbDRJInX+IWDi4VeRQz6mg5r9wJ
aQeP/QC/3ErWAX951A14ZOfJfNbdcvQtbfaHjw/E3ZJD6D27UC7yZcGFwIcv
2wk+RdZbKR6GQL3V1W94yaIRr9TGFGHeVDz2xgPma2h4Wa9cf9OVc/d3+Ozd
GBPI48cvKOLzVprEzOe+W0Ju1isL/qRY4QjxPTH/hdciTx94UlK+JG9caoSQ
m3UbCp4365LsDy/f03m8nf32Cn62wHeFZMP+lHWOVrJjIj/o3Igr8tNmvzn4
i9YjcX998UTy2RP3++LPbgj9k/Rx1Yt65UZ2eBac01sKeeVOkby+vEBg3GRe
QM/3G3wgZc6DLx3RBHyY7M8S6P8u+7Mo3u+APS95v61mSzivVfwq/njst2bZ
6njldo8W8J497um7PtB/dn0kcSqlryYlZH89aQlOTfLw6wPxn83dSYmPdoVH
1M2cHTyE7O+j+ja6OW3W+6DGko9C1qldWEX8K/uw0l6508hAj01Zix0of2bd
T9jHcx3yMqoOa+ZS+sC1uxoh7ntuPevwT/oyfDWgGT+5HrQc5eDdvlc/0ivX
V3UB95BoDngSxdeh+Ki/eqLifYPo06RFPo6+wyM3olFXq7e5mVDwvL2IDi9K
GYnDTAcf7H+8vuJ6mdezC0QRr7k7hvhHUfB4drCNHz15AvJi9IV0rEHkrdKe
g69H1SmfhQdDa53BXzfXeWzM//52Xt+nD4bi88lYAXs4w1Z4IMdPApeeBp4E
s3+DrPx/sl/Jle7Md/odebxyK6gi51ST4r46NaPcLnCQXzWPGLc3+MXOxy/w
LNSYGimur5FW2L3mqfYXhR5Id0Xqf+bFrEx+xC2eScSrrXx/02fhT+rXzK1n
xD4OxDPfg8PQBy2krmszuA6tTxjn9yrq19V72isLYjdk2mR45dauDPCOBXBr
aj34+8OalSaBZ5P9Ya2p6H/n+RfBX6bv/BJLvN/rseSvZJ8v6w14Y+c9ci2W
Rp1TIuwifTn60JxSEn3VyAoRcrl+VL2PWj/m+i5Cbh0ohjx6f+Tf1YFfXMWd
Lku+rdV1fXFL7Vwn8qlThkUy/vI8zZoS/EN/+LL0NFNZ55nzcE5pneBf/IY/
xz7Xh3rDoIEi7mTV/J1+VbIPhZpf1YfCWRCXOufaOZj307J/3P+rW6c/mszj
en6F+VvH31nyXuZ3ZJ1FxFvBLx3gD5c8A4G+XQXI12mJBovvcmacBoc/vwX1
fEcq831vcpM/nZgXO9/JTx6xfVURP7RWz4kQfzfCrtBm2qyPrfAVGD2Pci6e
rQv+KvkWcb2T7RD4gR/Gsc6OvS8lv4/48j+yL1HXPuAxy3cHB5YrmZgPV2uF
XlHnzp8PfX031Peq+mU3+FfyPPvgVdDNerzf83jErdS865nxh5+fi+2TvzN5
3/3PyT/Iftlmi7Xs63e5we/nk/21Wz8nPtAvp5DblSdTL3H8JTixNZXRn6ls
eDFy0w9Xq7SOc1nGq62gXeCJ39aknvvSDp7bfzE4xtcVxfON83uw2zb2kvXj
JeGHnNdOxNOM1Vewu6ZSX6zqAoyn6eAVvEO9W6BOxz4nxsV+1tTnP+qD1ov9
rfj/A/6v5P83D0X55ApfoWlxynnlCo9hHO/HPpXjbOR4Lq53TwRFivtVOCDt
qpjg+JN3jM39+NlTX2MvLsTfUnpG+wt95NZCrvSMMxO5sW9rFp4r7aVHRYnz
7niCHzEkpdDP+qLL5O0mpoTfKS5620jWizhYdYmDUvtuZGXhpzjJidepeXQf
JIefLQ3xvYC8YRdwGk2+l3wgkpe4aEz8h5QP4RvfVETUjTt2AuzINrPQSx00
5vleRaF/rMh/6Bch94ue7CV1JmezE88LTSHuY+7QxTrVf13E/W7SJ9c9/R04
p1jI9STx2I9lXgs+baPXgXLe93daPg0S9/thcznv+xuZdTHeRv3Z1KMrv+PI
9/APjuoFzvE1cmvFBuEXOUvwrwNx8phTwTu1OJLLKzeevqEfW4sPMo+JP2W1
i8/3bKR/jXtC8qjU7YPdVdPE71L6ocYi4tRBp1iHcv3oEbJO3owUcXRzSYzm
4rlHFuL/pqgpzmHrWEEh14c3Yb3VzUmcdss46v1nxQCHULeDLw/lfO5NPdv4
EPopHduFXXO8JudRH/q3uuupe7WrjiOeJvGZ2k+j8UslPtPceJW4iJVayPVP
57AnGkb37bsATikG/XLVfFnRzhHPmQcOUcnN9BKnKPGfAb6UoWnApcd9Av9z
xXnULT4+xfzIPoBGEsnfJvsAGuO2+Oqz3Px/wK8X+ht44VXHiRO0SSvWv1E3
0LdOxAdV31C7HnKlx5TcuNZIrHfrxE7i528M9EPNWHLe2afmXvrbmpcaUT/e
Nr3I7xjb36N/V9YmL3OJ/jt6cD/yoW/Dia+8JZ6j6nM12UfP/oK9F+ij9xw7
56v9DC7Hxf6xX5wij7asDPx+x7+IcbXj/IMeCFncXLz3DuJ0xvWV4F4LucrP
Yr+VXMw4mavF9XrrBth1Nc5zHig/bn2fSHF9kuFqPMXPrlIrpfy7kvxXxJE0
yXNq9h8g9RLj5twyqBdQfImPu4nnqr5gTq5D6Nt0r4WeMRrOR488XiDsYWfh
3+ix/VNV3QT+Tbrl4j5m7CbY21Nm89/j/Syut7eFi/PCHJxM4mpkP77jA4jL
7Uqc0yt3yu6kvmZMqfReuV3jDH1wXM49NS/2n5IHc2AigRPT518G/7llDHrm
q90r5D9dZ51Ie9i4kFf8/9bPN8nLdIoJD+rM9uK9tdUfiS/VKA5/XZpD2AdK
D4y9UV6Np+EZZ2179TT/Uy5/erId4d55cSN3q3ia8r/B8+8Hr+nh/5TzC/+n
ES2Xer742Z22YQeMalDOK9fOHgCnm4l8usJ7GOdiks+Vfq7qM6X8XD3VTGEf
B3geFg0S+lCPMyHYK3ePFhfxSjf8p6xeufX6rsDLGlFJ6Acn/S8zIi18Qw/g
PQ3wnab/HruiDeOj5Pof14Udax99yHjsHoU92TycuNirK+RVF2Zj3WYpC87m
Tmn8Vsl3qp3ORdztctasXrkzKAF5TMkLquSKF9RclFzxJTMvI0NZ33EfZvGN
f82MnF8SZ6vyquYr9IuT/LMYPzvbcHiGF0+Q8btDjKu9TMidsX8JudOxSgYh
r8T17viPnHcJ+0s+Flkv3+ocfpF7pZhX7iQYHynuH7KWfOVEycvRIbuQu4e6
yXrrEJkHL0M8XJsZYXjGQfGMmTHbCrlat9aoYsQZB/7pk2u/bRHX2+mPyXNK
ypfkglczTruS3nG2x60lTjT6FXomlPiDOf0X6kjLTvHrsZhR4v5GyTJxvPcx
su+t752PgLzAafbvzvG+690MoQ2819vJwAHY0xZj50ieycD1kmfSafcAvsC7
NYV9rtX9TtRtaXdlf3IZv9V/lP3L6xwU/ohbWH5Xhkl8lzyPbHk+Bs6jQk8y
8lzZD/RH8LX26k5h3vdxzk4QcTFjXwnDK9dqTxRyM+SK73p7S2HiLd0O+M5T
vfAV4mt3FhAPU+OXLkT1USL+Kt9TewU/gLmoZS7f/d8nYF47/JvFe38n9if6
cAzYiT0l+QrsP1/hJ0sesEB/E8kDpviKA9efg39V8cAF4lcfv1CH1rU39qb0
i7V3LvZF00B+B3t4An6FEaMPdvU/+eDR6NdR4KDMf8YiX/MZ/yUsn5hvaxr+
h/2CuIF55Uss8dyE14r6xl/yLjqD44f6xmdbM/AKOeGjUuNjfyH/bUzd7r/P
EXhotel+fWWV3y3Ws1VyMv7koXrUN8UeHfmfXPFgfx23+mJ85oeTH5L6QcXT
lH5Q+kTJlT7RD7bM5R1/PWQgPEgDuvrkWjA8rkaBfXL/pBP6ygoJFvF/d91C
yRdNnyb7rkY+8vcgH/+S87gffWQkX5/S/4qvz5jp+s+FMxvA2Z8rir2t/IK4
9cHvOBr8sYm3iTosrXVz9G2/Pb77aCNmg5vpmhF7Wf6szX3I/64Gh2kuWUQd
rcRhOln6i/FTeSL9KP0zrb8blffKnbu38Nd6xcT+V+t5S0X0ifILklgirq78
Aqc1fozTHH4bLSId58qJEob3Pnp69rtz/lEp3/2b0HfYXlY9XH6XOL/covCz
6/nKK7n42aXuY0fu+aeUV246y+hnXZA608D4px9IPens+MRNFQ9JqZPIj/j3
r3kJvmX7wh8S/yl57B8sxI8a1Vryf8r62ba5sEv7VgH/02gW9lrDYPpQ5P5C
X+P6b+F9u5WT+FKSCHg1o8chrlXtHv5pzFO+uLcWiZ1vV7mB3jjZVtgP7to2
xNuLtSBuWn0yvG/lm4rrnZmtqvnG83wN7rNvC3n+k/AnWC71s1Zn2devOfXK
WrGGoo4p0Lfx4xaBK1B9G634k8p4x1kbAC+NFQTeVdlv+p6n8GdcfUE8Ixr6
zV0m7cY5//j2kX5wL/Vgk5v75Pb9rJwvbeA/d1JtpS79fg3iHRcs/HppH+o/
kp/Sw6lnDNiNBX7nnNZWiHPM6LZT8sYOp3/SxU/kteT72z1nUC9dc0xZr9z6
NBm/4gH9ntT97S0bqDcYOweelqa8p/3+J+w/2U/K/AG56iel15wt/Aj3BfOi
O5fBZa096TuP3InnwV9J3uPA/pK8x+Zr7HPlt2oHiXt67HMZ15V1C/nI9wXq
TVTdS47oxLPVvDS8Tfyxwo/sryOTRF2b+64V+rDzB/pw9bA47/L+ECGeW3w8
/vShQ6yrQd/jF1WpIOIbgXjLmJTwEhwPQv5zU5GXMENqi3y82aK08Lvdj5Op
693QBfzAw9rsw4/gRuxJ6CNr4WVV18i8dzfIvx5uQVxTzqM7/Rr8OBUs+I1X
72surj98nHjLnnfEv/7tAI5xCPh8p1tXsa/1UnIe730iD/rSvw6NrPSxMiqt
h5+5OfgozX1NvdDpv7FztkZhD7fIDw/X1nX4TTdOw2NRfHJaOW/ss/jTqctp
XJQ4UVHJX6TWbdc14DeWpvXJjVQ21w9+CD58Pjzkzg/ZhJ1s37wkecxk/VSZ
OEJupM5Ev2/VT+HYSHE+2nvG+fIdxhL6HBkLz4V5x1nftJxxmPOF9dgniu9y
ChFPGDzZd70ZMyJCXFcggrrA/b8SZ444wHo9t0vEiY0JF8E9Vo5FPn0H9clm
vZSSv3A/+ambCegjrHjIZR8BM29F377WPsOv63Z8Rr2VxL85uyMEHkDFVcz8
q6nbl3GVwK9hfBl3SEx9TbQyxKvbHEZvFEmE//lB1r32KSvWs3trd3J5H/om
RP+9jve+xrRd1FF1GEofztdZ4I1M2gnc4yz6cLll7pOP6AMPgOZKfoDB1cR7
upmROzu43rxXS8j1HMWFX6nsH32cxnkx55aw04wmsq9lTvoNaDJuEKjfMeaL
enJzyk5fHYde+jHz8tGW+iSOnF/4J7Uj8FeZs3dFif+e4xh4xbdjqM/rQb9F
O1VT7KEC49FbCseVG14ed2I98LHqPDrdHv8zw/YIwyufbohzVvt9P/qjakOR
19NfWPARzOjGONVtAE/gkhTgIiW/nMKtKX45PUVu7D6J39ana4JfUSvYC/9s
VS5w3TVjf6FfSCP2d4anQu6s+UXwzLihnfN439MsNg/74O7FvF65FRIF7uFJ
oQJeuRG9NTiJwvfTeeVOqTHEwT/1Tu0bh6r1xbliuT0jvfPlFp4Or2Lb5355
wu2CR1r7Zt61pheye+Xux/bopdPwGplXmgg9p/q/a8srwd8e7z18MNkLEge5
eBT83JhJ8MQ+P0z8K/om8Enf2/g7ZUOxfx4dh2ds6wrOj/7w2lnNuhDHlPFh
7VqXFkIu48MqPh+IM1dfRF7i7EGxL40dF4WdYz6JxX8/lJg81aQfhVz7xPow
Vl8kXqLq7548EutC71Aa/FKcK+AnJ58B57hB5oviXxZyd8QLzo3H6NWAvpX9
aLTIkuDfXw8Q8WFzLfUC9ols8Jiq/EUY/T+1XYUyeOVOIROc1rMpGeT3ck6+
aIBfnFiDv0LF97amE36cW/ZLSa/cTIL9bGTKTVyxQAHinm+j8N+yPiog5Yy3
pqEvJg3M4r1ef5KLPIzkZw70i5f8zHqZxil98kmzqHNODt7KWHCgufj+B2fw
b59UFuesHXWO+Lf9Eb0TmZz8glxv5kTqlax5m7DjNxeiz87wH9ADW1ZzLsek
/50xmv3ptF5Ovqcw11tjfmXfKj7PYfQD/JbPU3uxgnX4DZ+nXp31qfg87SOT
WFdbguCVWVZZxHmcu9GxUzpLftRyL4mHX8uP/5KjIzz8xghxTpgf48CrKvm6
3SQNsUsXVIe/c3tJ1uORfeSN+gXjJ2nH4HtpugG76WgY+e1Kh+B1ucG6Vfok
EF+V+sRobsPHKP1xrYdOHED9JE+Rkzst/TLahLPOlT/++pAvDhaIq8g4mPkd
eAdL5jtMheeQeQNb4oWcz1+oe92eFh7X8zXF+2tPl5Iv2lwMvlLpx5n7ipBv
vSz7NajzqDq4X9UnTukT1SfO1Ltynt6Zzrm55AR2y6nPos+qc+SEsE/0l81E
HMS+OJF6uPRL2O8l2+DXfT+FuPiNM9SJNLgr9Ko+8ik4hByhrPvB5Lms2lXI
i3UuJb7TGp4BefXuyNeWZJ/fTs7635uuqBxXcJJzZd6hFH6k8gucp/hjzhFw
IoG68qSSV63tdezid7I+ffYI8Bzb22P3yfyaMWg5ceFPUwp65c6MfvivVWIQ
z5T6wbKPot/nxo4r5eJ+5r8OemT98WDv9U6TIvgrRwP4DfIpMg9hGAOJlz8q
JPKhjtWCONteTeRrAnopgrpj8yz4Q7PbffLs62PTP2Nff/SSqg86UQ4/Yld3
cFDVpiCPfiKfHE9wlI+mIh85nvjcxtTwJ89pA59qtcliX9tPVoo8pP5+Cf7R
TfrH6Y+6SLy99IMW7yP/u/u9L87ghung7ap9DvfKrWNv8KtH/0L+YhR5div7
NHiXpN2izjtltxhmX/rtKJ7GYsQb7U5Srvhb7M+xxP9vx1XXi59Vf5iwN+yc
v1f1yo19P1EvkD+m6gOPv694PE4XCvdebx+vA498+f6GT74mAfZPsqsRXrkZ
XI98fL506j7g0q+upS5u5AfqGuePFvabc/0MeeeTq/FDJR5AX3OWviQ3W1Xw
3t/6cRP3b/2XLz9lp1xHfjzFdYFDcSRvp571nO+9tSMDhD/yVY9R13SucSzx
77vh+H3VDgu53bIovE+KF6X/S2GfWfcbKpyz+C7zC7y7zttqYp9oHSX/c8bh
zP+7Zyofx/i8bhAi7n92OX7K4gHgv2LPxx7d/gw8icQDaNnWEd+fI3mP0lRm
Pb+dTl+PIyVFXsuKPwZ50Dv2edg9Fffg/JC4L/dEFPGWfBfJa075njp32R8z
wKet+h3L89fs20Gca+r81WbUov5M1l3qdwpwzn95Dl97u0zY20eKwWvR8wr1
j62yYFd3vY69lSe+b798nQ/s1PM7S/nkf2fh/NN2CfvV/I5+x+7YN+jxTEnB
TWyeDN+y5LswGv8r/GmjOn2drFUVmN+D54U/YUwaQT1UV/K2ZqsO1HcvKwpv
T7u4wg6xe1ZmnJYid4PGi/XpXElO3PdjM/LLQ0/wvi+7Rojxm7Eb3rTHO8Q5
91/cUrzHN3FLp9XNgl65OX6+eK55aZ/k+ZHxzGnU17n5Tvtw8m6xc5w3PxwU
+sPthD9oxmgucLDu3c7lvdd/NVyI21wbQLzrTWZ4O3dcIT5W9yj8o/+kpn6/
Af2czDS94DttiN3ibG5M35GY1fk7wRH8+UJdOZ+TnhDfq/hD9IGryFtPzEI8
LLgkz22kU4dzl7rjgD2c9iLnY62C/H9yXzjNR1DX87eWQTxf1XfrzbGfWxYW
+YIAHikrfaC17CkzeOXOlSYS5yzxDMqPk3gGJbcWwFcXwDl8B3+F1n8QOM8t
oeCu0szCDhlyh3U4O634fm1APyG3zz1E/qQLds6H90KvOw9jEccqD17Cjla5
uHy++DlTk4JLKAxORuG7zL4SJ2Nk5TyReStz6k+Mr6zjDvRPl3XcbuIMCn/B
L7mOfxX9VTWv3G2YiLqkZtXV9cSrb6cV+8cdj/1iPwH3a36i/tcZFpu8g1xv
ZqoJ4PObLy/qk9eNhr17vwjnwIur8FM1HyvGw2pPX3Rr8x7wUR2bUE/VinNQ
8VA5K2Qeba0Rx/v+RtqWjKfk8VDnrOK1NqqF+8bBPJAxg7h+dFff95pBWeDp
/fCpqvd6J/xfxjsb+GUtgK/oJOJyVokF2C3JM9HvNi563qnVvIr3Pu6tCOy6
Rssr+95nygv0QbFuvnPZrFkKfnuJl1M/K9ZU9IbExan3cdvGxz/6BodgjwxF
XnRTCd9z59VhnF5WF3Fy+594Ip5lFEoLPl7PK+IKeopU8LFkvSfjq+PAVb6r
DR9LsvTiPlqZ3tz/3hDO2Y47ibulX1nQ9/5F4eO15wws4pW7K+Yz7nW3K7l4
f8PKKK63SnyijvP+Kfy2tinEc+2WpchHDXgADn9bHvZd+N9lvd9rvYpeWt5X
4a4ZH8Wf9VMDod/0buB7tRyS/+RcZupRKkdhT5+vRV1tvZE+u0g/tZ94Yu8z
1PUXCYM39W16+AtixSDv+exn4titOpJP6deulPd93POdRf9oa1Zj37jZw1OC
A8z/IML7Xcb4JoIPxzIqKznruUoBgZ/RTx33r6vnMYU9rS/e4rPfjHjnhdzJ
FMq5lWKxxNX0pJ4uNf3l7AfkR+yRW4RfHIhXyzyy4pt1PgZ4yLH30uFPeuT4
Gz8id2fU8PEqGNkK8f91KC3kyo/Qu5RmfqQ/oeTK3zBHflF9u8HhXGssnmP2
jUaed+h4wUNivO/O/OlB4BXmxwN3MyEVfKH1GmJnPftB7Avn4UTq/PvR90Sv
nYk+kzfPYe926yHPI/LLqu+qVm8hfK4H+og4mF4LHpP/D8cu+7EqvnclV3zv
9qvtQh+r8bEul8cve1BK9S1nPR+YOEnEOfdGM7xyK1OwqBfQym1L4Rufv2fA
R1litO6Vmx/fgreoEpXUd5+sy9V6FT9P3Mm3nwP8/JpBnu+beIXihbM7XYUn
RuHlNt0hL1O4i+97naZdwffXcP151VydyMOOzuTT507+QaynIa/I7wyB59Ao
eRL+4thjRJzYODoBfuDz9LO2NuUQcsVXbzUkv2AkH1TEN87HaxK/Hb63pFfu
JNgDj+GtmWG+68feyyDkfz3FX9nahvq1XsGyvg++dycd72ktgO/9f8X3xP8X
D17SQB3om8lKr4mfGZIGfdNqZQ7DI1f+fmB+VpWAj/cidXBGTpM+yoPnklfI
kov6uL6tscdk/CDwPlVj4G9/cNR7Ek+YEUuMo10xIf27lF36QyPsrvHbqff/
own258pu4A5vrvfVk5qVFql6K/DA+p7+3u9xvjQhj/DkV7G/bKsV+f7zXcg/
SJyJ3fPL92K8FkSFe+XGi7nCflb5kQAfjsyPuDVP+PoqmlNn4Le0Bi+kf5R1
FtOlfRI9Ebxkst+H80NVcFvxP1G3oPoIbDkIfmtWNOYj5Czn3LJWYt2Y2xoT
/7l7gjh8kR7Ei4MWkweupYm6MDdRCPvjEnVqZpa01Isl/UvYe3rR2eTPp+hC
rkdryvXB1GW4Jddjt/97Hvvz0ctIcX2l+fR7krxJar9oR1ODY5H7xQ1Z7efF
OpON82/mdR/O306VVPjR5t5+BXzyammI/yTZSt5M8gdqpztRB3s7Hjgv6S9Y
F6uA2z+43ic3fpiE35TsDuda6mDw89sjRb2+ceOU5NPy9wPV/upZzfs+5tCV
5Lm/6pn/5IE67q96RozbkVdcH/cscaQd97j+YCLqNY5z3mkjtoILLBiF/yb7
qWlaYr7/e0u8h/VgFHm0U82oc2v0f2xddVzXXNSfiN3dOrEDEbFRGD8RLCzs
nIGK3a1MFLvFfIzZ3YGJswu7Hnt2otit7+P5nrt38335h4/HcXd388T3fM95
xIVF/eiIorgvngI3os9EPqP+DLgR8+VgxClE3ait+8HfyzxOgkdC8Dhp3WPg
15q2G3KjBezAEYtwHvvuhb/UowT8CMz3qxdag3iK4PutqV32t42bcbMWcJ7H
hiLuWnwj2vm6GPutNfNXjR9LcmnreNh7B1pgHLYgD0L1eo55iYh05o//6Iw6
pkN2OOTS0lrAA1/eijgGrwe1jYx8wzW3qT053/A23C7WQab1Re3PSy8TI56w
aQL4IJfnh7+lbjjx/xr3G0BvidwD+/ToOuSH5wdfq4gvyL/9vhNP8nfIpS81
0N+lsYRzM3K9cNgX6pjnpO/JQ91T2uWK4uPwKylnK1N/tAZj6J42WxyGHb8X
eHU90Wvo7xs88f1X4JfQwz3YDgHeROCaBB5FzjgW3y/qRm1Jhzgx+6Wtekzs
lzafwm+ti3yHGlxX8oElp/1mhrD8czthf4M/6D8Lg/rxnz5P4yr0+fCswHtN
Rf6aJPCuSeWKf8lL2+XW/mrQG+cG7y+rXszL5jj3uF6M3n839Msdu1vSdy4K
hn7Vbif4R/ccJLm2cwTOkeuh8LPlLRdJz2e9R99hpF6LfRk8GfM+uSjFafQ6
jXEebsqKeNPMhzgnkuREPIbjldp41HfQmsrQs6OSkVzptALnXJUtTexysy/q
BWirljOOF/qScjQR4t8V/Vx2uXn3JPzznUW9bJwDyjkv3Nvuo4FPGhRE60ov
40fxKiN5GPKhfiCvUF02lOIE8rTnJFcqjCG5cbQT8Chjwum9euaT2L/7q2A8
h/mT3Hy3lORKIoyLcrsO/EaqDn/a+kLwC0UvJL1GxHGkzIkpX0Aukd/BI2cW
BI+xeTQ3189iHtGCyZCPc+Ad4gJFmmD/rgkGj1uqQOSXxfXB9x4qm5j6+W04
xckt3tQvAcDT3BqPuurWeCYEUbtNeiCv3EPFOBR/TDg97QbLN0zBe8cNILl5
LQ/HNdZAzv9Wnn4kvIY5ajbGeXc74J8kjexrPTgU+9EYgrjbz4eI5+4vhnr0
/gsQn8mjeFC/GRekD3KHXZDzBMU7hFwNzoN7s9srF97Xle5xzWhH9qO6Lwr3
b6pI+JE8Ywhvo7z7zPcex2UWbqXx0lduK22fLz1zNPmpTXd34Ol09qMah8BH
Nu0G6kDFhWJ++65EPtvC/PBnbj+F/O7sYxBP/RmG+vB3Z0HP6ToM51224tAn
c4QBP5zzCnhf+UeOS4v6C8svQA9teAL3FfvHlDm7YAccBA5Qzz0K46BPwTlY
WIGf7HgG4IFdEeAB8PGh/utfrkOffPMUeNMpuE+l8fNoPWvuK8FrcAv8pkaO
dchXap0L+mj1a3hvztvof81E0AO5np2R9hY9L+rZmWw3S7/hf5N+cb4980Lr
ycC3Jnih1dVvUXeS68QpTVBvRffqinkUeVX76sPf9VzGfSfw2O/gZ9CGch2b
IhfRfo1h8M/XPQocVeE9+N6TH2Av1E2F/Kz4Q8CJPWhD/LfGrnL+9vbNennA
R6FVgB9392uMT+0Y2N3PU4MH4HRHrIdaUS76O6kN+aOMce2BC3r3APMYfa+6
o51po+AXePwCOLX4InhvC5x7SlR+H3t/lHjBQxXsQf/ecIPkUuxP+B0rfMG5
1DcxrQejTTT8AoXGUD0oY9FGrOfxHeGPW5Cc9q8YZ+1ZSuj3dVWOdyD+InAv
6rBOpNcYWz5THMP0lIGfkAo78rbUTp0Qpxb5IsyjYvxAPsnf7Yu8V90nUnG8
l+9HeST4KBSuuyrnzwd9b1tf0h/l1rPRfpZb8ON5xVfi/sDOfTELemztIg7/
lfHqNfKP+j0pau+/kWoA+G44L1X0X+SlSp+j/B3yXEdxP2bMi7iP0PdGXkK8
IFc55k9j/PxKjOffeaNW/vs75FfJ3yBXS7N+kgj6rXn/MNfLAC5Qi5pYzP5e
PToP6kbsyufA/2ie+RHXyws/utXPEp9hPzzgOrMfAzpjnEcLfwp4cnjdStNX
IQ4k+DdEnce4uHTUv2dJQ+xy/Uo48Sj+/byoXykP5fNcxGWyx8PuPpTZZZdL
jY6AX4DrWUtlmM+f61mLHzl7JcTLGE9i/Yh6UiLeWgl6i+iP1ILrHH1cg3M4
oRNwaD/XsH8E+qBk+WNZXzSKUzv6pM5YD/5rMa/lUF9V2ImmlBR23rBqqCvC
dpNa5QT0r8TDoHe964rxuQz+HO3LPuhX/adg/ZePK20ff7MZ6m9a/CebymMe
mbdEa6Fhvx7bCL/NIX+SK5WjgHuoMAN6Tb/Fnaj99gtwHu2pgjj4tOto/0ww
7WdR51SsB1Hn1EwYDj/Eoh44z98MdtH7A+oDH7t2KOQ6cCKinqNlb4p6jkf6
0fmhz+f63d2jqR3zZB/gmstgfJTzx2FXF54FPV7tgH7G/4A98pHrIeY4Bh62
wcfAq5aqNfmbtIrIh9Vi4oBn++IGf7zyE+03zYU6C42AhxXnknGyPORBYejX
Zj6Xbg0hv7TUqSnjhRhvOawbrVttVjPgHbgehJkSPJx6Nq6rI86TWOS9C7y3
0bwB+eEF3ls60AtxvTjUa9auv8D+WSLiWXyeR0Xhvp52Hf4Zse9yDQXem+s/
Crmo/6i/3YbzsPVo1Bl/kBx2gvAXdeR4IvuLdG0k+ACZN0l9uwp4Tf4R3/Xf
eY77j/OXpU/gUxL5y/LkRd72/uvJh9F6U4I3Q1/IB7mS5Tb0dmG/dG1N+1TY
L/ok8F3I40LhN9BMxO8WeiCftA7qlRjDuP4L4xOsugbMM6lNLUjnp8XnkKYD
/EshiYMd43l9c9I/cuPo/vp2uVxDxX5M1KuBXa5MnQF9ZXJX6AkiTzzqFdb/
tMqOc0meGQa80Pxafo73hoFn0hyeuopdbnx/Cr6c/u3o/FZzjoP8PvK7tUl5
Ktifl962oPal2qhXaLXTphXJ9c2mQy6dTAW7MtV+vu/4fs+Buifa3qIOuXIv
gvQN9TH87gI3LvLolDElwPPO9qbRYwb8AF7fSG8UdqVxCPV25XZRjexywatp
zHjreF7wcJrN5la3y5WiqOOleqPOiNXOi5nwy2ed7nhefdQGfMV7DgTa+6m2
3Ix47qEEnBsi7ha+Hfi7KndJriZDnM7wOQR85dWKDv+eld+XgHtTvFc+Uw34
cT7nhVzUbVQ2J3c8r7a8gf7/zY8h6qOlGAM/eb9nwMmn7YFx6PgZfPZjEuie
kI79hv608BHw2UIP//0NuOKTvsC9fOyCcyPyE3jqKj0kualBLvshPm3eVUva
x03z/gH9YfVHH7tcvzYGfMTP1njZ5UqxndhvHaeFOp4PG+9Gv4t3dMy7XDWO
cPKifqjVDtcPNV7fqO3oTz4f6PEnd0E/NIGP1R5Ug77UbDf0vc1cn+t9FtKX
lJIfytjbUfVf0PcqJq7lmK9LmEct1aOajv5PqgF5N8nxvNoC82jcK+nYF7rH
fsKxG43+2hc+m8n/oAzf43w+egd4sl5LZe3PKztnwb/dwK+c/XmjrDvqPw3a
RXWlhN6l64Php+i0juKrIs9F8FTLL8GHbNV96HsZ/rVS/YCbeZkL/lj2a4l6
90pvBect17sX9fWs/nN9PVGPTz92lnHyXI9vIOoaWX74duDt1asjz87Su1Ls
hp/w1UjW56ti/f/sgvvvzUjw1P0lV8yWdK4aUcgrkb42w3NjfsDufwccqd4I
+U3KP1ch7xqN+tEz9kPP2zca+nnrUeCZ3PQJeYiX4JfQC21CPqxbAZwLN2eS
f8V0r072glQZuCW553vYWUu/w+8x7xVwNW3nAqfKfgN93FWOt52AH/LqSHxX
i3OIs61vDD2OeZ6NAtmAk7k9oppd/t/9hXxvnyPgXew5CH65AA354rvnoG4J
4+fl/e7gU6k/zCFXliwgPmczxKOovX3NvTriOntLeNjl6rrpuKe6wx6Rbzyl
8ZR2LCE/ueqbjPqpFjOgn6cMdqP2Ot5AfobIHwmfhvMk98SydrnyZhj8cQsv
M77pCfz/2UsCx57zDvJkeR3KS8OQPyodRPzRbxX6X2si/EuxLcFXORnjLJd8
nc0ul+VNDrn0oDryGlcG4p4a/BL3Mdd9E/zGou6bHJ4UdsEY6NVSA/Zz7Zzh
sn+X1u0CeP1qrud7Cn5UI2AV2o90njOa+zHiu9bPLqB9pA/KAz/hl6Qe9J6K
iUj/0WdFwm/wyx3+6tmbA+zv1Seth79rfAf4oSfmwDy6/JAfFLXK2zGeI7tz
fOco/LW7FsMPo61GHKr5KtTruw65nKI+4tcf/Sm/TzvO8mZx4CctC/+VWYTj
PldyYj/MyQB+BeZXkR5fpHVp5fkKPzPn+Yp8W3k09EaRb2u2OM3xO6xPXS0L
f0L9h0EO+bfcOI8yDwi2y6WIWsg/EXUWGjQjvdd8OpvuD5HvrLsh39YIZb6v
3Pj9d31MrWEe1M/j9k33zHhfqT3YxyIO1c0bcdbbYx1yPX8s2SN/diT93X34
65QPwz/72eTKG/BC/CdPRvfm531kJ4n4nbBDlb6JmjrkMXsQD2EeBoG3UXxu
ged94TKcW0+rUf0O5U198PoZIeCrevUW9/8y8Fno/roHtfsevJeGEQG9Zblz
HkX9WbXODuDUllxEvmqZ+sivn4q8HmP3BMgjstM9br6qg3XXZQ/siMU/4Icq
OJ7HDfeCtCE3eNvynGF7DevZPFkFuKSMI5LZx8HYC95eMyP41a3zLXUhzEP8
FW6H+5/3X9yXUcOAs5iLOoNGljDUFVo5mvqjrFqPff2xGe0j9d8jwIEvjQGf
Z9OWFEeQw1F3zsp/FHXpviK/TO2I582u6wlvJOo2Wucz121Utj4PcPQzWzuM
b47TNN6WH0M6ARxqW9i5elPwlWmeHxBn3RaDcWbeXVG/TBswEn5xwZOToyHi
rffzUP6fvPID9svCMPCk+BYhPj/txyPYj6u2oy6DVwTFAax8rk4dgIdje0TE
B4U9IuwXIRf2i6EMdcil1p40j7JPWfhvuL6wmfML8jpTQr+wnv9P/yB5m9+I
r99oDXvucEHcv5OAMxf6iZFjKfybkxZiPHg85X3p4Jepvb6offz1379xr6Xc
BbxJtpx8DjwCnuGvdWvlcWhL8P5qOJ/lV0GID599DDyCtATncMrPiANaPLes
FzHPrTG1PfCxmyeTPqz3zIq4fo5tsK+TI29RTXEKeG7mA9Sv9YE/QfABet2G
f3h8UehpTRTSL5Xgobjfed3Kp8Kgt415BXtfzO/YZ+DjCIF/2KrLUIp5A+cv
Ax5c9Qev1OsXOA9H3Ifdz7xSctFS4DMdgfiG8ekg9svXAS76e64rId2GXNSV
UFMBdy54ddTxk+DHY35XuXZJ9J/5XfW7nDfG/bTWZdNL8Me+K472fxWh9o2r
u7wd36vnpHlXmj/xtH+veecfyPOOdI7PFwl+y4HTXfbn9UmXER/3mhXgkJdH
3qv8rB/yLwSfRmLwdRvFg8rb5UruYbTe1PHDmH/jE/w/jcqgH//p3Y72WS9X
ctYPtMvVbjcRN2c+H+Gntfh8fC8h/laS88eHjQVPTti8PPT3p2ZRO0al7Yjb
Nh9I86Xv64Lx/HwM8fozKZPbx18KdMO9XjQI+OVmh8DHdy8C8zi7Ifx27P8x
nvSCv6Ai6kRbea/rdOiBg1/iPPDPjbzgwTdRb4LzcK26SJyHa67fhXqhoo5S
pRXI36ntXsr+vJ5uAfKr+UcdX6Qv/g3eACmouiNvWq2XFPzPd44AtyvwYN+b
PvmD95Bn73DIzT4pSQ+UOL/AqotxtR/pZ9rYgfDnJEsHO6Ud4q0q8+KLc09P
mwp1szhPwsJj7Efcx5g32rFP5YdFsC86ZQJOhHFZqqsU1v3cyg7+PTO2FOoo
RJl+jvFJ4+Gif3/rqtjH04hTcC7XmKE4np/GPAB5BpW2j5vc5zz8J2NrFv4j
V84+pfWsnU0JP16uq+zPx/Nmg0SBPC8OuYiPaBt8K9jlRrdTwG9X+w5/7I+0
OA9f9kX+0tda5M8xLx6Anrx7LfB06kbe1705jjCK/OB643oOuXSuPPs5J9a2
f5eeqRHyXtvVrGGXS31Qn0Pdf6WYYxzWloCdOWhQAcfzS8eBB6pueYdc39WQ
1pOSdxfwCHVnwB76dwvpceqREOadeQG9ouEi+MWyVShnb0d9lQ3jvPo3+vl8
OvTzk0NMwi00b0v7Xdk4F/L5e5Eny/UcrX5yPUd5z23HOKjp59G8mrM0wjGJ
+IX6Yzz4S//i9RL+SrMZcK9Gktfwe7Rrinyui8X4nkLemWIij8Lsk7My5NAD
tUwbCI+iDdfBH9hgMPSW3nvhB2msV7LLjR7upPfox2tXdjwv4uMZouBvyNYE
fKStSiEvbC3n2zK/t3GkDOJ6C5M69HOpSjb4N6okCbG3b96vCX/Uz0WN7M+r
v9fDjzp7gSP/S3JtRlyz0YxAu9x4j7qBxo/ThGM1A5PR35kPUH/LuFnLMQ7m
Ug143ak7fO3vNScdQJ2sazu87c9rD33o/tZiTtZ3jPPbS7ALgvt40DxtAs+P
uaQQzq8pu8AL58N1HLy+AkcXnoDvzjoL/rHv7cD/O+UDzY+mTALeYM93ur/k
32OofbPrRvixXyagrsPbUDqfrLoPQdHwj+k1G9vfK9WL4Tiigrg348fM7+04
rpYUdpmon3Ua/kO1dvYQe/t6dsyXmbCiun0cjNuFgPe4H8m4WdSPk6+kwfnW
OgnuNU+Wi7q9C7/XtI+zNAntG64BNRzz1d0b4zV1P/KHGG9m+cnHX3LIjXCc
q7LXhAaO52PHwo9d8jbPI+JiesRp9Kf9ePzmvFej5itaP1qXO+CJnLUF/q7R
4DfRvMrWsLdv1i8GPo1zh2ra25d/BSEPVYkBzxHr80rHZ6iLNaYrcCmVDuFe
S+lDcmXQ/Yb29rX7L65T/kHHew3t7Qs/s3SkaGO73EzfCXbKmVmNHeOzyBfx
gqrHwa+8Mh7yreBZ0G6VhXznQbSfvBfyiAb+aGJvX+tSEPdKiWWN7O1L/ssR
HxmBumxCrp9BfET6T2/5I7frLfS8iIO3HEB4dREHV6+ivrbpORA49kcrEX/i
uJ7V/vwGGGefF459qifaAF62vUZdu1wNeY948OR/wb/EeAkpe0qOV+bmdc75
g5OQ1yfqWVi4Ka5n8ccvapf/8YvSOCneZR3Pl4HfQOo7Bf6Y9MCVGVFtgdsp
dR5+AuFnS3YbPPKuEM4bhJ6vvbyP+8wd9qDQc4yGxzm/HfgBnfe7/E7wrEEu
p2P/z2s+B7jOqbEV9otV55T9HqL/wu+hTfYOhZzXQ9WJdK8bLR855btuk11n
+uuOdat/OkU4POXUeNwPheMxPhmCYK9OeoS8wGjI1VErOL96L84xUWe2zgDM
4+DnZDdI6SdTXEm+khPnkloI43E0O/knzBgvwieZs7lew195CvrPitC/eT2Y
n2CfG223A3ezHfq0MiiE2tFrbsL8+zHOeWU8+PXurIbdOmgH9Puy/ji3S/eC
nvjoCcYzjQGeiDH9yA+p/FOB6lJJ6xA/1ZuedvIP+HiIPHz6Ef2UpAuY3/Ef
SI+28D/392B+A8ORd8/zKA2Gvq4cT13aPi9SoefEx6tUmVLWLtejql6lPKmp
Q4FzqIs6nnLJUsjfdmsIvbQ+cALSlrlY90+/17C3Y154gHz4pflpnZgZJby3
2A9aP9rhnfDb7cmK50OqI18/sJLjPFSmeOH839vbec6PyAq9bmqgY72Z54rB
v3f+AeaJ6zIoJz8j/7lYceQpeHE9l8ElwIPQcQVwmrv9MA4z2wOnXiavoz9m
mpGIS2YfAntL1LMYnYTOE63KJodcXehOdo0U6IH4jFqPzjf14U7wOTT66ji3
tT0vgdM6U7+J473TJ0Ovln47zn8l4DrqfcwcRPqYVd924jD49d7j/DcLX0C+
1emGwPes6M98h6jnJadIgfG8cQz9SYs6INqDWcD3f/yMOOzy9VyXGbgaaXx/
+LmZd1GdgDqh0pgfiBtwPMuoPwn7JdgFXoHKVan/0tgS9F7z6V7Gq8NPZW44
zXyVOs5P/l41cgTwUVXn4vmUiUluLC1E9QvNY+UQL03zGedJ3QoUd1Qq7EGe
3G4/8KKURr611rYy4XaVbR3pfpayrMf4f4hDHbnHqGus54a+K8VOL/znt9Yn
AHm+M+qCN/jzIPjzDmWHX9e3N/hQ1m0GH04T5ivIEZGa3ne+E9kTYv8qpXrB
D/87hHiU5T3b0P/XsEe0PNMZx9iYvlfvjzw1qclU4CDEeng7CTgTr8mcf8T6
wOd/wXP9PtYhV39cAG4p9ncOR3+6T0Lexv0bwJ0JfGnenagvXrs8naOG0Qx5
GV3A76rk9c6u2NqRBs/C+VOvK/tJnOeS+FG3Ik9B+rQSfl0fN8e9rMfBz2LG
+lWyy5Us8NOZiQqBX/zTW+DSPv+C3sLxI71AMMaT40fS886Iv88LAv65/iLc
D6I+CPtRrfog9RAfVALBr2bO9Haj53+cwL4wkD+oLquM/0+ZGvYo48zN+Gmo
U9mwB/ww36/C77F0KPwGD4Yif6fjBoxPrhKIb7XrCX+j4DkPn457ZpngLee8
0Zrr8b5y98k+Fv4NKeAcxX3lGt0d54OUKL2L/m78TcTNOmzBufHJE3xUot5K
irPwq7N/Veq9kvqvdmP5SOTtm/+dG/TvKzhPjGRhiEeWmwK7TPhhrjYlv432
qQR4ghIz3n7yAuAS+wH3pe3EOayuAM5fT12J5l++zXj17kvAI/MkqWNdmZmR
56XenIR7ivEG/52r4E982xh5Byw3Az0JpyLPRX1S8x7Xk61cFfkFHJfX23Kd
X47LGw2vwa8YkQ32EePWBA7BDKpAeEiBQ1CXX0ReQGUP3Ne33sJ/zXVVJMFT
xHVVzMk6/APvsC/0Nu3jSf/31RD/2h8N+fLOOMdSgTdXrFstO3h1bTxIyKcV
dcfYTjSTsX6YwLjT0Xco3qQ9Ggeek1Dwdajxc8ALJ/LyXFkwzv2TQQ9bEgle
17jLGJ8jLuA3+Hl9V3HgAKabvna5MmQ84qyTmGfjK9cTfHzPynu1P2+WbwH8
xjbUqTCNQjg34r/T36sj8iKfr1NhPF/oCeKgE1C3UxnN52p4UeD4i90V9SiB
354yFve0/6GcLMdovT+H713yEv6EoeDfkz5/BK6yQE74ZctWh301+wh4Mj8N
wnxliEPedtXeGNfZ4Jm0cMhNztG5pLRZVN4+zua+WuSnlf+95Bh/dWFn4Mkq
DkKcVtQhDfBGHrvAsbAeInAsZmzeuvbn1RmeiMff6eeQK8XqgN81x3vw6qTx
wnu3tEfe+OCTwfb+WHWyLgdiH3tXpzijuu0u/BCTj5F+INanktcP98KvOsF2
uXR3GfkBlVKDgMdkv6s0JRPiDp5DA+xyZQvn+/3QcQ6xP1ZKmhjytQvpPLTw
J9/7BdF8NBwE3NfJ2chHXrEJ/rS55/DeO+6R9O92bvDzt/OAH1J8b86ZhfF3
vsh3z3YSfsJUP9GPhbOQD7cdeBLZfxXiGYvuiTx28A90u4L8nxI/A+3jKU0b
iX15oxbHcxm/Gp8b932xW/QdilEJz8su6OFl11S391OOicO5VLcP7LatwBUr
MbNc9HvXdtRJ3gG51ng4zu3ryRHPqoz4qdY7AnE+5uUzK3L9U8HL93wa/IcV
INd7dkVeQ5ORQZgXXudxU4ET2Dkn0C5XerdB/CBbqIfj+Xlcj2byB9wbMZwn
u7Az8JEslxvAXhZyNdAN/kFxHnZCPrAkeGLNDNhfZachDngffKdanhzwU23/
AB4E5ie31i3zk8vbBkCP5TxoJXFR8GSdeY/6B+dwD0q9kc8v+Q7G87b6X39+
G9dvcZy3NsahcSDZJ7pf0xOURyv4r67OIH1dzlw4sWKTy11V+FGfN09ilxu1
ptPzFv5QxL+SJQHv6AyuF8PjrKaNAt9Q5P2fdM+MnQAe5FQK6Xki79I6tznv
UuABRB6xwAOYdfrQvpBjgMtXds2CnbBzIHBBa5Efp2ih4O3k88rKRxa4u7UL
MN7xuAfVcgGUjyy/u+jkh/nWH/yAnSoo9vGU77QKouer9XH0X/eLwX1ZeBT1
V49Ph+/6sAA8A2meYN9ny4/9vro18k4nvHX4k430veBv9ANPsIVX2Qa/qLz2
Hu4lzkeWG3yDHTpuqYdjvir5Ir+m4wbwvlyC3aH2X4HxeRzu4JXSq6UCX/r5
j4jziHhW/cyUDy7ifdbzHO8zD60ra5fLF/oj3ubz08cuVxpVAH/d6uOCVwrj
1yUHjacU4o46kLb27fMh4pt/6gTRe/IcQb5eOfCBm9cTQV8QeB5en6KuipGk
BfzDy2Cnme8OUvtGu9g42hciT/aIO+J3p/KRX0XIleJDYF+He9N5orQqAd7m
TaNg/x8OKuoYt4UZcH9zvpiFc+Z8sf8PX03yvulJvxb1mvXsBcG32SoWfITH
9sGvvacb7ECPEOiZPyGX5AfIFzNvMc8G2pFCcA5o7xa67HJliDv8da9TlrW/
V1lxHnZonxJl7N+lr80KPtseVx1y9W4Y8phmPfeyy7WXhyBPPx/+VN92aP9a
D7RzvmQOx7gVzk/fqxwX9Ti47kDtZxRv0ox1jvoXf9Yb9TOmN84lwe996iFw
KW4zFbtcX+aD/Vkj6uVBm1x+kABe3Yi2GezPSxN/Iw8kPKsjbquHbwqifnft
VtUuV+d4A8/XQ81hl2snZiB+l/+ah12u3GsKPWBnGOyJ8Vuhb1yeAbxZ5ZsO
/UTuB/5DUafYwn1xPohVH7kn8MCiPrLsG4u6fxyn0OeFwz/zQYNdJuL+hREv
FHz1UqO2+F7mq//j13U87wFchXIOeQrWPO7E+Sn4AbRZt+EfZn4Ac9875FPz
ejP3F0A+74yBfF/zuqpUFvJEqBurFGB//tWNVFdaSyXqyYLfSXozDfWmGccl
8qEEjkvKkB727L1yJFd2dIF+tX9WoP29xhHwv5h3NWc9tbnBgu9J8ANRnomo
K/ZHg6Z5/IV6l3Kre8ArnNwH/XwB6sGZqbh++pldONdE/Ti+T403ex37Vyk+
CvG2ZGs5z2B5e+rH50Kw8yZu5Hga8xgMz43zucYmrhOEcTNWx0OvqtgJcUWx
nrm+htyY63KKdXskF/wv+TiPhvedNrw3+c/l95Px/JXi4DuaOQx4AL/k4F8R
9aAX54b/e9hornfM+PxMxVDvm+trWOuc62vIoeWq2OVK1dLgPbmeOjna4XrW
K3cKXgz6EXWK//i36f/rgafdqhc/+AjGcU0hh71j7m1J94iS/EqQ/Xnzew7w
n5aqEGyXS6u8Kd4tHQGPomhHrsM4A65HYOFYuB6BXvJZdcf4z1yHe2dUc8wb
7y8tXz/cC79QX1UtAj+qVPQ98DYJD4BHS8x1lsscBD+kkhL6bPe5lC+pj5n/
k867bDUqof/nyJ9gDp4Av3oH4HzUYyWx3vqkQRz9V1/ws1Vj3OMs1IWRf25C
/uLQeaiD5mFCz2c+W6muEUnPMZ+t5JPUsd7knpnonjJSLwWPSOMTOD9L/8J3
7V8JnpAKRzFuV2siH2RRAfBkiHvtdQn4RZlfRfBXCH4VpdRvyl8TfiotQGE/
MuraiHG26trIX+FvEefP6ZngFc2SHrgLfq/2fA7J5dKJaFyVty7I02fCOfj0
yyvKvy1eBPKgZvgujt+Jc1XE70Q+lJVnyvWCpZ++iBv7t6P+K82Twi7ItNAx
nurb3qi3ksqJIzJPgQdNHn4f+oioX9nQC/dLqwj4QzgvRsow5T7hr0J71LbL
tQYfXlAcmeOnVlyA86ONKpHIw4h+hrySyWHg0bvsibpPrYYR/kS/3KqW/Xul
675D7N9rKPDTClyWnC4V9u296y5qv28Biv8av9KBV71xl2qO/k+Yh3vu0wDY
69lWUTta0db0nKivoT2/h+/i+hrGuxyIqws+MdcL+DE4/1f0U42YAH9Olu74
O8ZHqW2bYpxnIM9eb8X5FO9U6CN9gmCPd70OeVQF+EX5PpWunyH/hrhPtdc6
9A0/5m0O6438ugEZwd947xn10xi/jes5/oCe+6oD7Ud1e3GKM0pxv6AXdXEB
P5DJG/Nxqyb0xlntMM75P8NPkTsl/Aq7OwBv/Kou8iVWN2S8MfSH//Rb5Eku
ahVgl0u1c4CffSr4r7Q8YRj/2N+oe5LnC/xegQvRn76V0P9CO7zt7Rjj+uG+
aO3HeoWKuNL0XuRflRpWQ7yG7WJx7mkTn6H+EMvNtS0RXx/1leTKWZYPrQN9
aZCCfLRXqINgfktC57wamcDfy+th5gv4NxmXJfAYFi7rZ0gTyFfjHvTKBzvo
zUiH3Ki5Gu0eSwf/ocB17HqPOkTZStewy6UDNWldml2PBDnkL7KDh+sd8BJa
VTfsR863NRr1QTy9xF3Cz+jDj4PXoFd9zqM/gfldndxF7bEf429cpZBLHQ2c
2+7XUpK83g6n/nCoAeEzLf4ooY8JfozNnUPs42nUnEy8HqpfGYdcXpCK9ELj
+ZG6DnloWGFqv8Jz2AuF5wH3ku40cIBnTkNvTPMPxvPbFMS5ejyl71NSI5/6
T34W/bsH+MT0AgmEU1W7dEZ9wG/TGf+P+ZL6gT9KyT6P8aJYn2pHP4oP6oMf
VrfLjc+huG/kiABHO9n2Ix49w5P2pRU3aZscuIQCNzztcn1XGezbC19D7e3I
8irKo1QLuqHuyOskWIc1HgPPeTmDbB83zXsQ3U9yTPYn/ja5Mqkk1cvW/SIc
69DINhb6QeHDfB+xPjy2KPB+maqWscvVLIF0z6nH6/k6nk9Zn/xo0l94XfFj
5ACfg3ivNvoz/FcDO+EcijyFdb7oFc7x0+887c+b3ycE/fm3Wf4BnTNSqtN4
Pq4u/CZ7T1WzP6/0norzh+NEcmXcvyJOJN0GntM41ALryqPuVfKnlk8AjmvR
Buyv+4nAJ16qRKB9XqQOZ4j30kiPc0m5Nwvz9S0W51LiOWx/8b3mznyjnoNc
in182C+trfSvZH9e9eC4pNkNdslXGXbE6g7QPy/Oq2jvj7kxbXGM61O+XzDv
ZnxV2AvuX33szxt+Q5EnvGYD+DfmxWOdtNmG+IurKuJWwi449YP8Rea73854
3FbUXVK/cV1U4TcLQF1UY00cfYc+/wHW5yrg1vTjtX8ctPVTi4F+piTbxzyi
7NetH4f1uqmSg49FGlwNeUOPtuI+utoRfvLgVpTXLd2/xHgnF/zqzFepV/PA
fd0H/Ax/cBT0u0d14At4/cjNgcdRuF6Wfg3za75diHpfzeJcjvE0hyM+09eA
HXMJz0vhwIGocn7Mp+CT8V/F+YCj/O1yPV1O8ndok440wffKuKdmN0Ueael6
FN/QNiA/RZo6DniDYlscvPrmxgbAxd3VHbz6ejYdfviUmxFvDZ2J51t8Az4p
/b+4j87+BD957brQ98rsgH69Efas0nsXcEfl38J+EXnNQaPBk5IxGvFlHk99
QUkaLy057DvrHHiYC3bmkq7gPxd5Tx7JYc/cOusYZ3mjH/A5d05Av+b1o/7I
Tn5L6UWyYPvz0tKJkN9OCn3/7DP6XuV3HeCl/w2Ef/VxPPhDDrvBb907pr69
ffko8sClg+CdEO3rftVQv3jzFvQ3SSzwWpnBQ6ouBf+G1R+3Gr//rHvTHfwb
1v71wXkiN9jreN6s2gr5sI0vOvpjtPuH8ArqmbIN7XJz7tB3f9pXU8eD72T8
HOzrSnswXuyHtHD77IfUTkQ78iOUCfC/ifqnShBwDqL+qVYedcHUY5DL/klR
FyxdSsSdf+ZGnP1Htl90X7B9atabjfx0YZ9Wf+yidhP+gR3xzYPyaeXfWJ9S
INazNgP3stQe61yLAq+yGhmG8zORczwFn4m5PZrHk+87sw3ZddKoIcA1XbsE
fMgXb+gne08FUf8Zf6IXvIN8+fK1yzjmMVcQ7N9VWcva5XIlP/jZub6qvhb5
kqK+ql4lNfmNLbzNjs3u9P+xPUs65G09afyVZPU5r+RfakfvMwXx948tqtjl
5vAExHOr9Q92PH9rOfo5vH0th7xcGeB2tsWz/wHnjJSlA+0XbcAD3l/Qc7QI
f5KrXcNr2OXm2cs0X8q031ns/Td+tQcPrdyjrP15aUYT1J9i/gfxXsH/YD4M
djxvXkX/jHW/m9jl6qZ0ODeOp29qb0c7VshFzwUlaWyXGxdzQ08yqwIvcP4b
4nRTimD/dAGORWpzHrj9L8CxmCvPwK9z/xzwwC1/Avf+26uufTzVTEdpn5oV
fzrykfXpJaB3Hvurn/UCoB8Epqxjf96oVA311w5crO1oZ8EI6MmdGiJ/h+0j
bSbrq4uSOOw1I1MIcBfhNzAe9RDfNPRf0B/mAedm5cGFIA6nZ+hA/VTX7CO7
Uu5fG/ETj83Ipxhfhfaj3LYCfb/yCPxyUutKuEeytQLP2qOSj8hf2yUQdfpG
bBZ2SjnH9x4oAhwa/1j5MuzHEz9WfhzL1Rfwv1nPL4d/T8m6G3iWWbfgX83i
A3utTifcO5kgN+tthB0x/gPdv1ozjI9e+SJ4otNmZFwQ93NCJjq3pQ9dEf8V
8/7mF/TqGPDkWOt5YAq6N82tgWXscnVyJ9qPauXLOJ95vpSp8/D3yZo5/PbS
rXHI13hxF/dzxj40nuYCP8Q1FOif6rx+8AMsRdzReLEY98+MQyRXSiWDHV6j
IMcBOU/c2IN6JcznY2wLQ74J819Z8rjpDrk28AXm81Q4eFHCtwPXyngqkRcs
8FRS3S/Z7HLJhTo76qhAOnctv3H69BjfGyU97XI9kwy/qt/1oD9yC4/R4TXq
rOTdEmL/Ln39HcJlSi0XUXvW8/l20L2pN32Hc4DnUav4GvUJqoYG2uXKqHPQ
s3//C72U+V2NtyuBK79WkfVMxukxb5LAx0q5MgD/zPhYeTbiydY5HN4GuOrS
OdkPBr+Q+jg9cFwzrjjk0uck4LtYfbyGvR3j7DaBN4I9J/xjM1YhPhXcrqJd
btUL4OeNpZkcz5sdfwIX/Bz5R3rjafDzb/iKuG4kcN36vqlYD2/6ULzY0sci
v0BP/rqZ8HjS5RvEs61OD4DfP/di5B/1HdWT2p0Ce1KStgCf/Fojubm2GtZx
4FTU+eu0Avtx2iH4k3tVBO5R8Ma8TQI9ecAhh1w93As44K1vmO8d+XFa6dzI
S+U8a1HfRORZ6+syghe8bjnktxY+SXLjjA/4xzoMBu7lxT2J3nsV9bAtvM3y
YOAfvnwmv5N2HnzOWucLBulpB5ohb0zMyxwP3Bdn15F9pBePAZ/VhubYb60f
Ik99RBPwlMZu8sa8TgS+91FpkmupPsBfuXk0nW96Bq4Hvb8/+ETW+sIv9BzP
m7nqQA90P4v44xkftNM9mHDMSsOSyM/me0fvGIO6ALlDgZMR56FrKuLfffw9
aLyYv07k6csVOyN/kZ+Xiu3HOeCRurJdrj9pDPzuzZfINxH53UdP0foQ+1fg
isX+VdNnJz3EinvGID9anBuifXFu6HpCsF1ulj2PvI9+jR37S8//ujA9v+IT
ns8o8bkaQc/Lk4cCj+yC3SR/KAl+lReN4OeetxftRIM/RQmPYT8q9rVW6wTi
hR6+Ho7+7GwFXNPl+S76d8YPtA6N3RvpfDNHLiG5UgV4OTM4mOT6bFG/gHkO
Oa9cnbYM+fFboZfq31phfTx75md/r3YjD+K81TcrznFbDDyq6zXy73+UxbpK
r2Bd+p91jmfgvk8UL2n/xTGeZq7hiWncXrQBzwePg/5Pfdz7vhr8uHfht5eW
oj6o9G8R8AA8hFx9uJLiHMpq+PdME/3R5h34SnHGE89gHwgesG34Lm37R/g5
Rf3KGe1g54b3wPkm7vE0q0i/Nc5OR523fIko78ZY3x9x0PzewPFVmU5yOcs6
rvNrivpl4E/qfPm+n01uMm5W6Tm2BOkV7K+w+Dzvp6B9p4cw/2K63OC7mPoZ
eMGAmcBFCr/ByUzkn5QaAZ+o/bwCP20X5C2ZS8HTbNX7awx8lDG8pqgzC70y
RQ2sf84XE7gdkS+mzUI80YqPP1+NePPCxLSupG2+sKsLhSEuyPam4FcR9qYZ
8gB5t6JefBNP8H5Pyit4OoG///WQzgf5cN0gtIN4nxy2FvdmiWuYl2bzqD9m
PU/EZc69yORo5xXqZmmL19J3SxOOYJxvZ4Rfd+0L4KpEHnH2XsADdXuFvEOB
U2qLumjalpEOuRSUBXrw625Yp0IPf3eK9Gojy6SKdrlZOAp8MUmng/9J8Cr7
oU6e4RZK+o51j0fPBK6rbkuyA9RKt5E3eG0T8eooSa6Ab0PUMzqXA+vnwqhg
u1zviDogsldm2IuibvKG4oi/dsH5ZMyNhX/JlQ/+qYl5aH5E3EFe98ahn9vr
VdHvVDsd54Da6SHhbIxGWxHPEvHZUb+BM3z/k8ZNy9cdfvJbpYE72PQJfAux
OSkOqKVN7KLfCxknMLIE4vVpwKOnBZh8XzBeqJgHPa+mmKHY5fpprm/xvasD
LyT4GcwU83ztz2u3UYdX7dAWekU6D5w/u5EPo78BzlnMlzG1P+yTppBLj/Nj
/R8siLpOjAewcEoCDzB0rLejP9O2Iv46ajn8fC320/gYcxLonBd8OOKeVcpE
0vdKSV/jHmm7D/fseuSbK/dvYl/+VW9O+io55MrZYYQz0J4eZ5w546L3gf9f
7xyAOpJc99w8Fo+4XlgE+S3MVJhfpXMg/KpjKpFf3Rw6huJTypTs4J2cNaOq
YxyiUZdIW9a6sl0ue10FjjNvafAqP4hFXliRp9jvY4t6kPzEC/DyLRyNe6p0
eXwHr1st+B+q46bkHYu6HyIukyUTjafx7Qzw8gcTA/ebeSz8Eb67gUcIPAac
4cfbwEuPAj7HOgcOtoYfcPgj53trdrhB8ZiJRRrZ5XK17sSfKQWWb2Tvj952
LOpKbP3c2C6XT7/F/RTStyLGE+ewFnJNxO+EPZ2efwP3HNsS4++ZGeen4P3j
upOaW3vUVeS6k9r3lMAtCvs0DnVgtZXRde39UQZ4AofYOk2IQ54J/ABy0bwh
9u81/2V+0XPzKtrl0j4X1sOU8o5zRoo4h/t0q4n5TIG62PrDUqTnaacCobdu
uUx5efrkhxh/t7pNHOOfH/FZ4+qlJvZ+Sr+Yl3DKOQcuSK3cLIFwoktOO+TK
5he/KU50J86BCzKGdEV+1tcI2C9cn11P0Ql+KteUQnie7dylXekcllIMBS8W
34PS5yzAWQ1wU+xyuXsN4C+/5qxv/y65QhLks791OfIv5Gk3kv75t+AXFfgf
9UcXxs+URJ5mEuBMzIDBiFv9DHGMm9KzLu6l2zmbOuTNLyO/vtIWx/NGdhf0
rdglDrn8yBf+xhbsF/XdDz/aQ+Q7SE9z+zjGZ0IgzscjuVnfBt7J3L0PvNxs
Xwi9wrIveqKughUf71/URf26PMix79TFdeEPTA+8tLXvvh3Cfbg4N+69Y7BP
ZSkUdfX+Gk/Byypdr+bYF1LQY5pv82kt0k9N6QGde2b6mciHHJwS7fN5aE6p
AR45wXufFHq+4L1XwtNVcox/E/jNDFdVR1174+1V4FMjA0Rde9QFKJoAntjU
M4DHZh4PeT/s679xesrhIfD/FLvZ0P5dSjYdca6kbYCfcX3FeBplgScYVQ28
SU83Yhw8ovBd5+eURTvQQ9THg7Efk7g5xk2OmQM/fs4udexys8TWBvbn1cEd
HM9L17Y79BwtqCbOz0bfQh3f2w983caIqEZ2uZQFfN1q6eJUL0KsQ/NWPPb7
scYUVxFy5Yw/+Lx6fwRPV81Y0v/NbKcc/ZS61Ai399O4ivxxUa9Zi5FRZ5Nx
4/8HRxH1u4m9P/qncPhB/uItFPWapa2oF2rto4Sn4Pf4kZr9iuxHKjsfcfQd
h8Hre8oL/t7D5xD/u1YdcqG/LQHfrjwa/CrWuNWI/0X36cQ8wDv16YT4YIUD
WDf78gL/5fkY/uoNPw7TeHaXajnaecz+85W3YEcKvOVABXmSjHs35hWBnHHv
Fk5+OOQCJ/+f/Qq7UKzbLBvQ7sDF8Ovvgv/KaNYb/tV+E1FfTcT7Tt+GvtW4
U37IOe5QtT9ws0lCCtrlkuc0use1GVtK2eVKbhfVrZQ3NEB9uiblsa/jfrro
d4e80B/bVKfzRAlLDrvrNPzxYhyU+IqIz8U/zW+XG4dnQX51unPccuTifDbk
tQn5n3uFxr0D6qha993NI4jTJz/C/F1VSY9Sg77B/3XvOvzKDW8B//YzHfAe
d8sA/+U9EfylykTGF57GeXVuJtZV5a7AGYzfxvg6xBm1GtOCaJ5OPi1il8st
fkBevBL+Lg790Vc1Qbx+1CHEK0TexD8fgBuvdgb7S+yXpyvI32t8ljjfGfVz
1TKzUbfljQqcoMBVPtmAPPyKFQLtcvN6Mdp3yoGZDrka3AVx66jZDjyzmsTl
onYyZqPfVj7FLhf04XXrAuxyKaEJ8CGx8+m7RD6LHpkC9+P+O/BbiPzN9GuQ
D1XzOfJw/L/gnPmJespKRC7ga0olkFwbLoP/q1NPmmdlI+dPbQxA/Y43yHOV
0+B589UNxB/VMOARbi3EeL69RPOiddtJ61k79YbP4bfw73DeohLyGvmDnLco
+Iis81Pw3jcv55BLRXeTfq55HmNed+ab6p0/hp7nc9Xis+JzVb5jQr9dAH5X
aQDqh6oho8EbNgN4VO1kadqfyr1b0Lffe5BfWqkajbyIXm+gR/A9aKbxg7+m
6kV6Xr/rHknPn673lfTDIsGwS0T+7KxKLhr3vr1ddrk+2gN60YXLgXa5OR51
0/TGEeXscq1nFsSvX15AXoyol9SlHfaX14fqdrlSqjPwTIzfNl5NBH8I47eN
AUfgV/5nHc6N64gPyflRZ1acD3pkRvgRuN6rxeMn8DOll+NcEnl8126A93It
+Myt86TjMMQdmPdGO4B8c8F7I/94x/w5nJ+4dz3zPj3yoL8XPDOzsrjQ3pzS
drma+xz+bkQ/8PnlRFxGDkmH8R89OJ39eeUI8Ml6OacfQ9QTMRsMBn6sEPgB
9O+tye+nnb8CXvnXmWlfqHvZPrqSBrjUablIrvglYP1nV4o7xuG1B+S93Ira
5bJ7WvDtrLiJ/goenuYy8ncOD4S/TeyXyPbAd3Gda+U+5lfUuRb1yyycP9cv
MycegH0xZSzioWMr0LmnD08MHgbBe9BvPuLsHVtlt8vV94vg53lwKpNjPGNj
gdON7kr9lzJ+RDv7j1Ben95rBNblmC8Yz5xeyDeLfILvfQFeI61BTfijt09D
3u3YfZjHLR7Qj1NswPPMs6E02Uk8k8qb9cBlZMW8a9HD/TFufpXs/dezgn9D
y4q6b5b8wlfw4TP/q8Vby3UZBI+HxQfLPB7GY6dcSQ6cnr4nLXg5LB7geUE0
T6LOjODd2lsUuJlGl5D/yPy6xo8iuF+ZJ9nSA5nfW+4+Hnl++cA7reScTu2L
H/VsqKO+rZYknHgY5FPdkc84v44H/T7RATgCESf90gDjz7h0K27LuHT93i/4
heJq0bqSX5bBuqxXCryyXBdAK1wLftuJEdAf//nensahwxuKq1l5vaJOaD/o
N1IXf4xb2X30vFz2CuL76RpjHkR+0yBP4Ir63VPscnXGWfC3bu4MnoEY1A2X
QvqjjtWFrLALJqZB/Zd/88N+5DwmbVFq5LNzHpPgTzP3cz4786dpWxpAD9kM
XhHpDdfx4ftC8OqI+0LpvCPALhd1SfSS2x3joMyfCH7s2ykcer52cRO+J2sE
xS31KrtpfJQflYDDjtkOfYbz7s0mw+FfZpybMf8l4vWMc5MLZsL5n/4w9N4D
jYDTGNoXdfzyo16b0rkO4i5X8+G7xiLOqFTRab6U17+BRxI8w2VV5AnmucF8
m1wv7Ps32l/axLHwO55AP6WVlYlPyShfB36anZyP3/cH4SjUFC8c827VZRx4
E/qS4KNYiLim4D+36r4x/7l67Ho1e3/UiByw03Ol5XnhuJhrHOyKRe1l+/jL
wa8oT1wS+f7Cz3Z9W2273Hg9o51dblTuDLszvgPiqk3ADy54s5X7e6kdeXJh
yofVAno75EbaLeBF5TxBoa+Kuj96T+BexPNK8WPIt12AuuJKojbgiRriQXkL
2uGdwEf/Au5FTfIUPAX18g6k+HL4BnperhaHfjCe38LNsh0q8mjMIp3BK8h5
NIK/TguG3OKvM2+hzsjUltDzkyaQ/WwuV4OovenV25M8dW3wlfQLQpwz9zqS
y5/8ad1rF4bh+Zl7IV9zG3UnmjEfieCrn4P8f8FfbvEt8Pmrlfd14KK1/W2B
b7wyBPqyVQ/6LOIu/51vBrWDuhhyKOqva/me0XuV6FXUHz2wJfTvtOC3+Luu
hL7DK8DevjHMDXkylyNx3nrfwDk1BzznZgjuebHejIPY18bUA152uVYjArwx
uV8CT1cK7Wi9LsMPUGcA9LEaCvDrj7NAPvMF/Aae1YDPiObnf693tC/nOQX+
l+/PyS6z/NuhBcCnl+F7frtcdncxn15BwhOJ/H0zTQfosWlKgw/jSX3gxqLL
E95VaZ8eOP8ui4GPmPqM1rN8uR+dB1KHJ5QPoYU2o32h3z1NdreeoWZraqf3
cfhN6rRBvuYwL5JLVftBf00L3KlUrTzGQcpO/gr5MueDZPTGeb2kMsWLpaHH
USfiOfPtB36Df3zxY+aPhZ4mP8tk0nrOeAk46L/qpOiTdZw/05NA/27fPp7w
HswrYvEhWLwi6R1yJf2AfNTPPcPJDyP2u+RWgPLlzYgSDrnZazPy69vGgDcp
dCadS/LivsAjsr6hdozCOmR9Q+wPca4K/USulRh+ALEOfcfCz9WonaddrtZO
Dnzwr53I5+If+VQh8PaWuIBzt8Nu8HV1iARvYIMT4LM4tx/4wkZjgJOXNiPe
JN4751/Yqx1Rh0jIFb8L2Fced4HP4nHQFh9APKjvck/789qmrMhnqHKb/Io2
fgm0X+gOyeVMu+CXS7oG90Lq8QH29s0a5WlfS9q1yna5evs0cE7dD1Rx9OeB
D+SLU1V1yP0vgqdsUCVat5YdtCAv7pVSi1mvgFwN2Q476lJQNbvcODMA8bg7
wxx2otS2DtbR28Sol9EI61DOlxvnT6oqAfb3ahPrIg7doDjfR7h39EndsE64
jpj+D3Ddoo6YHPUS93AU5IrbDfB8NjGg33F8UA8+RevTeHbUg94r4hpXPuH+
4nxb8bzItxU/xvMCOK9uqNBvK6whf5sRVwf+u8FtwB/5uDediyIerf26Q/eg
MX4b4ji8v+RvT5EX4DHCIddedCU8gKgTbfHS7Gd9JnV2jKeI17Qtijgx2wXW
/mW7QOvK9//H5Ih7cb14wZ8v5II/X5Xawq8jxs3vCOKU425QnF98r+RTC3wK
t88XsMu1ZsnJbjXfNkN8rF4A9L+4HYRvkfLUCrSPv3pzH+kt8orx1e1yPX4h
8n1e53fEeRW1HJ0/Atdh9Z9xj/LyLMBjiP01yRd6y8LB5eztm2V/gw/zVzTw
P/U2gz9zQx1qX/hFjUxvgDtkv6hSDnnlIi6sDENeuTaN860FH8imQrgfT1WE
nj/0Z3vqT+QhssONZwWgX3eMhvwM+BuMdp97+NvHp+F16DMzX+L8E/u0wUn4
tZ52CDJs71W3d0Ue9cu1PD5oR/M+Qf4QOU32QLvcLAhcizlqnMsxPpsKkR9H
W7AgwC6XUv6ieZf3jQM+VJyTW0shDmp0rWBvXzlYjsZZrjO2sl0uLf2O+sIP
xgba+28mVAHfyNnDLrtcDstB54PF2yNwFMzbo/TuWcwxDks/kdzYCn5Raxzc
usJfvykMfmCxzr+l5jqFVSo42on3gF/iV9+ydrnychTzFUQ6vlf1fQP8bZ08
vJ7RT/UoeLnlypHIu/qIOtTy1DAaF6V+K+CYqtZEXO9LA+h/yY/QvAh/uB70
LSf18/s34GWY51bwVaqJcrnQj5ZkR6iHpxE+TPyYx3MjHubjA96JrpeJz9Xa
vz1/4xxLlwE45VvJED/J+43k2tskHoptHDTvucCXmPFFHPL0QSRXiyd2PK97
Ab+ied8ifICeNRC8SpWfI96xuFBy+/Nm6Ae0s24NzlPhjxp6AuflfdjRZsWH
yKPYcB/vK1AFPGZnXgD/HBONuEXhbxz3YT9YtlGUj6DeHeWIp5slO6N+96ar
/g75gzk4bytUCHT0k/3z+ujWfL7x+ryxhfNf4O+y2mF/l2bq9e39UQfWu0t2
0ei+nvbn1Rux0CNHgW/ZlDDvelHO26+COLgVZ+yEuu3ahVuO9pXHU8Bn/iUS
fGUNUM9dm5wBesib7LQvBG+D5LmO4zdTwXu9Bfl3es4l0E+OZIR/5in7e1/h
HhL1pyw/A9efUn+o0OsUxN/lR8sJJyb0Pmu/vIJeKLUFr7WeEnnlIp9RPl8F
fEcFwknPlK4Pw72QUXfR+B/C/pJiq9B9rTyZQfEC2Z3x1X0R/9Lb7YT+0+gu
fa+2cwT0uhX3vO39kXJkCqLx0icAJyX4mrIlwA/+EvezhQ/k+1vgYC1cHONg
pdtF6N5RH2H9y8MmYB/9zO7AW2p7bgGvxvh/Yybqdwj8vzQ8L+pUi333fCTO
zwc3wTfJ9qAZmJzuUyMmDfSPG4twXiWcxfPDCznuWdM9EOcS82JZ/Z/wjNaP
uby0I56uhQ7HvLblelbieQn1rqTeXLeR8ZDG6bcYNy/I1d+ME/0OuXrsLnDN
J65QXE/ftQzzwutTxKfE+jSN+UXschG3khMNdOCjjFKvkec+aynw0gL//G0g
/LG/ezvig0Za5kusmE5xPO8+G/vi1FHwdhysDj2nVTIX/X98c9rvehHI1f3D
MX/TjyFPxX8R59WWgn5RYDZ+p36KOPU+X+AfmL9XaleFzmHB3yvqs1s8b6I+
+5BDwHXr4LfXxr4HD2ob+CVEPRezaQHyp2uBcfBrcTxa6b4FeRw7g5BfIvgZ
Xp+CX3XXQ8xzQ/CeSqERyL97WZJ4AvQCVYFLf/8acQquTyR/UCAX9YnO7oNd
L3CSHxBfNvcjf1c+MBf891s+YT887VeNvxfnWuMh8HfMmuCyy9XsTxBv8CyD
8/ky88NXn+ZG/VMLQh+7xDzPqX4AT5I1woG7NjcY8Cew/izG2dKfu3L925Sd
ke/Z4zfw1revO+rd6DOaEB+62rYC9oWPD/wuO84DF7f4rEMu1XWnfagv2448
MFE/4sB4Gl/ZtToVPSfybQvHkp6hXpmI/cu8MWZJCfEM9ota4yb8oo/rIs78
YUwb+rtjb4BT6feipr19fdI/yG+KHIT77Wp1zHuJtsj/HLoAcVruv34G/jft
A+fnbr2O+s4e54knTWK+sv/2O+oBMl+Z9L88Zl52uby4J+ywDtth766YC/vd
3OFG/RDnsGsu8GfdXrns4yDmS0oEPnNl/RiS69c2El5O6FfGgCPwt7B+pfSO
FflJ6F1oOcSDZjwScsI1/YnM0vcyHtvCqTIeW/4CfKwehrxAqRf4GzWfCOIV
0fy2grc99RzEwbOmTYt2EJeX8y8BPqdM71R2ubF3N/KP7t3GvIj72hyBOHGY
7uOQD5ShH0wdIfghYSemhH9QvoVzV+LzWVn1DXkZ26zvRVyrF75Xaj0FekX/
pNB3Vy0BrvvdVvD0CP601C9oXozAHszPgPNZST4G/HJTGwuebIxnpvrID+zE
POIP6mG9ufIhvlaoF8Yz9yrgYB82pntfrbsBeir/GKM0zMeBX1xfXvDNpoFd
nHwW+A3U88gHvJwDeuZV94t23lr9bRDs3fnT2S/N/P+NEAdV96Yge0TEo7XX
84Df9foJP5Xg4Q9aBPtwZKTjPjJLd4Geed+P88XYPzB6O/A9YeMccmNKL5yn
h0eC71bwsq5M4m//fmnGbsTNpfTgK3xUl+bJqDqW9H7j9AzofwffwF997jDW
Z/EdyNPemIjid7obeNe1xiNwv7F9LQlcH9vX0s7C0Pe2M+/9VPD/mI0uQF9j
P5t6tx3y/faOx729YAh9p3G1Cfxfl/6p5RifjW/ht+pdzDmPT6dBj2heHfom
/8j5xoB3rGdDX7tcSgCPsHJ+pKPOi1Iige6vP/Xj6P+5fpzZEveyWgz5EJK1
3zlfwpvrUX+B3S70FuW6wvk3+NE7fAEubWhrIQdvttcinNspj+E+b1cI9tO9
INhlfs+KON47I6vL8T38Y8QxT+WgNDiHBG+2eyng/5p0CrDLjWkXgWss0NrB
420ezYHx1joDb7s4JXiRW3Sk9S30OovfmPU6oQda9wvrgdpi1A03X4E/WU+J
vDxlQn4Hz4CU+DztN+VAC9yztZAHrRR/TnaBFMvxapF/fYzjKZ2nJ4Kc6/cl
S4f3n/XHeSru02EL4KfKhvi51c9Y2CMijqndQT9FHFO+HkTnh5wkB/r5Oi35
u6UCa3EORSeDvPUU5Mt/DhDnD68T8HWatUqhbsG51cgbTZIRfHrFXlJcy+qn
JNF8mytvOepGKfsWE35PXXsjt12uN7wFfTkM9Sqt+pvTShOvlMCjWnV1GY+q
XI9zyKX94V+4v/Rj6w/W5ddNwJmEjwVvS7gf6QNGomkUJzI+fAWv/4BqpM+o
Sd4jf1fUzdw3CPUOOH/KqnPK+VMiP856nvPj5GOzFbvcaJgV99R553eZXWuT
H1XkGVl8ApxnpDdUMV+C95hxKXrqa/6Ocfg829c+D2IcxDwZESeBn28XSe3o
aeVENJ4lG9H8S/PKAV/+OQF8bX/xIeuF3IlnVf59CDz2wj/mG0y85/qvzIiX
nRg7kfr5zr8g9bOAU7818zyFH7zQ5AC7XHqcA/b42WOIx13yp/UoN7iD9c51
W9SNVXCfct0W9WwG4NGKKajbPGYM+h1/j/xCWvfuuK8yf6Pv1lpHUBzNrHEc
fo4XvzAed2AX6POnA3+iDASPym7U39RGGoi/GKi/aU7qTX+nRCMv1Vy+hfa7
/P0a3j9kL+eBbgQf6cXqye3fa7SPgd/8VTjnmfJ9keso8Povm0NPHAI7S3o/
CviKmBs4pwvMiaT2fRMk6q8E/6g2tS/kAzrQ/GpJxzvjHbEKcOwd+9awy+V2
BcCzyfeD+pPt2QIvwf/WXgWPtOBPHp8b9uTWpIgvNj+L/MqeeRGvNGvDH1UN
42bUvIL49LNWwBmuvol89lINKX/SPIV4r7Hqeg/07wXyQq/PS4X3Am+jqLD/
1bLQ48T9LofcQ15ApQicJzEnwb9XNxPial3aO85trc0q4Nn+XQJcFdeHNZdf
oP2jz+hA/dLn16P1rF3rg3Y21ES9ksdr4Aculhr53jm64f7zWIu4jHcX4Go8
8+L7GS9hlqiOvIyOrThuzriFJYfJz2xWTOKQ601rkdz45zzzTiAvXjn9Hes9
8BfzWke1p35WzQscTKqC8AvNu0xydX9p+N36jwTP88PhJDdXxiC+Wbso8HQC
B/IgK50XapLLQYat//qyajg/GWcl8PMCZyX1OoX1y+eecmc91uHOY/CHfd0A
v0fi0tDfqwYifivqLwg8hvgRcp/LkHdIlcL+vHmhMunPeqtiyINjuZ79JOKG
HGcUchFnVOOywJ8TO4bmV0n1i3A15tsu4Lv7vpnkRoZJFDfSQt1hJ4h84SdT
cP8ei2a+TdhNam34l7SF5RxyI+1+nMttkQ9o5ZMmAl5Om+jC/HA+i9YZ+aVq
ZcRthZ1uyZMAtynvA/5Hj0YekKiXIebLqpfBdqXIjxZ2paiTJeSiTpayfgH8
tXvRvuETQPNo8XPH/wY+9Oc95Mswn7d8H3IlkSTuI/ox2sSAF2zQNfD+9U9E
dfm0c8DdycvL4Xyf+JLscSPuJORndMQtPN9x/A71BfTSoWSPm6Wu5IQ8OZ7f
NwbndhPwXylZHsBPMjUW52uHTajPvHMtnh+tg0/H5Qce+Daoa6mF5iOebbNf
EuR5sF6kHNst0fym3kHnosn4QNl3FeyKRwGE11PeQK5nC8U93Eqn75Jd1fD8
xy3gvfL2wj36fRPGeag31gePv16J8Q9i/Hke//bniHm09ASeR33jF/Ck9pyN
/lwri7zuFAuQ/z0uGnUcslTDuq2VEvfVNNSVMxt3A09pmyngQ+XzQf69x4P6
uWuWp338pYC07tTOh5ccn+V4qNcNGhdj2AMHH4X8cTudU2aS3sB98Hkrd52C
/i+4UMEuV71CMpC+vfOh057a5wF/4EzU/5I2huE8D3EDX8bti8kd7QROAI5a
x3oTcv0or7cUiodDrrrDnr9yqYhD3hj3hzwb467PT0bvlXx14DZLPwRPOOPB
LD7kvJ0cPFfmWV/cLz90B65ATZIYetFV1Auy/B6T4lD/IG8U5rfgW/Qn2oP2
g9TFDfaO/z6cY/MjSM80PRP4HmecQ4eKuEc6V6Z1pMdvA57tR1vw+aTfBDze
zQn4rqAW4Al59xb3WFLkyWq+nPcu4ikVsG5FPEXP/wvx8F53UJ866uVrwueM
6knjrOzoQn48M2YY4tqinhHjG0U9I3VEIoo7mN2hHyrfBsCudO8A/Iuokzgo
kvCIyvev8BsI/aHoKNzraZI41pt2uw7GZ/hCx3qTq92m++nv9anlmkLnj5Lq
GngM7jPP3thNJfD/d4C7bHYI/o288KNrl0rBXxS5B/J3H4GrOvsC9v31o6hP
1A64A8mtH+yZv+K2gt/Vuq+Z31XUB7Hi4FwfRLvUmetCsv6wYKeL/n/jtgJ2
uTFgGtZfqa1cv4b1FvcRiPdxfRNrX3N9E6ku47vFvVMKfKx6r4GIx4q6PEd7
ol4L88ZY/WfeGPl41yDHPF5UUS/Sr1sNu1zr0gB2fbplqOu9uziej4vDvXh+
dyX781KXz7jPyvbBeSVwtilQp0Ea7OtjlytNY7C+2W9m5YWx30z/NBTnjsg3
aVYa/oRe9/zszysb8yPeMMIZP1X6zqf50uR73g55ZEaSCx4wK94qeMD453/r
NaSvbpcbc4pC/nkl8rLOtYMeL+rkFgyC/TDuOe655lno3FZHtoAe3d0P8eCU
o3HOzy5L4y/88KIdyw/faKeHYhs3fXow5jWyejH7+Ovxj+i7pKTnijnaGf2G
v/eap12u99ex3rheidBPRL0SUZ9RO8jnA9dntOowiva5DqMx5Ql42sT6f74G
ekvYePDQpAJ+Wx7g9oD2dZbu4I/g5836Q8EfOmxKA7tcSxsFe+f+L8RfRu9F
XP7UY8IrajV+Axcg4teeLZ/SubcdPGDKrkOY3+WxuN/XHAy0t68oG8F79r43
8r1310I/96L+8p966DQOIv9oHOL95lHgDvSUOSm/Rt+2GfkMYfHgq+gzkvK5
5F1hOGc4L1L4h0VepFK8WFG7XNGTw5879SfXTwe+V4nOi7hg1cvg75IPoJ8h
vcAzcv6Ysz7C1p3ACw1u09j+XerWdMj/aTLEITeiEuBPXpoY/LU5XRifu4/G
kV4WFwq+f8FjtuQm6it8ccN6COmM9zbLRXgJ+dJc+B1FXYY0qUm/1BvXA15P
2DXnytPzIp/LknM+l3ElMcbvMa+fFkUxX0dSeti/V16B+p5yVuBdzcSwW43m
fA+pqM9r2QWzdsGO7T7Lxz4OggdAfXDK2zFucT0gX5KKeae57gbjJGX/a5Xt
cilO2EEHqtjl6k3gLdXxmcAT9gz1Vc1Tg3E+MP+eGGfBv6e4ecNuikqGe7bm
J/hdGNcnvkvg+tRj4MUUz6uHxiA+/KZtqF0upz2D8Y3sBp6G3OADlPougl8+
NAp+crelyJO9tAT5tEG1mEcO976RbmEy+rv/7FbHPLLdqv6MyIfx5Py4MeU8
6H3bujW1t2Pmzuyi7yg9zCHXjuA+0A51hz7f5jnW4QSOp3uf4DwmtG8WioK/
bSJ41Cx//thjiP/+HW9qj7pjZjXg5Y1hlVFXt98v4KrjnDgH3Qv8w3L5Ojg/
uS7knzwRku8pynynnM/+JgL5mzU20T2sz88HPTD0KvBk8wPhvxV85sZM+In2
RSEu2ZfrZ3nGkF2nZ7/NeAPORz4IfUBLiXojIk9KvnMFeIY7yDsTcj0R/t5o
j7xObc90wr1oXZGnJn0qVss+/nqGx+DZG/ihpmO+3h0E3pR5yaz1ybxkZunT
2K9iPedkvNnk+8CjiPPkSTB9lxHK+YDcT7XlfOAY2+3wt7cje58Uej7dh8av
JOzvvQw+Za5TrHbLBn8a1yk2hvVl/YTH50Ys7vGjsgfml+toBIPnzTh4G+dY
hoFox6M1ePtzbUSeVMIAtFMrF+1z1bWJcbnopzIlG+TM/2/Jmf/fyLLcZZer
+1fQ/hHzLtXmugBi3lmvE89beh3z+8lXuD+C329FDthlIt66FueeJhcgvU5p
E43+rJ6E+OOBXuCv9q4Affv6C/gvHu4Azm0n8nT0L2/Bc8H8kJY/ivkhBc5K
G4r6OxbOas8t4FY2P8J66NYd+NyJhXCPcPxaqR4MHOr9IYpdrg39ifjR/XnA
SZxmnuQ3L6HPrL7FejLmVxmgYN3vK0n3jNX+y8ewRwQ/4cUcGE/mJ5Q+fkP8
nPMp1GJcP4V5qETcXPBQqf+0xH3L+0I+k4balW95sx7OeZrJppLfT28c4ZBr
sx9SPMJIFuLw72ltlpM9JnBWVjyCcVby6MvwX40Bv4FZeBR4ZBi/oS6fRnKB
31AyrAL+JM0W+OvSd0ee14MTpO9LGTfCf7juIsmVZZMd61b/XRr4xoGrHHFD
c/Un6O2cD2fxt4s834H5czjmZc8C7K8n7znuxuvfFYt81TI5HfMofZyI/X50
hIPPXw2sifqOya+wXcN5wR+ZXy4G+qEUegt5AeMy3CU9VnHmkyplhtF8iXoc
Zjift1yPw7z3FLx2Ih95LfQ3PXsjnN/LcI//p3fh+cA18H+cgFz6UJfal3Is
h7y8L8nVz1VJLt87if7PSYH41J1Z5EcQfG5G5eRYP8znZnxcQ/4HaSLy1qWf
a5BveQ38gtK2p1jPAa+Qf3I2MXAWYj2Xv+5Bf5dyJeoHPp0N+/FGLOb1dHYZ
38v83pm47vXEsdinKuKw0orKwOmmPM71YXmd90c9BTXHMuCpRd7xQl/Ik00l
P7Pq8xrxu6u/HPFr/d4Hkd+H+O5IF/tteL5Odsa58OW0477Qn53E+elzlv11
fF+M7g3+1j1FGO+Ee0p/uuI52Tslple3ywVvjFTdLzv3i/yTavxc3GfdyiK+
KfSf9ZmxHi5L8If3xvrRr0Wjfu3pFeUdz097DX6kDIuAc80KfVutMRx8g1ev
+TjG38yIeF32pcAHcRxK9trCdYyddpzwT1r5HX/5pcU8WnmvPI+izouVl8p1
Xoz3JuHLrDjyj2PAK8hznHHYuB24z+IqOeLO6vjEOPeYh9B6nnkI5U7bnM8X
MeB33RQGHKDwf9bMAPt04k/4jUS9Ei/kfZht0zrrd+w4SfOqDQvH+rk6H/ZU
8WjgrrOvqGAfZ3NDU9ibDwY66iCr/rVgf02c4uCHl9Kchp58JCN4oEOZp/0N
62Pv1gC/mgActfpjDfx3ucpjXa8Bz612qyLye39vhL9d5AusnY/4XLHKwDVx
HE2bJjHvIcfTWP4n3kb9SWOQXA5oTXJFXwH83fqVyHsTvPTfxpDeabi4vl7m
pzjHYtKjnuCdksApF4qDnnZvCPbbr3MNHeMzNhfV4TIqAGduNhiM8RzAOPPV
+Zra5XqHozj3s3o0tbejd0TdPfXpm0aOcZ7mBj9euhe498ojTqOVqwSeK8ZR
W/FuxlHLyU+RXa48B35D9Yjm+6yao59yw1/k11KevHbIjZCDwD/tX+KQS33B
2yZfyuayj6eRnuNHXJfQ+t7592FX596L86nmSfghl10GL2H7+iXwvbBT5Ext
kTfeK41sl0vhn4BbjatbwdH/W/eRB36iWXnHeJbLCH29AvgMjbzlqB29BPwA
6oJZje1y7UNRkQ8i8siL87/Bp5StN/mZdUlCvO4A89hWHV3X3h+z/1fgfgsl
CbHLtc9dKc9LKR4QYu+nGvEV+WDeqFuu74MeK3WLBQ9MfBTj7uthHfyDPB9z
yU+aX/Xx8LbUjvwW+Blf5pvh75I6LwZfStdaZBdoN8Cjot3qgzjQ8dqV7c8r
0Unhl8jyqoJdbk7dQnJtD+qTS0NTk1z2iIH/aG+KOvgunsdqkJuBSi27XD11
Bc/zOhFyfX4DPN8sG8ZhB5/z7ZoKvmbgywILNuJ/O34s/CHn62qLR8D+YLlm
ZsZ67nXPzy7XN+R30d8VW/7c395Pj1dYD6//gd7CvEPqjEL0vFFmQwN7/82G
P2h//vF30biJfI0jqGdsTPUAr47/OvjBDoJXRRJ8BQ8zA58W9hb2LcstPp/1
I2GHPMlJ32fuWonvynUWOOCo5MirYj1HaZ4UOCvfrw65Nutf7J+QoEC73Cj2
jfaJkuFciP27pOdz4SdvWxH+K5GPH/wNem+hslUc8iyoC/yfHudnl0uzA2jc
9I2Dwbso8l/OZoWd5ToAfxLn6aiTwGOsTWzjkGv/gI/UrBpe3d6Otvo68BY7
xjlxjBXfwr/j50XrUKuYkuT6g6tYh+2rUdxNcz/Qnsa/a33ozWlHkV2iFT7c
ktrZNRd4iX8PEw+hsnkD5MoR5L9XOIb896N7MZ49+gPnn6cix8V4Pyo3Sd/V
qz9x8FBJ6b/SuEi/AuE3e8U4kGnZYNeYt4Hn5LwVC8+ccSPH2bkuUqu74Dtr
2tNllxs7wEeml9QR7/iMOtHGl7P3yc85ZifnQzG/lhTmRv/f+gz8Bml3QX9u
cgf2W4hPYZKn3gl5bRXjXikaOC7LfnwfRONVfTPOpeZvUTeZcUdajAEe3WAV
fJIPPiH+lrsCzb/l3zvqTXqUMvMWrSs5ah74+h51wLkfkwf15QS/35Tr1D/l
nj/2wfOA5vS+zJ+QJx44FPn4zK/7n75FcvVpM4c9JW/pS35I+ex45FV/5+/d
nZa+y1w/NhTjDL+67Lse8cKNpZzyfO7Im0hIDr1a5OkM3YR1dSQdcDgjypPd
qr1Lj/spXxzyldjfJfUA75bWDHnw6p7ZkX/+reevAnxDscqwU/LwOe93Hrxv
mbbivq73HfMeUAw89VWnOPgTlJ4jgKP+vg/nWPs0iEvWyom4b9gp6PWC32M4
6jubmR/jnko1CedVbBDqUBxPDfzb9N2oNzR6AOld8u4UiANsXoFxdn+CuLMr
j6+9fTNoFvR1rgNu2aFcB1ztsRI480i8V4voD7wq84Rb9buZJ9y8WZL5/aA/
m09fIK+pzqP6jvnS98BfsHAA6UdaF/ij5MzpsG8ZLyHqRFv5L2sQx7fqLcY3
AG9GTAbgO/g81zcl4JzhHyEXdZR0ow/OP4FbLr6Z/Eim6uGQGzlnIt42oyfN
s9nkAHBElYdQ/5SAYIrDmjfu43vLoS6IkqkScFbJuR7T0p/gi+t4nf0PjOu7
eQ75Mte6UfzXDHoD/8yeM5hXUcf5EOxxwT8jCX4eHue/+XmsepHHziPvKdn1
ILtcn/+V7nslUwPwm55Igry+0afAg/cXH6O8MgDn8DMFuJpOW9H+/hDk7zxI
Td/3f/ig/n2Y396O8VCDvr6hOPiKT0oYf725wI8Bp3SgA+IdSzsTHlVO8dHB
g2d4yMCLu9XwsMsVt6MUN7R4EW9g/wpeRFEPwuIxE/Ugxi8Db6dYJ54pkafH
dbLkd82xrrhOlrB/hT9K+W990vd3mqLY2zE6lsH+6lWZ4nFSHfZvzNlI7/2T
92fvj5qW49pN7nJdmGuEq5Rmlsd5fX8d+4OfAIf5ai/8479vUp6OseYq8nTy
5rHGk75b2LMvD9P5YLbbQ+Nh+Xu75IafNuc4xg+w36P7VNynXA9IvTkD/ed6
QNLujKhTX5d5NRdd8OP34kfMe1wccBXr5jp5AEZPJT+kVOZcNbtccX0hPkyj
Zp0gu1z9hTp9uoE6pMKvYvyb7QHlNyw5jLjn6SpYn24d4M+Jzw7851/5m3I4
+NjEeSj42oxM2x3njL7xC867CV8Vu1yefBd8R9tS17J/t7EMuFOjxW3mR0L9
ZbN1UuSTFcoJf4IyE/fsvCPgeUkzEuei8H+OHgp72BXrWJ/6mXvITx4yBvHI
gZXoXpPjC5E9KYWfAX6mGPKLzZVsZzY7gbiGmN+E2sB9cf0aaz1w/Rq1a17Y
nQPPIp4eXQz55YnToY7cs+nwZ94sBZ7M2/Vo/K31Vi019NfDKxPT97K+Khcd
CT7TbgnQm0R8s+N+9K98DPzqfUzqv9wT/MhqHcRrjIeTyS4zyvwPW2cdp7XR
vf3gUNwdwuJWYNFFlrDA4lq8SHBvcSgavFhxpxC0LQ7FNbgUp7gFKe4Ut5fO
dyZPwvu7/9nPns3mTiaTmSPXdZ2a8IC+uP3i7wrnNjwpeZnX34F7UfiQXPck
7sIN8L+sSbeIfyV/QpN9BOzXg8FP3Ctc2H8eO5fBedx/8EMbzKRfc7T4Yn7q
0aeRb1b3Va0Y6+TIepK/IusF93vgL+W8HO4/3t5aBFxptq4Bu/73JLGuOY8P
lQ6cp+5l1russ+gfmrQd9dk730WI6+qP3cgs+bnDa2B//jnQz1r1NVY8Yqv2
U9YlySM2draX/D3Z33ZILvIfBb7q+3zxDPW+6kH+i8IX6e+/qncPv8/7v6tC
Kf99uf0T8j7WGhjgo7lrCgi9GqV75p1f6jo5cbcF7E5q8EN6rUZx/OfXM+Vj
nZ05KSIwDoPziPdLf/A80n+8nfAGedIRvdi3L6M/oDWnjub5LVLHUvkt9k9P
ycsqfl+0CiKPZv5zAly2wkN2r0H+s/0PrDOz0D1wOsYBt3H9ifBz9PjtuJ6Z
8fC38nVn31nziTrYMvRR3WM1ZB5M5gHyDKPu+yvxptfXvuQ2+O9DXuYLXOds
+JJmkp0V/eNj7Xgi7E6/jMRRqt/6mUPcx6U47JPDJ4s6nZE2HXp5sk+9fuEO
9TvZp949viHC/7zctj3we3vMDTxHre5n+HwfUvEe9dWoy265BG/JzCrwQgpP
q19Jxn0+WwtfZt1v5OlvxKb++6NBf4dOHeiD8KK21HdaKNZdd30i9B8qPRH7
n9Jp8fSupU6LtkMP2O2xJ+DfnYoTm3GTePI0L8nnS96WLfNdVkzWHU9/WPq9
Cq/yJS6VOBaZf26gifuzj24R+4x3PZlM/NcyqwN2Y1oG4q5aZcX893C8q8Hh
6zG7lvZfv/7HTfIPUs9B6WIpPQd3QCLyqX3oP6V1fkVeMtvECv7zGF1DweEf
qxmwO/Z89n3l7yl7kvHY4xZGZ0b5yUPRq9cyvZX6/PI9PTwJfMzahOAT1TqZ
fhQ6EsnzBOxW/5r4Tw+zyPo19VZ3Dvk950nsVH67fT4f+aLmFrz5ObyPVvx8
5AMn0kfdeTkSnclNkdSRKxwgT/PTYN7fnzqAE/7nFn7cqNacZ0979FbCopJ3
UnyEvswb5/Jw/PMy18U8NC/0/kfotGyfJ3jEqv+y6vdhH6HfrteX+SD5NDds
deB4rRH5c/fpDPgW+1rTLybhdPh0NXIH6tp2yQ/oAkj+mqezIflryh/+mv+u
9NOcX5/g/0j9NOvNVq6nfGz2iyJHiD8adJH9jmW/728f5/Yf7/UpkMfrXSpw
f3fo9+q2q4lfXgacgPkS3r1TM4z4robEHSsd/us34Z+s6VPGbzc6pSDuWibx
pCo/EKc4cUuOo/CJL6K7bixsCV+5WBH0+Otjtxr0475OV5N5R537vbEJvHrc
nvghcUPAh1x8j15N6iHiepwPZbmedys4r+yXocbZ65cRvpZ+Karfd83xrEvX
bmf3290OH/DnZ6bO4b8vIzd28+2ECL/dbj8Xfu+NO+Qnp9BnSs80lPy81MVS
81bpYik8jLIrPIyxHz6NsrsPion93arYTPatkDiZMMmLOAE+wTvPVPK/2jmL
eE6tq+lz8r6ty45/rXg33foxDmljsX/MlzpCY7aSX261lTxBjbustwcLifyM
dr8Q/LgbhQVexbzfRMSx7r7y8PWUH/6qDbzO7TJfqvRXZ5+BXzD2V957pWsR
G71CTwe7Sjzmp9Sl1E4PD+aL1tFHW9vblvy6On+zmfhbfR7A3ypL3zqzz0Vw
7T1vyP7p0s95C19D/3SRup+ME/VUi6mjZ9lfwf+95oW5gh+q+iC7faeIcbBn
zpwp/OURO6gbhq0mz2305b1b+Sv7qqoXDF7L+xV6trTfblXBXzS2DwngPfRM
mXnvovcMxNH6tcL4n21qsg+r+DpRW/ad3sSD3vpWsZmIB43b38JfU/5JFHhi
5pM7Mi8h/dUT8MH+043kvAlZxzKkw8/T0QvX5oO7cEY3E+PrnEgm+1lLfd1h
p9DHjtI5YHfPxCcf+3ZIcb/dWPSePEm/MeShH0SDj5y6ocg76aXD4MnmWsd7
ugo+pls+I/rhcbvzXu84C28z2i708n97ItZD7c/3zNcnNTIGvvfoUurit36h
j9Cgb3jvGv8DDmHiCt4L1c9x/2PqR38sjfTbtaiJwJ2vqB443sz+Lfn/XL3B
SxsHyU9Weg4uoTU4YW//Sj2avHSxr/ap6/RNNn67Sh074g31vshF7IvZdrJv
KvxA+rbEw7KPpFePln0kFZ7B06tReAaJW9Bz8Nw9/MmCuIyT7P+r8NJ2/RHB
66wwCpzYmD0BuzNP1pPS7QzsX9a6YthrB89jx+2L7nnPXwLHu4NPo1uzDP/V
vtKQ5x5eAB0jT3+Gfoje/mv/XcR/Hudaf/qCp+iQzfGNj/17e+phL26BR4ib
kv2uMfhdc+1e/OzeCdgXtAI8x8vg6L15NaocOPtlhYL3OzYGupMnVZ8Fme+y
J5OPlThqj0cvcdROrUKp/M/RmDGXOPCvZ4FxcxsspE7T6nHQf3gj+39MOcj1
y/1F37wN/ayZH6l3truD/1Dvlnh/jdVnZJ8OmSe5znrl9ugFT035OcfAf9oP
Zwu/Rs0Tr475ayy+Nx04HHvbbvS27IuMW2hZ7NMisbeoKfvcSR3RaxnAx9ZN
JfcFpQ+zVtSBjHHdg8dHyy7qOFqhhtX9x7vFurFeS5y20ptSOG194PA6frs7
KhQ/8MlA8H6yz7vX9606eVOFQ3YK5Ff6DeBTVP/WCUuoFy8vUdRvdzoeIj7a
XYr8kuL7jEbHSXu6VNZVZb4lT3f8nBOLZP1d1lvPzEK32Huvx0hcNHwTZ9wG
mc9JJvxnJ99b5lXK2+ANV40Rfe7MUzrzc9V3+KspOd76tyD144Z52ddCb5OH
3/YavRTVp6nqM/wB2adJ7920OuNJHzGj4iKdcWhZ2m/XW5L3dDvQL9scnxU8
/NAu1OnzjQ71j7Oe6Qn6dRuGy/Mz3/SkOQXvVa8aM1L830vy+UanqPDrs7vw
jBMV5Pyl0GGwp3wM6AlYRWbjB4+JJXD3Xn+iqJeEf+ZsTyj2cz1mb/QzH9dn
PZL5QLs95/fygaPyUz+ckZb9yOhFfWEv8Yuab+YD+BFGmRCZT2Af+TKoxH9L
+gXsZlgz8gxLYxX3n8cds0/2ATWZ97LftPMUHofyZ7zztLmNPvD/8n7w3yQv
WhvcEB1WNT4Zu6OL1aZ+Rb/d/L0ufSqTRMVPP5uZcf4ch+f1cgZ1edVX7vvB
+L1TowX6v5vTnjEf7sHTNKJo8Ge2vCPuqvBNBf/zMgpnoO/bczPSb7fOhZJP
GNakXOD486vBIdw7H6iPmW1HM87jJ+Z0fHb9WSn0WeX79TVP2Zo7gLxBtDjs
73k6Mm8nyT6P3v3Sd8/tP11cpxmrCONTpz242Nzobukf0K/QP0tdI5nP8fa1
S/A4PLy90vGT8YXqi2TE2sv+JPsieX1e5PGqz4t7Hn1m9X6Z5cqI77Wru/jP
F2QdvH4T+D5JK0pev+zr3WcUeIJdUeiXdAtcgTnvCXm3H7uIdUvLXUHUx42T
OcnPl7B4PkoXbmFb1rHZ9EO3QvvB790dD31/iZdW46nw0l/3Y7Xadhbrnur7
4/HLZN8f9dEPtWd9frWY/bHwPfqC1fybPNjJrLwvUg/N3xdbXE+0TTIfJfta
1kUfQfFHPD1SyR/xeGeqD7L0o/QCWcBFTL/JehtlM/5V1dYlA+d5nF5cp9Vi
osw/Y3c+pWH9bdOT9z3qdvqytT5JvBprW4AvY0bAK/zPr/u/rkcL+w3+99YR
4rkY6dCBt//oRl5nN3kYo+sK+mnWiULfBJV/+zABnkZFExyQqo/f2AnPZ91T
4hrFp8u3jd8bDQ2Mm5U+B3nAuJMD42w3RS/XPF2SuOmEzAv1PST2a/uPpfS7
V/H42R6sP7OvBeJlpSvrRMi8xFPqm/rD6+hYjY5djONln766I9lPzY2iP7C6
fmN/PPSn/pD9Q5S9y0DyG8NaSz0Nud+FLWHfT3sm4Ce4taIQRx5EL81JBO9A
9X8xtofmcHznsZ+xDtq5UqEXPrmT7KeJnrI7ci54Z+X/bC19WPA3e/QN2K3V
aaKL8Ws+nvxJyY3E3adnUlfdPTDoR2VbKXC0epN3aTmPjJdzb6DOHh5b7A8e
z6LBavA8a9KK+/Dwe1M30r++/fEafrtZO5aodyudfG+dkTr5qj/j1/rPWpJW
8OeKpQG3WaQ0+/6ZA6wzNbuK8xvrY5HHb5aNPifnFtLvtavM2/x6Tvbv5rmY
Y0I/Cl6tlV3kpdwNP4JzvnWP+Gp0+iBedCm4MmPBOuJZ1c96WVP6aR5cVcZ/
fufDbOKOCysK+493GvTgOiXu1OtTLHGnWtyeef12831bdAek3rKxXvYxkXrL
Cg/p9UGW+7698xn9elQdeRB8RrdYOWF3vj9M3bBNfvRtH2QU74UVXRN8PGeG
VzcUHzeyRlt+l/wCbbfwk8wt5eC1jX8t8qoKz+z1B5d4ZndqbVVHFnVJ5/aP
no6f3650/PT+tQoGxlnmdVUfLoU3U324nAyyL5zaLyrC87R+WVfCP57umO3k
26vBQ7EaZEHf6VB68G+Js4b6v9caElfqBjxmfMycAh/uJL7iCj2WgvvRcZP8
RCdHCnRZl9RHV7bPQ/bZRh9Yb/u3Fno0Sh/eTrU3i+MbZ2X/T09e3GfxSeAf
FK7g0E3qtfNiJPDbbSsm9cHxMehD0jIxfahfvxJ+tumSF/LyjX+ALzUjZH5e
8dwTxKV+sKQI/cATLQIXPbIn+aZWU9jXMnYfIq6z0QFN/ByGDqvZZzr21odF
n2VzamHJH5F9N3qTJ7WOTAnY3XzwszwceO706LFPyQO/IKQEvMzlsk4x91fm
01f8MtUHVotMDl5D1jXsVxnABdXV6Z+g+hT/vAg/NwJcvaeH/+IX4pl6weNN
rRz+07FYFQL2vvHIN708TF5Z+Sd3D4q4whyfq4z//O7nnfDlyyWOFPe9sqjQ
yTS3v2F9PhBV2LWEw/GTh8YA73Iokagj2Q+kjuunHuzf04sH9OqNCw9Zr3Yu
DvSh0ztewP9e5wbwsXrCsuL8Rqsm+P9N0AHQ4rVB92zRQvCfKXeiD9DskYj7
7PYjwEvc6gNvyGwj/AxrN31m3cX5WPfC0O3Sf8lKX6+8eXi/5rA+m1V3oqO6
LJpYT51ukg9WeBPx/9qT6Jb3Tib2FSf3KTEuXn+9UevJS5briq7I4/JCZ0Ab
nIY877GigfjCKhoq1istbQLqP7fxN9zorDNmwwuh/vNremcxnubzwWpdDJM/
wc/cekc+8EkW+vYWePFZ6kAyrgrnfOU3gYf72u7e7C3ql3rp7RX8dmvDZfpG
rLoV+F5jUUZ0NUPhwSm704S8uTUuPXyJR/A4jMTohVqdRoJnVvOhwM/wvfd0
F/GRfZQ+AlanKRHi/8fsCcwrazZ5P+3pwOB808PBoS5owfss+5jYG74F71Hr
FnzK8HhifJyDh/GfytMPRluSRsx/W4tPvemvb6gvq/6Aip/yQ/eK/uu3KqcR
+Z8vzzdwX/bUSPJC3V7fF/uKxEs7H17gPyTE71A4ba1JE/zFHGnR6VF9xn+L
JH5M8C84z5vonBsn+r8WcWLsM+DyVP/fA3akGM+wvew/Sm9hd0zyCdvLlAzY
k1EHseLeCugSuP0/gGeY0zgV9yX7Vjynf6thHavg/14tvCu6s4MKlglcT98s
rA8Le0g8MPkB+3pM1tXS5fIGxm3jWXSWRj5kv1XzsPsxcV/W8hdy/5X9Nf6p
ybrsUh/x+pjHWAsOpnw98OdV6B/hXujP/UudfzPO7DbieqXOvxt7VX7/deq5
pN70e9nfbTx6mM78HejC7ZR9jLrFo+75ZiE6O5Xii/mp8PPm0HH48cOys27K
+ojZPTPrgOJNlLnaQv4e+FilioDr+OL/iOM255Y8QZl/eDBHXL9hJSzjtztL
rlNnCbkn5qPq12bHy0Yd8FAMGa/JeT7+O/ICeRthv5pDXI+R4KKIc4xIqZ+s
dKTf/khdJmwafXTV88q3Dd7a8llZ/XY35Dthd1LHifR/rxMRX/g9dsIF4K2U
jkrB08yzA4+F/6wNeY8/oEvdp/m9AvwOvXlS/KgJT8L8dmPKNN5Pue97erNy
31d4WoXHUHhas1pT4S/ZdauwzqyaQ95nayPBwzXiHWE9+eccdZNImzrpycGi
j4lR+B15ifsTyKfJdUk79hF7zXfgEZSu1O3FzA/58fqKag75fNlf2Dte9hd2
WuQT12usa0O/9b6F0LOecV/wQI3ehcEL/fQGP7D1DOqxb69QJw37k3HskTbE
f51OouzsL/uqwVscvYT+v/GiinlixPqZ+oDqq7LDwN+dc4V9/ENyxmHmumTy
vvAjui9r7r9Pa9LsOP7f7ePxxT5r/YJevZe/ik9fAW39aYmzlfilIykixfdK
3r1nl7x7J39q4n3Vdy/tNnCDF74N4GY1dw3z7CzxiB1V8ulqyP4FZdFBcZe3
oi/qtCjs33fP44fIj1HggewPGo38pepvuCYtPP3r6PFbb+mPYMR9zr6mmWIf
0N9I+3vyq9r6cOoUrZ0hwr79FTziHdOJ46X+rdMCXUn7xhb2XaWbmnmwwJVZ
H5tG+O166Zjw31L3LuK3mzHOiflpP+tA/UX1PTxA/y9zVgS6NFsnivq1dr4O
ekOzi8I3VbjizjGIq9NeLeQfZ7PSCuZrC5s8nuIHyb4G7tbnmaSduGNbZvK/
teYJu/tM5gN7HQf3Xq59QB/M/GkPeK22+YU/5vWH6jGN/JvsS+4dr/qSVzfR
F5q/QezL9qM8AdyvFX+nsCvcrzFzUkDXUeEb3fhXi/mvX5tzB33DJJdUHx/6
l93LgF9xJmjXV4NTdQpr4f7x1DMNxf4ghH1S9TVbekKs10bmcQX9dmdXb/hN
12tRHwjZRzy+tu0H4T/EWMF6+GQXOhizNN7Dv1KQn48xlfi6dizhT+pFSn51
v28C+FsPZy7xt0b9yWJ+ulcniHqQY28R8Zqz9Jp4v426Y7G3/+eFiMuLnwOn
pq5/XFNwbDUrBuzGkNrkf5odoD6yaCDrT53c4CpDblF/eTEMXPVA7Ha9HYyb
0i+1MpMXTbdR2fnsmU1f2Q2Zxfz0eEMljpHHln2FPLvsK6RJ3J1WeRd44fvF
0F8dfCvYB6FRKPpHSkdOnkfpyGnVomf3j6fbYYzQ49USXQjgduxO70R+0m1W
zwiMfxT6B3h90hUOX/ZJ/0/3+z+7lW8k9dZ76DlYydPKvply/OufRDdN6tJ4
4y91abT/8Y7Tyd/pm1UmHvrgGQ+IdV4fsSpC/F+6CmJ/19ajd63984y45dqf
2HMOYT4Um8K+P/YKOMB/E6HLN20XfIPnEu+/Cry6fW1lpBjn1nGIfzOOQldh
/TrilL8Pk2fL2xj74KTUF4Ykhkf8cQx6Cw9OqnpVJf94qo+zJHWk3243HIfO
T4UCvGcbYoj6m/VXOvRlJK/NDJFxjeS12d9Esl+oPl9VHsOLkH1t9Gxr8ddV
X5uv9GxVHVZfWYE8are/0Ottcwb9u2JXK/jPr7/Zybipupvcr1XdTXvcUfKp
pd7F80PwN56Wg//epxt6pLNewZv4SpfYPWSjYzD3mJoP4mOMrAVfI8e0SK4f
HoSWsCt+a/5L5QL2Ae/gdy1ZGtRlPduDenedTegKq/vqME48D+UXefkc6RdZ
UbKHGJr/vUsi9jsnZ4fAfmTErkq+W/bF03KgW+71xZP9wT3cu+wPrv2vvkkf
B4k/NmMNDOCrzRmN2b/WbVR96JgPMa+Tl6puFA1c/6IDgfzn//p0SH3LmUXQ
4fB0FDcF/EYvLpO8PKvARnTeJG/OuL4S3pzyt1W9RvrbzsOB+H0Sb29+aEc9
teMyyW+VeI+bJeEVn98WiGv0fE2oazReR726ILrW1rmenwXO9puzpf33+x/e
VYxL2vkBvV/7RlTmyZjo6PBFgBs3R9QgT96QPl8eLvfU9pr+cfjfx0T3o/Eq
9dzEx/g2O/tQ/K0R4v96WSKvo2ecQD1b6n5o96jjuEnDRHyu+gF666rs56v8
T2VX/qfKK6p40DlyRIybu7wy/TQe0jfKPh5D4k4WSH0YyV+oWh09gnlbwTPO
kX2Cto4n/57jTFn+T+JVnhxAf7zybPgEv8r+2AVmkK9807yCHAfZx8+gL228
ygH/2a3/lD6knYP1bjvrGmHXUz0X+5L9+w5wk6+nkseJUrV44PpnJMUvXTau
eOA6702Ad5x0DvNH+TPPupCPqVpG8ltlPDsqM3mVcd3hJX+Fz9E/jwvYraMV
BB/enVa7st+u8v/mrI3ofs/oI9Y3c9MC/M9CT1gX740X+4sWZxZ+YJNf4Qc3
u4yedhwHPsjznbL/rFyXwq7y3q3cELDbYYvIl70ujP7qq73sY0takL/+Pfm3
gfGR/Zi+nIf6XTe9ifi+duXgZ7W4Rb1rAXZz2nzyyAU2ivFw8x6E77+Kfvdf
PhLHoZ47+7X9A+uipvoHdX9JnbRaknLSLj7WAfR79YzbJK9Q1v1/gm/5tX9l
D8xMHFe2aoThO48bt6C4PqeS5Jn17EFfiH4hrBevy4f5jzf6DQUnM5w4Wn30
C22o7/69CR37ggXF9zttYqDHVHuQ0qUQH3NoPHCMn9Dp9/rWSZ6anX2N0unH
PzxDfx79bi/qqjc0cLJjB9IXpm1p3qvlOcTv+q+tz4r7ln3zvP6Asq+eOf8V
792cA+D96g4SeoDa6OnkVScvI//8vDF+4JlNqRzffVmtY6A7mraAyF95fZAr
bBU8QPNOCda3xuO4nyg5WD8XZ6wRGM8xl9n/PnUT+57qm2BO/gjv6cwhzj9d
9pF5FDNC/ByTTcwfY2sm8X5a52qDP595X+SJzaXoUrq934jjnUQHDf91GtMv
RRV/r7arrN+uDQgRvEgnI7gCr47WX/rZl3ME7FoN2TeqjIsuo1pncoaI73VX
FkCf4e5P8AUW/U5/gRf3wWOMe4AuSq+E4ELHXCKu0aX+gOWSt/J0/KTebxV0
RI3ZhQN2PZ70q/sWJh7vgn/r7vtAnJ6kG7gGla/L3IF69sTPVf12d2gG5m3H
4uThJK/ZnrJC6a0pfwPdDoWnylpSPC+ryG36d1R4Dj/z5HjqDRfygNu8O0Nc
v/VxHOM1Ep1249Y8dP8rHCV/u/g2+PzsS8V8dDO0DuyrxrJw+uDO/IfxUzrw
Fz6K+ezeWUC+ROmBj9j3UbwXE6fJfiVS7+L1K/KKyeOIdd2rv+fLzTjm7RPD
b9cbtaIv5D+lJV5I4jriUH81kzB/PN3F06xL7vZGEeL/ZT8yM9891pnF2Rj3
G5PBG1f5hO5trF9EHGy0nUR++Bx9kbTR18gLSd6TcXY762Sy7UH7i6sBfTyz
yXXVT4d6+vW+6Iir/juPKuEnX3yX3293o2eiH1CcoB6U2wM9Ge3OwyJ+u5Nq
Ejhk+0oE30P+0xlRgfhO8iudmpIvL/mVZuQa/PPx++D5FvgZXkG58vhNSu9x
V5/gvPP1RxPnq7Y8wNc2Bg4iH97nPnVDxYOr3BG93Fn1c/ntdrT6wm4lGk38
rPgdA34R64799EEE4yj5F0Xoo6HXfIW+XM2m6Kcll30LCiYhD5dkFXp0UauI
erd+YSA6zUV+p/+IvV/yX7ozng1/4fj2+/8VcdalwRJfQV1er1NT6JNrhxOJ
73c+URfQPvbg+qp/FDwe8+hw4qO0JUXcohdbL/LGpkY/EefTbnC5xXugw9Bl
DfnVu3/Q/6XGSOlXg7Ny19QR/WetLRMkfl7iYAd/L/wALcZ0Mc5evn0l+qQK
V+zpmUtcsV75Rnz/OJvJV0UVf5c4Xj0juJevcbx6WEn4AhLHazWaTB6vPX6R
HqKjc3J4En1CTo4jvq61GT1e6Rd5z136Rf/xLv12R4d3aRQawj6idO8lP0vp
PHj6h1LnwdTQU1JxiralEXXhivnQd+r7vTiPk6Iy/orkiznFfuY8ii9W7yh5
vLzDwas0zAavJ/peid+W+Oq8F8EFzqe/hbIbi+YR/2fvQnyj+m4UOkX9RPXV
rVcZf1H21bXvNogU51P74Jpu+CHS7/L6ICi/q/sVcDVK/7nxp2dCd/HHs9jL
nBPvr9U8VOyzWk7iJk8v/fs6gr+k9jWPL3mHvs7aufxifdaLW+gWDogKLrGP
lpPnIT91qI+aZa5WDozDuNdivbPb78jF9UscQpF3zBvZF9Krd8i+kFqSbQG7
cR5/QPVnV3YVj1nVB0aI86r3ojf5U7Mt/ouH904A3tLrSzu1oPBbFA5T8b/M
h6HC7vG/uv7N/vg3fH/7j17gaEpMAVe/64HYN91Uc8CRb74Z2Ped7x10Az/B
F1Djb0f7S/KVyoILkjwssyR5AON6I4kHkzq6PeiLYKfIE8r50f/Rtv3DPpTv
c16/3fiFPrBWP9XPBf1JJ/dV8nou/QA9fzL9z9SzNv0R8NO+3AdxaIGIav7z
60ffCD1AN9Ma1uMfyZ+Yzbaib1O6JeOn0xfAXDtSrBt2quj0nWgKH9CK90HM
S2v6C3AupSYJu1O1BPMpIoGYF0bb0wKPYY5vwT7b5z3x2qxx4DRmNyZOyTEX
nKbSz1H6YD/GK+4ff808SP3izw48X6XD7zQ8KOKAnK2FH672QcuZBJ4jWYy6
/uPdRTvBe9Ruzv1XQ9dXK5WW+l/7VgGdfDtHA/DJB8OCuvoz07AuPY8atG/Z
Cs6iR1KBH/Rwj6HbxPNz+0Yn/zkdfR63bg5wzl12Vfefxxqbl/zT7BHV/dev
J8lHH/Q3owJ2bTX9083GecR6YnWaL8bNOjRYHKc9vgmvM2wD45lnq+w7bgX6
uSg+qRtf8g5KMD6W2wr/bctPgfvVZiyG5yg/nr601EvUu9KPW/GG7IJDqGNO
oJ5iJoQ/ot9oyXoVPoh6i9KxTzmCOnGuTAG7kfgVuMkobeADhlwFF9GpH/Nj
dV9w9LfRvXTmTyW/fHs//I0m97n+d1nQuQrdi67aofiM27W48FwiwXd7/Wji
SPz3lF7UB9u1FjpvhrkY3dHwBvhls7aKuN7JXhr7xFKMW+ht/LTPGdFbSNeO
dSZzDzlvD7Oe310t1nu1DjstzqGrUmgiuCDFd77RReSpvD6hufu1EnbZJ9Ro
2z/ASzWO5RN+hfUvfYH0DMRTX9Y1sd8Z7a/x/srzG0e/B2fQJzX1+fSbwbtW
Pgff7fTkCP9z0aacIW7P7vW7DNRnrd77Wf/ugVPVyr1Dn1B9ZJ1R6SYpXXG1
L3i64odlP4ikD9ivS2dCTyN2IeZvW+pl2o578AElrlj1A1W4YsXv1lKmAZ8m
+d3Wv7wXaj672XLCA5H1bf0d9W6zGfel+sR5fq/sE2fUXiTPw/tiFnpJn+Pm
6DbrHWIR74xIiz5FylfyPOgIGVYF6nYJ+oOXU7q4lQaRb092TPbpIJ5yXiQH
xyJ1bPSH6cFpSx0b+4rEcc38jveo7RTiDoWnUnlRiadytp8jby7jRyflWXQL
DyeEL3ucvLoxZhvXkTE3vL+L78Q+YyRPhx8vdRc9/TGpu6g1q6gH7qtmRvad
vZsCerZayJVs4rrr9iafVLIrPNbuhfFPNC3Mfx5t4hKu//TWwoHzF81PfbBC
82J+u7GqB/kCqa+inask8EhKX0Ub9E0R//F24daR4jzFT4YGzv/hGnoyT/eV
8Nt1G//H7vKoeOD4BIuYVwPnwE/auIJ5+GA31/8pCdd/aC/255uZx/P65gyc
/9IzcT3OzNzEHXK90neCu9bWtyGvq9aT0Df4M1k/4R+lpk+N3jOEPMLl3oF+
7vqCe/Bf/l0r8hhGP/S3nZuxI8T/f9U3ULNGMd+qpkcfQOkV7IoFrn3oCN4D
tV93a0scdaYY8brqdxCnAfOvPfpguo2+t3G3Fs+p3Q1VLwA3PmExfeTf/E48
K/sb6hp1OefMWXBMVxtLe2b8sPwXhN0c2B/7v+ngRTS9SP2h/VPmYdTJ8FXH
LKfeMWoOeKekI0UeRt88AbvqH3fje/oBtKsMzrH8Enj01ZcInqHyiz3dCVmn
cGc+Euuop9ObfJjIqxjGRur1indws7/od2l3eVbHb3ezxwBv/zBBQCfc/Lus
GAfr2Ixifru2lXyFE2N3Yb/duj6SuPLT2oJ+u/GkmNgv7PoXC/ntzqjq8Moi
u4Iv2PED55d5Gytj8PrNrOfwW2JEE/Uu/cYfjOeI1ZI/PLu8fzzNmasT8P9d
xP3q+cHb2GNLM/+OZEInbNdkYTc6rxXxj/VvY96LSs8Yt+F/Ece+Pqn4gPAL
DoD7cWJEFeOtXUsszqNvnIbe79pkAR1jq3Ql/DTJE/yyHoNjVH1pl0jdhloT
iV+O7Bfjb06cGcAfGqV04utRJb/Djj9sHZgOLr8U4+n+GS7s5k45ntObBvTG
zf2yH9nQbTX9dtV/wThvs18p/k6f6ZdEXvf11nr++1I6M06JdwG7tmcdz71s
XPqJyfPoK6T+cPH4gh/k6SD1qwJ+SdbXvvgVPC+pp2FWy1g38L1/6OQ5S64O
jI/eRure70+OPkRxF1zEqXD8Sdk32Mv3lkH3zIgyjjrOlhnU72wTfkLpEdzH
53XCTzMXlqGOGAN9Bo9f/N18/IzO4QF9fq/P4DTZB/4D+HBt/3Hii8tf9auS
+XAnj+Qfq/FZnZf66u0VAbudmN/1Putvl/aNs7PwD3ipecAROTdPEWeFZQHv
lOJDRf9zsf9d/V78/933Zf12Y8k31BlbdAnaRw0Gn3Cxq1zPZT7qoeSZxsnB
+zFtCji0xyPQC4seHfx4d+yus4u+fUqH/J9Hws/Vek3A35M8CE8vXfEgvuLd
q7q2NacwfZGSDEGnNz71bzvKMPIBfx7g+KntqENEl/1dVV/mMdXoC1s9JeN6
Yg/3dSY8Qvx+CJyCr88s+n6tZoNfnjlC5KOMvbXIB0aSl/jyIU8UlT55VmnP
Tj7o80mFOxTrvaZ0F1sOYB3JQb96zcvTyn4Asq+fGgfV10/xeb38kuTzOsNi
Cv/f04c5s5u8nMTNKv6Lp0NbdAd5wVLjqCN8t/KIuK54sSX/D9ygkXL2PeLr
UpH+8//HJxI/0xUnPlB5j5cfRP7ZPdc8oNvvtBgEHrXmTPL9Sif5m3iK7yA+
dlY7gKPWkphi3fP4cWcP05f22lDDfx6zzzv82KH58G8XFiN/mPYTz7tErIBe
veLXOZHxwdv0W8T8L/yLyOOYDaKwz6v85Jg/qbNP4/nb9jn880SpweHvXQOf
aOQM/Jl05DltKxI9uZ+I+6x65OOsgsdT+cfTSD5H4UOCOsbyo8+Hr2HdBedg
fvMLdf48NyXODX/J87sKR+V+Fe73i38vjttXTuCf9LHocbm/L0W3dNd68jnN
wFXqu3fQR2FLavKKCm/wYzPyKjK/p+zKj7GfoFPl2aWOlYdXkdfp6WnI+7Vf
rWQ8XzcVOr2axHd5cdCKUfTzi9Jf4G61cn/w3M8cEHhdd1BuqX+OPq374yrs
IZcCdiNeCLp/eWOE+O1W5dHiePNhvhyB49/sxh5rmhE4Pl86rq91HnC5mWU/
zXw2eZKZf0resZznOwbSH+LiA3iLSm850Xz8m6tdA7x+8/EOWQd6QNyfugPn
b7mDPF0qnqenwxDaWuxr9qM5OfzjZs7bKa7fufwyp99uJUsgxkFLWTHM/1w8
Xn9kOxEPejz0kRvgHQ/6PpXfbv48GXvZ/NSpzs6lLlNTR2dt+FyxLtnrsbvV
1oaI34eUQQdX4ijM7E/Zd5p3K+m/Tr1ldXgy8Qex3qs+cQUviXVB7Rdfzytj
aJHsXCc8HSdue/ikppHSb7dqhoPvTLZd8tmpDzoP68FfGh63hN9ub28O/qR1
TvDb568Q1wxbjj86cS/7RpW64Kyem+BKZB83L/8g+7iZ/aaH+K9Hu7ZE4T54
L5SfMK4+/uq0R5kcn905fRM+ZGPyXuqjLy4l8jVu7IoBu9Xgrjhev/gokLez
zU7gkbbYgj+i4iaj/Z0I8bPLBeL8ojnJAwz5m3pY3avgM15K+8yE1DsudKEu
+iEGebUtB+krsWUKdcPH08GlnzbBZ2SbTP+c789TT3z0gXzf7phKr5jrLN5V
7JtaiOTvt2kCr1+/QdySdpvUd5XP8TQ8eisvcbOn45qlJe/L/q3gKJVewXN0
+bQH4xl/mb8yD94X46JXbYM+Q1Jweu62H/HLRzcB77x0LnWZrgfRv8t5JJLr
kc+xynDyWVnMCn67tQM9U+N4eOB4p1Ny8rNT54HD+aYluKttZYQ/8+WKwFdL
P8R+eyad0CmQOGHvPBInbN2CN2FIfRW7zjXywJur4y80LyfOrw05Cc7wzP6A
Pqe+sgJ6RI2zB+rn1pxQcGkNchKX76Cvhz3lJf75ikqS9yTjhQc38FsqNS4d
sA89gZ+5eLbhtxtPDI7/1K1QYDxlf3mr9PCA3c11BBzXpbSso2tmo9tWsBF9
fzL3EPlXs0BMeANjC6BHsKDvBfL2Mu/0In15xun9O7/dvkYfFIXf9uJ3id9W
/am9vIfsT61Xu4Mu6/bOAs9mVy2M35xnO3H/g2H0XYr1LfNb8krMw/DQFa/E
qfkYXmNek+eyVvb77NFL7ndBnS5j3L/gyGKj82bOaotezaNr8cT5sxcV8amT
jDqT+XMJ+b7I/eI5PALrtsxPSH9PzwA+Xk/ZmvivwiPyBrnDyJv3zxjQozNj
RVLfGtMxoHtp/RZL4tVmBPUwpV6Qvrkk9d9NDuP8F/1M9RzfogNzbg7Hp9wC
3uXNYIWLC/Bwld2V+kh6fOzOy1QBXVAt54dIMS6yL7yn+y37wluXDsLnVvpv
49aJ+pq26FX2wP3OqkD/7OuTsnAeqedQNyP1qunTyfOU3k69q8hlMT/Nv0dL
XTj8fzePhj/89kSQx3RtvHheqk5qTErfWhwn66T2m2dS913quh9CT8kxosp6
ivTTEsbFnzh0KKAjZ59YCe6v696Cgfv9KTa/RxwP8BPtzoXviHhhUyyJQwb3
a5yLS73g76GR/vNoB9/DM/1pncRLSJ2W+ZWFnrzxsjI64vfALWh5m4HPyZwL
HlY79L5sMwt1lrthrBurj5OHmpO2mn+8/Dht8dNOGdSx6G0RZ94uDh9H8RMr
JWF9vlSR+ax4kScPsi/mvUTcHfMC61j7TsyHt8VEHOxM2DVEHBf+O3Wau/tZ
dy/nZ10aQd7cmfgsoFOn/XYY/NnrTgEdMHsmOEDjc6qgblgr/H/X+LZOwH7l
RGJxXX9Prhw4T6vjMn91q1LAPqYiOlK5j6JjVPwGephTkvH8Wq0Db9mdurAd
7TXr8HcNQ/3n0W/MAEeyD16np0dURfL+hkar4L9ft9CkmP/ZrbxrWJ9UPuTa
MfR/2hcu4T+/cXIs/QoP3gzzn8fY/73QHzDP5QsLHN8jW4i4j4dN4e/I/IBR
vih1hFoHiviv05q+gf3sMvuve303cdiHKPQ7TriAvs9Sd9c5ckTEJ7Zad5Re
qKxHmPXAV3v8lISS9zLhfFSOl+9dpw7g5vsWFLwd92o7/NVbvLdu/HCRD7AK
LEDX5WlnqcNj0fdD6Q5Nzc48GXUo0vHdl3N5MfWpomEV/HbteHxxXntKnP+P
Xy9+znIC/BF38kjG5+oCdMcXSZ2ob6ty/aMjAvk0qy39HI33u77z291xFenH
2p0+zp7e0aarok5nvhwVuE6n/1/wmZq8RT9J4Ut/M8CtDThU1m+3mxYA9xZr
PDo38vzutoXktXulicPxso6/Kio8uDk3A7p5ekRPMW+tOzGr+a9fP7Ka/gNf
6RMau3+iHvFsYED3zyqGHoJhyO+X1+OcDaVOtuJuhPjenL1EPdeMX5u6pLMg
MnD80qLoyO3YUd5vN8u1AYec6kyY3+7pTc0I6m7pN7PLfgpf6W4VScy4/mUF
9Iv0L9NPXM/ECZX842nOyy3y88aTTeTJ5MdY0B99lWFlwNt+FfcpfVGv75Xy
W2rOEXhAxW/VU2WFh/PvBPz3hcupRxQrw35cSPa7kOu8FYc8jNOwNf0MX98T
uGKj6Xap41Qd3OoBC73TCX3xYwbfYJ6efATfSvIitRE5Wa9WPsQueZHWgvzY
zQTgef5cJOzap1YBPTf7mwzU+zIG9Rzs3h+wH/gGHGkVdIT0tPPT+MfRTlZI
6gn9EcD7unPfdpG/g+vNfC9EHJfnCfP/m2zkxw+QJ1R4de295EesiBJLjKfU
DbD/GAI/83Bz6vBKt+rzDnh/Lc+C085zFX3RJ/HBYUT2q+Q/3gyfKXCY7pxf
qX9JHpO2tIy4D/3QvnD/OLgT8/DcozjEPep7r8OHMSf/E7BrhdDHsbY/IW+Z
YzPr4b6Bwq+1pqQl/3doIfpOp4tHiPuTeSpv/ss8ldUB/SHvuUj/3k4JftnD
M+9AP8oMoZ+p59c1akh/iz43hb9n1okN3/9Et6DfpvoISD/EODIWHQCl63W0
lrhOfajEz8u8kBEvhLxwWDLiYoXHXn+ZuFfmA5V+mjloFOuz7OdlVe7Afcl+
XmaCntX9z8vZOkfwcZyT0YoHxj/nc+KLHW0Cerb6d9sZt8duUP82akvWozXw
3jw92+zTo4rrqjRH4gEk/jDXBKk/sDowT4zfyoq8pPX2Dv0adOab0baqmD9O
lej07ZLj858Ovzhe9gHx+LCyD4i1GD1AL8+WKqmwm9WiEUcoXbI1M+AprUxR
yG834rJu/9fvQHzfm+us/1t+5v2f9kL2+ZnFOv9tGXDbqaaSH1Z9B/LIeX6y
veG3u12lDtSO78mX2I3BM+d5DJ4ybBl1HpW/ipqePtRJopDXdaaiCy11ioxF
cWv6j9fmxcHfmxOzfsBeMiX4t2wv6Q+g54QfkbIx+1wH+sKYW64Ju76kHTpp
TpwQ8XfFs+vXjDz2m5BUfrvVaYrMb9eh3jf4d66/4AihW+fo+QXu1D1XgHpH
jjvkrdasDvNfp1sK3p+x7BU8/kOP6Psp43qlw6lwJkqH09pN32RnHPVofYkO
fqXD+tr+8xuP69O35elq4gyrGHjRrh0ixE+3GXx6peuVFVyonatVwG5Hd+HT
tX3P/Z7Ji+7TugHgA5fuqe0/Xiu7lrg+Yl/Abmzdgv8QNqV8wL74nFr/4Vl0
v0y+QupOG0ZF3g/lZ84LF3lPq81R4Y85u5gnZmgTdLFiKF162T8iW2V0MA/E
rha430YXqNfLeq53v7Ift1k8NnyCTbnA0Ul/z167sQB28CGKV+v0KxLQHzPa
WegvLdmLTpfEr5q1c0n9DT5u1k0i3/glPiDurX8Jf+OPmuSZm4aKPJaHd92N
zpvCuxotTN5rWa/XRtIn3T5L3c/Tn5T4E6ty1Ar+69SHDML/7/AAXpGy31nG
evLtJOJfGT+adkIxr+ze66ifqDrjgir0Tds9Qvg5ah7qdT+CD+y0Kar43nbN
GP/DQ8AF/VqBdTJ6Bub/wtFSD+JsYDy/+D3UQQ8/C+hxaY0i4YfacdjHyyfk
+u3t+K8VI8CTFIsi5q3dIl2E+P7yPwV0S/RaUUWdzygck3yM0tHqVZ117Bp6
LKpeaYyjfqSPyZnDb9dmxcbvL3VB+IPmNPAbbuEU6BuMLJ8/cF/T0dvx1smS
c3i/5DqplaNfnPXLfXQgD71kn2iSQ/Dg/tf/+ix6EOt7iflgjqB+bVjfMY53
wH9617l1A7x1I1iHVbhEhTP08jYSZ+jV6RRfW+7LHh9ZxVmSj6zNSE8+e3F2
6rwr6a9pPl5a2j/ORs0jjPPpIfAY/ykt5rM9Db/dWPYOPIzCV9+ZSn6s/uEg
73LL/Ehx3PPm8G7bbEAfr8/3Ij5xGmWhrn5gI/Zys4Tfo5UPTyXPI+rX5kP0
btxt0ZSd83+qzz4k9TmVfpTWtTx6spvoT2QuQGfVGb9J5Ku+rLv0uUoXIviz
+sjKPNdNuakrLSsq7tdq9Jnxl/wITzdG8iM8/07aVT8dPWMrsb/oN8Cz2aO6
CH9d3x0u8wlSxyOF5K81m14iYB8p+/3Jj31ttFh/1LqkPs6e5QG7rp9Hz6/D
Uuzby2Dfu5K4VuUrhoSI9cXZUljwirz+gBP7c/4RVcGv3R9Nfmz9fnBy7W+x
bj1vjQ7SoEPgMI2hsn/xeZEndKxW6FIs3kT+70hs1s8bw0PEzyk38J9UPnZy
SYFn+zLPiCtVv/XY7Lt2uiTF/ONhTEAn3/1tXoD3bQwvINY9bRt2p+h56nbx
MrKuLvxd6kHJPu+d1lLX/rJM+e1uTQN7jIcp/Xa7+UHyD4lTpPLbnaTzWJfb
b5R6OPiBTpUD9O0reyugd+rW2A4ucLDUpVfneQge0Z7ZNZAPtK+cFrgg1YfR
yxPKPoz2s1Pi/7x1vtD+qGJcslQo4LcbJVLD1y0XVthvd9tp53YytJUC4yM/
Sm9c6d96+t5SJ9lOip6P0klWfSM9XfEt8HyM6axzKu523+9i3ymSp5zfbv9V
IVKMm9ElImB/l4V47Uo3xjOyn9CZceZfob/kw+f4488ztBDHy/6STsLcoYHv
rZhC1K+tvp3Jv8p9x4rMT107e1G5LytdwVB0Bm49iGQc5H6U+iT177iZWbdU
nv818YudaW4hxkHWI1q2Jl+3p3uhwPGjf8Seu2yI47se+9U7rrPyffH8NYVH
7VaRenaycQX8dnvUXdbfHZ5OCbz+jdmpB/1yK6///NZ3/cEhpB4i+Lt23cmi
TuTeAZ9npV0R0E+zNkejPn5zquG3a73ox+r8mwn/VuH8I3ew7k/8WMxv12od
YH4rfVSlSyP1UV0L/X4jjY3eat6Z4FRv7xffoyUaKuabnb0U/KYtq2S8pvhK
XdFb+0pnzHWrkK/IFS1E/L/KA+cjvrC6n2U+zy4n+gtYu2fix4f/XESeh/Mv
aY7ewu7k2cRzuDcFvPcpcF9G784F/Md78+qI4pXLvjz54JWbL87IvCK8AOuX
huL+7da21PX66vpbfY/e/wDqTcavE7i+LD9Tz5J4AG15OngFi38Vz1e/8Qje
yoei5K3agVtT12mGDkYHb65bxj+e+t8bwOPlisK6NhN+hBn2l8gfOrmu0rda
8ssU38z4uxQ4dxkva3G3wxNceA9c6868+EsRJdBBC3MVfoB4pgo8CKPwDjGe
+vJM8K5OXsNvODqefNMZ2Td2UAfyEfWsgB6ddfYkfa4TUVf04vSO1B1VHcGz
yzqCdbaWyF/pG5NRP+s4QPTJtfMUxV/4nf5lRjr4BebC8vi3ox8NEc9Lf8V+
cbt6Hp6L1AG+foD47odu1NH+OUc++x7rmHn+ptLBE8/djDGG9zpuDHS4la5C
1qRi/mhNBwf0BKy26aWu3+yAPr9ZawP16WnXWUcXHCFPuWQK+DnjcjCPuiI7
ceDx8Ej/c1T4ATfO8ghx/Ivj4NrqrRd+qXu1P3G86hv19yrqdF6/GFmPmFmL
vMHm15X9dv05dVDrj1Xs+/XIW7ppBsUTv0sci37iG/opNJ2IPmmds+BXJx8h
vv3yWovxevBVfVnh4zWpK/lV32r9h6Hk62Q+036fl3l87BA8aJUHTsHv2pnY
+HexYrC//QiuyGwl+cQeHvVf3vMB4yQvWOIGN3VkPku8t9KJUnhv9XH3p6Ov
m9Rpd+pkQIfn+mPmX69VxHsdTos8pdJ1d3/8TL5b6ompeFmd3zR/Bl+p8uGX
coJXvDU8rd9u/1QUvkrITvIS/UqAW0hXg3VY8ub0SovYzyVvzp0veeeqr3Rd
yUt/6dWRqSscoI7sFgyTcbqss3yugZ9XLhx8o5qfj6ZT581XIpAvtebsFvdr
pT8PP1TlM5OVQsc78e/5/ed3qv8Q4K04R9BbVrwVNW+dFtiVPrzXz1HVZQru
YV3eOk/i4aW+R53W6G98V4jxOLabPGjz0SLO1fWxYjysbd+R7ys9m+OXhwTf
34i52cR9Tg0N2nskQ2+q3L1AX2y32w50pfNkYR+PfZX97skq1q/JT8GRTiqD
fkW8XMJu/nMCfLtaZ6JtYz+t3lX4O/oB1ltj42Rx3c6HpeiWKv+5WM9Icf4a
vwg/xHvusfpRz125v4Df7vZOTZ7h7++C+vztTqArfpR1TH3c26xjRpND+M+/
5qPuf6YO+gw11gV0pexdtUT9yFyZknzPbznBO909Ah7rdXOFk03ETwNc/zcP
Avkhu73s6xQWK3A91nfDwJM/pw+RnpP+Pvb1Njzne+jUeevAVuq/evP3BeR5
8NM6kFd1z6eSPKG+4Du2R+DH7qxBXLYxJbr9oWWoV7lDgri7zKnBHV45XsZ/
fntKDMFDd47HLus/3lk4TugPuOH3IgLXM7Qp++Z573j8z32j6Tfxld1dMFas
J/qaJOQF//wLfSRnNvHwqwqK/8V5ZswAr/u6fJjjux53wFCBlzCqJw7zH29n
WkN/iD6zwGXNRKfpS3zN++42Fj+d9JnInz0pgD583lB48+kkH638+KjyusFz
Sr0mLccD6lbRC2Xzf6+1/C/4+S0HBL5X33oL3bjNH4oGrudZbcmTql7Kfx4z
7WP8iBnoG5sf4XvaSeG1GqunUudvLet0ThX0Lmo0Fs9XL/ZY4NjN17XIsyU7
pXhG1Afqw08wj2wX4+TpyqbKSnxx8T1xyV9j4f09yss+tXIP97NkNDpCR98T
J0wLRz/y+M/o/HRPwXv7tCHH3yL+covW5r0YsSNEfP/vPakvG30jxP3stcDR
PMtI35OeY0+KebK5Dn2sludCF/T66MdivyvVPaD3bkQtRF4zZyvDb7eyRhKn
96B/gTMgLfWjAQ3Ac5+8hT9zinXbWXvqouAlfYlnxXUrnECZd//691lP32wh
Oope/0pVD5L9K606qcX9ejrDz9At0coH85PuFFm/kPxXj9fQGjyEmTsbuDi1
/z5g/7JznUe3XuYnzZX4Z3bTWgHco3NhA/nw2ib7otrfJR7Y6p1TjIde+lcx
f5zLrdkP+q6TPGKpFzG6GDjwn44F+J5u7cuiT5Xx8+aA3TxcF31aybtROArF
u3HWVmZ+nxkp5o/mvBF4eyPzaLEOad80gUfT9rrgkenNkxLHJEGHx7mXL/F/
v+vFn2cT93vkBMenvwef/ZvWwt9UdmfUQDEv3bF94Nc0ncQ6nHi4GAc9/Wbi
u5+ngEvP6xK3D16QO3CeWdEEH8z8/W/2JaXfNTUNfZ9HJ4FvMa4TOJ/Yy9Hj
yJWAdTvNZHQvE+RW6zufY+DVrVrDBI5I++l3+JqHinNfv52nntFtGDhHmZcz
MrQhT53xxwBP39R+pH/9pKXkzw/eE8/XfbhI4KSNhC1EXGFF7GTdu/EUPYT5
dYmjnt8jjjtbhe9r8Bs88a7F0Rsc+y98q1IlhF3/ZbjAl+oZaxIXFyxI3T/x
eHRFks9mnfzwSXy/pw/29gbjs/ZUdr/dKD8PfbYlMu87oqmMH6ty3uOfqFdc
Kj2An8nhJUq/S78eAU9f+l3qo3DmHt/Hs2dUelzgve4VpY52B104I9dD6p65
4PHYR1vCO/jYJbr43paZyQfuPS74cU7+NeicnK9B3jcH+iR68RHYpd6pp28j
9U7dik3JQ0dbxfOZERIhnkPFCfQXSPoevY3a23mv8ywkbpZ1bTvitfDrrDnd
Kvjt1rai6F6mTYS/8GIAeZISydC7bn9VvDd2ODoeeoZO8OhidSaPG76I84Si
+2RXWineYzdzW+qeix+hRyPjCFV38PpXSpyDV7eVOAela2f/01DaqWe4b6Jy
nmptxbpt1E8r8mxK90nVy5Tuk76iBHwppd9ydgr62q2XErfL+qDqz2V+e0z6
51IX6OAA9ByeXQvY3fJ1iKNPp6pi+MZT/7AbnP6AWfS3yhYCXnrXI3C1f2J3
R18QdqvCC/I2f60CV3Auk7DbpQqS33gNvsm7/s1VhL66275OUf/3WhdqEU/N
AS9jff5MvbGhJvIR2id0gJzTe8GVNS4t/VGXvMJXuH17yGi5b9xFf+bvPsQp
MdpTl1sZj3n17SD6qlcYI3XLJW7tGXhOp3lS6Z9LfZi0JYROn7MvjcwjyfzA
iIzkexfUETw8T/8qUU/6h0WMyx2wmxOEfqa2ejl6FSoPlmW32G/sPXNS++36
bzOwHxoU7r9Ou/BRkWexOo4p4rdrISuoX8RaFmL4zuPuawjuSMPvMz+0YBzK
P44U58nzEb+w6UGu59hqYdeicrxe5gm6KxEcr6eQfdr7TKW+37gI49s/H7yM
bfhdRr8/yfOn7giueyV1ZL1AO+pxA6fi7xUJhW9YIR7502ulA3rRzq4D8OA+
TSKuVPoPnajT2SuKZRPnk/wCt9oN8FT1WOe8ccjXSqwzZugAGaejn+DGRg/E
rZOnaMC+6Ajx/a5H4N23JmQf6X8GHE+ry4FxdqrUF/dvJMmX2m/XBs0iz77y
towHOb/9QxIxnsb5PvCnR5cWfqb5aBr748USkf7jrQ6XqXM16i/9KFkfmSLz
DhL/6Z1f4j+1h9GEnoPWdTbX2TMjOKsfQsX5vXmYORx8WNS+5f12Le8k6rWX
lI4ZdrPmIPJjEj/p6ShK/KTicXjjI3kc1pti6DC9noxe043cEr9xVF6/jKOn
l38r/LFhR/GTR6K7YqWeQH1u5St4B2/PwtdIEC1C3JeO/qeH3+iSnjrC47vg
LSuwPrhVVrIOTEU/QXvrUveMtZb3TtadlZ+p6s4qr+bh3KTuhNoXvLy33Bf0
V+iB6LtSSb2sLqyfQ2oFdCG062XQdfqy3oqfH/Bn7N3oC1u1roj11h5ZAlzc
gKfwFNr/QJ4+cqCwWw22gq/6tXGAP+L0asr+FwN/z9MRPZaafvEPGgTs7tRu
5JV+JG/g6aX88Sd8uvDjQf7yhm6Cv+CGPGD/3ynzA9YrEd/aQ06in1roF743
zhLe58UlRL7FTHkQezzw+VbfxcQFWdFZ0mNdYdyuNaUOnm0z83yvxnEd1ws8
lJbqCTiljc/wJyTu0dO3kbhHo8CyQoFxqNOd+DGrWyBgH5+U4198rug/j701
9kIRr88qdUPMU8WXbPMcvUqVvx0em/Gc2zBC8DviXeP9kB8jSnp0zk++LuS3
6/G7wHNvnJV+XnIe6leSoRv1vgrjqhVGf/LjcOa59Df0i7mo10h/QxsS7Etu
pOtOfrDjPepm69+CH+iXRupBJAjoh1gxq8m6QOayfrs246M4v7NldTm/3T7e
Ez/pxFr6n1/rx3hGy0zdpUR11jE5nm7fquAwp56hP0mPXeRra8GzNb4tKv1A
8kvakgIi/2C8G1fA/73GnJ8M/zh6+b2CZRs6/4fdOTJH2BUuy9NLkf1evb6Z
SndF9X/vn4D1Z0F+4j53HHmT76cTd/wBTszpZtIfOfNomQ8HT6L4DkbNPKX8
drvVRnTYE9cTz9NcjW6J/Yi+G+7z8fk5XuaNV/Sh/4v5oYb/Oq3IKfCAbter
6b8vN364iDftrdPA7aj3/UEf8bytqJWL+u1Om33UEUKuBPRttHddwcNI3Vqv
jqZ0a3POlfxHmX+Q+oRGrlHUOVdG5Xt7fUSX45d/ZT5Z6q4k11LI50X+csJt
+E1dS5KHWnEXHqXE+dvxa4v6iHtVD+i6ONfysw9drivWOXfbX/D0i3djPX8Q
NaD3Yu8k325uShG0fxsLv0f2e/X0NmW/V+t1b/AtacvCBynRhXxpaAPZX1vq
m90qSB+xr3S2PT3SiB+LY5c6yVPfo9vwyxTi2gaR8DqjbQL//evP0s+RdRa3
H+/t1m4h4joSovuhDZY8xyi5qYNm3s9+/fNT8hfjXsv1Cr/XqBJVjL+zCX6T
p68YpZ58L9D9cq9143ldS4Mf2M7FH5B9bJ2nm3mfZw6B5/UGP986/Dmm+N68
1aW/JOsU/5wDB/+qQ2y/3U27F/+ga+kQrhNdKiN0iPipndxEvNBwIeOz7g3x
b8Txcv7xMR/9Cb7zSLCfmqpTG5lziXjWzbKOfefjVfye1wulHjvn0d4ajOeP
zeT7Ip9jS6lfui67eI4KT2J16wc/4lxskX+yLlFfsLoMEtdjJEWn0d7B+676
YDr9zuC3/sl9mQsaUS+sexj7py1cZ88h5Evl+Cg+iNKNdKPXQY968ELyA2PP
Sx7iKrEvG6vQ7zLiR6O+uKlJQE/AfPmWcfnhCeOueFt7IgT+3KkzQtjto+iN
G7leUGfoHIV8s/ITbp5R9TD4FvOzYX9UBFzI9knCH1A4Q/dDXuZNyzYhfruV
twl5S4tx9vRVblejXlL+XJjfrs3VeC5vCpQK2MdUkfy6ZrwXCaKjD7n4iLgf
PXpP6qDyeP1aYfyWWVepu6p95O8B0cTPrjX4u3zfnRmTwVk+q0397rbsD5V+
KXGyXot4Z+Ng+kONbgZu/2Nd7K0vcXznT8RLF26I82lPLzIPWwx7JPyPk4lF
fw1j0QXwacOG4SfV6Czs9t5U2Of1lf50L+LX++QrHHNjMmFP34q+3LmGoTs6
souYr/as1WJfs3vDZ7SG9xXXaTybBy76heQ5NhpG3riTy3NL3UfMH3vVOZGX
0IeA7zZ3/Up+r9UO8lp5F8h1Uuq3JFkHfuvNKfzn/s2FXuiX9R1+TfYU6Psq
vZGjuXnfDjYP6JPon99S10vdOMJ/vF7gDTjsC6/wZwY8Z56PPwte/2FR/JFv
jnI9Nd6jV1C1q9iH9Y8JxPgYG9DxtKZXF/lsT+/r6in+v3sq8hVJOuLPP6h5
QNQFZL85NU+8fnMdtqMjonQzzmZhX5a6Uh4vXupKqY/H319Ivzz3dBvy+SdX
09cv/g/weYdspv68cRV9AKNkAffWY2Um//W7WbLBt3wXS4ybHnMScdDE7fTP
OH+M+XunEtd/5g542SNHwvz3pd1Bj8yOkk7k0T2dpZxbiJdPdcvgt9tn16m+
9YovKfzALx9Rb3Nvoqthviwj8Kt6yFB0N9JtgS+2pCHXc7Ur31vvRQBnql9Z
jr7S6zkl/HZn5xG+r9U84n6FF120UcTPVml0M+zW6GbYO6/DZ61YHz5WCnQS
7MFL4OfsWRh4vsaUHfhp2wcHeF7G5Fpi39F/3wkOQ+lOvF5IHev/6Ecg7jOF
7K+n9MxPvhXjo2dCR8Q8hK6IMRSdEesv8h/ePJl1FfxR0aLlAvZzOeHffkQn
yknkkFcvvp96veyv4bwir676a5jWGdaD69i1q93QAW41Q+BvjTxh6CQU+zOC
8+xDR3EWeSG3VlXyj1/jHyQuWm8+hjxHo+jk2z+lEPNQfzqT/O2cyqy3o2Ky
n8s6kdLVV3Ui9fH48rLvmPWb1AlR9dBhBdC/3TkO/9mILurRetEO1GNkHdDp
zDrp1QHflycul7jrL88PHrszj33J021YRD4u4hM461QDqC/MJt+idwonz9gq
BXo4UjfPWjkQvvKb5MRZKs/5S2d4UQp/OOE+cd4qdBGtMHAsqk+K+XsX8nt/
FyWfXyYM3riss1jvy5E3lnUWt8MyxknOW3fFDnSPR++px31JvYL+9dEPiFY9
YFf6lnqrEQH9Byt2XVF3sMe8gH+9uLCYJ1bbLsThhaMXDJx/HOe3rp0T4633
Yl1yPiWEvzD3Uqj//E7Cuxz/7QCeT4ty4IuSTBDPz14wVOyznp+5crGIT8xY
VwsH7DumiXXDLTeMPIDkIzvZ0RW3/y5EXXx2IfggHfOjG1MsWmX/8fapsuC+
OmoBu+IHGY+WoPuzpEsP8XvyxvCju/Ur7z/eeB4LPc8s6DA5hsPxCYpR162r
1/cfr2+DD6gVmICeoMTJOxPmRBXHRalW0G/X/wHvpy+28/rt7o1G9FfQDhBn
dIZHZvVsKXApeh10zzwevawXmy0Hofs8gn7NVof+wp80SsSROkKSt74zPd9b
eoTIjxlL0Auyp2SlT1naH9ABWzlS2LVyudC77LaJ+uHky8JuTaffmV78G96L
Ny3F+NjtJb9mdALwvbEHC7ur8bv+8Sx5FVlHc85MA1d2PQl+8bRcYn7aTQfj
/0WwLxgv8Of1h+wL7g36YHr8+p/mRoif+44w/+/cEN9rpTksnru9fD55v3k5
hd1MdhseYJYPzIdv31LfSdlH1FONRzHEem92LAXuvSF4G2NHhMJLiI9Rar74
XnNtTMGH9vad5HvRV7mxIbXfbhaagV5ApMwnqef4OTH+Rsytl/z5Lm1dZuKQ
1EMK+Y+3/+4RwBXpqTYTF79aHKhXevoJSve+yULmTxLiaOc1Oo2Kn67y3oqf
rvwiT9/A84tY17087fnHGUR+8onJ96t+fLeXky/dOjCS62e/tnP9jB9VD76p
nesR+bS50cV81buelXokLegbUnNGUf99Of9+H+iLZJ75jXzL+CLUOzbJeFfq
bHt8Yamzreodnl3WO6xqoRHi+ws8Bwe4OAvxxmX082zrNnzqWMvEcVbi/fC7
m6eHf/39BfqwzenNPImqs55fBh+ptyH/7c2H7I7YB62zg6UujeRfN23DPih1
jDwe+jb69qr8qnf8V/lVzy7zq9qwXaLOpvwQc8TPYh22z09Xelngqe7/Rl0z
WdYyjn+8r32kj1K60fTRknw9dzn9HVSex+NdyjyPvrmk1DMBF2EmToa/NLQG
+1FkQ/G89OFb2a9vw5v25tXsOfCUfztR0T9uer2y9BuWH6vlVHgZV230DAtI
f97jAcl+MNWL4G/K89gbZD/o9wl5n5S+yuWc1QSe5N9t4I4U/z1vuKibu0/X
sa9tQldE5SG1y68DehTGrwZ9F1aUDxHnnf4nuKw8n1ivB70FP5Bd6hUMrBru
t1vZsCv9RruzKfI5Xv/fAxN5jzKdDfHbjWvUy/TDF9CJUnpBBeGfuBVDqGuo
vlTZ7+BXtU4X4F87W7KiA9W9ermAXSvKPjiyakDnRy+xRLz/Rsltch9nvdKW
p6OuKnmRzpqNAf64uXBiXf/53WYR1NFWFYL/ezQGftqk1ujCl7kpnqPzif1L
u7oWfHudjHX892Vl+B1dNfnx8hIacZw1egTx6ffoD2iLiou8itKt0lV/Lqlb
5XzMAA9oDn61Ee7Ae2+6BT6W0mG2e2X1f6/ZZgl9N2T/CDtbeak/QN5PT1GZ
+s2Y3/FTpN6dVW2tyFPZzwYGeLJ65d9YZ0MzBHjZbvyB1N0epA/Y9eLh4JzP
VRN2hQezV2Xh+5LOLxewO+h4mFU2sS+ret8PIeiVZQ3yyvV4h0VfeP3VPMkH
l32ERz3FDy69H/9W8R9zVMD+aBfnmTF1CNeD3o6r7YanU4f8pzkEu9bpF+qH
y7bD99y6A71H7S94W8UihN3oPBoczjTyovqLzwKHrg/5HFNc/60z1wReVeWR
EmbguQ+x2RcU7m5qVNapN4dL+e3/4dP+sxtP+rOe9zwOfu9mRvBaL7qxbqlx
6LIPXKbZQ9Y9Zb3gU2uxf7ltwLN75/8rn+JfiY9fl0PYe//2jfgZV+LVUxzC
v3p/lvpPw9zgGy+skH26l9Vi/Hm+2g8fRT7CvQ6+wIubQn8X+5GzpQt8OMWv
H5CC9bxxQvyaLHoLYX+Wk35tLwvU95/fmrEA/ESXYsyjl+AnzVOdLwRwkpJf
8B8fQfy9yXJwOnLc3Nw/gXfdcihgtyNuo8sUq24u/zhbqRPDY3gwspzfbk5O
D45X4e1X3kcfTOq9u8lysl5p2+Dl9Vub0z/+Hs9arhtGDfLnnr3PHnho/3j6
nOAaVqLPqf2vf67S/SOeCgXf5fVrqwIu1JhZOfAe2T/UJr7OJ+MyhWttnlPM
S6PmZYkTTifykFaGdeAtyvaIFHZPX2u9iHONzruF7prd+geBi9DnrsWPrkq+
ztkSn/W2yip0U7e9EH6xO3m62Gedw+hKWzNTgMtT60OmY6zzjbrTH7Yn+Rzz
5kf2xRpXqROpes3QLuDzLZP5fK9oC/E9iZ8TB3UcDS9V7l96sif4OZdvF/Tb
jTQmeqNSJ8HrdxCnAX0xr/XC/800lfN3XkAets0q4ruOM4XdHpEM3HPBWfh9
WVqJ8TGG3gYX/TQ1+ez1t4Vdq7+F8W84C/9xejv0l250EXkA1RfGXZmCfJLs
C+MkDwnoJJklMsKXSPRvsN9ulwQiv+zMKEi+QY3DieXkr1osR5++TzeBq7Si
wrNT/Q09nK3sb+hWW0scoXDCFdex36elD5inn5AqBv2X3+RM5be7HdCvtpaF
Sz0xqffV4JGYT07jGezX3cGfmHc3wsOUeWxthRwfmcc20nWkLhdC3ze32iTW
kUN70WF4SZ8gvTF5UmNfMRFPGVlHiLzQl/0U//XBNcHr0v+9JOx6CnTXtTVv
IsX4ybqSFbcV79Fg6XfJvhV2Dvwro2k96mKqv3DXPPAc5ed/de145MPj/4yf
LHHybsUi5LE3ruK5fcUndZ4fKu0/v1H3MvWLwUPA7yj/ZGEofXc+long/2V9
cO4jcMhJOhEfjc2N3kiGWeQ3L+WWvCTw2G72o+yPu5dn8dvtK9/z3kp/xr74
O9cj/RkrZk2RF3XiHYF/UqQ79bzj4Hz/h/8hn259M0PquoBv16/8DX76CnoF
Hu49Cnx81Yf3f/Hm5QCuwDLMgC6BkTxPKv84W/1r0q9hB3GGPYp5ZZV4qon7
iHdK6VpR162KP2cXjMr+qXDmR+gvZT23CvjtRg76zak6r7V0D3kFWedV/YM8
nr7sH2RP2wKesE1D/OSifcDffNB4Pgq3vGsxOqs3iGvdvuSTreTrBX5R4a+c
yeXwLyT+ysgwkHqIih/f0KfSSBYDPtMlg3xQ/FbUuW5FwJfJOUTUv8zvW5FH
qy71u6L0pT9ivSb0HZB6+Io/qHTL3T4zA7gU53stv+N7Xp5um6aB+8mJnrzX
x/zTZ/b3109EfxhjSHHZr7ah4P1qwxug75j7O3QeNq4S+DTnRZNAHUZvk0Lx
kcTHOSL78E6ML9Yfa1X9wLpqFwtjnGW/P1XX9vr9yfXEfLWdfUCuJ/bsdQH+
ndWoJfjytCkCdj3FfeqgUo/F62sg9ViMgi/Iby1+AR4jfx3x/XrSr3g33zE/
nUY6uO34QyW+dxr1vAs/Y8/SDt0h7Rx8w3YOfAtV3+81Bn93RArDb7faxgcP
vLtwiP/6zULofWvxm6Ty240pc7En6hrg0zl7fqQO/s2mMn67Vp77N4cfqRCw
J7r3XuhTn/mzkv967PmDwJ/Puxewmyc6C3/JWlJT5NOMDEXou3FkP/M+9RXW
zwb0y3UylBfxuRV+iDyyqvf1OhhV/P47uqpevePqYHTXS4WKddvDX4XtgI+Z
vF+gv5i7vhV4kQFL8C8iL4vxd35ZSh5g282gnkrnHvSreLYzDuMgcZupqcdp
p7/izeUeBd+t2YFg3u58K5EHM0OD/Vzc95Lv+hP1LCPXHvCWH6ZGiO8bGRng
x9kJZ6FT80dIDv/5jY/JxPHu5JIhfrveyMKe27NTF0sziPPfu8H+Miy/qL84
r2fTh0nqa/1/eqpZrxIHyflgfpiBv374FvuO5Pub+z6hLxB9GvVoxY+Ocpa8
xF/jqe8/js57NaQDei2L0Hvxzp+JfcRdmkTMH2cROAYty0F0fEbcZP4NrAeu
L+dK+EuKn7u2NXVk1QcqQRTxnunJKhCnl4q3T+AMmzHfPXxLFN4H68AUqUMi
806jwL1ok+7zPa1mtRHHTTnNdcYHN6rHaA/OrcgFkf/S4rzDL454Qv3l8lH0
n9vfAaehdMnuNBR8D7c0+5SnS/a+LevRknvwmUq3ZZyL7gXfu741+j1SV0er
lJj+0Z9N/KafwQM7sxaK+E77mIp1V/YftDZfwq9u00bm9ziPmToqfT467hTz
zf47HevzygP0IyzLc1f5QC3aeHRZe5Yv7Le7a3uKfUFP0FbwFaxD9EM3y1UV
96k+9tFOQT5UnZbokKi+kI+7Eo+XqBmwWweyUI+5Vx9dhZyFOH5VZvKQdU4J
u5ZkG9+7ZlA2cb+FO4rvt6vJ8az/iuuOiC/1GaR/pY2+LePclPJ6VX2ZfmOF
0iUP3McfaVjHPpZnPEd8K/lNB8hr9ygKfud+E3hJGaMw/+5tEeu2Wwnek/br
Z3QbrN6Rwq7wyX1Xkoe/2668325OC6Nu1eI38rLRxpM/fzuP+TlgTybGjXqN
fel7/Pn+GeGHSJ6Us2kAdZo1b4X/ongobqbHxNvjewjentX8IOtnkxPk97a+
jec/3k6wlv5Pm6PEkuNDnCZ1X+0f0kjeouzrPagv+1LiVsRlP36L/sOwknHF
/32UPKPJedGLKLEcvWLZp9XZeYd+UrJPqz32mlhX1fktnTyCuVMer773IPh8
c3DsyMDxGbeCh65dh/3k7inwmt8NBx+Wayh8reHo9Gr/viUvsaogOhI5R4t6
sdElJvyfJXU5j5xXzoJsAv/sln9CXUjxjNp1ZRzqtS7vvx6tzlzyYLkTfivH
U3zc6P+K+E47PVzm7WU+YV1u/N4kcUQdw02yENzOlp8EjtfIOpvrd9AR1Z5F
Roi/Pz0T4KnpKadJHdJdVbBLnumhj5dFHxDZ19XLa0le63/7nThO4hi9/e5Y
m0L+cdCv5RG4Fj3pjgD/1NGf0v/uieJHyOs5wbpsbm2fmu+VeexPp8BRX0xV
wn8e61kofpxZspTfboeVxy8ePbZO4PgTx/HHJA5Z6cgZBU+D789NX2/nAf2S
3LTomto5lrO/KD+hQz3xnMx6hcW4utnhzWlLJgr/WeEAtTT0dVI4QKvzQ/RT
MsBPdzdt5fchxdFfVXyroo/wzw7TD0TxR4xHxXh/ppAvtd8y/kZZ8qXW5tzo
wmUoDw62wWf2ia/0gpyl6dDnfCXzYFE0dOI/3hfvl8LVeDwXiavx9YOA534Y
HQ8zxgNlFx+zrdRPyB9H5AnctD9QR2iThnn+Vd9MuzDzya5/Z7XI9yodkmsD
wR88niL4ZMru7BwL/vv8btG/2ph0QdQXDGMPeZL4bcR6ZXwTCq6j535h17Pt
D9Q7/sMLiuuosYH39/pE+DWHVuDPF5J8/Sj043PnoxtjRc6vw98HwFOLWj27
4bt/r5+1Bq/cvFsUvFnuNuRVWowXcZS+NBn+SNhKjh8RBb2kqdHIW6j5Nu0Z
ONsbryId33PRNxZAp6P7vHJ+u9b7OHnFAj8X9Nud7RvJr+nbpP8vr7PrcnQz
5n8U67kz76gYNzvdYcbtftPM/vPYs2tyX6HJyacqPdJmNdlf0hjoDSi/fdsE
kU/WD6Qp6bdrhTcKv8j8cQJ9jZuD/zTW3AMnXDYteJNi63hPM21AL2fXAPQh
FD7/ZTL2j8tuuN9uzckUIe5T5jE8u8xjGGXOBfhBRpfH6AhPW53Jb9e71CT+
bjaIvm1qv744+rqImyKWBO17IoT+ntsnJ+tcpxeSt9JaPG/zn/MBPW+lN2KP
dXgvWj/kfrenFO+lWbuCuC5PX6tedfoUaF3QX5J6JlY2+kHaxRMX9F+P+1sK
8uG3Y1bDzrqn+g5Y64dX99tV3wE74egC2OE72FXBdbnvwUGb82bAQz+xm3xl
lnDydaq+NuytwAPbrX8nvlG4vkEHRd3CMN5X9x9vLa4q8LfOjAd1/d9rTltE
H/i+Ser5jzdT3hG4LOfMqYBd+7RM6pAure2/L08vNGUj8MOFnpC3P5BQ3JeV
jz66xp9x8LsuRxLPfKU7qnjHRt12Zf3jrI0iv6bdR5dS6dXoqdfA291QQdYT
JX7+fWyR7zP1XVI3BtypebQz9ZFWVcCfKh7HoGH4Y2Zv8phx78LTHPoD+D/t
LHkj6QdaabLgZ44rSj2o3mZ0aVq9Ik/W+Vgt//caFVahqzmf+absdt1VvC9t
W+UKHj8yQnxPuaqCD6E3rtJCXGevcPonpr9EHC/jIHdjPvi9Sw4F+B3mxRvU
m9ZnFnkFr46/bwd+9q6Ewb7JcVuJ7zOiparmHx/z1cfk4rg29QoHjk/5kfqU
nA+KZ6Seo1ZvYMXA9fyZS9Q/9L8k3/Of4eTlwlugZ75+GPUC1Z9xoUPcuucF
9dB1ss/y4PXg7G7HlPME/L+mLxDroOoTrTd+Sv5c9olWdqPaoYDdeDECHdwh
J+FBFCkHH2die/Sc1PcuvA4uVPEgVH9DmU+zGt0Sdn34POK+HJ+yieu73Ad+
VSHsVo6j+F1SV9ka27WT+LvUVbaan6LfhOLd9KrFe5d2qeQVyn7KZXtQJ/ux
WVG/3WmxE15VBvrE2YskT//1J8lzR7fN/PA5ofg+qdtmz1gq9g0rMgKc22/o
XtqnZ0aIv5d8xjq8aYXI/2hNjpCnSPoHPIvJMchr9E8q/Ez7Sivel1/fyvpR
E+LRMdFEfOcurqLyqPA1DlQjfxXje3j70fCjVT5Bj0690LzIfXn59pnU0919
5dHHUnjvV23wc+rMIi8h54mR9DrrT4nzEf7jrcoL0PPKJHGq0m6GLWIehucm
DlU42H01wM80tcX7YdUYA+5u9QX2ocGtJS5C4t4HJAN/eKg1eFulT/79Rur7
DrqJnv7DXtmfqbrM66jr/5Z9V+mlKxyy0ks3pnSTfaMUTvUG83lg3xL++zKu
7WT+jGgW4KHYt1tHiutPVzncb9e67mVefTwh/BavH+jqyvAfz0UL9dvNNWnh
R/TKKvLTnr5ZsrzC/9DcR4E+kmYT+l1ag7bBC5mJHohVsSx1pU7Ubexl1QRu
0Y5fhvgi7VixDuhbZ/Nc/sxNPHZwA3gT1Wc5FnU9bXKlzNjZN/8fW+cdaMP1
vf3RexddjEv03lsYF5foBJFEGaITvRNGS0SvUaKMiIgaNUqEiZogRO8MEoQk
em8v+7P2fM/4vfefGzvnnjNnz56913rW8zzL7AMPyhA9oNMZXqQf9bH6PsaP
i+kPqPG6vwzWz6wpb+gsCqh9353cN8qKHC9bAl69+L/ZReDbaP83s1Nb+ibo
/hqfvkSXd3gCny91GT/nf+QDx/qXjBy3q1YmfyxhVIy8HjP7CPLoK4vwCTvR
Cr7H5UfwaSbMLRd5neYpfGuNeYPop/G4Da8/24P4/8hvKl7Q82Z8+jb1gKSp
6O8z4gn821Hzicfybw3Nj5EoGh3pG/1Adb3Vz/+Ows/MbJWYt69OqfjT/XYC
/JxVM4ar+Sl6A3+bFo9D+gJ73ARwoePb1b5m/bAcPWbt+Oxj0u9V10E0b9+a
los4Tvvu/lpC5RHO+21EDyv1xGQNs6rvYfi6f53GtdSPNfZt/FwX3Sb/ey8R
vMcZ/aiH97zP81+vPfHS3G70xdb9RseQh7hH80q/YHQE/ruJ4GvdaICOz17M
6xdkoT75v/7m4MtBf3OL7xeLcfcR/XqsaX3xidkB3u2e/SG+ev9P0b8YQyso
nNNYNx+/l8L5pR+W8IWuxyGu+icB9/fd0+iVSm7FpybLPHTKouPw5r+t3tey
4lDX7b6S+7KEfjRusxfUl862VDos45gNTrc+LvHtTcbt91YwP5OGh3j4xpZ4
Kk90ypyvHjmf5qNtigdg3tsSEzluHe6j4lv94yYsrfyKNT/NurBP6Ue9zo3V
uDHzX3gq76cE5xh0QeFm5uUfiPP7Fwzx272/WsKnH3E+xOszLswj35F6ip9r
L3pAqaf87+ckeXfxI+T5RxuHfKHdJDU5L8694Yev68t6P9F5h+wn1sj19UPj
6VwVD5jLG9Dv5eE2dIj7n0fzPUcIz1ziujR5L7Peg/wIvCLvDepWWSeJ75D0
K9kzg3zvVO2wjn5kJ5XHmaX2F48cd9smpJ/4xCNW5Pf1s+Zmf588slLkuL1l
J3ho3/HwK7Qv7q3z4MsNi6IT+XEC/C63JP5ZyZuAG2t+yJypnCOPa7Lvvjue
+7txCXwUwee033jgO7f5vuA54Gz+7CbUwR+OIl7TfZTGX8XX6+0fCkdep7OF
/iv++REFIsf99Lfpvyw6SnPDC/A90VE6nf6J5r5w7lteK5VfOEm+wK9Uz0/r
QfAJlzdPHjnu117EPvT9x9SLz3+tvq+X5zK8lg+mkmdV+Bd8eMtm/I+2ftyI
63pO/iX8VbNWbuFpo6Mx+u74W+XvomcP+juInt2o+yh95PhrHbV6n0mjwN9e
/sd9/Pg2eGNXcLvA37jgU8ZrxK4Z+bnOH++BY0w2QuP+pCPwPytkrROa5/Kp
0KFPGRzyhfNKZGDd7lsGrtNqCuuo6Xz2mQPwlLxEx+CV/HIVnla63uwH0jfW
6gf+ZmVOQpza5Uve/9gDfHLLTwAfE56JPyqXwnWDvsCp8EPWfYHtBFfAhepP
UfGJ8/Qj/PJKRFMf0/qIr/JxbjYrFaXeX+uMClLvtqs2D/kD63r3//yldT9T
/KXN1qdFPyv6oOLZqG8mnAbvWPOuu/wYrX4nKEi+NboCPMNet+AVjawQ5l99
iS7U7JAd3Ku311p9r02P1P5u7RSe3eJo4uos8LjM7bk4z2PRZ8ep90LxKtwM
jdA1/wTe5axeD166KVal0Pdach1excS64b6lt2vBZ9p3iXP1zxfkyy/SwN/9
tLRaB87KslyPt5Q6dUP0aO7LBWrc/LUVOt4BJfGV1TqUiwfU/Gh82/n7Avi/
4NvGi6PS90Ge3zpxYtT3yQZ/P4gHBmh+WyNwaM3ncdqp+XLfuRgVOe4kgw+v
fcACfwnxAbP3fhcTeZ3uFZt1dTZLaNz5fhk+Tp0Gc351SEQeEescegqpU5tx
6Wet69S6n3vwPtLP3Zk7N9SHVPcfNOa8j89kzFfD1XX+VVz6WbrCW5D8t09s
/L4aXhXcQ86XsV3wTTpwLR/zKX09SqUgXuxynXNAx11ZUrK/SL3NsfeB30p/
WKdLWJdhLJ+j7otRtC54kuzzXteP2Td6DwiNGw3vKB8D64PMebyIcfsZ/DyN
cwZ6nNhV6DPy/j51HwK+08f4zluFtuBjfPEJeoEREvcUbxHS1zjuLupDPb8n
j/aHoeea1lfNr9aJ6O+ldSJ2UeHh6j6Mp/Fvdcb8h8/YyyLoKEcd5vkf3Rsf
nZ+/UvV9/0QrdOYpUteNnH8jwTbFC/SfpmoUGv/FA//J/2k4XkpwGp/KdFEh
XYbbhjzXb5mcurHoHbx74Fe6Xhn09ZN6pdfqO3DW5bNV/Gm1H4ku98WcED/c
bfMZvO12n4f0Pk4y9Jje/Q70LVlbRuW5njWbdaj7rzWjH5/mUVg3r4FvbBoI
3jU806+VIl5v7RzbNfL1dvmWBSKvx/rmW/YjcwPra+Ah8uJRw5mXurEkPhd/
g5mfwttMly1a/btYFP5d96SP2s/vqf0/4DV9Oo38N8FLeCiFJys+rXfsO3R/
4icT9HfQ/ZtGVUF3cONf+OpfbKXeVC2sd/BSVocP18DnfBQ+kl8QnbB3MVWI
V2ntngO/ove31Nf0+M+t0V8IjzHQCwiP0dxwiD4Cc5sSF319Hx/vKz78mI3l
1DzYJXuoeXGaL6O+MnMXcchi9IzeoNTkKfV7DFev2+Thi7K4tfKpCvxDkr3g
fnf5Hh/xS5vRZx5N/pg4Gb1C0IdIdILuktns51fRddolK8dS3/fInMK8nvPR
br0WHs+9w+r7uVdKwus+QP3RS9Nir3q/7ntaq+97Bx8x897oJWrd6b5ILRj3
cjnUnXV/ohtXw3rOoG8R9TU/pjh1Jz1epza86yyz1f4f6DtS/p3r9b+N/k/R
yR4YrNaP+3UzcLPUI+jjM5Y+bt7868I/5DnV39cZ1xw9eYfVhULjBeEP+zva
sl9pnnauEWrcbd4nNO40TQju9D1+ucHr/23A61c8Qodbu5rK79w138ao+Ty9
V/EV3VTvKX6XVegTfGgHjFTr1KlcoDnvg17Ybt5M7YfB/pxtPPNZrzB83fut
8fuNu1K9T+B/22+U6hOk/W+dLulDPGqnIH1krD8K4F8k69/PlV3hbP5T8nsr
LvUpcxf1YqNnyhBP2M2QE95CtQSFIu+Xb97lOicPwZ9P9+fKEUvtU27W8qLH
lDjkqAfe90Z/E3NlbjWP3uV15M0V1uP78eg2da/JucP6iH2N/lbrMs5GqfuI
b09j+GR+y3mS10i8+sca+oU0OyM+Y1JHuFOQOCbv/hh+S/xZaxQ+d1vN0pHj
7rg/yMfER8Js9peKSwMfiWNFVZzmnt6GX1XJ+9RFJnekj/xB9DvW8/HkCWOb
heqMftrj+BG1So0uU/u4HiOvNJ9dIg/4JlrFiUac3sT7J2eit2iUTY3bXceB
67abia7ibHd8cc7jO2F/nF38f2SfTzmMffnk5jKR8+wv38x9qd8V3oTgV8bS
36nL9myF/mU/fU/cZZ+qda/7jQZ9QqXfqO5PaqaNJm6R/qR+k3/w56uXnDpD
uvtP1f19q4Ca/6BOuvN38a3aQN1TfI/N+BfBK579oHg9+vrtf1rCe2+fW+W1
drqW4BdRDVXeqPWJ7sRO8MTqxqAjjpcXfF742M6NQ8TTBTdmiBz3e8VT55ER
9zK+sG/PVPuDkbEePphfXlO/Tenj6UzOEK1+t6of6pfn//m24gc6ydeKv6uc
p3kXgwukiVMyND6wBbhQS/T6Qf71ap2r3+22hHjFZhH0Es7TvUUi58f55Hd1
f41bCaqFrsc7Rb+n3PTD0uPuzT0KV3dPtpT+eMLDv3ATnsOofdKfWvrcLd73
n9L/bmilnl+z/Bp4gJOv49u+L026yOv3q/SW/qSfhHhE3txK4NeS7we+KJLv
G2fpX+yU9Yar9/38LvrxaV3om1MZnYxnDademWlCeN5up8Hfct5f4PryY5cw
6PeW5J26ofGvhqnv6RzLxXVr3sv8zSHes6H14Puln9D+Q+jK9brqJ+tM+jZ6
b0/Gf0b6Nlo7O1JPybmQeSjWBt1Emu6q7qHxWPsIvCAvbzn1/61vNpIfVTxI
Puugh3WqeOxLtYsqvrT1shF5ii/9dAZ/R3wr+gWNb9vPOuBftidplPr32JcK
f3LqDad+nJX+CEFfvzkdOdc+ak6cWP8geVzKPurvAh/L2vSB1b7xWqev93Ot
038VJ8Lr/4E42b12lPjeaUi9Mjn+P/Yk/Gmd+N15/f5f4cd2nqB4uU7+kuAw
mlfz+T3qc316FOX10tcgfy+1D7i/xFLrx54v/YXn3+ScLZ4S3PLmLPKxW4/Y
TzudKRY5D+aoj9W8WS9PMg89G8Hzub0I/nf6CfAeG8am3nQ6FfjOqBTwm+ZP
4XzpfOyM4udI/h74RUv+7tqnqGdVn6zqJuaZyeRTc2qp67X3f4/eJNdacI8H
2RjXvI5D4DBGsb7iJ0O93rTe5Xz/vAD7iq67fYRvmL/ojNTZ5Xnsa7GfPJ4M
X33ebvRi4x34vQ0/Z50vzQK/4r1WrHNZ/2azf9V9D/qW7q+t5jPIX2omQ+cQ
8wx878tb4Crjaqjz4k3+m1+G/d13y+Ab3HULfMGfj8EzezpPcFfRd5QdAq+p
rct5kgvdtPlnN/LHwRfF94w6oJmnEHHOl/2JuyRPdGakw6/2nc3Mt15vdxuw
f19uo/CqIA99pxl1yqOriR/ux4NfvuYY+ezf68P76oe7c6nPPU8+GvD8NxMH
B/mgfn/B37wfR7Gu5FwOeEQVztaOnDd31hKu/4c1xBvdm4N7LKoD3+X9fOxj
F8vBA3QnUe+TOpFrCB/vKXUi91w27Vulfvwxn4FfrB4a2lfNtS/wWasZHXq9
/d91NV/O1oZqXw9+ynvwYnt2iIocd492pP77a/dQn2Jv3u5o9f2jU0WFvu9P
w9T4ax8PK2Jc+3gYU8frcfXjFE2rxp1ZpRS/PuArFtxYPfJ1RlDXo4+DNxFe
qPOY/dPe9SK+mofpqYh7doxTOLB7+RB19/qdQ37LbvEonseZe6j7aV3kjmji
mDQ1qOMIn8Tv+6VaV2baE7JvyDr/KRtxbG74k25szhF/HvwNQ3TVZgp0f34C
Q/qu0QdS81rd9KaKe9xHuk74Bl9U6oTGG/283uzHZGT+D3+QB/S5dhOOwC99
LH4yxhXOgSCeEX9z9+ZD+JOyz7szVqv5s+qPk3H2c/f70/iJlc9WMDSe7xHz
/V4ueGp6vEIF/KBndcQvuV1h9A4HRqt1+yovEvxQ+kQ0NaLV3+V4TN43ZTbn
9Xc9wDfnlcW3suY2ldcYVTOxb05fzPklPuq6b4Wup1hRu6h7Sj3FW3aBfkkr
4b2b5XPTXzFubJ7r+zuEdwofybg5hPPkl47Ula51C+n6Aj6qxhcm/wm+p/vO
/L1C5dHW2Dbs/93FL27sZfzo35rK+pJ+NPazpvArumUm/r0q/TcvXeZ8+Ze+
3IEf4A7xJR6RQu0DTpb/1OvdnybAu75wRnxEt6lx691p6AXqjMCfJD24rvNr
EfjeRnv4jZPn4j//IDN57dEn6Ghjo/+yb8Nvdg58ouIFt/lE9ErLR8LnLpcA
3G8H55GTpHrs139vDj7Euhhi4ZfSrh4+55c2gt/ofsSbc6n8zTY7kidov6ax
9Ef0JsLr0XmxuciH9zMnSp2fdsZr9IcatJT+ax/hkxb41F3BJ03X0YJ6VuAD
c4j1lXm5wlG9M7fVvLldx/PcL7hGXLH2HvyHQsU+iHwf98p02Qdsnr9Y8vxK
fz7tm63rs9o32zn1u6onWQU24w9mX1P5vpE/d4z63iM5R5whGcizry2IYR7k
nJqSEj+eiu/hv3EWn17/l7TM59A6IfzWSOVSnxr2OziTrCsnbVf0gHtWoguf
8k9nXofvpdn9A75X1JfKf8DJUhuc+sLlaPV79nu8X6W+Kr5zrpfHD69SR3QB
8fKSpzz+ET649htsWIN8wNkGH1bjCa1Twj8e8zN89bk2/ISF8B2Nh7fwTVm/
FV5V6q9UfmT02K/2K/1j/feQ59/5gnNe86VrVIL/1zQhenOtq53/gvmZ+w51
Zl1H/nEt32/rAe6L1pVYrRWO415rqsaDPolLpM+C+5OaH29cZnwmf5rIubBl
tPgND1D7qXOsCf1O56+Hpyc/XvQ5rU//P3ouK/w7X+TrbNEjWC/k3JHzxYpf
9d3I97eStoY/PXt4SL/w6gfe/JVwH0azaDx8V+b8RFw2cyM4w9Aq+BN1qqXP
L/gJW47y74G7wXVHsD+4VZ/Ad+97E/3XhoFqXdm3WuFXIPwxHS8F/DE9L/tF
f5dnO/XK6yPR653agL67VoModd0fnlP6EX8nOj4/9SLytVUnhFdMPm6WhWfs
nOiJfkj4xsbxl8pX39hfl3NNv37wRfg2I3pSD9K6klNbWT893wnppLwPp4OP
P9oBnqx5Mp3+hfe+4kis0Ou3D0ef89NV9IMPmsHndP9lvsq8LXmP6GsS4L/k
rv2XuFX7NuQZo85R4xNb+Kv0m9B8RX/yzpAe2bxjN4wct+yFoXGzz3V8dj+B
D+Ysf7ad9RL0byJPK/9thtf5oxFTDbxB1z3XPMcfduA98GrNb5xtxajXaT2W
PKea76Hjl0Af8Yz4ximzFdzl4h+q7qN5I+aNS5w7X5RDL3OOeu2r+E/qucKn
6gzubf+SkPdf2wFe3NG9+FjdOcR51WUw+Wznrzivj5mKtxP4jKW/xvk0a7iO
68Ct1+OH713vS1xYIid122WNqd+8W0Ht/+ZHU9X54gydruKu13wh3j/cZ8Hp
txu8sazo0189R2oezyZS7++Mmop+IXMWeFOnOoN7Sp3diD0TXa3cL42HGDH/
pFG4U9XPtG8ZeOikOOq5MnbsVOvdaXBH4S2vfVHU982Tqoy8Xv1Y295R68N0
84ITJPmS5+LT++L3Z8Mf0H2T7wgv7uIb8cZ54mO93hzPUTxtvd7sp+2j1d//
9hSfnAfXpZ7WmzpM6sQ83+MWghes28v+rftCDl2m+pc5b7nEjdeTwpOuvZ/n
XXwrg/psyj7Z0MXEDo27yZPwPH9xq2jkPFsZMsBDmE6/VOMlfO9Xnwyu/r9x
lZc48f0QH9cI/LH1fUopeOIn8PF2fIHOoUYBeFnr1oH/H28DD3YfdYlX/630
NjrPtwr2U/MW6G7Gp0GHOyUXelnp7+z/0RDc7Key5G2CZxq7SvP8fNWwZuS4
91c38os1G3R+Hc33uogOKEvq0DrRfGMz46aSkePmpsHiE27q13PuNCOPsv0G
5HnDN4F37FgKj1G+n/tM/Nb2sJ4cr3VIz+VVAl9wem2nP8nmnbzP3WPk72P/
Yt1rf6cnrcgzy5ulI8fdlIfQzUn8EFz/vBfEN5tuhMadrPgAOKUGVYkcf7Xu
1f5u16sc9g/ZkENwzvKh19t2HM7pBemrRr7eGjJU/L3Im62bzIN1b3ACyac5
fyUe0PNpLgn7SJjTe8NjKRfuX2yUWA2O8/W6UpHjbtuZ+Ll0Lls19H3veAqH
8sYfiI4c9xdO4hwd9WXIT8WfVwQdUJO9VuS4U4b83TRWgntJ/yDvwpfUw5bv
Qzddf7qKr7x7Jufgw8rw0GIFPvPgzHNn4Fu1sjSvL3FW+JlbQ/PpflESvUPG
cH9qI0km1uUvCWtHjtsJp6j9wxiCnibwFRm9UO1D1od9FQ7jnvtC5enGw13M
y5NAN4qOQvA3r++PwtOWOOHZVHD3kSuqRI7buU7w/Mq+auj7IjiC+8FePa5+
/FJR6NkzLkNf/2dHNQ/+gxF6/Wn//JyR8+jG9sHZXv5v/ajvuXGF2ue8v/DP
Me/8ouoFlv0OvgQaH17zLryCT6uVjBz3v+2n8CArQfdQPOb8uYa6ae0unIc7
J6JPbzGc8+PeypD+2r5aiz64jVinxtlj+GSOHafmwR/xNrqBQ7nxDRi7VeVZ
Zlr2w4AvdLUEOG3hM1bkuFvgJ/DNSfUlDpE4rfnXPFfOQ86ro2cYr/11XDXe
+lGo/6mfeXAc9f0lnw109DqfbbAE/65na8B9ypaG3xArC+ev5slcqBZX/d3i
puRHu26BS5R5l3pA+mviDyB9JJMkJX7bmp59b855dK8foz+1jFhS/5K+hD71
F+OzldGR49Z1+pTZuV3OAclfDP8/+m6Wh4/s3eK88+NMQtfxny84m+gKY8M/
9w7FKRc57uW9I3qS3PhPVBmPLrLI7Bh1Pf/7EXzMrKF/q/+v8+6Yf+5uff25
uRqG8FLr4uZc6v1fng/hmc6pufj3Jn6ePnLcreuThzTag998EnAMe/8S6pQz
uoET6L4e7ir4Bj17UzdPEJ/nv8UThXM5f6aGLzQ1ifJLtFoO43xMm1DVowJ+
bNqs3O9i+/DNPn9bxV1WzwGcI+JT5DSg/qV9ijTeqH1HvRSCNzauFeJ3Oe/+
q/I7c8basP9t7emZrYj5CvwcBO+yl8zCL/HzX3gujtKPz300TO//QT8Ldb0X
ThAn9syhvq/9PAW45C8x4AraZ3JLJvLgHj8p/MG/emu4+vtv+vM68efRdS7t
z2N23CL8RuoIuj+jdyIz+bXm83zfB9ysRsGMkePOjLcVT8PslTLkN6j5G36J
qehtC4Kb2YuHyfMzPITfGpIv298Uqhr5/mbcNdRZZyTAz2pcT3wvZ+zDLzHR
lWj1eeXo92euukc/nWaLqctov+XiZ+mXkOZL3UdF/dh13td4ve6roq8Hvku1
euwzWVvg69sNv1r/cSkVVwf49tSnD1T8P7Ak/JP0TdTr3SzXic9f5fVWxPvr
vN6tWg+/THl/s+u+GPX6uu9pHIDrHJZT9Qtxkj7NHjluxo3GR0/wlkAHJHiL
W61huA4y4Rviu7ZBnhKaf7dJTdFZyk/6hArXsh+vKxr5ess8z3mapCJ6hD96
ElebRfV5yTxXf4JP//2T6L7On7Yi5829uor617Vmat2a58Bv7UINFT5u/nOH
+db+DykuoQOJi2+TziO8hrupR5TtTp54gPpywH+oNwy+RMXl6HPXd4cflWoo
/rjbF7L/j4mBhz9I/AflPPVvl2EfmfKWwufMfdk5f0veBb8tcgp9cKXV8A2i
l1Cvuhv2nXO75mNdtpnGfft2Drob6QdnVhgu9UHxl15SHDyhab3Q82guoX+W
MRJ/OOu7POgXNo3dqe7PKPqLu9dKkRePzUqcs6ow+8rwkmrc3jVc8MmEiblO
8dsssVb2l05xQuPvp+KcynhI+MDwmrwdN9lHuk1Gp/Z0O7rOvjbxyrYt4sMj
/eZ6L0bX16M2fNR6Mczblt70t014lnjzqqnwf9vMy3PYP7H41aDrMVo/VHo3
O/5W+MO6H9mmCoqHbM0S/zbto1vqCnlkylMhXMXtAh7irqbvsdca/aBb7hh+
yqcKqdcHekB/NfiG+EgEdVjtIyH+AMF1is+AWa50CPc2Z64Fd8h+Q3B16ScS
KxnP5030RAHOv+QkeZj09bDWbVR5q+7rEfzI9QR5+ED8sbXvk7EjAXX8JQ3h
K+3ED9//5EPwuwxF8LG/Th3EWDUD/Culw/k5Mzn72ZFWUer1NVqH/Nrt1FXI
02vT5zbADY7cB98bsAHeteZnnknM/t6CuNiQ+NmJT97lXWwQ8/q3HfWfwql0
fcoZMys0P/4TibcyLUO3KPG5+So+V5+XJQn8Mr1v7/kQnDwqCfFYQfpm+k8q
qvq+f2tQyOfQu3wP/O3BieqR486cb9ArvpEHGYP2cn//P+fd63+7/cJ8PKfR
MfqBbaRvTuCD3Yu+OfbsBHkix62NKcBlrsLjtmLNUHUo83B14s8Oh9V8uMtq
gfO8Df7mrlhFvWwS99efM4z6zrRLqh5uPz6JT9Lj99l/xZfPqksfIu3L5xoN
TfXvOfeIUxtnfDvy+9i5srDfdPwBnP+N/NTcQD3G25Gavp0W+mL7H/EH/Pc/
cP0GLjhHyi/BXc3j6nPcb3KCN37QiHPkzlp1TnqnK5O/ZHxE3eL+l4JjiO/N
4H3gOr8/0X3QFI7n3SOf9Ir9qXWy6sc7ZMLffnhb928J1Z2t+DdCfV2sojfo
8/H7e/goaby0UCH0p3nwZTGC9YAu0X9+iH1a9ge7zRTqkne/SBj5/u6OW9Gv
/+1ks0Ofa3zaROVB3oL1RUPXH30Onv+ONNofnc+dM4L8x14hepyx6LWNYaqP
id+7Lz6sGo868Af3Xb53MA+P/qfbDY+TR5tFxR9M8hrzDq/3NuPDbPX7nXzt
WBMVV7nr+tGPsTC8FLNpK3DMKQFfQPMciM8fDntjnPjZ/HeR7NvwTp1TfdBr
Txb8UPId78UF8vN/t5A/an5g/sYqLozgFcj7U6c0fwzzQ5ytleArHuyaIHLc
7pwYPUbWWeK7Jf4YpRPDg1xUQOl9TC819ZFJf+HTJ/VPQ+oCen7NG60FH/hV
/Bt7hu63/e+ywIc58joCvkH3z9R+pXH4IH/XOHymlSqeD+KfTuKDPBudrK7v
2Ok/UHiFfeIRfEDxkzTn74K/PvEqOGlK+LdW8X345FSpRZ0ysYz3WIF+NdVT
6nFzdggfMSP5co6E9A0QP0/jo9XoW2dKP3nhaVj1pd/8vT7S/0j0qh8Xhvfb
6SbngNcVvdVHKahvrj9aLvK+uFOT4/tzG56nue9zpXMxj7VH/3g2Hjz3r9Oo
c9NNWB0c7PGHKk60i09DxzEBnbp/JRX8rwNLuO87qANat5qJ/lT0SslW4W9y
dSH8rsbFqe/8Ba/eTXgXfGVwdnhr2xy1n3ulr7F/Fi9M/FOlO3qEPWXFx4D1
751OTh/Pz/HlCvxDtqbHf6n4Dp7LvgZ90yo75MFvP0d/mW4JeFHD3NTVjv9Z
IXKerceXiGM/Gke9us4V4vCGg5T+2llHPxOjWGniz1z3ld7EbjYaHWGiKQqn
ss/+B14keVygd5M8Tuu57No/c/1azzXhAzXf3sj3mOdLO8DhLrRAH6bj1fZf
Kd62XQh+ehCPpZyodMhBvwndn27WRa77gwPExdq39sXee2o/+GCxeo6MF+CT
5vvPydulT6u963OFe+g+rc6N1eTjlyrB68gYJxQHGDXnkEcWL55LXc+xdiF8
0ozfCv35Z33xL0o6QOFa3sze1GMedQ31i3mVmJLn7JuUM/JzvHvoIsx01+Gb
bwTXdd2k5I0Te9Hvu9c6eKdLcuEvMXARvm0ttqCzTXAOnqOu52q9ldRzA99C
Gde+hZ4VG/xP1wvWTWJf/qUCdYYO9Kcz92wP9bWynoyXeDMl/OMrk1X+YsYF
z/F7Mf9ab2LEFz+08nIODUX3pPnJfv2iiq9rjWXcTrwZXtTRDQ9VXi/4SRDn
a3/j+fAT9H7laH6C9KPRfAbdj8b5fCs+3tIf07MGgjtlKRni8VkHS+Gbce2j
EK/ANrbFqO81sXBM5Lh1/Bzfc+F2eMU6Ls11WJ1H1jvSv0LHsT0TohPZ1ZP7
POxvhUsbR+qIf0gj7rv2Qf1glPAjwAvNi5zj1r3BDytGjBv/O3/Vj1v4En41
zfPSR/vheea//kqV3+tzxG9wDB/6lL9ViJwH7/uRxCXd/g7hNl6sPdQ/cobr
R+5l+Cev6w6R40aiTPgyzwjzAK0BTdHZSf9xU/o+6/7jXqvocPyfoBr9UOIO
aMx8ir/E+wv43H0tKkW+3j5HPuDdKsP5OIHz3noUG3+VxaMVru7Oykjdf29l
9InSb9qKWon+RPebLpovT+T7W6XxVwlwM+1rpHGzSo3V/Og+rf7ALsRD88L9
3dwMafF72j00IePEFf6B6ipedUb1Sxj5er8XdQi34zz4REPhLXs7f1DxkDOn
JPU9raNMzrnsVhwq/ATB/9N/Th4oupuA1yS6G2denYSRr7fGg0tYXx5S68eK
U4i+k4nRe+rXBziYvN7dlVLl3Zrv4dRDr+2decJ5LniL9xX9JKyT4b4SZta8
nB+JZoV8C90Wv5BnRc+Avyc/7poS4PMH7oX8NNxHH1InvwleEYxX7P2P2n92
/glOfk/6zx79hjytY1f2f+kLbPVMRJ+XTuxXRszH+IZ8k/Ex+8Fb4OSnUpAf
TWqGrlDwZLtVez5f8GSjQHnRy4svTYn07NP29IrMg/iHJCsQra635Bt9NKIS
8lwf2x0at1fgb+bmJ06wdnfCR2JYffRtQ6ZUjvxcu015dT6Zl1bBzxR9tP2s
EHWWnz8i/3gifcbz/a3ySiMJPBlv6UTik7K9lb7LeGGgC0ndjX5YR75S+5mz
KCf9UvT5uDiaPhcVF9KXYwT8WK/NdTXuxx7A81ZxCuOzbil8wVxRSs2H+TID
eeXHTi417+LzadRarPiQ2ufTbXFKPWdms4nwJE9PJs/olk39nZv6E/V8eTVX
cR7lGBPWI4xJiC5udV3BUQVP6/wR9aenXfGvq/gJfrSj95HPTlmnvrd/LRr/
sRHw1axjC+DDaJ3dgvb4Ny3oTlxUbzS6uvc/gY+7rgy40IaP4UNWbBpb/f3G
ZOD/39Jnyvczwx94PDEUb/iFz6j76l1bKL4osq7ivav0L2arpyGc2emcBJ+R
dpdKRI57kxYRt/f/sFLk+5uVvgOH6br0QaWI15txS4GPXJ/FOqzQVz0XzuGx
6JHm4MPtDqjPeP3W5IM5YqnnzLt+SuFOVvqvlQ7Usy6Jn+qX5EcD46pz00+1
Qc1/oL84Mp38N0WFaF4HfmvMpq+92+kC+/zfnDvm/DHM89Be8Fg3p2N/rlod
PKHNXM4J2Yet663gp41h/TifjUQXWvJA6ch5CfK4hX+wzz4tx36sx6/upW9d
ngvZI9/fuz4BPlGdMB5uNy0bpT5n1jnqxvp8PH4Y/UjmwfglZP2Mes2GY+w/
g0aA92rdVlQa6kelqM9amajvOO9GqXEnWw7O05Sf8VynaMe+lOVr+Gl6H05D
vcH/4JMCkdfp3BCd1eGdjLv0a3CPvocfhPA43H81vwi88U19geYVBPUxqeu5
vYhr7dFnQj63/sRfFS7mr5gbrf6/xIHWcHTBxhGjMPPGc2et3Kte7+ZYwv25
QR3EONRA/b3bYlMM7y9+jMlTsO92IJ71L9XjeYrOBv7eOz98Us0DX5IO/XiD
eknU9WtfgvrPwOdnzIGf3udrcKqri6lzJMOX2Lv4G7zxq/WUT4VvJAc31n6S
ZRzyZWtqichx1+gAj3PGBXDYP0arfOfVfSUe/u1P0XWG+4kYk/aG6ptewcSG
+tzcovMQPYgT5w76uoKM67qt8xKczh+4nzrJgTPq+bW/zgy/Kv1uqSuJj9Y/
h9U69mf3hbfybJrSufu9Fqk4+TVerb7fm3j1jTvqvpgr7lBvkfqUHg/047pu
lX5ducj3MWdsgI+ycxU6WY2fdBjFc50yY6jOaMe+r/BE59JLiVvEZ9tvCx/w
Vd6tXn9X/AYH9IfPWWQ1Pkjav3pcT3wo4m8UnxCpI2dcSF3msaf7QKEbnRs/
Ee/bnH1CfsyuGcDB3uShlaxOHaXQPMEfRH9RZy18IOmfGPDnpX+i+0Em/A20
3921BvDcGs6nH8tC4h/TO8P5Iv2XNa9V91+2CrUM7W9O0dLq+zhvt1TPa8BD
LsO4/dbL0L5hPbrEubu1m+y3xMPOyLX46RQgXg76I3etQP1rbiX6Pc1Phk6n
6jN0ToPWoeeTc8F7tgf+c77RIZ2U9zE+6c7DTgkjx/3MO6lvVbjyVuS4kd6B
n6H9T9aAn2j/E9u/CH78A3VGd9LjuyqPPHcaP5MRf4LPLNjE+Eb8DAPf0aSt
iNf/yQn+nLdZU3U9c25z/96JFapnGfF/JN4T3yQdB2rfJPuXDjx3mvebZD18
uLMz6G+ZoxbxXomN1M1z7FXniLG+Bj45E8Hx3baCU2odx5Pr+MTeug9/af1p
6kTxGqrn2kz3HXGLxFH2yTjwssbeBWdak53+m+27sz9sQtcY+LzdRPfojMoU
8rdxG7POdJ36zefd6Tw0FOcbg+fRB2TY8LD/UpGy+Ch2X4R/yLXmPKdDeoOP
Z+/E81t8MD52BQ4Rr89k33YrrFM8Ze8K+7Zr5wRnSoIPgLfm8GmFY2TdoeI/
48BkdCUnYhH33hik7pf/uCq6y6yJ4IltSq6uJ/AJ+XxmjLqePvS9DXi8BYpI
H4cArxYcQPDqFO+gB//2OOdKlcHw18UP0Eo8A98nrxVxoDEktE78cTVYHzF3
q4XGs/Yjb91eP+T35a2eh35k1XK1bwX+XTm3cz/qRqnr8H5CB2E3Sxjqs2Uc
2BDqT+R3Q4ce6C77NBf9jx/C7czC9Oe1hp2h78Ze3t+z0E34lb4lX9c+WnGj
lE+E9efb1Mcv0n/TT9+MOCqKPqduv+nwAVqWxs8wTXfijYUDujCfW+DX9h4m
8Zjw1louwgfjRDHypIkT8b1/eE78eMvgZ7KwCP5siZqy3809IT750m9obLHn
ir/9ho5e+z6ZRRMyDz0WK/zB2jJBXYeb6GAO3p84xF9US8V1rn0vb+S40yWF
GvfSx8Db0j7Pm+IzzzE5yEu0Tj9+UnCA6F7gdHuoE9kLvuL8G9RT+jWL39qp
reCE05OH9iv/bI1o9e839G7msG/J9zrc4Fzvij+eff8Red/YvGq96Pc3Zidk
vyr9t/QvEJ/5t97CF/GkE/LT9hp8I/xX6rDaP9mZwuf6UyuxX54thX/XA/q2
O8/bsh8u70mdutMgcI/lA/HFlPPF/LLFJeU/kBXfBj8O/FhrFn2N7Xi9yNO1
bqvTLs7rTFHSt0jww7xvq+/p3M8Gb1dwVL+pxM0Vr6J3F18UY9JAfGq2D8Ff
/yi4qLcgHuf14ULkQ7pek28//I19S8D/0tAP1HjxJ3GS+O3oeDvw29H1u2Cf
gV+r/Vz/Nw5/0m7UEN+4Jlnhk8z+Ad2L9IWxJyZX47ovjDMmOfnihg34Hhj8
20makLw5Lf4POh98nVe9/reOY42MK6YrXHTUMHQo59Hx2Wl+RTdbfADzHI/n
2st/gHrJ1U7kr03AS+1uk/BZvlAXX5q534Kj9h1H/fjFNuLQyvig+s0qwYt4
w5/QnvxOtPp32r943gfvR5exNQY/j/Q10FEKvmFYNVW8Yq14zDkiOlntC+Ev
34i/kPCIjOgvqNO+hHdkHcM/2Zksz9GhHuw/wscz4z6grrprWggntGvhI2+O
ou7m2uXZr967Cf/7/F7460st6be1G91p7RbU06qhVzLe7cW5mXkDvIY06B+9
RvS18lvOpn53PSd+d0v6qufRbdKPdR93LDq7niXxR5afwDdM+omb7ek7HPQT
rLiB/f1hs9D38guvUs+PPeyour/O9C/wc1glcUm2XvBIK4GjGv1vsJ/HYl1b
onPR617H8/pc1vG89agmunbRc9nvr9yv8MDhY4jz0w5SdUzj0zbU48754qMu
51o++sX6g38Q/BN8xjudOEZd56ILnGM6ns+QhnO63rshvoSx5Rj8n4a3iSt0
n4vK8FWs0h3hBVU9ie4swSzyxIXUtdwLMfha9y6OHuT8fomjZL8d2gl/lYvv
EveJvtjKnFutf+viUvpp7IAHa/+zmfxW+r0G7yP9Xt1fx+Ifsp/1b/38gOex
Neenm/0YvOXmO+k78NsZdGfuJJ67/UmoT19rBm/GxEfFO70a3k7ZnXxfnX9t
j89z22U0+9DtbNyvOgvBterMlnql+KWMN1TcaF0vgd4ufxTx7Y2u6jl1v50A
j0P08mbl34J+4ryP6P6Si0+m5AX+mGro0CUvcPvfYJ0umcS53/80db6vM6u8
Q/847/7F96pTlvqQzmsWNGb9d6hBHlRzAjz5+fRJNe/0UHmWM2I5r5/7EH1B
zGV44InXcH51acp5umw2cfj7Bbj+4pWVztNPskz4PILDJPpc4Td2s2Tkr2Oy
sc8v7YJfp+5fpnFp6V9mvHeIfbtFA7U/WImrk+98Pz703Fs/5qQe3GUEvAbJ
i60nBekDmn4IccKs5MT5v82n3+6IlDwHVXiu/SfU/Z1xHfE/0PWany5Tfz9e
LQP3S+LD+dTjnT51Q+Nu4gnM22b6egTjKyaho+hVT+I64R3NhC9q/jAEHkKT
S+zbsg/45x7hD6f94euM2K1wzt9WwKNIdJ/6/rcX4MEsxI8lwKNS/afOEevH
y/ADV2ZR+ZTx/lCFY/izo+EpnAVHNcvtJp+vM1h0pdwXv2ARhS848evDF9Z+
dM1rcV8WTJC+5ORZ5p3suV6Pu3P6U8fVuGKJl/jPyz7vfYpPl97n/WjhCZ9H
7+99BU/Yrbccf3r909chnzyxlnqs9gOPqqnyFG9zd+1jA44886aKP9xr4X5e
RocxxA/ilxPoIi8MxVfuvEudJ804+p199AB+c2viQ6dHKvprLELH5CRrWS3y
/b2TqeGnv3ud+dPnwqNB1L9kHwj40rIPaP2s5RPPaP2s/jGzHeOcFT9/pz51
cePDT9XnWYW+gD9wcCP4mMYDOzykHna/EzwH3c/liyM8V7pP7o1p+E5In1y7
d6AzJo8ud1H8CMK6V+sZeeZr/p6nvif+Nq95Zer/C//ZWcx+rvnP5v13eE5L
sj/b9X+Af3XhDPtVDHxpr/ozzrVHe4krtS/BtV/V8+zkwmc1+JnwAXW+JnXQ
500SX6nRUdz3zqPxgZ5O3u31GXdIxadX/8mlrr/TUXxxc9VE/7J2RYh/ZTU2
NJ4Pz7JCL+o4ca6quMr+uCi+gBX+RX9UdAM47Las6jkyR9AX2HHHh/mXEX0J
I7/P/3xa/pB91i0ReT3e0oPo1DpVC12ne3MxfbbaPaWOIHmoneFrfAZ7HQzV
8a3f94V4HYG+3khJPnxwaMLI99f1aOPYRvX5fov01KMnZSYeSLq2bOT3c+6l
AX9c/i54lMbrvklNH447LWRc/HyqlmZ93dxYMvK6zDrgmaabqlbkuPdFZjUv
5ndx0VEWmkbcaLehn/iIrSFdp91/L9c/k/p4EDfWER2O1B+MN3S7weftd8CH
JydLJd8z3Df8UWV8qN5Yn66NXtheU0XlDXbZs+ieWwvP+lYN8PQzDn4ga8qS
tzcZF7p+M2EicPkS/4R4hfaUPuyrNwzphyv7dsbJxKs1bHxoNB54iT5f1sjK
IV9WN8+t8noerIjv5Yte0u03R/gS5Fle/vNqffhVx0ZFXo9/qR343ht1HN2f
9P+nt1L/XpA+9H39wUPhIS9yqadIvcB7cZ14W9fry+Qi7pJ6vTX8Euf7+Uns
59KHwuwUL8RX0fzwiPsc5rXa6/DnqZOd+HDXPOpxqdGjOZ9wLnjxLoETFR8u
/njgOa+eI3Sxb/UK4R723lGcL2/wlvU5ZezbzvxvbkY+V3qY1hsniLxO7Xvi
phFfL+kb637A/bKs4uATtYfjk5VorFonZuYGar93vmJ/dsdVQo/Qm3zEHC/+
ilKvMU6+pd7X252cfCKqFvNy+if4+NIn1D5eCz52jjGMLzxOvHHpFjz83Nvx
+clNX2mdV/q3GoXwGefKRaUPtXbPwZ9/KT6Qxqu8V71vmaBvEc+d8MKdDqfg
J1yTeu68F/AQhKca9EETnqqfLH71yHG7bz10NekE59R6vS7gnG73z8izxOfB
G4ufm1m5KHpPXWcsPkjrxrUeObQ/mFWbo9vSfRmmzSO/+jxH6HywvsFPwLGK
Sh8NXm8VGxStPv+9H9Q+F+iIT59RPGbnt6rkkbqP6rmPwYWzrWSf1Dz8hEvg
bV88LHw59n/vYiLOte/Xh84lrUfzHhrCk08C3vj7IPhOPyRT57jboz95xymb
/fzrt9iXJkt+VLsrvNLGQ8kzJC5ypl9G/7D7q5CfrV8D/Mc9XiZ0nRovfbVP
Vov8vubeBfq5Yt+68Dd1rsqT8BvZXhIeoM5HStDfxFo4X/ljBfWvaT+CM2Sj
P1Lw+trojsz3p/PclSyG/nFIUvQyGSfDO/1KxuM2oZ/uN1lYpxLHWuMTUNc+
eCxG/X+t0xkbizwl3Wr4TdqP+sEB2R8Sq/pUoBsVXw9jVOH4kddvbqoqfH50
oIGPVrE28GkXFlbvo+NVa90OzpdysQWfZJ04gxLhezh1D36eSfug+3ap47+p
ywjq9ety872lb5TTcxA6kZ9ekPdJnevVBsm+fSgeecrdR+jdXryNTu9CRfL3
iH5V6ncl4t7g+w6gLuwde8B6LJWMetOkPLzP7jT4EvcSPmSOfFy/nZ26mfAh
vaQ8z0H/RLkvun+iP7Yo607vGy3bc//GzOX76rxS+uJZv5auHnn9/vRial8y
M/QhPpI+odaVGsQVsWcSn/R6in78SVPi8wIV6YcjvCOzNuvTKNEjhDM4iUTv
96Knqtt4jcjf7anP8bUpejCkx7H7nrumnutnKUL33ViTso7Cr2z66xknysOv
PoeO3vq2kui5BB/OznwZu1KEeIbWj3fBVY//G+JvOEl6w2OQPEyPe5vxOXK+
7UA/cNHlmSNTUGfv86AK90V0qQnzU4eVvmaBrlD6mtlRSfHl1byIK42pvxf+
p2zkuL3rCvr9z+dFWRHXY62tQR1kK+sw4FG/xfv7u87Rn0j7A/w9mHpxvUJq
PzBX9sMPXHzRdR3nf/3u8UN2auajzvJfNL7pmehj6FVlvwrwzKktqcOaWfHJ
1/yxHF2oayzsG63eV/McWuGT86bfqfH3YuLpzV9J/zLxyTmwhH6QnZeF6qfm
5Qqqv7vdeQ1xWvMzrMPxRcCVq9LvW69zL28U63vgSPjPfcuSZ92xqLv/lEV8
xgQPLJgAXKB6xZAvtJ0iLc/5ePgLQX2q/hzW8YU45DtJ6T9rxB5E3vfnGvG7
AMfzNj9S12Ge2h2qv9iz6TPiF28vukJ5Lv4jH3eXdQzxPbwvpyqdrD1vCnWT
FVI3KRtXza9eJ3od6nVit5xRPnLc/eIYfJes4GMBv/3pE/p4FYPnHuAeteHB
u1XGws+skY767xP0qm6GuJxHOYhXvfZ5qQNmL4ReVfNJng8njhvzKTiA5jfG
T6B0U9bw2NJHWJ7H9EPUPLq1s4bmzftFzq9H4pcv72/+nketVzMdvFH75i/U
VZuVwtc02wLqFaVYD2YXC5+ysXGJd5fC3zA88YvzlvJ8yboy/+gtvknkEW5s
4l77+UvqVpWnKZ6VP6wY+WC/ZyputHdlvq3Wve7n9fJrzq284DxWT+n/NXEu
+9jjJbIeZH/Lk1vpQ81nW0Pj1s8Nb6j6vvAWgvUsvAUv7dSY0PvkHEkfrkTh
+ppbDR29Mfoe/I6t9O9zyx1i3OpJ/dmeh09XjgqX1P48rCt+S+s6KF9Wo/l0
1v/jbDoPxR/wY9H39lvHflZ1Guv24pj/1Ly0cvBdOPU9+crCJ+B4JS6FcD9v
biXW2ebDFSLH/SZJ+dz3juCTIHGLn/936k3bH1Hn17zuPU9i1Puv5DkI+tVe
Er+MBfAagn5MjeE9uNMa0zevAnxC52xS9KM//ADP62fOU+/WfPiqsn8GehDZ
P72bCaXvBrwa92RhntOS3xOnaT37hv3EB4Vv0hdU+xJnnx/DPExj3ebbwXwe
scmj9oOD2SkEB9uznOdmxU+c459/QJ+Xrne537NKCl+d67RvwONx9/VTnxPw
8eZOVOe69u0M+hlp385Gx8H5ttKP1W5ZHZ7N5vrqvgTP76q61GsapySvad4H
nZ3gz07Z2KF41R6In6GV5Ed4ZOkzUZ+N+yf7yvS76twwL8H/cdsVQFc2dDjz
rftuF+1AXf6vb9DtCO6n/X6Nfu15Pv6JC6/gcwteX5pa4Ip32B/sX35Ft3oE
nUFwPkbVUviwvwW+qzeoLXnBKnBd++c86DkceP7uy+7g/FP7E0dVG0sdxLtM
fDWuvcILNZ7mZr9Nv9EmMaHn2js9EF7spdOh/MiO3o6v3exV9BvtxnnhjJJ6
fbm98HTOraK/bVb8ed7kZxr7X6j6jV8KXYp3twv9BA9z/ropWsNnkLzbvl+H
1y1ozLjk6dYgF7yiqwWv7EQt8rh8uxRP1e6/l3jth9Po5paXY5/9BxxR+wDr
urZbuzG6hm7Utf0plxXe4Ddpxn0vvYe4fcMBfDkSb8Cn94OB8Gc2jxY+TxHy
razoOj0rL3HRvczw6bo1Jy8bVIXn8YO98Hn1eTrrN/Dhbu+Dn0g90c+6AV/m
ryawb0+srHT63m8/o+udMJD4QnBps0Ah6rtx3uhnJ33k3XKxZJ8updaPH3cO
9YOjcUNxgm1M5BxddDQmctzYnIn8eugpzvNvflD33TuWi3X46vVe5Ot/zASv
aEJrcMMp9HFzu6ZjXXUbSF5qLmI9dOwJ70H21SDvkH3VLXK5oMw3deShX3IO
vdjHeSjnoz37C+rQbZ9SX9F56/V7xOdzPqsQOe74aclX1+5ReZzeB7za5ekn
m/5ZuO9w9/tVIu+XUxRdqr5fZvor4HBDwIs0zmb8D1dRP+6jX/BBzkbeE/Ba
B1N3cWPhB2afp2+me2yFwqvdf+kv7JbbpuplrvsMvsQ0+IxWx2nUIwp1xM+2
6kZ0AFrf5PWgnr7+/STqc3U+kn2l9NWQ/iY6r5f+Jubqz9l/h2wCL3nHi1a/
v8qQIfL9zWusV+v6NK4/+3j2pQlvcV6OtrPzfeEPOHHpM+Xcz5ouctwY/FT7
eqgfcxT1kTf1m27Xk2oetH5T+4p7p5/Qp0Z8xa2qR6gv7Y49XI0nLKryNPdm
aXSIKy5RrzlwAL1cw+PUR+Q8MltV5/m4ED6XrfEtqSud6wXvZpY87+2ncT1b
slSLfL2Rn/jTa7uUOEP4NubG5uCcq7qqeTWm5id+jt7Fc3SZfMQpMwGe+Qn6
sjknGsND37JPPY/2e8moux3m3Av0Vpno32y93Q5/u0Z3uf4NdVg3i5vAu5I8
wrx+nDwum/bhEVxF1qdTgHq3fX+yuh67LPooo8BNzrtV01n/1WS//agTdWR9
f4+chB97uIWK34L9p38/cO/DE+kfJPjPq/8Pz69MfHhNJel34M7/AD+u5YPp
jyl5gXdzPPzY2fgUBX4vBeEBu0nLUgdYmI99oMt8ePVp/Bh1PZ0r0D/6fP4S
ofuSYfiwyPvil7kf8gGwO09hfWYoAp+qPvu5PWEg+9Q9wZN1/Lk2lvo817rA
+tR+toVSEC8+yUqcc+A5+eDAkpwvf39HH5/YE/ENyEQ/GK/jb6I3p05nb1kB
/yFXg1zq/arRZ8eZ0UL8NMAtgnj1nPCWvy4H7nXut9ZqvPZF6g6LZ9JvU+Jk
e6joGe9zrgX75LVfVbzlRXWpIfeP+PNUV56LRofxm/zwOXHIs9yM3xwifbXo
9+0+76DWpV23EfGa1GdddwM4V4ls9N0aKP0Wv08Kn+DLFdL/RXTig+nv6469
puIR+7OS8JY/Sc79exUPq8+PvqL2f//Z9Gj1uuYz0e22y814j05q3Er8A+NJ
0Yn4ZX7jeurN5Xz47HvwqHov8Vk4eZm8XPBDO95Y7lcy6a+t1/+DZGpf8voO
Qfcn/dDtDA3hHZ0M407mFun/2hceROAf2Iq8w3/6C/ik6I798TXw45qfGL6H
xgmTfgNe3WwIPCitI/jkLfyX2heHR5rxJ+LfleWIb++dxcexL/Ngpi5EHW1F
G7UPmena0w9o1AD0/sLzD85f4fl7N0uJjgw9i53byKU+T/K+wA/NJU52kqUP
1Tn9Ovik+dMb6noZeZT4JFs/F1P7h34u3NuJiZP31mR/+ycuceCp/fgc7jsn
PvOit/ouH35WR8ck5PoPqHPBL2jwvNcvwPoXXq41PoOcX6IPe8PH1T/2mzpn
rAH4itv/xud+FZS6mOS/dj3Jf0sb8Cj+K0Ac+3k9tZ51vqPjySDf+Wixylf8
5ff5+zYp2A9HN6JPmtQBjVXLeJ+p/cG9Zr/ErzIJvqx2VAX4Y7tG0re3TCv8
CortxC/ESwkPuWuVEA8mqI93/yzkd2ykxndR1+vttcuj1PtZd8AVO05kf14h
dbNOuo45nHWwfR55UBWp94nvnzF8k7pvdiPifzdWTqXDfLXfEHeUKM4+WXwq
Pjb5e1AvS70ffOaz9eAFhWKxT6R5SPwZ8xNxeO688P1ybWfczUldqsgAldcG
vls996v5se90Et2B8NUPX1Jxr/dhW/bP1T2Gq+tp8TNxdpFZ1ME65QEn7J2R
8/L2tkS8D+emnRF/Ov/8Wvi0F+nvaX/cBj/fb5IITi7Pe+Un96Q+/KafGD+Z
ZhA/ap3agrXRkdcf9GGU6ze+xO/OrHNSnW9eI/zu7AGxqevWPcj+/xSdp7t2
C/vIjVxqnVtOJfDfY1+Dq+m8fvyPnOsrYqXm+qVesD0f+f74XtqXkrpknNyq
HmFfqqH0627XMq3Vdf5O3zW73DvCSxddw8UX8BPEz8cucZ7nVPx8Xvv/q/+v
n990Lr6W701W/vS6XmNMzQ5/ayBxlLNpL/qjucRRbrdZSpevX+8vzIA//4bb
8MkF1zUOzFL6CP/OQtGB3uVcbv6u0gO/jm/V3/9RUs2b2/O5ui/uivHsv5r/
8Pck5rHYFqkLS/003ark6rozHQyNG/HSX1c48HSN21B/cfuJ38Ly+pUj398v
MwCec5Hy8AKy3mvE94KHbXy1K3TOGovpy24ZpwpGjnu/ngeXP3uFerf4Crrr
tit+if9u2cqMU89y/+wX8sX9H+9IdLupp0jdSvwVtz4iHvZfUp+XepaVuB86
kf6rk0SOu7enqHG7JTyKwD85ATwKKx96jSB/dBPyvW7HUfG/+xPnspktC3lO
53LU4dcI/jkNfzQ38W7Of8nH7d74IWhfYnfIOO6X+BJ7vZMQZ81rj276xEG1
/qwPPlb4sMb3vG1p1f4b/ET4N6rXXzyNr7zEG37VhOg6/j99Z9T33xYX35ek
CVn/NVvsUnyi5Rcyqr/TeWKWgczbmCTgt4W60Ufmr6aMn6uZI/L1VuJ66LVr
or/W68FJt4R9/lKYZ+UuSU081/33kI+Ke/YCOt5/BxN3pU/LubN/LPWpXYWl
HiH9oZ6Wod6VuQF1qefX2ScT/0wedKoZPtFWZ/wxjq8HRxpLXySvFn1J7OTx
1PVbo1LBN3n5FvzYodfQp3+YC78Iea6twp8o/NDJ0yM07v3+nHwhUbgftMbP
3ZsJqO+90d/W3Tkp/FwvbQ6vu9068bMF19J+odaSXFGR7+OdR09if3wK3CXm
BHlfvZ2MZ6sbpX7/hj+t/deqXOrzrn4U5kG93Mr593J8aB+2fq+u9LPOq3lW
72/DR7U3pIY3PzoN9+vYcDXu/9afeqj7XmPeh/to1NtQkvswgHi2atLW6vp7
5iF+nduOvEfPz6kG8MkWZAvFz16Zs+BgEhcFdTGJi8yKm7nvGg/JNRd/olWt
hQcl5/XKQuCPRXvB62y5C5zqqzTw0ea15Zz9Lis8kHuH4Sf475Lvl02gxo3x
ucE5kxQI9QmyhuGD7Lz1F/cxCfoRc3sMvn7ZauM7F10GnupBj/WTJaPCWwLe
SKmd4G/f4B8VxNW9Y8P7Pdlc8Sv8Ol3xW27+D/zXUZK/lBY9i+RT2l/C/FH2
N+0v0T7Mu7YOFCYevh4VFTn/9owK4Hjf54qKvF96Hfqtcyg8ydp5EN+2zvmo
v2xNH+I/u5Vq4Q8gfsjBeLd8xFUjzof8E4wL8+iPssHjvjVZjK/CpQfgePk/
Db8+wWl0EOmOwv9qQV9s7+IpcOz908RXmXzKL4zOyHnajveZcZ66TBT9++yF
ZcO+2Wl/xT9lZaJo9Xk6Xz6WIka9z/wGIV2q8Wkp8OvW9UPPl+67bW85G+rH
ZaWZrNaF1ThDuA/pP2tUfwh7aXfqxhveUfwlf1fekN+vrnu++oEH1pv7G+gl
hVeveRQ6H9c8Cmf7eurtLX8Ed4p3Fd/jG2PAFbQvYr8s4EUDm8MLk/VgFp4b
4hH6pwrJ+cX5bq+mrm09GaRwb/fHKfhvNM6ueMzO3ynhRTR7QV/vlRtEvyB8
s6HodvS6DcZl3frbxoCTtDb5vo2PUN+N9Yt6TgN/wju5qT+Jv19QT5F+tVbL
L6nn6H7HaXn+tT+qnrfX/qjqeyV+ruqxxoNR4IY/Dld+N1bdxtHqe4mOzJl+
GR+cgq2Z16JT1P7pbaePpu67F5yPNx/iO/NnLfLrGvDD3eHVqIduTkLf6ScP
wSHvC5++6Ab0Jl+sUffRurgSv8fxOdFf6/tVbCT75rVZudT1/rAAfOz+bPLL
lt+q6/TX45NpdGyNHmrcaLWOzDyHiOfFr96ZS77mlKpIfLKhOPvd4TXwlJom
wjc4dg7qKJ83FZxKdNm/7VR1AWtkT/aJ+gPVOrF+jo2+VM7ZgG8m56z197vv
cL+kb/tmn+c85VX6xY06DX/pe/ymjM3f4LuTxVTv7zz6hLqd+PIZC8DntS+f
3eapWqfBOdUpCXlCnq/Qm2teXNum6FuvplPxdaDfWWriC3+4cJ3IcaNOXDXv
xqZNNUOvL4+Pj/n3aaW3cuNIP+uzPcgLki6B97Ssi9L/muPy0G+924M4zI/w
lK7WZR6FHxX4LGl+1Ofpo9T3kXPHiY+ewj+bJ4QPG/XAp9zsq1UcaHZbAs6Z
jH7Tr/urqtdrXHr7VPIQvV8dpb6p9yvz4Mf0DZe8wLpwE3xkdgXqFIvic39z
E+/543KG9k+9bo0F/UL7pzvuB3ga4rcQ6FDEb0H7Sv2f+3gpQczr3/7HudiH
mn/DPnoe/Mm+Xhid3+jZ1NOvtpa+vWHfXV0/9eaCV+j6qTltI/zwxfh/2lVX
cJ5lLS28JsnXlhfFP2pwYeLD1PnxXx20lvpr/8vKT8BNgd+1t3Qi8Zvsk0H9
Qu+TtUYRx0l+4V+KYR/u35A4fVYi6o+L77HvJTmO72LO69SFP18pfe7CegTN
w3fyHKsSOe7e3EO+MfwbPa5+vPR1we9yjqYuKjibsTwL+9W5X8k/x3HfTafR
i22Rfy/njiHniHPqXaXXDvyTd/2FD4j01wj4Y1uP8u8k1DEDH4AzGdXz6OUu
XT1y3IsHH9JJ+I5a54Ev7kfwnHR92apWD9291JeNJKPU+wf81Tp9wF/sRdRd
/5lNXbX0n+BfTU9IPXEsdbcUa4hrL77LubDkC/S5uk/utOvsw2UufMr3+lvh
pda2n/HlqzeXeeslPkIFS4d4CMbSovA8zw0LjbsF23N+FUhPfnpntbpOv2lL
eHV325I3Z8qCjnL/XPBY0cPq76X1sM5gcNMgH99diz7UA2uDQ3+Nb4+daDL6
5I4bwvFtzT1cR7Y/4fUHOMYz1tOLNhVC44nfhr+X+yD5U8mj7FeJEvPc7urF
OVfqMPq1LF/jdyp9q61qCZk36VsdjK8YEhq3Rt6vGnl/vX758Ad8A7+yY+dW
z6/mmQQ8MeGZuP3WhcaNb2opXMx5XI+6UOLR+BFNzYKO8mvtMyb1u6Tin9s0
7LvifUVc57f7nnj8b3ww3PvVFI7mlDpDXCdxoPcsB3//9gQrNJ73bfKW+zXp
J3JiJ3yQDQPQLQyE12dPxm/Eb5wHfviig+r9gn2mRz74jmvp1xPwlxpEUUfZ
MU/q47JOKmShf27r+yH/UueOhd/7qgeh15ubCqBjzxAPXUZ+2W8nrIhR82jF
YV+JLeNL6JP1un8H7xPu36GfU63v1s+p5uEH/ZSFh+9Vs0I4hjH7EevjVTys
rjsiHlbfS/rA+v0PqjhE94HV+GSA6+r+pFIHCfw36pEfeZ+ljFJ/J/VTq3c1
Ne9uTGr4b7pfzJE0WxVeWeUuuitdJy25ELzFqEZfzSr4PRi1ikg9b24Yx2gm
vtjiy+TvnEMcJb5MWl8c8PG0vljy7gBnlrz7zfPCuLWHdbbnAfNRdQHrPF0+
tT9bsZrjgxVTGj395v2hfCfwE5D+JlqPEFy/6BG8Mgc5v5uBq/sr8/K5bcuA
m02+jn/U/D3gg28tUPPqD6a+YGTMp/x/jJ+uMN+Cc/rD9+K/MbsMOhu9Tupv
gRfapafww0UvVn8QfJF2pcGrNL46LB988e0lo9TrdBxV0iaf6HIdXaDuY5Ul
JeN/gGcGuumK6PK8FHbp0PgddHaa96LHNe/FuLWbPHUWPuT2ZeIWr+3X6AEP
01fd3T2C/XzldOKWyfOp4y+aTjx2Cxw1qDuvaIBeul/GDKHxK+jWvRvwi/W4
7k9s1MAPNbjOifQh8zIvqBwavwQeYn2EPjfAMWb/pv7tjxsl/AepU1eMT/7S
6S7ngPbhSf9dLnW/xt5V/NDgHE98QvUR8Wu3Q/ewlnzKr7cihGv8Lz75g/j5
k+fUK5Yd4nnZfAIf0kubQjx267vEqo5vdU4A31D3Kfg+icIlnadj2P9frAOv
WDaE6/jlJHpErRvNZ2i9ovRxFr79nVbwod8vAo9J9gGnB34xzuKW1N91PPA+
437fFSH+mNMBnzfzQTaVdwb97w5l47lr8kL0F5Iv370L3pfxSKnQeJ0r5GXj
cxUOje9xYtS8H55QLDSe8z/iioqp1Lmq8Q133QfoQDKXIt5YD67lp8E/zY7q
wn5zmLq/E2uY+jv7/jus60PwwTS/zq56CF72RnyWzEO1FK/ePX6P/hp6X81f
Bx34uZ7gPInoI+YtOKfiMx1nBjx5iTPdqxuj1HxoHn7aD1knvY+HecgZnqt4
3h4m/SE3FlbPnZG6Kj42v1YXH0jBYWZlZ9+o1wXfclkPXjHqF/79AxVD4/Hy
Ub/IOVc9p4EPbdRjhXub+ZeE8Cv393LEYUM/VN8riGeiehFfCL5t6Ph/2yn8
p2rPC+lirLoZhddb9gO+l+B1g04Q77VtFRp3MmelHla3mvjNSh/5n/Oq/dNu
Pg49+5mV6DH/ewoe0ms6dWAdV3SEN+6NP14sctxs27apXDc4h87fM/wJbyTv
GHzNdX1wbS30KTdSoPvYOZ86bbEm1CfmFJH5ZJ93VuELZw/7E328rpdlTIb+
8YT4mOlz4XkScKv/j/5X/X395WG98Bj0yE62jaKjFLxozBx01OPug/f0vw0f
puJjzrlHnTmPy+wFP1/SSvMX0SdqH12ZBzPDO+R991dRdys0gvmM15O67t24
nL8HFjE+/3gofvPapKYPTl0bf80Fgiv+V4xzZ2BffGjl+fK/Ok7eN9cCn9e6
1w/u4UdXe1lYDxu1Db7aNvCKQFf7K3wn89W+rT5X79tbulF32E68YbRphJ9b
EeINc2EC8i2No4r/qdusVJT6/MCfRHSaHyyjHq77fk7NDY9n0GzRG8n9vbCJ
86hXc1nnnDv2xRX4ZZRIxz47oRw87aE/4wNzM2GJyNdbEyoRt/zej3hmH3w8
Y/dB+uUUi48uUvZPd+zXxNsnpkSr/7+hEPzR4XnAa16Y8OUE/3GzXwnj9bHv
8ZzqcyVGcAXJO4K6l+AzQV2g2EhVF/Qb+PUix/2C4EEatwni5zE/gG+0rcW5
1+Ep8zD5L+p3M0vEqL/TuN+sU/jtrHkn5IvrnE2Kj+LxOqFxc0t+8twBn4g/
pOhu4ixGH5L8I+Gfy/sv/K66/t7q+y7x6V+5rQL+Gw3IUwN+74wfmQd/LfW4
NNvgD9Q7Rj6WrlW1yHm2811l355ynXX6kr60zjT6/BnJ8kapz9Xr8C90TX6K
b/D9HJWbelPxI+wzJ+PD/9Lz8MdU+Dk5WokuT/oalI2DLqBKVKg+ZV9ez35e
QuIL7RO1TXjUVZeK3krrsPriC7z7LLjs3/QNtIs1B9coGU/y9Xuqjux1KMv3
SrCtVOR9MTp0Ij7sJDp4Hc9/BY/BTXUOPoTeh0dnIa88/HuiyO9rf16GOngD
fByDfOSvSrz/+w0SRV6/+9kacJCLVshPyagCz9k+E50x8vVGfOoKztWpOZjH
TOSPy2urOrL+0fuDzkfcu/nwYd08SuGERqb06rz3/1hD3XzAEr5vnBzqfvhz
mqk6YNAv4+5c+GwxbanPPKbfgXNyAPtOBtGDa97gNtGDSxwd4APP4Hs7OaZy
f7S++Exy6uKp/m8/2df/1nVh/fzqurA9NXuY99uoF/jnywYhH2m/61N4PImH
CJ4svJ3+T/G5HhHuI+Yf+EDlOeadi+D8Wre1vjf9PuP/uEbxa2KyqnVl7LiJ
b12OMeW5HnjX3v79qo5mdGjNc5C/BfWaefAa3d/nhfyUvNKf4DvtDAn5L9m3
v8O/K9dU8AG5TvNUcuq5qw7r/RJdQpK4rG+ziPr/7pTr7dR15LnK89YYnZQ+
F1yvD/WpypVDfFpvY1b1OmdYCp4T7We7bZqaF/NGMXX+u83+UXpea0J99Ktv
1HeCfbjFlFA93c/6kLzg1f4c+Xq9P9tnH9CfUOIxd+mn+Lps2J8k8vqt4WtY
n+Ud6jY56JvpLmxP/HbHEd+nzOgaLraDL/o/f2D58dmn724M+Ye/9p1Qn3N7
RKiPgbdgETrrJlv1OPHnkBzUAyY1pN7XrRA+rvNSSz9j/KPMRy+pp96nn581
7hZ14GL70c+VrAsvV3itGh8O/Kt96h0BnrxkKjjL2TC+atjt1fPiHQz7WzrT
+XsjTxinteMWU3mOfn6D/WoLebKfOKngYOLrcnOi0o/o/n1BvUP370tSiH2l
1EDympju1OGcL0L+Y06NSuhxuhaLUfOn63E5KuLH93Os8Hl9Yqy6T3bO7uwD
I8Cf3Z/vMO8tR6O/0/nmFzHR6vNXNwF/0PtAqbFx1N/9H79o+ir6j49zLonu
zH1wnPWcPxXncetvqZd9mx6ehvhMWzfxybQe877m6J+4/7q/24omKk/0e8UL
+du7b22kz2WKzOD2gY/358Rtoo8O5k300Xp9Buevuwgcefe0qpHzadW6xroZ
Pgo85+0x+OEsg3do10hKf0K9P3yN75J38T3Wl/YhuXGL/Wj3+9GR8+xWf4/6
dPSn6MOEJ2YlHImOIsmWkC7AydAD/VW3CypPDOpHK7KTJ1aAJ+xmOkceHR+e
sN9pH/t33vPo3IfV4fVTnki+LDzP22V4fhv40ep1rSoQpxSoSp+imX+qcTN7
EXyu+9RS56Ux+ho8opzwObUvn9Xaxg9D+pO+igfQyS6ZpfQgzqJprMOjt9mX
+04SX3HxJx97hDhcx616njVfy8PHwOgvcXjV3+B7HRup4sqgXrm7A/uD8DYN
vf8Ib9P+vjt8KOFpmJXLwidsOBT/0VbpyVNW3M0hfx/KQ51S+/Ady3mZdXxw
iuKLOut/Jg6YMI34czo6JivORvj6wicJzpGkk8FZSm2grljwV3SdXc+A+xfu
xe9u73G+LEPPaDeoouIljZObq8qpOMc/sjpJ5Lg1dhzxj9T1NC8iqOvteY+6
T7Wl5JsJHoCTVo0diifttvC4/EZdhJ9DHd9MUxI8b30XxWd0Dsyj3lq6TpT6
/8tKqN/B8+iSd3uHmmWIHLfdqewvHS7pvhXUayYvog9sgw7wfzqnQye4JzvX
cbYx+E3ji9QRyvXk/J3SK6t6f9k3/HHfs+61H5HouLUfkdE9a0h3aZWKBh/U
+LTe55MnwedO+N7ar0Pzva18o0O6Qu9DC13o1r7gr5LXeI87E/+kDj/v1kl0
XtqHKhjXPlRTr/IcN+6jznFn3lcK33brdg/1yXK+/Bef5d9LV4+8HrMc9dPX
9a/QdT6jzug8qwtureP5uTtVnVX3ffY2iS5G+j5bbZvBp3sjHvZvTOK5F/2C
uWEaOpyLf+I75nbFZ75/D9ZtnEnUaZd+St38varhuF3HRQvBb93qk4U3KHW6
ieh+3e5Z1fyZ9RaDi88hTrbPN2Bey+xkP8hRGZ+f253E3zWsF3AerQ3hwP46
Cz+ghW/hM6N5DmPLc67Jug3iOt33yvhOziPOfT9rlWj1uflT6PdRP1Z89EjO
6fbUUWaeVJ/rVCiieOl2Yld0bbuZ/w6L1fPjPbsb5mHmTqH0Qu6+l9QTdD67
pTe8zRv4wztxxf+tMXiWUzNa6lwyz/9eV/fL/KG14PzhOpFtbsJ3/Y9x4MD1
pnPOlUvMfl54CfhGx7rs4+fCvtBel0/xB5M43L+0Ve2fOg43ksP7NUc8YV8d
MZ/nOuMV+tdpPlj/SeRvgv8E+mXBf3Q9UV+/rieaNVKig9P89hNfx7z+t/HY
CI07ec7xPs//Yz/Q/jbVSlCHejfMo/Br1gX/qXC2Nv9f9AKzlvA83OsYwgH8
ObfBrz4Mx/9WsYf4gawWXZjOW2Peop4+7zv2tfON8Bf9OT543NWGUgcWXPe7
4fhpJHxBPKN5R+nnURd+kCN/5Lgx65B6Dt3sj8GJq+TjvLZPobPYyL5hxK7H
vpQyNvt/S3CnAJ+JtZF8yknPehFfRDfOQ/bTvAPhK/ZBf2FmIC41RzQFx91/
g/G129W4X1DwW40rrucccbd+DN4ypDv9Zwv8p+I9p3AX9f526b3q/xuZW1D3
PztDPcfB85jiOjzVz+Ko5zGIr3rOilHXd2x3tcj7Yq7E/8ecvBPfuT9OUw+V
erE5Cf9X184K/j+gPfyPY/1F5y286KqVqT+K32+A24jfr1+/BHUGWW9OyjPg
q978aqHxxd/i3/GGP6pVjX5J1txbws+sDR8/bj78FI6vo07Y4TLPizcRHlLe
aFVHNU+Npc5+9lP4Y2/gz0bLk+q5NdoXVf1srLVT2QeKlWad7UuHv2/mrPAW
lgq///s64CdnhpGv3ehB3PVfbM67l4uoL/jlwRVyxifOvPqE9XBlyimVf8T/
JFq9/yN4Vtay/8h70m/Ev2vduo/5nAJ83+mJQj54QXzTl76oZp+z9A3ssoq+
qIsqVI+8L+b9hegrGnxPflq7Nv3aUsVifY8J8+X8BLdUHGtOmCu+/W/4vMUJ
x7e6X4bGi/S4xouMIeHz2i/Sgbx1wSjqwlqv/eHvEt++pfaxgOcg55Q1fgb9
uKXfh98oNXqEvtvUutU6XO1LYyxtID6x6AjcQVepG/aoTX2zMD4hflQvnhPp
5xLUy6Sfi+dGcb/GJwRHPfUZuqdE0fBotN/UtoU851frqHWteSlGI/oRGG0m
gv9r34Ny4BtO78/DfhrtjvO8Jdmm9kd/dgvq40e/VPxee+BHxGXiH2WnL4fu
U/AZ4w0eozuxeuXI9zeTX6NPWC3Zp3V956evVLxqH++s8EnzHr7ZzqZ9gc+n
/Fbf231Ymf1n8BG1TgMd/bwHqp+1U7aT6Gtkfy4l8fYl0TnKPm+fJW6xq8YW
Xarkj+3Ej/F+IaVLC+Lhj6Lp03T2jJw7Es9PaKzmx+06PlrmQf1476Wln5Dw
1TX+rPnq3ukn0kcU3Ma6hp+vlapTSOfo17eYx/fah/pqmQ3SUWf/Dv+u4Lw7
3huctq6h9yHpN1qefPTGH7qurn7sjq3g9xS+F/JdNwq2Ryc5qXBM6H1OnAMf
+bhUyOfTKiS8ju8/CPXZMUeXw4+17y+ZvIjvZU2ZStz7aw/20ed/wWM/iH+c
bwtP40xSzkfhabgVpvH//x7Pc3Ts29jqt+YjFUyLn4zmI/UrIr4iki/b3A/r
y9/U9wr8Ws8u4lz/NRz/v/aTVOP1Hfz3OuRU+a81KD0+mDc+hEf5Za/h6v0P
Zrmo5mnQ3OjIz/U/oj+ml3cN86nXm/9M5WP+1nasM62Xef9ncJK++MMEfQDz
4g/j7U9bK3Ke7ZnjwEn+eUG8t60iefSPHeDT19oAbqTr5oM/VH6YXoK3wA90
nXf5Gd6nOHyVYN4KwVexxpYI5VnOswfgOy3nRUfOm/XHGvW+7jTJg3UdRJ43
t3baUP3IaJObOtz1onlC85CM/lN+mzoKD/G9+OQ7ce9Q/51N3hTgk425TufO
JOrUH9pqHpy02dX12ZmXorvSfIYq+N3ZiT4UXr3MT/MczPMU7aMo838SH0Wr
dFk574RPfjAZeESVg+Tr2oek1rKrqv7bfmu1yPl3l32KL6L0uw/qEdLvPtiv
5BzU+5V7oa7UISWuu9EqRr2+xXXq6rpvYIMj8PKvNZW4SPDeZT3BS6u8XzVy
nq10f1AXsL+oEvl9nWWV2PcTPhM+jMTb/eBZme3+Lcx1Cv9w2C/UN8cdD/Vp
1fwELwbds9H/JjyicTWeKtxiNX3BzGdxh6vPvUdfMKt6Oe6/rE/j8mMVb5tv
++J3Jf0mPqNfj5UvFv3djNH4cb2srebBaNMFv6UkMj+zesBvrEx/Cr/DY+qb
W34gT+ySCp+bf7MR/+z8kbj6agznWKsJxMPHdqCX+x6eTOArMgUfKr9MV4n/
98Kn2tON6xacIdgnBWfwm7QN6ebcg1Iv27cX38fNO+FZPRnPOin9tzo33Zgd
4C0p9hKnyvMY7M/yPHrRo/CV0rzfeKmJnw93Co07DfC39xPirxXg+ffh//hX
4tPHU/vep4XnqvnGAS4tfGPvXiPRH4mf6p1MSt/hHwj79zqlpV5Qcx/xuOaF
pm3OfezRJRS/ue3z088rze1SkePGje7EN6kPyr5Hfur7SZSu3MymcSTxRRzQ
HR341xpHknhM+Ml+nSh00zqPiFsNPeOlPeHnvdJihf/bFcP9a4xd9biPs8lr
3uznYq8doubDeX4R/sbsg+Q7mtck+4DmNb3Wj0eOa/243++jkB++2Q3/CutK
cvz6gnzqcYx6/a6iofzaurCHedkST3xIZL+akhz9yc2TBUPjT1z2l0STpW4r
cd1e9mH7mVs5ctyIH4ffo8dVjnwfe0hG8nsdV+jrkbjCWp0xKvS5jfCz8rf0
qhI5bhwYgD/4KerSgZ9kp2Ts171fCn90JHFsmhzEr0V+j2LexJ8kJX2azJ8z
ZYwcN4/OZr1KP/T/+URNF53tb9Rttd6wyGb8R+wh4ucpz8sn4BLm+yXRp2ie
7btFqCunbyK6PMGTWxTBj/5ZbOEjrCBfW5QW/p/ECXo/1HGCu2YEfdvblm6t
xtfvA5dJMIH+ob9nBl869gI8SnCe4HsJzmPXTa+ed3vvVvU+bqt7vE+DHQrH
1nGdu+oaeWzifsRrPdZyPi4fDE4yYA55lK63Jt4GnyemBPUHXY+uWR4fyG1f
4gc8sx28i4E9hPcXm36UOf4kz5V95vW5r95392N8PNJQ97HivYDf9s3v7JN7
Wm1U+UpH0R9ovFr6oJvDR+o6iPqxCieAh6b9A3W8Lf6B5u5OnD+SZ3mHbPEH
b6DyxMAf++Uq4rpUnbnvWr/2TwLijVjXy0aO+1vFN/vYxwlD7zNE+jbluR+O
x75rqvuXUJdc2hC+5eTv0AsM+ZbPkX3A+n9tXXd8T+f3v2ITRNWIeSURo7VH
tNaVRGKX9Gu1xqUUMb9WQ6kragu1Z9LbpsaXqqiqrZcYDdFapQguvxpFatRu
w6953uc8uc/n+/3801eeXnc885z3eZ/3qXEXce2WKciHY33+pRXxPc/qibii
vSI/zve0DRjf4NmIg7MOCfF2WAdb4rq314n92TrSg/BVytsdtgvzuEYcxVlI
l6xBCnhmfudbeNvtEvD/zS1XEBdiXHQ+jW+uNMSFGTeoXQHxwjOtsE8wb+1x
tRD0WzMxjuwv21Y+8JVLE5+B9bFLf4R80pKq/aONegy/PuC8wlu28mvg+RBO
7qtLY7c/TvlZsK/MOhueZM9vp99viIt9qSO+ZiPOpPfc3MD7XKN2VeDep2YD
p585WOS76cUiMP87HFbsVT0rCvrg/meivO3OwEDo9V3ujHw73od7rUYctOUm
gTe762Bva21ht9nf+4V7v8s5vRu8ydh2ON843k15avbhwtyO36+0b/fd0sLb
7lT5QZzXhhGB639aIda73awT8Mfet8Fn1k9BvyLR+k34+2tUu4vXo1UtCuda
9/3Qrb4yGfOv8C7Yd2x3HSmLOg4UH5HrmuIjbuxG+Jtkj7mb9qE+yd3Bim6h
XgF1zM3prXGuHUOehRNeEnEsn3iokdAN660m50uS7iLltbnFa9XGe5J/qoNP
7m71r660D8E57vy9DHY462E640W73WmiobR3rQ0cdkAa6YDRuphI+QXv/9QA
9yf+aoUR0D+fHQJcjM/fEXnDxXf8K8XwthubsrA/77+JeK9fVTGfrUWtwd/6
vj7Gd2Y/4M9JSeBJnqlezdv/brOC4LEcRhxPtt8BX8XqOYdwJNiT1s0VIv7u
BgaSrg7OL+c06gy6hSZC33duCvRbLgwU/94Nni3Wk7SXPhxL9uop6JOVKA27
8adXwHEWHEI8eij5+wEvHgr/JcAGfsL7dutkxJ0XbRPxRmdMeeCfB2fCTou9
D/0u1l8qsg/6ABW+UPUBrvoBx2FdcfYvSF+Of/qdAoPpb0WHIqeuK+kR/VEZ
8diRh4ADmw2hG/NruNr+59Hu3vvI9vqnwavvCH1V8/QC1Fu8NAc66Guojgfj
tEHAZ63WfUgfhvzWkLehTxR9EnynffHgdVwNAo+twhXwV8Oh6+gk/gmegY46
rTLuEP9aVPb15t9lKF8YcX9jF/B/rfEUYXfIfJbkCKy31Ddw/aFA7P9PNoj9
xflzkpJHY5+EPqfx64/iOXKeJ2wXfpDltFXarb4HxP5prsd+K8dxCfYlNxn+
tYz/JsK/dq4AL8rhTcFfM+OPq3Hn0CGCH2V8ORF8avJ39BbVRV69W34x1ief
4+9/L+5rXwZ/XPY/1WtkHXjJM2cdeKoH9M93ib+5HpBe+IyCJ2Tng4j7OeAB
STs8FTwh42Rx8psITwiFnqE9+CXOdz4fa2cATw8eirhLo+ViXtnX87IuMeKu
Q7shfnesBfTYF/0HflKhROCiO/cI+9WpCD0AiXu0Jr2AALUOuHO9Et6PcCmJ
gxEOzPuP9BNp/3ELg38q6xbF/Iz37MjPxfdyXRvNJ4/JzfNIxINMrQmNL9nb
pVsj7zUtGLpVzPcYgfis5bwHe5D5qK33ifmjF0L8UOJUraie+J4RpHcO/RzW
fza3X4K9M6ET9BayzuL8+/EJ4m8BU5Gv/SJE6ETZ5aOx3qtS/d+8MZjPW98C
fs/6UWeXgRdRc0oHb7s1Ngm6jum1YM+0TkG8u9DlKPH35s2It4QUB6/7w5bQ
uyO+meQtz4K+DfM9ZJ0I4nvYlZPAz687HOsicjTisDUvgrfFekqrtkG3lOKS
Mh+KcGO7Rz8lfm3+dQY6zKk9FT06cwPVvyY9W+kndt8GPds+hxsp76+RHVsX
+ucybnXhF/BVZ6q8Gk0PR1y20Avy94Gn2WXGQMesTg3l3DQaI19S4ktsn/jw
WGQ+JvFYtOQfwJujfUDv/yVwnxWNxDpg/MSouQN4SrG/hN9kLcuNeE+u/tBr
Djiv8ELNIVRv5Upvhbej3UbeqJU0CXXDPDrn4v/3AL7rtAdO6JwoDx3tN03S
ySc/9ylwcubVSL+AeDX2pSakr0I69ruH4zyl/D65rim/z8pYr4yj0SMB9WBz
xyFu+UU6+MOh6/n8xbxqeAz7bY8bqAd/9bLCH7AObMJ1qR0UP07PvM58ayVe
zHw5vQjqS8pz5CHyGZ3J68U+Z4T1By+oO85l5+yMcPE38wDb30Jcddmry8KP
jskLHH7rK9jzpNMr5yHp9OqPvhb7gMx/LxQW7v1ebUom+FFH3oP99lUtqktI
eHWbKQLX0s6CDy/x+bLAhbSVDRDX7Yr4tVF4Br5/1lC0D0Y/O3u3Q/csMQh1
BNpHYJ+cjDrobsemQeL9mLfTBHaGtg48OrkPf9oL82HjNvjBzDudsBj88K2F
lHZrWUes28QZSlzbyDwh8FZz+jPg8LQe3XIZyF+j/AvJW6b8C2sZzlGZZ13G
FvFxexZ4oQbVKbMWgBeqnZ2s4NuybhfZV/JcIPuK81zk9ZTnYnz1M+kwE483
33LwyYlnLuMOVjD8youss004WCfS2e4+E/mGB46BT152JHDIlKuEZxKeY1aB
vxQ0p7G3XX99IHCV8V0QD2T/Ogk8RmPF7SLifT+Cjqj70TPRD+6C1orOv+U8
RJyCzju5D9B5x/FWqYdG8Vb3l77Q/eiIOjIyf/b+AMTrhzWEnob1FHom/44V
vAg7E3Uo9Blt0W6p9ts//wJ4432qB8H7Z2ns73oR1S+w3ktG3OdEKPY5ric7
Lp/oH/vKPrIbYQ/ok+sIv8UIG4y81cjMeNGef4WwV6x5n0Z4+9nZG43nlnov
0tuuDduJuh3BZygvm/LTd+aJEtd1SFTrAd3uD7vq3s3K3vfXTxD/20cPxMlC
XgDXf+R2rv+obz9Zw9s/9osM8VyuwyXtSarDxTxSqYtCPFLOQ5LrOmBsJYHn
v0imeUL5v4vqKnl/Ms7I/tGiS2I8tQbbES84eOeBwBOG5qnlvb/29Wrxns6P
f5BeKeW9np4D+6GIWv+X92fW5ZPxX9LlM0r5nI8nn8OOrLgf58uUdMIzH0Mn
kOoJyvVI9QT5Z8UmKXp0Rom3sN+TTprzRRb4ur9YYt2zv+Ca42AX9VT5cqyj
buzrrOSl6o3DkD9M56/sHzp/nf63EY86UgE469AhQm/Qiu3Z1NtvVuJS9EsX
te6Jm/kowvB8l9yfib9q5LeV9W5VRhxBbzMX/gvjG/upfsHzZmHedmP+ETx3
rVrvjPkSrFMh5zPpVLibVL/MiEcc3669Xelno1Bt1J+diniHtGeW+eE9R6i6
BE4/qhNdXOUJWO+hDp8z/2pzb7sdDZzTbaDie2bHaPDyP8uCXhzp0+ppa4Q9
p2VsUPgPem/iHVUprdg5dng07JXPE6DnzPGm6g2EnWlH8nPJvnodz3XaoP6b
Xb8A3r9a6Ocib+B+O8pPJJ2fuQeA5zCOyjgb4ajmqptRyngV8Md+McFHX8hu
K+wuvT3Wo7SXzifADolX8/q1wNHwx5d+IfS1JP4ct0XBJXN0V1AXXr93qSn6
geztXIOg07JO5eezXWHk3xPh7R8zHHkobP9IfI/sH9at4nbWrXKMeko+tfVs
Leo7+5VFPKHkKtofpsAfbHUfz+HzZUKC+H5jFdW9lXWW88BPPzAJuDLzHH5B
PpX5ZlgZb7v2zWKsu2srFT/IGZIWKt4vFv6OvL+xUfg7zv6PVH/n7F34S+NK
K/6aU+9fmAeJV2CfsP5JWcTx9cyFil9mvEgAT27KcTVeXHkIcGr9A+h3cXwz
aAzW14pdCk/DaXRD6GcbuyIKeL/X7gJ+DOcjSP+I8hGczdtbKuNlwa9j3ECu
X8INzMjBqP/LdkJcKuaV6ZOnxvyKs8z3pnW9YBhwnlG5FH0SfftO8Py2g/ci
85gmo54m8zSkv0A8DXf/BqXOdXadR/FelPctcRLK++b6ofL9qX5oti6iGAc+
j1KRJ2h8nLuW93uZD8zxJulPUbzJHNYL84HHvcoW8IhC8in2jF7pK9j5IxD3
kbouX4PPw/Wjpb1B9aPtWZ8hn3Xbc5wz55tBl+dlWFHxHpwft7elWFdW1jbS
G4a+lvN3NOIrK1TdZu3fGTg/clUR48u4qNm/idgnWc9H4rTXsP+zno8cF9Lz
sYMeUr1y2m/fqCTuY32Qhe9OBo9UW9YU/LR8PxC/kfJnd+E8dm+0IR0Ast8S
BkJP4OF+wsOIlzs1ToyLe2JUhLddi4mAbkaTMmRv0H2WVxf4j9Y4F+bJdMSn
tNR/ifEzS/ys7APuqOK3YUfd9BnHENTzCI8k/4js9q5JWBfaYXFeMP9EK4jz
Qk/vXMB7vbEwVdm35fW0b7tpo1D3hNr14er18rl0vV0CeYcSp8p9EvV6OX+f
7WfK39cc2HHSvz5Idl5iCvhOZH/qSbHAz98oDT2Ba5hX2q6lsPMurEJdtRwd
SOiRHWnQ2fs+2tyC0PEbd1NpN3fsRT5OkUnh3v63nvvBbtgXDx4c69RVDoYd
EmS19F6v5QvF/PTvhbgY24FLkrAf7a4OvTjGtVJoXP6DOjuyLm2ZmFKiffhp
hbdjnSwFvm6Gq9gz1mri4x2JAf+iw0jEwUu9C33CXaiXrr2RBX5LoL+Ib5n/
91jEv2T+0etFxXrRQ3/AfkXj7lYYiH0yIS1KaZ8/H/vgxEpKu5k/CutodwuF
h2nqlaPEOBEPUM4f4gEyj1HOQ+Ixuk4g6r1wnaxhD5HnkkI4H+8PV+Encn1t
eb5QfW3G2736S+LfUz1T6UdQPVNn6UjlnLUH1EH+Ut9OSh69faUieFz0vbIf
6Hv/S1df+yGK/hY/uS5IH8waFYR1yv7Rfoyffawf+NS8DyR8j/bJ75fB99J5
NxN8YJmf8m1RJT/FflEXdnEC9Gado7kEr8YN9vMXf/M6GnEV8b5ktc6U9S5w
AftMmsBLuZ6Rczcf8IJd1bDfEr/XvpEg7s/15XPWBemp/vtP9AfrLA1cJOJ3
ZlgK/BTWK0vdgL8TdoR7241T4NfqXcar13euCZzmFHTApN807Sjwn733wL84
chr7wKFPoBubTvFb3odL4G+JM7MfRziz3a2Geg4uDkf8OKkH8qZJX0j7Iwx8
yst6fe84mhk/gTdL9dath9DTthe/ifX8E3T8ZNxnHfSg7CoHSQcS42X4fwud
UPLv5PXs36VVUfJQjO+pHm3NPcq5Y+RCHRltZQj2yWEP48X/79kC+tKnSS+U
caSdwRiPBvEcvxZ/a1oA6p9e2oj5djQ36QlUwrpq2Jx0Wojvt/qAym9gfY9k
nC/GsoaUzwZek5VUAXFJ0pGT+DPpyLlpq/BcPpeTF3IehPhJvl/9CNgbIblr
e6/XM8dGietPd1D1bc69FPueHV2xnvf93c/zYn8pckTh2dp1V+bJ/tte3Yl0
OImHM6MK7LkBfyn7lW/dUmlPUt1S8ynHTahOdG2KmzzpBFyK7cNZ0GX11Udy
FpxHPpcPf14/+jfpOWsCR9Fyaahz8OoV6nyRPpvkhZI+m1nsQ7FvmPOLwp45
9Ap8IYrvSHyV4zvEo5Z+PfGo2S+Wfj35xdo5zoel/gluK/Lt5a/gLSVer48N
At/Ad/+8kVVTGZewRMSHtnwj2uX1o8DDNJZlQd+W61k//hQ8g6hBBfA+xAua
Ad1X2wnA/HmEuuTutSDUwysxT5yzWjXoouvnx8EvPfqiBb039AGePcA8i+0b
Lu5f5gL0nzffh11B8V957lP8l/XxpJ1A+nhOW8Tn3Va3gDMUB/9HC1oC3Prd
5fHifbp3Qb35ci9JD5Pm+czZ2Df3rRDnIetF2PEFwato+j7y70KuYP6P6SHy
iswbKu5nr1qt8FrleU28VtZ7lOuX9B65HrHEH6gesRu3k+JN5KfXfQo/8zTx
+Ph8D4F+svtNYri3XZsCPoBVIT0c30W8kefNURfhWjLhOcQnDG0h7qOvW66s
d6foXeDzFvP8CZcgHNuqUQT2SLkLaB+WD9fvn6TGFx4jTmfUVHmnehvgeFY1
1NuSuFyeQPj1m5ORR8P25/gm4nusgIim3nZ3Qw3iwYaSLj1wLad3U4VP5WS8
RLxp7TD4pYR3yXlOeJfp9FFwS6fkPrHOOY9A4smUR+AeVPM+rJD8Sn3AnH4j
vyOpioqH7H1f+E3Oy12KP2W2PftSrBt/4N7Sjnq6RKm7nFMny8E+oqNesHkm
DXha2iHozp1T67PzPmO9oZ6/7hrw8Oz1byu4nxX1SPAh9byjlPmj/x2DOvIF
0hW+olZq/F/gBfaGjjXl39krxmOd3+Z8E7LrEmifbNoe+jOMz/wxIdLbn9IO
WREIv9WnHoFdfhTiYVMLBaGfqb6D30LYqZ+ocW3O99QW/V4Gz6V40JQ56IeY
5CCl/Vwb7Esb1bgh629oHZ+VRjuNe/jPiK+8fKboHtsV5gGvGzCglbfdmnse
vCj/GeCFpWyGLnrrTqGi325NU/nPNQ77ifcz/LD+2H4uVpjs6XTwlUL/iBf3
W1UO8/jXJ9A54TpoZRaDb/a5TvVqqf+p/q972Vby/ozRzXC+DJmAPNA+94Dz
HO5TQjyP7Uxe12Rnsr0t9zeyt5n/kDOfwX/Qby0S8U/tneL9RDvpzhmj1Dws
+41gsQ/YV5oruHG2fySek29mhLfd2Qe8jvnSjFsyX9oe/pqiM+COfoxz4fwt
JZ/OaReNduLhyPnMPBzCMeS6IBzDvqfWh3ILt4sS15/Porx1sqO++hi86BQ1
LyBbryD7v9k4nrc9G8cT33WpP/ztT8DH1luvF+eovSoScYABg4FH3e+CPKwT
JWHP/loMceoFPVEPjuqSc91Grkv+X/XLznUGftF5pDjXraWoa2xMHYc8rugi
hA+0E/uwe4J0dQZEEh5Lduz0wbCfCe+V5ynhveaY3xD3J3vA7LoA50X5Qahf
4j7HfuUcFbiM0eMG7B+Oj1xCnoJd7IWi6+Ikfiu+3yhbBzxxWo/m5auwW2ol
EZ+ZeFwdEH/RK6u8a71xVa7Lgnp39z6Gn1qvPXh3WyOQ5yj5t/BzfXVOWJ+H
fzl+NOKaeuX5hvc99QO7wsW/4zwaniecR/Nyj5IX7Hy+C/VZj84lO4Rwxcmz
cU6tLGh4x8V+8SnuWy4cOmfMgx2dBzhMTTX/lM93exbyBaQ/+3U/nFOU/+UM
WwL/netQUF0k6TdRXSRzB/I5ZL2GSW+BH0I/yaP45xwU/X62k7BHjaujkCcV
MQlxQ9KJlfEs0om1dy9FfTCOw96JQxy3i+q/cPxRP5aJvBjWrWoMO1mr/hv8
XJpX7uSN0NeruQL785KN0GeedRB6ON81hc4p11O7EAQ7fGov0hOm+X8e/gX/
cnhi+F692zPk2bF9ewH5+4Z/LHhMfF6/XQP91iEP8F7eJ4uthN+yju0fwpdI
F13izxw3J/zZ+G6OyL+R9sySqeTnpkBPchbqKRvrIoQ9x7wvGRcg3hfXb5X+
C9dvZfuH7UCyf4z7Kr9OL5ICHsmiGYp/am6MFHpV7mtllfPRjSsO/e1JmljH
xpshqId46hOc18mq3cv8W7fhRhVPWPGb0MlxrDFKu753hC7a591GnQLmBY38
I0qM17rlb3nHy9yZC3ytd6YjL/L3lvDTzxQB35Hiv9LeoPgv11GS+xvVUeI4
i6/uCudBS/uE8qA5XibzzjheVuQn6FrIOH5JcR+n6pW6yv2JX20YweBpM7/9
FuqT2lOOK3aX9fpwcX9ZD53nIfPVQwoodfe0LZbAfyxXxQesiRh3/Voc8ADm
Y0c0gH13aK8ap+g765HggZwn/QCOB62E/ozk57AdRfwc88ps4OG8D3ctC7vi
BulT8vUVMb8lj5pxJOJRc36N9I8ov8Y6Ekj5I8R7WYx6o9a97sTzpDys+FHC
7rXGFmzp7R+jOfRTWMdD6j+wjgfVK9RYf4PqsxjvF4V+IOG6dg3oZ1oTGmL/
KN0VeoXlbwNnuDRasd+cT0cgPnj+Dvw11sc7mAY+caHlTbzjpV86I/rX7HME
87BlBvbVkFrwx3/bp+qfJxCvifJS5b5Bean6nYdRGEfSvS92DXWJuB4K7yfE
E7JOpCJ+1/0e+nP+GdQJiBgT5Xj62cnYhjjLgjOtvO3aU+hmWuOrBol/x/bn
7t6YZ367gXfyvmSPhw5Vb9Wv1xs/xblD/BCjwEXkNRA/hH855xrhP85WNT9u
7kzw4RNfRXr7zfl4LOKw8T0wf9g+LI/6BVZLFzgnx3mrB4WL66OWgN/tHwxd
qd4DoK9e3Aaew/7gnePwQ4gXJHUwmBdEPAcZdyCeg5Oi6m06nyG+o+1JFbpp
2mlD2HHGuL2wG3/x2a8CkW/lRE0DD43zpKqn4/wqnA4c9OklXH8uN+y5F5sU
HMyudA385F9fAw6WvzPyBX7cCHuS4onS36d4om0sgx/3dBHs2+brxXqzpm6G
bgCP74VCiLOWjmvqHS87b2n0z5XJyvXM23T6rgUOXBz1mIyBnyK+3Cesqfd6
LX852DMDF4VjPBC/Mwbthp20Zqvij7uN3oM+fLEvlXifYUXDr/PZ/53A4YJX
YEcca+7tNzf4W/Fcd09yM7wP5oM2Pxl5T8WmwJ++T/qovXrBTiV/X+Kl5O8z
T0m2E09Jq3e2hfd9rHYU/3p8tJm33b71I/Cuy+kKvqFNjhXv7zzdrdj5eqN0
PJfiF0YJrDuOX1gHHr/lHS8n1xOFb5YTRyb7nvAKuS8RXmGdCf2veIS4Pqos
6dzCjrI6TwP/mX8ePCe7XT+QD3lRzK++Xxvr6kE3RbffWrYW+3WJL7BvEe7h
lB4XJZ67uxTFIyjOtW0N5se1ifW87WYk/B394hQFbzT7UL28ygWEPSP9ozzR
iDMdT1XsKzsqRowj6xNK3Jv0Cd1vhjX0PldrUBf77NJOTb3fa6yqgv6vpuY/
Sr3oDJUfJXWnqb6DPNe4vkPNdmW8/eZshr3qBKjryw0qh/3ZHgO9PsprsC/N
F/wlc3+BQO/76/nQX/oj6Kw7AcBb9NdqIb+U7KUcfiDZS03U+lDWdfDAja/6
hCn9H0M8wG5/veVttzNJ5+fWHCV/2drSD3nxWSeCRbvUs20L3shFNU/N/GA7
4iPXT4Z772O/eBPrnH7yfKe4Uja/Rfx9dZeYz8xv4Z/E2SjOZT2JVfJh3XIH
feJiPZEvnO4veCDu7L04HxNNUe/bmR6G87FIL+B1fK4tJlzlQQx4tnfBf9Yq
bIBffnewokPCz2UcXvrLhMObO35X8usN9wbst1ZtUAeV+f/TLsLPzVxNdW1I
N+zzH5BnMWgTePNGOeS3zhsq9nO3+xGyS8kPvd9OxNF4fKX/ReNrfdJY4d0Z
hxfj/ek8leuLz1Puf7ZbKP5uJAYo9onbvyHszGZtw7ztTrdDOOdqIN9Wzje7
gDJeXnxb3C9yMMWPaJ2OJ34G/ZgHxeNrhdZRdJ+cc8BD9NhM7GOMS7BeEMWR
3c5xiCNT3WqrKul0Xh6Mc3nA0VeCj0D8MelHE3/MqP8u/JRhQbBzMr82vP0g
7XPqByfmrKLL5wR2BF60tpPIIzYqgiegpR8W/W+k7BB1OSVP9c/pmJ9l6gi7
WL+E52opy6Az5RcDnKFJo3Hedv7x+uJ1x/me8rymfE89EvwZ2f6PXSeufzqe
9OtovnVbKO6v932p+ONawQnQA6d6nXJdUL1OM1Ll//C6M4wSWK+NgsCL+G57
lGgf953yXP3AUvhZyePx/uwX9zsh9ivLz6f/PzwEPJDqlRuF1gncyfzwhuAR
mXXA05bzsynpdFEcR96H4jhmXh/7fP544OxDqwXhPUln9ecOmOen0pt72/Uy
JYED1rsv8Bvn+jToR7WoLPK3uX8kf4/7h3BIGTckHNK6i3iZfP8DiJe5C7cr
eoNGz7eB216sG+3tHzP/POTr8Y/H0We9S1yL1juvI/2bp7FKfzJPo5kf6V9h
femZav6dlkp5Q4O+U/Jh3cdL0Z/9fc6pW4QHxnUK836XlQ86J/aoAYq+hLOg
LvKII39R9NCMm3nr/6/3l/Xrab+S+yftV0a33ajLwPePqRcu3jfruPrcMaOx
/29ReaSsH+KO8DmXP6A8O9LbcbeeF/Yk6+3Y5dX5aYQTn5b8MjlPyC/Taqn6
eNk4s3jv1sTfZH/tGuWPEB4i+QaEh2jb1iJfg/HAoQ/C0d+Ig8j8BYqDME+V
z195jvvwqNkv4LrwmtSNLAzeWONaynjpcYfhX5Fegdw3rvohXt6nH3SJOD6V
2o7yo03kDRTNQFw+803w6lsh/0LisYuhE5IdH1fag4AjZesMe9/f3AT/wo6o
F+19T6PjAuhpPD+s1BO02r5Av/mr89askoLzcbWaT2o+TMR5R/aJ7z7Adoj0
l8kO0UvFgH/nNwj5xRF7gMNmfK/kczk/L8f8n5mq4EXaxHdhb/v9HuJtd7tC
b5frBeuvb0YdBKoXrD94DB4O5Wtr1x+Ax091D2VeMNU95HiTlzcu/p6dRXgL
8VprQy/CzjMSOpMUn9WHzRP2f/Z3iX9/7zPxXOvlc+wjhDfm5O0S3vhhQWWf
0fd0wj5G+7nkFdB+7rwTW0AZlziyQwqr9VXdNMIT1qt6TazLx/Vk5XhxPdnI
9dgH3iHe9aOO4eJ7FkYgzyUYutyWP/Rw3PEqzql9ofJ8vHkl4t+Rnew7T+SP
1inbA/zL0d8g3pfPucn7JLe7ybrgnfL+L9+Hn0t2u/xR/E7ef81d+GfMb9n2
Onj7dC7LfZjOZT7vZDudd/bmHQrfwPRfE+B9rjfPy/td+rT8073vL/UnPfHQ
7L/thhWUfcAJKtDI+B/34f6x6/dT6ik7xEf17Qe2Y/l8lPYwnY++/cz3/+fX
TulXTSvn/D81TiIH
"], Polygon3DBox[CompressedData["
1:eJxE3WOUXM/Xt/Hf2OqZ7p7GJJnYtm3b5sS2bduZ2LZt27btPNf+77rX8+Kz
vrs6mebp0wdVdWIbt6/czvO///4LvPvff16kB6QttTd84As/+CNA/i+CEIwQ
hCIM4YiAxWSkqaNghQ12RMNhaqdpu+BGDBIgIRKZOta0EyMJkiIZkiMFUiIV
UiMN0iId0iMDMiITMiOLyaymzobsyIGcyIXcyIO8yGdInR8FUBCFUBhFUBTF
UBwlUBKlUBplUBblUB4VUBGVUBlVUBXVUB01UBO1UBt1UBf1UB8N0BCN0BhN
0BTN0Bwt0BKtEIfWaIO2aIf26ICO6ITO6GJI3RXd0B09TPY0da//dHmQ5aI3
+qAv+qE/BmAgBmEwhmAohmE4RmAkRmE0xmAsxmE8JmAiJmEypmAqpmE6ZmAm
ZmG2qeeY9lzMw3wswEIsQjwWYwmWYhmWYwVWYhVWYw3WYh3WYwM2YhM2Ywu2
Yhu2Ywd2GlLvwm7swV7sw34cwEEcwmEcwVEcw3GcwEnzN/K3p3AaZ3AW53Ae
F3ARl3AZV3AV13AdN3ATt3Abd8BX+r97uI8HeIhHJh+b+gme4hme4wVe4hVe
4w3e4h3e4wM+4hM+4wu+4hu+4wd+4hd+4w/+4h9k5eIBT3h56Pdf1gPe1D7w
hR/8EYBABCHYQ5evEDIUYQhHBCyIRBSssMn9ItqktB1wwgU3YpAACZEIsUiM
JEiKZEiOFEiJVEiNNEiLdEiPDMiITMiMLMiKbMiOHMiJXKbObdp5kBf5kB8F
UBCFUBhFUBTFUBwlUBKlTC1ZGmVQFuVQHhVQEZVQGVVQFdVQHTVQE7VQG3VQ
F/VQHw3QEI3QGE3QFM3QHC3QEq0Qh9Zog7ZoZ+r2pt0BHdEJndEFXdEN3dED
PdELvdEHfdFPPmsMwEAMwmAMwVAMw3CMwEiMwmiMwViMw3hMwERMwmRMwVRM
w3TMwExTzzLt2ZiDuZiH+ViAhViEeCzGEizFMizHCqzEKqzGGqzFOvO615vX
Lu/DBnPbRmzCZmzBVmzDduzATuzCbuzBXuzDflMfMO2DOITDOIKjOIbjOIGT
OIXTOIOzOIfzuICLuITLuIKruIbruIGbuIXbuIO7uIf75nN+YOp2pv0Qj/AY
T/AUz/AcL/ASr/DavLdvPHQZkGXhLd7hPT7gIz7hs4duByT6T+vY/7T9hfor
vuE7fuAnfuE3/pj6r2n/g2zceMATXvCGD3zh56mfmz8ZgEAEIRghCEWYp342
8hmFe+p7EUFaEIkoWGGDHdFwwAkX3IhBAiREIsQiMZIgKZIhOVIgJVIhNdIg
LdIhPTIgIzIhM7IgK7IhO3IgJ3IhN/IgL/IhPwqgIAqhsKf+DhTx1N+ComQx
FEcJk9IuiVIojTIoi3IojwqoiEqojCqo6qm/Y9XI6qjhqd8DqWuadi3URh1P
XS5l/VKXuh7qowEaohEaowmaohmae+p3Sb5HLahbohXi0Bpt0BaykdseHdAR
neR5oAu6ohu6owd6ohd6ow/6oh/6YwAGmscdhMGmHmLaQzEMwzECIzEKozEG
YzEO4zHB1ANNe5x5DGlPNLfJa5tETsYUTMU0TMcMzMQszMYczMU8zMcCLMQi
xGMxlmAplmE5VmClSWmvwmqswVqsw3pskOeCTdiMLdiKbdiOHZ66bt9J7sJu
7MFe7PPU34795AEcxCEcxhEcxTEcxwmcxCmcxhmcxTlZNnABF3EJl3EFV3EN
13EDN3ELt3EHd3EP9/EAD/EIj/EET/EMz/ECL039yrRf4w3emvqdacty+x4f
PHVd89asuz7S/oTP+IKv+Ibv+IGf+IXf8nf4i3/4306Xl9YepCe84A0f+MIP
/ghAIIIQjBCEIgzhiIAFkYiCFTbYvXQ9IeuLaGoHnHDB7aXf0xgyARIiEWKR
GEmQFMkMqZMjBVIiFVIjDdIiHdIjAzIiEzLL4yMrsiE7ciAnciE38iAv8iE/
CpiUdkEUQmEUQVEUQ3GUQEmUQmmUQVmUQ3lU8NLPuiJZCZVRBVXldaM6aqAm
aqE26qAu6qE+GqAhGqExmqApmpm6uWm3QEu0QpyX/pa3JtugLdqhPTqgo6kl
O6Gzl64HupBd0Q3d0QM90ctL9016k33QF/3kbzAAAzEIgzEEQzEMwzECIzEK
o00tOQZjMQ7jMQETMcnUk017ipfum8l+2VTqaZiOGZiJWZiNOZiLeZiPBaZe
aNqLEI/FWIKlWIblWIGVWIXVWIO1WIf12CCvH5uwGVuwFduwHTuwU95z7MYe
7MU+7McBHMQhHMYRHMUxHMcJnMQpnDaPvd7UZ0z7LM7hPC7gIi7hMq7gKq7h
Om7gJm7hNu7gLu7hPh7gIR7hMZ7gKZ7hOV7gJV7hNd7gLd7hPT7go0lpf8Jn
L/3t/0J+xTd8xw/8xC/8xh/8xT+v//63Y+8BT3gZUnvDB77wgz8CEIggBCME
oQhDOCJgQaSpo0zbChvsiIYDTpMuU7sRgwRIiESIRWIkQVIkQ3KkQEqkQmqk
QVqkQ3pkQEZTS2ZCZmTx1uNIWclsyI4cyIlcps5t2nmQF/mQHwVQEIVQGEVQ
FMVQHCVQEqVQGmVQ1tTlTLs8KqAiKnnrNl1lsgqqohqqowZqohZqow7qoh7q
o4G3/tbK72xD6kZojCZoimZojhZoiVbm7+PQGm3QFu3QHh1M3dG0O6EzuqAr
uqE7eqAnepm6t2n3QV/0Q38MwEAMwmAMwVAMw3CMwEiMMvVo0x6DsRiH8Sal
PQETMQmTMQVTDamnYTpmYCZmeet3S75js6nnYC7mYT4WYCEWId5bt7EXe+t2
9hJyKZZhOVZgpUn5fZZ6FVZjjanXmra8F+vM+7PeWz/bDdiITdiMLdiKbdiO
HdiJXfKZYg/2Yh/244BJaR/EIRzGERzFMRzHCZzEKZzGGZzFOZzHBVzEJVzG
FVzFNVzHDdzELdzGHdzFPdzHA3lP8QiP8QRP8QzP8QIv8Qqv8cbbrLPId3jv
rbXkB3zEJ3zGF3zFN3w3Ke0f+Ilf+I0/+It/kIOSHj5ae/po2wve8IEv/OBv
MsDUgQhCMEIQijCEIwIWRCIKVthgRzQcPvo5O0kX3IhBAiREIlPHmnZiJEFS
JENypDCZ0tSpkBppfHSdkpZMh/TIgIzIZFLamc3/y0JmRTZkN3UO086JXMiN
PMiLfMiPAiiIQigs94Wi5rUUM3WMaRdHCZT00c9QPr9S1KV9NKVdhiyLciiP
CqiISqiMKqiKaqiOGqiJWqiNOqiLeqiPBmiIRmjso9sPTXx0G6Ip2QzN0QIt
0QpxaI02aIt2aI8O6IhOpu5s2nI8oIuPHhPoSnZDd/RAT/RCb/RBX/RDfwzw
0e2BgT66TSDvySAfXaYHk0MwFMMwHCMwEqMwGmMwFuMwHhN8dJ9zIjkJkzEF
UzEN001KewZmYhZmYw7mmnqeac/HAnmvsAjxWGzqJaa9FMuwHCuwEquwGmuw
FuuwHhuwEZuwGVuwFduwHTuwE7uwG3uwF/uwHwdwEIdwGEdwFMdwHCdwEqfk
fZX31Ef3o86S53AeF0x90bQv4bKPrjOukFdxzUfXP9fJG7iJW7iNO7iLe7iP
B3joo7/3j8jHeIKneOaj2wyZzLrsudwvXvrocviKfG1qSVku3+At3slygA/y
GvAJn+V54iu++ei+5XfyB37iF37jD/7iH+TEmwc84QVv+MAXfvBHAAIRhGCE
IBRhCEcELIhEFKywwY5oOOCEC27EIAESIhFikRhJkBTJkBwpkBKpkBppkBbp
kB4ZkBGZkBlZkBXZkB05kBO5kBt5kBf5kB8FUNBX96NkH0pebyHzmgujCIqi
GIqjBEqiFEqjDMqinK8ed5DjD+WpK6AiKqEyqqCqqauZdnXUQE3UQm3UQV3U
Q300QEM0MnVj026Cpmjmq9v78nk099Vt+xZkS7Qyry/OV7fDW5Nt0NZX12Wy
HmtH3R4d0NFXt7k6kZ3RBV3RTW5HD/REL/RGH/RFP/THAAzEIF89PjWYHCI1
hmE4RmCkr67TRvnqeu202e+R9miMwViMw3hMwERMwmRMwVRMw3TMwEzM8tXl
a7ZJp6llv2sOORfzMB8LsBCLEO+ry9RiLMFSLPPV82HLyRVYiVVYjTVYi3VY
jw3YiE3YjC3Yim3Yjh2+ur2w01e3GXaRu7EHe7FPlh0cwEEcwmF53jiKYziO
EziJU/L+4QzO4pw8V1zARVwyr01el6y7bpptpMu0r+AqruE6buCmLEO4bWrJ
O7iLe7iPB3iIR3iMJ3iKZ766Hyr7o8+pX+AlXuE13uAt3uE9PuAjPuEzvuAr
vuE7fuAnfuE3/vjq9/gv/pnnJp0EJD38tPaEF7zh46fPz9fUT8zz9aP2RwAC
EYRghPjp8hNKhiEcEbD46TGzSDIKVthgRzQccMIFN2KQAAlNnci0Y5EYSZAU
yZAcKZASqZAaaZAW6fx0WU5PZkBGZEJmZEFWZEN25EBO5EJu5EFe5EN+FEBB
FEJhFEFRFENxlEBJlEJplEFZlEN5VEBFVEJlVEFVVEN11EBN1EJt1EFd1EN9
NEBDNEJjNEFTNDMp7eZogZZohTi0Rhu0RTtTtzftDuiITuiMLuiKbuiOHuiJ
XuiNPuiLfqbub9oDMBCDMBhDzGc/FMMwHCMwEqMwGmMwFuMwHhMwEZMwGVMw
FdMwHTPks8QszMYczMU8zMcCLMQixGMxlmAplmE5VmAlVvnp8rYaa/z0+7uW
XIf12ICN2ITN2IKt2Ibt2IGd2IXdfrpvJvtle/z0XNlePyX1Pj89vyjHQvZT
H8BBHMJhHMFRHMNxnMBJ83incBpncBbncF4eDxdxCZdxBVf99DfwGnkdN0ze
NLXsh97y033R2+Qd3MU93McDPMQjPMYTPMUzPMcLeT145aff4dd4g7d4h/f4
gI9+2ndI+g19ov6ML/jqp8dn5fshx2u/kd/xw0+PccnxrZ/Uv/Abf/x0XS7b
vPvNev2vn7b/kdKxyQOe8II3fOALP5P+pg5AIIIQjBCEIgzhiIAFkYiCFTbY
EQ0HnP663SvbvC5qN2KQAAmRCLFIjCT++puTlEyG5EiBlEjlr8cwUpl2aqRB
WqRDemRARmTy1+2ozGQWZEU2ZPfX3/8cZE7kQm6T0s6DvMiH/CiAgiiEwiiC
ov76O1qMLI4SKIlSKI0yKItyKG+ygqkrohIq++s5FTm3UoW6KqqhOmqgJmqh
tr+ew5Pzd3Wo66KeyfqmboCGaITGaIKmaIbmaIGW8n4gDq3RBm3RDu3lMUzd
0bQ7oTO6mLqraXdDd3/9vepB9kQv9EYf9EU/9McADMQgDMYQDMUw+QwwAiMx
CqMxBmMxDuMxARMxCZMxBVMxDdMxAzMxC7MxB3MxD/OxAAtNLb970l6EeCzG
En89dibHzZZSL8NyrMBKrMJqrMFarDMpbdnmWU9uwEZswmZzv1uwFduw3V+/
EzuwE7uwG3uwF/uwHwdwEIdw2NRHTPsojuE4TuAkTuG0vx4TOUOexTmcxwV/
3U+R/ZWL1JdwGVdwFddwHTdwE7dwG3dwF/dwHw/wEI/wGE/wFM/wHC/wEq/w
Gm/wFu/w3ryHHwypP+ITPuOLv67T7pvfr6+0v+G7v+77/TPbV3IO9we3/cQv
8/5uNa/3N/7gL/5BOmt6wBNe8DYpbVm2ZBmT3wcf2r7wgz8CEIggBCPE1KGm
Ldt1YWQ4ImBBJKJghc3UknZEwwEnXHAjBgmQEIkQi8RIgqRIhuRIEaDHilKS
qZAaaZAW6ZDekDoDMgbo9ytTgB7bzUxmQVZkQ3bkQE7kQm7kQV7kQ34UQEEU
QmEUMbcVRTEURwlTlzTtUiiNMibLmrocyqMCKqISKqMKqqKavD7UQM0APadZ
i6yNOqiLeqiPBmiIRmiMJmiKZmiOFmiJVgF6ri+ObI02aIt2aI8O5nPuiE4B
ur/WmeyCruiG7uiBnuiF3uiDvuiH/hiAgfJ+YzCGBOh24NAA3RaUfqHDArTv
3nByBEZiFEZjTID+tshvzFjqcRiPCZhoUtqTMBlTMFWeL6ZjRoD2251JzsJs
zAnQ40tzA/QY0zxyviwLWIhFiA/Q/n9y/EP6A0otxyGkvZh/W4KlWBag2wLL
yRUB2vdkJbkKq7EGa7EO67EBG7EJm7EFW7EN27EDO7ELuwP0GNMeci/2YT8O
BOj5fjnvf5D6kLweeS04imM4jhM4GaD7nKfI0ziDsziH87iAi7iEy7iCq7iG
67iBm7iF27iDu7iH+3iAh6Z+ZNqP8QRP5fnjOV7gJV7htanfmLacw31LvsN7
fMBHfDKf92d8wVd8w3f8wE/8wm/8wV/8g3Q+94AnvOANH/jCD/4IQKBJaQch
GCEIRRjCEQELIhEFK2ywIxoOOOGCGzGBul8n+3QJqBMiUaD2d44lEyMJkiIZ
kiMFUiIVUiMN0iId0iNDoJ7/kPO3GakzITOyICuyITtyyGMjF3IjD/IiH/Kj
AAqiEAqjSKD+LhYli6E4SqAkSqE0yqAsyqE8KqAiKqEyqqAqqqE6aqBmoK6D
a5G1UQd1Uc/U9U27ARqiUaD2QW4cqP2Qm5BN0QzNA3VfVvZpW1C3RCvEoTXa
oC3aoT06oCM6oTO6oCu6Beq6rrupZZ0n7R7UPdELvQN1HdyH7It+6G9ygKkH
ymeJwRiCoRiG4RiBkRiF0RiDsYG6PTGOHI8JmIhJmIwppp5q2tMwHTMw06S0
z5jlfhb1bMzB3EA9ryrnD+dRz8cCLDS5yNTxWIwlWIplWI4VWIlVWI01WBuo
20/rAnWbaj25ARuxCZuxBVuxDduxAzsDtR/pLnI39mAv9gXqNsV+8gAOyv3L
feMIjuIYjuNEoB4LkOMAJ6lP4bS8dpzFuUDt23w+UPs6XwjU80Nybugi9SVc
DtRjcHIsTrYbr9C+imu4jhu4aepbpi3rwNuBuh6U8wd3qO8G6jbtR7Mddo/2
fTwI1N/uh4Gmj3WA5iPaj/EET/EMzwP1GMML8iVe4TXe4C3e4T0+4CM+4TO+
4Cu+Bepy8x0/8BO/8Bt/8Bf/AvU4gwy28YAnvOANnyD9TOWzlVrSN0h/C/xI
fwQgEEEIRghCEYZwRMCCyCA9lhgVpMuPlbTBjmg44IQLbsQgARIiEWKRGEmC
9L2ROqlpJ0NypEBKpEJqU6cx7bRIh/TIEKTfs4ymzmTa8v8zm7+R7ZksQbpN
k5XMhuzIgZzIhdzIg7zIh/wogIIohMIogqIohuIogZIohdIog7Ioh/KogIqo
FKR9jCqTVVAV1VAdNVATtcx7VRt1TJ3AtOuiHuqjARqiERqjifmcm6IZmqMF
WqIV4tBa3gN5/WiH9uiAjuhk3lt5jzujC7qiG7qjB3qa7GVqObYkx5t6U/dB
X/RDfwzAQAzCYAzBUAzDcIyQzwejgvQY5mhyDMZiXJAeCx5PTsDEIO2LOomc
jCmYimmYjhmYiVmYjTmYi3mYjwVYKPcRpOe24snFWIKlWIblWIGVQbpsrsJq
rMFarMN6bMBGbMJmbMFWbMN2+XyxE7uwG3uwF/uwHwdwEIdwGEdwFMdwHCdw
MkjPCcu54VPUp3EGZ019zrT/7/zueeoLuIhLJi+b+gqu4hquB+l+kmwb3aC+
iVu4jTu4i3u4jwd4iEd4jCdBOsZOxto9pX6G50FavzDtl3iF13iDt3iH9/iA
j/iEz/iCr/iG7/iBn0G6DvmF3/iDv/gHGTToAU94wRs+8A3W9bof6Y8ABCII
wQhBKMIQjghYEIkoWGGDHdFwwAkX3IhBAiREInO7vD7p6xFLnRhJkBTJkDxY
92FTBOs+bUoyVbCeO0lNpkFapEN6ZAjWzz1jsH72UmcK1nZmZEFWZEN25EBO
5ELuYO2PnIfMi3zIjwLBuuwXJAuhMIqgKIqhOEqgJEqhNMqgLMqhPCqgIiqh
MqoYUldFNVRHDdRELdRGHdRFPdRHAzREIzRGEzRFMzRHC7REK1PHmXZrtEFb
tEN7dEBHdEJndEFXdEN39EBP9EJv9AnWvuR9yX7ojwEYiEEYjCEYimEYjhEY
iVEYjTEYi3EYjwmYiEmYjCmYimmYjhmYiVmYjTmYK58H5mOBuU3+bSEWIR6L
sQRLscx8/jONjOa+l2NFsPY3XhmsxyFXkauDdRtM9sul77D0WV/DbWuxDutN
vcG0N2KT/E2wHkvYEqxj2baS27AdO7ATu7Bb3kfsxT7sD9YxYQfIgzgUrPVh
0z6CoziG4ziBkzgVrNuOp8kzOItzpj5v2hdwEZdwGVdwFddwHTdwE7dwG3dw
F/dwHw/wEI/wGE/wFM/wHC/wEq/wGm/wNlj3U+U3U/bj3tF+jw8mP5r6Ez7j
C77iG77jB37iF37jD/7iX/B//xvoLH3rPUhPeMEbPvCFH/wRgEAEIRghCJW/
DdExRuEhOs4ogrSE6DL30IyXkrFCkdwWBStsIdov2k5GwwEnXHAjBgmQEIkQ
i8RIgqRIFqK/XcnJFEiJVEiNNEiLdEiPDMiITMgcou91FjIrsiE7coRo/zTp
p5aTOhdyIw/yIh/yowAKohAKowiKhmi/FOkPUYy6OEqgJEqhNMqgLMqhPCqg
IiqhMqqgKqqhOmqE6DjMmmQt1EadEN13rBui+4/1yPpogIZohMZogqZohuZo
gZZohTi5D/l7tA3RdUI7sj06oKNJaXdCZ3RBV3RDd/RAT/QK0b4SMqZU+kv0
pt0HfdEP/TEAA0N0bPQgcjCGYCiGYThGyL9jFEZjDMZiXIhuv44P0e3ZCeRE
TArRdebkEO0bPIWcKq8F0zEDMzHLpLRnYw7mYl6IjluZTy7AQixCPBZjCZZi
GZZjBVZiFVZjDdZiHdZjAzZiEzZjC7ZiW4iu02Tdtp16B3ZiF3bLa5Dnj30h
el5Ctkv2Ux/AQRzCYRzBURzDcZzASZzCaZzBWZzDeVzARVzCZVzBVVwL0WOZ
18kbuIlbuI07uIt7uI8HeIhHeIwnIXpO4Sn5LETHQj8nX+AlXuE13uAt3uE9
PuAjPuEzvoRo37Sv5Dd8l/vCT/zCb/zBX/yDTMDgAU94wRs+8IUf/BEQquv0
wFBdz882v20yz0AQtwUjBKEIQzgiYEEkomCFDXZEwwEnXHAjBgmQEIkQi8RI
gqRIhuRIgZRIFarf4dRkGqRFOqRHBmREJmRGFmRFNmQ3mcPUOZELuUN1LoQ8
ZF7kQ34UQEHzfAuZ2m7ahVEERVEMxVECJVEKpUN1n6pM6P/f5xlm2mVRDuVN
XcG0K6ISKqMKqqIaqsvrRU3UQm3UQV3UQ300QEM0QmM0kddkSN0MzdECLdEK
cWiNNmiLdqZub9odQrWvXUd5LeiMLuiKbuiOHuiJXqG6HyX7U9IfsDftPuiL
fuiPARiIQRiMIRgq7w+GYwRGYhRGYwzGYhzGm3qCaU/EJEzGFEzFNPNv8n+m
Y0aojmueSc7C7FBdB0rOMfXcUJ2fYB45HwuwEIsQH6rL6GIswVJ5jViOFViJ
VViNNViLdViPDdgYquOzN5GbsUXa2Ibt2IGdodonR/rj7ArVZWx3qPYXLGhS
+g/uod6LfdiPAziIQziMI/JacSxUt1Ukj5v6BHkSp0yeNvUZnMU5nMcFXMQl
XMYVXMU1XMcN3MQt3MYd3MU93McDPMQjPMYTPMUzPMcLvMQrvA7V/epXJmU/
+w31W7yTz0SeOz6Gaj+XT+RnfDGv9av5PL/hu6l/mPZP/MJv/MHfUD2/LSnn
uKX+Ry2Tz3jA06S0vcL0Pf1iHDKP583tPvCFH/wRYOpA0w4K03VjMBmCUIQh
HBGwIBJR5nGssMGOaDjghAtuxCABEiIRYpEYScJ0WZLlSLbfktJOFqbbpMnD
dIxLCjIlUoXpOenUZBqkRTqkRwZkRCZkRhZkRTZkD9P9lRxkTuRCbuRBXuRD
fhRAQRRCYRRBURRDcZQI07HpMka9JHUplEYZlEU581hzzf5ReeoKqIhKqIwq
qIpqqI4aqIlaYfo7U5usg7qoh/pogIZohMZogqZohuZogZZhOi5UxoS2CtP+
w3Fka7RBW7RDe3RAR3RCZ3RBV3RDd/RAT/Qyfy/7kr3JPuiLfuiPARiIQRiM
IWa5GIph8ncYgZEYhdEYg7EYh/GYgInyOWMypmAqpmE6ZmAmZmF2mJ47lnPI
c+R9xjz5bLEAC7EI8ViMJViKZWHaj1n6My+nXoGVWIXVWIO1YdrvaF2Y9j2S
40lyXGk97Q3YiE2m3mzaW7AV27AdO7AzTM+L7CJ3Yw/2Yh/24wAOmvqQaR/G
ERzFMRzHCZzEKZzGGZzFOZzHBVzEJVzGFVzFNVzHDdzELdzGHdzFPdzHgzCd
J+Eh+QiP8SRMf4efks/w3HyWL8J0O+El+SpMj7u+Jt/gLd7hPT6E6XmKj+Qn
fMYXfMU3fMcP/MQv/MafMN3G+GvyX5jWMpGWBzzD9bdDfjdke8WLtjd8wrX2
NW0/+CPA1IGmHYRghCAUYQg3GWFqCyIRBWu4/k7ZTC393KVtp46GA0644EYM
EiAhEoXrcZVYMjGSICmSITlSICVSIbWp05h2WqRDemRARmRCZmRBVmRDduRA
TuRCbuRBXuRDfhSQ9wyFUBhFUBTFUBwlUBKlUBplUBblUB4VUBGVUBlVUBXV
UB01wvX3pbrJmuF6nk3Ot9Wiro06qCvvpbyHaICGaITGaIKmaIbmaIGWaIU4
tEYbtEW7cJ3XpT3ZAR3RCZ1N3cW0u6IbuofrNl4P8570RC/0Rh/0Rb9wPc/b
nxyAgeF6XEqOVw6iHowh4XoOfCg5DMMxAiMxCqMxJlzXX7IeG0s9LlzXU7KO
Gk89Qf49XOtJpj0ZUzA1XJct2UaaJo+PGZiJWXI/mIO5mIf5WICFWIR4LMYS
LDUpbenjv4xcHq79L6TP1gr5jLAKq7EGa8P1Oa/DemwwtawLpb3X7DvLuTYZ
r7kxXMdsyv7JpnDdD9wsj4Gt2Ibt2IGd2BWux8d2k3vk/rAP+3EAB3EIh+Xz
xVEcw3GcwEmckvvAGZzFOZwP1+P5F8L1mP5F8lK4jh+5HK7juWRc1xXqq+E6
1u4aeR03cDNc53m5Rd7GHXktuIf7eBCu+/cPw3Uf/xH5GE/k7/AMz/ECL/EK
r/EGb/EO7/EBH/EJn/EFX/EN3/EjXM8H/SR/4Tf+4C/+QSYQ9IBnhB7vk+N+
XtTe8IEv/OCPAAQiCMEIidDfpFAyDOGIgAWRiIIVNtgRDQeccMGNGCRAQiRC
LBIjCZIiGZIjBVIilbn/1OYxpJY++NJOg7RIh/TIgIzIhMzIgqzIFqF9hKXO
bto5kBO5IvQ8RG4yD/IiH/JH6LGyAhH6e12QLITCKIKiKGZIXRwlUBKlUBpl
UBblInSuxPJkBVREJVRGFVRFNVRHDXl9EXoOVs7FyvicWhE6Xqc2WQd1UQ/1
I3T+jgYR2n+3IdkIjdEETdEMzSN0fJaMzWpB3TJC51uReVdknHGrCB1rHEe2
Rht5/AjdJ5H9kXbU7dEhQudxkPkcOlJ3QucInb+mS4T+9nSN0LqbaXcne6An
eqE3+qAv+qE/BmAgBmEwhkToMj2UHIbhGIGRGIXRGIOxGIfxmICJmITJmIKp
mIbpmIGZEXpeWo7nzaKeHaHHqOaQczEP87EAC7EI8ViMJViKZViOFViJVaaW
XI01WIt1EfodWR+h3xOpN5j2RmzC5gjtayt9bmVs6xbaW7EN2yN0jPkOcmeE
zoEnc+Htot6NPRFa7zXtfdiPAziIQziMIziKY/JYOIGTOCX3jzMmz5r6HM7j
QoR+ly/ikrxPuIKruIbrETru/wZ5E7dwG3dwF/dwHw/wMEK3Px6Rj/EET/HM
pLSf4wVe4hVe442p35r2uwidN+k9+QEf8Qmf8UWWmQg9RyLnSr5Rf8cP/MQv
/MafCN2+ke2cv9T/IJOpesDTon3KvEhv+MAXfhYzbybLvT91gEX7EwSSQQhG
iEW3u2S5D6UOQ7hFP+8Ii34fpZaU76eF2yIRBStssJs62rQdcMIFN2KQwNQJ
kcii+yuy3xJrUVIntui2tWxjy3G5JLSTIplFl1VZTpNTp5DXi1RILc8faZEO
6ZEBGZEJmZHFouvyrGQ2ix5vlvO7Mq9pdto5kBO5kBt5kBf5kB8FUNCi40EK
WXRcnmxbF6YuYkhd1DyW7DvI4xWjLo4SFl2/yXtYkrqURVPapckyKItyKI8K
qGjR4+mVyMqogqqohuoW/f2uQdZELYtuh9Um66Au6qE+GqChPL5F+4M0lsdF
U4v+Hsqxu2bUzdECLdEKcWiNNmiLdial3d6i84h1sGjfWBlj1JG6EzqjC7qi
m0XHmnUne6AneqE3+qAv+qE/BmAgBmEwhmCoqYeZ9nCMkNeKURiNMRY9HzCW
HGfRfjrjLdpXZwI5EZMwGVMwFdMwHTMwE7Mw26L/X/7vHIv22Z1LzsN8LJDX
jEWIx2KTS0y9FMuw3KLjjVZYdMzRSotuq62yaB8POQ+y2tRrzXmRNbTXYp3J
9abegI3yXLAZW7AV27AdO0wtudOixxJludpl6n2mvVva8j6Z3Gfq/Thg0fnx
Dpr7lHMZh8jDOIKjOIbjOIGTOCXPH2fktVl0LP058jwu4CIu4TKu4Cqu4Tpu
4CZuyd+ZvGPqu/L4uI8HeIhHeIwneIpneI4XeIlXeI03eIt3eG/Ruf1kjr8P
1B/xCZ/xBV/xDd/xQz4ni64zfll0v1v2w39T/8Ff/INMXu0BT3jBGz7wNSlt
v0g9Byfn4q6ZYxD+3BaAQARF6vjrYDIEoZHaFyGMDEcELIg0Ke0oWGGDHdFw
wAkX3IhBAiSM1PVyIjIWiZEkUvtEJyWTITlSmJR2SqRCaqRBWqQzdXrTln5Y
GciMyITMyIKsyIbsyBGp8yvmjNTvYgveslyReg4nN5kHeZEP+VEgUsemFSQL
oTCKoCiKoThKoCRKoTTKoKzJcqYujwqoiEqojCqoimqojhqoiVqReo5czpXX
jtR5T2ScZJ1I/R2pG6m/JTKWuR51fTRAQzRCYzRBUzRDc7SI1GOuLSP1uOt5
XnerSB2bLnVcpLZbo02kHgdtS7ZDe3RAR3RCZ3RBV3RDd/RAz0jdVpDtBKl7
mXZvsg/6op8sWxhgSD0wUuczl77eg6gHY0ik7i8PJYdhOEZgJEZhNMbIZ4hx
kbruHk9OwERMitRz1XLO+vh/Op/KZG6bEqnjh6ZG6hiiaeR0WXYitZ5p2rMw
G3MwN1K3k2V7eR71fCzAwkg9JrjI1LXMMUL53WxitkviuX0xlphlcqlZLuX7
nNm0l2E5VmAlVmE11phcZZYZWV5ku2ItuQ7rsQEbsQmbsQVbsS1Sj2vIMY3t
1DuwE7uwG3uwN9Ic54zUY577THs/eQAHI7U+ZNqHcQRHcQzHccLUkidxCqfN
e3YGZ3EO53EBF3EJl3EFVyN1/hWZz+4a9XXcwE3cwm3cidR+dXfJe7iPB6Z+
aNqP8BhP8BTP8Bwv8BKvTP3atN/gLd7hPT7gIz7hM77gK77hu3xe+Ilf+I0/
+It/kMG+HlG6rMsyL79dUkvKdrMn/+YFb/jAF37wRwACEYRghCAUYQhHBCyI
RJRJaVthgx3RUdov2EE64YI7SvtXxZAJkBCJEIvEJqWdBEmjdPlJRiZHCqQ0
Ke1USI00SIt0SI8MyIhMyIwsUTp3l4y9yEqdDdmRAzmRC7mRJ0rXf7IvLst0
Xtr5kB8FUBCF5DVF6TlhOeYufV6K0C6KYiiOElH6nOV5lkQplEYZlI3SOVRl
3u9y1OVRARVRSR4fVVAV1aJ03JOMeapOXQM1UQu1USdKx7bXJeuhPhqgIRqh
MZqgKZqhOVqgJVohDq3RBm2jdI71dmR7dEBHdEJndEFXdEP3KN03lzl4/5j9
qx7c1jNK+4b3InujD/qiH/pjAAZiEAZjCIZimNwfRmAkRmF0lI53l3NXMt5v
DO2xGIfxmICJUbotK9u0k6gnY0qUzh8ylZyG6ZiBmZiF2ZiDuZiH+ViAhViE
eCzGEizFMizHCqzEKqyO0nFrcsxHxrGtob0W67AeG7AxSufT2hSlc2ptJrdg
K7ZhO3ZE6fpIPo+d5nOJM/Uu7MYe7MU+7Df1AdOW/p4HyUM4jCM4imM4Lu9D
lM4xcJI8hdM4g7M4h/O4gIuyHOEyruAqrpn6umnfkPvCLdyO0v3rO1E6pk7G
1t2lvof7eICH8vnhMZ5E6fHYp+QzPMeLKB1b+ZJ8hdd4g7d4h/f4gI/4hM/m
vfuCr1E6Luob+V2eC37iF37jD/7iH+RCKR7whBe84QNf+Fm1b7L0T/SnDkAg
gqz6/Q226nomhAxFGMIRYdXnbSEjEQUrbLAjGg444bJqv2Y3GWPVdXcCMiES
IRaJkQRJ5XGt+p1KTqZASqRCaqSR+0I6pEcGU2c07UzIjCzIatXxkdnI7Fb9
HuQgcyIXciMP8iKfqfObdgEURCEURhEURTEURwmUtOo8K6XI0iiDsiiH8qiA
iqiEyqhi1b4v0u+lKnU1VEcN1EQtqx7brm3V49ufTV0HdVEP9dEADdEIjdEE
TU3dzLSbowVaWnWseSsyDq3Rxqr9nmV8R1vqdmiPDuiITladd7Yz2QVd0Q3d
0QM90UteC/rIfaEf+mMABmIQBmMIhlp1zjAZXyFjK6QPnPSFG8btwzECIzEK
ozEGYzEO4zEBEzEJkzEFU626Hp0mnytmYCZmYTbmYC7mYb5V54ddQC7EIsRj
MZZgKZZhOVZgJVZhtVluZJlZg7VYh/VWnfN+A7kRm6x6HR3ZBpXfhM1Wve7K
Fqtee0WOv22l3obt2IGd2IXd8n+xF/uwHwdw0Kr9Fg+Rh3HEqrXkURzDcZzA
SXkcnMYZnMU5q86xL/Prn7cqqS+QF+XzxWXzeco6Xz7TK7iKa1adt/e6VfvY
3LDqsUEZdyq/xTeteh5MxjPcor5t1bGld8i7srzhPh7gIR7hMZ6Y5eGpycGm
fobneIGXeIXXeIO3eIf35n4/mHxg6o/4hM/4gq/4hu/4gZ/4hd/4g7/4Z9UJ
YDzgCS94wwe+8IO/Ted9CiADEWTT45LBNj1WGUKGIsymY7/DyQhYEIkoWOVv
bLo9ayej5T7hhMum36d485vrph2DBEiIRIhFYiRBUiRDcqRASqRCaqRBWpPS
TmfTed7Skxlset89zGcttTxeRjITMiMLsiIbsiMHciIXciMP8tr0fFw+Mj8K
oCAKoTCKmJRxblIXtelc5jKneTHq4iiBkvJ/UBplUBblTF3etCugok3H2FYi
K9t0vq7K/7evRbsqqqE6aqAmaqE26qAu6qE+GqAhGslzQhM0RTObblc1t+k4
Xtk3aUHdEq0Qh9ZoY9NjUG3JdvLeogM6ohM6owu6opt8rvJ+o6e8BvRGH5uO
H+pL9rPpdWjknGl/6gHSxiAMxhAMxTAMxwibzi0sc0+MtOn2/CkzB+8o2qMx
BmMxDuMxARMxCZMxBVMxDdMxAzNtup0t29iyTSu/e91Nyvk6qeW88Sz+32zM
wVx5Lja9htJ8cgEWyjKFeCzGEizFMizHCpv+tq606e/rKnI11mAt1tl0rpD1
5AabLqPx5juxwbyu8ea9HWtS3uuN2ITN2GLTPsiyDt1KvQ3bsQM7sQu7sQd7
sc+mc5vtt+k5QjlXeID6oNwPDuMIjuKYTY8lyTGl4zZdz0nf8xM2vZbVSfKU
qSVf/afbH6epz+AszuG8WWYu4CIu2XRb/7IsX7iKa7hu07490sfnBvVN3DKk
vi3PAXdxD/fxAA9teo05ubbcI+rHeIKnNj1OJnM5PTP3L/f9nHxh07kWZc5F
Odb1Up6/Tef+f23T+f/fkG/xDu/xwabHRD6Sn/AZX/BV7tc85nfzuD/wE7/w
G3/w16bfd/ney3d2s1nu/pl6uFn2pA+PXNDLA57wgrdd51QuL9MrUvvCD/4I
QCCCEGxS2iHyNwhDOCJgQSSiYIXNrn0t7WQ0HHDCZdd51eSYlJs6BgmQEIkQ
i8RIYtfrxiUlkyE5UpiUdkqksuv1rVKTaZAW6ZAeGZDRrmNqM5GZkQVZkQ3Z
kQM5kQu5kcdkXuRDfhRAQRRCYRRBURRDcZPSLmHXfiMlyVIojTIoi3J2nTOi
PFkBFVEJlVHFrmMPpP9sVepqqI4aqIlaqI06qIt6JuubugEaohEaowmamrqZ
acu2sfyf5miBlmhl1zmw4uQ9RBu0tes2tlwTrB11e3RAR3Sy6zjIzmQXdLXr
PNzdyO7ogZ5yn+iNPuiLfuiPARiIQRiMIRiKYRiOERhp13GIo8jRGIOxGIfx
mICJmITJmIKpmIbpmIGZmGXX+Upl3tLZ1HOkbdfr+M2z67UK55MLsBCLEI/F
WGLX6wgutes44WXkcqzASqyy67bHartuf5w280LI/BBruG0t1mG9Xeca20Bu
xCZstut4Mbnmh1zvYwvtrXadU0/Gnmyz6/iT7eQO7MQuu15HbTe5x6791aSv
2l7qfbLM4QAO4hAO4wiOyvPHcXndOIlTOI0zOItzOI8Ldj2uepG8hMu4gqt2
Hdci56z+d+5F+m9y23W79t+4Qd7ELdzGHdzFPdzHAzzEIzw27/MT815LP8Sn
du2L+Ix8jhd4Ke8BXuONvDd4h/d27dv6wdQfTfsT+Rlf8BXf5DnjB37iF37b
dZzlH7uOXz5gxjD/tWs/QulDKP3X/tm1D5tc7NQDnvCCN3zgG63X3vAj/REQ
rdu3UgeadhCCEYJQhCE8WsfUyznaCGpLtI6RjiSjYIUNdkTDASdccCPGtBNE
6/ZBQjIRYpEYSZAUyZAcKZASqZAaaZA2Wq/hKtdyTUeRHhmQEZmidb5Wmbc1
M3UWZEU2ZEeOaB07kZPMhdzIg7zIh/wogIIohMIogqIohuIogZIohdIog7Io
h/KogIqohMqogqqohuqogZrRun6vFa3bDbXJOqiLeqiPBmiIRmgcrd91+c43
oW6KZmiOFmiJVohDa7RBW7RDe3RAR3RCZ3RBV3RDd/RAT/RCb/RBX/RDfwyI
1j6EA8lBGIwhGIphGI4Rph5p2qMwGmMwFuMwHhMwEZMwGVMwNVrPI8r5RJlf
aRrt6ZgRrfVM056F2ZiDuZiH+ViAhdF67m4RGY/FWIKlWIblWIGVWIXVWIO1
WIf1ppZ5J6S9ARuxCZuxBVuxDduxAzujte+jXGdgF/Vu7InWeq9p78N+HJD3
EIdwGEdwFMdkGcAJnMQpnMYZnMU5nMcFXMQlXJbHxdVo7Wt2LVqvw3advIGb
uIXbuIO7uIf75vXL+/AgWueRfRitc8nK8i3zu8ncbo+oH0fr9ovUZUz7CZ7i
GZ7jBV7iFV7jDd7iHd5H6/V4P0TrNXnlfKNcV7OH2VeT/jbSb/wj//4Jn/EF
X/EN36N1HP8P8id+4Tf+4C/+ResFXT3gCS94w8eh203yHfOl9oM/Ahx63cBA
h147MMihc0XJdWuDqUMQ6tC+OtJPJ4w6HBGwIBJRsMIGu0PnH48mHXDCBTdi
kAAJkcihc4jFOnQescRkEiRFMiR36G9RMpMpyJRIhdRI49D9pbRkOnltyODQ
+dkzOnS+9kxkZmRBVmRDdodeFzeHvCbkQm7kQV7kQ34UQEEUQmEUQVEUQ3GU
QEmUcugcWqXJMijr0OuVlHPotU3kGNZv06esvLzHqIhKDp2DrLJD19FVHLrO
rkpWQ3XUQE3UQm3UQV2HngeXc+D1qOujARo69LqtjRx6HdfGZBPzOTWVv5Hn
iRZoiVYOHYMT59BxOK0delypDdkW7dAeHeT/yf9BZ3RBV4cep+tGdkcP9EQv
k71N3Qd95XmhPwY49BzdQHIQBmMIhjp0jNo5MyeL9NUZxm3DMQIjMQqjMQZj
MQ7jMQETMQmTMQVTMQ3TMQMzMQuzMQdzHToPtMwHPY96PhZgIRYhHouxBEtl
OcNyrHDotZE7mvdlpUPHQx41131d5dBzj6sdus0gY3llu2GNQ8/5ryXXYT02
OPS6U3L9qY3yd/KcsAVbsQ3bsQM7scuhY53lN12Wk92092Av9mE/DuAgDpll
4jCO4KhDrzEg1xo4Rn0cJ3DSoeM1Tzl0zOZp8gzO4pxDjxGeJy84dHzlRfIS
LuOKQ+c1l/nNr1Jfw3XcwE2HXgfxFnkbd3AX93DfodfCeUA+xCOHnh94TD7B
U1kO8Rwv8BKv8Bpv8Bbv5HnjAz7ikzxXfHHomGu5nsdX6m/4jh/4iV/4jT/4
69Dzif8cem5CNpw84OnUY4ZepLdTz3XLOW85Ri59iqUPk/Qr9uHffOEHf6eO
L5BxBgHUgQgyGWzqEIQ6dR85jAxHBCyIRJSpraZtgx3RcMjfwQU3YpAACZHI
qdcfjCUTI4lT+4slJZPJa0EKpEQqpEYaQ+q0SIf0yICMyITMyIKszv8Nhfov
G5ndqfPUyrZ3DuqcyIXcyIO8yIf8KICCKITCKIKiJouZujhKoKRT54EsRZZ2
6vzs8v0sQ10W5VAeFVARlVAZVVDVkLoaqqMGaqIWaqMO6qIe6qMBGqIRGqMJ
mqKZU6/H3typpG5BtkQrxKE12qAt2qE9OqAjOqEzujj1OvfL/9P5KLvS7obu
Tt3X6EH2dOoy24vsLZ+hU7f/5Ln0RT+nnneU84/9nXqt9gFOvV67kHogBmEw
hmCoU+fyHkYOxwinzjsjYyy/m2uejuS2URjt1Fr2n6Qt8xmPIcdiHMZjgjwn
TMJkTMFUTMN0zMBMp54Hn+XU4+SznbodLdvTc6jnYh7mY4H8X/l/Tj02FE8u
dup1CpbIe4ZlWO7UfhgryJWmXuXUtmx7rnbqtt8aci3WYb08huwL/Kd91zY4
9fpUG8lN2CzLFbZim1PnkpT57WReu+20d8h75dTfDvnd2EW9G3uw16nXvJNr
eMj43n209+MADuIQDuMIjuIYjuOEU88nnnTqNbZPkadxBmdxzqS0z+MCLuIS
LuMKruIaruMGbjp1PXILt3HHqdffuUvew32nXpP+AdmK9+Ih+cjUknHkY/IJ
nuIZnuMFXjp1Tme5JtYrp45fkHkAXsvzx1u8w3t8wEd8wmd8wVd8c+ox7O9O
3V75Qf6U5cyp27O/yT/4i3/4z8V6F57wgjd84As/+CMAgQhy6e9UMBni0m0C
ue6VzD0XSjsM4YiABZGIghU22BHt0rkMHKQTLrgR49JjwHIsWGrJBGRCJEKs
S69jl5hMgqQuXf8lI5MjhUvnWpc6pWmnQmqXbj+mIdMiHdK7dD6jDGRGZEJm
ZEFWZDN1dtPOIY+FXC7dbs1N5kFeeZ7IjwIo6NJlpZA8JoqgqEvHUsmYqr/m
+qLS37AYtxdHCZfOBV3SpfNBl3LpXNKlyTIoi3IojwqoiEouXd9XJqugKqq5
9LxHdZee+6hB1nTpMTfpD1qLurZLtz/qkHVRD/XRwKVjeRu6dDxvI5deC1We
r1w/o7FLr6fRhGyKZmiOFmiJVohDa7RBW7Rz6W9se7KDS3/fDxMdqTuhM7qg
q0uve9SN7I4e6OnS66/3InujD/qiH/pjAAbK+4TBGIKhGIbhGIGR8r7Ke+rS
65uPcen8fmPJcRiPCS7dDplITsJkl567nEJOxTSX7v9NJ2dgprzH8v5iDua6
9LzUPHK+S6+hvIBciEWIl/cfS7AUy1w6l67MqbucegVWYhVWYw3WYh3WYwM2
YhM2u/Tc/xaX7jNvdem17+Q48jbq7diBndiF3diDvdiH/TiAgzjk0mMkcqzk
MPURHHVpfcy0ZX//uEv3+U+QJ+U2abt0DO8Z8izO4Twu4CIu4TKu4Cqu4Tpu
uPTYhhzjuEl9C7dxB3flNeE+HuAhHpn6sWk/kc/PpWNepX5m2s9d2ndCtg9f
UL/EK5eOb3ktyxTL0RvyrUvneXlHvscHfMQn+YzxxaXXdfxKfsN3/HBpX6Sf
5C/8xh9ZZlzab1f670rfHFke/7l0QkkPeMIL3m49NiHHJXyofeHn1n1wGSco
4wX9aQcgjUzrTQYhGCEIRRjC3TrPjPRviaC2IBJRbr02ntXUco08aduo7W7t
0xXt1msJOkgnXHC79XqaMfJckBCJ3Hr9oVgyMZIgKZIhOVIgJVLhppwTIm+Z
TGPqtGQ6uW+3npvMQGZEJmRGFgzl/w1HVupsyI4cyImxHnpNKMkxps7F7bmR
x611XtPOh/woYEhdEDXkOCsKURdGERR163XQi5HFUQIl3ToevRRZWv4dZVEO
5VEBFVHJrXPeVDbtKqiKaqguj4eamGeue/8Oc2W+ZA+dz22pXLMIi7HZpLRr
uXWeJZlvqbZbr7Nbh6zr1jEZ9dx6jEOOddSnbiDPF43QGE3QFM3QHC3MZyCf
xTZPvTaGnA9tSbsV4tAabdAW7dw6557Mt9ferf3/O7j1emYdyU7ojC7oim7o
jh7o6db97l7mM5Mc7aF1APe3jlyL3tzeB31leeb2MPRz6/vT363v0QByoCzf
GOzWa6/LNdiHyLKCYW7tfzGcDOXvB8jfYgTtkRglj40x8lzk7zEeEzDRPMYk
t84tONmt899MIadiGqYbUs+Q14VZmO3W4wRyvECuRTHHrfP+z5XPGvOxAAux
CPGmXmzaS7AUy7AcK7ASq7Aaa7AW6+RxZNmW/lnkRlnesBlbsNWtczPKfDjb
qLdjB3ZiF3bjuMxdTO7FPrdec3W/W/sRHiAPGlIfcuv34bBbr/2V8j+dI+MI
7aM4JveHE269T7nvk+QpnJa/4XnOxBnqs26dk/sceV5em4deC/eCW687L9ef
v0h9CZfdOmfPFfIqruE6bri1781N0sr93iJ/cz+33UrqO+RdnOPf75F3uO2+
W8ciS19l6acs88ZeM8edZazzA1m+3Xr9pL5mOZTX/8iktB/jCZ7iGZ7jBV66
dV7fV+RrvMFbt87L8sb0e31H+z0+4CM+ufUav5/JL/jq1u/WN9Im1zklf2CQ
p5J6sKdeI/0n9S+3js3+7dbn/8et19eQ8Wr3uf0v7X9urWXyYmnLMTEPak94
wRs+8IUf/BGAQATF6D6N7NvIvH3BtEMQijCEIwIWRMZof4hqHto3PYq2FTbY
ER2j89jKHLYOaidccMfo9eVjyATS5rkmwDTuZ6qHjnVOyO2JEBuj19osxu2J
qZMgKZLJ43vq8pCcOgVSIhVSIw3SxuiYs3QxOvdjejKDPDYyITOyxOi8zTJn
s4ynyko7G7IjB3IiF3IjD/LGaL/VfGT+GN3mlTnoZbu3AO2CKBSjcxIWjtF5
CWV+gCIxOkdA0Rhty3wq8fJbQ7s4SqAkSpm6tGnLOHI5dlMmRsfpl43Rcynl
yPJyXzHan1f69VakroTKMTr3mxwjqEJdFdVQHTVQM0bPv8j1AWeYbdWtci0d
bq8try9Gz48v89I5VWX+YpnHuC6314vRc17SJ6Z+jF5PoQHZEI3k/UCTGL3u
ZlOyGZqjRYxeT75ljF5TXo7Ht4rRa2zGka1jdB3RhmyLJzJGUV6fuSZKe+oO
6IhOMXr9687yGbFcNOX//D+izgLKiqNpw8uyuLuu33W5K7i7u7tDgODuDgGC
BvfgrgESJLi7S9DgGoI7/M+bmv985+xz3qq5d+f2dPd4d1UPx+7pbX4vtDf0
cfYB7Qt9ve2Yp2NfP2879vdHB8BAGORtebgHo0NgKAyD4d523SBkj9B6YBT8
BKPVR2Es/Azj1O/U52Cifsfb8sBP9rZYqb94W27HT5R3o2KnqE5hGkyHGd52
bMjGZzOxZ6k9YY7qUPUH82GBfo9tHe1lyP7V28a4aKzLQuxFsFjtBEthGSyH
Fd6Wa10511d623PIVehqWANrYZ23xaZbj26AjbAJfoPNsAW2Oipfub1/1/+h
f6DbYDvsgJ0wM6HlQfgTe5e35bDbje5xbOWyk7/X28anaC6t5nPt87Y5XfvR
A3AQDsFhiGCdR9ATNPFRb5t/rnnox7CPa7nKpf/3trzSipujez/dA2psemIv
eweqd6GKSXva2+LSnkHPwjk4DxfgotbvbfOoLqNX4Cr8BdcgmG24jt7wttyc
N9Fb3lYnU/nstvoB3PE2+67j31N/hwfwEB7BY3gCT+GZ6kdtAS+gHmXOorzZ
2C/hlbflbtL8ttfeNsftjfoQvPM2+73jf4CP8Ak+wxf4Ct/gu7ceplj+owSo
JyQEL0jk2MrPIT8xJIGkPhaHKRmaXDZlS4GmhFSQGtL4WJ9WfabFbsd30qGN
HG3sZXZ6H4utpRhbGWT72Bi5TGhmyAJZIRtkhxyQE7x9LPavDzqFevZF/cAf
AhyVr3kZgT42N8OFBkEwhEAohEE4tGIdEWikj+UP9fMyW3lE5SsGcRR+NLh9
7LgX49g6/smPxY6DeNjI/9SAXFon616CnRv7HH03D5rXx87vZzWmXfOE8fND
ASgIhaAwrOA766EI9mSOHUXRX3T/gxaHEjCNdZZES0FpH8udqbyZZbDL6neg
PFTQ9vK/FdFKUBmqQFWo5tjVHV/zQWqgNaGWj50PdC4oTVlKQW0f09ceZteB
ulAP6kMDH8u119DH8ksoz4TsRo7fGG0CTX1sfkQz1amzLdoOne+FbJ33Wzgq
v6XaC1pDG7V/AquTH7Dbqq+pTzoq/0foAB2hk9pd8cLQLtAVujl2d8fv4XxX
/6Nr+Z4+dj3fC+0NfXzM7uv4/VRu6qK/jyF7ADoQBsFgyMWyPOpHPoZszfse
ij0MhsMIGKl+DT/BaBgDY+FnGKe6ggkw0cfyR+l9nt7lTVL/8LHrK+VH+MXH
ciR0oS/4JbLjfhdHdR6YwucvPaz9pqrMMB1mwEyYBbPhFN+fg86jj84VPra/
zPOxfUb3COHOfcJ81ZfqChb6WMzYRehiWAJLYZnTzxQTd5lTl/KXq6/DSlil
/1U/gbWwDtbDBtU3/eMXyrQRexP8Bm8ox2b0FboF3Qq/+1hOA40tUo6GWP7H
DX+wfBtshx0+lmNvJ/qnj43N0LiMXdi7YQ/shX2wHw7AQbjnafkoDmEfBh8v
y+mi5zNHfCzXvFT+UfQYHIcTcFJ1CqfhDJyFcz4Wh/s8egEu+ti4UNXDJWfb
Vzn1Ib+2cg+jNdFm0AKu4F+Fv+AaXIcbcNPHcqPfQm/D33AH7vo45yEfOzfd
Rx/AQx87Tz3ysXPVYx8bZ/bEx8ZzPvWxccrP0OfwD7yAf9WfIEh50tHXahcf
K9dbeAfv4QN8hE/wGb7AV/gG39UGvhz/oQp16ulrsXITol6+Ntc+ka/FtVJ8
q8TYSSCpr+VoUq6mZNjJIQWkhJGsJxWaGtJAWl+bX5LO1/Iop9f/QkbIBJkh
C2SFbJAdckBO8AYf8AU/8Pe1WPQBaCC4fC2uheJbBPna3MNgNARCfS12TRga
DhFQkf4YiUZBtK/tw9p/11FmN34MxDoqX3MYNf84Djve157PlWYdubBzQx5H
8zp2PsgPBXwtj15BtBAU9rV7Kr2HLYJdFIpBcV+b21wCLQmloLTzW2V8bd8p
i5bT96CCtgEqQQBldkFlX8t1rJzHVbAH0B+qotW0/fDe63952qXydf06Vvmi
+Lwm1PK195q10TpQF+pBfRjK9xugDaGRr50rdZ5sjN0EmkIzaA4tfG28Sku0
la+NkW+NtoEffO3ZqJ6JtsVu52ux/9v72v71o/oZdIRO0NlBdhfoCt2gO/SA
ntALekMf6Av9fO35VX/VAwyEQTAYhugzGKY+BCPUV2EU/ASjYYyvzZ166uTy
GIv/M4yD8TABtie2fjNR/Qcmq+587Vig48AU7KkwTdsH16nnvsqnhD0TZvla
rgvlvJiNPQfmwjyY72uxqTX+ZwT/s8DX7qV+RRfCIpitPFPoEljJeXUpulzz
aRRnUTas8LU4UCt97Zm15lVrfrXyHCvvt3KGr+Kz1aoXL2tjqfw1qlPWtdbX
xguvQ9fDBtgIm+A32AxbYCs84vd/V3/1tXvhbaon2AE74U9fy/+wy9fuWW87
961fnDzBZ5xcwVLlHd2tNqc8nb0slvUe/L2wD/bDATjoazF9D6GHfe3Yr2f2
R7CPwjE4DifgpK8dp0+hp+EMnIVzcN7X8n9cUJ/xsHGjF7EvwWW4orbV/8M1
tSfc0HbALbgNf8MduOtr+VbvqQ7ZxvtoAHXj0nwt7Ifg1rtz9DE8gae+Fg9f
sfCfYT+Hf+AF/Otr4zSUx+G/472vHfP1nO0V9mt4A2/hHbyHD/DR1/JzfUI/
wxf4Ct/gO3j4sR+Cp5+No0yIekEiSOxnv3vfySGRBP8sx40zSez9Z1L8ZJDc
z2IkK1ZyCuyUkApSQxpIC+kgPWTws3xpGf0sf1omNDNk8TM7q+PrmKxnVtkc
W8dm+dn9bL6Q5grlwM4J3n5m+zi+L/iBv5/lBQ1AA8EFQRAMIRAKYRAOERAJ
Ufo9cEMMxDr2WI0RR+P9bExtgI792LkhD+T1s9xm+fysP+dHC0BBP7uOKYQW
hiJ+lmunKNqfdRbzs/e9xdESUNLP4rqWQks7dhk/8xWLoixazs/JsZvYzrvl
8StARagElaEKVIVqUB1q+Nn8qZpoLagNdVQ/UA/qQwNoCI38LG7OcWiM3QSa
6vcdW/em8ps72646aAEt4Se6VCu0NbSBH/zsmKp+rvwdbf0sh0Y7tD386GfP
yDqgHR1bMQ3ld/Kzd7t6ZtbZz96Fd0G7+lk+OL0v7obdHXpAT+gF3RTnDe0D
faGf6hoGwED1M+ptEDoYhsBQ2Kkx2TAMe7ifxdQfgY70s2O5jhmjtC3qO6x/
NDpG/QJ+9rNrr5DEZr9yrsXGYY+HCTARJsFkCOD/f/GzHPfSKY49FZ0G02EG
zNT2+9n4TNWlctzPlg9z/ey6fh46HxY4Kl/3Jb/6WU6ohX6W3095/upQpkX4
i/W/sBSWOfZyx1/hZ+/nVvpZHqpV+l0/y7GzBl3rZ/MhNC9C4x+VQ3Mdy9b7
mR3i+BtgI2yC32AzbIGt8Dv8AdtgO+xQ/ftZrvgtSc2W6rpFcd7+9LNnZbv8
bA70bnQP7IV9sB8OwEE4BIf9LLbUEfSo+rLqAE7ASTjlZ/l5TqNn4Cyc87P8
a8q9dh77AuzWsyr0kp+p/MvoFbiqelbf8LN4W4pprxxR1/Fv+NnYqZvaJr0b
QW87yP4b7sBduAf3tZy2eoCG6d0PPMR+BLP5zb8T2vwuzfN6zLIn8BSeqT5g
l57Zoi/gX3jpZ8f4h7ofwE7F+mZhz4TXfnb8ewNv4Z2fxW3aQ32/V52iH9Re
HrQbfPSz/N6f0M/wRet27G+Or/y531EPf84l4AnlKXcbfi8hthck8rdjbWI0
CSSFZP6WL0a5YpL723j7FGhK2OVl9xKp/E1TOnZqSANpIR2khwyQ0d+OE1uo
i0zYmSELZIVskN1RXZ/KzgE5wduxFcNEvo+/xbf3RV3Umx8alMRyMwc5fnAS
s/2xA/xN5Wv8vp4dBep//S3GjmLtKEd6kP4PQiBUdQHhEAGRji2N8rfxq9Go
G2IgFuL0O7RNIa4f4rFz+VscHsXjye1v88w1xzwPdl7IB/mhABSEQk49ql4L
Yxfxt2dRRdFiUBxKQEko5W9z1UujZfwtjlJZf4urpHFw5VTOZJbrvTx2BX/L
K1QRrQSV1ZZQVeuivIUTWNmr+dsz1epaJxzUM2h/m3Ney9/uxWujdaAu1IP6
0AAaQiNorG1iXU20feg16n0v29RUbQvN/S1HX2W6YwttI9oSbQWt/a3slfm/
Nv72/vQHf3uH2tbfxva2Q9vDj6oD6Oiocv518re4e53RLv4WN0/x87pid4Pu
/pa7YSr1MiWZ5XCQ9nD2Bz1r7Indy9+eoev5eW/sPtAX+sEIytbfsUcmNX+A
v82ZfM62DlTbsiwvtGTbBuEPhiGOyh/qfGeYv31/mOMP1/qdvqOc8SPRUfAT
jIYx/hZXbyz6s9pFfdjfxrZNQGvzexPR39mmSfou/AJTYCpMg+kww9/utXVN
pvtt2TP9zdccAeVY0XieWSyb7W/zMuagc/1tDKNyX+sZpp5lzmPZfFgAv8JC
WOTYix1/CSyFZbAcVsBKx17l+KthDayFdbAeNkBptqUiVEpm9kZ/86XfnPxl
0rIs28Sy3/wtLt1mp362wFbVifqo4vD52/FtG2xXXXAMzJ/Mjr0p0B0sS40e
ZxuP6VyHnyyZndt1zSTVuV72n3y2C3bDHn8bDzQgianGBMlOksxiHuz1t+cN
+/ztmcNp1rPf3657D6AH4RAcVt+Do+r/6vtwAk7CKTgNZ+AsnHPs845/AS76
27H1kr8dPy6jV/xtrOJVfxtzNdgZd6X8nIr3rRydf/nbvazmtOi8rvO7nk/8
5Wkxr69pjAHfuQ434Cbcgtv+Nsbob/QO3IV7Tr9VHx7l+PfhATz0t/c5ynHw
CPsxlOGc8AR9Cs/gOfwDL1QmeOlvcw5f+ds8yNf+Nhfyjb/tO28dZL/zt7wd
79GyrPcD+hE+wWf4Al/9bd/65pTzu6PyPQKsryRAPSEheEEiSBzwv2Of9P/9
JGhr/rUjJMVOBskhBaSEVPKpy9RoGkgL6SA9ZICMkAkyQ8/kNk5OsQo0bi4L
y7LCo0QWDy4bdnbIATnBG3zAN8D2tZLJTOX7gT8EQCDcoz+60GidHwPseu5w
ApsHFIwfAqHO+sIgPMCehUSgkRAVYOeGPPxfdIBdh7vRGIiFOIgPsJhkudDc
AdY/1U/zYOeFfJAfCkBBKBRg8U6V66kwdhEoCsWgOJSAklo39VLKKWNpKANl
1TZsSxq22TOJ7ZcVEtj9TTlth+ZmBFhujApoRagUYGOHKqNVoGqA3Qdq/dUC
7DeUd1P5N6sH2FjXGmhNqAW11eZQF+oF2HOA+mgDaAiNoDE0gabQDJo7dgvH
bwmt1GegDfwAbaEdtFd9QAfoCJ2gM2Rz5tNqrvVqD5t7rbmPXfisK3SD7tBD
bUZd9ER7QW/oA321XdA/wOZCaXv1XlzvxAewbCAMCjB7sOMPgaEwTG0dYPku
lPdiBPZIGAU/wWgYA2PhZxgXYHlPxgdY7pNqzmda3s+JPaAYBMplPyHA8tnr
fX8y2m4i/gHKNQmd7NjSg+gv6BSYCtMC7Dv6fJqj+zXXWNsPM8GbMswKsHcQ
s9E5MBfmwXxYAL8G2LjAhegiWAxLYCksg+UBNkZYuSRXaL1elvtbuURX4q+C
Lp42bkzP/1YHWD5m5WVeE2DjmtcG2Nhm3QevU/+DDfoN1UWA5cnZpDqDq2zD
NcXfwt4CW+F3lQG2wXbH3uH4O+FP2AW7HZW/B04mt/jPe7H3wX7Vk+oSDsED
9pv7cDjAYnIfQY/CMTgOJxz7pOOf0vfgTIDlOlSew7MBhuxz6ltwAS7CJbgc
YHPGr2jb4C9IRN1d0zoo33X0RoDF6LsZYLmKb6G3AyxO/9/onQDL06YcbSep
s7vqk4ltjOYzJ4bNvQAbI6/4Xfe1bfAQHsFjeAJP4Rk8h3/gBfyrelOcC/re
Y3iJ/wpewxt4C+8gSDEY0Q8QQJ19hUDNKcP/FGD58D6jdZS3PsD26a8Btl9/
c1T+NOUdRD0COceAJyQEL0gEiSEJJIVkkBxSQMpAG6v139xm7NSQBtJCukBb
t35T+eTS42eAjJBHz/DQIvTNzGgWyArZIDvkgJzgDT7gC37gDwEQ6KjLsRWb
LyjQYvWpHYOxQwLNlqpdQ9EwCIcIeEHdRaIvHZUfhUZrmyAGYiEO4iEX5FbZ
IS/kgzoJbFxdfuwCUBAKQWFtW6DFnyyKFoPiUAJKQqlAux4o4VwTlMYvA2UD
zS7n+OUDbayZ8i5WwK4IlQLNruz4VRQrB62a3OIEV8WuBtWhBpz1sLh+XWnj
TlCTZbWgtsoPdQPt2UA9tH0KywdXH7sBNIRG0BiaBNr8Ms0t68U6mwbafEnd
d6pvN8NvDi2gJbSC1tAGfoC20E6/AT8G2jzQDmhH6ASdoQvs5rjVNdDmpnVD
uwfaM/oeaE/oFfi//tsbewbHvj5oX+gH/QMtBsWAQJs3NxAdFGhj/QejQ2Co
2kRjvaizIugw/OEwAkbCKPgp8L8wfZoy4DEae0ygqXzFchobaLGdNB7zZ+xx
MB4mwET1xUCLkTJZ/ROmwNRA2yeVq1Kx6KcF2vOk6doOmAmzHJ3t2HqfMyfQ
YiHORefBfFgAv8JCWASL1T6B1s+XBtr+ouciqzkeLMNeHmjzfVcEWgzVlegq
+ECfWI2ucez3jr8W1sF62KD+RL/YqHaB32AzbHFU/tZA26d/hz9gG2yHHbAT
/oRdal/YA0k5H+0NtBgzQ5122Rdox4d9jr8fDsBB9QE4DEfgaKDFmT8WaLFh
0sFx7BPQlHKeRE+pbuEMnA20OSrn0PNwIdDmel8MtHHil9DLcAWuwl/6fqDN
vdS1hK4jruPfgJtwK9DO/7cD7Rrgb/QO3IV7cB8ewEN4BI8hhn7thifYT+EZ
PFebwAv4V20daLne/stnrzYPtOPSa/0/x5m2KQ3Z7gQWa/4Nn72Fd/BebQgf
4RN8hi/wFb6pP4KHi2M8eEJC8IJEkBiSwEbOO0nRZJDcZbHsFNPuvO5FXfbu
NCWaClJDGkgL6VwWgzq9y66BMqAZXZbXORNalnbJjGaBrJANsjsqP4fL4ork
RL3BB66zrSP5P1+X5aiWdnPyVfth+0MABIILgiAYQiDUZe/8wlz2DjAcLaF6
RSMhCqIddTu23jnGoLEQB/GQy2W52nOjeSAv5IP8MIPz1zQo4DKd6tiK76Bn
FnpeURC/kMtiKBVGi0BR1Qt+MbS9E2tJ+bOLu4wSLlsmu6Tjl4LSUMZl7xs1
L0/z88ril4PyUAEqwkfqpxJa2WUxp/S+swp2VZfZ+x2/GlSHGlDTZTEj9P49
imNALfzaDrLrQF2XxZ+vh9aHBtAQGkFjaOKyXD1NpdDcZTnRW7gs1l9Ll8X7
a4W2hjaqB2jrstzg7VQfLsv99CPaATpCJ+gMXVz2DL4rugfthnZXn3RZ/Ime
6ksJOUegvdUfoS/0g/4wAAa6LD/xIJeNjxuMDoGhMMyxhzv+CBipvueyGD86
x+v8/hP+aBgDY+Fnl83RGoeOhwlwMKU9w5iIPQn+oW4nuywvkuIe/4I9Baaq
78B0l+3n6g/qG+1gBstmuuy52SyVh22cjc6BuTDPZeM9antxTsBeAL/CQrjN
7y1CF8MSWKptgOWwAla6bA7AKnS1y+ISrXFU/tWUlrd6rZbBetgAG2GT6hs2
u2z85yMve2ewBX+r6hf+gG2wHXbATvgTdsFul12L7XHZ9dhel+W02eey3O8a
Q7cfuyV95YDq0mX5xQ6pjyp3AcfEL+xrn+Ewy464bJ77UfSYy64/jqvf0kdO
uGys/UcnF/dJrUvrcVlO7jMuy9N9Fj0H511mX3D8i2pPjrWToCS/fcllcZov
u5x4maorl80h1VzSv1z2XPIaeh1uwE2X5X+/5bJ88eOcPnIb/oY7LotPfhe9
B/fhATyER/AYnkAFtvupy+aYPHPZO/jn6lsum+vwAv1X7UW9vETXJLI+9kp9
C964bGzyW9W3tl/b7tgfHf+Ty+IPK6/Sc+c3Pjv9OpPq3dGMjv3VZc+0vqHf
wSOI/wHPINtm5buXfcupg4TYXkF2TaR5oomCLKZDYjQJJIVkMFjvd9AUkBJS
QWpH5aeBWbTHTEiLnQ7SQ1wqy635IKXlU8rAsoxBlkstE5oZskBWyAbZIQfk
BG/wAV/wA38ICLI4+4GoK8iO0w0hCDsYQiAUwiAcIiASoiA6yPqAG41RGVQ+
+Il2iUdzyfayPPTKR587yDRPkNkb2Ya5Th75vPj5ID8UgIIw3Mu2o5CzLYWh
CBSFYlAcSkBJKAWloYzjy9Y7knK0XVnsclAeKkDFIBs/PRgqYVeG81y7VEGr
QjXYlNLyh1THrgE1oRbUhjpQF+oF2XVgff0WNIRGQRa/qDHaBJpCM2geZOPF
WqAtoVWQjWVU2wyiHK3RNvC3cgFxbPsB+2AKizepGExt8dtB+yAbp/1jkO0n
epbbAbsjdILO0MVp/65O3SkvYbcgy8Os+OLdsXuoX0Iv6B1kcwk0pyBZIhtT
2IdlfaEffOX3vkB/+bTVgCCz+6Q2f2CQ5bsa5OjgILMV93YK9E5t2jO12UOC
7JpJ10uyNc5NvmI2DsUfpraHEU75RsIo9SUYn9qOMaODrI7HwFj4Gcbpc5gA
E2GSY092/F9gCkyFafpdmOEgeybMUv+gL1T2tLlUs/HnBFk+vLnoPJgPC+BX
WAiLIJB2W4wugaWwDJbDiiA7L+ucvBJ7q6PyV6GrYU2QPf9SDjzlv2tIXTfw
snECa/nMm+/6wjrs9bABNgZZ3vdN6G36+GO9m1adaN6Ich1jbwmyefVb9Xvq
G5Sxk2KYqD/zv9vQ7TCbY/8OdKe+D7tgN+yBvbAP9sMB9Uk4BIeDLF7KXOd+
7UiQ5e/SM9uj2MfgOJyAk3AKTsMZrSe1reessy7Z5xz/PFyAi3BJ/RKuwFVt
L1yD63ADbgbZ9U42rn+z6lm2zkEsG8313W30b7gTZPuR9qG72PfgfpDNN9Oz
/wfYD4MsPuKjIIuR+DjI8mI8CbI5Wdpnte8+RZ/Bc/hOnf2DvoB/4SW8CrIx
uq/RN/AW3sF7+AAf4RN8hi/wFb5pXeqfeq8WbDmvlfs6QbDlgfZEK9MXKnhZ
fraE+F7Blt9Cx2Pla1DeBsVLTcTyxMEWc1Q5+hR3NAl+0mCLT5cM3U+590Fy
7BT6LqSC1JAG0gbbPIh0aPpguy/SONJUzjozsCwjZILMkAWyQjbIDjkgJ3iD
D/iCX7Btj7bFHwIgEFwQBMEQAqEQBuEQAZEQBY3o39HoCA+LhezGrpfG8iMp
91hMsPXlWDQu2O4ZdL8Qj51Lv5fUnnvomUdu/DyQF55Tp/nQ/MEWJ7cA2j+V
5U8rqPph3SmhULDF1i6MFoGiqs9gyz9fHC0B3XT9hHZJYPMO9E6lFH5pKBNs
74nLouWgPFSAilBJ7QstND452PLiKQZK1WA7b+o8WQ27OtSAmsEWR6+W1gl1
oK7qA+oHWz7LBqrrNB7/5buvq1i2rCcB9hzNfwm2WF1KmShbqlxbjbAbq+2h
KTSD5ioXtIRW0BrawA/QFtpBe/gROkBH6ASdg+15bRe0q+om2HKSdQ+2HAC6
1u6B3RN6aXugT7DFc+iL9oOqlLd/sL2jGoBOY30D0UEwONjmJgxBh8IwGK7+
EWyxu0aio4ItH6Puc38KtvEwHVJbXq3R+GNgdxrL+yZbOhb9Odji6I0Ltph6
iq03HnsCTIRJMBl+gSnBFsdZ8ZynBtv7s2nB1vbT0RkwE2bBbJgTbLGE5wZb
POF56HxYAL/CQlgUbO/39W5/MfYSWArLYDmsCLbcuyvV1rAa1sBaWAfrYQNs
hE3wW7DFb0iq9xvYydERbOsW7K3wu7ZT2wzbnTrcATvhT9VLsM1X2I3ugb2w
L9jGXe5HD8DBYDveaW6Cjn+H1F70u8PoETgKxxz7uONrHJhiaJ0Ituu/uf9/
/4J/Ck7DGTgLVzl+3+d67Bz23ZQW+0vjzc7jX4Bbei/C761JYyr/IssvwWW4
onXAX1CYz7vzebfUlhtVOVKvsfw63FC5oAq/cUt9EL2N/g13gs2W3oV7cD/Y
8ioL2cqv/AD96GFx3B+q36scae15h55zKP60YsSsTWtxYzS+SO+pU8JjvvsE
nsIzeA7/wItgi72tGNzKDfRvsOUHeom+gtfBFq89I8fJN9ipqYe3wTZe853T
b5Sz+b3WA4XS2liMj9if9H38z/p+WssZp3xxX/C/Blsu1KGJLS+qVP43ln8H
jxD6M3hCwhDLC684+8p144VfgzpOhCYOsfywSRxNGmJ2ZcqUDE0OKUIsfq/i
+KbE7sW29IRU2KkhDaSFdJAeMkBGyASZoSfr6pHG+liWEOtnWdFskD3Engfk
QHOCN/iAb4jF51Gq7odO3B6/EPP90YAQ20/8HQ1EXRAEwRACoRAG4RABkRAF
0eCGGEflx8JOjmNxaDzkgtwh9u5L55A82HkhH+R37AKOXxAKQeEQ2y5tUxEo
qrpkn06W3IlDi18cSkBJKAWloQyUhXIhds1YVDFm6VMbqLOqaPkQU/lRig2A
XxEqqZ2gij6HalA9xPKBJE9tOUFq4NeEWlAb6kBduEyZ6qH1oQE0hEbQGJpA
0xDLGaPcMc2wm8uHlupL0BrahNhYogbU2w/YbaEdtIcfoQN0hE7QGbpAV5Uj
ke173bC7Q48Qy/mleAk9HVv6SrnV0d7QJ8Ri9Ck+X1/sftAf3vOdAehAGBRi
ea2VJ3lwiOU3GIIODbFz2bAQO58Nd1S+5tprXLvm22sfHBFiuY5Gql1Zd5+0
poUdexTLf4LRMAaO6dyk34VxITa/arjyzaa1nNmnnWPm+BCL/au4vxNCLO+3
cucqh+5E/EkwWeWBKTA1xOY769pzWoiNwdUYwtt6Z4M/A2bCLJit/sjvzUHn
wrwQy5E1H13vYf1iAfwKC2FRiI1jUIyJSoozgb8ElsIyWA4b6R8bklu+zBUh
lj9zJZoutdVbBkflr0JXqw34zhp0LazTb8OGEHtetpjj0yLYqD4Ov8HmEMu7
ukX9CIZRF7+jf8A22B5iz/J3oDvhT9iluqDObyt+I/Ye2Ku+oX6vfs1vHUAP
qo4hfypT+YdVL3BU7QbH4QSchFNwGv6h7c6gz9Cz6DmVUZ+xnRfQi3BJvxNi
eb71jv0AdbwfrrDsKvwF10Ist8b1EDtP3EBvhth5SMd55dS6hX9b60llY3CU
Z1b5Zv9m2R24C/fgPjyAh/AIHsMTeKpyQqje22ifoczP9XshFvvpBfovvIRX
+j+OC6/RN/AW3qm8lPu9yuxh9ocQ85WHuq2H5aJWHqaPIZaX6ZPWHWK5AJQT
9gv21xC7ZvqGfof/EhiE2vVUglDLreqJJgSvUHsPoc8TOd/RPdnDJHadohwm
iVmeBJJCMkgOKUJt3kjKULve07VeKuzUkAbSwigve7al51p6PpGOZekhA2SE
TKEWxyVzqL2zz4JmhWwOsrNDjlDLS54T9Q41le+DXuEe4jL4YvuFWv4BfzQA
AsGldUMw9NdpONTi+oeiYRAOERAJgzhuRoVaX1Ofkx3t+G40BmLhoIflOonD
jg+1MRK50NyQB/JCPsgPBeAm7ZyS7byFFsQvBIXheTpbt36jCKyjzi+zTxYN
tTHxGg9fDLs4vMEvEWrz3kqGmq25cPI1b7aUs73qN6VVL2hN1lcGuyyUU3tB
BajoqHyNpa2EVoYqUBVWci1RDa0ONaAm1FGenVDLX6g8hrVDLb9WHbSu6pv+
Xk9l0PVbEhtv9zmJXYt0ou92gPp83gAaqgzJ7Rl2I+zG0ET1lNaug5piN4Pm
0AJaOnYrx28NbeCHUDtHZHb2Ydk6V8jP45wjdP3Wlu+1g/ahZv/o+IWp+5a0
+ff01tZq8w6hdgzoGGo5MDuF2mdaLruz43eBrtANukOPUIux1IP66Q498Sen
svgbisPRK9RiCyquYO9Qy83RB+0banGzFT+7n/ooDICB6o8wGIbAUBgGw2EE
jFSbprbPvtOGo9CfYLT+L63FZxyDPdapc/XNn8HNZ3fSWT7ccfjjYQJMhEna
BpZPRn+Bp/SDJzAFexnbNBVdjk5Dp8PZpJz30JkwC2bDHJgL82C+llO2BaGW
G+JXdKHqld9/BYtCLfahcnwuDrV4TUvUr0Itzon2o2Whlo98uWOvcPyV6CpY
DWtgLayD9aH2zFXPWjdgb4RN8Juj8k+ktHOp3u9vDrU4eFvQrXBD47uUUwj7
D9gG2/WbsBOKJ7JtVx38CbtUr7q2Q/fA3lCzpftgP+Tl93ayvUN0LsQ/CIdC
LUeucuUexj4CR1XvioWjOkxvsfD1/vi4ygwn4RQk13VMqOWNPxNqcWR03j6L
fS7UxtGd13K4CE/4/iX0MlyBq/BXqG2/6kHjHa6FWg4x5RK7rnqAm3ALbofa
nIy/0TtwF+7BffWrDKZ5Mpj9APshRCq3uqPyY9Na7mrlrX4cajkBn6iPwTN4
Dv+E2twxzSErRH214lj4gmX/wkt4Bamow9ehlpfiDfoWPJVfPYOpfMU2a+7E
N3uH/x4+wEf1H0/6EmygzT6pP6S2GLrKNac4up/V90JtPGigc0z7Ct9C7fyi
88x38AijDtOZnSDMfM8wi3WvuKNanjDMPhtOubzQRJAYkkAhtiMpmgySQwpI
CcdYVSo0NaQJM1uaFtJBesjg2Mrrnt5ZNiehLc8ImcLsHYvy52QOsxw6F534
rXM1lll5QFk+jn6RNcxyBCtXcDbs7JADcoI3+IBvmOV59guzGHT+aEDYf49g
PQJRF5RPY+fjIC2HkDDri6Fhti+FoeEQAZHwkDK08LJnXVH40dA3oeUCdWPH
hNk8iVg0DuIhF+SGML6XJ8zyjudF88FyD8sPnx+7ABRUHUNhKAJFoRgUD7O6
UD1k5vtzE/6vDmWrHu9rLCd+I/pGyTCLIVMKLQ1lwiw/elm0nLbb0QqOfcSJ
TV45veU9lsrX8bEinx9MZbZU15l69FiJ5ZXD7Lyjc04V7KpQDapDDagJtRy7
tuPXUd2yjrpovTAb118/zGJuKnZBgzAbp9hQ2xJmeekao02gKTRz6rWZU7ey
9/nZvMjm2C2gJbQKs5hTrcMsBlUb9AdoC+2cdbWHH8MsprbiaXfA7gidwmys
g2L26R60M34X6Bpm7+n0jk7Pnrqpv9Afzup9DvtVd/we6lu0U0+0F/SGPuon
YZbveSrf64fdXz4MhEEwGIbAUNUFDIcZtGs414l32e8Oss4kioEFI8IsxvPI
MLNHOX4nrl1+wu6Abub4PRp7TJjFonpFnY/F/ln7EIwPs9y9yuGr3NUT8Ceq
f4aZPdnxf4EpcIDfn4pOg+mwk99omNHmk8/AnwmzYDbMCbN7s6McszqxDXPx
P7AdDdiOj+i8MMvDpXxcyldYx8lZ+F8cY20L/ArzWf+vGe0+Y6HaKr3FelTM
R+X3UB6iRSzPjy5Gl8BSWKZ9C1bASlgFq8Ps2e+aMHv+uxZdB+thQ5i9A9+o
7yajD3na85VN2g61VQbTARnM1rXD5jDbJ7agW9Wn4Q+tG7Y7yN7hIFtxnpXr
Wzm/d+L/CbvgEeXfje6BvQ6y98F+1T0chENwGI6E2XuiI45/FI7BcTgBJ8Ps
XdUp9HSYzZ89o//X+VZ9Fs7DBbWltgcuYldGL6GVMhiyL8MVuBpm+YD/Qq/B
dbgBN+EW3Ia/wyzWzh30LtwLs7kr98Ps2lr3fQ/CLG+bcqY91LY769Ics8fo
E3gKzxxkPw+zd+gZM9k7/X/CbA7hC/Rf1au2F17DG3gLKZXPGg3OaPresT+o
jPAJPsMX+Arf4GEqmyv9PcxyqOmeaxPHUwWc0rk3AeoJCcELEkFiSBJu5wO9
X19Nf0+KvwZNhiaHqxlsLIuWK8a6crSOSmc5e1OwLCWkCrd43KnDLT63Yggq
luBrSBNufTptuOWQ1LzIdNjpIQNkDLd4R4p1lCncxlYplk5m7CzhNpdZc5qz
hts13S4YTVmTo9lYlh1yQE7wBh/wBT/whwAIBBcEQTCEQCiEQQf2l3A0AiLD
7f5a+TaUdyMKPxrcEAN/cH0Ui25Dc1Df3hAXbs9rF1HH8eF2TNOxrZ3mPOHn
hgvYdSlvHuya1GdedLTy3UK+cNv386M/cm1YAC0IhaAwdGf/WqW4qOhqtAjL
htCsRdFiUFzlUxwitKPGdUNJ7FJQGspAWSinbfO0mNWKXV0evwJUhBKUoxJa
GWZTvironAy231QNtzwD1dDqUEPbALWgNtSBulAP6kMDaAiNoDE0Cbf2Uls1
Dbe5VM3Q5rCP5S3QlmprzkOt0ExeNu6sNXXcGr8N/ABtVe8ct3dAO+z2qi+1
n7YbOkFn6AJdVWbVHfSArBy3X9M+2/nf9ByDe7KsF/QOt/etetf6DPrg91UZ
oT8MgIEwRs+APCz+ySD8wWoDGBpuz4GUG3JYuM1dGa4+ACNhVLgdx39y9gFp
WscejW5nnWPCDdlj0Z9hXLjtq+NhAkyEQdTVJHRyuMVDVfzpX2TDVNhKG05D
p8MMmAmz1J5wL5Op/DkwV32dZfPQ+bBAv4//K7oQFsFieE1/XBJusZoPc+G0
HV0abrm5ZUt1LNDcPuWgWBZu8zWXh9u+l5XvFKPOSqSwHCIrWLYSxvJbQ1nf
jEwW12xVuB17V6Nrwu2aUPG412Kvg/WwQb8Lm+A32AxbHJV/jP66Ndxifv0e
btdOuobKxrFoJXWbBf0j3PIQKwfxNpU1Kcdo2I69A3aG29hijTH+U/WWwVT+
LnQ37Am3a7K96r+wHw7AQTgEh+FIuD0LPIp+1Vh59DicCLf97GS47Wun4HS4
5apqofNcuMVkOYueg/NwAS7CJaiZ2XIrKq+ichVdDrd8RVfQq/BXuOU2Vo7j
a+qP4ZbzWrmvb2DfVNk1DkXbSt3fRv+GO3A33PK4612Z3pndw78PD8LNfuj4
j9QvabvHjv3E8Z+qPtVX4B94Af9CQo5bL9FX6k/wBt7CO3gP8RnN/uD46s8f
nT79yVH5n+FLuN0HKd/aV9VxuI2V/44+1uSQCM5zEXa95IkmBC9IBIkhSYQd
b5NG2HVeMjR5hL2vTYGmjLDzQApHK/rZvN1U+KkhDQTzO2kj7DyaLsLOq9L0
jv3YeUatZwEZWJaFY0/GCEO2jkeZsDPLh61s/xDdR2c0e4vjZ+WzbJAdckBO
8AYfGMYxzBc9Qj/wQ4+i/mgABIJLZeW30kGQyhxh4//0rCokwnLSh6JhEK5t
hUiIcuxox3fDKsoSg8ZCXIQ9wy3OcSEeOxfkhjyQ10F2PsgPBaAgFILCUCTC
4oZr/EJR7GJQHEpE2Pwvzf0qGWHvxp44cX0156YUy0pDGSgbYccD5e0oh10e
KkBFqASVI2xOuHLkVomw+RlVI+yeWvWr+2rZm536rhZh1/TV0RpQE2pBbagT
YdfKddF6sIt6ro82UH1quzhHNUIbQ1/OrU3QptAswvK7No+wa/8WaEtoBa2h
DfwQYflI2qqMXG+0Q9tDKtomjWKDYHeIMJXfUf2a31sLnbA7QxfoCt2gu2P3
cPxqrLMn2gt6Qx+VMcL2935ofxgAA2FQhOXTHIwOgbv08QfOOUM6NMLsYehw
GAEjI2zevObPF6ePjIqwvFM/oaNhDIyFn2GcY5f3Mz8Pu+p4dAJMhEkwGX6B
KREW035qhMXkV2z+adjTYQbMhFmwjfPObHQOzHV0nmPfd8qv7ZiPvwB+jbA6
XujUc3vHXgSLYQksjbCYWssiLK7scnQFrFRdcd2yCj3iYapczUexV2Ovcdpw
LbpO/TPC7A2Or9yzGyMs/+wm9Df1K9gCW+F3+EPbBNsjbJ7xDnRnhOXjmQd/
Rlj+0V3obtgDeyMs9vI+dD8cgINwCA7DRv7vCHo0wuJLKdbiMezjcEJ9NMLy
WStGlHJan8I/DWfgLJyD8xG2/AJchEtwGa7AVfgLrsF18OC4dAO9GWHjCCvy
+9kT2niwWyy7HWHv/CumoB9ix7H/naT8d9R34J7aDprpuSb6EB7BY3gSYbmK
n0YYsp+hz9V3OYe3gX+wX8C/8BLG0x9fOfaEzOYvUy52/OXomwjLx6ZcbG+x
h1LWd+h7+BBh57CP6CdtD3yJsHwO9+Er9rcIO45pud5J6H2E3j99V11EWr41
5V3TfI0E+J4wmm1PiHpBokh7/6LxKHoHkxg/SaTll9L9veJS6x4/KcuSQXJI
EWkx8hUrPyV2DGVJhaaGNJAW0kF6yODYGR1f8w8zRdr4IeWCzIydJdLsrJHm
az/KFmn7UvZIq0vVaQ7snOANiVNZHA4vxRSPtDwRvtpeWMy5wR8NgEBwQZCj
8oMjbR86BgXYhwpCvix2TxbCZ6EQBjk4d4WjERAJURANbm0zxOp3Id5Bdi7I
DXkiLdZGXjQf5IfJHpbvWnmu31PuAiy7wz5bEC0EheFKFsvRrJzNRfCLQjEo
DiWgpGOXcnzlfC6NloGykZYvvlyk5b65ppxIWgYVoQ/nh0poZagCCz0sNoTi
QlTVNrDvVNN28H/Vtd30i2Ssz4v2TZzZ8vDWiLRcvLK1TH5N+Mp+VgutDXWg
LtSD+tAAGkKjSMsh2hhtAk0jLddKM3Qp/b4C+1zzSMuxfgB/G3XTAr8ltILW
8JvzXE7P59rg/6C+A+2gvfolnGa/OgUdsDvCNtb1h8bIUsYY6KS6oP47R1pM
jS5oV+gG3aEHXE5qdk/H7xVpz0B763/1f9DPsfs7/oBIy109EB2kfpLJflM5
/gbjD4GhMAyGg6fekaNe6Eh0FPwEo7UdLOsIY7DHws8wDsbDBJgYaTmHJ6lf
wS8wReXUWEt0GkyHGTATJlGXExNZvmK9S1F+b71PmcVns2EOzIV5MB8WwK/q
I44ucuzFsCTS3gktjbT3QnrePpjtXIa/HFao71P2VF6WS1151FeybBWshi18
dw26FtZF2pjG9egG2Aib1M6RNhZHY3I2R9qznpx6TwBb8LfC7/AHVKc/bkO3
ww7YqXbkGPAnukvr5Hi3G92jzxNbDkvlr9wbafvQvkiz9zv+ATgIh+AwHIGj
qu9Iizt9HO3sYeeHLuiJSMtvrzz3usbVta7muZyMtPZT252CT5TzkWIIYp+B
s3AOzsMFuAiVWN+lSMsNejnS8oNeQa/CX5H2nFf3j9ewr8MNuAm3Im1Mg8Yz
3Mb+W22k9oF7kXb/IGTrPuK+o/IfqDyZ7ZpcuXIf4j+Cx5HWfzs59iDHf4I+
hWeRlg9XOU+fY/8DxfBfqNzwMtLiuv5KnS+AV5F2bfcafQNv4R28j7Rcxx/Q
j5E2LuUT+tnpm1+c/nk7q+VF/or9LdJyhyqH6Hf9TxTHa8qfAPWEhOAVZdeC
idDClLtXRus/eo6v5/kvITGfJYGkkCzK3q3rHftu9pXk+CkgJaSC1JAG3iez
8cZpoyzvYrooy02eHs0AGaPs2bFiL2bCDuc3wzJbLEvFtMwcZWPTdU2SjeNS
lihbh9aVFc0G2bU9kBO8YUdKy0HsE2Xj9TVuPxD1xfeLshzOirvmH2X5RRWf
SHGKstAvU6S2Y7aO1QF8HgguCIqymNGKsxUcZc9sdAwJwQ6FMJUdIiASoiAa
3FF2rNNxTstiIDbKYqbEoTsTW87Y+CjLs50LzQ15IG+U5YjMh+aHAlF2v1gQ
LRRleTKVLzMP+28+KMyyIlAUikVZTLZ61FP9rJZPoWlyi91dnM9KRFm/L4mW
gtJRlnctJ8ehMthlo2xOmuajlYuyce8a/664P/L7oitps1DaZBVanmUVoGKU
vQOshFbW77C+KqoT+khVtBpUh2lZLPeP8v7UiLJrhppoLbU31HHKr7LXVVmg
SSa7vtJcCOWWrM+yBlGWk0G5GRpiN4LGUTbPqwnagu81jbI6Uv1oPvZUjnFt
lPcVvydt3lzfg5bQClpDG/gB2kI7aB9lOXB/jLI8uB3QjtAJOkMX6Arp6bsZ
M1vOyzpJLQ9bN5Z3hx76PegFvaGP6hH6QX8H2QNgIAyCA2kt1pG+r3hHelai
d0yD1Yc0FkFjRrGHwjAYDscU4wldyH4QynXMSOxRakMYDWNgLPwcZde949Dx
UZarfgI6Udvlafcok6JsXMNk9BeYojr0tJhjU9WOMD3KcuEqroriq8zAnxll
uWY1dkf54Wfhz4Y5MBfmaX+KsuvHBWpDlRcWwWK1BXW4BF0Ky2A5rFA96jwM
K7FXqY/ASZ0joywf9RXKthb7Etpasdix18MG4WHjS/dTpxvxN8FvsFl9H7ZG
2b3Z7+gfsA22w44oyxmh3BG/pqKMsJNlf8Iu2A17YC8MTmc5Avdh74dx+Aei
bG7SQfQQNKRP9ofD2EfgqNoMjsOJKItVcBI9BafhDJyFc3AeLkRZfCXFVrqI
XSKJ5Q7bl9ZyjGj7lF/oVCrLMXSJ71yGYhyLE1IvV7Cvwl9RNrfuGnpd/Qlu
wi2tX+0Od6CJ3rlnt/Yclc1iqt1l+b0oGwcfQv2HKf4TffF+lMXweIA+VL1F
2Tiqx+gTqJLZYs48xX4WZfnTnqP/aLsp7wv0X3gJr+A1vIG38E79KpHlANZ9
xnv8Dyp7MrM/Ov4n+Bxl8cC+oF/hG3yPsuO0RzTnPvCEn7LZGAuNtWgOCVnW
hWODF5oIEkOSaIupnDTa4ionQ5NDCkgJqSB1tI3l0piuNNGWSzpttOWTToem
hwyQMdrmwGdCD/HbmdEskDXarveyodnhEXXUSTHYsXOCd7SNPfRBfaPt+blf
tD1D90cDYBLrC0Rd0RYbU/MIg6Lt/ewkD7umCY62Z6RS+SFoKIRBOERAJHTT
2H30A/0lGp2Tnv0X3NgxEAtxEB9tz41zobkhD+SFfNG2n9xwnjN855ibn2UF
YBXr/CWrXW8UxC8UbeP4C0dbDtK1npaHtAXHkyIsKwrFoHj0fylU/lPFipFd
ArsklIq2fD6huseLtrzkek9dJtpyqCl/2oXEtq+VZVm5aBvTqbGd5bErsQ9V
QCtG27ygpHovre9E2/lR58kq0TZWT+P0qkbbeEGNFUyY4L/0Oh7VWNZV94No
DagZbe80+mnsAXZtqBNt7zvqRts7j3pofWgADaGR6gKaQFNopr4ELaIttn1L
tJX+F9rAD9AW2kF7+BE6QEfoBJ3Vn6MtD/gV6qdrtMWM74Z2hx7QE3pB72jb
P7WfVkL7RFtO6L5oP+gPA6LtOl/X+AOxB8FgGKI+wjFiKPqayhiGDocRMDLa
zk+j0J+ibQ7waHQMjFU9qnwwHibARPVluJzadLJjb6ee06rv4E+Jtjqfik6L
tvE709HPlOETzMCeCbPUp6LtedecaNtv58I8SEr/nK82hV+jzZYujLZr+kXo
YlgCS2FZtMVg0LXacuwVsFL9GVbDP5zrnye1nPBr8NdqmyjjOnS9Y090/A2w
ETZFW25yPUP6DXtztD2v1bi3Xdmtz+xEt6Bb1XeizZb+AdtgO+zQ9+BP2AW7
YQ/s1fphPxyAg3BIbQhH4Cgcg+NwAk7CKTgNZxz7rOMrx+o59DxcgIuqe9rl
kuqLxriMXoGr8BdcU73DDbgJt+A2/K11sU/cibZ7UOWY1H3o/9fLXZWRerqn
cqL3nb6lGGWyhzp+07R2fnoQbe+IH6oc8BiewNNoi59wh+8OQZ/hP1c7wQuI
oM6jlBdd6+R3XqKv4HW0PX95E23HhrfaTv5/B+vJnt1yOmme1juWv4cP8DHa
jkc6LrF7eZTMZO/pP6lPRts560u0Xc/rWl7xPLTOryybns3sb9Hmj+PY8x31
cHOeAk9ICF6QCLbwv8H0syBIjJ8EkkIyKEH5kqMpIKXb7l90H5PKbb+vOcWp
sU/xvTRuQ3ZaNAxNh6Z323dOZLfPFEM2A35GyOS2+x3lXM2s36PcWdCsbttH
L0E27OyQw1Fd4+raNie2t9vOoXrf7uO2d+6+bru39EP9IUDlhuWcb1xoEARD
iH4bLia1MTSX0DD8cBjEdkWgkRAFa6jDtRDttnE4G7NZXms3fgzEQhw8Y/v+
gWFp7D13JOeBeJZf57u50NxuU/m6D8njtvuSvG57V6H3FIqTr5zx+dwWv1Vx
XPNjF4CCUAgaetgz6MLYy/S8Ei2qbaKMxdDiqksoCaWgNOznnLkPyqg9ubYq
i5Zzm8rfyfFrF0ygnsqrr+Sw58UVsCtCJXCzPZXRKvo8uT3/1HPQqviLWEc1
t411re628a6ar7YfargtN/xWlm2Bmvi1oLbb7oHquO0+qC5az23xdDQHqD52
A20vNILG0ET9Q/sr2gyaQwtoCa2gtdti8WgdbbB/cFuelLZoO7jpZfMP2+u3
oQN0hE6Qh7J1RrtAV+gG6XQ97LZzQxTHjB7YPaEX9HbbfXMfdL3ObWg/6A8D
YKD6ktti4Qx22xgZ5VMfgn2O7w9Fh8FwGAEj1YfdFp9C19K6pl7Ab87X9Q3L
R8MYGAs/w3TKOw4dDxNgotvyu8ieBJPhF5ii8sPObBZ/T9fL09x2zTwdnQEz
YRbMhjkwF+apX8ICt8V/fM618a/YC9XesBiWwFK3xfdd5rYYv8vRFbDSbTE5
V6mfu+2ebA26FtbBKt1DoRvcdl+50W3zvDVnfiLXV5vcVreq49/QzbAFtkLe
5PZMVLb0d/QPt+W43oZuhx3aZvhTfY0+84x63OW2ebK71acSWa7kPdjvKMte
dJ9j73ebfwAOwiE4rH7Geo6gR9Vf6BsX4ZjbYrkrpvtJtv84/gk4CafgtNuO
UYrLr5j8Z/DPQnHq8xx63u2cB9GLcMlt1wuxmqPktuPLFWf5VfjLbTERrqHX
4Yb6NdyC2/C328a9aPxLW45ld/DboM90r4V9z21zgu6jD9z2DuCh2/JZn3Jy
Cj9y2/szvTfrCY/xn7gtZoeQ/dRtcUGewzPs5/APvIB/4aXWAa8dlf/GbbHh
3rr/C9f/3/gR/jzeue0+5Yne0WB/gI/wyW1jzD6jX9Q/2H++qj11jkO/g0cM
/Y3tSYB6QvW0lvssIbYX7Ept8zqPcy2eCD8xHOJaOwmaFEbxm6MhGXZySAEp
HTsVpIY0kBbSOSo/PWSAjJAJpnN8nQaZsbNAVsgG2SEH5ATvGHtX74P6gh98
0nszNAACwQVBEAwhEBpj7+7D0HCoRNkj0EiVk+NZFBodY7nJFRtcMcIn06/d
MZYDNAaNhTiIj7HYzrnQ3JAH8kI+WEL759c2UbcF0IJQCApDkRhrH7VTZ/pD
UfxiUDzG7BKOr1xbrkSWb2uM80yxJMtLQWkoE2N5BpRvoCx2OfhOn0uQkfMO
dgU45WnxI3qiFWMs93IlVPmXK8fYOVfnXsUA1rwTxQFWvPDj7JtVVMf8X1XU
B41MaHmwi7Av5c9pOdeUe022tBrf+43+UR3djFZjeY2cFgu8BsvqYNeMMb96
Tvu8Fn5tfRZjds5k5iu+r+L81sWuB/WhgdoFRvN/aShPI+zG0ETfUW4ImEvZ
m+LfoO2axVhZmkMLR1s6tmI1t0JbQxtYzv8uy2kxChWr8Ae1gcaAQ1vss6y3
ndqeNmiP/gi9+awcdMDuqL6bysYnK8bXeX6/E8su6NjA/3bG7gKdsG9DY9rp
tuY7aH4VdOWzbtDd2c7MrPc9n/fA7gll6UehXBf0wg5DU6a15fr8KOvrjW7k
+33QvjGWj1fPYxWnxEt56FnWP8bySQxAB8IgGAxDYCgMg+EwAuZojD6MxH6G
jlK7oYdZ1yEnrvtX/H/hJ7WJ6jSFxdUfgz02xvJW/YxuT271Oi7G7tWUo308
9gSYCJNirJ4nax+DKTBVfUhzAelH07Cnwwzow+/NRGfBbJUzxvL6KCfHXOx5
MB8WqLywUNvE+W8k6/8JFuEv1v4JiVj3LQ6Yn9jHluLfpf2Wxdg46eVoM65j
V6ArYVWMxSlWvOLV2GtgLayD9TH/TaP6Ly/xEPbrDfgPKOfGGItTu4Bri03a
N2KsPjbH2LW1rqu3YPtTLj+Hrfi/x9g+5+tp+52+84fTPkuoy21oU+pwO7pD
/Z++tBP9U3XuIHs37Imxbdmr/2Gfbg77sPfDATgIh+Ab+137hBYT7HCMxQU7
or4Fx+A4nIix90cn0VNwOsbGvZ+Jsfh6Z9FzUJ99YBLlnqg2hQPU8fkYy5N4
AS2qeV3oJbjPMfeyY9/1Mv8Kdm762FX0S07L//wX9jX1cdb3G1zHvhFj+Upj
+U483MRP6GXvom/F2Lin2+rzDrLvxNhcAb0Tuxtj43/uxdgYoPtqN3gIj+Ax
PImxce15qeOn2hfAndDWF+2ofJVXcZGfO2WXqvzKTfqPtpnvnNF9umJc4v8L
wdh/8d0Mnma/ZNkreA1v4C28g/eO/cHxs+vcyzH+Y4y1pdr0E/pZ9RVjOR++
otdZ701Py22vOKffWPYdelCWwSz3iOUz8Iy1mJmKl7knveUiTxhr+cj38D2v
WItpngj9mNHmfyaOte1IgiaNtbxZydAI2viS8pBip4CU0I79KhP/nwq7FN+L
Tks/irU5avtYvhfSxBqy06LpID1kgIyQCTJDFsgK2aAA21nI28YAZcfPATnB
G3zAFwYntGOOjj1z2M/9WDYf9UcDYBafB6IuSOtl+QeCsIMhBEIhDMJjbR5C
RKw9X5me2p6xROJHwWyNzYi1+ZFuNAZiY+29dBwaD0fYtlxoc8qcG23mqPw8
6HV0kKc9G9Azgrwsywf5VTbF7o21bZiXyGw/xy8Ya3G39Jy8EHZhKAJFoRgU
hxKxlpOlJNpCcyE1NzDWtHSs2WWgLJSD8lABKkIlWOyMWa+MXQWeUp6qaDWo
Hmt2Dccf6cRgq4ldC2pDHfUR5bhk++o69n1P8+vh14cG0BAaQWNoAk1jLQaW
28fa3tfH7BjHb6b60zapvOwX5aEl9iA+b4W2hjbUS1toE2vvpvSO6gfstrG2
r7eLNWS3j7W4mIodpzkNP6qsqg/aN20Ki1uaDu3Isk7QGbpAV+imdoAe0BO+
sR/0Qns7dl9v8/uo/tjuR7CNZX3xtzvaz7FXcu7pjz0ABmp7nM8Up/ghDMYe
AkNhGAyHEap7R0c5tt7N/hRr72dHo2NgLGRlHT+j4/RZZsujpXxa4/EnwES4
R9/Ky/fye1m8uSB0Essnwy8wxbGnOv40mB5rc/1moDNhloNsjV+erT6r70A4
x4plGpuMXZO6mI8ugLwa360xgOgMvdtj2UJYFGtjpxejS2ApLIu1Oh3tbfU8
gPUEedr5T8gO0dzpWIu/sCLW7vW0T62ENFltXatgNdzisLgGXQvrVDewATbC
JvjN6Tf5nP+Rr31zc6y9W9yCboXf4Q/YpvaEHbF2/a2Ybroe34n/J+yC3bF2
fbAH3av1wP5Yi8lQR/N4sA/CITgMR+AoHIPjcAJOwik4HWv7Yzr6/xm0seam
ah+gjOfQ8+q3tOsFNDuf5fCy7/3tzF3QmObp9L2LLJvhqPLCyL6EfRmuwFX4
S3UJ12MtjteNWJuDUDyzzUO4GWvjfm6ht2EFvzWKY+bf2L4arxprucd1n38C
7qrPxVr8p/V83heK+JjejzX7Qaw9Z3mofQEewxN4Cs/UF70M2d35/nP0H3gR
a3Np/421+bSTOJ+/xH6ltk5oc/VeY7+BtyoD//vOUfnvIZ4yRqW2GDAfYi0O
jOr8o1Pvsj85/mf4Al/hG3yPVeAV0wRxZnvCfY4LCdH2lLkRpPAxbeLYKcGL
zxPF2f6aGE0CSSEZJIcybE8KNGWc3fd+Tm73wanwU8MGL0N2DTQNOl95lVKb
vSCn+U3S0Zfx00F6yO5jcWaz8T8Z4qyvZEQzQWbIAlkhW5z9Vhbn92T/6GPX
D7n5n+z4ebwM2YpxmseJdVpEsSASWk5B5Vt0KVcM35nGspyoN/hAJfqJr34j
i+0f+o5fnI0/We+M8dWcNX/VAUzgmn8SBGKH81suNEh1iF1QecVZvzu5qfw3
3NOe5vunIJjvNWV9ISo39125de+FHaZ1QQREQgP+NwqNhrm6bqX+3NiNlSda
5yjsvOksx2dV1p/My/a/WJbHQXycxY7NFWf5kpV7SMfi3Ppd/S/kg/yOyh/P
uecy6+5AmQvgF4TbGkvgbfGd+ypmi/Jus7xwnNnSIrDMWd5H+U/RYjCR80Nx
tASUhC2U8Y2uDeJM3zp2aWhL3ZRBy0I5KB9nsXOrJrL4uRXwK6qt4mw8UeU4
G1N0S+NjWU+VOHtnr3f3VfUdCOV8XV39EmpCLagNdaCu+grbWQPqYddXnUND
OMZvnoBG6oM5TeXr+abyO+l553E9r3G+ly2nqfztlGUbNI4zbRJndhPHb4o2
g+bQwrFbOn4raB1nz3Vkt3H8H1Q/cRb/Trae+cjXca1d3P9ygUvlV/Gxdqju
Y+MANB5A87YDqf/2fN4oidkBjq/yq+yx0Bl+ZFkH2Jfc8v52xO4EnaFLnB3f
u6r+fS3H4aYsFse0Pftbtzibr6+xNN3j7JqxB9pT/QV6q49AX1jB//dD+zvb
qO0boHaHQdA1k8UOGOjYg9EhMBSGxVneqOHoCBgJo1QX8CyR1flop+7lj0HH
ah9Vf+V3x6FF0fGOyp/PPvcrPOX7t+h7U3SP7GP2VE/zJ6hfw6Q4y2cyGf0F
psRZzE3FUZsaZzFwp8X9F+LSY7rqRH1QzxfQR1wLzYqzcayz0TkwF+ZBCvbB
+egCCFTOcdTl6M6EZi9U3+HY2VzjkrAXwxJYqv0QlkMwZVuhfQBdia6C1bAG
1sI6WA8bYCNsgt9gM2yBrfA7dKRuGlDuTugf2v+wt6Ex9B03ZNN7DD7bzrIE
/NY7ylTC2/JF7lCZ1b9YvsPH9o1afPdPlu2C3bAHvrOfRuewPO2KVatc7Tp3
q3+rT+9VX4T9cMBR+QfhEByGI3AUjjl1oTo5HmfvGE6gJ+EUnIYzcBbOwXn1
Z3jP8eei2gQuQwbKcAW9Cn/FWY73a3EWy/o6eiPOctv/iH8T+xbcBg/2rQRJ
bHsPUz9/s6wB23EHvRtn/ef/+53sYr7ma1+8F2fvBu6jkTo20d4PsB/GWQ6Z
Lr7WDo/irG13Uea6lOsHytEDu7tiwLL8CTxVGVn+DH2uuqFMR5LY/ZjGe25m
n/8nzsZPaBzFC7U33/8XfRlnx9BXcXZM1ZjPRfzuQue3VYZGCaxfNHL6xmuW
v4mzMr5F36lO4UOc5eb+iH6KszF0n9Ev8BW+wUBfU/knqLfJum5Dv2uf4hjk
Ec9xwtPm72mMfgJ8T0gYb7nGrjixI7zi7f1oIvQOdZcYTQJJ4y13VBifnaYO
ziS2fp+M5ckhRbyNgdR1jcZBjuY4lpJlqeLNHuv4uyhTucQe/w1CkV0+sfnK
+6KY1IpHnVplgrRwM73FUk8Xb/nrFS9SsSLT40+iz2dAM0ImyAxZICtkg6Jc
P2WPt3j0tRLbe6gc+Dnj7X5F9y3e2D7gC37gDwEQGG/XHLrecGEHQTA0zmF5
hUPiLZdCKNoLDUPDYVZyu6/vxf9F4EdCgXSWr2B/Mov1oJz0UfEW517x7mVH
O74bjYFYiIN4yAXts1gOUY0fzo2fB/JCPsiv34Dv9MnSfO6pZw74haAwFFFd
QDEoDiWgZLwdx0rF27HsbFaLe6b4Z6VVJ7qWQMtCOdiMXx6tEG9jqiqiZ5LY
Z8o9VCne8g/1o89Uxq4Sb+M4q6LV4p33ZlA4s8UXrM6yGtBB8QTRWlAb6kBd
qAf1oQGs4ndeU2erkxiy30BDPmukNom3/U/jmZRHsTxtUA6asLwp/Mt3m8Xb
MVHHxk20Q3NtB7SMt+cDreLtuY3udXTcbK3+Rru2QX+AttAO2vBZe/RHlT3e
cut2jLdcu53QzlofnE1pY0q6YqdMZnmzW/mZndzxu/FZ93h7F6c8X1eUg1D9
ChZw790L7Q0XqNdzsFRzG/H7xpvdL978/jAxq+U6H4D9jXV50F47/SznsfId
y45KYv5AtSvLBsVbfhXNp1GOlfksG8yyuegQtDzXCyX5/tB4i4+iOCnDsF+x
3/7M+tyU6SHffZzU7BjH/yux7eu3fMy+4fgZOV4OR0c49sh48/W/WkcsOgr/
JxgNY2AmvzMW/RnGwfh4i60yId7iq0xUfXGMmKR9je2fjP7i2FPizY/SM02Y
ij0N7rLO49T1dO1z+g3tt/F2XJ6NzlEdaH9hm+eh89UesFjvIfQOne1JS3l/
VRmSmr0w3vy/qa9F+i4sibd5O0vRm8lsP72VzOYNav7gMn2f4+DyeJvrvyLe
8o6fSGyxN35Gx8ND55q0Er9dOZGpfG+2MSes1D6i/UaxJdAM1ONNuM3/rsEf
yvauRW9zfFiHrofVnHNWQflENj9wA8s2wib4Tfu79oek1v7l6Ac+fNc7gV1z
zHHGmq7xtPf4l5x39oq98Fpj7vjfrfA7/OEgextcSWVtNop1lqJc27F3xJtd
xvHLsk07ddygb/6J7nL+fzfsgb2wz1H5++EAHIRD2hfhiLaT31gHR7ErUTcl
2Z8ro8fwj0NXtu2E9i/21UtwEju1jvnxNiboNHpG+3K8zaE9h57X9+EiXILL
6ifZzb7ifFc5S5S7ROO7PWiHq2rXeBuPOIb1j4Zr+NfhhZ/ZNxxfOc91L6B7
gt91rUCd34y3mIa31IbqM+ov8Tbe5a7aTNc98XbNlc7PrrvUD+7DA3jo9OFH
8FjrgqfwDJ7DP/H27GeV8/wns+IjsixLYvvtf+OtLLJfOv4YjncN2e9eYb9W
/cBbeAfv4QN8hHNs6ye0G32pR1LLefY53nJ6KZ+X4hcqH4ViGCqGxxd9Fm/z
Ob+h38EjF+2Ry67TPNGE4AXlOEYmymUxAhOjSSApJIPkkAJSQirHVl/X87LU
jq3+Lz8NflpIB+khA2SEhpS3MWTKZZo5l9lZICtkg+y5bF7MdIcczrJS1F1O
1Bt8ctlxY1Eis6W+qB/4QwAEgkvf97Vjjn5nvqOPnPYL0jZSjmBHQ3KZHary
cqwKQ8MhAirwecWkpvKbst7s7FfN0CXsA/Opy0iWd+TzKDQa3BADsRAH8fCK
9suF5oY8KqeusyEvdj7IDwVyWV/UGKyCuWyuq8ayaBzLKPpJIZYl0jwitAgU
hWJwUjEV9FvUWwmVGy2puoPSUAbKqp3VXtomqAiVoDKs07yZXBaHv2oui2H2
L2W7xzGmGn51KEE71HDatKbTvjUd/xXbXp+6eInWwq8NdXKZndjf/LpQD+rD
Eb73f0ydebxP1Rf3zS73uqZr5hqueR7uPE/IlKmITKlERChNxqSkaEBmJTIk
GmQeGiSZJWPmIURCkVB63p/f5zyv5/nj/Vpr73O+5+yz99r7nO85e691R7E1
kF1lH0F+50Aq/XVef7vsJpuBHnBFPjA5Xs9o17/eresdey/SvbWOCvkosrck
7A/0x4K0fFqeh8fR+6je9X0pr9/R6vuofCM8Ee1YO32jPUdQcwXlC6Af6Seh
PwxQe0c7xtBNyvMXNGZMGkjeJco1SG0Hg6P9nV6x2cvDkGjH4moNQ9Fz0aY5
i9g+noFnYRg8X9l1oXp4Tml4AV6El2C46pjzjFA9V/QatXr0+ZGkV+Wyz/tR
6KNhDLwMY+EVGAev6nec43GGhNfQx8Pr0dYnBOk34E2YCJPgLXgb3pGNwmSI
xG6mICsW9NpYxVabSvo9WMPxpyGnwwyYqbJE2GetfNdqn5xVvN/qypZKT6LN
ZrFttlAfRs6Ntj8DzTsaE+41k1o7+T75H0CHco6r9Jv+F6ru2edD5Hy1JWXa
wLG3Y2sLou0TVf5QP0L/kLyF2i/Ez5PhsIj0Pex+MfK/Qkb6EvhY9ci+S5Gf
wDL1HfhU7cM5Pov28+7nyC+inVYbysZXwJewUm0Eq1VHsBbWwXrYEEilN8Km
aMfA/Ur9IdrxNxfTtt9E2xdvGrb7LXo6chhtsBn9O9gCBbkPF4Dvoz2HQPMH
tqL/ANtglPwbYnubK1A3pHfATqG1X8jd0fYjJn9iWls5hvzRMA072xPtbxv6
rrGavLWwl7wfox0bcB/yJ7gpH1X0t/3oB+BvxpApcBD9EByGI/BztONZv6i+
FGL9aLTT5TQHmfSxaMvj0dZPwEk4FSD9NJyBs3Au2rESdX/U/fJ/cRNzO32Q
chXi2L9EW56Ptn4BLsKv0fYVIv8Ps3M4JuGlaMfx/J/vqmj7s/pfPMbgmL9F
O/bYlVLWrwRpleV3mKL39tzn59E/r5K+Fu2YpbqHS78epBWTTbHZ5DfwD/L+
hBuqS/gLbqmuZMeFPaf8NvoduAv/wF7s4F/ZDufbqHnqsmPIEUP/glzQWfMc
kXkgL2yv4nlckkrr3d763J4z1VLPtpoPyvZ8bMsPj3IdITH2U/FcTsfKUsys
AuR9pv9lyEoF3Y6KVa62DCUvDApBOBSGIlAUisU4nkRvzl8cvRcyIsZ+/+T/
r0SMY6GVRJaKcbzz0jGOd146SCuOXetSrrsy5JWFclBTYy+yIrJCIJXWXIjC
jA2RyotxjOBKMfYhrLXDWkM8Qt9K2H9kfuvq10qPoe+cYryvzP5VdKwYz83a
zbXvhaoxwZxW+mU19JNa91XA/yOqxzh+3Cqe/Wug/8n11UTWgtpQB77WM0WM
/fwqjlY99PrQAN7lOA1jjPQp0Ej1A00gGn6mz8UgY+EB2ioOGQ8JkAhJkKwy
QyqkwfFIr+tVzAOt7U0nLwMyIQuyVTcxfv+hd48H87vtmsFmrr15jP07yc/T
fejLqaMWqn/KUhta6hj05VY6DrI1sg3cD22hmuoN2qG3hw7QUeWHB+ES/aZT
jOcS6L1DZ/QVyMXY6UPoXWKc1zXG/2UeRnaD7tADesqe4BHoLRuGx2L8Hkfv
cPSe9vEYv8PuE5Rf8wSeQO8L/YLr7IxdR1XyO6EnY/zeWP5T5EeluXwCRPqb
Yi/adRv23599BsBTMDDGfX8Q8mkYDENgEccdGshnYqyrrzwb9JdhsId23KZ1
2DH2Syz/xPof9rzqFTmeerjF/fWFGMdHfTHGMVJfQg6HETGOazsSOQpGwwyO
OQb5MoyFV2AcvArX9WyAHJTP//vHo78O/Wm7J+hvE9DfgDdhItxiHPhKPinZ
/jVyEnlvwduybfpBHX2f0PE17irGPfJd0pNhCvxWyn7u5ONOPkc2coypqgv2
ew85DfLQHrlgOvo7nG+yfP6U9poLrbeQfxz9L53B9kP8rr7mxkQ5Hu1M8mbB
bGiEjTeBOehluEfOjfFcs/dj/J7xgxj73i1ewvF158kuYD4siPF8n4+QC9Vm
MY59vBh5lmv/kTpfgv4xLI3xu/lPYrxeYJnsKsaxyTVH51P0z2TrlPUD2mJL
Lvu70lqT44xNC2nXz3VO5Beyd/gyxr7SVyJXwTeUuyjH+w65AttcCatjPHdT
/wX0n2AN6bWwDmaSXo/cABthk2xY5dOx4Fv4KcqxyzcHaeV/F8gtgf49bIUf
YBtsj/F9aAdyJzTj97ti/N9E/1F2y4Zhb4z71I+wL8brwbUWPE8ur+XWmu6f
yN/PNWdi0/vRD8BBtWmMY9scRh6B+lzrUdr/Z/R7XP9R5DHVOZyAk4F+Kkg/
ie28qrmMgf5abqdfx/b66F0inFE7wjn4Bc7DBbgY4zWcWr/5a4zfLx7iProf
m7tE+rJsGK7A73A1xs+kivl5Df0M4+VqmMLYcb6in92uk/8HRCrOI+f+M8bv
Um4gb8b4XaWk3l1K/0v9DP5WOzC2lNUzn+ZPce0vwu0Yx/H9nfzTtGFubPyO
ys62lhz/LPmtkXdj7NvyH+S/Mf4WpG9Css978B/I6V5OyAW5IQ/khU2aP4XM
H+s4tyHIF4L/j59j+59BpPxBx3r+uPwd99A3UPloIW8140koMgwKQXhwnOcL
Ombu8ijfzwuTf6WKpdK/VfG3F+WdL+s+odidRdg+jryiyGJQHCqQfpvrvAGT
IIK8TPpzhp4l0EtCqVi/L+/K82/pWMc4LxPrOGFVqeuy6OVgOactr2NCNte1
hPI3RT5MeSNjPd5KrxjrdCWorDrj/v6gvlNgn1VIR0FVqAaXC3hdVHX0GrGO
i6X4WIpJqnXDiku6k/LsgpqxRnotZG2oA3Uhgrx6yFjKWx/ZABpCI2gMTQJd
sdGVjoYY7Q9xEA9DQ91/NU4o/Y/WhyL/RY6IslQ6EZJi/T4iGZkCD3ANqcg0
SI+1nhGkH+KaMpFZqrdYx9hbyX2kKXozaA5zeC7YCX0j7MtPsWLl2+8+trWA
kQUtWwZ6Kx2b/rOHum2N3ibWfuzuR7aFdtAeOsAo+kVH5DHs5AHkg9AJOqts
8Cy20AXZFV7Rmi5kN7hOPXQPdMke0BN6wSPQGx6FxwJd8nFI1tpB9Yswxy18
Ar0v9IPvOdddxvOtXMP3BT1H9kny+8faN+gA5FMwEAYFUumnYTAMUTvBM/Bl
lHXJZ5HD4DnVTynrzwfpF2Lt7/pF7UOZ5ul/UJj1U6FOy69CxZz2raBvk5oD
fwl7f0nXSJmHx3rOn+YOag6g1r3K19oInU91DKNhTKzjkr6MfJXfj411rNJX
kOOUB6/BeHgdJsT6WUBrUt5AfxMmwiRdNzZyEXt4C/1tqET53kEWp9+9G+v/
H6/pOTLcfWsyeVNgaqzXPL2n9uLapiHXam0V9TQdfQbMhFkwO2i7OTA30N8P
0lHUxQfIqsXsz0J+LeaR/hDmwwL4CBZCUfpVDOdahB6LHMPYtxh9SaylYjVJ
/xiWwiexnru7DPkLfWd5rP33fBrrGKCK//kZ+udQgf2+QK5QW8NKWBVIpVcH
tid9TSCVXgvfMv59U8Xv4g/AOtl8Zf8P7g/rSV+jbkaHWZfNK70BfSNsgq/g
a/hGxwuk0ptjfZ+8S91/p7rkGWmOfF3w+y2y9Vj7W5Vfr63oqdThDyofdrFN
NkB7bEfuiLVUeidyF+yVT1HVk76Nxzr24m69W1AZyPsRuQ9+gv1wQG1QyDHW
FWtdumQx5EHZoGwCOzmMPAI/w0nKcxR5DP7k3H2pgyfhOOkT2q56LOjnZT03
n4r1s5LqQ76TTsfal9IZ5Fk4F+u1YFrjpTVYv5A+DxfgIvwKl+Ay/AZX4Hd4
gnNcVTuo/iGZ+/4fKhPcgJuQxnWkwl+05V/KR95C/g23Yx1XRvFlVsEKuCP7
5VruIv+JdVwI9TP1N63/a8O2ody7WoW5rdRm1bHbCMryOPo6rXUi/57qmWeU
/5ANc7qecsRhQ4WcV5r2fwVbL1PAa+9ysm1PLveLXOi5IU8glR6BzeVF5oP8
EAIFoCCExtlmwpCFIBxa0/cKI4vEeQ6K5oVpTkprtXGc514VQxaHiDh/Z9T3
yF2UuQTpklAKSkNb+f/SXMhwfydJln+AOB9f5ykTyFZQFr0clIcJUZ7PUQE9
EirGeR17pTjHmlIMxcroVSAqzu/xqyKrqS6oz91QHb0G1IRacR6jVCcap7RO
U1JpremrHed1fXWQdaEe1IcGcY7/1RC5i3bbA02p9+bwOX26EfmNoQlEQww8
TjvGqkwQDwnwF9f+d1V/40wknRTneUrJcf7u9Ky+o+f39zz9LiX4rfwhhVPv
C8McBzyVvLQ469OD9EmtsdEaJORNPYtyrOEwld+la19kBjITsiAbmkKHMCO9
GTSHXvLTHZS5RVBuyZaBPgZaob+M7FASG1EMQ2hN3jry2iDvV7tDO2iv80BH
tavWYSIXRvgaVPYH4RN+Nxb7X17av+kEnePsO/AvmElb3pUvO/K6QFd4OM7+
lh/T+3euPQJbWc11diN/UEHr3eOc7gE9dW1xjvv8iPpEGce1+6e4Y9upjnur
DyAfRT6mdqTvPY7sA09AX+gX5/nUTyJfLWyfzEr3D7bLb9UA5FMwMM7+fQfF
OTao/jvpf1MN2q0WPE3+YBiiMpLOrur/bUPjrEs+Awuom2eRRbkH9y3osWsY
6efgeXgh0F8M0i/BcF2j+if1tpIxZ6TOVdi+n/VOZ1Sc3zGNRjbSewhkCa69
LnVSH14mfYyx/2g5+wIeS/oVGKfrhtdgfJx9tstf++vqs/CG+hdtMpOxbwZM
5h78JnkToTj1OQn5FrwN78C7MAfzbapvDVzzgdyOaa3Y1uthMtunqO/GeS7A
cT0nY9uf5/a7WsV4eS+Yb6959++x3zSYDjNgJsyC2TqPrrG657PPRX8fPoB5
8HSYfVJ+iD4/zj5v9e5TcU8WkP5IdguL4uwPdXGcfegU1/uGOMd3/oXyf4y+
FPbpvgifoPcvZ59Ay+Ic82N5nGNOK/b0Qur+U9Ub94fPkJ/DF7ACvoQLHH9l
nI/1k+416Jn6zs+5ssL8f0n/m1bLPti3N8dbg748zHFpPkdW4NjlizpGezR9
b636KqyHe5H2YyObWajvjfx+A/pG2KT2Jv0KfIW+imMtoc5XI7+Os1T6G/Rv
YXOcfRB/h9wC36uO4AfYBjHsGwtP0map0A973E7+DvXZatZ3BmnFa1Xc1l3o
u2EP7I2zD6MfkdXlu6Ok4x8qDmIGdr5Pba936bo27jn7kWV1T6KPH4jz2jX5
etP6tYOkDwW2rGs5HFzPaMoxhXp4r5D1I3FON+ce0Ax+1m8iHCNH8XHaBP7D
5CtoY6jvM3W1ppWyHVUfLG3/PhHyo4N8mHIeI7+b5vhQnjXs+y7yeJz/u+g/
jL7r6f39CfJOwik4Hec42GfiHAtbfkXOxtm3iOIIKp7gOdkyY2GbUo7TuIZr
XwtH2P8XtSc2c15tG0ilLyAvwq+y8QjHd1Kcp0ukL8f5nncpkLoH6h5+q7Lv
4+oTvwX94gp0pk1+R16Fa+rvpK8jQ6o4BrWegbtW9rcg+aH+g21/xtmn1L7A
n4auQdfyHXVyA70Ofb02XMZO+3K8/FxbX9rwKHk3NSZxfX8hb0EDyvQ38nac
5Z1A/5XflMXWLpSyXrqw03fZ9g/8q7bnmPeQ/8X5PWqO+OBdapxtfBXHzkle
LsgNeeIdeyhvvNdoaH2Gvqnni/c8Cs2dyI8eAgWgIOTknLkKu73V7mshlPww
KBTI+tWsF6It3mDfZaTDSReGMyW85l9r/xWjrAh5LfTuBdmBdm8PxeLtp0Df
rRQ/u7jKGe74QBHoJaAkHGGsKKXrqW7/lBp/Ssf7O6zm9xXSM2ao78u6P5eJ
t38M+ckoi14OykMF2EmZdkMkesV4r2uthKwMVaC91hioHIUtnyts/QHKW5X0
xLL2BSE/EHO0ro686+H2t1tddUi719A15vfvroVZPh/o+eWjkHqoyT59yzg2
Ri302vA013KF/eqoneBJ9HqqZ2gA0zTPiN82VF3Sv+8P9fWczmu/85pTVkXf
eOK9ZrcxsglEx1uXjIFYeIljx8W7TdWG8ZAQbz9gh7mGxHi/g9P7N93nkuJ9
30vWflxbCvIe7ZCKTKR90pDpkKFjQBZk6zewlnv0GmgW7zn7msPcHP0+mBdu
XxEt4u0v4jHqtyV6K9kuZYyAzbLncKdvInshO3K9reOtSz6CbBPveT33I09o
nIK2gS7ZTu2rtoGOcIo6fAD5YLxj2Z4t6ti227XGkLwfkJ2RD0EXGB5lf6Bd
4/3O43F4GL0/7ZKieC3ovSlfX2zwUWQJtneXjcNojtuecbKdfBur3Cqz9ofz
YX7vuo3f7IBHyXsMHoc+8Y4B/0S8fb9EMib1jfc8kH7IUdUcU+zJeK9P1TrV
/ugDVJ/xHp8Uw3Ug+jqurzG2e5b2HUR6pNZX0S5Pow+GQ9w7X+Sah6DPLej5
EHqVyuXkGBrv+/szqisYpr4R7+cA9ceJcDSv/b4cQz6vPgQvytZUd9CokPUR
QXqkyg9nuYZlXONo9OocJw29AOcfQ/rleEulx8qmaOdXkOPgVXgNxrL/eOTr
MAHeUNlo8+erWyr9Zrzj2SuWvZ7pFYdqAfJ7tk+U/XPe46RvIyeRbsjY+5au
kzr/GT7jvF9UM9LTijrO29vs806858y/izyJrAcN4E4x+xCdS5//AJpR701h
stqS809BRlCnU5Hvxft/1LR4+0zVPLXuel5ke0koAdNlS+TNQD7M+Wciy1CW
WfG+R8wOpNKK+6tY34r5fY28OWpTeD+QSq+lTGs0HnHMdpTnA/WPGka6YonP
Q34I8+M9r2uB+nY+x2QfGu647E/p+Yg2v0rdHMeOP2KfhfH2a7sIuVjtV9nP
dPn1TYDj54cl8ZYhgf4xLIVP4h37e1m8438vVxouat6MxhD4IpArAv1LWAmr
YHW861Z1rO/Qa+L9XXotci/1tgfWxTsm13rkBqhMP4iCjeib4Cv4Gr6Jtx/K
aK71W/QY5OZ4zyXSd5vvtB2+h62QF7u5n/7SDVv/Qf0Qu92GTK3x/+bNbY/3
3DnlxUMiTKQed5C/U2MLegPyGsKueP9n2o1sznH3IJsi9yJ/hH0B0n+C/dCC
Mv5TzHrLcKcPoB9UH4fDcAR+jnf+UbjOuY4hj8uWYXkN90n1x5OkT8FpqMSA
ME//D5Bn4r2OtBacRT+nsQE7+EXtwTWcR15Qu8GvcAkuw2/x9qMlH1pXdH3y
cafnMfSr8fY5J99zy7T+SPFqAnkt3vp15B/wJ9zCppLIe6WG9eQiTt9g2814
25/WiP2lfQOk/w234SV+d0e2Cv/ALPrKm/J/iH4v3r68umEX3eE496Zj8B/5
ORIoB+fpU8z61SJOa22B/HppfcF87u052TaprMeF/fomzbNhLvIGsO0C99rC
jDnhER7j9d8vN9vywBDaLC/yeY6ZL5BKl6A9SsG+op5nkJ+8kAR/4y+Q4G/+
Y/X/HT0UkrHDJDhR2O/o9Y1P7+y1Xi6M7YV0bM4VjiwM4yhHkQTX522thZMv
oCr+D7BYfs7Cret/gdJF2bcYFIcIlQ9K6ricszCUQi8NZaAslIPyUAEiYQ+2
8znnqoheCUZiP3doxwjyKpMO57mrCjIMGYWsCn249mrS9b0dvTp6De0b4vWV
1/T9jnv1Gup9HZzQOhCOV5N9Hke+xW9qoddOsA9a+aKtg/4M9VYXWS/Bc0Xq
Ixsk2Id4R+rgHm3WkHQjaJzgdzZNEvzeJlrn59gxCfarofWBWhv4Nu32LsSS
H097J0JcgueXvBH4Zo4nnQCJUIdrqg2TSzgmqeKRJiV43nVLSEZPgdzYUd5I
6+8UcjoVfTJ2toCypqGnQ0aC1/trrf9g2q0P5toXMsn/r5rHSo2TWaSzoSmM
LerjtMEum5FurvMn+LvnlODb56HgO3uLBI/TGq9bJvj/Titk6wS3/cNce5ug
re5P8D1W/hL/5ytFZed47ZDt4S1+20H9BbmUvtIR/YEEx0bX++sH0Tvq2SzB
a4gUj1FxrBVnQN/s9L2uM9segi7QVeeHmdjODHhK77S49q4lLA8HuuaCaQ2M
/ot2Y/9W+p8MM7DvLTwvPc01dCe/B/SEnyhfL+QjCY7L2jvBsVnDa7n+HoXH
ZGuyVdhBfe6CJ9B/5Vh9ZQt6T6943dCP9JPQX+NCgp8t9Vyp/voU6YEJ9tc1
CPk0DE6wXSuejt41DSE9VPabYP3ZIK3xb1iCx8A/+f1z6NeRuajzJlxfmWJG
elnk82y/wbYXEjz36kXkSwmOj920hmOdK+75d0Fa39PlQHg4+4xQ34VRMBrG
wMsqt8YSjSu69lz28XKLPj5Aa77Iew3Gw+sJXtM4AfkGvAlP0DYTkW0o22dc
71xOtxI5SbaSYJ+CZ/XtTXYk+5T9wzdV7cdKc8KnkI7m+qYm+DqbBHoDzStG
ToPpMANK0udnBvqsID0bOQfmJlhXvHClNd/+feQH0E9zwOW3kj44j/SHMB8W
wEewMOgP6heLYDEsgbNFjPRzyI+RS+ET9Sn4nb5SDrvZUpL7HunbZehnyM/g
c/gCViR4TP8ywTGDFS9YuvwCKN2b368kXQS5Crka1iT4vn+thp8JDgT3f6XX
yrZgPawt4bi9it+7gfRG2JRg/6zy0/oVem5sIS+Uoz5fxxa+lt3RZ75Bfgub
4TvYIjuCrfBDgmMxtmW83oa+XdfKua/Ih2aC4+IOoS/uRN8FFyv42U9ro7Qu
SmvmdpO/R+0BP8I+9UvYn2C/bfLfdgD9IByCw1CaMahUNa+/GBCswTiSYKn0
/uCd5Wzqqgz7JcPPbD8KxxI8l16x6b+p6fj00o8nOH0CeRJOwYtF/C73JeRp
1T37FYYzCX7O1PPm2QT79TyH3Mkz8y8J9h8q//TyU3+e9AXIU9x1nA8q1HRd
H0IehJs1Xa83g/R+6uZL/qtcVF9TefT8j7wMv8EV1TNcVTvUtPyhpvVr6O21
LhQOMAYchP3UeSp1cT3B8bK1RugP9D/hhs4LfwW63qcrrXc3ivE8jX45Qe9x
kQsp83j0W2z/O0D6bdmu2gb7vpvg7yX/IP9N8DXqum7AvQT7AG2JPjeP59e/
j/yP/ByJ3AcgF4zXO4JEx79ek8Nxr1/k+TuP5iNLsi0v5IOb9JNc2Gt+9BAo
AAUhFIZo/TOydE2P5WVl27RNIfImIPsyhoWjF4YiiY7prnjuP2s9FemjyGKB
VPoNrq94on2fFKQPR6CXgKX8riRySV7PhdL/BP1HkF4q0enSyDJQFspBeVib
w0ivAJFQESolOtZeZeSvXEOVRMeGOMhzwzNcaxTpqvAt5aqGrB4gvQbUhFpQ
Gz7jPlGastZBj1F/oH+Uhrqkv6A+6iHrJ1oq3UDXB42gcaLjrin+mvQmQXqK
nmsgOtFrmWOQ+SlXJtcfi/4z4+18zUFG/wi5iP8HzzOWx5NOgERoxnUnIZMh
BRZy7lRkWqAvCtLpqg/Gz4qQgZ4JWZANTXWcQN9VyWnFJ1EMQMUouUedNSfv
d+R9yBaJ9nneElklwsdtlehvHK0THRMropx9NbUhfT+0hXaBVFoxRhVbtH2i
78eK+6L/KPq2rW/cn/E8UI12rwEd2KdjomPmPaA2yeW4HrVz+boeDK6tZSCV
1nqwO6W9Pkwxt/XtX76r9O2nE9s7B+VcFLzzfoh0F+jJMbsiH060r0n5EI+o
Zp/i5fN5TbrWpndje3fokWifPj0T7eNH/yFvYU9/wSDKvpWxv1eiv2XcqObv
GYql/kii46n3Rj6qPgOPwyH6xiHauBPHPMP9szNys94ds+2JRN9z+yb6vqv8
foneJv3JRKf7qy/xu0xsJruYpdIDyH8Kng9zTMSBag/spz/bB6E/DYPV32Eo
PAPPwrBAl3xOv4cX4MVAfylISx8epBfRDktkG4xBI0iPhIHF7OvlPq67OYwi
bzSc4prHJPodjt7lKJ74y4l+lh2LfAXGqW4Ys7ZiYw9xX3w10b4I5YfwNfTx
KmsRn+Mvtj9VzEi/CVdr+P//teC+vj/4/y87TSadBJkVHePtdY41Qe2R12NZ
i0qOTx5GX3oj0WPWYOzzTfSJiZ6LP0nliXA7vpVoH8vNSb+N/g68C5NhCkyF
a5x3Pdd3HfkR96hFWrtJ/jR4g3JMR86AmTAr0XNrZiPnwFx4H76PsC65BT5A
X81z19rq/h+8lWual+h4rIrFqripki0DXfPRPkz0nLT5Oi829B4s0Hij8UPt
GEilFye6r6jvLFF7lsVm4GPZG3ySaB8/X9a0f99lifahOIk2W47+KXymfgxf
wAr1AcijZzLkKpUf1kBX7GMtch2shw2wETYFUumvEn1f+hq+gW/VDwK7kf38
b00G1/hdomO8bEl0LJfvkVvhHnX+Q6LjZbes5HYODY45jDIvom22oW+HHbAT
dsFu2JPod0fvU8658m9LugWyFfyY6LhQ+5APyK8tcr/6BudL5pgH0FPK2X/S
wUT7UDqU6GdlPScfRj8CP8NRyOA6jiV6LbjWhCtexHHSJ2QXifYzdwp5OtDl
e07p9pyvHZxB31fLvtzl0/0s6XPwS6L/a5xHXoAHsaGLyLo1rEvOKOm4kL+S
fwkuw29wRfZe29esOvhd9U3fvirbhuvQtpb1u7WcPki/+UNtm9/X/if6jUTH
pLqZ6LhUBWrbz0NrxsAKPPOWL+VtWu+agK1tRf6V6Bh0t5BD6eN/I28n2g//
p4Ev/rG0ZUP66J1Ejzd3kf9AJ56F/1Xbq49CFGNsxRK6iToe9iDUnOi5KXMu
SQjluW8h17Y7eDejdzR5yP+cMuZF5oP8EAIL5VsMWTDJ7z9CkWGwsrDjlRVK
ss/YcGThJPuOVVr6+BB/C3g9xPcrzVMrkuS+I39c8stVlHQxKA4RUAJKJtn3
rPzOlkIvDWWgbID0clAeZnBdFZDXtL5e76+pj0jSFaES7GBsqALPlvb71UeL
+x1rCmVKhsrsUyXJ75ejkFWhGjyGvVTXtemaYEQhx55WDGo9E9ZSGaEO1IV6
SY5h8lA5xzGpT7qB6rCsY8gvZ9syaKj9aeNGyCP6hoc8hGyCjIaYJO8Xm2S7
jkvye+t45CnKO5F2OxFi34QJSfZP2J9re5h7YHdIJC8JkiEFUiEN0iEDMiEr
yfHjs5Gvcu6myGbap7bHouaBvj4Ym37R+kbyWiRZvxCkpSvvPLKlys8xWyFb
Qxu4P8nxhnRPbJtkHzLtkM2RdXiOaC//24zt7ZMcl7sF19EBvWOSY6YW13wJ
eID0g9AJOsMS/i/e0ncr9nkoyf6q5be6S5LXVnVFPgwHqJs52Gwr6qwb6e5J
Xu+hdR49kuy/sGeS4/71Qj4CvWVXEY4N8EUNr9l7VPYAjyc5robicfVBf0K/
TbKuMV7pfvAk9IcBKg8MTHIsqGr0mUHoT8NgGBKcq2dwvi/pt0PJeybJuuSz
MCzJcXcUa+c59OfhBXgRXkryb+I4xnDVD+PbCO2j7/LI5wKp9CjkaBgDL8NY
+Jj9X0GOky0kOUbla6p/6EV7vI6cAFcZM6LLOG67YsVuzOd4sW+w7SbHuFXS
+ptBeiJyErylc1K2l/XsgP5OkqXSY6iP4lHW5UtaPqXf4d75Ltsnw5Qkzz2a
muS5SJqL9R56oxp+r63323UZF6eRNx1mwCeUcSZyVpK/Teu79Gz0OTAX3ocP
YJ7aMsmxyecjFyT5/ctHSY5BujDJsd0j6YuL0Ber3niWXqJyYe93NK5Tp9eR
uenPH6vtsaOlKoOuUf1d9Zlk/4LyM3iZ/R+DT8n7DPbSXz5H5uL3X+ha1e7q
m7AqyXGlVic5tpTmmirGpuabriEvA9v/i9+vRV8H62EDbNQ1lfb3xU1J/t6Y
K8RxBw/AV+R9restY39qihX0TWATP9W2jewLpNLfJtl+FKNZtiSp9NDgeUtl
UzuqDaeV8Lp+SaU3s993sAW261ssMpxjfsQ5F8Ab5G0l7wfYFsjtgb4DevCs
3V1U8Zq+jZS5cpR9G+5k+64kzy+vwvl2o++BP/Tsgjwc5bmyP+p6dC2wHw6o
PuEsv5nJvudK+DtzJcbOinBIv4UjUJ9njXr6Pox+FI7BcTgBJ+EUnIYzSfaf
2SfUc6c1h1qxNRRj42zQBueQv8B5uAAXdX2Mbb8m2Y/IJeRl+C3J+gN1nL4C
vyd5He0nHPsqeuVQ69eSnL6u61Z/4zc35XdUtoH8k7wb2OQN9Un4C24l+Rnl
VpDWezX54f8bvQh9O18ux3a8TfoO3FVbU4//IKNLe87mv0met5lL/mTQ/4Mc
yTxnQC7IDXkgLyyhP+dDfozMj1zDmL8aQtCHYUtvQYFkxzzT3KKCyV5PH5rs
sW0heliy/4e0o1wr6ROFSIdDYSgCRaEYFIdV3N8jkCXgvL6tJ/t/XSlkaSgD
ZaFcoJcP0lozrLXDFdAj4QjlqZjs9dSVkr2mWv6wKqO/QB+sgoyCqvA7Y2M1
ZHWoAW9hR5U4d1XG9Jqka0FqXvuR1Fq/odh9bfLqwG5su26y15UrVrtitmcy
dlQkXY/8CvIvhmwADZMdW0kxpRslOy77Ra05rOJ4BY3JawL7qNNo5PNsjwmk
0uvkNyPZMSN2RDhuXEXaM446XkXZ4ti2g/4Qj9yJTEh2jMJEZBJs0pxDbCQZ
PSXZ/VUyoq71VPQ0KMlvu7JvOnoGxGM3mcgsyIamai/q5nfO2wy9OdwHLaAl
tILW0Abuh7bJ/k82mOsaCu1IXyrh99h6n/09ZR/BsdqT3yHZca51T4uiXB1J
P6C8ZH9rUTyUXylPp2THihoOndG7Ih9CLpCvdeiS7JhLXZEPQzfoDj2gJ3yB
PfdCPgKTQrxG4kfoTfpR2Ss8LpukvWrQntXgEdr+LOncjMN92LYLO3oi2WvF
B+bz2vG+yZ4HqvnMO7jWfkE518GT6Pl5Zjlejv5S1/OhW7BPf/Jf0/yGUo6l
OzOHkT4g2flvB2n9zz4Z4v/YT7FtIAxK9nODnh8eCuTTydb7UBdzStpH616O
MzjZcekPkD9E9oscinwGnlWfhudkczCKfv4CcjTyRfVnGA6xEV4DoPPEBs8t
en6ZV8oxEBULUf7nR6hfwAfU2ya2fQ2jdDzZPvWxl2taJB+UyDEaQ2AsnGXb
K7Ij5DjVZ7KPl8HvX0t2/1Jf17ff8aRfhwnJjpn6BvJN2I89zSzre94L+k6l
dlbfhoPcrxO47rfR34F3YTJMgRn01+kwkv7/Ou07XPN/yH8v2etZpiGnaz+Y
CbNgNsyBufC+rhe+59xbYF6y1w1/iJyf7Ji/C9QvqJMnsIWP0BfCIlgM4+hX
S9RfYCmsoa0+SXYc1oocL622fXkuI28Z9dOPulue7Lik0vsHac3r1px9rVvS
+9n38/p9rWLAyt+a/K7p/8Snyf5P8ZlsiHv658gjnHNvSX9H/4L0Cvgy2frK
IL0KVus6KcNkbPldqM64toa8qlxvdb33QV8H65N9H1YM8Q3oG3U98FWy12Ep
lv3X6HsZByqH+x2d1mJoPa/WY3zDtm9hM3wHW+Am5f8+2TGOtyJ/gG2wPdB3
BOmdat8cfr+0S+2N7UyG3cl+970n2fpjpZxeyviyl/SPwXbl6/243svpnZze
IctvzoxS9qMzmWead2Ef+7fBpn5C/sm59ic7dqtiuGpsOJDs8WEs97d5Rezj
7TTHOEj+ITicbF+M8s/Uhb50hPTPcBSOwXE4keyY0yeT/WytZ+xT6PU5bhPd
I+p6vtRp8u7WcGynxrkd6+mM+hWcg1/gPFyAhtRvAygU5fW6mjuoeYMX2fYr
XEq278LLyN/givoZFM7pNYRaSycfBAWr2ieG/sNdVdlpn2vI6+rrqhO4oXaD
v5IdH1txsvUf/RxyTX6vq7/FtrLUSxk4R7neokx/k3cb0mvZT0IMfWAMfXp0
CcfnvpPseN13kf/Av8n2CXwP2YjfJ/As0BT5H+kcKTznQK4U++nSu57cKf7/
qG9n8rWXh3ReaF/K+seUYyONmZcKvUsd50txPCzFwsqPHgIFUjx/6jW2F0T/
Jrff84em+N1JGPKs/vcgw6EwFIEnS9vnZtEUn0vnKZbimEvyC6F4RfM1/w6y
ySue4niCiitYnT46g+uOIG8kY1oJZMkUx3QuleIYz82xvV2qJ30vIq+Mfi+w
2XLI8lABZpOeVcbf7PXt/kPK/xrtcYDy7YdIla2I34fovWVF0pXgE56dKiOr
wEG2HeL6d8gnPOmqUC3F/luqI2tATagFtaEO1IV6UD/F35UbIBtCI2gMTWA5
x1tWy+805Zdd7+q/px9E69il/Tz5C3VxDmLIe52xJhYZB58yDsUjE1Lsw0L+
KxQXReNIT8qaSP5jHPtRSEJPhpQUv+NYXp5nohTHplJML8XxSiOdDhmQCWm6
F0IWenaK4ycvpS12U1d7oSl5zXQ8eE3rcijjMPa/j3QLaJnimNjr6X+tVBec
qzWyDdwPbVVfBRz3uB36i8j2KfYdJx9y8ZSzA+mOQV0/AA9CJ+ic4vWcU7D9
xbTtQ6Tfr+g18l3Qu6r+oFuK41Z1T3Hsqh4p7jPqL3pf+SHnn1fAY11P1UcZ
f+sYSP+YybF6kfdIitfBXKGP/AYrsIWWjI+9yX9UdZziWLgaT/6u5Ljpj6cY
6YqfrmccPevo+4DWASr2rvzB9MYW+6iP5rYtPoHeF/qpzvVcpf5M+/3J+b5m
n/5BvrYPgGMcsxZ94D7KepN9miF/0Jxd6roSdfMU+7yj70/q8+w3CNkB+TRy
MAxJ8dxnzbccqnEDnoVhKfbltZI2acKxHqENe8FzKZ4fMTiYI3GUsfF58n5G
vqA2TPH69ZeQXeiXw5EjVD8wSueCMUF6dCC1/at89s3+MvrYFPuXegU5Dl6V
fcHOMl7fqne+USX831prt8erX8AE2UY++3yS7/ndeu9D3h5kHersTfSJUIrx
vbRiGqlPch31YVKK17m/hXxbdZbi9QVaZ6Dvx7pPbtazAPmTZScQQ9vGcezY
+o4vrbltE+kfU9n2nuyWc26O5J6KPh0+KGRf7hq/m2NDhbHXGaovmCVbgTlq
X44TIl9h7DM3xXG3C1bx8/L/npN1LJgHczn+h8j5sCDF8ZF+kA9i9IWwKMX6
4iC9BD5WfXLMpch7iluMXAYFqLOQSo7dvpx0ubIe57LYp6nW/6MX1joa2C4f
Kim2tcX0+ef03Er7fE7eF7ACtvObL5ErYZX6EXW1GrlG9o6+NsVjZyj2tU7X
T3vM0rtd9A2wETbJNuBP9v9D40t5r0f9mrxv4FuNDdj5K5x/bGmvT99M3new
RX2noGN8K9a37Px78raq3Douv9umcsJQ6nWHbAx61LU+j+v/AHah75Ydwd4U
fxP6nWu9UsYxcuW/90f9jn66D/kT1NY3LepmP/qvHOMI57pQ1v8FXmX/8XCA
bedq+VlT5Vb5x8FB8itQp6/X8nuE+vV8H9D/st01/d/skPoR5z+MvIIdXdX6
NfXDFPtvlB/Hoxof4DicSPH7Hb3b2YqNnlQdIONL2oZly6fIOw1nIFxtSZm3
Rzn28dkU+4lTfPlz6L+k2IaLVLQdy+/E+RSv47mAXM8xL+raITfHyguX0C/D
byqz7FrHTHGMqWspXud5HfmH2jtA+g24CX/BrZTgvYDiKKPf1jVzriNwB/2u
2qeO/dIVZ7wsBv+Q9yRlrcFv/k1xvCTFTbqH/h/kSOVekuq48rlS/U14onwP
oueBvJAv1b6e5f9Zvp/1PVPfNeUjOj/bHuKcIcgCUBBC4R2eh9/gGSI3xwoj
PRN9FXVYCfstRHoUbR6O7E6bD2XfwuhFoCgUg+IQker4RF/Kdyv2UIJ0SSgV
yNKBPppxr0yq58v0K+P1XYuxsVSuuyz5SzjHUuy6XKr9lj3MuYfR/uVJX2Pf
nar7Ml7PWkHXkN9zYSYV83wYzSeWLzDNL9acpEj2qZjq72KVsM+KUIl0ZZjI
/XQh595C1W6FKuS9rD4KUehVoVqq/RpVV/kLer3GnWDNRg3VCfaYWd/1rXpX
PWt9hdZZ1GR7U66hFjI/5aqNrAN1U63XC9JaU1wf2QC+4FgNVZcwoLZ9zsj3
TGPSTSBadQcfFfB3ulj0OIiHBEiEJKhEfSan+r4uOae+9RT01FT7UUhDpsPa
+pbr6lvXdyV9U9KczY+p6wy2deJZZH11x4aX39tM8j7kv2oWMlvXCc3gDvU5
gXPfRa6kLSvw+/LQnG33QQvZE8cqyHFGI3NzrpayC34zGXtrhd461WU7r1hQ
qV4rpHVCCXB/qudCt5VNcYx2yDL6/pXq96cdUu3DVe8LO6ZaPpBq/UHIwO46
6dghjA2QTvpciNPtytrnQ2f1E+iS6jWQXZEPQze1N/SAntALzlFfj6TafhSr
vjf6o/ASZR8u/yZsn8JxHyPv8VTr7wVprVPtk+p1qzHUVX7G4tjS9l0mP/Xy
G692eSJom/787inom2rZL9W6/vtP0/o29DH8vr/6nL6z85sM7G5MDusDUp1+
CjkQBsmm5bcAORiGwPs5PI84i/FoaKp9dJVuYP/K8rP8Cb9/nu15Stt/uvyo
yy90ZBjXRx0+I3uSLyXkMHgORuo3yHKU4QXkiwHSX4LhMAL2lLLvmpGp9l+j
+MeKgzxK9qFr0+8oy8up9rusd4dj0eeW9bFeCPQ5sE5x6rWf+hRl/RyG6DsZ
dfwqea/BIsrzbX2vQR9P+qTey6RanxCk9d/uDfQ3IXdZx6LPg5yY6rgaiqkx
Cf0teBvegXxcRwi8m+r4R4Vz+93p5FS/P52CnJrqWEXvIctT1jU8z4yk7kdr
mK9tu58WtP10jQ3yv1jZfXlG0J8Vp7cUeceRM8mblWpfBE9zjPOMYbNlq/S9
kqqTVL9z30Fb/EveXLU1fKDrJd2Zcb1LccehzY/tpOT1seelOt7IH5zvQ/Q/
kfORCzQGpVqX/LSQ5+1fLuK4SyX5zULyU/R8gVwMS+BjWAr7KnvNxyepXvch
/5nynblM16DjwWfwufqZYqOoLinnOJ43hnA9N8o6poNiO6xg2zG2nSjjOOWJ
jCNfpnq+md5jVYFIzbEjbxWshjWyU/UrWB/0p3WBHAAb0DeqT3C8TcgCFfz8
9xX61/AN/MJ+3+r6w23fI6jbzcgwxrQPuM9XwuZW0De+I+9Z7Hhcbb+vnMQx
x0b4WnRNrcr6nrAl1bJOoL+veUmpjoWr+KKKM5qqd23k/QDbUv3uUO8Qt6sd
1b7IV5E7tQ92NVXPhToGY8TuVOsd6zqtb/F7ZNcce1RNzy++WNJzjS8G8433
pgb/6fU+Tu0GP6V6nN+f6rFeSD+guuV+N0LzadEPQb+Cnn+j7y6HSbfmesto
bheshiPkpfOMUpq6eBqbHV3K5XyzpufbXWAM/Zl0NflqZXw5qrZWP9d/Jurz
uPZFnlB/hUFhnvd6Cv1SLc9RvVrc81T1TeQ0+WegUT2vMTrOcc/qGtWecB4S
ND8DeRF+1XFUt8G8wcuplr+lWte86PIV7atI73j2wCf1vA5Y386usE8y9tsk
p9cW/046lL5+FXkt1b4orgf61EJO32b8/0PXiM38iezDMW+kOu5OF67vIbip
cqTa/4Z8n8gHyoRwrwe7Rf7fcBtqcI9drDlPqX7nq/e9d1V2ynQJ/kH/F+4F
SP8PcqQx9kIuyA07sdk8yLzwEDaYLy1YNxB8511Ie3wEnWv6XDpPfvYJgQJQ
EFZzPdcoS2iaY4UqZmgYeiEIh8JpHjOLpHmMLIosBsUhAkooLb/VafbHUwpZ
Os1xjcsgy0Iz2iIayqGXh0GMjRWQp8mLRFaESlAZqkAUVIVqUD3Ncy1rIGtC
LfhUPnGRy5BrGPvHwstQh7y6UA/qQ2P6/hTyG6A3hC7ol/lNIc4/kvGoUZr9
hcq/fafy9oHSGdmY/CbwDzZzoK7jBip+YDR59/j9XYhJ8zONvnvGosdBPCSk
+X+s/sNW4vpmcc7KyETykyAZUiAV0iAdMqBpGcedy0TPUhvJ3wpko/fQM7/W
sHOs45y7KXltcnsN9Gqow/aWWqdN/n3I5sijNe1v9z70FrBBz3Rp9jtUT890
6M9xfV9RR63RbzOOtkHeDzHkRUM/zvdTTr9DaUt+B9IdgzpU/f2W0+lZOf3b
dnAi3Pem9uhvUcYOyI7wADwInaCz7BUGKJYddEHvCg9DN+iua4aeEMn1VFZc
SMr3A+NRL/IegT+qWyrdkTZ8EHqn+blc/iAfRX8Mzsu/FPJpytkH+USa/W/L
93Zf9R36cX6tbaR/9yO9m+t6ErmN8bG/7JI22ELedo4zQDYOA+EY6UE6LrTP
7ZjPg9FXyBcEZR2CPjRou2a07WjGmWdIv6Zveownz6IPS/NcWMXPUuykTHgu
zfGGFWt4KH3oeV2T7FF2CS+iv8nY3JR9s+EI57sCL5F/KcpS6f8gB8fI1ci6
5HC2jYDebBqJHBUcW+cYDWE1HP9ZPuPlO74IsjplHcO2Gsj63FNeRh8Lr8C4
NMcIV6zZV3VtsIl6GY/8Ru/JdE2MLa+rPmnDH2CCykn9vKHrUH0pTgh1k8D4
1ZkxfiJ5k2Q78DasZIwbSduMgJP0w3d0bsUhhXfT7NtkMnKKykX9XOPYT3Gc
EI63Wv7ZyN9Yw++6FVf6vTTHk56GnA4z0jz/aabOmcs+FD8p4PWbswIblX1u
5dwj9H8tzT7L5LtMfitWyUcBeas1z6Oe/cfKj6zeOet981y23eEe+b7Oy1hc
QvM/OU5JZDy2NRI+SLMPjnnID2E+LICvKhjpH8Gz3IeHwVTKspB0HeyqbhnH
WE+AZ9l3GsdbxLbFOq984Wks0dy5En439DHppWme/6V5u4dKOw5wQ679ber6
E/URzQlPs1+S5ci5jHGfIj+DL7hn/8jvuuubqNJqwzTf779Ue8GyMPvLOw3b
6vqdot5Fr1I9wRpYC9exr3UqC3VXmt9vwg7Wqz8jN6jdZJP0rdDcjke+SXUC
JSnP17IxHUP/qWo5hs63aX5OWKA1F7IzxoRf4Tv0thyjXW7rvxdweiD1dSGX
dSH9PGxhn+/V5vBDmmPs6T6v+PCKFS9/selc/za2XWAc2o7cATvTvC5ea+If
qur474r9vivNSE+pyBiDHse59yD3Qg69A0S+mstp/S/Zh/yU6/wpkJ8H+jTK
/h7sR2+OvR9AHoRDcBiOyI5pv5/TAt8q6JOC9G3K9BIsK+9r79zI16xnIT0H
vU07tM/juOKK/a16Lp3XfuljIrmn6Fwca7T6OMc4Rrqe5m1oLMnpuOMn0hyL
XPoHQVrx3k+mOea7nqMe4Dd3kKfIG6x5Q3ldL50ZX06Td0Z1ovccRbzP2WC/
IXktlT6n48J56E7brdX3mdxG+npdG9suwq+yBbgctNFvGiPhKtf+uyS8E+45
nUPoP9dkV2n2SfcH8k+4kebYj4r7+Geg31QZqI+/kLdgNuPy38glWj9Jnz8L
t9UP1SZ6T4X8J83PV//CPfgvIEc6z3bwOH1nosZt9GLUybX8jqu1lProSX5u
8vNAXsgH+aE19nh/aa+9CUn3c00B5EX2L5jucT403WN9GLIQbOU6wtMdr74w
sggU1TnTPQZ+XczjYD3GtBF1/R65eLrHaPnHnsqYcoL2iiCvBJSEUnAt0mvx
tCavNOky6faB0F7zLGibktxHypJXDsrDNNUT94hdyAqkI2Ex5a6IrASVoQpE
QVV4OZ/3/zq/f9M4r48xLdCb5PU+dSnHuFyW1dKtK/7uTspfAftLp56rk1+L
Mt3HsTojWyBzyO9I4HdU97NyXHsN9jsW6nc/NfUbXRfHKt3Yeu0gLVs/1cj2
XyfdNi/bf5oy1CVdL9265HuUoT6yATSEJjxvNUp33lTGg7nUWWPlQzTEqB75
bSjEplv2yGNdcynjkPFQWOsv0h1nUr5G5EM9kfTOXI5BkZTuuNXJ6Y5dnSJ7
kG+rPNYlU9ON9M+DtGQaMj0ob0ZQ9owgvZ3jj6ZMmelGuraX49hVuZZKjY30
KPi2kdObgzFSuvKz+E02NIW95D/KcR+HLxm3LlKGZumOw9IcubqK48vrvcR9
6fYB1SLdfqBaIstis62QLeQPGJoxHi2MdOzC5MbWFcNQ6bqKWaa6jvS1SrYO
riO1uK9F1xidx3kqfxvy7ld5a3vuQtPaXhvTlrx2slfOMSy3n6s0F/93yjOH
37dnWwfZVKB3DNKKFdU4xPGitIYmCR4g/0HopL4HD8EOjtUFeQ5b74qMy2Ok
P6zrZUxq2tBrJbuR7p7uNX49kD3hGcrYC/lIuuO/9kY+Co+lW89q5HQ3nhl6
wOPofeAJ6Jvue00c1xYrf3zca/uR9yT01/a8jo89QH2VMW92Bcf51nphrRvu
Sd8swTNLb+RT7DMQ1nC+QeobMFjtB0NhKfX8TJBeHuhDg7Rii2tO+n0c61nS
w+A5eB5ekC3AB5y7A2NoEiQHUulsyhGJLVQob12ygtZC53K76/4nvW6QVmxx
zYdeG0jNiZb+EucYDiPSrY8M0orBqririsc8rKrXAo+SLcEY1QuMhVc0LgW6
pOK2T1CsDqiq8SEoZwNkkuJ4sE9Cbsd6Vvx3xYHXHMDX0j13Q3OpHqzr+VTj
yTuCLR0O8f/s1zUeVXS87wno75D/s57D0d+EiTBJ9ZbP8qV81udyrLdIz67r
2ISKSatYhS9zrLd1HFiG/hxlfFftEEilJ6c7zvYU5FR4D6al+36p+6b87Wvu
6OkKnj86L8oxXRSr4UADx+m5ngOb4lqny7a1zi3d66q0vmpmumO3K277LNkl
dTY73f/N9Y1B/8/npPsd1DT63lz0X9nn5zzWD+d1+n3ZCsyDD+EnylUgj/WB
eZ3W2sE2MD/d81z/F3c+n2PQ5wzSC9h2l/r9CLkQFsFk6iYf5Vuc7nlFS5Af
p3t++8YKlkovhU9Ul7J1XSu/C5NvXI43SfM0tb4i3Wv6PlN7Qw3uYRG0RxHk
Cu7XReVPX3XNviuQX0JO8lem+/4SE9xjFItjczH7C11FerX6YLrvCYrjPpNr
X4u+DtbDBtiYbj+wq/jN3pr2JbMp3WPqVypzJe7JyG8CvUao04o7rvjj36LP
Z7z+EDanOzax4hLv5FnpO9JbYDN12Jbn0O/RW5I/jjrYir6X31yjXA0YT/5A
/pDuOESKR7SQvrWN9PZ06x8F6R2wU+WTD5t0rxfbjdwje9ec30D+mG79Z56f
jsA+tT/shwOBfjBIt6E8h2Q36lv6DRyFY+n2Kz6M6z4ue4vwey/FrVb86lzY
x4l0p0vAEY2R7HuR433Pc8YWOMn2TJ7xSlG/NFOOU6RPqz2gINf9JdvS5QOR
9H/Ic7J9OA8X4GK613LU1Tt/9EtwWfYCV+B3tR9cg+vQOdQxGP5A/1P2p/sg
3Eh3LIWb6qdwCwbR9/9G3oY7snG4Sd3d0rrYRo7dq+9O0g8H6X/YJx/X9y8y
hfLfS7d/bD1zbMLuFyH/S/ecnep5LRc3tp4jA7uFXJA7w3XWl2PlQV/I9sWQ
Fz0f5IcQKJDh9XRaO9KNPlMww+8bKmr9AIwPsw+MUPLTuM7vqPMw9EIwkP89
7egz4RmO6V04w0gvkuHvUvo+VRS9GBSHiEAvEaQrcE0lkeWRpZCloQz04ZrK
Znj80n3vMdLFNeeM6ylH/nDS9ShXgzD7VX6Ztr3HfX9sTr+nLZ/hd7VD2L8C
+tCKjnc4G/uJzLBeMcPpY/SNPFxXJdI7qLMnKttGtnJ926Ay+Xuw009l/5rn
RD1VIW9epOfdKNZdFOmqUA2qQw2oCbWgNtSBA4zRdZH1oL6uPZ99LizEphpk
2E+U+kgVxonK8mshf/xNHL9c94yV1fx+MRYasv8nlGc5/M5xP+L6GmU47nwP
jtcY/SvK2gQZDTGwMbdtLDbjfy7scsRlOLZ9vNKBnpjh9ME8XjOZhP4tx09G
Ds7l96War6h3pinkpcouMqxLpkMGZEKWykgZyuudG/ptytoU2SzD452k0op5
+q98JqDfB0e552znWltk+FtnywzHem+FPMmxohjj/qV+LtewXbfO8DOU3uHM
CN7j1KKOlujew7arPLfdj1xRye9xNtTye53bpHtxPy/Ffm2pv+HBeyW9I2vL
/u0yHLc4heu/hmyf4W93+oYnXxp6TsxmWz3okOG1St9Rnu+hY4aR/gDyQdUP
945UyOL8Gyh7J9kM9lYd4hv4+7Te3XUm/6EMP0+2xbZH0jfacZy2mmdJfld4
OMP6xRCnL2hNBPe0buiLsdnOXEf3DK/1W0R+BuftkWF7k3+P//2GbT2D4+k4
Sj/A/9NepB+B3vCo+iv94Wl+9xj6MdrlcZ1fa0GQT8huoR98zfhwv57vYT7l
uad7O/JJtQ8syuH/WAMy/D+rFHW+gbosXdExfZ/SmAKDYBu28rRsDoao/8J/
Jexb5Bn0Z2EYPAflaMcKUJvj7MA2nifvhSB/OmWPRN7Rcxl5d/M5Bv1+yvJT
Duu7g/RLGT728AzHutC9STHXRpAeKTulrKOQoyGR+/gYtZO+4Wc4Jt0V7iEH
kF9TxrHkhXKuV5Dj4FX1McrxGnJ8oCcF6ddhAryh8SOf7aZ6Put/RjqttmkY
6vaSv483Nf7Uss+OurW9Jle+cuQrdCLbJsFbGfZrrLjrx2o49vrbGX4OjW/i
eRkbYTW8Q/67MFk2S3/J4lxT0Kdm2J+m1te2UGwl2BFp35nyofke26fB9Az7
GpqBnAmzVEeVbL+z0b/jWuYgq4Q4HuFc9Pcz7BvyA10LfKh+Dgt0LPkihQj2
j6E/fiSb43oXZng9iNaFKE7NKPkWkc3Da9jaEuTHsFRjT4bv37qP59H31cL2
jynfmMvYthw+hc80zkC36ta/CNJv0bYrkF/CSrV/hsfS1bAPW1yT4Xcfb8Fa
9HWwHjbAqfyOLX46v9d+bczw+q9NyDDsNBS+Up+Bb9SvaIPjcLix40p+Kzsr
ZF+Mj3GNmzP8/adjZX8D+o70FrUVbJUdhjqO1Q/oY+h/25DbZcdQu5SfETrT
Hl1gPn33Q9iZYb/TjXn2i1ZMRtLZes+aYd/OP2u84T6wh/Re+DHD+j7oWcH6
j0H6J/WBDH/TycrpePZtkeGUd458gyIPZNh/5EHkITgMR6AE+5aEi/I7pP9X
5PUIcfzbm4UcA/eo6giOQ+sq9s8h/yknSJ/M8P+QRvzmWa79GX0r4HynyD8N
ZwKp9FmNAdTBv9CC/c+RbhnIX/4//VJ+p+UzWL6D62A/59UPdQxs+WKgK296
fcdXVZzVqvl9r/pVx5BNN7ENXM6wv7HfkK04xxXZZqDXiXbb6v+E/ldcJf8a
hLAtH3xDG1xXnXNNC/NbKi3+gD/hK/bZlMfxq29kuL8Pl28R9L/gVobjWjxZ
yX7mVT9/B3UyIJ//E9zV80GG30veUT3BMOx8YHHHTlLcpKLcS/4h/1+4B/9l
+F1bH/r0cGzqJZiqeTmMwzkyPQ8zJzKXdAgtYP/9el+o2ON5yMsL+SA/hEAB
KAi7wh2TOjTTcanDkIVgI+0fHkilC2c6vtPOivYrK5+yWVznb5xnguagwyns
tQj7Pc01FkUWg+IQASWgZKbXEazI4fmGx/P6/eUJzR1i260Qxx9XTHbFYdd/
3gzsuzTbykBZKJfpNhxDXxsNWxkny5N3P88zFZA5KU9u+SPJ9LcafbOpiD4l
l311ymen/E9UyvR7r05cT2X0KpmOWf0ZbRaF3ggbaJjfPvyqkq4G1aFVtKXS
0+RPnHPVCPQ1lZ1+uICl0jXZVgtqB9QJzrW8suPZf1rZSFdc+4QGjiH7JdRl
v3pQH5ZQL0uhgJ4zsJWzJb0mtUGm/c2PpF4bosdzrEbIa1zvOLa/Bnnlb4F7
WGPyH6CuO+n9D3o0xMD7IZZR+a3Hqr2p1/BI76O8eSGOU6XnhxuKUaVzZfod
pmKCJ2Q6TmgiMgmSIQVSM71GWrGzFTO7G+VPy3RM9PRMv6fXOifNgVlP2f8r
ZF+EP/Is9RNksE+a5vRQH0cK2rZl19pPuqR+p/rMzHQ9ZiGzoSm8zL4x9IEh
9LF8lC8Ke6oCzdjWnnvAGfrviXKeAzgbmpN/H7TItN4ySCtm9GLO0SrQBwfp
mdh9Dep2IePCe3ovy/Y2skdoC+10nkyPyVvZf3yo1/Br/b78R7Sqb38SHWSv
ah94EB6p4jjsTdk3J9c9XHPu9M5FcSMpfyedI8L+hDuj/yu/LMgucD7KMZ6r
YSNV4TL2sYfxaADHSqe8n3K8c5TlLLxKu44LcV5XfvswdIPugW1EB3oP6AkT
qd9+/K4X+h75oFNf4dyTaMOoxl6b3TvT83M0T+dH7PBuefu8f5T8p6jz/tUc
p1sxunsXsv9JxbhQu79LW3Tm+Pm49gzavR7tk4lcW9a+eeWj9zGOM4c2nQ2P
y+5KuD37wFdcyxPq29APnsy0D2L5Ih4PeTl2DfpKLciJ3oJzP4vsz36bGc8H
qIwwUO0c6E8HacX6LRvUnXRJ1dtv1PXgTPu5lm8S+cWQT4whmY59phhoQ9Wu
XNsG2vEZ9GdhGPyY234qnkN/XufUujHkPI49HyKphxdJvwTDM+2vZQTynN7d
86z2ez77R/qvsmN6z+H5aiTbR8Fo+Ku0y6x4xWPUH2BspvfJVcX7qW7kr/kK
7fJKUIYQGKd+TB1/hf4q+mswHl6HCfAGFMce1+lZGf0g55mIPE57Tcq0L1J9
P3+7qP2Dyzf4W5l+P/K2xkGO/Q7yLr97FzkZpmQ6rvXUTMe2lv5eptPTMh2b
fTpyRqal0r0q2Qd8TphJ3iyYnek55pprPgd9JvfK2UXsm7uWfN6RF0Jdvo/8
INO+qOchP1S9cV9IpS5TdC/g+PPJq6P588iPMj0+6tl6IXIRLM50bPgfYEmm
48Ao/o1i33xM+iLpXvT7peifyF7hbIRjmK3I7RjyyzMdR/5TZKruQ8iI6o5b
pphln2e6PJqzdV89P0/qubIL5fqCbZ+V8bfBMwUda1rP0ytU10Udo+zLTMcp
e1U+79knSvNbyVsFqzOtDyzg9Bq4pXEJuQ7Wwwb4J8oxRDeib1Jfg68D+U2g
fwsf85yyFDajfwdrq3p+eNcCniOueWhbyP8+02O7xvWt6mvY0Tvs27+G48f+
oHrNdDzU7cgdsBN2wW64QPuFUaY96Hsz/Ryi5xH5RfoLppR2vB3F3flC5+c8
P1FPP7LvPvgJ9kMX7ocPwQH01jwPlKIvlKLNDpI+BIfhCPwMLzT0fET5ojmq
MtCOx2TzcCLT715PIk/BaTijtoYkbGMsY9dPlGEX+nZoGuW4YufY/kum0/9X
Px+kV+ai7eCC7Ah+hUtwGX6DKzo++/2e6Zjjw7CdCbCHe2cD+kUjqAezQh17
/ihjZa9Ir9W5v7HXlmpd6VV+fw2uZzp+zx+yl5p+j/cnem3FNlO8Uuq0FuPF
DfJuwl+Z3n4r0/PXGjAe/Z3pWJe3IJz9b2c6hvF8ni+Ws/2O+jykM/b+o3bn
uI3k76ai20/xudWe/8I9+A/q8lyUI4vf8l/hRa4hJ3ou2MY9IzcyD+SFfJAf
QqAAHKK9b3POguihEAYrOdcKKIQeDoWhCBSFYnCGsfJadc+RKK5jco6ILCM9
BHZThyWy/L2qLNe1DEpmeb2mvlmVQi8NgyIdm3BKVcehnVrVSFds2lrYwRDG
7zLsWxb20y7lkOWzHEtebSp9bjWnK1A3FUiXC2RqqPUCVRxrrUstj6uRbKsI
9Ui34Xf1kZVIV87yPI/pikOE/luonzVXwOAC9rVUr5Df1bejndvCCOwvin2r
QjWoDp1pji6QVNlzfqbqOZj8mlAry/H40is7Jl8m9VWbvDpZnrumGASKBazv
Q3XJqxsV6FH+dvRhqMeSDwJ5N9r6yqAf1OM3M4o5rq3WACj2/Gyuv7jmAar9
6ftlaI8GWa6Xh7j2C7RDQ9KNYBp2T5XkYJjJ8UOo498qDq50ScV9bpzl/3gv
aX455dob5XUwc7C9JmyLDtpKbRaT5TlWl4I5PNll7IsgNsux4+OyHE8+t2JX
ovfMY1tNCOz1Ic7RFRKzHMc9Kcux3JORKdJhXqjrYHuM5Z1o6/OCPMWT1/0j
jX2f45rT1QaQmWU9K0jLz1o2cmI9r+0eAU1JN4PmcF+Wz98iKINky0BvhWwN
t3mOaYO8P8sxxv9mrKzL2NaW9ALkMOr1eWiX5XHiwVDHF2ifZT8FCfStDujf
c80dZROwuqznNj+Ivoyy5cDufscmO5H+levrrHqCLtAVHoa29Ovp1EM39O5Z
ntvUA9mQuu6JTKNsvQKp9AOMZ52oo4cgrpH/X+gb/yNs6w2PZtmniXybPIb+
OLyNXb5TwHG1FFMru47HvxmUbRrM4Fx9ZFNRjgevuPAaX+TX5gnyryL7IvvB
kxoP6nhugdYtjIX+5A3Iss3J9vTd62Xyn5JNFbNt6t2bYjV35J76AAzUceAP
6uzpLH8n280YPzjL67KHZHlt9tAsr8XVOuBn0J+FYbKPQCqtMfBSAY+Dkvof
L/15eAFezPLz7UvI4bCW+90I5Ei1geYOIEfDGHi3qH0JDpWvpCz7EJPvyTZV
7Yt1Nde+CsbKbuBj6nEpjNMYgM3WgWPU/Ql4Vdcgv8zI6ciylGE8+mMN7Qv2
38AfrPzSRbHt3UC+nmW9Hno++WyjjSZkeZ78G8hj1F8kZfk5zEh/M8ux5BUr
WzG0J+r6kKNhkmxWdgDv6NgwGabAVHhPfYZrmoacQJmm61zU44wsz2U8Gua5
jTOz/D9K/6f0/0o+/vV/axb5s2FOlp935mb5mUc+BTWveHgBx2p4n/z12PcH
GgvgQ5ifZX8cC5AfwUJYlOXnM8V2X5xlpC9BlsL+Q2if7o38TP4xeUvhE5VV
10LecuSnshvqozP1WJ7ffka6fJhttEKYx69+tNWGXF5nqVhOeamD08UcO0Rx
Q2ZT/5/zuw3YwhfIFfAS53+0mGPUFuZaCtF3vyR/ZZZ9EqzKctzD05x7MHX2
TJiRvjrLtqF1TFrPtEb2hy12ha8Y97uE+v2s9MuhTo8p4nIvptxr1cZ5Hcf9
j1qOZbJONh7MO5WfwuXIz2C9yq16VP3Us8+ETUEZv9IYAd+oD3Hs05znFCzh
uMU0v6SmY9o34D96P+R+xqjtmlMme6FONsueY62/F6QPUc4HqZPDyMqUPwq+
I38LfA9bZRuy/UKOY6N1LFpHovUkijO+s6pjhm9jn/aK4wg1eJbarjEEygV1
oLqQXiSv0+9yrA70v7cLuX7eqelrqEq7ROqbLnTk2EVgj+Jiss8u2C37Y4ju
gQ3syfL2vapfZM3q9gMnv6Y/krcP+pN/LsL/efR/5yfy9svG1Fd0/XAYjkBB
2n4U4/MY7uE/kz7FGHdUbQ+d6MvHkSfgIsc8qe1ZnotyGvkTfWUf5GPb57Tv
vGJ+B3wmy++BQwt5/or2z8V55nG8k1Wtn81y+j7Kfw79lyyv7dW63vNZjo90
QeeFlsUcs/7XLL+H1vdSvX++RPqyxku4onPCVbim41Hv17McC/kPXSv33T+R
N+AmtOF6W+t/S5bn13SFW1n+Bv53lr+Da+6v1s9rLvBt9acwx827o3rAdu4i
07kP9KDPdYd/SP+b5TnEk6nTd6Eg136PvP9UX/JZnc2zNOTK9ngt348av3OT
zgN5IR/khxAoAAUhVPtDDY5ZCFk9kEovZhxZBJdpu3DyFuo9rPpVbsfBGEXb
FCa/ObIIsigUy3YsYMUd13ofrfspnu3YwxHZ1ksE6ZLIUlA62/quqk7/xnNC
mWzHCFQ89zBYSB2VJa8cLAgz0j8K83OwnofLk66Q7W/k+j6udQdNG3vtQWS2
20htVTHb34n0vag1v28FRyPsC7kS2y42dDlV3spQBaKgKlSDK+y/hT5WXfUE
NeH+Ip5bc52+VIt0bfgkwv5C5du8DulhjBN1kX3Zp08VS6XrQX1okG0fTfK7
0zDb3wcaZfsbwTLq5na44wLv0/qI4o5h2Tjb97qp0CTba0Ob6V0Vv+lQzrEY
5btO64h7RnmtsdYZR7NvDMTq+uSvItsxzRXbPB79jbJe16l5U5ozlUBeIiTB
FGy4U337s0smfYL6SEGmZvsbW1q257z3p0zp6BkwjbEsE5kF2dAUmgWyeaDf
pzJh19GFHEs6L/bTIttxRFtmO5Zoq2zH1LoPm2iN3kZ1D22hHbSHDtARHsj2
PfxBZCddZ+DfSH6OzlKXZ+Avzf/T3Gy2Nw78/uodnvzOvqb3TNj6uAqBL0vy
H2K/3YwZXZBddV0N/L54KjxMulu2fXt0R/5T3L5g5AtPPvF66ByR9lkr37W7
qPde/L4n+b3gX/RHkL1hSYx9HTyK3oP66A4n9c6U9OOQXMHfA/LAZO6DR7mm
gkU816UP25/I9lyGxdA32/7/dgU+APuR3ohtbpD/bPIOwiStn8l2TICBHK8/
+gDYwZ+rp5ADYRA8ne250FqrPRj9GY7Ru5Hjbw/Jtj+2tvSDTsW9TlVjpsZL
xY3SmCOp9IRIz/FXjLCh5OeOcjywZ9CfVV+B5wKptGIbKu7sY0UdF/Z5jTVF
fB94Af1FeJ9yz4Vi+rYmO4HIcMuK4da7KgYJ6YeRIzVe0K9GIUdnO1baGOTL
2X6vNDbbazNKMn58LH9PpMfBq9nWXwvSsjnFxGob2KF0xcYaj/56tuM/Kn7k
BPUrlYX6fhM5ESZBJZ4xKsJb6OO5b7+N/JqxoQx1+E624za0hXfRJ8O6ao5z
r5iIio04hbwPNAYg35NNwlL5KsJ2p6PPUDk45x2tMYaZpHNSjxew91zIUshZ
ahu4Sl+eg1xP/UwobF9b8rk1V/Wr88C8bPt2lH+qD9HnwwKNQ7KRSo7VvRC9
P+dfn9PPRHo2WkTeYpWf4y7J9rOLnmH0rHIzyvH12spnIOeO11xB9imJnSzV
+Sh3zkqOF32XNmtGHTTjmF/FuZ/IN8jcIh4D1AafBEhfBms5ZyE9Fwf19yny
M7UFxxqneYrZXo+jdv4C/VAh97sV2p99WnOeLzUG6Z0o99uPYSPlX5nt95pn
69h3Y2XOUYX+PZbfrsr2GnF9z9Yz2OpsrxdaE8i12dYVu3hdtuMXr892PGPF
NV4fbFM6nfrIgA3QmX7QCRrQzyqQrlbNth0Z6LJtxTZSbBbFNNoQ2PPGbG/P
4Hq6BPtuynb6Sco9AB4h/yvZH3wD38LmbP+vK8l1loB87NO2of0PfZft9xR6
X7EF/XuIwp62In+AKeF+htiW7ffE22Uj5O1APoX8VXMr0HdpjII9sDfb/wf6
FPL/A8W1vBOs6fpR1wI/wf5sx+86DB0YD2dxvJnhjsF0INtxmPRN66DaM9vf
zA8jj2Q7rnt9rr9eNcebV9z5CZzzZ7YdhWNwXDYd7bUHJ9BPwik4re3VPf//
DHqa3jFmO4a9Ytn/gTxH+pds+5X9lzLNCGF85jznybsX7jyllZ+zsOWsQF8V
+OS80MRzEBQ/vT/yQrbvlxfh10AqvQL7vYS8HBz7N+RMzZtAPoHt/J5tXVK+
xa6qrCof/e468g/4ExqUs98SrcUfSPse4tr38yy9g35+g+03YWOofQnVwq5W
c2+L+z9EnXd4EMX39YEEQockhN47oZdQQgktvYFKV0Gk25VeRVGqiFJEuopS
pAiICIgoVUGKgKIgSFcRUEClw/s537Pv8/vjPPfO7OxOu3Nndnfm3uD/yH9t
Hf8F12+0tb+fEsSnEU5mXJegXjfVb7yHHQIxXOum/+zgFvF7Sfee9p7B9+TZ
JfWvra5tNmuPinzR/U5fvVvU3/F1LrEndZtRxOc/dJ5J32m3kP6LUJ//lH3m
OzzvLrintgEPQJsC3vx1iLktKzQbCAmowh/p+z59uqS4z0iGEpcdtKdPhknW
oC/Xsj/CDMrfSf+kuX41m33ahsHnjDcvGycK5wL1kOf6IDd8nnjPAZprn6nm
uXcXdc4bb338QN+3tC9Eeou4/KBAQAsGfBrzZ3i8bcc9oKyNWQ92oa0jiIsE
hUAUKAwSCvhdTh9Li8TbZmZR1Ym+KAYtDkqAOpTvAOOgJHwpUBqUibf/4jJB
uCwop3vqW67Kw/craL5CvMMVwTnZoCS/NshSUa5XIq4yqAKqxttvvfady499
NcLRoDqoAWqCs/RBLWhtlQvUjbe9hHrQ+qAB+EE2SqANQSPQON4y3zDgRZvE
O02TILya62tk+47nr6BdVhVwXGy8v23qvHzTePvFk3+8owXsK/BsXvsNbMa1
5gHE612lBTQO/Ih8FpJdLfhW8YEt3+K259ungr9P6j+W/k93zOn/1TrHO1N7
CEFrtXeM9+q3ifcZiVU6TwQfr34EN4rbhqrsMCcSTor3mW21udo7GfpEQBX+
g3qmwKeCX6jnC4ydE9A0wifQq+nQX5G90yAD/gLzdSZ0HuOtXUAVbg/yNrAt
tIfi7Yc6EuRmjn+Y8CMqG88dh/4dTvxq9EYH4j6Jtm/6jvH2S/897dBJcsKa
szO0C+gKusXbX/yj0PnkmZ1yhEaYF30siBcdqT260O6gh+or+aWdekrmZYNI
vmfE0y7bKF8v+N6gj+RDckD5UBv/8zVfsqJ9hZWAruH5a0E/tWsVU4Xlc6k/
/IAg/lR+X3sKPA2eibdv+t4F7Z9e9Nl48ysY35uK0ZfFPDc+R/zzqi9lG0gZ
BmVxP2Yv4r7ciry9RB9tgf4NFtAmV6FZK9gnl/yNvUC6F+PtW/ClgCo8ECxF
Lr6hLoPi7Q9XfnHFiw6GDgFf8cyhas8Qrxe1VhxGeAG6rXNd/3caHu9/TyOg
b8pfUU3rtZFgFBgNvmE9sKOYz7nqvOuCPP5v31v2f5hTx5BmPGNnKuUvCF4m
HC7bNOissfG29f229r4ghxPp01eIO6r9wuiWV+HHgUm1vWfwcZ45jH6NpZ16
yN5PEeuYv6nLGehrpH1d+YFTla0/hhV0X6uf9zQ2L3qtvH2VyWeZfLRN4J5P
kduJ0i3c11f/Iwp4LTUp3u8Tg6jbZI016AfU+yh5Ton3vJWf9G/ATwVfM/7f
lLyhS9sW8h6CaYTfAtPIvz16+qD+nUDfJm46mAEO0W8zobPAOwFVWN+NZkP3
sRZ+FzqFclbS9y3aa7z2ePDMOcRXp31mw8+QzSLq/S+oSR7PgVrgC9k3AHNJ
uw55nhdvP9iV8pufH+8x+k6Q74J4+2KUH8aF8C2RkUWqb7y/qerbqvZ4v0/4
A9Ac3fcHZezFeFkseWN8H6CcXQvYjnZaQf+r1Pdbrfu1Po7N7/XyD8F7ut7X
X8njb159eU5O5tcw8GG8z3XJf7vsMEby3FMR3i/Sj7oNqGp/1R+RbonGIunK
kmapdBKysize/9P1X3255J9rH8f/35pAa4TijJnr5P0vOA2/It5+4+pQjjHc
9wtxE2S3gviieWx3fFW8bY/rG/RxzSPSR5TrE+kk6PfaHwJ/WnsX4v1vdhbr
uVDtledZ64i7W9l+5bUHTPt108t7z24EcWtpm85aCxL3KWnXx9vXruYQzSWf
Ed4APgfLC3nvtPZQf8saaCNxmchiBP0SCTowjjapfLTfE9qnB7+CsnwMupF+
LXK8BnxB/E91bPdlIWXYItkI97pB34W1jtBe8C/jvTd8q9pTbcK9X0u/0hfb
oNvBDo137W+hDy+CrmAncaUY47vibStK7xx69xgJvqENKzSxzxr5Qm3HMx/j
3erR6rbxI3ugu9WOte0D5hv4b8EelVFnlsrYz00m930W0HzR5rOQ53XZFoT+
Rj6j0aejwFUmgr3x9rf4HbRZVe872yd9H+PzIaU0T2i/QLz3XB+I977riyV8
buGgdJnGMPiTcVipuP2sXajsdjoMKiLzR6A/qPw614nsvqG9HDl8nmpYdp+v
ukYZI+SfQLpQ5SLdT/H2u14oxL7Xp4b734/++0wr43N1K8DPKl+8bfseh/4C
TgRjW2P8ZLxtisg+juyKhNDHvxIXWsf8qXiHNQ9qfjuvsQA9IxnL6zWT4n4l
r7PEbWNMnIM+Rvwx+uQ8/AXwW7z3JsdwTyN9365q20i/x3tvif4jy979Hxo/
ajNQnj6ZQrtdgr8MerGenl/aZ/OvEP4L/A2W0u5XoVnQL9ekF5HtHsjHdfh/
pNPibdvgv3jbN7gB7coa/SduuUib3ST8O/RWvOdBzYfTZZ8Xeife/gTlS1A6
+13KvQM9nlHN/+hkLz8L64m7XLta0vuSo6t7nroXQLzmrvvgAZigb3ysrXTo
pCJtcR/5yAqfDdyjzvcL2A+9bPmuolwrwR3k7i4IIU1O2nYfca2Kme/bxOEv
uG8CemFXoCM6gehw+yqWz+Jz0F90HgCUKOlvXP2pz1MglOdmBzlAGIigjXNC
p9JuuaC5wRzymQ3ywDdEb+WF/pLb3x+/l98NkI+4/OBl2YJO8Dc0/TtsiIzU
ZI5sAE2TfW6ud5FdG9L0po/DE+w/MiLB/iTnlbCd9h3ck7uJbePIRs4V+vZv
6S/SRZeyX9SbpW2jthBxNeiLO/ovxxi/C/0SuYwi/i5lKAwtAoqCYgn+j1kc
+oDylEjwmv0AuqBkgn2pydaC3h9lb2E995ciPpS2vajvFPq+kmCbu+9RxjLw
ZcEYrQWruv5qh9HQctB5IdY5ohuqmR9Ee80B74LypKkgeQDDG9u/RCX4yioz
Y6oKtCp4Xd9oo+1Xo5raAFQHfzA+L1byunk/919CvmokWN/8kc/+A/6pYX8C
8nNQk2u1wArafj/teRB8Th0/o+y/kr421+qAuqAeqA8agGbIU2+dZwP3SB9D
3H2d7SbvXswtDdUmkuVI61XxjYOw7HRqb0OTBI/J2ASPUdHMcuZlG3RCmG2F
ZnBPU66diLC96MXQsQFtlmC+ufpK5z0D+m3A/4Vc/Mv93xA+D+Iks5F+N24J
3wq0Bm1AWxAfUIWzIkO7uP8S+SQQTgTDKpjfFOHwDWS3JjJwUv9aabukBNvP
l7+QZPgNdS0j18MtJymBfPzBc1MT7DdRPhPlLyKNcDrYz7UMtQVoB2JDbHvh
MXR3e8IPKQ/wCOgAkkv6nEgKtCPhTqBzAPFdAMMtS9cEn7s7R3laMo90I/xo
gs+f6+z5Y/Clkcfb9MHj8N1BD7ATfXIYnfxEgttjp84fVbWv+54aQ9AnE+w7
rBf0T3TmP9zTlbHbm3Af0DfB37p1Ln6o/lXCf13R68MS1OsqeuRv/ZNQnShP
f+kBypIT+R8g+eOZT0kGC9uu+g7SbC9qW5SyQ/k0154Bz4LnQCV0R0XwvNqR
cfIC9DX6PUznQEv5uS8m2G6j/j+9lOAzfwOhBwv5O8Yg+MEJtqNdOqfbYggY
CraiO4dpjGo86L8CdGSC6aiAH51gf5/dwXdF/E9K/6bGqB8ktwn2Of0K9FVw
G3m7BcYl2Pf3awn2/y36esAPQ+6GRth/81XWBV+zXh/PtTKRtmkbSl+sZtzv
k+1W+nGH9DTxE0gzEUwKxuFk8B7PmKJ6g6mSee3fhhbi+dOgb0lWkdsG1ezr
KSrG/p7m8ry3uTZdeoB7UnQWinGfC/2ZQt8u5voMrs0Es0CSvpcw3t6BL1jI
dspmwx9Bpt+FrkcOYmVLDV01J8Fn1oYgE3Phz6NH50Hng4s8d4HGDO35RkHb
DFtZ0H7TFybYd7r4t4LwIslDTfvHaBPr58s/uXjlo7D41kH4vQR/81kJ3hev
czUJ3gckX9ryo71YcpnV/2bkg7scdSkPPiT+owT/v1gCzZDMVbOOk++u49r7
rT07CfbVUb6y/18uI/wvbdMPXfdPbX9HmF3N3xWWSz7ACskhcSsl17TBqoAq
vBp8kmB+TUAVvksbroXegy5E194PsU+Ig7KBxTz5vf5hqN8p+xuFzH8ahNdD
PwPXSvkf4JQa/g84pZCvFy/v7yb6frIDvM0a6i3QgfbYkGCqcIj0kv5rJPie
u9T/jvbqSFeA72VDPsG+nL+Q/CF3bcEW+C8TvG/3KPdthZ+n/zha57JO+koy
QnsWQCd9DR9exzZ4R8faDu82jT/47dCf6IdjYEeCIf4HvdvTnrkKOs8a5F+r
ur815Ebed0pfQhdS112SI+hujXXKO578n+LZK7TG1nsJ8d+CPWAvSKPe30H3
gf3gAPhG/lNVX3AItOX+BNCBtIcJd4wyH1rZ4T6ypQz9AfwIjqoeYAtl/hl6
oonDij8W0OMB/4uuSx9IVpGpzXRBKZ3xTLBP71+hpxJMFb7P9dPwD6BlZI+W
Nvgkl9+v9I6kd6YzXH+Bee8s9JzGpMa92ob+vZBg27bHKPtvCbb38hrP+R1+
KTrsD/Ur70fxOp/JuL1I+E+VkXuaoL8uwfdijF6GXgF/Jfjssc4d/w1/VXKo
cYAcLgfXE/xNtK/+f/GMfyS3PPdfaC7pOnTUf5KfWPvclq/taMpTDRQh/SHS
3uD6YWgjxlC0fCpk8xnw1LI+o3qT6+2C/YfiRbUfUX6X9N6v9/+3keNbXLst
MJ7uaMwFOrOH9i9C7yeYKvwgIcv/nKVnBY+xdgyRPTTZNaxnnz/y/ZONayEg
FJSlvbNDS1ewLZ0c8A+QtzDomOzet5ITfkEuj9M29akjz8qV6H/4uaF5Em2z
J2+i7fb0h88H3weaP9HfpmbltE3tgvLjQdxpylQQ2jDafHiiw1koc4TKX8Y2
4GULvjCIJG6T9pfl83+jQoTL5GCdyvOSyacytHgp+1KNUp6htiMrO6+FCRdJ
9L78otBiiR4zogeC8dOfMvSlr/pCixNfApRMtNyUSvR50QHaz6Z81W6gnOpO
38+jXytSlnmyNULcTu29SzS/PZ/D9SlXRcJPox9v075DKeuQUrbTsVPnCrP5
PInOBumMUCXSLkFnbJJdBtIto+8qE5dEHlWgVUG1RPu6fgh93hS9EguiE23v
/U3arDr8UfgaifaHOYnmLUL6ydCF6IGbtFse8Jy+dXBvTdKdVfuCTYyzWoRr
gzqgRiH3a81C5tW/CsuXYF34eqBHIftD/5p7B4LVzLf1iW8AMtBpk5Cd9uQT
o34HjcAHzI3va88P/H+MjaGFfaZqBOuV4WAc/fqD5rdE73N6ua73PUXLPlak
5Un72QaH2h/MEsLLQGyiedGmYB16ey7POSn7kWHev59L++1kZ4DrzVVOdG4m
88894lsQvgv9UDZD6K8a4f6O8X4Tz1v6ViOfafKdVol6ttW5mHDb+Jbftzju
bwlaaRxx/VH6sDV8G+UVaztjbRNtayweepI2KJvb61etY19h/E+hrSaDBK4n
Jga+6bUPBXThmUnEJYMUMFs2V6Dx2v8HPca8dauS1wPTs9tGn2z1TWEumqz9
Kzz3MrrlEkhX/4DMRPv4bpdoG32y1fcfbViKst6AzuLZs0H7RNOHEs3fCvMe
bO3FfphwL57RGjyS6LJ3AB3Bw7TVYvTRCfq5E+HOoAvoCroFvPy8K/wo+Jk5
/zHoPv3XkK0c8bRdd8kaeJd54QloT/CkxiX92yvREF8W7Kbc5/ReFun18phI
r5lFYwqbX8Z4+Fhjo6D/eel/V2/pL9AX7EF28vlXaJZ0ntmPuLWMzTUR9gUv
P/DTmpoXfZu27a/+UhmjzYs+lWif5eJ1Te8xT0M3Qws29ndKfa+U/2X9R5UP
5me4vhC9+azai77qAp7TuG/sfW8nwD/yV0fcC2ofytSSus2jvX7W2VHiXgID
QSXW7FVAgcK+9jTlHKT2ok8i6O+JyPp6+mYSdDDxjyE3QxJtg1/vP3ugt7l3
KHF3oMOgw8EIcJN2GSmKzExCNkfBT4aOhl6lfGMC+nKi+VqUfyx0GDL5CvRV
ME66S/np/zlj6XX48Yne8ye7PhMSbdvn1yrWq1vD/U9jYqL/a/zO83+TXqPu
y+iHScTPiDb9LMr8ZPhw6h0C/wt1PQl6RpkXncL1NxJtv0u266bCZ2vq9wvx
onrfKE8ebypf8J7OdoI3kMe5pP2YNl5RzPxbiQ6/LV1KvklNTesEvP5NvR78
n5qe6DMAM6AzlRd4J9E6TDptb1nLtuR6tmQKzAH90BtzlQ7d2wQMifEaRWds
5yXarkgcei2O8VQY2Z4f6KEFgS5amGi9Jf2VIh1NP/dE976s/2DgX565SPUE
74MPwGL1HfPlh9BdzD8fqa/QYUsS7f96DXLZlDaep31u1Gmp6gAao++WJ9qO
z0n6sn+UfVp/nOj93mdow0msS1cQnljE//9WJvos2irptbL2w7ga/hNQrZht
4zegjI9Av2LcbAVruPY0bbAWui7Rc6D2zmsPfQ7K/S7zbVbk7FPi10s+wAZw
j3uzUvZo7dmmLJ8neu/EgAjvn9BZ8tO05UbiR1He0WAb2EQ4jDlvM/QLsEUy
BLaCr0DOEP8rlH2igeiZx6j3aJ1LkR3SWvYl87XalLy3QbeDHYmW451qY7Ab
fAMucO+rYGx1n3W4Qn9fBt9yrYr+ezY1vycI/yV/fGAv4ZO0Uwhl+S543slq
fqbswy9tahvx8qEiXyojwT6uXdMeVdAdfbCKdJ+A/cQfAPMow8GAKvw9OKT2
RJYOQ4+AH8CPifbpORedcBT+J/AzaKt3Bb07JXqf8vFE71X+BXpC5RNFR3xF
+buR/6+ET4HTamPa4DrxV/VfifVXNq6fIX4K8954fQeGPwc2RznNloAqfJ74
lGp+/7kA/xv4HfwRUIVlj+lqVdtnukj4T3BJcodcrC7pf2Wyza9v1tNK+czZ
Za5fAX9JV4Grif4Woe8Q1+AXked1jT3tzYb+C/4L6NP6zwxtRp+1ADfhb4E6
yFt72um20qkOAS86lXa/A1+gut8LxVeOcviu5BncV3+w/nucuAfwA2QnnzG3
QftxkpjTqiBP1CVrkv/X6b+dvlu3aexv11OC9cKQ6n5nmFTd7xDiU8oGYe4N
ATGMgd7ISij8+7JpGsx7mvPiGM/Zic8BwkBOcJx5JFdAFc4NSjHvZdPaFD4v
yBdAfH5QIOB1Xef/Cib5DGBDUIt7wwlHJPkft/51r2dOejjK/jaraM8DcTWR
j/rERZLuu8J+lvIoBKJAYVAE3KVuEfTtTa0VGP8JtFl8U/tSvBD4U9yA7G0E
DzW2/XzZff0NTEE3FeUZ3WjmqfCxlK0Y4eKgKW1TAlqTMpSE1oG2QPc0B6UI
H4CWhpZJsp/7stByoDyoADpRt7GsBSom+Vum/EFVgq8M2pWxjbwq8FVBNu1v
gr5Cnvvoh+gkl+UyfV0dvobKAWqBM+ifCuj/Uzp7lGSfkPINWQe+Lihd2HY3
ktCdiaCeylfTfg9yodPrqw+hLWnfVeiPT8AHZf0vU/8xw5DlBqS5z3vMMfgY
+IagEWgMmqhsSV4LrCCvpvDNQPOAtgj4fvRj3yLeuzaY/kis7fi44LrCf1Xx
N0J9K2yZZHt6sqvXCr41aKPn0AZtoe2Rt3n007vamkc4AXxAuyVCkyhnJHJQ
CJyHP1fDPm6/ol2SuP51cfu9PR/EL9e/Ep6TzLWUJPuv2Qjq5PC/R/2DTE2y
/R3Z3kmgHm3lu4373kNWOzMW09R3+pabZL/TGhMZSR4XmepjlVnyDx4Gj4AO
oKNkQ2NPeoHnd4a/QPn6Ii99KltuJQOS3S6SlyIeC+K7BuFu0EcVpg7hlPdp
ZPMxwrWpX3JR6yO1idojUf94uNYdDKG9bzO39IB/QrKKDH2qd2Hoe/RRzyT/
g3gS2kt9Wdc+Q6Q7F9MPV2SXRTZaQG+uz6jhfWWPMHbu058doCel15C/O+A6
47iPykV8X/Ul6J/0P7M+Wf7UfhjWVAMIPwWeTvJeM71v6b3rGcLPgufA8wFV
+AXwG3W4EGLbgFsD+4DDmbc+LumzmPOpw0L5USDty2T2EnR0fscNTHK8vit9
GeLvTPp/sA0MSrJ/t8FJ9k3+gDoNgR8KhoGltNNw6GTGfu5S9v02gvBIMCqA
+NGgZzX7oM9JW41ROcAW2qRnYfsNlv9g+QgtUcy+MH9gPh6b5HJEcM8r8JHQ
K6W9X+lVjT3aOi9Yo7UsZRlH3GtJ3u8zGeyoafvVt2jbhdB2zFGvc30M88NS
nrMdukzPk04AE8GkgCr8NnI4AR00HVqihN9VJxP/DW03Jcn7/vXNTv9k9A3v
DeKmgjfBNNBb52eg3+WynzL52Xib8HTJSpL3ZytO/su09tO6bybxs8A7YDZ4
FxTl2pwk22o/Us+22+dqLKFP2ze0HdV5SbarOgOZnl7FfTon2Fem/WXzCS8A
C8HdEv5OvQj+AePzPfVHeZ9xl+/O96VLkry/cTH0Q/ARWBLEL03yvsdl0Fp5
bSt3uconOQIrwSrVm/X7OtrsX8bFasI1oZ9AC9HfazTeaNc59NFa+HXgU/CM
9nPLT0Re++jcQR+NJk2G/jeDRcQPQbfk4971Sa6D6vKZ9CNyE61zXLT7hiTb
Z/1c8TnRn2AjfAnqWaq85XeT5JMxuRlaJcR78p7Ufp4k+yqQr80tklPG5xfg
S/it4DPyOab1J/PGL8jZV5I5dNdksAk5S6bMX0v+Kf9I0FXjifB2sAPsBN8y
HnYl2c+z/HfLj/cq6vUyzz5D3XZrfOv7VTFDfC1oJGvSb7gWAf0WugdUp33O
VrPfafmf3pvkefI70JhnvU7affClkJv90APgccp4UP3I9el5kCnqdxR8r3TU
6RD0MLhN2WMZP4vpu6Y8u7nWoBpD6IPR4AfJCe09iveNbjrHFWMf4PLz+GOS
/ZoelZ6inZ8Hq5H3nwj/LLkinzw8/xh8NfKIo2+rQo8T/gWcACfB3+iJa6Ae
z/2V8CnlCZqiT2LBYPTGn9x7hriz4Bw4D0LRRxeS7Fv7kPZN0n6/Ed6f0zaV
D0DbEN8a/E58cf2TloxAn9f5RpUb+qtsiSXZJstdyncJ/n3WHJehXzBGriTZ
J3sr2uivgP87yeGrSfZJL3/0E/PaHo/2o/3CPHONa9fBPyBE9hSh/0meKecN
6E0QyXz2lr6pa9zkcJzsAieA2xpvyOsdjekk6z3td3wDek/l1fhWmzAHzGAe
6tzc/qFO1rHvMtnEln9W+WaVDY6RsuXaxL57syTbl29W6AaCn4Fs8M1p77jq
3g9xoKj90IYQH5rsd9js0C+RqS3gKepfl7asA17l/lfAp7R5jmT7RJBvhDD4
nCAXyA12UZZrUfaTkofwdWjeZOu1fMke1xrjssGcn/AU6PP0fwJ6Ll7v0zy3
APEFQTiYqXPilW0/TXs2IoiLTPZe82MVvfe8EOGPqcdy8BV5RxF+gXL+EGo7
1dKr3ZG/wsT3gBaBFgXFkv0tuXiyvyeLlgj4ktBSoDQoA8qCcioT5SgIysNX
SLYerwgtRB6VoBHQytAqoGpAF2UxfxhZrE5bNpDPA/qhGnGVkKPo5OBcZW37
EJH/kJG0Y3Xia4CaoBaorX4izSfoi9U8cwFt+q3OQBI/R2ew0V03wa/cX1f1
APWTve+hAfQmNAbak3I0hF6k/Rol259ZY2gT8Dey1Qc5i1VbIetNoUvQcR/J
30eyfbs1h7YAcaAl2I/eTEKWHkYeWqmPkf/WqhNlnAV6cq1Nsv2rTYyyjXTZ
xr8CP4w6hDLP5MhqXx5tSRcPilDPBGgiuMQY6Ui9LkKTkl3vR5rbF9w3PGM3
SCY+BaSCofR5GjQdZICXZK9ZNoHg24H24KFkr4W0znsY/hHJtOQOeeoIfUDd
hzLGOiXbV8wQ+M7JDp+Pta/7s7H2T6j/bPJRKH/yslH+N3r6arj3xiwnTRfu
+Yp2mISeLoX+XYKu2A3fNdnzjeaausjEn8jmBs11PLsb147Tno9Cu9Dfj0Ef
B93BDwUsiz3AE+pP8CToBfoE9oB13nsaY6kb46c38c/zjGy5vT9I5ztkS1k2
lfuoTbg2Icq6ua/ajTG5Wee14adqjzB1uwb6a3wjr51p/9357EcuK/XLEmu/
8QM0rsgjH/37FPzTydblz0Cf1RhFnz8HXVHKMvR8smWqHvroPnX9oK5tFY1i
DurFcyKYk17QdfKbSL88qX034MVky8xL0IEax7TXIPU/+m+w+lVyr/U9bfo3
GEp4GLhb3P5BleY78tqPnKbTHmVoo4rah5yL9TDXRoCRYBQYT5+8DkbD/6Rv
EqQfA/8yyEYee2SvgOeMJfw6bfgKNDd9vJVrr8KPAw1qmxdNZLy+prTgrOxv
U4/x8BPAcNrlVcbua2Bi8v/cvGeZBJ2cbKrwlGS/u+q99Q34fUROR57mUs+p
hDfTFutlO5W83iR8gz4K0X+CZMvDW9CNeR3/Nvx0MCPZPgS1N1K+4odnsU9n
nSebyrOfg84kzTHqNEvjj/qOK+S4dbTpB8R/Cn1HeaCH3tZ/G+kKMLqq7WL0
ivC7y5xkv6fSRFnmSq/R3/OSbUdJ34rmJ/td/R74r5bbsQn1aVzC70YLuJ6X
ebQH8QvhF4GH6Z/3NIahrYj/Q+dGKvh/ZfMa/mf5frL19AdgMVhOHT5Mtp2A
lCy2FXCTcXALfET8hWIOLwn4pckOL4NuoyzLJc+SZbCziP/b6Oy4/t3om4i+
jayUrqA8q6BjoaslW9TzE+iaZP+LWQs9Kd8y0MY0yqfQQtW81lR6+W2X//ZX
kJv1hD8DL6DL/qJMV0Ej5PYkumkD8a3QNx1kYwa+P3QjtB+0LOXeJNlItl/7
/6jvv1nMy7+9wnO1d1E2Pouav17M4Z1aO3Pf0OKuy0tc30I4AvkqAKKLG+Jl
R0t+pRtH22ek/gl30DZg5u8vk/3fV/98t8J/q/0u0KaRtpev/XtqZ7X3b9BV
5HVWbQZ+BEfB11zbLdtf5PckGIOcXeD5x2ibiTx7G9dfId+W6I8xjOntyf7v
fYR1wWF9u6IdKoAd6jPpMnA9p89f7k72GUzZ0l2g80QqY7KpwrK/sEeyC71N
2fdKh4AXGb/zGHNtqOM+6R2e3wDs1/PRFzv1nRo+hD4+CP0eNEG3nUHeilOX
EdqbW9sQf5p6HiLNIcbNuUb2KSP7WLIRJD2t+VO6+pj+RYZ4vu4RfD/TdzTZ
rdW3MtmuPcxzjoAfwI+gGvWoXtw0Iui7V1u4nqqj9sEdlZ4DP2u8g+OgDuWt
B36Bf5tyh9IG06EnCBemvLvorztVba9Wtmp7tPCc/Tj0JGl+BQdqGeL1fX8b
bXYK/iXmymWF7XN1CfS0ZJwxux6ckY4ErxX2WkE+df6Kss9Xfb/5CORD/s8l
25/C+WTbX74AvZ3fNsb+oV6ZtM2v9E8UzzxM+4TTrmnUoU5O+6uUbfje4Dfu
6wP9HfoHuJhsHytLAj8r3cn7CfAn8ZfAZXAFLNT+Yp0zhv9b9dOZbNLVC7G+
W00fXYX+QxmvJfu7+zl955QtHcWDf8F/0tfSM8k+P7eW8fkpKEx/RoX6vFq4
9lJyfW4R+3dZCQqxNrtN3B1wN9m+0+Rb7J76nHLd19irYKr9y+Lz019TmH8e
SP9TjiPESRFWrmyfFDrj0Z57h+t9Tu+YofZjLH+/WUmXDYSk2IdvKDQ7KEp9
B7FeKAbNQTgM5EzxO1YuaG6QB+QFL1Y0ny8I639bucD+Y/4Uv8fpfU72CLXn
WPuNH67tcz1vak8PaWoiXwWh4SACRIJCKfZprm+eUSm2Z1+DetagXoUJ/5DV
57iLpPgst+aHovDFQC/6vgd9Vxy+BCgJnqX9b9PWpeBLg32MwTLQXNo/AW3D
9dZgFmUpp3jkvjz0IvNXBWhFUEntCpagg6qofKBaivdMRQc0S8BXB8nl/X++
IOVczHxSI8V7iPUeUFJn3AjXArVBHbA0h/1zL0MWzpe2zcjCOT1uNWbrkqYe
qA8agBjQUPUPqMJ/5LI/1s3cE4keqV/Rtnp1HqMx15uAWLCe8jSFNgMzWAM0
h0aT/6P00V36KD98VdBCfVzQ/x7jAl70JejGGv7uqW+ebQtbj0mfyXecfMi9
wLieTT/NyWqbFRUY08l1bfOjJc+YqfOa6JBW8K1TbBdAtE3Ayx+29j3JP3bx
7PYFKD+AHahjeZ7xMLQtaWfntm3J+BRThUcybkfo3324banLhvpa8kpIsd/W
xBTrgaPV7TtbdolfA80YJ5/E2F+i/OW1pZ1OhNofShL3DAvjuSAZfgrpblG+
FPhUkJbivQvpKf5OkKGxIhu3svUB3079r39p1Ps+aJ9i/+PyPT6Q5zyU4nd7
vde3JI8MytUizPzDKQ4/kmJ7KR2gK2WHHboK2gk6jWdupq1G8MzOhLuAruBX
zUfgeeo3nP55Vx+60Rt3eF52aAp91410f2kOpM97Er+zkX3Dy0f8ef3/138I
wo+S7jHwOHiLfA6S7nOubwLTCPcDrUnbXX1KXld4fg/4BNoxHjwBv5b4NSVt
s7daEdvt7Un8rCK2h/AT7b1SvgJZr+aRnb6C9jN/u4bLLVseKpvKJd/1WkM+
meJ1ZEfyriybq9m8Nl3GM3pxbTg6pzf0Zcb3sGreL/41uMm6omU2l7uPxpB8
bbHOHKPv9WoP0Jf4A8jdSeSqH3z/FPMvhtqnunyrD1D7Rdiv0Iw6bh+10yXe
r56CPp1iPzPyNzMV7CJNGvcdaeJ+qkx9n5GeSrGvXPmHFi+fuQpP1BnOij5n
/1yKbU29jC6cSdmfJ9wC+gL0IOU8BPIRXpjV/foiGAr/DnnmlGzDD87q/7Y6
a9eDuN9ok9Ho5JdI+xsycI+5qGlj+5UpgTxW1/9Prg0Cg1Pc5wfo+/Hoi+20
wzbQnDwv5vNcqTmzob5HgGTJToj78GnC9Zmz89GPDaCbcjtuD897l/ptJDwb
2pX0scxXNemPjmXt6zm8jPdTyubVhpb+l64z1zp3+g7pz1LvNrTjVzzjtvZe
Q/tKRpgT+0GHaG4hr6Eax+CpBt6b+RL3vkwZx2Szf+dHAvvA+2rYVtZw0o4A
I8Hr6JxZ9MlrPGcebbZSdjKJ/ya3bf/K7u95ynuTsr3C88aBZ/RNv7TP4I4m
7RPUq5jyg3+YsnUAL8OPTfGejHE8+5UU5/EqdJx45Q3Gp1h3TgATQTfZf4Ee
psyHwGT4RNZJU1L8j0v7iSpqD32KfT1/TV9Ohc+LPsgP3kzx9yN9O4qhzLdA
w5LmdZZW4faUtQZ1fkhrUvojEUzT+E8xVbgBeBt+KnWfnuLvTte590nafQbh
Xll9pk/n+YqDfcjYTI158A74nucfArOls5jzuqO3v4O2CrXvatE2AS873O+S
7o5sLtGuD1H2tYzDOSnezzEkh8+JTiH+T2hJvVdz7V/9q4V+hN4fTj/2Ir/5
hBdIt+byd4Oz9N9Cwos0D+XwPmDtB65X0t9r9d12HXiP6++DTui0jjX8HfUX
1g8nkaUPiO+MXOQnv3602WLNy9z7IfSC7OKQf+3C3gf0UYr36Gqv7hL1UYj9
yIlfGoSnIB/LVDf9I1a9GQcfQ6tGsw4BK+Dnks/sGt5T3CHOZ4917vgV+bTl
vlelT8O8534l6Qui+yLAcvptD2NgVYp9nZ+hvqtYJ58K9XlFnVtczbVPwBrp
bsmozvcwdtfBf5riPlD7i48t7XAZylUarCfuM7BBOgN8VcpUYe3xlu0B7fP+
l774B3wH342xNy67v6F8IXtTqjvYHFCFvwDvoX8W6d8YaU5ns+1v8SvzOqz9
sPqvpj2xOhe6hXve1FnLFPt7z9PSvOhW6H708gnWTAegXxH+GmxLMb8nzuEC
lHG74nn+jhSfnbqAHphY3XakZU96dk77XJe/9Z0p9pO4CxqNDB1jHOyGL0Mb
vqa1J/QatB999w3xx+nrPxmXL/Lcb1P8Lqe5ag/8XvAd2Afm06c5pdeQ2b6g
IDK1n/gDtN+BFLfj3qBdrzY2Vbgz/TaA9h3EPFgSvkQl2z6Qrc2DGofgEMgS
Yj/tgnj5az+cYrsQbcCsOPtEbwEGSf8iV0e4fp92aSH/pdAfgnkpmrSXyZ8m
yXKlru3oyr6ybOnKh1LpUPtR2s2Y2FXYPj47EtcZ7Khr/7vS/x10DoFnRjB3
hIOPGW9HCf+UYn55ENb1D/VuCaZT1m8Zx9/ksM3Ugo1sN/Vn0h1Te6fYp+Yy
6acU4wQoqnk3xXshtSfyV/hToEO4z3Sfhj8jGdY7jGzswJ8D5zXGweVslvUr
0N9SbJ+xfAPr9shGPicu/8Ahje0jWHx8EM6D3PwunSHdDP6UbFK+S9ASYbb3
fxN9clljEfwF/gZXweK69nXwIfSadAX55Y2zD5LrhH/Wvl9of67/m2KI/w96
A4zRniXpdsp9S3LAtdt6DrgLxlK2ecT1aOBvaF+V8He0e+p78ED3pNoH4Y1G
ttOYNdV2IGUrSzazpJMeox1bIFeb4kw3xplfyDjIRvqQVNtFlf3/7chLKOHs
YKL2olPGzaTLQXg/bZGXdgsL+H1BuGvwvVzfzfXPJGeq/5s0pB/Oxfqbfy7i
PqE+q7ObF10n/7jwI6B5Ug3xeaFrocMpawZlypdqm//jyvudWu/TM6CXoHH0
50ul7Ve6FnydluZFWwaQf1fF5ec5P+kbHLRJPe+FKwi/hvuHhjhP0eEBP50x
E8716XW9x/0n5CIi1X3Wu67ntJtBPyocybVCSs8a+TThc8jNV+iqKOLelW08
6GHy/ZM1dhH4jTq/ij67DtqT3xAQlt30aCnz8tsYyWAummq/ofJrKj+ixQh3
o24ZcfZZJ592Rxiz8YzH07G2Y1CcNKt4dn30V4lU244smWr/EOn1Xc9SqV7X
vpPN6zmt65rwrNLEb6XNhiAPk5vaz0oZ4sqCcqA8qJBq/SW9JV60Yqoh/nxd
6y7pLfWVID4uwBrySWtpXSQ9JJ/Dn5P/DuRoI7Q112q3dL9q3q3EcyuDKql+
b9f5ENl5fVDG3xonon+qcq0aiFYZQI1Un1GvCf1HMgLdS71rQ78t7O/IJ6Lc
b6sZN2tAXfRXHcL1cphfm91h7fPXHv+6ugbq69lgN/V4hDLshNaiXWOIa6jr
9MepRrablYIsNCKuI32xq6j3LeyGdsnNuCNuL/NKY8llqn0S6bxKbKp95kaG
2F6s7Ma2oS2aEt8MDIY/QDvsAOvJewP4R7ZjKfMTYAr5T0EeelP+SchEjsB2
hGxIZJS3z9TmqeZjyzqcN7vtDuSGLiphvxryqXFP9qEoQwvSP0J+D4M4+Jap
pgq3grYGYfBtUv2dXd/Y65TxN4VVlG8JtC3X4kEk4+Qt6paQ6jEvqnBiqn3d
RWkeoT82c99h/W8K7KXIbkoSaZLB+Wa2Tb0syjY3e+RwG6gtxP9U2mHxilO7
vEi7LSdudWnzH5d2WLziVoHJpF1EPzQt4zNgKeSVCtJAutoMZIJHqWtRdGA7
+PbgoVTze7I7fBiZT0dPZoaZPxKE/+T5x8AfodbPf0Nf4Z6H1b7gEu+bc2jv
DpIZcKS57bXIbov+BZ+iXL+CI8yHnVJth0v7VWNBZ8IvhNg346DsPksg+3my
oyeb0F1SbRe6q3QIiKI8j9Xzvq9NpW2jW+ukktofxDzyqOYU8LieSxt1h/ZQ
/4bYd3iS/gcgOwPjLIvb6lk29Z1d36n0n/wJ0vfU2JXNNWjWxp6DVzAGijFm
VkKX0ze9uNYbHCXf7IT7wH9APePJYz3P7Ztqf+vyK3aNOvQj/Dd0rv7963t0
YfsN/w998Blt2o8yrUcH95fOaGm/7ANS7cNPPplnVPUc/TT90hiUZa57iutP
a7yDUrRNzWbm1+Vw+EB5n3U6CG1F+87kGW2R06N17c9Wvud/p8z9Ke9v0Ge5
9znwPFhI2j28Iy3mmS9w/bhkm2ecoGzFKWsS6fuQpjZ91ayM9zRH6gxiqm0T
vJhqWwXyba655BB4ibhc8p8AHSS9EMim9tndzOW9eDcL2T7aEOKHgqvk9zbP
/STWNutWxdrvj3z+DOP66+T9WhnXcbhkOsz2fnsVtu/1XZR7hGSC/EdCB1KH
EOL7lbGNleH0571SXidovdBAvoXUDlwfnWqIT+D6zlz2Gb4depHnjUm1f+KX
oWPBK6nmXw3C48BrKmNw7R51GR/QHGXMK35CEFeJsj2AVob+w/PbhjlflXei
5F/nWaBbqtiP+G7ZDQXfgMnETwFvgFDmwuxgKnx53vVHlfH1lDD7dpSPxxuV
7I/qzVTva5iW6r0Nb0HfBt/RrzNr+71jJXQdY/8ybfoXeECbZqWMn5H+ADKQ
V7ZNoNH5PP7nkN+hMPucn86zZmiOaeFvuDNTbbteZ4HvkscM5tJZqfaxHBPI
pPTHVd5jlkLf4dqP6ILZ0HfBHDAXdGf8P65zv+if/NpjGdR9Plgg2aEd51C+
gdTzpUq2IbgEWVzItQs5/I17kdJRj1llbK9K119Ebz9exDriPa4XI+4rrs/S
medUn9PSeS3NC9oPoW/ExaAfEF4seQBrsvvdZVdp29a/hMy/TNxHXFsCJkaa
XxqEl4H8pexXtT9r6B1lvXbSeP0+p7+5L0+1vS3tARpTxrpTOlT82DL/p0ul
R4dkNy+6gmvl0FFlwQrwMelyMl9WRq+NlH1d6jtK9raIX6lyMN5XQa/z7Hep
52r4T1QnUBrZKSsb/NAcue2zb0OM1xlab6yFNqTfW2jPPliX6nHVIOC/C3P4
DfL4j+dMbeZ1idYnnyJnn2o+Qk5aIZ/XkbH1khXoZ9BppC+CzvuJsdef/J+q
Zb4Ez/4e+SzY1OcAazb2t/cN3DM7l+0qdtc/XXTrBdoihn6No10+53o0ZXmT
9swknAF6IicbpXNppw/zeNxLFzxTxvY83+Q5U/PaRoDOK2RjnXtI31IYE1NA
a/qpLdgkvUUfb4YW1p7VgCo8mPfsUZTpQQvzo4s4/D5tsUX6q4j9Ts6g/XNT
5xbIbShy8GWq/2f/CxZW8X5b2SEuBbam2p/4Rq2jKM/eOrZJ/xXxj5Aul9bd
8NvAAOTscEv7nP8Rul16gzHUkPgdqfYLIB9AdXjWzlT76oukTPdL2PfUHPp8
Melv5LIthFM6iwLdRdrd4JtU/3f8Vn2p/qc9ErSns779pOyVHKSazq5sflhz
+5bewFjal2r/luXBP8zt+wkfSLXP0oPQ78EhcDjVvuOPQFvRj/PJYwR9dlVn
AcEPqZ4rDiDfP8IfBT9JlmnXg5TpZ/hjoBftdxz6i2Rc/jWQnxMaa41sQ0vf
ZEuAk8T9CpJl75b2jWvq79s7wEny7UX7neK5maz5zlGWdtBTqfYXfhp6BpzV
eKesEcjuXe67D6JJey7V64ErIf6Pcwl6XmUm3wu6pueAP8BF8Kd0D31yCZm5
BH+COak9snIZ/kqqzx/8lepzCYlh9lF/lX7MR/pajLNRjKO/uX6Hdei9KH9v
fZQ6jKbdrhLftIjHzQesp5swPobS19eIz0V7XE/1Pr5/oP+C/0A27n0SnI32
OLxBXBfyHEyev1O/m6l+z4gJ6i//5fJd3oz8moKdyM9zsglHmz8f7vO0t1J9
vlb75OU3VXsSimndo++I8rfA9VDS5Yj2ORGdEVnGPPQozx1Evnt57h3STEBe
x4NYynWX8L1U2wxXOqUZLd9hYFq012FPBOvv+6QrRJtGNjAv+pBsWcNnSWP+
A9uoSzZoKZ3DBCFp/tcTCl2KjCyv433E2k98HGQn/gXqt5vy9kO+w5hb+utf
J3R7Rdvp+5Jnbg3zGu0B5cvBPWHgmNa81OsnaE7CR6E/ynYG/BH0Qe40j7+T
2rcN/y35NQm3XfA/K9hXmnym7UXe94CjlCESeSgkHxrV7KthPFhK+SPIZ7j2
Rug9K83+YeUnNh98fvAWzywA/ZGm6EifRattytmfvfR0PeS7v/bSkiY8zevi
QYyb7OjOwbK/Wts+3iK4dg6ZesAaIBL+E/KrjU6s1dD27gsRV6uevxtEpVlm
CqfZx6h8jRaBfwj5fa65z01JzooSVwxMqeL5Q98lZW9b3ynla7N4msd9ftq4
SS6fIS5BXEn1IygNstM+oWAN4+ThWPt4Pl7Ctp4rwpdJs/1L2cEsC18OlA9o
hYCvCHpT3jPUqRL8HGjlNL8vji7rd8bytNkx2rkc9L72jdMWVUhTlHYqrv32
uk/29EE1xZOuOIjiudFp9r0qv6vV4Q8Q1x0dVLiyfUzUIK6m0lDPc61MLwZ8
LeIfr+n9j4JskSvuLG12EJnZSB/VJlwH1AUXWpkqXDuIq5dm+a6fZnmvT7nK
MNbLgTDqlgtULGuIrwRtQLp+1LEvSOaZKa1sF07yk8J951tZR0pXxpC2IWiU
ZnttSyhnY40raAby8ijpu4E3CDchPhY0Bc1A84BvEYT1f1B2V/SPUOdQtO9E
/jDjuDZL9s3VHgWsSzRHyvDcMtqqFfFtaNOhtMfGRq5z6zTrgGaUoU1Q77bQ
eJAQQLz8gSdCOyH7eVrbnp38T8v3dE7qfxDdfkhzC/eHyeZ+lPdDac5oTnsk
ce8Q5v1O6IRbPCOZcH9kJb/2u1C26mH2Xf9YLvuvF1+ltcPiZ+RyeJ/2InDv
BuoRR1764P6Ae8fIlh/xgxj7pxu43GkBxMuPeR/WMO1o30ztvZQ9C5DA89K5
ngEy0+ybpV2abcxP4PkVeP7fMfb5sAGcASWKOE5h+WuTr7b6tPGzLbwnWPuB
20v+aI9JyMkV0mXnfe6vMJ/j13n+16B7eFcbSHlfAiP13xRsJO52Sftwv4QO
fYjnZCGuKahK346kTNWg/bg+v559qHWlvl0a2N+3bFXKZuUw8DD3htBuoeAR
+CrUZa32kHJfB8Lb6YdS6IHS4FX0QEfiosmzOlhMuq2UOaSW+Y/Al4Q7pZkq
nIM2uMP47JzmsytdoF1BN1Cc9ngUOr2iffFeA4+lmSosP/LyIf845X2ZZ02m
/I9rbuDZ3aGjgzhRhWXTo0ea7Xo8Ac2bxz6t8snnCWvgrpSzp+IJ52/otpQN
5yclu2ANdZ+rPRXw43lu4xjzfYLwrPL2p/tOefut7auxnea544z21IEREba/
L5v7mvv7c31Amv+lr6CNP85l3+7y654b/MK83p5yP0Waz3XuDvoM+Ir5+FmN
5XLmj4c5/Fyadc3zab4/F+hN/i8QfhE8Tz070Gf1iR+leSmgCsuOVXnpTu03
0f9H5qQ8mltppzDwUpr9+g5Ms2/fQdDBGpNp5kXDWxviI6A7aL97YGia31s0
/wyDHw5GqK+R72OM89P6RpTL/6bfohzTZC+qrL9jjNd+hgr2N125oflSQbgD
efSgvUfyrMgYU4VHqf/BGHCRPP4Aj5A2mbLsh4+vY78nr7OmeJk0hWmzxmBR
nHnRv+iv7MxpFZDtsFb2uzk2zX44j9Wx77kXidvEuHpF/agzxPqHnOb2iqe+
HajHOMJLaM/XoK9LVsAM6jarrPe2aI9LOrQbum0C1yaqDlVNU+nf9WAS/JuU
aXJAFe5CfaakOe4NMFXXwDbacgc4Qb+eQi66oJ+ebGBb2PJxL9vYsvMiey/T
SP8WeBtsjLE90hcoz0t1LBvT0ywftUBNMCPNED9Tc4Xat4Htf3+IzE9hDL1D
XGfCicj4wJw+K9BZ3yuIfwKd9VNR2yp9l/AcMDfN/1Plw1D/V+cRPtPAY1q+
K2TrbT5xi2LsP30B/Get/Z99A7QBZT1OP3Wp5T3+cejCFuAz0res5nB7rn9I
OywBC7k/v+a7aPtqWJRm31Bqi/ek55kHz2n/KPmfr2B+fmWH3+f6B2AY/d6Q
ZyyG/1C6RX0MloJG1LEo18/RznNz25ecfMq1y+99gO2hy3Qf79/LNV9IpsDK
NNsnWgU9SP1XQ9/lOZ9I96RZb0pn1qZea9VnuWyTTHa8RsrGCXEtWON+Cl2v
NgK7kOX6vEdtSLN908/Vz2BTmveGb07z/vDxpGtIX11GTr8gbmS0baLWj7O/
Z/l6PpHPdnJlI3eLdDjYGkD8wBjbJ1pTzPaKdGYxXLZGKXMtnvcVab4GF3Q2
jTEaBb5kztgCthF/RPvviCurvexp3gc9DiTS9jsI71R90nw+dje0HLKdRn7f
wH8L1qIf90Avobcua48i995Fr+4l7juwD+wHB0B31ioHJXcak/TvayAPdSvG
8w4Rd1j6RHaVqGsh6Ad5eTZ98R70ffTBYnCEND+AH0F/7j8K7Uj5f0oz/2WU
wz/DHwPHwfvaV5xmmyEnoCfV90XsB6sfeYU0tN2DJ2nzX7mWJ6fPSEWB17h3
PDiV5nuzl7RNsZLkcVr6lnt70tZn1Pe0xVnoOXA+zXNwaDAP7w7aUOeL9b7Q
mLhG4AL8b+B39ZHsRyPfv8nfDeXqQ59FQf/g2g3KdjPOPunl70G+Hi4S30Tv
HzH+1/gn4ReZzyvmtj25G5TxEnE3y5uvWNRh8c9w32X4K2nmtY5SuBt9+DR9
/yj0L7WtbJZSx7/hw1kvFgRX07yuiS1qn77yjftKqP2ZhVKumpIz0hUBO7XO
Zj2/Wmc9uG9aXn+/ikTPXyf8D/gXxNF2/0m+Cvp6lWZOMx6ZvqE6gFvgNni+
qfk7QfgV2dTTtwz4IcjL8xHer38vzXuDhjQ3L92lsHzTHwb308yLlqBNH0jf
oauypPNenW69ng06iLgvafsTyGoI4QzaJzTdfkGyp9tPSDyyeEF7eSt4P9mT
+scPbUzeOUgTBqbRL5XAW+Aj8C/jf4m+XRbxnsS6IBvlyQqG5bZe1ZmqMO1P
4f6/0GGr0BXlaffBsr0AcqV7f19uaAp1T5NdP3RzHsJ5QRT3zizruU/fG09T
nnzEn4Hmhxak3gWgEQFVuCA0HOxAz31NH0TAb4VGQgul2/ZkFPQKfVMYWgT8
S32LQouB4qAEuEy5Tlewr/pfq9kuU0niH+g9SGkpf2loGVBW9yDb5dI9l96V
nV/4fozLYfougkzNLO/zgFvifCawAtdHo8cqQkvm8vXtuZ1efIlcji8RXFO8
+Bb6phrIvGRffpYqpdvXks7hVYZPpK3ikMUWoEq6bVPILsWT0LfIc4HmR5DC
HHuUuHKxtgnUD51blfQfs07pRfv1AWWb+4zRTtIc47kHkc9q6faJfpXxnUya
pa29H60K4Vsx3ncfTZpknlOZ+lZP9/fkGunez10T2o1rtaC1QVfKeZZwKPfW
IZxd38OhHenPhdQpSWtr2mYUGANeBilcq5du/+ZaX+k/gnSa9prrn1sGZd4L
HUp71SfdcOgXueybchO0AXExYCH8sry29RFJPg2JS9K5X+iXlKmx5AfaBHqK
Oi+njapxvS91jSVuOvUvg1yXA/1z2/ZbU+JHILMX6e8/wF+MuWbpHm//kU8l
2YBgnFSmD6JlvxWMZd75HGymfZuTrgWIS7efmZbQD0rap+vDhe3XVf6C5Su4
Fddag4OtvcaVvdtBXC/KOGqjMus/G/XaxHPaEi7HfYvRZx+AqcjnY6xtu4Mu
sfarc4uyboTGk/b1UM8haeiKBMmVxhBtnQSNbGMbK1/qmzsoDyqCf2NMk9PN
dyLdHzo3pf8GlCOF+IbQ1IAqXIH0aem+TzQ94Gcgb2/Xc5xoRrr5ZO7LlExB
s9S3nBRoaJkRVbgdfHvwEGjXxnPHP7RRJa7fhcaFmrYMNT+WttsGPgMPc8+z
2svHfY+kmyq8ibzC4F8oa13SIf3/bNmKKtwRdAJDSd8Z2iWI6xjwuta3lM85
9Yb+w5pnJP06AnSRvdJitvnUivvrUJY4aNdAfiXHb9Vzu8zSXrY8fqby7RZQ
hZvqPRj6WLr9yT+ebnv3T7D+6QG6pxviX9Q/CvqmR7r9h0iv6yyWdPsT0h3g
SZVf3+ehd5GfWVzrHfBqjxxBm8gXSg3QJ92+weUvXP7BnwanGMd9pRNBfzAA
PCV9i3zOYE68Q188rTFJPhN57mbKcqu8z4M/k27/BM9C77dA/6Ub4p+X/m1o
m+OyN/4C4dv05y1QJLf/K3aTHWLG4Ytce0k6nzwKgyk8cyDhydBB0MFgSCBf
opkB37+l/X4OgA4lbli6+6K0/pdDq0BHQPuQdmS6edFR0vEaw6AV7TqYtnmS
tnhZdUePDABj4V9Jtz+fV9Pt16hZDn8/7UjZf6FtO0HHce01UKyl7WG/Dj8e
3OB5x5CXm63NH8/r8GnmiyK0Sd3sfs9smcO+M8PQOUuY29czt05It4/w+Ebm
RSdC3yXdVvJoWNH7yVbSPpOIr8tz3wF1wGS1GzI7RTJCvReAJ2UPlWd3zmr7
B29w7VvK9Vw+86KX0Bmt0Sc90TlPgKnEnyS//rW99tIaLCS7/Ta9me73pGmS
e9CS8lypYpuwbxN+EV04nPmsD7p+OuEZYCaYBdZo7yx0tuSc+7pXtG2G9cV8
tn4QdXiXa2ORg+k10fMNbAtmLvJ4QP/ouFaQuldn3T4X/gx1e5b1+TNR9g2s
70ojaa/q5H+H/DOR4SjySOJ5iXnM9y/jsM6oXgSlyDMv430H+nUXmMdz54Ov
GpoX3RzjtCXyOr34S0F4FPm1hi6hHfPpO2xe74cSv1/f4Qh/19r8Ap63hLwW
QnNz3waNUcp0iDyyaQ2iszBcew+8Dz4AizWmG9N+3LeHPp/L+EqgbuvJ/4hs
uVb0+v3DdPts+wj6O/JYg/JMRZZTatonoGxWrkMG1oKayG4NfZvU+VXSLwXL
wHLwM+Ucyjx1Aj33seSggiFe3zZ1LvyJFj4bLhnoK/mraF6yoHBVdPIFaM/G
9lGuc+Y3kKta5LmCdMfp0yzUfyV8Z8rZKZ+pwqvA6vT/40U/ka6UvVRoDejf
5H8VrE23j78m5PMTMrGO8KdgPejN+PpMehLaU2fE5RcFbCDuc7BRY4d+3QTd
LD2b7m/uW6BfShdQ1gFgq2QAvJPf/NdBWHbmt0HvyKYXbbaRum/XOGXO3gHd
me5vfIrTtV3SE5Q9Vf/yaJvdhL8BV7j2bbr3UMqeZAe9o6bb/uDf+WyP8Auu
PaGyQjMpR5r8erTyHue9pD2a1z5r1e6DuPad9BJ65pC+m5DnPsL7wYF0f1/Q
t4WD8N9LHunbBqw56uv8EfrtEHGHwZFAl/0gfdvI9MeAT6rjNEfTLes/6owo
+VbNb6pwJPHlwE+SqXRThY8FYfFFwFjpx3TzqY0cfh75eA6U4D3wF+kUxvFu
+uaEZCPSNhNPwh9EBmLo34alve/813T3eW/0zKl0x6UjGyuR/Q3l/F7cDV0S
zrMKgmzkdzrdVOEz8HOQo/OV7Ef6LOFz4DygmbLw2CwX0q1zzmmdxH0jKO8t
8BVjcCv4TeMv3Wfu/1Ba2uMidEJl+2LQN3v5Y/iTuHyUq4DeweE7NfJ/R/nf
HE3fXpZ8tLFvXf3rW0Iff5vHev4K1/4Cf4Or4Bq4Dv5J9/N2kebfQO/+p7wp
yw3oTaVFV18Ht+APoV/7MwfdTve3/jvp/vY/TjoWebtLOJYxUxq5KlXfZx50
9uFdUIB6LKB/nuX6PdLdlwyn+11f7/xFdI5AezfI4z30UT7qlxdkyUBO6IOO
2stDObISzgZCMqzLDtO2v1c0L/2mcBbauiD3FNA/DNJVot+zZ3ivjvbpZDLn
5CAcBnKCZoEdbNnDzkU4N8gD8oLDlLcr933FO+FWkI+4y7TBpRz28yUfOD+y
LslP/CXtk2YNldrQ5zceoV0TqEOBDNs1k02zCsF+vYLEhYMIEAlu5/Y+sDfR
vW2RpQRQSPH6X4osfowwPUYbdW9iff0B8j6HNVE3wkWR556M56gM+2gvDC0C
imbYd7t42YWPYF0yi/YZr7NXFbxuKpZh/0u/IivF4UuAdTyrPW1XHd1fkvA8
dMOjrb0nZrb2PdJPj9IX7yL7DanfuUqmjQO+DGVrGW77KtkqWReepd4rKUum
xjRlLsVzS4PzcT7/qLOO+v7wqmzVEF8WlAM1yaNGCZ/tqd3CZ30098vnwqQs
ttVfPsP2+vU99xpYHmNbNiv03YX2rKD2p9xLdYaKulUkvA9aCbqcej+vd274
7pStBPqhimQOVAuofNGLj86wneT52pvJsy+jL6tneC/sSu77GFpDZQa1MswP
ruJwbTCE9hkG4tAxrcCCUPuQkB3tIfTLIPKpo3ugZSlfGbCettuLDD6gnPdB
Xa4foG/2g7d0no/r9YhrSfggbddK+8IYT+/D1yd+FPVfC36kfE1Iu5w6NlCf
kv9vrP2Kk1cM4eGV7F+wIfxx8stPX2yjrF+DRsQ9TlkbQ5uAb3jGLNnLARcZ
Sx8S/ld+pDRXoWvLVrWf+R8b2Nd8FPlXI10s9x5p6/ZUu1YJ2rgpCKU8Q9AR
zeDrUZbm0GXIWQuNRdLHZRjiD5W3j6S88PPymm+Z4fAGxkIr+NagTYbzbZth
OwiyhxCvvqAdblGvOvkN8Q/xjCPNbFPnN/Ahz0kgbSJIz2Of90nwyeAMemJE
SdvFahxp21jyJVw6v30La72RQrrUDPNadyicBgYwJ6erLozdDOgc6ppa13ud
dP5ftgkziW8H2mf4W8NNMI0yfU4eG8HlCt7DUoNx1FNjijwW0OfXcvg8aTjP
fkhyxHruLeodCd6hb1ZXNf9BtMNptPfD0qPUfxR1GQ1m0g65eGYe/ZNhDHcj
Lgt9+GicbXxNpB0e4Z4OoGOG39GZArJMZnz/yDp6HeNsJrK8KMp5dCLN7AjL
21zQmXAXjQ/quYLyd4XvBh7VuKH8GZX8r137DPTe+phkT2MTVGhs2iPgS9HW
T8B/SVl7Zvjc2zjuLSp7uJJj5DmKdL2CcdwrkD/xf2meod+eoRx7iduG7HwN
nuaZvbn+HHQ8MtBHfdDS7aF2+kPrcPJ4ljbpy7URTbzOiJP907yWR8lhP8l1
Zctlv0AeWwV8yyDcX/IgGWO+eAoaQp4DGb9Pwz8Dns0wL/oS8dnCbdd1d37v
l3uO+OfBdNrthQyv5fS/WmeHdYb4ReKuUPYkneOGv4tOuAcGKm2Gz0eM0jlH
+fkBg+izgVHenzWqgH1dy891fuRrJPc9jn7rg5w+RDkGlvI1nXkspzUTeX/P
uBysPLlvCHRohv1Y3mtuX5ayUb0UmRuW4f8eoQ397yORNIu4f3iG+ffyO3y8
rW2sytZqPeJHcL2+9utmeByPAqPBGPAyGAv2UtYJ+h8A/yoYB14DJ6vYhuJy
dNENnvsx9HXiz7M2uU4bdNG3UK3PqtkfrfzS1ijq9/3xpBsITaLPE0ELvU83
tz0U2ULZ38B7q2qDifT5hAz7e6+p/wSMiZugqWxrEt8MmlDd/gvkx0D1Vb0n
gRaUY7LKRDmmQN8A76CjJ8kePvxk6HbaP4Tyv0l4Gngrw/9H3pYcgBlgHXnP
hF7l3jDKNCvDPt5T0RG7Wjr8ToZ9JR4oZF4+ExWeDd8EPkbfpOnnVbL1JZud
0lVq62r2iyqq8J6WTi9+dpBGYa0lZN90bobPHvQu7LMI8wgXRH/Ohy7IMFV4
IXQReA98QRtW5hlF0ZXvE/4ALAYf6tl17OfzLHJxqLJt/H1E/CbaeiNYAr80
w/uDZQczLofXrJncN5nnhUhX0j7LSLOC+5dDIwv9nz86UYW3VrYvcfkUVx0b
x7tebdEZH0ufwK+ArgRV9P9WPGlXQz/R2GL9m1jftlFkI+Vb6Br1IX23Vn0E
Ps2wLX3Z1RdVWH4y5C8jG3Q94c/ABtWfPvgAfA6/UX2ODC3hmTNZV+Zp4D3S
2is9M9gv3a2AfbRvyjDEy1d7BOMqPL/Dgnj5cd+sdgdbJOuU8UvpCOgz1Pc5
UBL9X15nMvTeCLZqrKLzEprYnq36WvPBw6zDe9LOX0l3Rfu8AI/PUjbGNjrG
g6+5tg0UJe8Jmp/y266p+m072BFAvM5u7YQuoW13SaZIv1ttV9AQvx76jWSf
sTkdfCu5BMMLmt8bhNNKeU+B9hYMjbef6B+y2x9ui3D7xL0Zbr24gjH7XYbt
/+6gAvvgW8XY3lpp+mo/4UqMgca0RSw4QLhlVVOFD0J/aWb7litq+fyxziFv
Jc/vuXYow7zolsYuz+EM+60uQr8UBim040T0/gjyP8K1H8CP4GhA321jXv5m
D8qvIPxQ+mwGz/sZPhT5uEZ7/AMOo6cikMdjGeb1H1Thd7RW1Du1yquyM2c2
AWWy2lfmetKdIP4h6nYywxB/nHXARuT6InldAn1LOp2u/wo6M+e3aWhZl1xL
9geFmyosv+Rb8vt/iXj5eFb4FNeSqG9cuP2Ry1/5qfzm5aNc4fmyDcrzT2cY
4s9InrivBYgFk+nLJ5G9s8Sfk9yACwHE5yfPUvG+pjjtx/wN2kffZun7mfT1
74T/ABNK2O5vhvYskVdmlH117w+3/27tL24MsvK8NxqbKnwRmb3I/XfQOTnI
70/pQuIvQS+DKxmub3gT11nv8H8R/hssjzdVeAjPvKp6hvtMsKjC10ByvNNc
D9Iq/I/0H/gPzI1wH47Iabt3ByvYD8YXuW0L63qcy6990o9o743O/jSwDXLZ
XttDW9RpZbpXIO4b6kV3Z6FZ/seLFqH8j2m/OfPpDfKdQ/xN6TfyiS5qnynV
i9rf76KKfue8xfWalPeF3N4r/WYD2zT9lDzWgX8lx/m8h+g2aTNJewfaLt5j
rFVVjznxTYKw9jZqj2MedPj5CKfXfeJFtQ9vjcYd713roIsD2dcYuCt5otyn
wD343qS9n+F17CyQorPLGvf6HplJP2d67GncZYNfxrwdAh1He74K7vKcP2mP
UOLy65wQdDpt+TZYF+99htq/WQP+LGnPVPY3uhyZ/k63k7l+fg7vjzpPliNo
6GT6IIzrOcEXrCVyQb+EbgF9GRe5M+37OFX7vVnjtEaHnGVtl4f4vJne4z6g
mve8d69mP5fycXmSd498md4XdEbfskB+wh2rek9MJ2iBTP/XaArWINNPUN4e
oCDxFRnr4dAoyjyLdiocYj/zhYOw/v9+jIxEkCYSFFLagH+8gsOzqNsIdM47
0KysFUJAYeKLgKKgGHid56Sj98ZBW+vfX2O/T1fX+IEWzzRfItPh67JxA18K
lAbVwm1baT/lbo5OSaHtS2q/OH1ShuuZ3NselM00xJeDJmh+0j73yv7+r2//
5YmvAGZm9fm9ojrLSrgS+FPfbaAtatsfy8/UqQrhqioDiAa39O0m2nuhqxN+
lHANaGvauj26eQt9V5Nwc+Kzo8trZVp/S28X4p7ahOtkmkYW8NmEuvAtqU89
yUeM/0Vspez1CTeQDCBHzQjHwN9r7XfehvCNwBGdwdD530zvvx8g+7TIRX/q
FVPO69cmXItVezDeRtIPu6jXTlCpoP0HVoZOos5NSTMB2kzlVzuARcxlV0vZ
76neefTuEw+trD1cefy9Mk7lB63A/Uo+Z/EA2ppwG/B1uPm2QXgy42oSiIdf
o/Op0ESQBJLBJvRYSqbtMcguw/gs9p8wIYv1YwTPKxRufm0Zh6NBjOw4aC3A
vWlgLn1QhbGcrj6EDqC/p5a2Lxmd9dLZM539yh1hH/R5ItzHeYLwJ4zPKOr+
De2zQzpB/2yhGSpnM/fPNdpzNzpkHf3yE/edQg7GVLFsZGa6fdtB3wizP/D2
mfb7Ip8v+VjHPJRp/y0PQx8BHUBqNftNlb/U5eitBJ67FHq/sveSdyRNNury
J/Hb0c2dCHcGXQIU5B3imuYQrn2q/dLEfcizrvHc1YyHboTH8JxDyHFcpH0l
fhfh70iPcu0x8Ln2bYTaLsDjhLuDM6TpAX0C9AS9WGM+qbFb2u3eC7436KPy
sdZdRn594WO4r5/uq+o5rn/Aq98VHgB9Knjm2LamCr/VzPZBOkCfJnwD3fBM
pvm19Rx+Uf+x0W2zcvjMsOy36Azxbeak1ujAdOr4LOmfAzkYJ2/q30Omv8mG
hTiuBP38AnGvUaYXoS9l+ryVzl3JZ4n8FQwkbh9jI66Q7aAPIjwYDJGOK+1x
MRR+mHQf9R4OHQFGglGgAIN4bwXbCb3D+uM2GK1+ALXI9zmwmX77Qucpkamz
yEc96hFBfV7OtA9dycQwyjACjJWeQx670g5d6jnNPeT0gdbY2lNLm6eWtH/b
BVH2cRuF/B2hze5GmP+xscMzCb/C/bfJb0Qj/+/Uv84RAf0on88H65ywbH7s
Y0y+msP2zIrRNq+qDeA/pjzFVHfoJOThI2TrRhND/DjSfUJ8T1Aw3PwaEE7+
4XqXp64bq5kX/bya/b9Pa+i9nK9JBovZ7m1D7nud8AcRpo1izTcp6G/x+g7/
CPdeJe846Hzunwd28KzspB0vXady0+7FwWTGZ65wU43Vr7UfguuTAv0/OZgD
xur8Nc+7x1iconENpoI3wTTJLLio/yJa4ySYppczv5myvc3175CF6dAv0d1b
wGnSF6CuRasa4p8krkhVX1NcVsb7pQiP+2wBr/E/Q21Sz2OgGfLVvrZlcLje
M6Evx/kbcddYfzMOQe+fgJ+BjI2p5XVNBuWblWld8gd6+R342eBdME7fyDQ2
9M4IIlj7FAKL29onsnwj7+a+uaSZB+aDBWpbxs6EcMvB/5cB9b/mzyPojYWa
W0An6tC6od89Kuk7EnHvq19BXepVTzIg/aXxS56n0a15GX8fEV6S6TxuNrHN
qqWEl4Es2q8NzQr9WH1U1TZaJqKjVxBemel11apMr7N0nkhniSZzfTmyu4Q+
+Qjkoz0fZbzWYQ5YLdnVfAX2Buturb8P0o796c9w9MpayQBlW5dpfl1wz6eZ
3rfbUGcE4EPz2+ZnFsZ6W/L9Ps42DWXbcB3l+Yw0G6SDA6pzveLnFvL/ZP1X
3kh4Jv24CTojoAqL35zp8BL5ZOeej6CtQQv4Ocjh65R1dazPGX+hPkMmtkge
wVZwsrTt5eiMhM5HfEVcG9IvjTXfKtbhr+F/pk7boKUJlwU/h5seCze/nWs7
QDhxOwOq8PaAP1bN8RGxDu9SnSnjW7JpTXg34W/At9Kl6Po90CZc3wvdzxpn
Pe9+32XaZ/sk7VXjnnSwkeYtpbaAfq73niBOe+WHgX3cc6mJqcIxtH0D8Bf1
2a868q7REkxCjic2tb96pZ8e63uGB8/QHnxhX9D+uj4zSHMAPMx9I5Clg/Df
g5DK5jtQv0eizCtO4UHU4VCm7Q3F84zPQQI4HOj6I5nm8zGnZZb1ev5QjNf0
U5CnpvJvxvUfwdFMfz+eo30TGsvQgmpvUI36/BxQhX/m+jFwHPwCTkgGwK8a
/1x/FbRlHJwiPACZOC2do7GTafuKp8FT+bz+OpfpdcAD2vq85iToWsr7KYgI
IF59qv4VVfiCxku0006jLTJjLQOSh7eC8El0VSfq+Vumw0qnvq6KXFfW/z1k
6XeuJaIL/5AeVlnQh39mGuIvSZ7kG4Qx+zttdznTvmqvQPtoHBD/F/xjpCnO
OvTxgN5paF62I//m+nvkfRW6hXz7o5dCuDaBcT0eXFOZKcvUauZFr0P/Af+q
nsjRWOaw3NT1P8I3wMJC9oU6hToWYb0znOflCbdPOvmm0ze9jsjFs9CbmfYn
cAs6mLh35DeH8twm/LrscyGbd5Qm3vk8pfGPfs2lPbr6rgmKU+cllOsjcDfT
tEC0+XvgvvpQurQda13aJAlkhd/N3Pggt2WrR1vLWijh4bm9B/0J2nARspKK
HstG+hAQGtDsAS+5yQEdTNoXNa+TdiWyWxvZ+o62yYpchnH9Ga7nRG5zwldk
PfQMa7Vdhey3VT5bxctnssLyY5tczb5sdV5dtle/Abm4Nz/tcVhrC53bzu49
VD1pk/hC3t8ifyyJtPkN5osORe1LdCjjtlRDf0Ndod9pPCcP2Nfa/G8NHX4+
j/eLvAAtmNv2nmTrKS/XuiGHXfV/T/bg9Z+uhecdvddnb/E/s4L/+wenf3F3
0DsbkLPPynueqhzpuSo51lThimAw9asErYCuSBRi/J1mfmmfVWlcyj6uZCNz
IPfmoxyDYs3nb+cw3Z8lh849trH/sk3MQ9Np/y9JU4DrBcHntOnblGUjdDft
F07c8AK2+S7b7x/puwBxke3se7s1bVcIPgoUBkXa+Uy1/nHo/0ZRwlNYN3wh
W4egGOF2sdbXX5B3B/rnkRJ+J/ikjN8Lirfz3vgS0FHkVxJaqp33dnxPG0Uz
H0zl/sWxnuNKt3N/3qWNysBfpg8XVLBtedlZLEvcdv37gr6IPJeHttB/bxqj
Avwf1HMUbZJcwN+JU6B3KGtFrn0d7feh52jnoqTpTN6dwNs8rxLX+0gHQX8k
vx/oyyOgP2UaIN8ihYL3c65XBdVANKgOtpLnTtp4XhPTfrHmQ6v4u3t3yjee
+2uQNp4y/cYaPRrZL4gM1CSuVjv7aWzPWKkNX6edfY8vYAy0beM9YnUlu9K7
6L8voPUkm5SzK+jBmIukPSNAfeJHIzfz9K2RvmhAuD/pNyPPMfAN2/lcWCPo
kOA8ySbasTHh8cWtC/OQ92ZoE+JeoG6Z0bZZuUfrduSpCHN2Me0raOew4r8F
TQmPoT0XwTeTHFGu5uofEAdaglagJmvWCzH+z7+UMbUEDGntfWDaI3aJ+1qT
7uL/I+qs47Qsvve/9NLNssASy9LduXTn9i5KKKEICgJKCaiAIp0qXYp0l6iA
KKB0N0gpktIgqPB7X5/r+b5+f1zPOTP33BNnzsQz98wc2T6J8vxO8zzZr5Ad
i0ZqD5VpDyAFYc7QDnOT38b4NwFNo3wX8AfE+b7uYALN8HtEWb/QWh58C9AS
9Mhh+5et4FtH+f7iNuovkX0z0Bb+0+S+p1r3VUdFWd4nkUd0lPuuedT3WPJQ
FJkUBzH4R9f2/C4WPg7Eg4QAlftTdCBRekTcSdA5tOUpxNkOvhPt8BXoRPq4
QcntHguaM19IrzvcdCYF96tR/j48rJy/Ef9HPbbHrwPoGOVz+uPQx07KM3gd
dAZzaZtFynjv7hTQJcpnSSeAX6VTjDkHqvsbcleefYFMuql9qD/Xeqf0VWde
pFuSIegp+VL2txUG9AJnGUcr0A7KgwZZbUNI9oN6q9/Qf3iVkbHtNHJ+n7Gt
D+7HlPeNpraj1hd3vyj/x35Zyv+538N9jDbRjrLeomxbNO+XPGk7n4D+8OGM
aYnEOwB+IIiljIOiXBeS/2DwQZTPfA6BPkPOvbQXT3eVKT3psfKf1jY0P4ry
POhjlRv9OU0eh8OPAFt5p18524SXPa5K5WyLS/w34XbLbvjMkrZxP5J3Bmmf
h/SLcjQFc6nPVpQludZwdNeE7u+B1keHPomyrfs6yPZNxqdP1U6j/P3oIP3a
dOhhyv0Zfkego6N8Z08r9GSM+qfi7qe+Ju0X2hOgewaq2773WPwz0+Z757Xd
wXG4LxPuQErr2XjJi7QnqNzoeCRYqm8huFPXNl80m915dC8b6eeFTlK/gT5P
hj5o7HNr+3LbhsSLUr7r6RnymMLz59A9pNGF8k+NMr+6lt0x9J89kW8s9GPC
PYe2yW1e91vLnRw+GUhs6r12onJP571pxPe59BcsrOl9eFr/0zrg+9RLbc2p
mrpcVWm/XxKuWh2vzWov0g+U5TvaxJv4XSe+P6mzTTU9rxc2Beb303lvBpip
fglZzqDvmQU/W20OHZoDPU6bmwudB+aD5NTxCcasBfCriHthlHnRuvTjs6mD
WeC0vj/j9wt6voS8fg2/SP0Gcv8GOp16W6z2jk4tgS6N8pgg3Xldd7PjXg5W
gJVKS3oP1kTZRtraKNv9WgddH2W6IcCnY662BVneCvb+//WhPgOgs21zkc0c
/XdTWybMJmgb8voSvwH0qZujbDfoNcJ+rn1PagPI8Vv8t4DvwPfgB7UhEBrq
tbw80BjdF0P4GyCe8bsPfgnQ93Dvr21b3duivD/7VfA27rvUZ0/odvx/BDtA
MdJ7taxtR5djHlmbdl4L/MSzn1X+Uqahpc1XYA41Fn3did9+ZL8PbKFMu9Rf
MAaNaWo6NMC/gR51B49Je7fqCPwaZXuld8vafqni35vfaTQs5vMa2pfQNad1
XLp+irh2g9MB+muA36P6zO114z9x78V9A7pPfS5zgrfAfvhu5PFAlM8fXiLO
IZQlP/EWBH9XdV2qTn/h3bHIspLuQMF9irwfgp6G/q59nJTjHjisvgQcDUD8
sSjfbae7tXTHltZnj6svIq2M+s8a5bE9E+XOCDrzPI4+OFhnjoN8juE05Y8J
tW3uZuVsn3s0baUDOALfn3CL0Oeq6PZF6voSOBlliD8V5TP8T2r6TL/OV0in
ipLWaZUxl23G635i3VOse6YjibcuOBNlmrqZ+QrURyVwFv4d8jJHewbgD0ba
3tZ5+KchtvN5Af43cDHK9yF1IHx7cEn9JbgCrgb43wPuP0B3ZLOQfvRv/ttf
w12bvvpP6DjG+WzJaC88W4rOpyNPv5HmddUvuKl+Gb9bUbZtcjvK9k1G0K6H
g7a6T608MqNPuMOzrrgvIMPzRWyfRXZadO/0Xzy7C+6BaGR7j/Bvo0tfoxPj
0PP7auOUMW2IbXA/iPKeyh7JbRNxbSnbnCyHnB7yrLn2b5T2uaGjyHqivnnj
PwHaROcX4a8jl6vko4T2qJVy/apuUxP+iWQKEpi3hZJebjABfRgXaip3DeIZ
rzsNCPdXWbv/j78TcP8Z+Carb7M5eeeZ+hq1PfQyB3nbqzNxuLPC/xtlXn5y
/wf/ArwEEkoyENzMNHmATwGtTH2khKYCqUEaPZM/baeQ7jSETwfSg56M1Rmg
l9HFjuR9DrRTqOta9dyYPN+hzlOS59TgPWTRX/tjkUtwbVO5Zft8eirbQj9N
HWYkzjPQVGo3mXyXRSb85tJe54Bo/dfDfRM5d9FaH2m2IP5JFO0qcWQsZVvh
WQiTt4zvztR9/7r3Pyt+n1A3R+s4jmwgO6iOfsXQF0xXfnDnBLlAoey2l5qD
thmSwf14TuhnuB+RvydgH/VzAFzm3RL0tyG8VwyaGxoKZpGvwpR1JnQ2eK59
erW8X0/7y25o/0Z521U/V8h2LyIIXx93EWgZ9LcotJj2T6tMIB8IA/lBAVBQ
eY32JonwaOdJ+QlFzoUVXt9dc/ieP933Nw5dj8B/PHQuMpoHiuCegFwmqW+J
tn3eYtG20dsFuRaHLwEmwk+ivn5F7iVxN9NeC2gL8lca2hL6S3VTuTVP1v8a
/b8pRlsqAb5pZohfDJ0reRB2nu4Thf5Of/gG/Uc5+BD60vLQpaR7Tnvs9d+t
jO0cfgvdh7wq8LxitO/91p3ff+obp/QWzJDdKfJyEFoFd9Vo0y9xV5P8kFl1
vUs9dCMv/Qk7inhrRNuuzpwQ2wiUfcA8yDAV+ajYwN88axKmAXXXGnmXRJaN
yvhe98/Q0zFgHf1mLcLUjjYfGW13Du2x1rkc2lBt5hi1dA8+/nWjfe+L7n+p
J9k1c74a8b8xCJn0Ia8dYOdqnzdj3rw6dncC9Qnfm/nQ4MK2YSwb27JpfBo5
ni3q9eYp+o9JuD8ow13m1Q2l57rTorH3Hc8l7TjK0gj/xtH+5t6ngfd/S46S
ZxPQVPICzVXvqnPQClygX28NbQOOI6+20KMhhvgxRXyPF9kIIutBZ8lHFP7R
Cqd98dAyGVzn13XnB8ic2jbwYnkWw5wiDhoLHV7bdyHEB9LXfk7t6yzBu6Hk
uyT0BvWRoL4COldjC2PAPGii2o/uBIu2ruv+23bQV8CroD3oADqCTuBD2vsw
kEt7YGgXr+H3erTrrA46Gwk6BrkuVC/H6DdOgNf0fSfwrVzfzDsTvgvoCo4F
5NI14BbfLdo2jwrRdt+AfxN0V5/Fs13kezf4N7lpdfL8Fs9SohfFcvl/+Fb9
h6B9dMttW9+y39mDMAsI3zPaawb6jqZvaCmlx4H7oXVP9Ns8/7S49zTLBu8X
6EOxWr7jZ47OoFIH7xCmV7TtXPSGvgv6qA3oPj7QV31EOa+tyCZyPWQRxf+e
fqq7vLYjJnti82u5fUjHzujeCvLSQGsWuN8H/aPt92ld+w9g7ngCHX0fOoBn
A0E1ng+CDlb9obNfUqaCOX3PhPomrSNoXSGc/HxAmMLQUchhCPxQMEx9AWNF
lVJeIy9C267I/5UlyHENuvUhzyOJqzZYRFqn8LtIPVwGf+q7tcqtdRzmaOGg
kP7r4jccjAAjVW+SKfiFso+CltM8rLHv2t6IPLvRtlaR55Xgs2jbwFwTbl5U
Z5LXEP61bD6TrPUf2emWjffR6i/oe8dIR8nfWOksNB06N4J6rERaxyhzCt09
jHzGSbfJ+/hon+3Tf6QJ0bahlqOa7eHspIyjdI+NzqaU8lh4Azox2uumi8Ak
9YtgCpgKpoEP0MnP1XcxVg8EX8AfRG45aHeXydOXuLeQ138o93OwuLHbUHud
hSL+8RV8h9kEaF/a5RDeG1zG544akp/GOk+vdTgwPdDXzAj0PbqPeDhz31F1
fEe07ofWfcXX6FtnSub6xgu9gz4WoX+sTVyzcadmnr4DeS4paNtfc/Cbq/YH
lhHXAe29ruP9b2/W817N+YqH+BdE+3507Y/XHekLcR/Q3b3QUdRlL3ThHfA1
7kXgPvLvB/bSf2xCtt/gtxgsAeHUVQ90tTB0Ie1jKX6p8voOFN2Fkhb/Bejb
smifzemb3mv2LZHzRq1dgZBI88uj7V4R7Xsm9X1YbUHtQGuVK9W2KNdAsAr+
MHWxOtp3iW0EoWAD4W7rvjmdz6Bu1vB8M/4R1NUEZL0gq+9L0lnKniAim+2I
bmvo9Ye1qht9E6GN55dtLMq0Dr/1YAO4RzvrSfk2Sn+oo9nIcRb4i3Cb8Bug
dYds/h5zA7oZv2/VH5CnLdDv1P8TdgBpfA+/jT73B+hW8dHmtwfcb+r/Dv31
j/CNyWscYSvSt+3APaSS52rrKONP0J/VFyGXndCz0BLo79voYHH1AXl8riIS
uovnu8GftIVfoME1vF/7N+Leq29fWq8j3K9qM/jtifY951GgJ/57cb8N3Qf9
TeuXpa3H0ufnxW1nsjm6tpq+bj9+H9b2Ou4B+Mr0GQez+B5sjTsHCHcQ/yKE
LQYORdvO9GHo67l8x9bmSNv0W6072/E/Ch4ji0zMR47BHwcnor2GqLVEtV19
D9F6gNYFdlW2/YgLGs+ou2a0l9ehBdG/pdAjuE+qT0b/T0FfkO5/4DT8aPL6
GTgjmYJzag/MDc9H+06eC9DXKEdn8AA51qY9ZUXXf4v2XYbj8vk+Q91H3KmW
14cu8uwSeI9yXo62/YwU9HPrmIeNLW/bleXLep08LMTn33TW7HXq4jPqekge
24jbTv94hfevglD6yN/Fo4+jqL/kvP+Rxs9oz/8awKelbq+p3qV/9MvtsvvO
wfLIthjxXY823kKGPcHr6PgD8p2lrO1fyQ6W2kMa4uvOsxuSj/ZfIce3Mvn7
5YEm/rapu3puSn+hD5v6O6u+sSr9W4E83AZvNLftcs155mkvNek+R18eor8H
0Lc7hClE3Iepo7/g76r9qT+K9v+oW6XMiz6I9veTdchnLW35odonMkuTzfdn
laYcl6Cp6JPTaE9lAfcrGme1Vr+Vdx5Jt0Be4lgVabvtFwPrCFpDV/8wEzyJ
to1G3etcpLTtTcvW9NNorzn/DX0G9upzN/IoSpjeRXyGVudnn/NsTVrf03Yy
j++eqEt8/+D/L/gv2vzsOnZrDUZrMWeglaFtycML/F+CttRRUAztRH0D7W8j
NFmMzwImZ1z5SGfhYvwtR+fL+yPr6dpzpW83tI90DWzzT7b/liK/gsg6BeHz
6juT0qeOU8bYzp/s/bVDVqlwp0Fn04KX1FfjUl43eK57h8JsKzN1jMuQJsZ8
cMAdRbvtid61gS6izItBWp5NqmYqdzpoKuLurH336E963BnAx7oPDTpM96FB
X2Mu0Rn01d4t3FlibONqDcgKv4M4skE/q2NetDPIjl8OsJ5+ZAXp7UZmA/OY
XxVwj0cuOQlzoYz77CqMhx8hp1z4hYDcYDltZyLvlaJth+KuTpvMA13AON2P
8IvJZ7VsXhvrRfp/IKNroLf+6up99H94CtuUa0vfkBsZVCB/+Xi2Dn0Ng97R
umCM7X0XiLHN74LQMPqlWvQV6bSuAQpUs82KQjzbzztzivsO8OmZXabwGJcr
PXUfRhqFlT5p7KQdDafdRqhclCVXHvOiWhf5l/Lfaeo7LkvTL2ah3ZSCHgx1
mvuhg0ER3hkILQrdQh6Lqb6QV8kKHpOL4y4BSoJSoDQohK6VgZYF5WJsZ3Zm
Le/HKkaei4PyMZ4bfBuYHzSq7TWblrqDRGuPId4jWkH6gMxz8F+zInwlsIR8
PNeeQN6tjLsKqAqqqa7A6hCPB2o3PxB2l/YpEfcHoAbPa4IT+NeC1gaRoA7I
Rl3WhWYuZ9SDb4vu32zqb+f1cSfX9zPVRU7b0JUtXT3/j7y8AC0JX5/yNZQc
0gX4gFv823VsR173qfwV6TtVGvGsD7rUOMbPZW9eYZrE+P+PznZeQn5NcTcD
d2nDi6i/e9BQ2n0f2vu/utertvcua89yDPnvL/sxebzOp/W+AZS5Oe+3AC1B
PP3Tj8ybWsG3Bie1T4P071GONoG89KSfbgvfmz4qCnqNZ9FqC8S/HVlk4v3J
9X1flvY+tkbnYuFjdEcs+TpU1HYLdF5Q5wabgBjej1WdocNxykeMdXAi5dlK
P/oD+Jb+rwN9QCswHv8EwkzI7XFG400i7sva5wjtV8b3nfQB7XDXIs/3KPs/
zC1eUVrUTzfazjDa5Ku426sfBR3BE+S3Arl9yzudYrzX6aDONoF+9DcXiTO9
bFyhf83Ba4R5HdxO6TPrneE/pM67xHidoxcYUcNrFzo7rfWLkcjqU4G4uxKu
m9qEdI/33oR2B2/F+Dug7rzuAX81re+966l6AIm0nb9ol23ree3yY/IyNJjx
i2e9lDaYVc58u4Z2vyu9Ai+JcwUy6CtZxfj+WN0dGw59T2OA2hX11l99MPFO
1F5W0kiFHqYEA/AfTXsaz7OBMT5f+Hk6f0fRmc5B+L2CHMci7/Gy0Yh7DnRe
Jd+/qrvQo5Fn6dS+G07n27/Tt2308dvCPr+tc9z1dIcrdbyCfH1AHKdoE6dp
w2fBENxDlT/JGyxE9lmINyNpfKQ+CQTVch+sb5661zaWMMPxHwFGgk/AV7pr
I9g2gLunMP8W9NMY212TzbVRMf7Pr//7srFWo4LtrH2me5Oog78jvA/4fAXb
9pSdc9k7l637z3j3ub6pghGEj05jO2Rrg7ynYTTPx4Cxqm/dO6Z6CvI4mpk6
rpnN5wPGq6y03aF5AvNpMAG/ieARuvoQ9KP93KEO+kC3FfVZXJ0bnlXRZ78y
5vA8YVKM5wqpaQPt8/kcnuxc/4n8uwX7f53+302O8ZxocqjnRRr7finsdbwp
8LPR7VmNzE8NuKdBPwdfxHhPRyLj65fE9zDAy09n3a5Q5wuglwNU7i9j/C18
VhnfwZKirs/E9dR3FtreLfB2Vd9ZqLsMN1fz+Vadc53OuzPAPPqNE+jlTOk/
6Em+34q07cyvSGe2dBGE5/W97i+Q12r6hrn4DULfBhQylXtNZfOvQgcGqNzl
kWGFtL4rfn5KU7mTk24K2V1g7DxPPc0jjvlqY03dr6t/176cPvSL/UAxyrWY
sqzkf/IZ2sMhzXMZ2xbwzn10cKH0M8ZU7r70S7uI6xB6/XWMv+vvRa8Wqf+l
br8Cl5jnXgFrdUes7vTRGQX69a/oZxeCqaSVkvY8nzx+w3uHSf8wsrhO3S/G
fQGZv4Y+tNJ6BDr8CXwW3lvCs6VgGVgOVmjc4fmrlGEeNJpwK/HbkMnnTVbB
r5YMQTXiqhpAc+Jqltx+b+quENA5ve+9DUbXh6EfayUz4r1JOdfBx5Uyvz7G
7ozMibZSrj26J5g+ZAN+G9VHkodp9LUFNGfAvTtg/25zjO0hH05me+uytS77
6m/q/xjPZ9Eei+tbBvXTH/9h+SyD28nMSy7/5xa9kM74NOCXDn3NX9tphzPP
Okn7+5Z3ruuOPe0dyeEzXDq/pXFqZVXfl6Z707bgnkza30G/B2XQm5XEmxk9
+gH3VvVDLXw/fhswl/S24XcP2gf/o9T1dtwzeed3dHA6dDlyfEXn+KEp6JNy
0/5DwK6AzPby7olitg0kG0ER2oMe4zsTKlA3O2JsuyoKvi34SX0mbXszY9jP
GmfJYyHydwm6M8b/ffUfeBN1+Rmy2IXfOK2L83w8NCdt5rzuFSEP64h3t/oR
6R46l0LyAeuR2zrtV47xtyt9w9I+hHkVfBfcTcq1h2fPSOc0fHHaz3ni20r8
84j7FHpTjWc36Z/K6e4Z8lIWWl5zDML1JZ69vL8PTEOfLhFHMtpOPWS0X7pN
H9eVNnNA/UNgb9dB+I4644DOrAS9CH8IvxaMcYehL4jzCDS6hddvBtf1Gs5E
1Qv+7RmnTiPTs1XtPgaooqDj0CmEL6k74eArojsnNeZC15HGKbUb6GmFRzZn
VDe4c9L28+p+q+zeKxGZymHPBsKfi/F6xHnoG4V9n/Gb0AtKDx37DXoRZKD9
pAdjGUNa894l1an6EPKdiE5cgQ+j7krn8fO2YbYN/nN527CQLQutC2lNSPsg
tD4kd+NsvlsiF/W6oK7/J+o/4iXSuhrjNSWtX5VmHCgLftf4kt22SGST5A/c
18CfyifvXFd9N/B/uRvwN2Ncr6O13s5YX4D2+g7luyUZhNtW4mnoeNK8jd+d
GP+fehD4TyW759oPo30xcc19j/Jf+NeRjYsYf/u+p/6WOO9DH8R4XauAvrFr
PAOPwY/0F8toQyvAavqQZdTp0iDfsb0E/R/NHGcybWoS+DuLx77/8nj8e5e+
+AlxjC7ve2O2tPDdMaKxWc3X4tkXtIUcoZ6fbKc8sYzLT3kvhdaWyptfkszu
vyUn8DwA8d+G2a637HvPhf6D378am2mL/0l3wUsQFMs8gjgmprTttJAKtqV2
Hl37k37rAvRd3klGuF7U1WP9T6J8yXG34Hk1+rwKZby3QfsaZFdbvKjWB1MQ
rk9+28iuW89U7pSxvmc+VazDyL80ba4l+Zikc4Ox5scF3GnkRhbb6FMH4U6r
b/HIchBxBfPsJOVNC00H0oN45BVD3fUlb9WJoyboTNimOhukvr+67y/S3UWz
kPkE6nE8mATep3ztCdMRFESnw0A+kIF4u5B2N5A/m+970l1P28h7c/ya0KYv
U4aMhCuO7r9DPBeTe14ZXMQ6KVv0WjfMFOt1RN1XWxcaCTZUsH/mWPOiP5H/
LHJrzRGaXftbkW+e8ra3EpfKNleuNLd9KNmJyqZwYFUqn0vOAZ8TjED3O9fw
HuJcuENAbvBmWX/HD4312fE8sb6LTTaSJlSynaRRlOdf0p1ewRCfl3D5wBj0
PIjwM+irpoMw/F7Ja7tuV+g//6L/3aD78wv4zvo5yO5HnZvQ3QA8y4T88sdq
YQsdDNCCseYv0p4rMtYUgg8j7vwgHP4+dTeKMa6w9LeAbc4GpTIv+h390D7y
9XF+26QeGOywzcr4nIXOWETE2r6i7LFd4f/MdfqZIrG2zVY0IMNiYHYFu//H
8+ygzhtVsU3E4rG2kditim3Qloj12Xmdm6+AzpUlP6Fae6hkXvmTTR/x8pN7
KnoapTNhoDj1XBW9LqHvj/RH7aF3iXtqCtsXl23x0oQrmNL7nldSzpKkWQos
oJ/LzNxjBOnlIWxjwq0irnJ5fUZCZ59Kx7ofW40eDeN5N8r2YYCWiTX/YZh5
+R2kzZVk/KqG32F07hj63Bpdrp/S51N71fBZVVG5y/JeBGmXizXEf0DY8vAd
s9pOeAX4suS9AniezLacZce5Iv6VwDHSTNnYVO7LWazTlcHLCh5vn1UwL1oF
/8bQIshyD31ze/rO7jobDfaR372gQT3zokpfEK98VA24qwXwv+f4Vw+0jxog
kbYzgfwklbQd0nn6j6CzbKm8lq117JqEq0g+8mteQLkqaF0L1FJbB5GgToDK
/XlKnyPVf8Z0vFOauisF+vNOP/ra90FdtUm1x1jzDQJuoTdpvl3R/Dup7P6O
/0gLGWcWgJ8ZxxryrBGYF+L1nMbwTUBTtQXwAhmdCPb+2eax3pOt/diyk5Yc
vGQ+0I003qjoey67V7T7//jsoXYf0xmJFLarVT3ctr1r6J4B4lxB+X4gTGgq
U7mfUc6WPHsKPVzI/1eOFTJfNdzuX5BrKeLZXdt8WZ5tpU9qxXutQRtwpKJt
iIe0NC8qebcFUSBaMkcvjpDfcTyPwR0L4sAV/gfEQzvhP6asx22N311xjyvo
MovvlNpu8TlD7a7OHDVBegFGItfxuC/Tr86q53STVF/kpZ36wgD/aqzdksMn
hPtefV8t78OqTl/VPtZ2zzvE2gZ6h4Bb/h0DfCfoa4GyTSSOJaT9FViAzu+h
rvZn9neCTIF9niOIfyyyO17S+z217/N16QvP3gKdY/39UN8RPyE/pSvaXv2r
KdwXLQ1xf/SYPruL+kva5Wraf1f4NdBG6Go3jS+6GyKX111zQJdV8x1Ng8EE
xalxJtb8pIA7Czp6iXZ/Jcy0N+l9X8b8uynsro9udifsW2A77T699gfRjj+k
L+qB30fQubST3si+BmNDT/z2UN9vx/pb9DvQXrFOr3Mq5yEEefWGvgue6Xu8
vkvR156jXpPRf5xPbRv2+nZ0Qf1FSdse6kP4f/HrRV29AyYT39RUHvc+5flL
7S0hzC7dE6O1MeLtpz6NOUdFsE2HwkgnEV3KH2qbCFr/Ok4f0BM599Aat+pe
Yw3x9g9Quf9GZiWIv3ghx7ME93D68I+pmxFggPSY+Vg+sINxcWCsbQMPgt5D
B5ZSjru1bNt2W1rbwR0caxv0H0AfMr6/JB/JKN8NsnlJcy50JYhwWXT/P2HS
8W6Plo5PfHAluzsgi6GxvgepLG37BjiTyvzNgPtEBc+ZryKTYRqvSOdDaDx1
1w4dSoB+hPtjsCGV6bpU5vVc4W7lsi28X+rZHt5wwoxQ+wMttX9JYyP+6Uiv
eajvJC6iM1o8/xS8V8/tsl89zydHaaxhbp9EWbrg17CC+c9i7Z5AOcfrfLLa
re7fQ8dmox+/EP8YjUuUtwppjIV/Xf/R69vuSHfyMpRwH2qdj/oex/Oesh2S
y7aPZVN2fKx50f6UaUKs99w0q2S7PLLJs1370gvaPvxE9SN1fedoBxBLeuOQ
5yT8J8d6f94U6NRYr41qXbQyOlgF3CbfjbXGS/0OU32nNpX7vTpe83sTfKQ1
DN5/kNt71+bi1wzdTkn4z/H/AnwJpoMZAVo8j3nl/zBprJaeEndxMBO/WWAT
fdLGzP4Gsbyuv0PMxr8vc9V+YI76cnQsSvYWNFaB3Oj2cOqyOvKYRF28ndf3
6zTO6PXgRvW9Jjxf9RlB/xfr/4OT6XdykqeFuLPy/lfQ75mDZqUcf+ksI+5F
YLDO7UMXg1d5vgQaRrttSryTcrjPmwxdGuu9Uss01iCPL/hPvxw+gb6rNc+n
0i+uKuK+cEWs7V7K/qVsqe6L9F6npujVFu1fpR4XgJWEa4ScHuv+Q/rHVbi/
Qsbp0NXV6lfVJ2v85tlayZywuUJsR3Md7hWUayVYRjnX465APvojk7rkbQPu
jaBcDvvL/vUz8Bp93ib8R9OOPgOvUM5O4NX6TvMSMt4ca5s738ba7s6WWJ9p
Oqd782N9N9v3qnv0bntt28j5AfdWsA2k0X9V6I9gB1hL3D8F+J8Dbu2Vy4tM
RkEbRvju2wYR3rcbzH+EnYS7SZ3fRTb383v/0s4U3sO0i2dja9mumvjdAXdF
ZL20vO1qr65v28vbwEzKdBz3L6oX4nzCfOg35H+U8WUBdbKRch1BbkMYu3/V
uAH2xnoM2Se9oZw9SHc/fC7qZiVhk4d5rWgJGEC9fEzbOqA6oc2cRUcPxtoe
vfZ2xVbzOfCr9PF5m/qOed01f4gwN9DHlyX97bAOcR+Ote048ZEBt/Yoan/i
ZNpIdcpxBL+jseaPxdp9XP0+enICOpH0X5Cv/8BJ3KfAMsad07Hex6H9HGfg
z4JzoAM6fhQd7VjCd1PoXooLoJ/OYKXxWv5PxNWUPqJ5HZ9tkz5ILypRZ9nQ
9WK05biMHmPjoeehF2Jt1/o36EXpFjio7ww6v0C9X471ftUrsbY9fzXWtuh/
h/4RKNeRAL8JPb8GXU7dzqf+etFOmurMTay/NRdFB7OrD0fXz8C3y+G+W314
V+h15YV83oj1tyl9o9KZnyD8XpL2TfxvxXpf0e1Y77GvFthnfyfWZzTfL21/
7bufhwznoZP9i/ts4IfEcUJ6Vs/nFP/WPDyD1/d7kpe/pA+6d05n4EnzLu57
Krf6v9TeM3qvru8U0n1CLcADnv2K/pasbTtCsieUO6332v5Feg/VP2iPGzqd
Bd1/hPsxeAKegr/BM/mhg4/Ac/XphP0WXR6VxTZR/sHvX/AfeAFegt46uB5H
Gy5gPlmc3cHI4B/KNItxPjnuFCAlWED++9Kn9qlpu9uHyVPbZP4OnIrnGdH7
BOrtAeW4L1s9yDE1/nWgaaDJ6O+DoVnR7+48zwzdRr/zI1hIWml5dgn9SwdN
DzIozgAvO/ZyvxP4/zkK3brJGDOaNt0DmdSFz8Tzu6TVCJl9T/kbQ9dAa+KX
OVC2LIHy6j/HpcB3k5nILK3mNyBrnOdYkvU10smGuzZj73fE9Rp+5yuZFz2t
/0M8X8Z7OaC/p/TdQP9Cd1DHjynjo9q2lyC7CfouWj+w3vI9upFE/TwnnuO0
hZy8vxRdWw56Ed+Zio7/BuFugreL2MZ5zsr+ttoBviPIVdl1EZXMdtBFz9Y3
L1vtV1PbRvtN2u8NkIt0UiPvxzxLA71OGu15Z2YlQ/yrICtpVi/nNv+f/h8h
o7EtzYsOLeC96iMLe7+67KDLHrouX7iS2lTu6chuB3n/sYjzomfyj0WGIeQl
t+qYNDKo3VOWZOpHkMff9c0HBdzn05jKna+QbaSXJvw84llKvucWtFtUz+Un
Kvc92u/35O8+NJT08oC8oFFdU7nzgR9aOpxsvsve+5lKhvh3yc8t+s4wwuUH
XwV539bX0AK4wwmTOtj0Xn3zZeB/h28e7DNu++lP8jEul8S/IO+EFjLtVNm8
/EVzF/J6l9avHuiuU8L8QZjraUxvpPn//LWAO1ztNB3vQI9pvw86HBHnNcLL
oEicaflW5gXxRaF/I/ticbYt/yzAy8b8rULeR35b/0Pwq0A/elW6Vc/7EbQv
oSfpL6ZuvwGXGP9KKB3oBN3PTXsviC4VDshEsqlT2Wkr3WVpbK/7YUHbvupe
1raw1umcBM/XQ58G8tS9kiH+LegB5gGF9A0GHbxKfZVS+4OWhpYBQ6jbL5vw
nwT+DWRxnHY5lOdDQGHKU5uyvAYdncvfdPU9tzB5La7zG8m81liOd7MXcjyK
Q/erlI/zGr/W+mV//ajG6frmOwXcFQhzjr6wIvRN9OMlfdQL8CFl30C/tQn8
Ttlbk2YE/dBF+Epxtlk9gPwMApXjnH5EPrfFKioX+nudcai9/nfjrhaA+FOk
Wx1aA9QEtQJU7tpxto8jOzmR8FO1tyPc9s7rxFkOh8jnKt2vQRol8K8b52ey
TSy7xJlId2J977X+qonvRk2Wyfejyibze4Vsl1kQPxX6D6hHHPVBA8mSeK8V
ss102UpvqDYIGoPxwYb4CdDfdEaJ+UUX+Cb4NQXFqJdm0MfE0T0A8RXR9+b4
TyRsC2hL0Aq0Bm2kj4xll8AnwbYPvjqd7Q7taGi7PZ2pl7aEi4ozfyyN3ecq
+53BpJEis8urcuse4VjKNiTYtoqbNbPt4qy0lWje2xTi70t7GdNjVI+0jW3E
tRVsJu1NIL6q76hph2zraO6ofhAdiYOuamA7y3XJXzzuhDjbnQ5H7/5Cx6I0
r6jv8ziJcZ6TqZ/ugl+S8q09sNBX1L/S/74a5zUSzXP3Qhsxhk6gDoek9PdN
fdv8XftlyUt76QP0sO4UoP9fAvKRr+LoSwflA5qpgff01KC9zkWXa+oMAXF2
VF+m9wNU7sGU7QRt6RRoQ5udr3lFBvvpWYYc/JeOs936ztAuoCvoBqYxPn6u
zwOMOU+Q9wEwE9m9wbP25OlVMDtwD0tpxoOB+r6v73NgYzk/20GdvRlnm9vv
pzMv+l6AF32XeI7yv6672hIyf5e6GUDe+kCfkr/pZc3fA28RpgfoCdbRD20A
b0vn6MNagGKSFTivOQFjXXbwN/rxCTpVqJzP+xyj3o7nsj3Fd3j3V+r6MPlc
RV5aU5dlC5uWK2xe+7Rk/3dKQe8r1p7iU9DG5Ku4zjuCXsTTG7wb533HCrcP
2gd33zjbP29HvY2FXiPO/Mi0n8oP2qXwXKRLZa9nddJdLXGG+I4N7D+v6P93
v9rSz1Xv/QN13Yb20DbYdd8mQFtBu5LmLGQ3EzRu5TbalTimwV8kzQFx5hsF
3AMDfVdkK/ODAu7BcXbLfxft9jSy/0B9PahMW6sE5jL/HKr+DqRDh9ODKU09
79KcaynxX0MvPuT5R3G2n92U5x/DD+c/z3DoCDAyQOXuqP2DpLWOd6vUtF0D
2Tf4hGeLmQOkIs3XeVY3ve0ay9ZvsQy245oDnQ0BbarYjvwm+tFPea8tdXcl
q+8OW8y7I5FHOsKN4tl/Wk/k/c/glzDWFqBP/iOPz59qP1M2wg6v7P40P+Uq
wn/b0YQdAxpStw2kN7T7kejy5HK+f3EC/Ng4rz/KLus49bngAM9qIMv71NOE
ONv/Et8uv92vkr+16F078nuQeN9BRr3BRJ5N0vvFfLfrZOUb+hO6PgV+A3P7
E5R1quoWfB7ndROtmUSje8XJw63Uvuda911/IV2kPP21fyzOdHqc+Zz0R1mR
zQz4mWAWmB2A+DdJ9030N5p4epX191e59T32Nvn5D1nNIdwC9GYfZfuhkPdR
aO/F3Dh//3qKvD6Cvq39TXHefzZf74CUlHssclqofkn/C+GTk59k4aYycid+
aB3fVfODztOT1t/kq0oAX/HuW/jlRkfjkUPbMl4j/jrOa8a7dD4cLMJ9lT76
C2S+jri/wV2+he2rLoY/Sn30pV0/In8PwSz68QbBXi9fwvOlcT7jd4p5Q2vd
ORLne8b0nVDna0YS71caX8ChYh5nlsd5rNF3cNmgWoH7Hcowj7rp1cz7bLSv
RnttVuoZ/VFvMJ52tAr3avCA8qyJ83/NfdTt2ji3C9nW/TKdbe2uU//KsyoZ
fLe87urVPb3rpS9xXnPaCK1HPW4o6j3APSp5H3DDMJ990BmI45l8T7ds7Jyv
5fuHN6m/0t1t9Eeb42xHPCNlyxBYI/kYffwX+i3PnlD/Q0FW2tYWpQsqUbYq
oD2y7UnYjOj/9/j/ALLpnm7tXaLMW3Fvi/N+au0fiQfL6etvUMfXQTj53C45
6D9PnPdMNAcPydteytKHOCYSZgJI18T1uYNwx6DhyKg/bXx4kO990D5I7YGs
VMV7x2R7U/op/9SUr4y+i6ZxWz9N/Q0l70PAKe3higvcPYQutQQ/475IXzdR
+wagO3HvRh9/AXta2C5CTuK/iF7s4tlvDXx2dDf8L6BkOa9PaW3qX2Q6X/dD
IJcC+v/F+2ML2x657JIvBL+qPkJtQ3QGfeIUyvZlevN74uzeg4z2gUktvS9/
b5xlsC/O99vvhxZGtyujC/eqmF6lvFe0P5g0D6jv1x0bPMtH+L8amC9dye55
Vew+GGeIn6u1ePrTT8p5X/Yh/A+DHuSrCfk/iuyOqE9J7X1k3aFHpZO0jR3N
fR+R7ok/ht8O4kuNDHZBj6svRJdPSO+R7wDq8UpZ3/Gr+wt0z69wkufZoafi
bO85E3p2Gv4MyBVqXntk5O5Vxt/t9M0uGB1KB87iv4f0qvPuXmi1AJV7DWWb
Qf9+TuVBP85DL4D6zBvvILMG0A+K+3/VkOK+T+l/dymB3xSWeJ61MsRfxC+U
vOYF7Sj3Jdyv0Ce0A52IbxRt+7LkgNyf0Q7+AX9Tf8eDbf9E6zp6Jv/N1DHN
JIgmF3RF5SWNc+Aq/O/gD9VRBDLUGgX604jyvCD+/0BR+ovzOT037Ye+bKCe
7kpvVXawlTRW6awtdZiGfP9E/b8Ophb0u3ovIoO/O1zTmF3P9tFlJz0nyBGg
csteeR3QAhltpt/bAv7knevSRcpchbSu0nd8Wsjf/zTH0ZxH86Aw3gkjbzfw
+4z53ahcXoscgt7cxO+WxhWQVfdXgrbURxtwP9z2RfRN7Q3K/htx1CT/NcAJ
0vsD3Ikzn5TK7i6MiffRzb/wvwu6krc7rUzvxZlfpD2iyOVqRu+VCNcaO89S
Uxfr+X+cuoj3AT6I817A2rz7SW7Pc2frzE5N2+bNBGbVtFv3Nj4k/E/QR9DH
oBq6lBbZ36Xun8SZv5fO7vG885j8PsW/L/r7Siuv5+t+rtGMT5/pDAzl/x5M
iLBd8oHaRxdnvlLA/Qx3MvrLF8S5M5uf74I+h5bVeSMwjXyHg5Dctr2cEzkm
0R7+IcxU/EPx30id/Btn/drN8//gxwT7bkXZtZR9y3L0D7PJ8wuejUbvR/As
G3ipfjqH96sHxVNnjJ+5qduH9IfJcO9gzvEhOtQfPfgImjzeVO76oLHO9TT0
uUududRZ5BSESQlSgZrEfRl9qwWNIN3WlKF5a59HTR3v86knS/keuYtaU8Wv
OfHVAikInwoE4/csndvh9gamaovih8J/mM7vDYO2qOrzrl+go//yvEhVn0eI
ou7bgrSE60m7G0rbSRfvO1zSQ7/WN+lw/wfMgHs77ftH6q6RzvHF+wzhysBZ
yzx5bANJ/YDyMYi6HE+aA9J7TNquuS7vBGnNGTlmhq+jvciUKQt8XHrT+PT2
iw+4s8b7LIrOoShM4ar211pwNmh2MAPZzyzsMwQjaSs9ofVJbwdyD6b9baYt
5SBcThBDGX6O9P+KXLh3Rtqtc70huDOHew/V57ybG/da2l8oNBllrYZOLeQ/
/9cgiTLkibftjW7kKy98hMbrsqb5cIeBJejlLWTzA3LLj/tf5N0i0nyBgLsg
9FXi+4X++SOoDA7JJl4h/IfDv8JYf4h5XT30ukFuf/e91dTfgfUNJZxwDSr7
vPVr5PFb4i+MXwXmHpXCbDNcdsRlL/xlVdsTL89cq2wyU7llR1zPZXs8It53
FxSBFgXl0OM+6OIXZWzf66287ouXNLTtNp2jKdLCMhAfXNDuMMo8jHrIDy0W
byq3+HEN7R5PfgZq3g19L8P/PzsiOz/FCVcC9CJ/q5Dx7Uy+00/finWv30Od
l+a95bhLpLOt3/fpZ9/Tmj3hThVw/koSRwpoKWhp8Bsyn06aaSpbb97l/aJN
nE4ZnpcFRxoa4o829L08ukulKePt5mY+21Myr88q68xyHt4vp74i/n8q/j9e
lCYeVAG+YuCZ+EoB96sRvr+oHbRyvPP5fzIVlfsS7f8KqAJ/Dh24m9m2SMbz
/EfqY1hV3xdVNd53Ru2h7PeKuJyPkNlD0CejbbN3rW2b74+q2+6UbE5VJe5q
hK0OWtJ2aqh/ArXiXTe11WYy2LazbDz/Qb8eqbYLGjfzue3bpTxunwMzSa+S
1kRz+Y4u3SuWvLnvE5tGPs5Us336rLpHgDiyZLG98Hrxvg9a61f1pc/xPhd3
k2fTkM8qyr2A+BrGexz5N8L2brYExhO5GylPoInaFu4p4J2c5tc2srsnaMrz
t6FHiPsBc4S1VW0jQbYSmqneyOcbyLAD8ulDmypQ3DbXs2f0M+2Z6aa9UuhO
l8K+P+5aLd8nV5ax91pVPytN2LJgCeX4kPibx1v/WwSo3G+W8r3QWdTm0bGW
+LWK91pFed0pwLutcbcBjxl3euCfljr8nXJ11xw/wuXXnRxdsvleDs2R9uM+
qD6UZ21591B6y0H3busOj4M6n6Q9FxnNr8hmt/jXC9itu3ajpIP0tdHQPeQ1
Bvq65vqa79B3/MI7e6jPWPXhepbNd8bEq2ytff7rUhFTuSX7L5DNIfqIBLU1
jSHZbav74xyB+0Txf4IsH4PxmWybfVIm87LXLrfOAFfj3X28UxI8Re6loKk0
3wEZqtoenGz7ySbcfOYxScS7ALqLOVhd5L8bOoX8T85ou1PteJ6R+F+JN8R3
Rl8XUD8foWcHae/DqaMdOqsR6Pulg+r/ZSd1FXX4IXnKTdznWrvfT89/mfbq
x6irDvG2ExCB7GqR3j19o8fvLdpRUfSnFfOyGbw7hvyMBpfo0zrx/LV48xcD
7jfJ91sgkXFhJrIbRlvuDf86zzqDLgG6MKf5rqAbeEPvaiyjvpKD7kpbYylY
rfN48b7HeHVV/yd5G/cu/JsQ9zvxtqMme2qyLdEL93LazoD6/v+u70BlGRum
UEe9eZaO/L8LzdfUeyT6xNuunOwjp0eueQifQbKG9uXZYMaLfoH8KF8/8P6E
bLZP8x7u98E04u6JDDpQJzVL+kyUzkbJZntm+qUE/PsTbkC856yav56gn7xO
XYykPPUJnxVdWE+8J8r6/4fqagT6Opp6G8h7g+K9J38TGKx2p/2O8Z4HKz7F
KzttvXP6PMIQ1Y3+k0P/0h446IfgI40h9IOHwXPSWEFZP4432gX0S+F3NvA7
Op/8GAyXDAg7UmsD0HnIbiZx7KAvGqG0qJtytMex1MtI3J+ovAW8D3+97ivR
eEV5HoEH6O0zyj4Kv7Okc4t85OK9z9T/oH8DiXu00qtuW+SyoT2X8k7CXZp2
s4L3y0BzosNz8B+jvgk5ZkUPxsKPk97wP/ou+Ruv9kA7eIu8dNGav9Zeyf+s
xrbT9kMFwPNI9G4r9AW6k4N2MExnpajrjrSBNOThAO99Vc/2p3KTj6n6xhjv
s9gToQnaL4UepKhhW6cxlC+6tW1lTeJ5b8JPhh5EllOgU9WXkp9d6EfhAt7T
8jnx7qcvnMazzMwBslb23f81STd9c99jrvvM12u9g3Hsc8J11PwHWq2yz6Vn
YtycTlrLM9sWcMYmthW8i3h2gi9V/7T/goxvbXVXvc66EvdfYDrPZoCZYBaY
rbGbcHOgc6UfyGye2htlHE2dxfFuvNYtwV9VbMc8FP/5hPmOPAwmvQ7kLxwZ
LIi3fVC5LxDnR+j1Qvy+kk6iH19DQ5DDSMJ+ChoWcdv6PJPbV3HmD3fo5/pn
clmLVLPcjqELccR3pJjtkI/R/R+89w3YyfO2yHNba7dNtVHZnV7MsyVgqdo3
/gOq2TaWxuEhAT4qm92y+b4s3nbflweo3G3Ql2jkEFXDdjBW4Lcy3najV0G3
Rdim/fNqtmv/b4j3ncn+eoPAPjTxoZn9TLza47IibpPi81azeyJYTZxr4s2v
jbd7a1HfJ6Sz15Uy2va4bJDLhpVsWciOVXVkU5/6udHId6yv470G6PAZ+pun
hH8GivDuk0ZuB+vVz4CNoCVlnErdTNO5VvqShoxjXfUNgWeb1cbhv423jdEt
0NGEa9DC6c1Hr7/WnIox7zvNEYirKnn/XrpPmX+AntZ3e3RwEbhG+lvxe5HJ
9HYj86fJ5+EI5/V0IM/K+ynGpZPI/gRopf85xNkav21q78hze7xtk8tG+Y/S
rRamcn9HekHI7Epd23SXv2y+y/77ewG35mCaf6WvZl40ndpVoC5UB7kY23OC
mbTptKTfHF3ZoT450Ff+HCjjdPAFWMT7SY19p3455aO4dW+nxhX4O5XNy1/u
XfC7wS+gMHOcqsjkWoT3X/2K31P6t/60iyTtJ6xru+WrAjoofhO0peyN8N5K
sIdnUY3s3gv/O+/sU3jofuiBQD4E8ZmQ0cHAuKGxoC11uJR2fkhlJ/51xNO5
kc8XtyAPXehLW+l/sNbtq9k2n9bFtT4epvzoPxf0P53tAsPT+3vUJNraYeK8
TvmPqC9rY/pTNfNH4SeTl6lFvc/rGO5VjXw//Xqd2QbHVe/4VUYnT8Q7TE90
fzdt/6TaLXX0sdZ/9R2DucF+9OgU/vugXaqbdmpjKn/xp6FnwN5MpuFZzWcm
3s7Z/F/hLP7LyefxjP6vcC7ezx6hD09Aaq0dqr+hbSzL57sCdE/ASehN8vIe
YT6jXF11zlt9a0Pfu/qcOnkGQtpY1r/xLIJ0Lsa779tJWarm8t7lS/hdjrft
1yvQq6pb9VHk9Q+NjdB0yOZ38tKqrO22i8p9jed/SvbgBtiifEEvkKdb0OB0
pvoeIv52vNeb38F9nXaWCnoDegf/v8DdeI819+JtY/sf5NJAd2uAjbSVzfnt
3higen6fsL+V8Z5Src0+wP1usPlfC9ndkbCFq/s+i9fgB2S2+yHPHql/iXe/
8Weg70iU/AN+TwL+4uUvqv7maUDX/g7QHdXMPwPP430/2z/QgTybhwwbNfP9
yLojrHpD/0/X//V/CTOSMJ/quxL8eZ6dAy/gX4KgBEN8MmhyMIR8VCX/HwSo
3N0j/I7C1kE3Pg1z/ege0mktmVvgnxJEMJ6/Vthlr0H/Vx38Vdz3NspW/WDy
mcA8sTsyrEOeUvFOXehS/d/I62f6lqfveKl5lgYEgx2644xn32pveFX3mVp7
Vr94gfylJUy6BNuuLkAap5kzDFB6YD7yOY97MPnOFWzbuLKLe6iIy6Nyt0BX
Xqnjb8at03s/y2OQPADxT0DrzL6fR/f0pOe9DAnWr1U8ywi/OpMhfgZtOZPy
hG7mR5eukV54QdfB7rq2Yyh7hnd4djej3xHEz6zvu9l0R5vSKUq//DF5Gw72
6I7aBK+rZ0Bui2jrGTOYL1jM7raZfd9YZearo3TuhPcuaR2C9LIk+Jx3Vuge
9CobtAz9R3ZoKei7jDMf0F8GQ3Pgl1PQehjluoZ/YXQsF34hoDx5zQ39ivoN
hY6AflLZ+wVQmSCqI+gUZR6J34TUfvYG8Vwo6DlpHt7JC/KBGrSnMGhN6ETK
kB9+CrSA9JLyF0wwr3mV3IXgP0RPwqHDAlTuJ8juLOk8hV7kf/f5qt47qzuW
ivNeYcIVC1C5Z1E/c8DPyCcCvyKSd4K/WWqP8Tb0bmR1224rhn+szp7Qv9/i
/0GPMO+JPMtY91Fj22iXXfbihBuJDL5jLnmOOM6CVTozw7Mc1Ft+wg5i7lyC
cIOhC3m/pOQPkuhv3uX/Ycecvk+jdILv1HioPayUfVdz2yqOgM+h/f7EuRqs
KGqIXwktw3tz0IHLbbwXtGY17/3UPt7ruC9TrrKE2UYeyyU4b7J7n6W85+Uz
23iePgPsrWf3C80Z0YvyhK9O+iHoQg1oBdwVE9wv/Ua4c1rTwh1GHfQt4H3F
lXEvQwbVeb8KfFVQDZyg30zSGrTOS0oPEnwXXc0E7+2vRV0+pu1kJt5DtO2c
hKvFsxvIaBv8AO3RIX/1yEdt/OtDL1T0nRgrqrheVCeRPFve2FTuByACd3Pw
sI3p67z7FciKbi6FnkV+dSRH6n99M1O5JfO60HrgicYZwn0SwE88Gwmtz7MG
oKHqj/I1gjbR3mtR0BQ0U/2nIm31QaBlgtc8ZB9+WjafqdF5tVaSHbQjZWqt
PhrdbKO+C52+iF/bBNsFj0owL/vgchei/VxjDKxLYzyI3j1Bx7fxbjRhYsAo
7Ttk7rybcLtAacKWArE8iwOpkcFSyhwPnwA2NDAvf7llazwxwbbHxWcPuINI
KwnaLsC/kmD3MOYFr0Lbq6+kv+oAXZPBtsdlm1c2elcgu4vI/zJ4O5PDdWtj
XvMRuXdQho6SNXRRRd8PrHuCOxJfJ/AaeAPdu6J93uj6nqLWS+mk+Dfz2a07
v2UDXvbfdaev7vZ9nTC70KmUjXzWpjPujsi5C/QZbbI7ZeiaYHunL7Pbtp/W
f1ul9npwN54VRO/egL6puife7tBc6Nca5LYarNH3GvKdCLYXdf+co7HDvwUK
6awj7h6SD/I7TH57Sn+TIQfoO6AX+Jr+dzb/Ga5Qd70TvG/iXdU/cuwjPSGO
u22s38vU5+g7N+ireOkX+6kdIbf3pMfk4f0A/by++Z6BO75019cjynafvucx
NJK6qAsu0i77E+4v+sN7IFcq7+ufprsTSacskO3Z7vr2jpwHEHag+gnkehq0
ruZ1vxERvpNmez3fSzNI7QJ8oDIEqNxDE6yPwciwP3GWIv7i+n4B/z5YTzmH
EeYf7TeCrmdO8aSMbWW2Ur+GXwTzy4+lmxpPoTOp2yj09gee54POp6wjVOfI
ayv8SNUJ+fsE+inols13A+qOwLvUyyj1J9DPoKPVZ6FvYxKcJ+VH/KpmdkeQ
ZhxymIp88vBOPlAgq79TqK+5ByZrDzUIJv3K/H/4gPqvKx1Az9bidySH+feb
2K07gQo28r1AY0mrFjo8DjqZNGrSPsYn2E79DO23CPCyVy93QdrSN+h0fuhE
nk1K8FgsG/eVitnOqvjENHZPhp+a1XYVda9Vnxq+26qO7lWp4Dv/r+jbEjIv
DipRnipaR+Ddi9RtFvL9QHsGtQZE/hORawZ0LU8l69OPxLFC/y8ow2TyMUXj
Ezo3NcF3EE6Dfp5gm2m6j+Ai+vY3k4wv8Evkf9Rtxpn0xHmduJum9P3if5ek
L6bNNszlfSU/04a+TPA+W+2x1X1w2wp4PbtMW/NTAuvbJanrocTTXucjeG9t
Jt/5HE+9rUbH3kXu04lrP+19XxXbZjqJPE+AGQm29xeaw/bMS7W0TfN0zEXG
6k4b2WvMa/tLssM0M8H34u8BsxJ8j+ViMFvtBZn9kdN9jfqcZtT1YPJ3obX1
Q/3a3qLu20bItgvugzqXpXZO+NXZbddyXoJtW/7EfDo15ZmP+6T2TqOXf/Lu
AtzDtVe6nPkJ2e2WDbeFuB8h7yU5/R1Y34NRv6BDvFuesnRCdmnoA/6p4ntd
g8nbV+qzCDeIMXyg1sZ0Vo46/lrpaD8Xc4ER0EUJvh+zFbiATK5SV2HQb/B/
qn2aCbaPfaO2bWQvSfA4tjTBdpW071d2lrJQxmxabyP99IQbp71XpJ+d/K0q
6nlRW9rkr+jbMt59m+f1KERP6DctfSZUZ0OXIdMV0ocqtg8qO6FPNF5obCL8
pcbmOzW3e7nGROSYAqyQblGm46ArdbAS97vE9UhzP9rOqgTf2f9p4M5+2e+Q
XQXZV1jNsx9l/0T7FnSWNsF7Si/rTAK6+IL4SiLntfinx52GstXivQ3oQ0XS
LoV+VoJWl97oHvdAn3SUtCdkML8+4JYdmh0htkuzCHdD7SFpbIh/Ca1a7H8m
aoI0zRXfoKjdR0h3c2lkBTYQ3wtk8RL8qPNElHFjgvltWe3+IofXp+eCTTxb
WMzfiHojl87FLafq9CGZSbeG1sP0DYPybSbst2AL+C7Afx9w/wC6FPf76p+2
JriPEsRXLmb/bQl2527tObjW6RfV8Pjav7Hp1zU81orXM7lzh7uc60Jc/+sC
OvAFz3IydvUk3XK0hcLEO5X+/QfGg0nQyWA7ccUimwPaN93W34+fUyc/yp93
NtIWeqCjB0r57uKmhElB2Xfw/D/KnpDWdl8lu60Bea4k3p+gPydY5juyW+4b
a5jKPZR4dmr+kuD1sd1qs+jaaPL9C3xtyrMD/fgVfjv0hzbeY7oVWhUdSkue
g0EmfS+lDR4m/7Wo/Jph/n51nLyc5tnH5GUPccxCT2eS5l74faCOyopckpOX
6pRnP34HwGXmjS1wH4QvGKAfFjNfpLBt2sjGtuzU/ch/h0faf6g8ogODiasf
dXEY9xHwgHqohS5fYdzeT920og8+muA91A8L+E6OY7jH8e5Y8ArvH2YcXY5c
j+O+ji6+Q9mOE6Ytz05Ag3U3GHk8wfOTuB/if7eG6eMAr++6p3g2nvzuREaV
yO8B4mlDOYKQRwbaxgfo91RksLWK7ynshEyP825K+putGf2N7nSC7d/KDu5D
5PsInEmwfVDZ25O90OPoRCFkXjDM+qE7rs8SpjlpnVO+iScqo6nck0izL2n1
AWEZXWaV9zzPLoDfwEX1UfhdUn2AebqXjv+PX1PmRaC25pEJtjWZkX7tKnwZ
wtfB//cEU7mvBvg91Nkf8NfAnyAevzjwR3HTugH+Os/Csnuvvu7yP97U9/l3
4vkNjeXQmwk+C31L7aOJ41JZbmu+hUzvI8OVlHFMA9usvoP/P/nJO7r9V4K/
qfYHd+FXV/ea7Wp9Vwf38NtIfA+Q5X0QrH1AtNm5tK991FkIMq0PvS/dUt2r
/ZDeZ1qLJ89B9BfJtQ+/rSH+57ruu9WHP0rw/7a1hH8MfQIq0BdcwD2Y9vJU
bRU9+TvB/az610fk6wnYwXi4mHFtEPE+U99GefbqnHKC7cLsIp1/4LMTNhv4
F/46+X6bMSOWfNwg/v/wuwl9AX0JUlJHKdD31Oj0JOoxKNH752ZR7gnIrp3m
XSAV4ZIlWieSQ38iaApom4KW9c9t/d1a369T4r8c/jp9WDL93+edVPidJ57K
yKgptAo0daKp3GnggxM9Rkbw3k7tHSeONeQlLf5rtW8Xmj7ROio+Q8DdEr15
QflbQEfoext4FBK4oyfe39r13+G7CO8TU1+fkfd+J/4lpJ0JPjM408RU7iwg
K7iDHLdQH9ngs4MciT4jM1136hFPTtyX6U+bUu5c8F8SZwi0Knl5pbjjulDD
cWt/1Xfat9faMpP99J0gd6Kp3CsDfj8H/HcF3HXof0NxF+Pd79Hx70raxnEF
7ZdBh8tB8/A8r2RKOl8i13zw06FLeL4Y9Ccfd8BtMIj8zCzuvXazoGGJvlO3
CvJpTBr5cX/KXLYG5fqDsAUSvb60nTldPvqBgrgLgfBE33sejr7EljDEF8Y/
ItFnSXWmtAh8efR5LP1cUZUDFAcbkOFv6McF2Z2lnyyRaNuA+gYcTv9ck7KE
kv465qnfMZnYBF8y0e3yNOW4QT3kpr5L4VdK+7Kgh5HFIbABdxncZcH79c2X
C7gP0p+OYywoil6Uxz2OtCsk2pa9bNqr3+iGzr2Zw3a6f9Y3blCRMJWkezU8
VleWvJWfFub1LUpufc+qmmibztWgPZDpF8h3EmWbCCY1dh392Nb1JL56ot3C
kpr2l1/9mvbTfOd16GttvX9iJvK4Qrx3ia8FcjpOHfdFLjUSfW9yTWgtUDvR
e70uBO5Ej0z03QW6w0B24mXv8BbjSh3860oPyHPfJnaXojzdkNVM7ZWG1qY+
a4F6avvajwt9WdH3u9RHNxqCKehAA6UJ0qKn50LMNwIVGA/Lg9uUaTX9V2P8
Xpc9M7X93LYzv1tjMHE0xS85/WZKcEh7xxJ9xqIq7+8jzPu1/B9Ktmz0P2pG
QIaSZXNoC/UNYAJxfgOa5PA6jKjc39GHfQ/GkMfvaeN/Mt9ppb6thqncW4jr
Crio/ooyri3hfqC1yg/aJvqs7+Egn/1ty/P7xB0FXUG82aGzqKucpHlR34g1
pgao3ImBelZ916Yea5Zwm4tSu6JvvQH/O3VzFawJjBmicrfWvrFE75uPgcaC
ODAklZ//18QQ/weIV7sjH8VBIrJ+S2OnbALgP1s2D9RXaW+8+g3GiMzU/SPt
swK9SCOOeVVCuP9ny17CBt6fCxbobnLQjvdGo0tlqa9X4Ocz9sxL6zMwr6p/
pb6zpqbeaHPtE21ju0Oi7W63pr32Qo9aQuOa2kZ3aIDKZrf4B7Sfk62Cgjom
en6peab2SJ1j7F/P/K6Kzl7SR3XieVfoC3TmoP6btLXtnZcB92vSOfAfZeqc
6DPBOhs8JpP35miPTheNOdR/DWTQlvlZBOVYTTkyUh9ZQFee36Y/iNP6aH2f
X+4G3w3/BsxH34C+Ca4y72iEu3ui6VuJ5n8i/Fb6nB7wT9CblMjvZ56fQQ96
4lcC3f4OnX4b/ltoat3ZG+hz9/JuB3SlF/xgjTclPD/dhn9v/GY0MF80rd0N
abcNdD4X/oH26ENfIV+dS/qM0deNfJ78Y/5nZCBcX573A+9JH4j/A/RpKIgk
zFriDkcePclnWq07gSc8G8j84X3Cf0WfNIl66g8/AAxM9FlsyWZQouUTRvsa
DP0APEfH7+rcC/Q6feYm5vR/VvL+Dtmb0B6POVq3BJlJv18Gz280t9F9dtPA
Q3TqpO4QIY4hxPkO+n0ozPfIaD9Vuwq2MduPuuyCf9cw80MT7da6i9ZfGqNn
JZDLMerjKCjR1Oe+I6mndaW9VhYJFuucKnJ8Ldj3Iul+JK0tDSdfH4MKtJ2s
Wlsk/g/BR6AvOpKKfPyKHD7Gvb2l39Fa1G3lnfp6yRztLmNWH93phx72hlam
Xxqi+RJ0Ju1kJPKYBR2eaFsGI6AjwSP64s+1ZhQW2KsZZpvbF9CNT9CfTxK9
5jaAcq9Dd+JJKw78Q7k+TbRuDQ31Wsg22u8w3h8KRiV6nj+Nd2rpHjztpaVs
g0hrLXn5kTRWQz9o4rx+RvjHpHeMsPdlx4z6OYEM6ya3/W/lSfn5h7b6n/4X
U3dJ+n5Fvf/U2HbZR2s85dkYjQmUtR/1MlZjtOYL6g/Up6v/0NhG2v2Q+TP0
cVKi79aNR39KI++y4CPmEJPxnwKmguvI5iVpXpVtCcrwCvo9LdG2OaKpgzHo
0JFMPkeu8+S6m0730vVE1mcp4znwOeHXa50CeocyfwntzRw7Uv/PeX8n+rSZ
sm9krjNd7THR52PyMlaNpXy5KH9dyvUCviTtfqrujSHMGNIZDZK19r3cs/AL
1/914psNX4+05iDLboSfSF3OwW8umJfo+3p1R6zu7P2zhW0it0aHrhe1zanz
9C1ZCPM5/JdhluV8sAAsTPR9tV8l2kZSxwz+D/kUOY5D9geYBxZCvwqCO4T7
OtH3bcdlNf9emN2LJJdW/p+2jLx+o3whh1qUNxIsxn2YsHd155h0FlmGoXMb
kcFS3MsSvV9b94MtV98Bfbe07Z7J/pls0VejDCt4thL8ks53xz6jvylb3Tbc
30A2VyjrWc3bCBPUxPcxFCds8mzeZxOE7FbzLBn0vQJeB+5Dffcjnbdy+t4q
2ZQ4WMt2JYrpbEwx27Vfo3EBrAOZeGc9NDN0A3Qj2JToPTGb1W+rf0Ffu4Ks
tQzx07U+i673IV8d9V9Stg8TvX8nA/97btNmv0s0xGuv9vdyN4OCLeSxfFPv
uR5Y0ntBOxNPB2TeCVQOd1l65HR5xJ8Mtnux7FOC880M8RcCZ5RTtPQ55Rnw
P5DeTGhtdHYfsrivOyZoY32zeb1Ne/EvE98lsJWwlanX9s283jNJ+zcIP4X+
Og/lDAXDQt2/qG/ZRvjN5He+7sAqahtkGvt+oC1ul06T7jLqvithl0NPUe8/
4r9D4yb4GezUOCL5Ud5d8G/orBZ62ow0rqOnOehPcoHHuFNTP6nAbukM+BXs
AQUYHyOJey/8++R9H3Q/iKL+DkCPUF/3yNcDcBD3IfA36nM40ffs3ajke0qO
4M7DnLguedlHvfxVznydgFvvpkRe0chyTwrf13VU4z5pPgVzebYWmpWxapds
SxJuCHPK9dT9McIdByekV+AU2B3l7xT6RvFzlKnuZhO/DxmcJswW2mNV0q7S
1GtR+iYwMqe/C6j/Fa/+WP6nA8/O8N5ZEFvKa59aA9V+hBY8+w2/ltBzGtOa
Om+iyqt42bTaCt+J+cB55ZFnp0AGneMnfxcS/7c0ElSOOmEoCNrc2v9TVqAb
T9GVu4Q9EmWIvw9+09hG/V3UGIp7T4jTO0NezoE/8/jdMtX9ziXCXdZ4pX6N
51fVt0F/h/6hvod2npm8ZAJnS5oXPVPScVxLdDyC+HvQPzVmgBvgZqLtGekc
1i21TfX/ib7LUH3WINCMuvwLv+bQujrbSnlvMPdOIq2WoF0u820C7ruJvrMz
T6Ttot1LtD007Wu6D/9AdUL8J6NcJkG8yib7j7JNLhuQ+ga2GMFup09rVMvf
XxrWcthTgfCSt+Su/4ZJtLuHuBOKmn+UaHc8evhY7SzEfGLA/QQ8lR7Tvt/N
4Lv6LtaxDTvZr5M9WZ3V/jvR57X/Ic/76HunaO0yzPbts4cZsnvfsJnvzhct
Engmvk9LY5DuswDPiO85+CfR/MJIuyuTj6PI70guf6caQv/8r8ZZEMqYnRtc
o53dr+pzuPeJ+wXPXmpMSELvWnq9Ohl8cpACpEyyTfFUSbZ/nBoarn3z0GH0
afV5djrKctH3EPEJzexeRz7y4/eEPB+hPDHQ1PitUftCLiWQ0RrCpYDPEel7
cjZRV8ey2eaZbIr20Hp6ku+Z133zaeHvIMvbYADt+XetiemML2NsNd7tVc99
l/qtdIT9W+dhoL2yuA9WXzwBWp54I8lT2dL+zpCBMBmTfAYwLX3uUp1Nxp05
yWeFZB/6mupdtkwQFyr3P7voWXi+gL51PsgKn4c85AMzeD4LZMMvO8ghGu2z
a7I9qvNrRUgrQt8A9b8MuY3A7yU0VS7bRR/NvHcaaVYmwSnNbE95f6Tvgk3L
+JhO58MC8pfsJWvJXXoqd07SzEA7yAVNzzt/U+dPwcoQ2zGsSlsorzuuQAhh
iqFvTeiQGoPcuNvS5kKhz5q6DHV4Jw80VO0dWh13LdKr28zlmR3k83mj9C0F
/jPo1MI+7zwNmo93wsBZ2QtAN/PDj6ptXrQA7vohpnJLf1Q2lUv8hoC7JWmk
pt4bZPcc5HZOz0O21fI8bwDpLUBmBaXHLc0XSrL7CPn8ifTD4b9FdrWpq2/o
A1Ogc/ubeD7UnDwU5nmLEO/Z03699+jzB0YQt84c4H8NWU1UPwr9h7JlI+0Z
9TyGryVv30JTlPRcWnPqEOQeQZxFQBRhz5D309m991L7LotKRwj/NXO0YvA/
kecGoBEoLp2v6XWhEvAlQSlQGpQBZcEiZFIOWh5UUL2TxlDeqQi/HllmiTbN
W8Z86Sj/B2zMONWLcbIS4YpT7y9pU6m1vp/keyF0J0QV+KpJ/j6gNcNqAdlU
h8aR51hQA75mktdxppewu5jOmyeZVxi5a8Pv5nkktCH/OQpSp+G5/G6dwPu3
aEs3wRbdj0oeMpCfW5QlGvdHyKMu4ebX8jffBdAVxFtPuiMZ0o+PJ9w17Qcv
ZxuFslPQQOmBP6ivRtDV2guQ5D2C2ivYjbprojiIc3Bh24aRjZjt0J3Ms9NS
V+lBGPP0poTrQ91n5H9FWfowqjioI3xFyriPfA5G/5oR5v2K/hb2J2neALsL
+/5c3Z2bDD07jY5sJN2yyKE949TTBl7r1Z6P5pITMtgFWsC3BK2SfOZWZyCW
tfU5CK3xtca/jdor6N3MdyStRacT0vibaxT+p6j3k2BDNn97uQW9ks3fiq9C
H9KvRRNuYyXfixsDfwJ9iVUd8982LsnfP+OT/A10IrLYR3kScBdgzBhHWmNB
Iu5O6HoS9LP8XtOtItuZuF8BP5POq9D2oIPaIDq4GTSn3jtKZlpPL+Vv8pEg
vIz3x5Yini7M47ZW9/f3TkleX04DXkvy3iLtMXodvnOSbRl0SfK6/0tkXw3a
FXc36Ui47zzUXYhdKeviPN6Pu0RjBfXbFf1MC30b2ZdG32LIQwr0ogllrhzp
O1feIJ6J0LO07c7UV1fQiDAJ9NETitnOcTB4k3DvaF+jzqyDz5q5nsZAu0Pf
Aj1UFubtPdVW0KcJpJE61PctXaWuoxkHFpc2vgGn0fe3Cft7iO9iekfjm+qO
/Dar4HvCx5KXf5FVD3RsVmbr/Mqc1vveSkf3o9CuSoX6vqh3pdOgb5LnceKH
5rW7n9o+8QwEJfPYbq3seR1k/MlDGUPBe6o7sJW0+kPP8Xww42xq2VQCkdW9
z1v7vXWWQPuyZTd7KWkPIPwx6udEJv9PPkQbHojfIDAYfBCgecuZ/yDAa05V
hHp6SPjC5b3+1ymwBjhE/ZHupuF/yyfo+3D05BfaWK8itqc9NMn/Ib6lHobB
fwhKEMfn6N5H8DfQjQON0E1wnff/rGtb56OYU36sPpXxoFRe7zvSORt949C3
jibNfdffH9BfeDaN/jKb7AbxzmbcB5DL6pamci/XWVD15dTHr6Q9UroMkrWw
ndXkLcz/WMfuffCfqq6jfYdqTnR7DfqygnyNoqyj1O7AaNCa+nojre2zNqSu
StLGSoA8uiOGtjtG9+GgP2OSvM6j9R7dRaI7SSL5b5xWZxF5Ni7J54H1jWS8
+s4g2xzdgy7dQH69KWveCq7nHLz7FulOINxXPJ8oHUfHPqRsb0In4Z6KLkyG
7qHu94GL9DONaVvnaAO/Iveb5GkKzx+nd7trlN1t73J6nye5qLNshF0HphLu
JuU+K3lAn6JzT8B44qystgn9SncFqC40biKLz6FnKfsX0M/Ja0rSqxPuex2/
VN1q3EA/E9P7rH7Fmh6PDxHXbK2REtcL5Nmcuo2hvFvoHztEem9WlM4mV/NZ
oelJvptgNnjKezOSfP5HZ38aUv8zcTfWXYopfM+G/gfXpv+dQ531oCyLqKNU
5Leg9mDRJ/1GWt9CLyPvteRllsYF0pwNfZbeNs/nJNnuufbFhtEP56tqW8Zz
k2zP+ElGxlT4pxl9F9QL8vIfOEKcV0jnTjrbWaiFPK428P+7QchnIEis5/tk
PqLO5hNHFurzAn3QBeTRBDm+z5h0kzYWp/kXzx/W9t3cupdb6eiCppfQhRrr
ieMraDlkWwDkr+n4FfdFZNlFd2nQlnOT968Jtwh8A75Ax76kft4nf40I26y5
5883aI+L1cehhyXx+4IwS5L8nTVHK393XYM+bCKvS/FfBnZpH0ph75MbXtr7
5sSPKG13z0o+Xz5Tezuopzp5bKdQ99jIPn0F6mw58aSp43tfFgX5zubxvNOT
+dXtSN/nvBA5rVB7CPU3Qn0r7ECfVS+v991NIc4I4vqIvBeBvk+7/gR5jATL
0eURtMWVvP9C9+hCL6MHYyjTRsKNA+OR1UZ0cHMb26f4KZVtVLxC3xBCfb6q
+1h473Xk+1o928Z9QtzLWtkm+wFwjLpao/kR+rlWYzhzwdbJfD/eOrUJcIe2
vgGaSedxGvibd35Qq45t25eFbuR5tmCfq3gf3f2JujivM+bMjRYgl008jwg2
Pz/g/gMd2gwNpb/5VuMhbWhLkvme9e1O0FjazPcW1EDXqhe1O5vOO0faTsd3
yidxrwv+n8mpoDL8TCtrXpRiBk3Q/SiE/ULnWaB3oX2o5/3k/Xven6F+W+tu
SbaPLH5ocbu3qm9GH7dBUzGGhPK8UhnzF/PavbCO7+DanmRbKx+Cnbz/I+7z
aW1jfgf8T5oLgTP6z80c5Ghqnz27r28y9IHB6X12aKfmD8T7PXG+BXbh3i2Z
6XxCHpdB+V/Ps98oy46m3sf7i9o79Bn52qMzpDpri7xaEb4NKEM+klHWTUHm
ywXcDZFlqhjfJfkrMiup8zNlzO8NuPcQz2Dy+StpFCKuPdC9YB/Yn+T7O4fS
vxTV/j31UcR5iHePgNY6G8g4P6OK7/67U8h3gM8sZzvxP1OOMPSgOvEeIJ1q
Zaz3/4G/0ZOPkfUT6EHi3Um5fwYHifdQkuMfVsdlPFDV8wfNFQ4HIF5rMaXy
eP4iu6QFUI4E3qmf1XMMzWk0nzmU2+7/i0NzDb27hHIfUbjmhvjdtLmjmsNo
TgFOgF95tgechL+U0Xu6VZ5T0jGta+luPtU/uEfc98GiaPOibbRfjWfnwCv5
fLfvB/gXRDYnacPn8b+QZPp6M/MNY3zXYaF0/7+eSpUxr/qSW/uhvwG/ET6G
PDSnn7ioPIJ8yONic0N8fjAe2YTU9/rR2FS+m7YpMi/EXOk56UwgrrXI6jLv
9y1s2V9JsvzjY1yXKrfuONLdRleT/B/8d+hRaCh1mTvEfD/e7as8iKd//IMw
KRkT/0jhOxOvQq/9P6bOO76qovv6EErovbcUeichEAiBhE7oEFpuiqBSFKki
WFBAEOlNUaoiItIUBEFAQUWliSDSpKmAgiBdAWn6fpfrPp/f+8e+e+acOVP2
7Nkz95yZvbhWDllcgP8OXdT8Dw3GvvwBHxLky3V+Qu/Wye9y8PqM9vaFd0V9
xn+J6k2NvzRY59SUBj6U+fSa+kT5hnnP9agYv2tqgO49C7/BvZtQlSrGaBFW
y1D65M9e/n+h/xl/QW219xleHnudJ5vx9Qbq3GO4/dt/WsMYnlPLev3xFv2R
AM+kM/b6b9vFfrlu9/KaPAybEAFtI/1DZH4aPbrTy/uz5Sfzb8LhuZ1O59Pu
9jL+mjCX5FN/hXzdwEsji3vSF+7lLeNvqvng93vZf9dm+qMfRT8g/hB6lufP
Ylf+6eU9+H8is5tQFHpSF9qJDrRINCZdIvfnIvtPtYcY+pdn6mgssBb/h2fm
0IeF0PF7zHW1axtvMVMKOo992k+fZyY8Fzv5JlQgzONA4yGE64tYW8yrYf/h
e2hLFq41p64jsJct4H2Yg08gl0fh/bWu4342aAxlXaDs7IRDoRwp/q5Whjks
J+F30OUE+uYwlAjl4lpuKA+0n3K+g27rvXGcueKlmN/7IccB1Yzn2AO6T3v2
FfF7cqWp3cBc8U5FvNc+CzqTl3zXIaN88MNF7PcvRnoLf522DqDt1Rp5v0PB
wt77IK643mHoXUZ8a38LPY6+FI71f5w9yGdRVZ9hyU/e8ZR1FN08Aj3W0fht
BVKM5yY/XfLR9RZjchJ6WpDrz2k+hReGikCD9d8SyhFiPPX89E9RrhdLMVe8
uPqA+yXgm3j+a9YLJVPsU2t30K/WH/R5Ka6VTjGu2NTMxhm7Rl1HYfvfoo8H
0G+76ad+8HHI8Vd0J3Ne+4Asw3P1tB8P/nIo+lnZ56bLEY9pYpxG4R8Kq7Eq
6aKxH2PIczPzzGp0Jb62cVeFuboAHsZz4VAG4Qh4JFQeqgBVhMbm8B4EnYs5
zDx4Bt36BaqU4jr+EKznDNr9L7ozJsThWcG47NWvUEf6chPPx7Uw1rnkWJk8
csKTSddB+2igKlzry/h9Xmddkc0grp3K7PAnIY5fKun1/h8ljbsu/HVh1wt/
e0Qdh1/GNm0vYzz735FtKHZnTAlf17WMMsavF3a93jdVpdxK6M8zxBOwIdWI
JzZ2eSq3reYPrrWjHW+jPyuxKS3KGLuuIdfWUO6HdRx+tabjPXmuKWmeJs+2
2IR20LtdvJdb2PPaz92FueFdbMJC8u+NLaihvoBvDnG99D7sCP1ak+sNkN0E
7OL7PNukkMMTg/Fa3O+Pff8A/a5NeBDXKnHv18zGQn+Msupw/RHaE5Xi9bHO
0Oss/YaKxiZ8uapx++ZyLZo0X9O3w7EVI7I6fL2s413IYzp9OjOLw88G43Wl
g9JPKIVr9eEbu1ru63ReDt6e/MNIO5K2faz1TRbH3+D+QGi86kkc1f2vX4dI
h2hDLHkNJdyffGOhJOxJA7WTa18Qb5hiLKCf0f+nuBZHvJHGPXSVMi+RZ0na
VxpaST/vIM2qIFf8EWTXmLRNoDfKmB8t77Bw0ISBdhy5pJB/+Woew3JhoH1x
DI//zmfqnGZWxuMadOMdxusSKIF0C+iHhdBW7OSWzsZNSUxxXDgqZRmb2+nb
ihXtT39RHfvXb0qaDdr7QbuaybZALaD3G5krvlh2jrwflDGd4Lnh6PgDnb/g
2dfps2Ml7Fdc/sUrZHcaPRPGvNBSdoR2ttJcQDk9mD9aa+zT1krQ6JI+B6Vv
87Kng5FjOdr5dogxKZR3G9kCxkqS5pTMLlflz+b+esLjNX40dqDZEaZZ0DzW
F+mJxrlpz72sjNEO8I7QDZ5fSjmFQ7z2Ccni9U+fmsZQ65RizPBb6PmnbR0W
jrji8rEkv53/0Jb0Ej7rlZc2DqGPO0uPtO6n/DmsebqkGBu4GrQYHW+s/7dQ
V663QlY/k/YH2p6s8VXCtk7vT04G36F8oHdK0EPKW6kzELTpR8Z0N40fdOOO
1tf6Bkb9uoaYR0Y5LP5WMFyc+vRnLXmacMdq9ic3DJpB+vHk3Z38pqEfg7Bt
rza0PuldgPQrS5IxjrPC45BbjxRj3WuOL6G5MMphzfuK9yTcS2M0xetGvRvW
foma5D0F/c4X5bWT1k2r4WOae+/FWPh58vhV74Oz2kei/CM+iT6OZU4YRD+O
g9fl+SmUs1trFCiEtPOD4Qk1HH8Z+x6g/DBsUCo8DUqH7mAvTtOHp9o6LL4S
Hcrg3kvk/wK0nPwfIX5bNgYZf1bD/pX1XVF+S/Rt8VJ1xydwPwLbOotrZQmP
oA5Nqnsv1uvI+yhjpSZ6UhA5F4ZqI9svaPcOaBprid6U8zmy/hJqxfP7yKs1
vA/XH02xX+XH4ANp0yTq8TjhHaT9GupL+Lcy3je1jvJHVPe3kiaU2497CXWt
r7eDOvwX7fmM/xGfQttyOdyfdANSjKPwBHwI9bpUzLitdaL8HlbfhpMo70mt
KRgzrRK9zhtIPBW9KIJeFMLGNKSfCrM2uIWtyZ7FZ2lWkPYprQF4fhC8ZJS5
4jspqwtt7YqdGqyyNXaggvT7MPhw6GloBPQM1AEZlCL/6fCZWc0V7xAMT4PO
oudnoBe0x4t4E8pZmdWk8M/IoIL2QbH+Gyl7xxh4hutvI8dRxMthzyLowx76
f6R9zAmmXzQPScdJ+xy8TnPva7vX3HvbhPv2o9YV3LvGeP2a9MfamhR+ges/
YlcO0NbRhKO4Xhd6UXpHeae0LyHEpHAl+DPIKiqH97w9jjz7ZfFet8+h97j2
BfwfvVMnjzEpxmkXXnsBZHIXuW6q5zPiOqeepYHPqmtvo/Y4jiX9xZw+nzOP
9H8yLvOT3034RnTok+rex/E3z2zl+vPUpTxtv86ccxNq0cx+b1rC36Qdaynn
YJTxQYQN8lqiMd3lr7wSNJ5nx6V4n6D80JeC5kOd6YfPeDYbc0Ft9CZnqGW7
gXRrkf8PtHMc5U/BDrzM8z+hj/nJPx90gz69Dm1N8N5DccXle2BNZvsf0N7t
3tjUA9j+HtjjQ13d3+PJ61nSvpXL4QnB+CvwidCrKcaXF/a8cOUnEc9OfXJk
c/hZ+uIj8ulXzv+v9kf5uu7rnvhzWRyezPXa5DG+rElhlTclxfvHP0g0hrIw
k1dnNSm8ATpDP/ZGLqGk+Yq6fEcbvwwxKXxG/spk17CffzJuXitKH0DrST9N
4wd5hUq36OfpxGdAnYP17RLlsNqg+ARoLP/bJ8JnSj/o/4ww/4fUf8nC8OeZ
I2Zx72FWr+MU1lpuH//XOlLX2YR75/E+Tu3d24B9vwwvjj7N4V6sdCPFpHA9
1pNp1Pf1FLevdTn7Y5Bfho3aH1DG+JpzlR7dTEJnSupsG/Hi8Kt6905dykCT
5aOB+lYIho8lOv6m7Bb2LCvheYTnB59dAK9Ce++SZ3P+O2wl/RboY9It1NoS
3lbzHTY4c6z9jexFh6oV9/45YV8u0hoJyk9d8+nbruZC9SnlN2TueYt7b0NL
oHegpdC7Wv+UMSaccJmFw7xMdjja82th1gPvpRgzflSiw8KOV3wo/fkF9m1Y
F3/37cNaYLnahHw3F/S+u/3k877WB9F+VxDfzu8L5mhvCFSxif/DvaJ7XF+R
Yq74U9m9J3qldIr5ehX8ls5qc/897beFZmufOPJKoK9Wc/9DxmwTFtRzqEsy
6WbDu5LmSe0TR76JzHlrSNcUXhU9/EBrMGRaUu/Vg+84vkCXQhj31cob7/tD
8j7G9YWJjv8vLBxwxRO1zwAaxBi5RP3aEv6MNn1I3muhdSkOv9PVcdWvSzvX
V6RwRrJpL3mkRTssPpJ7ndqZKy7/MfIvIx8yH/Hs+hTjFy2gHl2yGKs4i943
oSMh8FlNjYF9J9Z7UbS//R5zaD1kViqz/RRt0BxCmz9OsS5vhDZBD7BH96Hy
OnvIWu8Trn2KXNKy+T++cN/ebev/u5u59wRz7010ZkuKsZlPk25riv0n7mOs
lsXuH9TZPOHgpPg/+R/af03aCOr0A333Gu0cQl+8hI1tSt9/RrptGuOk3a7y
5TOA62NZN35O/AvNWYS/hPehvdWamiu+A7rHnPQV/DnKL0N9y0E7dD/aetwP
mqU91tTta9J9A7Ul/3vkUxSZ7iS+mzoX4vmC0C7izXRWgXyyky4btJtre6Ci
5FFEc1sFYxnL/+sq8pje2u/uFO+R1z5h95L+W9kq2WnyepV2Zw9zWPe+C14X
1739Qa54eA3LayDxetjjSJ0JS/G41fj9PsgPpjiscxwNSVcZ/gPxzLRNwCny
x/txnH3yNqN+Z2jXIe4fUJ2RyTSoLX27TufpuF4pyrhgYaQ/ovrT33exrVeZ
M69ArzY1KXyU+7+39ZjXu8HupDvGtb306zjq9qNsKOWdZy6sTf+n1HF6pb0I
P879E5pjKeuk2oAsXko2KVxd75gY04nQjZbe6yw7I3uzmnl2VWef1ZJ/u0Po
9vfY3FPcL4S9KQI9jd0ayf+rZ/X+grSnU+yXc3xj+3ysynrlJ65VJ78nmWsS
WF/Mob2h+t+E3SjL/Z9T7FNqFXVc08A2514r2x3xbskOV2pvX17DwuxvclYL
+6oUhox82f9CPr9y7zfoDOFHg3p8RO8nKadJPZ+3Osu9c0qb4vBvwbhwn4X5
3A5+nvgF1RvZ/q55U/qMPrYg70U6zwq/FNQv6d7eIFdcZxj/SPE5RmFTCaPq
THun3x9MM556/EzdxsEvq6xIyoR6UXYKdLWD/QFUZS31AnJ7DJ27QrrH4VeD
4+sadJpxkxc9yQN1j/R5uuspfq+ud+pDoBrI4Qhz9jHooPYpIIdJ5J0h/Hbt
YyX92ETjU7dIst/qnZT5DZSXdeVN7ufLYZweyVpnH/7k2l/QFH0T5bnStGU1
MukVZq64dGQ6ZcyE/uLZ5/lvcAtenLzeRW9u8fysavaZkNrYpLVmGnwINng4
9Cl6dVvzFvS3xi529K7sUYq54pNzGZe3qMps6jrt0/oHqkrdFiCL4/J7qbNJ
PPN5Hn8H1DfAHuVsm2SjvtFcRB0fEE+B5yG+i/5vSZpIZBgBPeReTezr+9qP
gOy/gw5A62jT14zxf6QHOn/EMzXoxzTK+JFx9a/6JKtpfAdfe4F63KUvvkLe
hZk/jkX7jFcp+uipZOMpCJ9xLuP4oxw+q/oi6b9nPp3MtXDyntHIZWcKOI1w
xjMTDoEKIouJGqfh1hGdU5I8R+q8HvUYBV9NPpehYvL3wjNZA45nC1i/sgcc
vhrUt1DCY3SGmro2YQ2eg3hOqA3zdS74l208nrYU8JjSGPxv/JH2cl3jlcuu
hQS54r8Gx2vugOep7MGyQ5BjH+SfJbuv5YGK8cxxZLeRax9Dr2If8nL9BulS
0P1UaDKyy8u9/FA/zS30V2f0/DfCx7AbC2l7voD9AOYP2C9gL/o6JdH+/GLQ
pQJcn8/YOyp/DcleTx6ijFt6l0l9c2qPOrLPBS9I2kJQYSiUZ7JDoej1Xcr7
G8qFbJ/Wfz+oCGleoU9PsoaZVsbvr/TuKlsr47gJp+El9HQ7ZT7g2aIBh7f9
f3Hx+9n9fbNYwN84hXPcr5mxjkOD79J6MY6Kc/9wor95/gldpb6rsZlv1PC3
oIX69kCakgF/g9U3In0r0js/vRNsGe33dc20L5t8FzV1+qnhfkbhl+s6Poxn
47n/TR37RpSPxEvR/m7TEZnsYnzsquP3pnp/OoS19dBC/jY4E90sRV7T9V8S
nol0met4TGk8nSDvC8UYC5S1EIpj3VkmYP+usdwvS/gZ+uVx1liFC9pv2P56
rnMJrX/JJxH7d7yJz/zoXNNd5rJyAeMMJcf4fObhTA7rurjiYQHjECndfsoO
D/i6viGebOzviJdp/x9QBvkvpbxy1Osj6vCM2kwbdxbyt+KIgL8Xb2ecbKKv
N0MTea6q9mpyLy+yKcV/kTvMx8/Lb5W+K2BHygdsj0M6+ZuvvvdW4FpFqBJU
OeDvxBND/Y1c2KLCGJUPS+ElCzd5eV1/t9ZeA33HrsIzq+ivwtzfii6+oD3Z
ZbwnQWki4Y/wTG9oC3W8B6/KM0ej7KdU9vLrROPGCwNe+O+yndUCtp+nI71/
pQ5l/cu42YgutMzh8KZoxz+oZXyi620t87Bgf2TnP+RsxsiBuvbdqXl/KM+9
VzSIlahvqQHr/ffQTyWMnaj9RQuQaWILY0qNwbZ+Sl47cxtjvhj1KhFuPPni
4Y4fR8YLGPNXKGM0c0kk4Yqh3rM1Svu2tFce+qSk+6wn+UyCvwrVoA4RtLsm
vFbAXPGbWneQd+2ASWFhxZ/Ddo3h3o4K3l82CL0uo+9Y6GkM+tY5yOsHw1mh
LNSvdi3vl9NeuTrkV4f+/RGKgl5Hl9vSV0lQFPcWkD46YMzpugG/k9f7eXHF
S2nNgb0pDf+a8ntRfnKEw+LfwGNIt1Pn3+FPIdPOrO0KIIP6Aa8R0iuYNN9o
rqlGm3+kvHCtD2LMY7neOMaY8sKWV1iY94prv2KDgPcsCme+Qrix5kUKVwr3
9dDsjjck7V76NC7gdUPOHF5H9NH/A3QkGSqOLFpTt2LwRqRLoLx41SHgb6Rr
JVP0Jwuy7FLU4cH5HS+DjpTWeX50tQd68CJpI5qZv9beYe1drcy4mwSPoeyV
dfydpwn5Z+gdJfV82MHYd/908D4l7VHS3o8E6QX3E+FNoWZQ82D4+STHH9E3
Gf2/J3yc8p4j/2f1XSqb/QfnRG69443DLuzjZ3KYtwxeFza7wpupYw1kUB2q
KN9u5NektvGZ9a1ImM2tAsZ9TMzkfePaM65zlA9p/wMoCj3NVt/+r59s733l
Sqe9kN9FW5broL6VvEdAPtzu8b/uLlSti/e5aY9ba7UVPhkdHUf9BpJXm4D9
Hwib/t8YY9IncS0z19rK9ge54sJkX0Il34bakK4f9Bu0HTv7CeWUYczPbW+M
eeFXtwyGhWOttMKxbxYMi/8WfF5h+SeoyRrgArw2fC95ViLPWdqPH2MM++kx
JoWfgI5j16fncBkihYVt3476toc6BHnHYLiP9tUi50tQWWRYBrrczjjswuVe
Xd58ZDBchvb+qjOuuewbZjD2qyzzyCTNweQ1h7HdiXwD2lvMuKyUy+ePdaZa
Z106B7zXtg/PxWA7uhDvqrkMGt7M4XN1Hc9Sz7oeGeyfqJzuI5HCL8PHI89u
AfvFPpvffaV+Ub+JK67x1TY4xrQnQfx//ai4wg9Y63aHl2Nu7hFw+9Xe4ehn
T+Ivob8Pi/osmc6RhWNbIqEHpOkVMEa8MOGFA/AE89oAKBP/uf+lP0pg20uT
LkVyCTgsXgY+if8Qz1GPcujtEHi7Zs5PYeUnfHmFdU3xzt08X36Zw+fudeb+
H9qQyv00KD1ICmdobUzZ2aFK5b3PuCpUpbz33Wr/6OPIdz912EkZu+t5v+n3
Wbz/9ECQK76WsbeCtCuhR2QT9L0D6i1Z6X81OvkhMj9Hf7ehXye1xrZhG95s
5rP8Osevc6p9SP+obD/0OLQFW9U3YL/vX9Cn5cN9nkr+CfoFzDe0dviqzozQ
9mySNfHWOmMBfyJgvwnymfBkwN+9BsI3UZfNUDJtONXafu0uQK/q/4vypqz6
rIMrYQ+TsffPyqZBg2SPqMv4OO/Tlc+eP0h3BcqZ077fVyL/waS7j+yvk2YZ
dn4I8aFQIe1VDrdvjlryp4KebOPZeJ6ZzvObk4ylLhz1jtijy9TxKpSprik/
fXMl0j7/OsTZ7598psh3yrCA+fCAwxcqmiuepYZ9S8mv1NPEo/PyHG0bQXgp
/3caIoNntBaj/0cGjJEuLpz0UUH+v3viiq+mvrnp547MtaGF7NPs2YD9m4kr
rrNc1RnvBRr4fIf8IeiMx1BsSVvsetNWnhdHR1l2z2kt2NB+6MrD+xW0D7gu
1LEztDbMvkDlB/T5gP0+Pqhn349dWV8uROcXQDG0/UID+++vKz/AAfsDHq25
Ctv0erRxmALknwa9qHEMvUdfPc8a9VKi/TsLC6t5br9TKAafTp9Og9LpkzEB
v4MYK7tFXsnoeRrXw8J8fxI6Ppi+GgSNI00i67GX4S9EGif9IDRediW4119Y
R3vplz15/Q5nAveulzcehHAwXpGeMy4jkcPEgHFohBui95oVNMcHjAUv7JJJ
AeOXCFdFmCp5C/odgM7mT/7/+nUEz02BL6EP/6Z+38e4r75mDv2ugfFsnov1
/jDtEytN3T/Bnm8hPjVgPKYdYcZkCos2LrjwV7Xvf1rAfo50DkDnAW5C52QX
kf907s2ANtS1n5x02nUbOzAzYEzZ7c2MNzsqyZjos7i+Hrn8RrmlqFMv7MgX
2OXZ0hfqdIi0P0DPMJbejjW2WDXavY31y6oi5st1jizS70qFuSPsnV+RXQPS
zyGf12T3WU++Tdp3kcdreu+k/eMBf3PV91aF9S1WcWE/CgNybsDvYPX+9Q3p
kfqMsfFXTmM2PxZqDGfxPjEOP0RXHkBvkv4H2voZzx+Cf4EuzwsYA1xcOOAK
zyccWt/XxLMHw3/R33+2/z+cb3HF/wpe0zmPO7TzGvK4Ws2YxcIrLssYXCD5
k/dC+FHqtQi+GLqNHK/RhrcIr5OfJ+g6+XWnL7pBb3M9oZ3f0+o7TkvqfgFq
3cLvX/ReZglpcmNr3wkYG6cC4+l78sjIbOzhUdoLwPV1soO05SP4s9BOdOg9
5BNLmlP0w0loKXm8K9vZ3uFlwfgx+jIfaaeVcDh/c8ff416SzgpDywl3oR/X
0Z73Cc+hD2ZD6cjqRWSxgmsftDYGeV34D7R1JdfONPe7U703XRXwNeWlfHLE
GCNGWDF95X+QZ/Oz/s1Ne5IJ38YmvY1e9dDZ8IomhWXHpyk/vccgr40aS1BZ
+mUN8Sep1wfwU6V9zllnUnSGT2f5BsCrsob5UPeZKxZBY5DhWuLFqFMT1tmJ
et9H/dtDbaCR1C0J2bapb7umeUh2biLxFloDB4xj3QgalNPvcvUe9yOuFy/u
8bw+4HfCGwJ+LyxdaYOetoU+VhugQ3Xdz/JFtoD1U1gd+1cNh1eobxwjYRj9
pXfCpH2cem2SXrAm/ASeh/7ZDP+Z8Vww3Od8z5JuifYEM862cC8vdbhCHS9B
o2U39b6A8fyaztBA2SMdFtca4EGky3kzl8sUV3wreX0a8DeyN7g2D2qBvs7P
ZRxtxT/WNz/qvR4+LhgW/vZnPLedMssj58XIbwJp34L/rv/d3I+AZiOzN7i/
r5H597kdfp1we51VxAZ27GAMbsV1NmlEvP1CzpANy2FsbfHDwXBZbOoQlUtZ
palLD+xZBa0/kd821Uk2E/pCdiNgnGthVidkNSksHGuFxYXHnURb7zI+/4Z2
8Ewl5FER+orwdO3llV5V8zeD75p6HPwS4bGgPeX67jUXfZrOuN5MvT6RXcOG
z2YcFCN9svZ/Qe2y2fePfAAJH+sbnl9L33wI9aHNL9KOhvUdFt8ZMCm8pI3X
yoMI7wqYFBaG8lzWDruJX2Yd8Qn13EN4b8DfPEqoH7Qu5tlvubZPcwQ0gWv7
4QegNOr5PbxoV58ZPaxvZcS/13k4aLvO5Wg+iHF9VJdDWtsQj6GuNanHvvb+
JiNfeAOwfYe5/xFj+Ah8cHOfWeyCTidDYwmPJd+5jIMqWX2uW+e7j2pdwLhO
gK6h9/2hj0hXl7n4O+r0A318LOB9ZD/Cr1Df8+hYGv2RAU2j7RtJHwI/zDy2
jbw70CfnGXu3uH6cZ05AJ6EyPPtklO+d0hqQMqJ0fl7f6LBRp7nWEn5A6yzK
/b5AEAM0xTig+sarb72n6defpGva90cdfg6YK16XsutBj9PmRchioc6G045f
ZFOh7hUcFj8rW84ccg7+K9STuj9N/60oazxfYfguId1v3CsJrwWV6Gyu+CDk
vwW+GZqJns6Gzge8TppDWy8Ew78H4xfhDeivWOiS7KB8OcoOwY9oj38HU1vk
mASN55lXoMuSu9ZeUOFWxnztxP1rxHtT9rwOxu0Wvx5w+A1szgPaVpA1/hF0
52i895LrDLzOwsuX3i/Yq8XEf4J/jOw2Q5ugvoz1NYz9D3MYH/lGwBjJCh8I
xvvr/xB1Xomu3yT+p8pFB/8M9X/PCOhF7PoY6MuaxucTrqPwHcMKuC+092Mm
6/ZfWB+0Qz8L6P8F9Bf3qmnvGvPOAuaqFcg8g7x/k6+UcJ9huaV1QsD9lDXB
1/KG+2zLHa4XIH2+BH8nTQh+K/1bYz/e7yquM47uqt9jHG6Uz/Hu2otKXWdT
dhXafE/zdyHTXsZL5TB/F66Wz9+Gm6NneSmrBXwG64D7pB+DvJP1PZL/beN0
VkvfxQI+16vwgWB8ifygYEfegR+QvkMXdV6Yvn3I/RWUUYFx2UV+p4n/G/D3
a631pjMfZ0plfoKWdvE+d+13f491xbwufpcuHoOO9k80ZuGT+s6kvZXUc5d8
HWivbjPjCS+Gvijha3qvKDnJz04z+vgj7f9E9uujLMOePBtCuYeoexZ4Vigb
VEvnopkvshNuhF7EQX00N6NHS6RPQX1fC+/Y0r4S3pfPn1p+HzyxpM+A6izo
4uLGaA0lr8PczxHkik/kv2dJ+WbQ2UBkMTfeWK45U73WFu57LfRpOev5GvA3
EdXL6FAu7rdlTLfjmTYVjUssbGbhXutb4QJ0u38LYzW/iXxLt/BeBWFxC4N7
D7qcmzz2wttQ/yfp575t/M6uevAd3ulqfkf1Ezxd/gHQrQztDe5of8bC/M1D
Hp9XMJarwuLC15Tv//zx9t+/mmt5uTehs8P5Uh2vXdPphBXwIfJeqHOZbVzn
ZXmMMS1SeDmUP9V7aRujc+PzG0t9ZWvzfOj4WcbXLf7nTiGvAqT9i3xr07Za
0FLGTUGuFUp1Xwg3V/L/Oo//o4QkeH+V/JvNQ28Lc68IVDTVfoBHIvupkhN1
fAN5PE5bopBTvHwz1vJ3lUf1nQi+S+coaMf1asZvLkp+fxT3mL6B7hUjz2v0
0cc5vf7ogF7V4n9we9q6lmffwcaXRL+LpxpvXljzwrLuHGs8a5HCPaESpCmZ
GsTQRr+HUk7zzu5b4Warf+91sp+aiZR1K9F4DH9pHxbp53JtJHNgKdKXhspA
wzrYZ0pZwuWgMOhjrl1r7v9l4cRb67VbHP/DChvzZz7hhXHG5C0Ta1zed1va
r7y+cVzl2YrIowI0J7sxJF8LcuHxKpwTOeSuazzCV5HjYcbvAGz+Tvo0ItX+
YyLh5aEKUA7qvY3xM5X+HK/vYfRNRa5Xgiqjp5HY6F6U/bAy7dR7hzz2Oyx7
KjzwOObfyqSNjTWmtPYRSaerKG/4T9jJqoTncL0G+adRfhLl3UTWHzG+71Je
Ne5Xh2pAL1DOKvI6rPPjlFGTa/N49nPiq6nLq4zJPcghBX3tgv6+0cL40Ju4
Vg+bMoW+qIWtbUifdWN9GAu/SfxGpPFOIjv9H2aR9uptJt92lY21Jcwt4XHV
oszGefzNYCf1u4c+dYuyr7fttHmb/kPTL8cpc1u8sYpbUG5f+IvkG97AeJvC
wa1NXnWgddRzLRRFOBo6r/3N8BioHlQfGonuxsJHwRcXMObtW/BHZJuoR7Ek
4x4Lo7M5vLS++0jfgrwhFJdqHOBG8NeamxTeQn2mUOcXZR+5H0E/FKHdd8h3
IrJ5BYonXQ/WOueRy4WCfs8ykvSjoMbcawIlpPpMaj+e7QslEu+A7pyPNU+o
6PBodGEl4U15rM/Ce3801mFhwCu+lzRNef4+vFmqseC/gn7nmf5cexQ5zibP
a+jbHHhX9K+5bAn92AK+W3ur63uPWxX6sXJH45plp80NoZakeYO8diG3Mcz3
7zKnna7gvU6TtK7DZs0h3ZsVLTOFxSWzE9w/pf9L6G8f+qA31Eq2k/y+glrI
rxA2KwYdSYGf0VkBnb2Hr6dvWpO2DdSAuuVtYGxY8ZoVHc4vO0U588nrwyBX
/BHG7Bl9g4IHaPNZ+iwx1us7+SrRGm8RYzaJvJOQwwjm1Fcj/Zxwj8fn9bpK
vojaptofkd7t6R2fzsRLz4SzLoz1T6sYj1k4zPJDeiXZvlUfRY4TKhqrQTjM
q+sZi7lrXWNpbdN3DuLVqG8zvbNkDMyr43VDO/KvijxGM/b+QL45sGe5oCjG
11HkeSSbMZ+fijHus9Jcbmoc71/1jYv2tCePncQ7pHqPUUf4N02NUx3A3nYi
/hG29Hfq15lwTe1job1dCJ9o6zVI1+A6pD1t6QC9gGxWkGcy15a3d7hbquPd
pfeaS+s6vcbJ9O5+Rs+Ohvehrl8l+l1tJGOpgM4xp/q7jvxhyC9GhWivT1+j
jbvou51QL9m+cvaDcwf5XuW/SgnyTOF6INU+gFLhl+vZT5B8BF3QfsN2PiO7
U7avgTHzxLcHw99Spy+px6B85l8Fw8WYo5rTtjTyTIcyoEegK8ybm7S/jHAf
6FHoRcbVaqgr67blyHUB47keeh5bwOHHUh1X+6VvYeQ/XGsjws9TzzjmoU+I
T0UnJuc1V7yS3kOl/gdV8h+26L+xxhqt2N77DrXnsB/3+0MDUh1+Ihh/E7mu
oE7ZkOMJyn2Saydb2GfVyWC8LjIYKNsJfwp+WntU6hrv+D+M444mhYXDHhvk
ig+SzLUerWv8bWE8C4N7CNeGQotivR9SeyGFwf22zlbw3yOuhnG6dW0P9KfO
ruQxRrxwfoXxK4zgzcj4BmPxOtQbuzOMPH8gv3zY6MWsT55gPn6ffIZz/ekg
KTwCGk89Xu7ouEjhXPTrM5oboO8rGk+6V37jS+v9zzF05KjOYegdZqrrVL6g
2yAs8d/QxTBkel7nLmQPM2NnC9qGFkDP68B70Mf5CD+X6rCuKa59Is+neq9I
LcrervP+0Dzya8i6Kx9tTEWfa5E+Df5WHvvPku8s7VvTfr3qtPkF8hgtfUs1
trIwkiUztU1tfInrY6CxGoPhDo8LxneT70qtF7ANK7pbXi8HSeHx0AQosZv3
Ak/Wf0Gda6lnrOcR1DNLPoefyem4wreDce2bPpHFe6fzd3M/q7/1fyalhP2K
RupdF/SKdBX5PK4xQnxiqvfvau/uIsbdo+TXJ6exaIXTKfzgPKQrQR7Fofk8
F4YclzIHvcqzV4lnQnaTZIcId4ee07e3jt7//KP26GBb+8EX68wG6aZAb3Hv
7QbGVJ5KfBo0HZoRDCdi69szv2ewjk2Dokg7hHK+o+zprLdTi3u8vdXR+MAF
6xjHeDHxovCZqeaKa039fBaf1XmQ///wmQ+g/2eRd2md5ej4fzjMwj0t3NI4
qJLbYGgA7eqJPelR2ecE91GfWal+brZ0kvxeYX1/kzzzJPh8lvaXpkBNc1hn
dxS03mrP/5xU7/t/DV6S+fn1VIeXN3R8O2NtCuVvp74HixorWvVTWPx/ZYsr
3qGAcTjPUK+5mkOo4xvw/LQ5E7paIIvfrb7JtVdyGfNU75SFe7qriH1ArNZZ
W/kkkl+TjsYSi0KXTqAX83juENeeRRYB8qvOfJAKz8X4mNzQ6/X5pFkALUz1
fscO9FVN5PIlz22s9H84xDuC8U3QS9ibeHR2kfSS/BbDe9GG68hgC2NlOvKa
39L4qDpDoXNBOkfxFuniSXe1kzGUhZ8sPFlhKkby7CLKWcL9mYy7GdBb+Y1F
reuLgmGlHcoz67FHxXg+ERme5drbqeZLUh0uQp/+Trp+9Gt22voKOvAsaSfA
3+F+nmKe+7UG0Fp4KZSXsfgFebxLuG1nfztZRvhPZH8TytfWvm3fS7WvnsH0
10J4BmuM3tByrt+kzHvY3/KM4e9LYYOhN7h2mPF5VGf6mKPelxwYD42gjjy3
gngn+Er1PXWdStsG5/O8qvn1CvGdjW0LdK6phb718P/wcfrgO/5TTMEOrEo1
Dvg90q/WGGMeXxPkjyU5LL9vMyN8jvlT1js/Jdkv0YcdjW0pXEuF/8P+TjUu
tbjid9GzDwnXKmvs67WpxsT+tzS6pf9F0D7C+2O8bk3VfwbyXke6X8m3KP1b
XGex0LmPuLZebS5ojOGdjOUB/CerSt+fq+g+TYBqkP8G0n2cahzhjUGueGfS
jyS/TRqT0GZoi+YRnpkLfdTAXPJX+Bz9tFV1ge8qZb/q8qn+GLLoK3lwbyrj
dzq0hOuxjK3L9E9sNZPCkxjHo2nfZ6n267gt1Vi+21Pte3N7ML6QcrdrTmjt
decXDbz3U2so+e6s08r42p+nGmNbuL7CIRa2b1PtA4G+SDXNzO1rNbhXXe8w
uVaO+Jii9oUp3Lgdsptd/H+ybWX/v5SPlSYV/H1ZfjN+bWjfGTo3pvNjdxvY
77T8ew6EHq1qv58Duvgs9yCuvQz/kbE6HN2fT/p3Sb9MZ4hSHda7szOsW/bQ
D6vQiwql/Kz8mOr59bT/KcodCP1EvV5Bj65Wsm/Rr1PtX1TjRWMlEmpJ+Gnk
0aqlx6fG6TdqG/N7e+pQDN4Tfd4p+ZPm5cr2ySmM9Z7F7ENdfuuEVyfcOp1P
ET712Mrew3Cvkv9/bmEM7FLejOedbY1b+SlrmSs8t1vrx0r2f14Y+7+Y+XwP
1/ZCrcirJdSY9KPyew33Ldf3U+63yGkq4/AIOv+0vmc0sa/+Xcjje30TpZyS
RY2Rm1jROLnjC/us9YTC9jX/tOTFfLSI+/vIdzG8Gfn2R743Cjgsfl3zBvL/
gLaUpa+T0enuUGFkmEU6jPwvcK8lVI56PAbPjx7mg1qrz6oac/G7VGOsLdTe
qM7eEzOXur8ORbf0HsK62M+N2Pj9pL1G3gfgfZBrb+h7ratoz+8Rfscj/8B6
z6OzGfr/dJBrHcsbO0AYAj8Qv0d9D2ldib48Cx1CnoeJH4GacC8r9f2goHGi
xIUVpfBSwkdJswS+QHMXbTyWaixc7RXv28l7cvXeSu+s3mUt0oR0y+CFkXUI
fdAbWX9EWwpit/cUM+6g/C7K/+KshsZRE4Za4wrGuhfmvc7nFWJdUAJ+kHJK
IKsfKfcd0n6g71U9jGcqLNMj8H7kk7WAcXy3U+5MzVvoyTZs+af042buH5dd
buHzg1qfLZJ9Zxydpx4nuHcBfpDnhqCTJ4mvKeI9HHqnrPdrp7i2CD6IZ2rS
P8Whtvr/zXharHMDrP9Oq2+hVHSuJ7rRuKzDAegOMpqq/ZfM1f8U8F6QviJs
3s888wt0JsiHVHb4Ui77Td4EHeX5QsjmbKrxKIVF2aiTSeFJtb0f5Jzsbap5
o5IO/wZtIM3oOj5jtk57OLV+wM7tov8+px1Z6lhOF7g+n/XnPOgP7udkbA1H
DoNKGz93ADbuzYYOC0dX8fPJfjewWucX5H+YPgitZIzg31ON8yvMX3HFHyfd
pObejxhNORe5NoL63W9mH6UzaXcc/VoUPaycx+s9rfsuQf+wXngI/UH4ssYr
z/0EDUI2f1FmB2Sdubr9VPeDqjPGtzJerqj/0a+b6PpW1iDTKOMe8v+UPl+O
PFIoqzlrvCTq+RxjNhy5DKb9Z/VugqXhVY1FqC/tu57qfYTaQ0j1M1UkQXJL
42nWL2x/3o9oLzl2cyXP76A+N3hmVk1jYE2lDzrAb3ItO2M1MrOxqHbp/C/X
cgRlLtlfQ2bbdDYZefzFveKUeQv+aUfb0Mvao5TqNZ/OzOpMd/HgmXBhz39Y
2GeOS5OuFHSHtL/TtvPQGcqbX8Xn93R272v04Bd0ryPhG1E+J67z4jp7rvPi
On/+N8+nULeFOk9GOBad/riTz4pVIb9l+t9Bec+QT4dCJoU7wneXcrwTdE92
qbKxBsWFN6hwEn3UBqqvby6kv59qjN2ylPOA8EPocDPvV7rc3Fi5w6jnGvg/
zBvLyadhYeOyCp81HvnGoBdn9T+9nrHZhBv8T6rD4sJtG9vUZwz+1fpA69DW
xmrJU8h43ZnSjN0trnjmNIeFySt83l+C90Kg0si0E/W7hr3ahk7Va2o/7L+X
9f5C4eQKH7dbkAsjV+GLDY2r/HMV81+qOPwrdT8Hdcjp/R8tqFsWysmBThTX
97AqDovnLGhSWH7Rs5LuIn01kbYs097fzMbC/Qa970MZ2ZQPlxczFrITPoPN
OAfNQucWIocO2l+pNNAOxuYydGMo4+k4MphSyFjNXWo73Jr+L6LvEqTdzNhp
jz5tgueS7KjPOmgHetWRvEtHe07uxdojoO8YpKmib7zwhqTJR98VgPKm2cZN
aGlSeArl3WUuyZdmbMYjDMKF6NBiqB9jpjf5/FnG+0I2aW8I+po/zdhkjbEH
vVoZS7cA194hn4LwpfAq2scvO5tmUrgz/fgR8v4cPQpBLwtz/VfWa0XgRaG+
6H0LbGMxwsWhYo2Ny1GCcEmoFDQA+W5HFn+hC6HY+0/ox8eRZV9oXVfjB0sP
86C3eQubKy685hpxxm7eig6VJq97zN2HuN8HXdlIe8uk+dt7Tb231DghPjCb
sXSFnzuzsXV7TFC/y3E/DLrN+AqHR0ArkUnpJvaDOZK+J1mmSK6PaGWfNJ9p
rwNyL8+1ClDFNMe3drK/GmEq7EYvKnH9YCdzxXXWILf8t1CHyurfNN+bH0yj
uLB4P+rkumpdUJVr4UH+eiuHRQqfQK+T4ozFK3zeocj5JnX+C6qWZixCYRIe
5l57dKcPMqnO9U+R17bCXoOsk88W/nvU4HpNaB26VIB7haDzPPcr5fSgTd2g
26X8XrlWmrHmLuo8UZpJ4WwlzXWvTpqx6HQvKkgKay/56Ua0TX2U1/7Q5Rf9
aerSWesp1hN9yKNMLftZjaQ+97B15ZDfIO0HQe+iyacuNApdG8/1GMJd4fXg
/3R0uH6a412qGp9S2JQftbPv6Viu/4tuN2T83afODdTn5LUK2pTNZ7iuMx5b
0+aG0onW9rfdk3HaI9H38zTxOa8S6MpXms/pi5Po8dRS9pUXTv2b0DejapiP
rOHwGdnhKu6HY7TvWebpUcUta8l8A/llaW+uuMIbqzmudPId+j40lfpNifa+
c/H68vtAuGRnc8XzkGc26rkYPgA5bKrmOshP/V7WXAsZ43GqB/kdha6StkpR
7ydpxPX62MlHmJfPMa626FsOz+2mj/ZCn1LGRQZGPOlmaN1KmqdkT9LMh8Y5
/Cr2bj/0iv5DUn4dyqkNNVFfkfdqYVGlee/+ukRjscmnm3y/rdL7T6gT8kok
TVOoWZrDebM63os5bFK8/Wx1kj8O5F62u9uidmgvjPz1yG9PGnqXl7QvIoPf
aHvlxh6L8tuquiVCrUmzCZ1rTxu7cr05ZbRIc32XxPv/ekvCryHPXMgwFBpR
yLZUNnUDfbQeKlzHfkflq1S+R9sQP4b+tiSch3JaSa8oozV8IvKrjS5kCY6f
NmkeP22C42pdlM+1vAJNrmZM4CTNKejHVuhkVfNTVR0+Q/iXwsZuFw7VcGiY
7Dr5PwYVgmKRwbOU2ZZ82kGPUOfN5HsK/WmvsrHh46jraWTfC/3/VvsMuH6C
OXQneX1TzONHbenI9U5pPmPwbifjxo/iXiXms56N/B9H9/7Dk49zXP933iTP
xXq3gc69DT8Y53gb6AHhVvDOadbNH6HsOkMtH1xVfX14S9+LC6ZRPJVnAlrj
xhnH5n+YxvcZnw+hipR1lz7sorkDHspYrQw1Q18eap8YdLOh///of9DfhXzu
ZI3eEyHTZyhnBDSMZ7qSxzbSfgZFsY5IJh6d2WuBH6Ex8g2jNUQ54+qKnwuG
R6KvDejbtazFupOmB9QzzVjC8ksln1Sd0d0AOt0FntzZOOeyw/8g15nYzpa5
fWZCZydOae8Az/Qij9Way2nPMo1n+vFP+mQGMptV1e+cX6/q9856B6M9B3oP
o7GhMZKSZl9rAbWNfJozllI1l8fZDqUR7kM4XfZV5zihG9KHIsYWzUjzeZtH
0oxVJDxzhUUK677wl3rDr6IPn/LM5+T3mfovuPdEe1D6cL8cOpTEuuxRwrt0
ToT6vhTnvr3cxFzYSurzrcjhHG39QO8l+P/yA+u0g1Bz+jMnMn1M403rDHhk
Tq/J8jOXfFDE+GLCFlsNzdXij+t9uZ+GnR9MuekRxvOMjjKmZ1RNn0Vux7Ol
mAOOMGf1I31/rYWoy45iJoW/ghdGPwpBk1p4f2Ru1jknddaD+XoB/Xu0hvei
DEjzfpRK6FBFaLzeJVc3Ttg52vlSK/8v+Brb3qygzyfpnJJw33W2LwzawJh+
gnyeTDP+bavqxsA9S/6BAj5XIAzEDZ2Ngyi+q7XDRevbJ5H8Eem/azT6tQf7
epF2zsL2DEzzPnXtV28OjUReEZTXlDo9xb3nyOOF1sYaHaQ5mrbnYIx9RrmD
Ze+xq5eoc9ck+2rRPsQy0DFsyhDuD4XeKe8y78X4rH1YUZ+3/6kMz0Ado42J
dIox8JO+t+qcMTL4OqfP00RgY0uT/hx6U0/nj6EnGrlew9LMnw+Gs9EXw+HZ
Kxgb9SXas7GIr31Ux9crUPdbFXzGpyFrg6fTfOZ5RJpxxoSbWljnPtG5ghHG
nRQepLAg5RP/lOoOPZNmfLRk+mgrZUyk/xZT3oOc3gP0Y27fV7pL8ALI7t2c
3ncmv/K99X6We/OQSyf+U/Tn+TXIYhPhFpSzF7tYSnv8KDuaeElsRl34OmT5
TKJ9hW2n/mXR78+zGXv+CDZgF+kGoAONeC4O+i7MvhG+lW802n6S9dR+8h5F
2dOIj0KfnlVfQ92pw2fYjvX031n0ezzPb0avJ8AbokPPS95ptoHy2yj7t0d+
6Chvb2v7HNe588y043vGxgHoNvXNwrh4h/KXQKcYDz1bex5SeGo1xxWe1trx
CuQzmjJeTHP/qR/HFja+7X/908i+NoZF2/fGS6TLge6EQmcY01/QpjDWEz/R
5xsYm1up+5DsxvEZCj+ISeiKXo7huU/a29ZdR9ZzeC5CuD/kX6OdfbLLH/sZ
dK8o8p1Ln2Vrbjx54cqfRTZjyWMc9HKacWOFf/knMrjZyFiuTXm2pL5bwLeg
u3Uofzxpl9POEdi3p6H76Mdx6jiB60t5/hWtIYLhMS0dn0Df7kMGE+FraOOr
XJvFWKxOOXeh1Vy7A9+OjG7Bm2qvjd6bkS6FdE+jZyVqG781KbcxXHsTfxQq
HW9c1fVVjbn6AvryOro/mWenpBkDM6Dz39ofoTVbMfO2uR2+z/X1jYzZmhea
xr18wfD1zo7nYB33BjZ+s/ZuJNlOyW7JVshOyFfmE9WNPyrc0UXMpYca22fB
dO6/T38dxBbE8/+nETSmiN/f6z3+DO4H9I1P/0nQ4TyUlS+4blycYL8MnyD/
16oF1wvwfFAnyspWxr7rhQk9K81h+bBXXH6v4tBLAVPO5t596j1Hcyc6UQzq
zr01tH9LM/u2v1PLXHHh9/wPz+cU4Z+gqpRdt6Df/esbgHCnZRP+jDOe9Llq
xpH8Gnt0hPC0eNvicOxmM/hd8l8X6nIm0D+vUZfX04wduRE59Yi3/H6uZizW
udx7A/q8s0nhL+BnoN/1fi/N4XlpjguTtSztCSvm8M7SjpdFRzaFu+/ma22I
LGN0zpjxsEBraa19yOdF5riVjY29W0576Grb762+eRTKbH+2C9Ps0/Y4+noS
msKYCKe+O7G3EfB2wW8y6ttFpB2ILM7oPw/h5DbGXX0k0efDR0Cp2leouR0+
hXm0J2M+GV15W+t7zT/QetqxFP4udI16CpN1WZoxWX/q4LhIYV1vH+96qr7C
6hRm53uSM9crdfR4UXh5muMKz27nuMJlgvF0xsUY1ubr0b/u2NOe2jPT9D+X
THqVlul9flakmSueVtO8RJv/tr//xxWXn2D5C46Kd5oVwfRF0ImVBFaluZ6q
45JQ83dCHQ6go5Owcanw1VxfA30AjWEtcoDrcxkjNerZT7Fk+WGax23+og6v
DcbPU/91mkehQvT/bZ5/Bd5M8z3/6cbSz5VpKyLNNJlxUjCYRmm/zWU92Qev
T59l1t56KIT7x5iDjkPj9G2dPJKRZ3ts5HrSd8huUngD9LHmgzRjwAoPVVzx
2jWM5SpM1zbUJcDYuAR9pn2t6EOzSPRXtl6yom6ZaetV1gD/Mods5toW6FX0
eSu8BHpaLLO/JX+a5m/LGehFM71rSfCey1MVvAfza/IajK36CT1+hXpOgJqS
bkYX7/V8FDtQmHX9IspfCP1O+B7XH+TzPrv56Hxhxn8O9D0UOh3rcxIXqvus
hN7PSz2HaN2m9qT5bKnwEl7i/8iL0CTquo3rkzMbN+N39Ls//CLptmsOyWP5
fE74T+59Af+Jen1D2ef0jbS4MWYHFzNGknB0B9DXF+mTQ8yvlbgfQK4VituH
Yaz2I0f+H6ZsTe4NRg5faj3EMw2KWA+O6fxHEcf/FxYfWtB4qjvSjKkq/lUw
LBzeTfEe15lZAwyNsI+yhfJl0M14t3rF+zXpEXOmPTpHQ36l6LtvpB+EZ9L2
2UW83tC6Q/7IhWOj8xjyt1GRth7S+gAbspNndqUZy/XjeOO4VifPr2jnbq5X
Q3blGMN70oxP+3lxY9TuJf6t9BmKJM0A/o/Voy++I74fSurisHgbqHUXhw+k
mRRWOqWRrulcocJbg/GZ1PM4MixF2b3lN4a2DGQMfs/9ejq7RX9mq2ycAGEE
jNF/eygbY+ggad6kHfPjHa7fxfEJ5DsKO1SLvEeT9iWoH2X8QJpDacZZmIZM
D2vOz2TfMDcovy8yz0G6I1zPCb8Qb664zoMI1/Qy11Kp11G1qYmx7YRbrnc3
u/WehOuXMhknKwMdSYfa6GwF11ei/1voj++0voGOqxzmwHJZjMcpXM68tGEr
bR2pcUe//aZ34cwL5+En0nxWUWcWTxKeqjV6mm1jMWhwK2P0pECnpfvQTsbr
N9DpeO8nOQnPS31/TjO2qDC5hc0t3PQb6OBN6BfujSfdGfi4eO9JEMaq9iVs
o48ebWPM3JP5jPnasJXx2+UrSr6+mpFf7eLGBNe4OZvmsfNoV/Sqp33iv6d3
c1y/Tr3PkmY5dU6gPr+mGetHmD/CRRA+wm9cq5Fgm9SE5+tQ12goL/J6JdTn
JXRW4i7jqEke79ddTz12oUdlyOsg94rU8Xut82nG8v6EZ9Moc2pFY61eSLPM
JDvtQ67Zyljzo0lXk7q2Qt+WkN9SaEOi32tNjPeZqgLYiKXwMyWMX6AzVsIw
+JO8S6LPE7H9R5OMGVYmSAoLOywNmd1jPN2HjhB/WX2JbgzDnpeM9Puh36GF
wfXhRelXmt8h7cAW/AHPiDWOu9av/RL9DULfzPQtrA769zQ2IqqAcVqF0fo+
srtM2kXYjIXQPf5XNCavK1wrh02YT7k7Wbe06GjcpGXQcuSxgHH1JvRDLft0
+oH+qkSfVIRyMeduZv7bCj1NX4fq7KnO46IjV8m3L3W8pjUD7Wqvdbj2n3Ct
vXybc70tRm4W69rISsabuJFmzIlGNe1f4Sfq2YE0N7neUe+oE23P/oSeok9e
ot9fhKK0F5L2HGCsTSa+gbG1HvqLdJ/l9l7YqdS/C+P5Gn36JHUMkH8KlISM
trKeukXa/IyR+9iN27K/6FNz+T8g3I0+eAt92U2Ze5HLQOq6QX6jmO+zan8a
c+Ut/n/Uxa72pE/+5pm70D0oLJf9IITnss8Y+XW6z/VQ8nkAf0h9esi/LfQv
9dhNG1eQ3yHqNVfrep0VgJgeMj0kfVae2we9QT3/0byIrvXsZjzsf9N8Tdin
mdIZV9oPQp0uUN+T1PcKOlqRfq4Vah+YRTQPpft/lDAwP4wyDmZIurHDssBn
MT8Vx+ZMIK/D+p7CtQfYgWzw7NAP4fYJrfcwwiivitxnaT9WHmOVrCzibwDC
ZSiCnhWEWum9Njo1hmoWYI02k/4rCP8a3disPTe0bT1jKZT8N8JzwHNCudKN
4fFYbePEvIycYllztMPWLiNdbu6/C3+XdcB1+mq39m8h0y/QTX3o755on3b6
JrJG5zi5Htbd32K1P1vfZp/CFp6l7mf0v0t7gskzL1SKdXxJKB/hhT3sR1D4
hcLEe7Kb/Qvm594SZDyojcMFgvHy6E9F6ZDGDWNjJPW61cCYOOrXluj/XO43
oD9ioYI89wbxQun2xXsLnbkDFSb+NHazIXUrQrhouv0SvY7cpiKDtfDGpYzX
K6ze6cimPfnULOv9TsLeHoXN+Zk++o32T9Z5ddJ9RyW+reL/15+19n9shau3
cHwj95vQX4lQB+RXjHKf5f59KBf2PaGW/XrIv8dV4nVreT0vnyFPlLGPyxlQ
Dvp1NXqeE96YfllNncoiqxH0/3jGwSvQV/TBc8RXkEdu6pYLykpfViphHxCX
0ZPH6fc7PH8buqN38PRBcep0Q2OR9pcgPJh6v13T36X70I8hyOJR+Bn6oyT3
3+xi/PqQeGPYN8ZO7kaHm8C/YeztRj7ntXdI/7NpfymeuUe/naV9PxYz7qcw
P+clOSy+u7b7Yp/6U+9P6NvnqM/zpRw+Ud7xv9Rm7HQqzz1L/n8jjzvQM9yr
BB+pOSGT+ceM03jqVDrddVS4YlfHH6e9ZeB9dUYaPk/YZvCLlPMbbb8AD0s3
hvQ+8lpKW2tSt230wY16bk9MV4/naOQbA31JG76CCnG9XynjZAkvK1DSc6Zw
yoUdGp5uDFSFP0xyXHiq06n32lqemzQvXaAvk8P9vb84cnyfMttBb1OHfDw/
Qu9keTaJ8irT9shgWFisildDVvfI9wb9d4CyClC3/aW8h1dtUP27ohONqPtG
ZLqOsVmcOb8k4ytOe93JrwK0FN09RPnTSb8FnVmHXrbHFlbk3r76xutsWtoY
mOMyGfNyMuWM7eywMEsVV1jX9rZxP2ai7VmKO6z+VFyYmJr7NecXZ1yOl7+K
JONBCAuiTTn7ltyf3/4ll3cxPqhwQZcH+e4gKfxNdfupkI+Knsi2qvw8YEdK
0qaD2n9EvAI0nz7/ijYsgD/Ut0LNAZRfOd3feCUHnTMvVdN+DNKRwRyd69a5
q1LGcq0FneV+FdKep6wTXK9KOB+8J2ubaunGkNZ/M/kk0H+16lzLrfVCTu+X
VRrhzW3HTt1A5jVkMxHNAugpnv2XvsugTfu7+r2P3v98hyxWNPH/mJqk70+f
7KfuA+Cx5NWIdjWAl1MduT+wpjH64mobpy+G52tzfT36/Rd2uh/3+9b0Pqf9
2iefy9f/DN67qL13PHeGfltR1+eSThU0DtFe5vL8yKkO+UVBwyinCjY1mnBd
KAY6Wc3fLDqg5/WI10/33rR9yGAYbf4Lm/UnNFRrLNq4gbqP5nqs+gJqCJ1C
7nHpPo/yHu06Rp7vYHMapfu/eTw8QPvHUEZjwu8XNyb6iuLGKRReodag+r5b
kDYlsV65x1qnCFRU/kOYYJrwXCXGQoLma+b5nvo+Qbgp1AzarTlQ380I90OX
clNe1Q5+r63323f0Hq+Y343rHflo9LEDsrtEW7qRtoX0Ic77cLrFei+O9sn+
wnq2pcZeLn+vrAT1R6739N6IvvpAe6/1HYn8Q7EH7+j7abq/CV/U2fBw4021
5lqbdH+X1XnvNoz1bNW9hs5e3TiPSenGetT7uNqhfj8X1tLnZIpBq5FzArZr
HHKoxPUqLR3WdXHFJyD7GfHGgJdPo17B/YttyXsH7W0Hb68+Rqefpf7H9N1U
8yHXljdl/RrisxyntZeRetXk+TeZZ5sz1ufCn9AZVOqwEzs2Cfm+QR4d0x0W
75RujAiFC8Dn5jdXvLC+r9LvC3QWAf1omsfrqxmMia3o7jBk1Zx5849u7pdv
afMv2JzDNY3TNxdZvUDazunGjJPv7Yasc7oQ7wolQ3WwB93URvSpO3xqT+/p
7oh+REIl6Lce6k/tG4e/SjviaNsw1hazsQ2vQYXpm17pxs14CfudIv2FUqH7
6EZaus8JnoLS032W+TBr/Dra54TNfpK+mEH5ObBtGVrzwdsi47Po0OPh9h2w
Kaf9F8kP6Hc17AtUPsQfkX7D21Bua+hR0vfW+ks2EtlMrGOu+OuE03m+KX3W
ljVQrQRfe8D4idD+opre16X9XcJPfJ16Ztb3E/jezMbR3J3ZGIuxwX1gfSir
MrxqgvEcH5XNgzdjLXEFnbwG5WhlbEfha5ZB96qTR00oFF15LN17g7XXsEg3
7z3sEWI8TOFsKiwu3M2WCcbL7JDF4UIhjlfl2cdVD3jDEGMIfkRdc5LXDPpp
ToJ9ZchPRj+od2afmZ9J3/RNN96YsDCFrdmP+GOEu1LfA9zfH2u81nE8Mzaz
sTEzEvweKRUegPrzzADoCegQ+b8Tja1q6XMAuyg/ARlUp84b5EtItho+lL4d
QD9/izyiyf8IZRYnzVLSb6LscK4NlL6hnxOhA+jxO23sz1wyl0wLhljuOr8k
DMz2jOVm2LmGDey7Rmetdc5a/1uTqNObccZLFG7iFcbWDp1xJq/u2NVp6NNR
0h7Ja59O8ueUP9rh2diH7vFBP08Bh+X3UP4P65fx2W2d2z7AGGlNm1rpPaje
H5IuGn6feuxCBg9p879Q9dzed12dMVCNPh+kdSuUhlzeI88BZYwHeRe+h2uD
yGeIKN04iS9SXs0oY+MdJd9E+CrG6ZGWxp+dS3uimcceRS79yedL7NN7bY2h
KCzF5BDjzSof4e8MTfd1vffrqr0g0G3ZF64PhzIhy07aj6n3aNiGYcgqUj4K
sPfvlTUm5HLpWWbjiAmLqyTt/hZK1xodme7l+njK/BbZx2ETp5CmCeXPoF77
uPY05cyS7aHcEozH4snO/53W3sO9FD4i3fkIq1G+OJbp3TrPPsP12diGLg2N
a7wrxNjGOpM1l3G4s5LPNY5MNxbibXSoB+vPX6v7ecnmYh1jfQvzW9+rf6A9
B6E3ocnQv7RlCrwK9XpJ526wNdn5b7mVOT40q7/XnoSfgEZRzvZEY9ZVxm5V
gVZG+br4s+nG8BV+73O1vY7Xev5+CetIMnn9k8v7Dfvp3Qb9+Qvzwg3qtp12
lKRdVXVmFT6YOfMBeTxNH7VgTonETkREej0jPCdhKxZGz+tQ50vk8RV9kBXZ
ZYHmhVnOxaBxlDklO2OF8HPUJYN0z6c7/EgWx4ty/0Xsa2H4C+n+/67/8dpD
HtrMmCNTtUdf/+3ph6cYE8cof7TmMmRxj3o2ou976ywR8h8QZ6xc4eI+ndVh
4Xgq/hrj+0WeewkaAx3k+bHwF6OM4zeO8Ov0+TzGUsn6xuYu28z43C+n22/F
HqhGVmMIn6Y+v5PHUOb0k6wnNsu+s6YZr/8dXI9g/AxvYCxeYfL+o+8e0hfS
H0ZnKiLLPJXtj02+2BRXuEE5Y/sK4/cVjSPGc1f5/azgd+oNaGOMfArQ5itt
jcEqHEvhIA6hHXspb7jmvmrGXFyFnZtIPsco96jOgnLvfcZVgs65xht/PXO8
z2pdpN6FqdOr6f7eOAkeT7omUEH5FERf8+v/PtdDWDc8RF7bmtk347/cvyx/
Iozrc4QfYhdHaR9pssffFK0FNBczRqbBp6cbQ2sD5c8g3Jln2jBftIY2kEdL
6hkh3BioMnPGTOk4fFa6/YNpbftMe/snb8/Y6abzLC3tD+wN4vnI4wh51EK2
x9HF2vCqtC+hjP3gKjw73fES0Q7rmvzxpQqnKtE4rOKKJ2J35pDmNehX8vse
OQe410TniGhriXre13E3yjYrO3kW5LknsjpcKqvj4t9HOTwn3nOB5oAI5J+V
MZqZ+pygv/+mT99q6/Cdto53ijI+4etabwXtorAKhUdziO6sojViuts/D+pE
vEs5YzQODzGuyBvcfxOaBzWPdb/q/LUwJIU/KOzBjsTzoCO5oSWsVwpQxnzJ
PcpnlOVvSWfEzyKf1uRxsIDrqfpq7bUg3Wf5dI5POIT70MWFXBsp3Ybio81H
BeunMwdvRxo38fME48gM5PoinlkMHcZWvgV/W2tC0h3BLvxY0Fg0KfW8V3YF
dAR9yOhpH6DqH2Erqk0Ki6u/RAqrjd1pT369N4UPQ593aA9UHvtp1PtAvRcs
ov+oyO8J2ruE8v9gfDyswjySbvtQN9lh8aI674tsHq3oM/xrGa8fQm0YM08h
Ax7NdJq61+D5v/V9TPuTyTudvkmJM6ah9iuNTDRu3JRk42+F0Q+1GBczWhgv
SL4y58gHXTnzpem+Jq54M+QbjU06rvEfZnwpYUqNy/p/GFOZOtvnyxuxxgD6
imduZzV2mbji75Lfbfgt7bkO956SSfBs1Gc4ti61mzHvf8IOH4w2b0x8Gc/l
CjdX/D39t4HeD/IVwfBK6Jtm9rv9HH22lH56F1ql/zPYyyvYm9WE1+h/BW34
IMgVFyaa8NCegH6u7bKejPY5FnHF9Z6qM3KuEuFvtT9w/UdkW5f214NahTnc
MpvjH/LMWuhkgm1jlya2j4/x3JhqxvcbSHgI6Zcmmg8OhnNm9T2Fr7A+KowO
XNWZGHRqncar9mehU7Xos77cC2nh9uoDrdqeKRj/KN3YjOvTnWZ9MK6wcBuV
5hiyOQ5F0oddkW968v9hTCYH48LcKi1/exqnzPujSL8VKkfbNkh34St6+qzu
cuz4Mu5l1h5Q6DBl5MxkWeidsfwwyx9zDuzuQup6g/go2jsSuk4+vbG7j0AL
sQMfp9sPUXYogf+aTUv6HUw6z12Ej0bfPkRmH2TzPCa/OXOgkfI1gc78A+UO
MwZO7Wjj4GxMt+9m+W2+1sgYhhHYnk1c/wTaxDj6kHRfkmYtfDS2erjWlVBp
1pYTqWMZ+GbSFqfNKYy/h9HGCpnWzvkIe25LusPKT3G9z92qeQoqiR2syPXP
0q3rv9S2Pv1P7xXfpnUa1I42x2QzvqCwBRWWHisu3W0FbxMM18/m+GXs7mLK
G4Xcy2Tz+IgNc/jz4Hhpkc26Wk7v25jv9mMLv480f4l1+wGt1ejHH+nDE9DL
5PsFz40P8sx1HZa/eGHXCdPhy3T7T3hW52+xd49AU7WXi7ZWZP04Fv2Yhu7t
0Jhu6X3Da4v4jNed4DdT+TrqhC7EYBPW0/ZqufzuVO9Qm5ImD3XOnc3jIwfp
ylPWH9j0n5HpTzq/RV5f8j/rMDKcTDiEev6U6Lqqzj9md1h8Le3c0M57PNtn
c1hcPn6/oo6jaxnvL4U63EaJb2mPrOwMVBndOIhcVpPXq4RX0a4G/Lfayb3j
2Nldsp/kOwnZPsuYuaez5XqXiy3YA0+Pta8j+UDSNd17rorxna6T3zXpL23c
rbVJssPiwqOJRC4VoJfCzMfVcXgj7fkaO7MBfhRbFS9/gZX8zk3v2/ak+73f
xyX97u8T8lsHrU12WFh3ik/RN7No40T2iDOWwjzWxHt5PtCYe8huCvGfyxnr
8P12xqETHp3CY8McF9Zbdug8tr0edvNbnp/MPLEP/jNtLyW5ozf5GE8FoO80
99B3++EHoGXa0wr/oKqxqYVRPT7MPpqf157SdOPKJbPe+IHwBOrdiPnvDOP/
F/2np4xDSoOsk9DB8wn2F9sO3aqLzFYyX+yW7zpkfYB8p5HXGtrUFD09rLmF
ujxPny+HH6LMyfTr1KYOH0l3XD5dKteyX5eDyPYQtIp+HKz/W02M7aczUK2C
56Bm5zAmovAaH4mzv+wiyL0O1wdQ5w8YA7HI5Cj5v4NdOkV/HCP8Y7rzFN6c
8lX4XnbHy8X4/NZ7Wpvy7HHS9or1f0a9V7mCXFbSD6uhpu1NCg9p6v/ts9CV
NYzh2eH+tjqXPtxHuR+QZlldY1UehU6oX7i2jn5Zq/9v1LcDsq8V4v3c2tdd
Fl25jm6Ups8/JZ8yQa64/pfqXVh58lygbxXkNR++GRv0CRTZwBhzqfT3d7E+
P70WPQ3AU+saJ1I+oa4yZ3RjPqyPfamADE9SrxHUu7HOd5C2NWNtUWWf37xG
vkPR2SnUb1qo3wufIv16eCP0IQ4aTx9cRD8faxb0P4d8TmtdAC0hzyzUOSSH
8d/k03VRfWP4SRdO9TKu32n4z7LZ9EXtit6vtoW6flLX2IBdadsW+moq+f1C
uuebuv8ki/lBWUwkfBZ7+Cr8Du05k24MHMlZMu5P+mW07Wy6fT2e0/8H6Dfo
MezIefhR7MjGbD5bp3N4W1p6z9ZuaDTPb6QdLyqfIFf8XegaZS5JcPh/9xXW
NcVfym6ueALjsIn85zGW+mq/F2OnsL67NDH211OY/Mb0eUPaMKmpsQyFT3gI
vl9+uPLav7HqfgH6XfVHbr2y2HdrY51t5tqldIc/D8b/gC5D6eSdG7nkha5o
fZcfm0+Zycofeop2f13XPsu2oQ8X4DuYx7/T+3nG53Z0d1u0cQq/z2EcHuHx
KHwgGB+lOUlnlOjrmZQzHB0ZTjiJcVKH/51XKXdD8D/qK9pbhT5lp2+vpfts
/WM5fb7+errXmpqjQyh7EfZ4D311Q+tP5PURtmMa/R9C2gvkdZPrf0If0uYm
DeyfVL5Jw9H3ksitLHwfMnwL+f+Vbj9q8nUXC49hzJwnbb1YY/MIo6c2Y+lI
jHEvhX+5Ndz4gZpnbvH8KmQzrL2xTW6nG98kGlu5EP26Q/wO929rvz9pirGW
KwH9zfW7UBn6qzQ0Uj4AOhvbRP53pbOP67uK2q5v8vDh3O/C/c5QnpL+zqpv
rCepx0z6fEaow1uaOq6wri0in78Yx8WZI2/BH/DMDNZuRxhf+8KMd3gGqlXM
5w0uJBt38z3s8bJcDvdv5nh8hNeFucLMtTZUeDzt20W/p9K/xxgvdWnrYs3p
dcz/F19Wzve1mXhhfWO8ntJ3GNYmL2SzbRvB+CjJ/4M19PFqqBHpH1Lnf6B/
oe/ow0wZmTINIr+X6POtjMvLDexj62VoCO3KzP2WOpNOnW+hM0Wo/234BWRS
Hp0L4X4zZJAFXk97fNCptPw+z988s+8Jt1Bc9xW+qb1plFOI9k7Q/oUM4yOK
C1dQ4UjacKeVfQFkyzBuX/YMk8LC75OvhGzBa+eSjCOoeyKFhfOnNLpfOsKk
cGhRP6dnlPYHxtc79PUSKJTr/ajX58gqB+EBdX0tNBjWPc1Xf4V7ztoOJSPn
P5BLCPr9BTpYQWeiIoyZWJ069EwwVzwn+Rwg7xNNLUPJ7y3423XNFS+p/bnh
lmk0/RwF5SJcpZu54rnhj5DfLOQaofPLxCtRr6e0d4hwPiiAHsbyzJmmJoVf
o4zqjNecrAu2drVNyp9hzGT5NrqGnm2s57bfCXOba6LLnSsa+1b7ALQf4AA6
MEDf71krPQGPo9+rUHYBnvsUGxLHuP+U8TuwvPdPaR9VQe5NijEOnkjhQhn2
z344s/21R3Cto/a8xbiv1M/qL+EACi9OmHJZKb8/uvsl9fuVsbuNsn6DT6bu
2/XeNcPzp+bRQdR7AnWbqfeU5NmCtkWjV5mocxHSJdGefNjWK6TPE+b+FGai
8BNfRjdfYxwVJd2NGIfnBuPFoOJQHsZFLNcaQiXUd9BW0m6BdjF+OhWwv+ZL
zE+bKftaB+dzjvuv53BYfvoV/wyaA30KlZLOYcdDaE9pwmWg2aUdHhfh+Kv0
7+pIn5nT+UbVS/VTeHw3xw9VMFe8FO2Mpp2l4WW5Np/wEO09RW+qhPt/xED6
e3O038sIg+0Z8s7BHBLG/94yUDmeC8vwt+oBGmPkITw/4f4Jh1EYisJOFCks
DEV9I2rB2Hhbe0qwX4vqGG/y8WYOt2pvWb7RxniL4YRrwGsFSdd0L4N0vaUj
GaarlLmIa2fhYyhnLDQ1xriMSitSWM8kdDN2nbAXxQcEw/KHFJlhn0g/NTXu
uvDXu2MLe2A7k+Er0Z2eXCufYVqV3de0j0H7Gb7uZRyn422M5RSOvr7JHBcB
f0gePUj3CTQ3s300yf/jRMbKP+ilXp4pzYNguur8b+vCmKqRz5hebcOM8TWL
fMuy5rtO/0YlGINImH/C0BQu46oYk8L/+e+lnrWwQ8uoQ2/WG68z1p8JNVaj
8Bk1ngowH31On85hPde1id8NfZLb/nfkh+c2+YQxzufzbA99B6Veuxlne0t6
DtZcPEb+f7i3iDQVNS4ijYn3DHV7Ope54l/RN60otyfxvIy/SrJR8NGh/o//
RYTfl93MYYy/FcRXRRiXsXA5f1OcGGL5FtA3EtbmaYRL6bsGdAk9L6b9Izqj
1cN7hLVXOEX7LUM9jyssnhTqNcEvoV7rCdexcoaxHRUWHrLiVTLsE6sH9VxD
f1fT/xD4W5TfFRpWy+FTWR0/WNj+7FOYT6pm2Lf4ZNrUhj6vRrw6tEbrN2xX
msaAzuExJvZBT+tMq87QQTXpk3qMvTuhxiAS3plwiGrIViL7RSV97vdmfmOK
NUKPfqCtuYnHI6tGUHXk9lmEn1F6hZfFOL6Hdn4LDaxnUvgdZLkKGzWrvL8R
yie+fOMLZ+QsdelMXWtKp6Cvyec5bEXtDOPMPUsb62QY+7J2kM8IhoUxFpVh
zLG9yG4PbfkWXrar9yrd0/t99K4bOlQVPpO8Z8g20gfNkWk8smwB3077elLH
zyL9flW4hsL9ld+QDuXtRyQr/dGf9O9FGAc4t2w19JD55F/kvpBxMFSvgBin
w+DFSV8M+oH2/U7ZD5H9ier2Ky8/5fItn436L+rmfKNpRwHu14XX5vrtvH7/
WoNx0LGmv611Ke/zpe9n95n3pYzvQV18JiqG50awnqmKrsZpzyXz2Fb+q9xH
TzbDP0aP6pHmV9q+B/leQiZ74fW59i59HAt/hnn6AtcbVjNebm/a9gjUryNl
6LsMduMMc1tXxkCXHv4v0UC6DS9AX29D5mOZN+KxRTta2L/2ukz2SypstwT5
nKK933CvIc91QDeXE16HLGrS5hpQBfonlvqUwzYVy+92yEY1pP2X9O1V/0NL
GitvdKRJ4Vt6H6x9Y7Q9Mzwuw/ij58k7pZffvwu/pxHXp9OeadBc2jSvNvYU
qklf1s5hfKQnaf9dnVmlzH95Ph9554Vystb4Ktb4m8JcHk2aF6BGMcY+F+75
scr+rzgbmQyh7t1INxj+HrqwjbEXn/GfK+NMZJupPM/WKujzpTpb2ph7TTL8
fucJ6tIdm7Im0uFCjJ8nZUM0lvhP2QGeQNpc6FVihufYzZTbVGtmzcm0ITf6
8CEybo1d/BH78TH9W5u6jiLdi1BLrWl17inD2ITCKhQJn1B4hvIvhzr952Pu
NGW2IN2JLj4z2QKdLpLZOFNfUU5v7WMJNVaisBPHJHif0kSoIu2sSoPb0p9z
yO8ctn5WJpf7eYTL3h7kipdGQC251wpqTf1aZxi3TuEkKEVn6xlXRSnjIuuJ
oYyLYdDZVm7XxVZu28Ps/oasb8mqU1n6pA15vUNdIljvhENZkW8WKEllQKnM
W0OIt+5qHwvtVAf9j2Rds4N6tSf+AW1eA4VAI5tbnp1lp2lTiM6iowtLoSdY
n21kPGxnnnxA+R149r7Wa8jwA/ovrplxzo7r2wFpOmZ477n2o2v/+ZMFfZ6j
N5Say5jCGbmMVSo84E4ZDnfOcFw+V+VvtQj5ddFaqoHxMHIWMvbhbexMK/qs
Km3MjdyES6vvz/oOfRb5nYGu5DKm4NuUNRi+iTrup+4ftXVY1xTX/7TSuYwZ
fZzxdhL6mftPYsu7UvbAIFc8HzrQs6NxEeYV8pyhOUHzxtzsHs9vwF+hShOg
2si5IFRK7zwzfL6rG/x3+LYI68i31Lt7hrniPTKMOfgc9Xk+l7m+C/fkei/G
TU/oKfIsjk3NSdt+wU53oP/blzYWaa8MY5P+RxqH2NQUeEXs3Xmee4idegAV
QQ/a06aOUJL2wmXYJ4N8M+h7zdwK/mazWj4tuT+Ha3VzO659jee59xv0OPdu
MGa+KmQbItxVnZ0U3upt+HT0expUm/alUsZZ8v2CfD6H/kK3/qzv9956/z00
2WvN7xlfadIFKCPDexQvkv58bmOj9IF+03/nLvYJJSxi+WHZWcSY04d5vg7X
MnSGi/x35DXulsLiN+njRzKCOLJQCno2HrvWO8MkvMceQa6+UDgnZeeG3o52
WLw/z+1nzPyDbPpkmGvPjMI/l/9/RJ0HdFVF9/bpLQQCoYQWOoTeIQklAUIg
AULvkOSG3pvSlGIBlKKigAoKgqKgIIpIEVAQFAGlqIggHZUqSBNQlO/3vM/9
1n+t7OyZc+ZM2bNnz9xzZvZjrrhI+2l0Te+SC/PMbcZyd/LpFmJcSJ1LEFf8
DvPHN9RrPPIM51oR7FIYzxRoaa74RdJNpD092juckeq4/PfrPaV8+PfnWkHK
GQCf0NO+k+VD+WXq/nxL40DeYOyvkO96eGn5gCHtoFRjSpYPMa6kuHAfFZ7I
M4O53wE+kLXmm8w9QzQXSVdDjBsp/kMuh+MpJ4pnh6Y63CgYH6H9q3q/09m4
5MJWzFHfpLDwTYVN2729sWpFCk/Sd6sWxug9k2KfLMPIuwHXa+tcVar9Smnd
frut1+7a3zCC6/nRrUT09H1kO5L4KKh3iNsrrvYr3Fa6j9xGE/4DG30bug5F
kWY8FN3QYXH5i8mPXftE/l+oz1V04B62ciFlvFfAuGSL8xk7pHx+Y4nsQG65
u/ncWWbmxkdZvC8iLcRYj9+VNykszEddDwTvyT/qwxaWn0hhyXFwZWMslWWN
ta6530vqnWRccO0njPAC1LEZNnk646419mM399vAx9DOMdr/oPen+u1GH43T
GhZ7URkd/KqS66O6VKHN8eSTHmKszoLoWr82Pn+rvd8DoQyeH691HHSX6xnI
I536PU78Z+5NSPVv/IlaK6MjkcwvW6nfK4yTLYWNzSX8rukJ3mc3K9k4kT/I
fwtUj77ZyZg+hx04C00in09Js1rvl7BF58g7G/wmZU7m3pRU4y0KY1FYi/8L
tzf+4hOaR8nvSXhdbGQdaCjyTNBZffTg+fYOi7eCR1FOZWhqqsPii7m3NcT4
i2kVHN4W8n+4jDW6GadReB3TUo3Zoe8yR6DpxBchs9cbGhNQYfFDZYwXqLDu
6bzbE6E+87Yr1Pdl13pQTi/9tguSwvLZq33b+bCBM7ROYx0xhrQR1OF2iLni
8jf0FvF/4G9ir39i/vqFNe4mbPiLFfwtTti4+UKMj/sj/XOVOecofDi6Mh79
GQfl6mS/TN20nuJeFFRZ6wPm7Q9Za16Fj0cGQ6CnqM9Z8huRaGzNP3mmrdaw
2nOT6j3e2uutvQIvc//jBIc1F02FP6N1JTRTay50pg92bRllX0E/7sp2Qusp
5/2KxlNT+IOKjh/Rbz7061Ckx2s+xmVtqCBlzNJ8gwy+C37v0HePY4wTTEam
jejEaWzJbNI8B81FTqHMSUeq+/11ImP9ea4Xoo7NebYJtvc65d5jrTon1Vg6
c1ON39Qbe7ecfu+CDe+k92iVjAl/qb2xCZOgSoyXQozTrJRbAB27h3zn8XwN
6t0F+zGfcHHqvRIqAb1A/DJj/36cwy8G4zd5djF60J+61mB+O9rRWALS43q0
ORH+Q33jSt7Vt8RU+xjdDl1H3z6kHm3o7996+Nz7f/RjKforhPrnyem9THPI
cwHP7W9qH+zyTTC3pc8Xv5zqd51657k43r4W5HNBbbxBnx0m/SHoFdIs1DjQ
WApyxV+m7q/C+1PGFX0fhQpR7+8YP1flBwKemzZuJ/w59Fqqz8t8U8+4jcJs
fJ1r94Jc8SXwJsijGZSHvsoLnaW+vYnnIL/H9d2dMdgWm/w69fyKvq7Fb/fG
2X22TpipZ0r4PLjmGfkxFAZVK/L+Bb6U/I9jd95GXkPRgcbk8Uaqz2DovIbO
ZBRBV88xfs5Cd+iXu9DE+j5zqHe1b5J+GbQcekv2KcgV1/utpaT5ALv5gPKT
6YdtyHdlqrEZ3041KSy8Rl0XdqbiL9OfC6DL9NszyGsmtLecv8XtDH6P+6iG
f+fq9+536NA7PH9Q5yVLWJcWQcO5H4mNWKX1WZTvnw4zHkkW6hPGGjKRMf0u
99+DGjHnjmIsja7lfXpVtG9de/aR8+xYx1ujV8lQR2QxCfml6UxVqjF25Yd9
DeGj6L9+yNWjzh1p/0z6o1Mun5u+B31K3a639zp0KvQz+V3Vb4Hyxu0Tft80
xsvzyG0O9Avj8yZ9kZW6lma8DyplnOkH2JCn0c8vqEs07X6fsltRxw/ga1N9
5iqGeu+hbq0reVxLPwsnWC8jaW9n6rFOY17nO7AdybXty74wzxaDF4QW0c5C
yO1D0q2HmtI3t7THg3C9/PbDJb9vo3IY2+0l+nMBtIZrdbEjq7UvAnmPRQ71
4Vuyes/kyOr29ZFKmzewBpmez+1W+w8gp2jaeRM9/4f4Wco/A32cavxwYYX3
5/oG4oGWPlcgHG5hcDdlXH3C9Y0a0+jger2ngefR91DkkRXqhi2chE5011lK
0r3G+NoU5JtTHW6BPclDnrmhWSnGcxKW0150uwL1rQRtId1F/S6GriCTSqyP
Ktf12SSdHdM+niH6Ud+d+uYzKZxMXxTht8RO1h2F5U9MNk12BZkd4PmpPLcf
+SzJZ/yyOVCgk88n5i5pLDi90xIenN5xCZNP77mO056foZKUub2k7brsu3AP
i1HO1AqeT2oG5xSdjdQZSeHU/kxfbWzs38Y9WxmTT3h8pbEdLbG7LaDvon1t
WTefS9T5xO46p4pMPuG5DdBO8niS+Epkvk1rcNUl1X7q5KPuQ2R1kbrmod7t
0N2NhB8j34thxpavSv89SrGv9OKMm3Hw7Ni5nFAU6XZo7Yv8Mnf3fq8yyCEE
fgb9Ow19zv1I5FUr2M461OcLrtWGv0Qbd2q9zLw+kX6dUNU4yr+R7j/6sxDh
z1v6+7i+kw9n7HSC7+KZOhWMiSdsvOmN7CcpsraxPX8o4rrVRrcORduX6hvB
fSIPW3n9WSC4Bv2SvAowFsoxLiryfG7G2O32xt673Mi+k8qRdoj2cUDt0KXd
PHMaPZ6LzPcQXq336uQfig6/hCzW5zPOm94dC28nG3LsAz9J332V6rPJdalX
A+jrVHPh1PUp63doAe2B17c4yr5POBv12ZtqrDbhywl3TfhrwmZ7kvY+oH+P
0+ah2NhvSNe6msNDgvG80fZFIXy2S3rHSPn3yOd55JG/lfFCxYUZqvAIzWey
o9EOy5+F4vtTzfMG7ytPhYeQ35Fyfl+u8IRgXPR98Lp0oBLtKR3qPcTaS/xq
I69jtJ4RZqKwz293M/55r8bGcaxGmo9lw6j7Ac1R6Nku+itC7yVbGY9O8tgf
rFcI9Apj+RS69W2qfZFcQJdqwb8jHk3eB1ONGbRJe8K0BqPdp+QHSGtJyrpB
HSdRv+tBrrjOw3+ib0CYjL+wmSH0VVbqNwnZP8/Y2kN/FWJMH6Keu/OZFN6j
tSLzwQ3aEa55gfFzhHK+h35I9X6TJTUtt+ZB2X1N3mfijUG7grZtR3fy0u5n
o43HtY3rOdDTpsSjc9oGCnNK2FPCnhsYZvw5hYcE4w/qGVPglbb2UytMlDWU
VVZjFnqc+ADa1x9qHGo/7/L3/iN1fAw7eBT+OPybLD7fVBrbO554xUTj+kyC
5upMK7KeA59I/Bl0uRZjZnCcsb2yqizakUV7f5H9KXT766wOC/dR8VLc+516
RQb5G8GwztMKb64mef6Uaq74eNp9gudP0/YMxvCxVONn/Rzkivci3z5Qa+h4
qjHdDkQbY05c8Re7GyerIGW91N0YdZe416my8c3KIvexjJcv6OPnqNOJVGNS
/pLqsDDzFL/UwWfDdUZcdRAW3j/5jYsnrriul+3u8HTWj09BC8nzJNdjWH+c
gn+ps6nowLLq9oEg/wdNEowRN5x5ojv9NL6k+2ZHfvvrkp7LZ1cX0v2EbI6j
ny+TtgJ5nibPOXX87UyYvB2Yt7ehm2+S9kyqr0XxTPHubvfZVGOjCBelA3SW
9dlP2NwrDf1b5xz339XvwTL+Vr5c+3Q0b1K/C6kmhduie78G4zlbmRRenGIf
otuq249oB/IfhA17Mo+xMMZEGA+jbEHjzZ1P8VnNrNRxv3770aYwnXvSHn3W
2YPL+NxO7vrGJBU26W+UM1P7ZCQn2jqKto/Td2DqsJExFVrfOHErmhqT7Cnm
id95pm8B84XdHF6FXj1Buvo6R4IMLnLvWAXjdv+dzTjezdD3S1yPg19Odfmv
V3ZYdVL87W7GfhPu2xWuP93EPq+E6/oNMr/KtWzY7muaE6HsjPFs0HX9rkFG
cdiPSvp9Q/1vcO1P6KbWFNRvEnPZMPprsr4tF/UZv+F1fA5Q+FTCqerIc9O1
Fxy6gFySqNNH1OU4dvzbeOPZCdfuAWk79bTPrfnN7IMpibZH0LZblNeRa08x
bu9S1/+a2gerwB9a5vfZrfBsPtNXHztdQ/4RoKLoVR30pXaoMY6Ea9S3oDFQ
hI9ym3yrMnZaYU+iOvh8pH5fnaeMktis0vR5ibb2PXGHtMXh1aEP0fe1OvdK
m37S93t4UeRxlzRydKP0JTLbd4W+j+tZfSMXV1z51KS8vyRH6D40Ghk/SPXe
de1blw/seOzsPNJ2SbZ/iG+hv1PtN+gf+FbSvYd8HhL+mrrOlJ8Nfk8s7mSM
16NBO/ov/D9oNuuI7uQXwzh8m3Tfonsd0IUUaDX9cIFxcyTapPBv0KNU+8TZ
SDkbw1y+6qGw+O/RxpJ7yP0O1D1TGrKlLlXDHBZWoeJndP6COmWrbewq7dHY
iiwyp9lfcqcc3uemPW7atyrsvENtjZfXmXVNjdr2o5uF9Ec1JtP8u2k8ZbfD
VrUkj2xcSwjyQykOixROhO9Ap0qjH5/Ds5MmB5QS43DOYHw1srlOfknoy3PY
h79p3/Pwxzp7r5H2HLWi/s9wPRfpc0OZsVWZoKz0fXaoDzp0iXLGk+5v5q0B
2jNcybbuJdr4baT3awtz7Kz0EeqHPf5G797lywdZvUP58eh7Xf1uoYx68tVD
vfdCa+T7iPETBxVvaZyVkDS/E6mKnEIYH+dZ10ZQ77xcf5q+WEHeb+sbSS/7
B5NvML13eTGz9z2Gkq5g8N19NfLojH4uwZbfjjLGV4fOxvnSmmk343YRNvCX
yvZtH4atuaK989iAJ3VmjHb/nNW+RPORb0vq0wn9nkq7FlCXXPDCtK8CcqoI
7aZ/VqcYo7QK9mMndngXOvwY+j8eWlXcZ2sWobOHmbOnINNI8nuFNI+K+jfY
cukrffKZzp2TV/kwn4O7AlVA7gPo/0FQfurTVr/V9e6d8HfkdQgqoPZD4dDX
yGeXzgiSXk47df53GtQAeezGBj9Hvz1V2biB71S1X6gX0e3stYytVwaZvQBf
GbS9ssFnGWPDyWsheczP6X3jz0NbqWsE9qZ4Nfv6lM/P08grLcp+XtOhEPrs
V2SaF16I+hWGevZ0+EaY41ORdRF4n85+dnYFnyEqmmY/pt8whlszv0cQz0JZ
0+njqoz/YdjM5t2sjzo7IOwz4Z4F6P8Z3C9G+hDuP8NYK054n3xAoYs59P09
v/FWfqEv2qB7Y7i3ibo3gb9B2Uuh8UmeY/pig7dAJdKMFbONfv9C6w769lG0
z2UMbOCzGfJdGFHO766kI9KVnqWQAXpTMs24V8IHUlzhcOS4GtldR29Kcf8F
xtN8qBG61Jy1yA+EI7k+k3Y8C31BfAc0BXtfmuvZWKdmh8ZUNqZdGdmRDuaK
C9dO+Ha74/zNTt/rjsIHJNofvPzC5+xh+6Z7Ci+Svyna/zFjY2A9n3s6R/7v
km/ZNPNyaQ4/pN3l4buQfQV4VdKNTzB24R304y+ocFavjUYE10fCjxPOoMLi
wh0cSx88wAZnp90VyWcPulQIakF/V0pz+DLyvAqtQ7U7h9tPfA+dUaU+J5Fh
mPzuILPKpB/WwvjMa5iTD1Y0Tk+HKsbtEaaYcMSi0nw2VWdUM+jLBPqqCtcG
kbZqmvEgL1H3fW2NxVGNa43og+rwGlADdKEs9SgT7m/9T5T39/6u6Heglvfg
r9U5ynwee/G0paZ0Gr4K+TaCGkYZNy4cXot72+mvz6Hxld3X99GTKxr/5Fc7
zZhudeB1ZVehrsjsKDp4LNrhX6IdV1jXDjEO6quuUDT6eUr7UqnLYOr0lPaI
ce13ZLItzJiXwrvU+4F1PDu3lq9/FrzXMM061wjqwjPlkVNXeCLyTSBNYpjD
rYLxaNLFQLHQk628hv0aW3ga2e+hDgO1d4b2NFZ7kGG9cPOLUb4mrniR7t7D
upo+KhllzDetdUtBTdJ8rSm8WZp/E5SmbUtp1zrqsYRxG8f1eOiu5Ch/T4zd
r5B5JvK+q3er5D+3oHFVTsKbk/YEvAV8PXxWB/M/uzus9zrFgu92jmA/WpKu
Qh+/h9b7aH2HqcK4qAY9g01JSDP+nPDoUnimI/RDd3Phuin8uH7XMCfOgFqR
/ibXPixofjsY/h2734gxWY7fDomkaQ2djrGP56/1PYEx/gdtC6Ff8kKzg3sG
hcMmPDdhvAnT8nI3n6Va0M4+bYRj17GDSWHZ+KbwRwWNXzoFeT+OPJ+At0nz
XoqkNH9nPBb81vhvJfs2FaZaqVDjBWp9Jpw1YawJC1D35fdU8WSef0ZnIAkn
Ur/J5T2GhO2ocOtE70t+VM57iYXJ2aeOfe9ovZuITZ0Lr1LN7apazT47l8fb
b2dtwm0pow58JTp9jfn5LfhzHYxH1457HYknY996ogNZO3qfTnb4PO1BJ//2
pPmb9fFVdO8ffRvFDqRwbQW8AzydfkjT2Q7Ck6n3qYJ+97YI6opNOc9YG0S/
XCjj+9Ir6dd27WPBjr3XyLiJwk8UnqJwNFbxbCfSddYYg/LRj6dizBXvgz3q
DVWnP7qmeY+f8COE4dME/Y1hPHZFBuGMtYIpxpRbFGscuX6U2YZ6PUH/dpPt
C5bxZZS54t2C11T+6t7Mzcy9y+SPg/7okWa8OPFFiQ4XpS09ZSsbGPM3exXj
/n6JbcyEDXqRstMZA73LG3+N4SIYg0y9eKa32gPdp83LOhhTTBi5w2lLOHkV
gJIJvw5fDM2izM9kq6ChOnOCLE92NeaI7gt3ROHkYFzYcMKFGwj1pZx+0gfS
96Ws/lAq8X9Zsz6EqiH/7cg/Lc1njdLhx8jvRKLD4sKdu0QbvuD6LmgVcm5N
G9/T72DWLiPR7+dZj7VAPwLoUEB2hzquYc2RpZTxGCP0fpb+G8y69Yss3o82
XPOPxrzWhnoHiV08kujw11Ud/zTK5wo2RnmfWn/Sb6TM3ol+/9yY9t7r7nXi
Ln2D6mG/7vLvPpG6Tta3GsbAAJ7bwpq7PzSW+b4g9SsEDUzzXFaffhukeQV9
T0fvhnNvZEGfM7qj9T9z2l14XXQ/lXb/Qz6zeG4mNJa6tMEWPSJNUj73oXDm
hDfXKNkYcsKPq59sLny5KVzrBjWQ76M0c8WzI6+fm/p39I/oVgtk1hx6jX6/
jwzLMa5CKxsfbkiaMX0exRrXp1NrY7kNTXN4dXXHr6EH03oai1FYc9tjjTe3
CrmtpKxhpL+qNqEby+nXApQVT7pk5sGJ+o4Za0wpYbS1RL6/YJPGaY6ONU7b
Tvjm7k6T1sPv6QfUMIbJi9Iv5ocW6EICVJQ8w+jLsVwfTrmtehir7g/6+grP
dKc9maj7CO7lxbaFQEW094qy38hq/DHhkEn3IpHvSK0FyXdUmrHcRqeZFBam
W99Y95fw+kQKqw/HkOYKz79FPcamGa9NuG3j0owVVFD2v5oxQQ7TL3OZ1/dg
kydVs16OJ93hRIf3BuNDactj8Mc1P3HvDFSYum8M97lf4R6W7OFz1DpDXZL4
GGzvrSjPqZpbNTdMSPM3yM5QVtKvRF/fTvLZsmRoIvcnpdkmyDZkkF9iIWPh
KTwgGFdYY6l/rMPCy1NcOGHCCxtF2SnoWFF+c7Zr4PoLW0h4ahHUrWtr46eV
Yi6JxXauR+fK9TAOWRl4jYo+93lRey+YgyuhKyPq2efkZOqXAr+CLpVlXEyR
rqKHBXR+lfE1mTF8Jhs2WWskqDYynAofR/8nlPW++z/b+8yO/ERlIPcVtHce
+p+VsTctzft4NW6XU/9l0PQ0Y5JHk/fuyn7/+Rr9OIzfbzNUPrw0tiBDdgoa
xNz9Kr8ba1LmNdIv1r4w6F2ur4IW6X2xfNlgZ5KoQ7bqxlF/iryehmpJBjq/
Q5tbU+dnuPYbuvws/He9l8/t7+0zVa+iHjf6Lvk2ulRG7x2Zl2al+ZvlbPgB
ZHyJvIpQhx3ZbZe116oc+lgWWo6NWF/S+5W1V/ksQ+U56To0hn6dQT6j4SO5
NxrqiZw36vwG5RWEhtFHc0g7F/oo1vOI5pN07G8GNI/r86Fq6M5f/F7eTH++
QPxFzQm0Z3lP77v/E5nEVvF3CmGZyn7Jdm0NNw7nefh52vES119mvC8Qh+6Q
R9bqPge1kfav1Lv4qvaPU0X7lrDz17Dxr5B2oeZaaG9l+99cLJkzzn/XfjDW
VwtpS7de9sMln2nyl3aOfn8PfVgDvap26Ls1/Zyf/vtP+8vRhQK0YQht3am2
w49T9mukfV1yoZzf0PV5MfZBvLiL/bxspx+XcP9t6ttUvpIYo83gS7WGQIcX
Z/F3qze0bmFsla5mbEdhPGbN4/eE5ZmTtqBTGxjHb6Y5/HGS471Z3y/TmgD+
lt4lEX4LOkXfndJ+TPJZDH8v3LhiK7j3I/PEyjT7QM+EDB7RFy80NVbDTWRU
A96LtG+nmRR+B55F+zV0Xgp5PdfKeB3C7bjRzNiew5FhXvnYII/h6PoqnqnO
+N5P+ncJv6f1UZrD4ms0dpFze9o8AlvaiTEWTv4P9O0Jnc0OPa89UqT7AFoL
zdH5LGhukBReDH2l30fQurY+46GzHpW4fpS2/YK+9mddV4q8SkOv670ntqQh
evp9VtvZd2I9V2yiPd9T/uYC3u9QtYkxB+TztC26Ek4Z98n7HpS7p8Pi17AF
yZQ9Adk+0vfZxsaQu1rY7V5Wwm0Wzv2WCOPeZ8QYc1HnCBIof53GcRmHv090
fDx8GPQh4aPww+jPoKIOC89Y8UWar8Pdx4uCfa0+rxY8E6CzAXp9Po9/7arY
n/z3tCMX+TSmnv9S7/PEk7BDpXkuGf6x7B51ewn+D/e+Ysyspw4X0dVW1O87
6jmPtj3GmHy8un+XDmT8NSvgde7C4Fr3H/SqADoWXtIYU8ebGmfqJcZ2QO/Y
lA+6NFzfWbXOQx96aL8PZf1JWeXpo0GJfv9Wl/tPUOfj1H8xcq+CLJtQhwnU
syn8Y57ZAH0CadG8Ef4pVJGxH068EvwQzx0UNTYf18Thmdig4cQP0P4btcwV
38Tzm9Vu4vs7miu+BdoKPdT6Gr4N2g7tgFYyJx/Dnn6E7dgQ7XfX27mWD734
o76/rXQPfl8RLptw2JoXMRcumzDebtKeaa3t619UupR9/hfE1hWCbrNW/FQ2
oKMx2T6njC+gndBg6j0E2iUbAz1D2urY/2Tyyc/13WnmYcHw6SAXLpz4nmD4
K3hJ5tKv4XeZT4aR7oMgKdyzjXHKtO4RPpnCwir7hXpfov3f6/1TD5PCwri9
zzhpXtB4aJOxDZsYf+exuZVZV4Xpdyp8LHm3lg7ot3tj4xqWR3/eqOv3FNq3
uJXxdAV9OKx92ZR/trrxdc5Q313aW9/Q9RIem+omUli4bPJ5/02a94rpuq4J
W03pf67qdNpf/VqY91j35PfGoa4+a/FK8DeCfit8yjgZj+3bBN9K3dqh320z
G5+oLLQvzRhstZFTZBGH96c53hhqCsVBS9CF7O193mBCY18XLls9+usA6cMJ
n2UcFIfPpw7PYusbs6aIhb7lfm9k1re0MYeEPVQCPrWDbeJ3sjmMnWmVjfvU
gjymIKvJ0FjGfcs2DrcIcsXPNzMGmbDIFBY/mGZSWJhqS/T7m/lrFZSdZ3pp
3kA/D5GmPe15U/7u0ozHJiw2hds3cfyI1hCsTw9hL74nfB5ZnYt3+GQvx9sw
BqOLWj4/cD2WcExR46EcZE5tRZqGjOlRtPdH7t9G/peg11k7xFDGC1yfX8zh
2GD8KOmO5PDeZtU3jvyaFXU4ezCusK4JN+s6OiFsOeHOKby2reNtm1gW7YLt
UViYc/K7NhJ6JdyYIj9p3YKOrmDuf0zr/Kr2dXaPNdBfUEHkXQT5Hktz+Oc0
x8/Tv6n04QX1M0XOTfrf8d5Mk6j7EcbxhBzGORLG0RhutKEvDlLmJWS2K7tx
JoQx8RQ2owbrkOnwjsnGlMvcyXxlMLyMNfKL1DU7NjRMPsSYw28l20eavkHK
T1ox6vw7/TxCfitly+BbpIdcv0ZfP036E+jicWgpeTWnLi317qGacf1O8MwP
6MYX8mnIMxtq27fyo9zG7BIG3i9pxneST+8pjO1evXwWbzTrmJNaRxb0Gc6k
At7fKz+F03g+G+PtVJq/P9yTzUYGMfTdr8ikLZQc4TNxC/TTEBn/xXrrPdLN
ijdu2pgixk4bH+SKL0d+W9CtdxlTCeQ1GFkWQ44/cH9ajH1xnda6mXujoK+j
vHb+BxnuwTaNQwdz08bYjvbRdibN899Cym2DTArXtE8FYdS0aumzqzrDejbN
Pvnlm/+cxgW0X+9rSPciNuYUvCgyuiA9YQ79tqlx14SnOAVb8SSUmfzeoE9/
Jc1v0GX0qBr27HfC19CnQejNBe1v0Dt66Psexvu8yP2hTYwhNa+icaT0DS+C
/u0AP05bctDWEx39jWYW+hMtPaUfzlPHc9Am+ndUvL+/aNy2ruVxPBwZDIMu
UUYV7UlmfCUW9R7aKgneR/uoiM9Rb6QuR5BROep5Oc0YN8K3uaVvEtT1PtE1
pYyZKD2WXgunUeNF4+Y6bbjCc1eh66xTCpDf++QRz9rnOv2/lbZcSzMGmjDW
hI8mrvgbshPIeUkT46Keq2Zs1JnIYDb0ldZf1DuEunSu7rD4EfgfaS5b5Sqc
ib7JAg3h+XnY9fmkKYcOlIW+49pe2RfSjYo1Tyr6P/eXmUqw5qnLvFMSnoyc
U/RtGv42cn1Gfsxi7RvxA3R/HRRPOK68cdq/YuzOpn0Lkv1+VO+O9Y65KTYz
HVqj37+hxosRbsxq6vsb8n+3iUnh/tRrOnr+Ke26X9zfprKW9/cp4R/ekN6j
YyHodwZryQFVfG55uPa+kPZSQ+/hacEaJama9X0Oaf7kuZvQrTRjCpSIM65A
RX2PYKw3hk4gr3ayr9CL2ltZ1N9y96EbBWhbH+q0DZ0pX8Pf+h6nnbel1whu
BGkSdXac64cp/wD1HU2d/qINWdGXbIzL4tjcO5p7GL+/kVcqafLpXThtyQO1
auXfL/rtclf1pS1N0bEmOe2fSf6Ds/ObrH4vY+8Jd2+KfGVCoeTfkvJG6j0P
6fIisxDoL/KJY+5uX9u+w8swHnJQ/1xQafTge2T9HbblntZatPEXnTdLsk0U
PqiwS+5zLwX+AF4U2f2dZv9o+WhvGNRZ56+4dqGeww/THJ+G7m9H9v8Gf7vp
d9t97l9Gp/6in5c19VkP7Y/8Az0pS3wMdSgHP839WxWN7ZdCH92hvh30HpW8
Hkm/0zNlSqP9d+nHv6AT1LmE3r8huwfQbvpvBeVlJl0yNuK+3r8h6/rMoW9X
M37hJtLfo5zfkM8H6PabRbxvtWdR72PVWR6d4xkBP4SNu4VcD8P/xQ7sQkeK
NTdum/YPKXyigvdVa0+13gXonUAFxmxHfW+ifs8jjyzpxnvOCu9LPbJjF7IR
Pkj5e6BDUHKk/fTKR2927p2hjnWRyWTKeZN+eAKeg+uDyfNJwicYr2uzGHsy
MYfxV1rD89G+AlojUP6HiKYU+rQ2k9N+AO0h/W7aMhRdXNbJGBbzk7ynVH0d
0dz9rffiz1H+nOD7Vr13fdDD6+GlwTVxJmzEI+qWk3olMQauZfU3lWT4HcZJ
XvkN437m4vZ1JNzv/shjINSXZ3PxXG4oDzSO/MdCVcnnKe7Xx7Y8R/rD1LNg
ovkc2vU8NIF+HE+eZ6oZL1l7YsKKeQ9sq3Dvg42lrX1o10fo4OBOHk+NocTC
9v3TGj6FObck1ybBv8B2PQFNhVoX9NlInYucSz+UpK4loJ3YthDq2qWw38sc
Zq7+HsrLtZzSFeRyWWtP2nFF39S4ng/KD42p5zEk2TZkPDdGH8LSbR9nU37d
isbQFH6mMBzr8hv1LcZqW9peDlkfow3vFTIembDImuk8lPREe1hoZxhl5tcZ
c669y5jfqe8WUDjxQlDhdPsZ09ks+cwIQ3+KcK1ounHe9Ls8JxRB/GXqsrCi
fzcJO1qY7gnUOTHP/1z3ZLpMPYZT/2KqPzahIDbnmfzGEvjfu6DWTvMjMnwJ
ORRPty/Co+jn4uD7SL2XDEsyXlMB+C3tfSpl3xbNaX9Nfu+8muj3OyV4vmS6
eUJThweS/4fo/OzG1nvtTz1Iv5Ti3k7KXE9frdae/95+f523jNclf6JHbZKM
QdiKMRKDvqwK7unYy7034ryvXee8hPcn3D/5oZc/evk/ECag8ACFGyh8OZ3r
7xLhM/4vUPeuEdadfbRrdYTfuabyTE346R4+FzCZ+u1H1suxbSk1fRboQi37
vr2UYpzRk9BPzA2Zqd9t8oum7x6n3sUoZ3kXxxVuFWEsg5YR9qufl3J7I48O
zN3XaX9H+IfIcDS2bWyM5zjNb9cK2UdAc+p0Te8QySMS2W2PNIbiXmSzizxL
c20o5Q/RWWFk+C4KUDif1z4dOvn3Qpl0c8W7MSY3MtZfo21fotv7Wvqc3gCd
BdBeAu174Nqz5P8DPCt9Vpbnp/P8POpZhzILMibPkvYQ8/nX8JOkWcLaf7ve
/bOGWIn+3qVtOVhTNEBn/mQ+qsO115F/fdLdy+K1dmPs0Fvo5i7t10/y2Wf5
eNf55wU8/ybdu1717uV9YOWoRz2d9YbXh8/J7TMnJ5HpO7mNx1WBexWhadj5
/qwLttY0Vpxw4hTeFozXRUaVSPcOenyFPCoTvqo9peQVRbiK5oII2wrZDM3h
I4LzeFXNc9SbbvhfWJzqZ6pGOBdtzglVJ1xDYxqqgNxqaSzTltrwRujbT9Rj
Lfp0l+fWwVcii3egaOodRlufhZYi2zqkr6t2pxsfTjhxOhNQn/gU+qhjU4fl
R1rxz1sZ21Hnqgd2Na7dmEr2sSb/arm6G7PiLvd/TvC8rDm5Mn20F91oQF5t
ufYKNngrYyCN/FeRz3/UN4b84+rYh+25XsZOrVbE+Klhpc0Vb5huP+/yAV+Y
Z37EHlbletfO5oo3jLCc7nF/FfH80EehDocF48JGFUaq7HIG8eegy+TxArIv
2tPv4ldRx3ehdtS5JfemkCams8ON0h1XuGUJx6tS3n79NupkPMBo2eiaJoX1
zqyt1jpJXl8IL+8wZcWkmxSOTfdv4qKUOTfe2I/6nS089zn08VHKnFvca/op
yH4Lv0+rFLFsJLMPKHsJ/bCP/D9m/gqrYTyzrxhPdxg/X8MHU86A4Jrsbhuv
+YRV15iy/+L6feh16nmMdG24d76n8ZiTdZ6+rXEQLtNPB7lWCjtSsq5/K+l3
Ujaee7a03zk8Xdp4xcIt1rpDZ8ASO/tMmL6j/5nFGGoVChlTW9jai6Am1OMN
dOZ19HShvp/Ut8+jepRdF2rK/SK0oy3jtJnmN3RrNuuAyGTrgXQgDrvTTN+4
ST8Def/J9TjSJtKeFMKt4f/yXBzUFPn2Qt5ZeH409+JJVwlZvot+VCZdc+Kv
YHcz06YetC+AnfyWea4F11uqXzV/1/K3Y+Fe1qzjs7IZebxnU9+91tI/edC5
dfBQ+qY/ssiAPqCdb9G2tWXt3+l72juJ+u6lrzrAE8j/xWZeR78Ev8S1VtIV
yllDXquhPvTXcXRhKHPmVWgHc0AiaVpDbaDOyD4p3ecv9vQwznmL5t6Hl586
1etkDPDXoKysDbJDyaSfgx1vEGU8uJWspdpyrR0UxfiqDLWXrmIHv6DsUPp6
YFHjji9ALw4wJ99CdqNbei+7zrSsg1ejrDbILoVnF9Pvy1jrvQndoD87099/
wr9AvvWZt3fC+2BHdjL3XMR2Pk8fZ9PecO61RP9XoucH0blvkWNu+uY58u5N
GX2hyfT7CurSgXI6yu5Qv+7Yv06E/6AvT+ubdbp933ZJt/9bfdt8uYq/b3Yi
vy5QV+5FlzWmW0P4VHT9L3RkmtbClP2R3s8GeTfS9sSehcR6v4H2HZykTg/1
Xkd7B+jD45T9hvZoUPfupG+czZhvXUjzMrwz6c/SnjXI8PVK3tet/d3fa6xp
H5j2R/F8Mra4aT7joLxGG3qQ123qEYm8SyL7PPpug/7nYM5tgRx6cr8XNLu9
/T3I78MJ8uzNtT3kv4z14g1oeWZjvSkufLdazJknS9L+IO+b7HBvZNmr9v+F
xYswnv/hmX+h2VyLJ36fOv0N9dEchR5FQJt11o+61dW3Ivp+Cjo0grRJ1LWv
5N3LOEzCY6oGbULe31D2AKhfurHghAmXvb79piVpzyzXR3I9uY3Do+Icb8Iz
acRj4U+id+mEA+n2e69vKPUZ50nKT+tM9K0/fGOk8S17YZu+r228x9H6VgCN
gWrLl0y6cdteoj97IZOe0ECu9YvzPf3m0u+0pZQbqbNlUFmoGdSdtOuQUalI
+02Tz7S/SttPyCCe3UKZm6FXocHE15M2N88N0byvNQx6OVRrXdYMgwg/VcBy
eRq+QN8GsDvJ1HFfZmPWKYxaZxqgs6/wGK51rG3ZfMqa6SJrgWE8/zvj7HRW
43bprOaA0vaRHUGaR8xno+TvgnQjoCTWKn9gGz7R92DmzMf0fk1yl00kXTxl
Vu9qGh28JlK4OTwXz44hPBba2tlc8SNN/DtVv1cbUb8r5N0A/grXPubaL5IL
8UBrYzEKL255FmPGrePeWmhbZ5PCzzOWxmnMI4v9xY3R9lRLY72VZzzWwV4e
5TdYZGb71Y7BdtZtYvy0n/T7o6ixw+cy5p4vY+yXnciiC2O7s/YAp/sM7Qn9
9oePYM5+g7ou5Lkr8H3011yocXf7NysU53NlN1r4nFl/yh1AXRYm2+/cD+hT
bHPXQVhuqseX1COUduStYWy3fDV8XVzXhf+Vuat99gsHaQzyTcFWtoeexg4e
pC9mwB+TvWlrX4nvMAe9RP1ehPIU9rnsSqWNZS09qImM8qNHG5krprfw/hXt
Y5mNjKKZg/pQv8fJ7z7PxRCfkG551kq0TFdhyydy7UPtkchsrKYl2MDx8H+Q
QXbq2hV97VLAPgc+p5/Pcu3VZONBSp8nSZ/4XdaH/Fogz8yy6Yz1t/L73LN8
Fujsc17mkSltff4vnTkyDarSzbiAWXi2Qhf70hvEGnCI3ndi+yZr/SbdQ3ee
6Wu7cb2nfTmMJq9vqccB6NNOxmnbVsfYbVmD557vkXZdkr8T6XvRO3pHxL3Y
zA4/ke64wmqn4lqPlde5bL03bmN/HXlI8yT3BtLOqfptAYXSX9Ph15BTWcr6
I87YtjO4lsHvkF+1LmXOPw+vTt9Xg2Lp06/Icylt38dg/yzePm/205Yd9GcS
cijY1HsqB9Dm/ln8vlnvnf+FVtH3a6h7nebGHMtAL0prHqbdteEB4k/JxqQ7
vlBnh5gD60BXehkvZksHf/8Rjtx00jyv7020sTD0D+GRyCJHU+NCDaavB2Xz
b2vhvMVEmhQW1pt8DeqecFGfC3VcWKkTu1su17KY38ji8CrswR7WWl/X8m+8
kgn2cyV8L32zehI9PVrac/Qz0EnS/Y1sT8Fzoqu59buI69+jG/8iv4fQLXT3
JjQgs39vNIvw749AIWNabUOmuZFznnj71/o82Vxx4cUJX24rdWyBfOtz7VFz
71PSHqVP4T9UMc7gMOq6I6/9BspnYA5+T/xB//7RyONYZ7PvQjOxO3fCvf95
BvXsj92e0dPY0CGFjQ89Jbi39A/mtW20+yY26jnquQ8bN4a+6om9mEkb8jBW
ZsHf03lJxskB8phHX7+FXXmmjv3X5qW9IVAlyonrYT9Qs3lmFu1YwbrkBPNC
PfrjF3hZntnf13iXTyOzncizutbJjM8hjO/ntG7M6/ekV6H3c9mHi/y3ZJAu
AYrOZoxfccXf4NmKrHHuRrtOy6nbs/BlvWxPhAX3fLqv6Z7CM9o5LjwyxYVd
qHCRto4L6044d01LGkNtDte+0z51+DxoGfN7I8rvQ3/FwncnG/PtQWeTwvr9
I39v2pcsn29zKeMT5PU+4/oGeV2HZqEvh+KMfy3cyMXMl/M1Z8cZJ61uF2Ol
vaD1PfQSdIu5eQG8W6T5s+0cjqEvl5NHw3hzrfUUzhtprrjSKJxKnQtxfT71
fjndGFa9Y41jNZuyP+P5lnXdZrX9MdJmrWOZCANwe1fjYYzgubrIKJ58IhtY
Xk/zTDN4BDq4ANkVC7c/84vx3kP4JHnlpU1PRBpjTvhykuM08r/f2RiTKldl
joDadTEO4dO9HRZvD18uu0hdcte1X8bvGD/fQqOwY68xNgqV9ZkRnRfpSj1q
UN9HhXxO8r1Sxk2diexeSTfec0FoIeEfsRNvaf8S4YnYg4XobprW4/HGnFN4
abzjCncMxvUuS++x5HdqJOX/UNr+vBaTTwQ6/ap+yzCOf6d9q3va98465uCe
jO/BtKERYzcW/dyNbPMxnktzbQzzymjotXTz3l0cTkB+f3D/xdb2Fx+Sx/7j
j9CRP0D/drY/okNQH8b2BezEFnRsAfUsT9/3ZdylQvnop9HIYTRj5xZ9Xknn
E+ir19Nty4SRp7D4L7Tru9re1ygcSmHwTVC76zosnk794qERdY1nlURd2kIf
0xf1yaMhNBdbsoQ8O9KehsxFbXMZz+AP5PcEY34qbZsWpETq2Ap6Id64SJtp
w1KefZV7b8Db1MMe6kx7Dn/T0fecv3PaP84/kgO0AvtdDHtzDzv3t77fst5u
yfNvahzLxpV0WHsfFE+gv5fDE+v5vGd5aDF91I28mjKHRmDrfkVes5jX3yLd
INr5AfH07A6LZ0CzkUE/KLWu8QbXdTEOobjiCVyv2NxccWEyCYNwBv1TnfKq
VQniAaGvqbT7LPeWa/8/ffQWY2oFZS+hbnvJ70Apj5VexAdCC+mPvjy3kjQ3
scfhXRxem9Xx6/Th28TfSXdY/Fpen7MKaE8i9vQbysyK7PbBw9HTgtCqdMt9
HbKMoG7fdPH+Fe1d0R6XJVA+2nQePR9E+ATjLSq7semEUfcuz35OXY9Qv/no
7vvU9XAvk8LttKcPvos+3A0N1NwAr1Ha+INbiNfK7rC48N3eI89F9Mti+Wcg
PJwxPwxaozaxnrgKTaLsO9i3n6Ce1C+Ftryf7nCHco4Ly0br3urM2e9h10Kw
F6sz+Qx24eo+k52tlL/b6vvtr/HGX7sA7ysdoA2pshPo4lfo0pLgPsaF6Ps4
9Dy6ivNU3nf0vonnTqtfSP8BdYmkX2eSX6GSxnQTXpuw2tT2tZK51snpxvKa
iTxPRPr9xawufp8hPlvvD9L9Pq5Mst9jJSHTj7SuhEaS/mPK+ySHwxvSHU+i
Lzph/z4hvjHd2H7C+FP4f7iB0AjtLZNMGa+b0o3LVRoqX8yYbW+0NZ/b1mHx
+cGwuHz6SjdCaN9mns8L3wLfCn2W7vC2YHx7us+FnKGtO9KNIVYNu9gC+VSl
L1vCu7Au+Jx7v8Q43D7RcfkTL8T9tcgjqrjfzUnvCvL8QvSxSbLX4pXaeG2e
Df4F91dS1iXWuneQVyHZJmTSkXgnKICM5iPzeVDWXv5depz57k3KeI++ejfe
YfGUhvbJnx2bsJN8A829J60yz0yl78v1dnhMKb/TGat3U7SvAvYlAxnfYAz2
RN7hOm/DOuxtdGkX+fSlXvO5/yXhZrT5COV3Z810DXnULua54FKY/VeNV9nI
/AB6G067FkMnGPsn9X6/h89h3WCOSkVOacgtNdFylI8mfePORdkFsAPHyHu8
zq1iPwPMSZWp226t0eDPsQYqiS40bmY7IBsgH52LtKcUeSWE2lb/FG573Ru5
7CE+nfIDPPcec8nO2v6WqW+aifLtgn0+wDj7inTlg9+g9C2qtN7vwiPhTZHN
19zfxbPNsVl7CVdhXDfm3gnKPAndp73H0c1vuFe5q+MK/8Z4+lNnmpFVH2Q0
GFv4JPXax71f6ZdStGM/4QPSK2T3Lfw76GC6cdBm0P8/0sfTg1zxtcjwEPf/
Ri8+11mH3v+Hi7Y5GBfOn/pCfdKkhf2vy1f5YZ77IsHvG/W+6Yr20sFfQl9e
hi4Tn9jA/gbkd+BgA5/T0xm917XOgZ6njO955od073OcgB6Fs7ZvrX3JeexX
pgzz7+Xm5hXoox3Q51AV6naJ3y2bkM8x6rYE2Y9EHiOg+ObGJhNG2SLK+LWM
zz9+RrqO1L0F9fiRMrv2McbAUcJjkMmTrD0+wTZlR28W1jHWcqaufvdQJdLx
H7jUmvIvIO+b9Yz3Jx/M8sX8E/msrmdMh2OEf4aOQwMYJ9GUP077OtKNuzan
uf2p/UK8qt6jwiN6+/6JYFjpdP3peo7Ll6x09TD5x6Hf99QO7WHielvS5Cxj
7EM9r/wVPhnMT7iIP9DGo9D4ONdFddyLTELaGbft9bb2I5Cb53awVjjF/dP/
Pw33b/cxKSx8tzPcm0jZE3L6XcXZdPtYlAy+zWE5yKffozL26yfdLcO10rLh
xE+yXv2XsZCOHTvHsxP6Gl/zZD3joAnLuon2pNT2e6siUAQ0iWvf1jI+mjA0
CrKGPsv1WsQrUbfa8HPU+ffmDp8n74HYowvYxrrE60AtoAs5zBVvShkv8Gwz
+BV0ZAR2oldZn9HbB4VS95tljAF6gfw+wgZFaD1G+l81PqHfoS+pSzvqVhwd
qordu9Lc+CrrtK+DZ8ZBF0n3mPbZQzWRXajeJeVy+PUcjsfw3CXSTUYO1ej7
QYy7I1y7zLV/M9kn6NbaxlIrw/h8O4+x1ITVIlJY+GrjoRWk3Uvbfsce75AP
APqwVqTff+g9SL36xiATFll+2pwlzPugFN5Wy/ErlBtDn0dDS0O95u0e5/Vv
9+AauBLj8Rl+N6cyN/yHvQqga1ObGqdN+GxXNQdDf0heXC/X3lzxYl2NRSmM
yoQ441Mqfp17N9JtA75hfP5JeEYW76O7FOu9dNNLeF+D/PZ9zlgMpd4/0U+X
0IG1PPcBdDPd53x13le4JpeLB/eIcu807T6V0+H7wbiwwYQRdkzvKplrH5ef
I9p2i3xuQ3egAtiaZ1l/vQFVQX536IdHTYzjKTy0MdBd0jWqyRyNzJ5DBzqT
dhZ8dFVkwfgeCf+LNPfSjXf2V5ALT64Pc0QB5DNee0KZmzbTF29TRlppY58V
p52Fm5srrvNk05DpaMovS/ryUAJ0nzwfpBvXUWHNkYpHIKPCZYzv9qCM39lq
bvs73d+3hXv2T7r3z46lXcN1ZkH92t1nflaiS6+G2afcQ9K9xTzbhv77WGu3
cPs07Ebe66va581K2pQXXWseZjzPJ6l3LPnlRs7/pvs9rN7H/ke4B323X2cl
SPcqcnjEtdfgE3RGQntWkEtH7ZVsbn8awoyT3CTHFObeNd3tT2kea9lMAcqj
bnWr2h+A/DYJV0t4WpkDJoWFq6U6/ZHTdTyIDLJw71CCfZ/IB8oVfl/Upn1/
kW4L9c7K/eGEs8EntDNumTDPOtPucHQ0e8A+Utu083dK4aLpfYLeK0wta653
C0N1Fk77NNsar0X7Usb3th+uIciyHWuIvMhnRznj/kj/hP/2LXZ0C2O9NeEu
lDGL/B6nXs/CCzMmqqOXCaxzPubeu5S3tKtJYWEDVSnjd9+N+tlngWSv/Jr1
No5balmHVW/Fc9CerbR/S3FjjQlzTHhtF4Jh4ZBJtufI9wyUk/R7GJflQ41J
JhyyN4KksLDLBtJFA6AmyLYj6SbRdynwtozl9tA8rUHpg5xQVIIxx3KR7wBk
NbCt+WRkO42ya9DfzWv4XFk1+jAUOSboDGdPr1vSsFFH2hkTaAM6dJA2BXg2
jv5fy/2E3N6r8iNpPmxhDJ161GUs81pRbHumWH8vEl7s2C7GVZKPU/k3FQZR
l2jfy8P1B8h9eX376o/n+oe0Pzf17of892LLvobyYAvylvU3DeGQXchvXLI8
pJuo8zKh3pOzp6v35QjnTHhn7XI7nER72mQ2Hq+wAYTJKyyyDfWMRzabdfPr
2J/XoJ6Us7id57U0yutC/UICDs/o7XibCj6PK4wqnc+NDJ7RfYI0U3Q+Bjne
I20GsnmF/gpDjvt19qqz5/h02p2Wy9+r9d36O2hxQftxSUaHbyR4LSvsV+F9
C+v7WfgXuY3zKoymElX9nqMkvAjrxSTqlJd6XkIGDSg3DeoX5IrrusLLsc/f
6LcHdS+neZVnorGVsdAG2ryavvgPeaYipybIY39ZX6+Sy/dECq+pbz9jv9PO
BTz7BGMjjHwfsk4u0dL4H8ID0buOLJRVFV4KHV1KuteR0Tza1gmdulLc77iE
5yfsv/Os9/JRp/yi7sZqO0lZJYJc8cq0fw1rz4nkdYv55Q40kPavRO4nNC6R
5xkojDwKQLVJXw/qRj0LEv+HvjiL/oUTLgRVjXJZyv8UlJsxWRa7UDhgvMNK
PFsRehX5jUPW46Ei3BtL2y9WdLhoMD6sh7ni3RsY0+xSFnPhniks7DPFdX8E
aW9hv8uhnyu62Yd4vyj33SXkV0T7Xzp4H/h5dKcw8atQWB7vZdae5mklvOao
1MJrkOT65oovR74B7v+X1bhkH9M/S7raJ1YEdfwFXixgn+rtea54wFzxpY3t
o+3xosakKo2+RkIlSHOGfEo2cFhc41V+z0oG7PvsE+xGOrKIifNvwGa1vL+1
Hjp1t6P3NJUKGPNQ2Ifpif6tOlFnG3n+IrScPl3G2isKvVlEPSbRb8ey+4y8
zr9HBnwGXr4i7yfZX+T2RP9G0neZjGDf7Qi+K5Vv9kXIuBRzxafN7I9BGA0d
y9nWHGYMzqEtg1kv5Wa8jS3sPR7ntWef8reW9Jg4UNbjYh31KRJiW7eVsfAK
MvgMXpUyjyD7avBO8GMan4zr9pltW2VXX+eZ2jofnd/h14Jx+YGWfZStLE37
ykgHc3qffwuofaT3CireTu/PmTd/pG7tgzxAXX+Ad+A34mbK/TSPx8ZS2rcE
WkF79uscMGN8ANc39/C9KqwD+rJ+f6Km323/GHy//WtL+3WvqH1P1H1nXuMp
CU9tBHQqwXs1hyR5v2bl4HeicYn2F/gdbS1LG9qU8x6uyDz2iS88uzf62NfJ
ribGwqzGuLvTyH4Z32f8Dma8rGMu2UI9FtG+Wa19llk4RTrPfJE8s5H/b+X8
G1vv1rXHJzbBaRsnGINJuNDCYSpHPcpDL+iMR8D+kOQXqUSK6/qJ5hGNCcZ0
JfgM5LcOPXkz1v23RefrWEvtLev4UcKHscEvaj+NvpOT/jR0FlqCrp8JxisH
3Le1wh1ukt/xP6nTp9oH18LhqIDjNWj7k9rPnxzcD0x5B+XzTLZKa4UGDotf
Q59fZuzvlb4FzA93dTiuhu/Fw6sHfK1GwOdKawTj+3N6b8OmnPYXJdwtYbjV
5F6paPtkq0V4KjKeDq2p5D0F72tfEm38hDq0ocwNQa54bdJXivI5m25ZjLXd
NYt9mMh/SYD1eRX0vVqI8ZOEV/QtdfqI/ArpjDjXx7czZuDX9OEfjP/t9MON
Ol7bLqMefxCepHNVTb2vVudqn0V3x2KnxkCLKWMpZb4JbdE+dJ0Voz5R+mZN
v72PDuxkfI9ivHYnv67QLdr1J3YttgD9hC4vp+3XsK89Svg7rPaNRhG+pv0s
df0uXt9ThR2yT+/JoNyMu90sgb6EUtDn9tCcYD+rf4W19ht61he7+1klc+EN
K6w0m4P68BLtq0i7t1H/zdjLpfLpkNs+gpdQ3hT93iR+DZqHTNcjsw+hOgGT
wqMo50/y3am1Zy5jSPVsb+youqSpB9WH3kN3bzJ+C6s/ShnzQeE9yGs69jYn
Yyka/auE/Rta31hfwvwaAm8QMK6q5uVz1OUDyjif23P/6fLGSVNY+F+KC/dL
XHHto9vZ1L6SbiL7o9jcM6S/SX3Wk+ZD6JbOMyHvG3mM3yi7MzTe5zN1TrMf
9xtSh0YBY/kNIm1l8rzPWmCX9h+zXo/m3hzsQgz8Kv06QnLRWSjszFVoEzbr
PG2IrGk86TJQLGkbQwtocxjy3kaaz6AmGmMVjZOWq6Hx0IRLJzy8jehQ/lD7
5/gFe7qVfmsq+UT/7wjv/9r1MXWvTp2rlTevjmxG0o7rlD8GPkt7KSv6G2ZB
bEtklPe3TaD+P7Cmf6y0MaqETyV8LeGe/oz9/BGdjaLsyqHGf1Ieu4L5FEOn
92CzmwVMCu+Gcmi9jL5OLWJ7U6uGz3CnMLe2hzIx1h4wnqcgs1rJtsH9yK9t
e6+JtRYWDmt5neVI8V7g+qT9F1vyEKpFveICxh05gv7NZixUoQ05ZJehdyjr
rfbGlvsyr0nhPPl8XfE9ea1vf+Yx1tx/jL9/oXjynVbeXHGF7+R2/L/gfWF2
CstxuvamwavRP5fp45mEI9Gj1vGWmXDl5uubcnvjnPUJMR5aA9rQDPk2zGks
OGHINQ8Y/61CeWPACSekPLSgrq8JS07xZ0lzlfJmwt8mv6vMYWv1Ti0QxCrr
7HCDEMcL8Vxh+qlNMCx8R8V7IKct1HMzFEde6dyLh6fBa1NOXailxjBySwh4
7+j36Gs8drxYM/toalDAGNPya3Er1L6RW5H2e3h+9PtDfTdvYhzRQuWNgSkM
M+FIDNf53lRz4bT9pD0O9M+LpY1LJ3w6vVc+rX34XTyGj3JtQl77SlT4XIjj
rQv4LLXOVCdSfg906x3G7G1sT050/A68doz3BlelHXt6G19N2GpL9FuKcvqj
Bxt4phbzWhrPn0SnQpFNa/IrHWYMtXOkv5tiv6ZDO/hdiOYNzR+dkWmTgsaM
F+aa8GH1jHw4tNGanTGeFDA+mrDRkgkn0O5fsRMXGMSD6Z9u3RweWcHxEUGu
+PAK5kdaOo244jWgW8ihVgX7xf8zxNfEbwXDui5eHbrDOuc21Fa2nLw/au96
DaLvnyB8ij6u1c3h9bkc1jXFGyGzKJ6tXNthfTtVfBX3JiLDxqRtp3U+lAk5
vFTR51N1TlX9sQQZp3DvHmkfpy86EN5AHnWo3zfUtRzyrAB11HqKaxtDvXZ6
wLyaB5tSJN7zxjRoAf0znz5/inl9dAXjNxUP/t44SZmdAsabq6Nz8XqXg43v
LNsSsA+uOK511W8r6pFYxeehuwWMo6Y16nT9/qPf+6CfzbBN3bl3m7F9F7rE
umYw+f4eboy0HtzrCU0KykCyiGF+H64zF8Xsv/ot9Gxle5+f077kqtArtPEv
9PpuF4dfDsabBde5Wu/2Uj/R10e1ZmBtcbWozyT8hP14Apn8DO+OjHrrN0u0
/aD2CdgXqvaVdM5vLLO92a3P0utE6rGGvvgA6oLudkcGT2M3SmMTvkC3a2gs
Mz9UQi7fw/uS30s88ypynsd8vTvJ7xSqMQbSeLYf91OhecjsKNc65TWeX2f4
07RjD+vctIDfXeRPMKZ3Tp0vDvVcOSLIFY+E58rn+AnKPwm1o85HKXsQduEh
47MM9w4x3tID3t8bgJ+GZ8CfRs+6UXZ//b5hbpmhPe6y2dLxgP2L/A+vTGfF
stlnq/y1fsqc+meyfYvPow37WxqzYS82bB90uIl/4yezrloo3zaM9cuk2Zhg
ezGYe3P1vpf6/l3F+8Hlg60LfdW5mnG/eul8oOxHF/fzN91MCus8muzMEK2P
4QWw8eeYF4cSby0fEwnGupSfLq0BtBbYn2S8N2G91c3rOTLQwve0RtgiPwfI
5Z8sPv+2gbVrF33zpJ6L4e8x5uKxX5XIv1yox7X88csv/1963w4NCxiPbyDP
vIeuVNe3HeR/E7s8EjnHUa/hpHmILMqgi+Wgl1p7L+zgUJ/fegk5jCDNq/CR
8HLUsyzUG1n0TbGdmMd88QK0h/qeijdu2xkoAv05QZuK6LwqfR6O3l0kXTZ0
vQnPTmYcjQoYw240vH8X+9mWf+3ryHAzct3D81+18DsDvTv4iHFzq4bb8Ddz
WU7te0e2W7m3D93rT96z6YOZjPvn4PNCvPdAexC0R1h7hdNo27PU+x10YQJ8
jMpu4O/3W5jzN0N18vmbgLCVhLEUx9h/E9nEw9fRF2uhx2nDPn37pR3vUOcM
5LkBWkNex5D/M8ivI+uEp9HJ93WeRnsla9ineBQ8kvlkbMDn7wtgJ0syz82m
Tf+gn9dZa/Wjzh+QVwJ1PISujaDfJyH7iVAov1mGYauGQse4/5P8RLQyP9/K
4Z8JLw7eE0bXT8F4TWxHDWgt7evE+mMO+v1VpG37gAa278X1rV/vVEjTWetO
5PAAmXQqZWww4YL1pt29qhovVd8b1vFcaXTpCGN9HO36nba3oe3FqftJ2vgG
9d6ALjwM9e/u8cHf3trzoP0OT7fxunglfdqusbGGte7T+k9hrau1xp7GmJwK
raa8dpWMyZUdiqB/L2NjHwsYA7wk1JVxMRS7URhdWky5F7QPKLP3oS7kfn2d
EYAqaK1Nfz7Os9zKtA35X2fM3NLefNZxRaBI7m+mLb9zbY32O9AHPZr7DNTO
Sj4HtQ8b1IZ+PpZkfri8w5OQ/wT5aGjk8GMJjis85f/HKXsf+X9BXZfHem+O
9ugI420s/RYBlaTuLahXKfjrpP0ZOS2BP0vbNsFnhhp39Dpj6XnynZzXOvMl
sgpJMPaZMNDkjzoW2cbRPzHw+A4OX6f/N9GHM2jHiO7Gss+TaJ9sE6nfZOKf
MB5zMOayFzDmZwnkVxwqTblLsPdvQJNI+1Qdf3coT76TNRfSrlTmsimE0+DX
GZ9/QB9AXVKMyda0lXmucIe30N/D0NVyyOPDvPbn37iqw/Lrr/jyfMauegs+
McgVf4g8ZpFuWB+HxZNLmev6zLzGJnuC+jyR4rAwyhR/MnhN4anQI55/Ev2a
mt9c8e7y/aPfFrK53exLVH5Ed9PmJvRPY6gAMuzI/QYVHRbfh/wLEi6P/Kbz
/AHa8D3jrysyDtH5RP2e13qwgn3GpxT0d0Wdn70HfaIzufLF0te4fsL0G5jP
Pi/vRdrvZfWKxkDbEeLxPRE5zqCsF8nnJahsAcd1fX4D1+2pgOsq7Pi86HtC
Zp/TO9DH5/bkS0Dhp0l3nPJi0IuD2MZj6NrteP8GkM9+vSfSOyKtaRZFe43T
PrhfV/t2n6F948jnvW7meWjzY/AezNPP8Oyz+s2S7DOY86jPB9iHHdRjDfwg
4zJR9YUa0N7PGvn76ULKL8L8lbe3f1Pu7+ffleKKz9I+FtIlSo7NHBbmnuJ3
tKcWOdyFj6jl8K/aA8gaYxnGYDJ62JcxmBrnc1w6t/YcaV7Btsykrl+EGy9M
4SF9HI8obCxdYerO4voY9Hd0rNPMDhhLS+HngnFhgZXWu1Xsbe3K/4f9dUJ7
UwLG/DoHTaGdVbo7LC6cD4XFhZnzOfNMZuzoVp1/QYfyQQULOSxO1f6HkSas
tFGkucba4O2aPq81rKfXWlpzzQkY4+yFFIeFdab4Pqgo7Yiu7LB4MygCioXm
kvYd+jkXNmJJF+OWvdjHbfmgj3HB5gWMCyWuuK4LJ0zhZdiMcnV8XmB+wBhm
wi17QboLLe9mH8RloE/DjQOUmsMYLPJJuJX+eol0nWhXR2gB4fnU6zJ61JM5
+2XihZHP39jVMzzzCvGz8Ovcn0lbX0HvF3Jtkdbk0Gqub0enm0ND6fPNlNWZ
9DOpazGufckzEUGuuHDA2oUZC6wG/fM8z8+BzqUY10t4arquuO49H7yn65WR
a9kq9rNZlLljUoQxJnQWbyP0I/p0KcbhIoyNtbThK+SxRzYBGYZyrzr6shd9
GKPvEOR5D/1/hfDL2lfDvVcDfp+u8GsBxw+W9/fKQ/AKtGFCjM9XjKWdP1P+
MexPZe53YB5dwdweRbgKdCXO2C/CgHk94DNeWbATBZnvDpNHiuyD/CbpvIj2
gJPmEGP443zGqMpM2i/6GFtpKjKZAq2hzK5BrvhntHlpwHtRhe0kTKfHCxi/
Kx80h7a+wf3G6MnT2MSW3ayfH5H2FLLNydzRIdq6JD36kOvzw8wVj0iyfhZL
8j6Uwfzmm4Fs3yR9H57/jfLeTzFXXHZA/uJkC3pTj8forz7wXNjGE/ompz3l
GgM6mxFweGWK42Wo61Lq9k6y9Tmjr3X6s+B3Iumb8NDegveq5bT5gukrIb+K
sgvIZBj3Vug3W5LP6K4q4DO7TdH/OM332KXDNSxryVm/HZrSj4uoW84a9vt0
hjH2F3q0knzeDjh8PxifSRnvwD+XLdOcCB2h/jdUltoW7vfwFer7XXyrAsa5
Ep7auwFjYunafMqdB9Xu4d8q+s1SMoe/Qenb5TjkOI52j4X2YHs2kF8otnl+
Yfsekg8i4VvqjOr7zA1roPfI/zvmpdUBh0vwzOIQn9erSd61oWzo3aY4+zES
V3xznLGhnq/sfRK5mGvXBHx++nCU9838GG4/+V8nGUtqYYjPSeu8tHD9hOfX
MMZ4KMKSEibKCtb4jajzq4zFFrRpBf11gPRLG/m9vDD8FF4SjB/I7HoXpo9S
2hqDqll3Y1CJK54dWqoz7dI90vbsYb86wrv6gPhV5oD7zHXDtS+K9qxEXx9Q
93+gtdzfwHhtQ5uGa7+zxk4b25PeUcZmWkQ936dfPkXOMxgHS+jLToyTb2jT
Vq7va+XfekM6+Pee7NCUCOPe6P3fiMJ+9/ehxjMy6qAzleh/B9Jm1R5jrvWD
1nP/A+z0eX7HxBbyWWKdKf4duk25I8mvN/m8zJzXkjIH6nxAjM+RzYTyM8/e
RkZh8Oz04Ufk97HeA8ifHLIZzfPrkftO5vwvoMHU/QZ13qC1GzbmKDq4R++n
kcc5+uUsND+//Q/zl+kq8iRZpu7Uvyd5fqJxB38hv3ERlK6jvqmiK2Pb2C9C
8+bGKPqYep4h//VBfi4YHkd/DC5sDKDxwbBwa5R+Y8Bptc9qKH2wlzX4p1zb
FPDzm+FboIGaM1nvvADd1pwmGwGF9jDfFgzXr+x7CosrvqO7ffsIS0v+fRTO
6OC4eCAYFgbUdp7ZAT2tdQP8ofwasF7pi7ynVfD41DjVXoPPs3pPoPYG6jej
fi9eYMx9wXMJzBs74bugLwP2FS3cQ71/E/ZhHHPyXvLczb2LlXz++RL8P+rX
QvvBoQn97AN9T8A4VsKzEpbVV5pX6Oc6UebF6ct68Kw8c5F2nCX/npX93aAX
fHQO44FfZO2xQu91K/i9zAvowXT6cEdFy1i+LLKFOSwumQ+KMVdcffG1bCDy
/F3fJ1nnpkP1kryvEZOVqT46n4ie9OH+4WhjGQrD8B34K9TtSh+H3w3Gh3V3
XNcxG5leYNzupYxvoA7ofkpr22HZ431aB1cwroMwHTbpexHpe0AR2iuFvixs
5LGqMfs7/dORMbyf52bRztG0/U3K6s2zR6qYKy7cBGEmTGzu7z256YdXubYF
PXuIrd2U19/9c+msJzy9of0qyqfiI8bLBvo+nnEwA3k/CjOOlHAThZ8YAV2m
Xgeow7/kWb2cfwtly+5rd6nrnVbGCi9B277l2hT5gdBefezuD+S3WvtftCc8
zDrSjWe/05xCeWf6OCw8wHEx5sIHVPguNuYOdDDgtd7BSvaFIWwWYbQMQ1fn
6tweuriBdLUaGQtKWN/CxjrEc4dll5HBAJ57WMJpagbT/ap90JAcL+1HRvug
L9CD+tT/P/qkLzI4ovlEa/WKDoufgrIjv79pxwOoNDYlEvocOWXj+lnCZ/Lb
F9oPPJOVsioi59b030rq+2PAOFJHAw7f6u64sKPOxhhLqgF12c2Y+In7dWjP
s8jq3XDjiwpnNAHeItE8D+PnXWR/TPNnBYdfT3H8CH31s9oAzxHu/hFO1zra
9m1mz10ftnF8N3U4HjAu0l+0ZZ7O3GSxH94d5PeJ9r3oPSny2wvdwpad0Fij
nbfDzXVmWWG9N3szzOvVftiBf/m9+EvA4ZMJjo9CL/JQ15Nc/4+8fsC2fA+N
ifb69DgUxZq2TyGf6T8VMC7U/iiHhQ+luMLCqlJc3xJOB/xt4Uxw3hzS2thb
wt0S3tRzwbBwp5RWzwgLpGBfY5cJw0xh4Zopvof+mwn9Qh9W1zqUaxuggoyj
UoyHktCblbznbhzyOcz4ucxcflb615i2lLfeNQrqpHRT3xy1d7ic8uLeOa6/
wnrpDcbR0gifX59fxmeWNvGb9alQ410J66p/P2ODNUo0KSz8x5300/mA9zI/
xnOD0c2R8Neow6vQBe5F0d9VoT+xBdljLYvMPUwKC4frX/J5BupI+3/C5peh
TZnrej/zDWxZxfK+pntHoXB0/rlo42XLDkjHvmc98zP38mkNBg8jr/OMq18D
9lv5Ju0vCC+KTtWra/8C7/KbdRW0nXTfoI8taWeOMvaJUCeXz/9r7/EKZDY3
0fspRzGmSzJ+SxMPJ8/fyP8CtnEv9dis842sp4pD1WLtG+A18syGnL9tYz9b
B+AV0J130Lu3ob08+zX0e8DUpq+vZatkrvhFrl8KGJ/rcpArLhyuKwFjFORg
HVAzyXnX4bmz4b4vfiWYVtfFheVVkesfwivD11On3Pq2JB0mfg76hPXKZ0Gu
bzBP0rd30Z8LrFPb0Zdz6b9V2M123by/+yPtqdcagz7d1sHhzh0dv0g5fxC/
HjA+0XNVjUtUi7ZlL2aMrt3YoUrIbFeMSWGtA7RPr0o279XrjPyeRa+iKtlf
0TrSlYBXgFYxrisWMKa2foP3yW8/A/IxUA0+gX6+nNf7NEbSnkna802bB0ND
oWTKe8j4Gqt3HvTLS+jxDcr/E8qNHMoyTwxijXlT8mdN81+sw7eCcWG+SHaf
BelMUHYy99rHv4j59X3ynUc9F1CH0tiYslAN5DAHOVWVTQv4O+EdeCpt69jX
5+jGQZ8k+h3QRvgo7PpdySbG4b8CjmuOblnQ87RI4R2J3jej/TMq/yE25d/6
xsPTO7esff3ebaK+42X3O9V75PUieS2o4jCm5X9xkcL3ubZS7wMo/234PcZK
UZ3Do4wHWs9n87nUP7hemTqMQWea0M6/udcUfgzZHIeeIrNZ5fzbLrStcbVy
YsP3hJsU/gp+jHqn0F//aH0Z8G/brMyXcVwrUMZYdz3pj1as5xJq23/3ghjj
sMvflvxuta5s3qpyMEx726BLF6lPFDL6lzz/RleH0v4h2X2W8j9kNB35PoJ3
xoZ1goY1MX6J3q/kQjfn028h2IfnG5t3I9+51UwKJ2o9Rjsrsa6aR9p05qAO
Nf1+rWgh47QU1DdD9OI4+vczFE58LfX6L+CweAF40XD7RXik+auw8bQ2hft9
j977ZMpAvtjFXKyrh1TyHkpYplX1jV33S6LH3Ffal0HaZTyTju53J68A/Dfq
moXrSeRXpIe54k2ina/yDCC7rFy7jczX1LWvY/k8fp/6/oF9iGnv77bao7Yb
eZZEjg8Zg/9AVeivbDxbtad9XGt9eJS+CiFddq7ngHJCR6nfsUIOd0h3vAby
rA7l4tp/HYzLdZD2tEemH9PGj6ADmfx7tAT6NrKxsV9GwVfx/DtQIeqYm+c3
oBtZsRUPmFde4Pm/y3usXQmOt2XINIZ8ogsbS7Ex65JOJYzNJYyumvB4KE+G
8eOOc+9nKIH0g7GFIVzPK6I+H1MOXZ+pCHII5Vo+KLaUMbTkr7YJcskEPUKu
K6jXn7RtPfNLgdbGIBuL/o0jo/w8Nx7+qfYlqq1FvNbQb/VP4C9X9pnxvEne
+6w90M1DHBaPhxpTzk3W3p92MJ5f0SbGEZNfmrAM+6YJRR7VkHOBDId79XB8
Mnb1ZmXjyzZifn2La/eb2ofgE8hsKfItyb0CPFMcXpU2roxxm/I08XjTWHuB
8m4yTlYgl7eIF6Scnsgse0n7KMgB36Z9yshrUqJt9MZ2ttFZSN9D4wv+VFe3
JZY2fYgsy7NGfoHnwmn/ZPTw82jz8Ay/CyzE9dPU/4OGxt1ehm3pGONvhL11
9gJ9LkTaGVrfJHktWZj4aerWPtmY9oWYE5rQ36Hcb0E9jlKPfPTDT1XtB35L
E/uCz6uzTqRPlG1FVkUy/BstspoxsSQ3fQ/agUwzU7ei3D+OjvVjDn+RfL7B
fnaPNlabMNvkc/8+dvIa7e2o/Wb6Tskz1eGruVcsw1hfm6nbZH1/ULnIcRW/
5zpp3qaOL2Kb/yri8IGujr+NzT6ETApik4qTx2PYpOWUt1t7W2jDDNIdJL9c
6OAh+In6Ph+tc9ElMowhXRJeAjmWgp5AV+Yz5uaVNY6M1o7CSy3OvQaMsSvy
+UH77pf3d+L3uV+LMt4m/wrUd0hH40QJL0rh2NaOix8o47Bwrs5oL1Kk7XUp
yu9dx2u+Xej6TNpSt7bPnc0tauwn+QeXb/BCjOW1NTwOT0f5Wgb0Jddyokef
ys+Q9m1wrTKDdhp2oAGymA6P5Jn2jI/SQV4GXlZjOcn+ytKRdV76LQSa1ddx
XZc/M+GGyJfZBJ2jYy5YRhktocX1HF/Q1d+in4TOFDY/W9jhydiVFMbSRL0T
I95Pcxr1TO1ozCr5m1RYXD4nta6N6Op17ihk/TPxU5RxpKPxG+8h8wj0/ZG+
DzTzubdyGT77tpm1WHPqm8K88U1Fn5nsFW5/89UIv4tur67g37Al0JsRPPsk
47RXUftGK08+18p4fMgWCYerAtd+pU8qah5BHiW1j4Px+i/24m/yro9eP8fz
VxgLT2m9nM/veIrR3qqEe/A7ZD39/Q1tXU+37oNXZGw8Yg69yf0jjIEk/Q7A
vh2oYftYnHpVorwG1KMffRFaxPhXwsVSmv3BdMKk70seqVAZ+ucBtuE+VDnD
PKSp8aSEHyVsK3HhSQnXamqwr4Rn9Qjd+w+aqO8ZlBnF852195D8q2R47OQM
jiGNpb1aN3U0BtZjyL0B67Px8POMnwHUo39jh88F4ycoN08R7wGvSn7bWxuX
SuEdrR1PULrW9lv6W6xtjeyMcK3nBH/bYqYz1eZeub7G3+wRax/m3zKvHC9v
nG/toRTm3PwsPiNemHFcFPqHvCsWNg6dwi9T/wdVHRbXPWFcFStgvLlQxlck
47N+RY/XdehOtQyPpanowFPh9tteobH9uFfPsJ8s+ch6v5X3QWg/xBDanI3x
toK63aA9F3RmWXvGaV+A8tI7Gb9L76+F4VWcNVoDni8Bn8ZzuannQ34L1JA+
YGNrwj9CX4qQpnAr43kJy2uizjzRrxfoi92MmzjKvU45FdHdxuhgU2gY7RqD
7LLl8juWn5gbjmu9A93GfixkDD4sbr+y8ilbi7IqIrvZ5FUJHkMZLyUb00Th
NnUdj6OM2qQ9hU1bz3j4Ctu8FNucN6vPPYYGufbqKKy8dzLO5jWyX4gDpI+F
P077v6QeB7SeJq8RSd6XPVJzH/nWoYy6Go+kG6XvPozD76jbV9X9/W609vUy
tuqRphXpe5FnM/q3PvFjtKlmdWPn1AvyE8GwzoUlQRPI82Jb43MOon3dGIcN
eLZhhnGTuui8eLLtzirmssJBO5S59f9dE1e8K21bQd3exU6MjbW/mxXQk9rL
3sqY5Ne0L4xncmpvaxtjgtVo47BwwhSXH5Ouje1DoxH1WE//nSjisPgD9OlK
R2N6RWc4fDUYv0vb7kF5ijosrt/KN9G1W1D5Ts67sPYUUo9/eK6PvlH1dVg8
RnOEbAD9/zNpplf1O4kZ8JnI6wLybpxh31jykdURnZhSyHhnT8CbZPgblvBw
mhL+WX7SMry3YRs2OY7wUHSuFuUOK25MkniuZWBLU2oZj1K4lEMIN2I8x0Al
SVuD8Vq3uknhl7m2Jc7fuBZS3qgm3l+lM03C1MpRyLhaekegdwXNM3z9heC9
/oy1FlxrCRUj3gJ9Tciwb0352IyH18rh72v3pNtFLU/JdwnltdLvDuowKNL+
9+TXcztrgnvYiVLUbxL61Qx5fkB/dcI2T2P8ZdFePn18QZY/YlenYdeHoz9P
MQaGMD90ijUWVtOixuEUFpp0WHHpbxfKe5M8uwZ5YobDIUVdP+E9qa2KJ9Yy
JnPLosZ8eot1VTT5f064KGPlCvHanYxf+Ay26ukg5U0ztmEFjfcC3qv+WAnP
e8eRWZT2o2M3qsD7VzcfoHfxtCMXfRdd1Wlk53Ihj4lNvFYMLe69IJ8n+b3A
beztEnRxEPVvo70YyOtTvQOWrmhs6TuU/Jjw/Jfkf4k6DGc8tuH+Z+jarzoP
oLkDeS5Axv8V+H9EnXd4VsXz9kNJQu+9hhIIoYYeSiD0khBKSGgJmCd0pSjS
BESagCBio6PSFUQFARFEAUGUJoIFqYoiioKASFXfz/29n9/1/jHX7O7Zszs7
Ozu7Z8/ujP/76f9fI8bRZt7b0sy21BUOT3N8X1Xfnfwm1L6fYOv//EAJFGYK
CPkG3mZA/8eU/14P+yTumOFzxE838lli/X8+whp8dUHfHdcd8k7kKcdabip5
TqP3fmK+LEJ8O/SPZxx8xVxxCllYiqx8qLPmbewD4lRr7yvMIT4bONDRPpDk
F0k+kS5pf5ay2kNXFPLRWTqxmu8b6hyuzmG/igw+yxgrQt3PIk8JkuVuDrft
5fg98h2m7Pt57LdsCvyYDJwgrQnrx1ggnDniLdo7mfBtzbkdrBMvSh/TXzUK
+b6i7i3qvOx8+PY34+O29BttiqH/PwizzcRk1nGPgTdR32jmqS3owcQM+y1r
Qjn9Ii0rk5g7i1Szzdf91PcMemI6cCzK723N5f9yXXi3K+M9Se2v7jNlfyMr
eSnvfIz/79ekn2OQhw1xDnfNcDyaMl6lXYur2g9OOGlDwHVkU5Cx+UEO+6Jq
A43ZkdU5motC7PvvPPwbyvp0ic4R0C/hQLcM26bX/Kl5tHuGfQldocypVe0r
dSIwgTFQVfM1+CPy1qHeUN5bpp9hyPc/zN0/k74WOb4MrgZPbyDn0eBmrP/D
4OGPyFJP2TrsYF8EPaRX9X+uqc896PzD4/BiFHS+q/MC+mdH/rrAJ71sM1++
5xrqDDywE959AHRhHghF3v7l2W/Mz8mUW0X73cSz9bKvO/l7HwVk7ef7b5/R
t58DO3Wms7HPoglPDIZztrQ/hCvA78W8Z/009B+kjHSejSF+n7prQkcNYCs8
6km9L1dx/tda2B5zA/rjOfTy3CK2l5OSYZs5qeB18PNrzZ20768O9tug8Jgk
x2sT7kW+LPA5N1CD8fkvfBpE/XPVDvI9hHdPwOdNjNve4MbIWkt496vO8aBr
2na13/az5E1jTKRD/5Ta9lPSW9+y9GefIFa8JvhJ6s3MaV80/zBvDe3mPfdP
6eqQUvYBNYC5oT8wmXyjtEdD3/Tl/X7AVmRgO7ohhjmxO/KxjLaUgKerdXaD
tEWUvwwZXAFEJtoP1HFk7om69m/dLMZ+nu7R3q/SvCaWHpcOr1fWfoXKkX8A
dTyg7oPUvZ7xepW5PoV4GO/0Y176CllYiUwXbGsbReeppz198nlN/3NIg9bs
5Hmtm2Vesi8bcwPy2Aa0zhF+2NdndrqD03neHyhIve/Sb5Xp/5HKT9rO5pZZ
+W6Q3Oalf5oBd2nzmBb+r6Pv8kcy/M6v8ORCtL8fduisJOH+9NX7LexTsSW8
z0++96FtJWlbwO9C90rGZCr5MihnBTRPRhYSaGsx6Esj/F4z+94TLQltbWcs
QN5b8Ly47gSB66ODc8suA2VdoEvjatmvhfxgPsnclY22VGNeSYDfnYFWTe2z
e2d7+0l9DJ22mfg14n8AmZR/hTw/IA/nefc/6J7HONpNPS8n+3yU7tNL58r+
l2x/daFfBvLeoAz7zRgMHqIxAb/uwu87tS0Xg5lTrvFuGHX2gidv08dDyfe6
vgvAxZHrr5GxEvrfUd36Vn7a+yJD/6Bz+oEnQctk4Ah9PlB3QqB5C7wYmB2Z
rG+/BIvgfxXoWKp1MLwcTtkflHT40QzHZQtdZ+R0Vm4+4ebMWT8BM+DpYzyf
GcSnUh1W+gj1t/ahivobugy86dnc/qr0bT1K6zbaUgI4WNNnFHQ2QaCw/FLJ
D1XbQvZjJt9e8r0t/16vMD5aQPtL4Ay1GdmPoF1PkPab9BfQgL6tr3vUktuS
9q2mfNWQi0297MvooeaQUl7HboCm9UAx6Qrqepz3cjKeR3V2OQ2BdGj9Jq/v
YtQiT3f6KLaK77PI5o3utBTUvUV4eSLO+2VfI1ungGKdHNc+2gz1F7AAOf04
yeczdU5zKLTto9xjyOTvtOER6oyL8H/A//0DBN6RjSjprR6+s6P7OoqPpb6q
yPU/rGevonN/K2J/tt+TNqaU/VKlsCYbDS/eKuk7ZJ8x9x8CiuosFO0cQznZ
Uq3nVtEHx5N8N2B8Ne8HxiE3C6GtGnXVQy/WDfd59kzdP063HfgnKeMP8OPk
qQ/dm6F3i84mU08yba4SvHeu++fxtPvpRNsAkw2WT5D9TXyb/opu3UU9Yylr
Twnfi68Kb5pQTqMS9omksHDVNPt8Gpfhsw3JlNUD2MO8/ElHn3m4R13jM2xT
s3kn240+F2rbxH/pjrvm1I6GoXFOO9/Ovu0/qGa/VBMy7JtK4fSSjqfz3kTp
ozj7LWrNerKJzt+Lbt3HQBZKlLI/q1OU/Qj5Nmu/uJZtT8oGZRT4RfpyHjLy
XBb/b36pnP8/K3wjxPFJlLka/veB33fox8497COrOfP/edo4IMF8F/+39DKe
HAwPQF9moFuzM2azw7NswP7ajiu9TTGHs1V23rqUeyPNPK0b5K14PEX7KRrn
7R2eGoyPpj2fIa+DI+xHS/605tLWVPh3ELl5JsO+p7bRlgPAaJ1X5jvrDO1Z
z7ufAqGR5t+Hvey7axrvnEB2k3VeJ81pHbt7PtO8Jrt7d2t6nXQWeYlCR8zj
3TVdjZ8Lhuejt7+Fr4lp9oUSoB3TKftr5DwHfVEPWQjvaL+kCi9DHrfSjm0R
Xo+/EmO74bpXLnsWulvehT6bQRmfMD/PBM8CngVmAx30r7qb/V/dTbUPLK1l
Ygd4PSNQeAd8mMr6bUNn24ItXcs+uBoNcHh6nH1mygdUjWL2B/Yc/Txfd0Do
51TqmEO5uemvluTJrzMIQEnamxc8Kov9Qmm9KTu7zzFWSyFv5ePsC/coen8a
+Ad05n14ey+H92XvRHpvVn6E5UP4J/UHbf6UfthfwD7j5Tu+APPKXPIPFF0Z
BoUPyDaS/tuzBljLe/9KJ9HXD7UP19U+P+X7U369JnSzjzH9LysMPeUL2ofv
2Pb243scmZmX4XeGsMb7OsF3x8ZD43501oRI70M8SzlVa9vH1UJoX9rPfq+a
dbCveIX1THHhpcHwEp1lYw6tqLOhyNR86noU/Dz4GeT2x0b2UaX1pNaVWaFr
rtYs1e2fZTvyug34rZ7Pw1xHvhqgLwrRlkPISxHa+5z2/cAB5KkKY2Q2/d4j
1fbhOgyw7TqdqdyQYl/Q/XnvATqwOmP0IfWdpc17Ovv5cdYVeZGv9/TftLJt
/MeGew/zOX1v694++F5+y4J0xBO0cyrz2Aek5S3iPMqre37p0N4t3PedZG9N
95/uMAY+5J274Cvke4TxNgBYoL0W1sitgJ/oy0vA4/RPPukqyvqgnW3MXGho
OzMvZPic0ErePUKfbqT8Ysx/R+BjKegpAxSsYnvLsrusOUZzzT7m+P2M58/R
/+PD/f9Gdg2PNvIZEO2z6xzINtYh7wNnaONm8txKc/hoVv+XPwa+Dj+Haf9T
6yb03D1oDEk0Vvy1YJrw/SB+IxguCd87MD7nae82n/djmwFvAeeQ/bNABO0v
Dwwi/AT1p+o+Ku0cR3+nEI6FnghoKJXXa51WtDOUMZch21XkeRG65jT3HdQB
jNGXiPdknVhFewvVbHNB9uxmgcf1ts+lmN72AfmT7sNR/hDadx5enQvCCea1
WXXsm6o1+aeiB2rRZy9n+P6P7Ei/kmFb0o3I8wvPc7RzWPiRNN8d6oWcvUq+
RUBLaOyU1eVdhoXPZLEvqbPMs7PLONwXWJzhsLD8TCms53qWBp2teD8eKJbd
dawsal9QVak7EjnaVsftUzvX8d4SylmaYV8Tsb3tb+JMAdPwM0BzQrpSVkno
Xka+XLy3XHOV/s1W8T+BxzvZ95R8UCm8Hfwh+VI7GSv+Fvzcxxjfii5awfsr
gcrZjF8Lhtfw7bUaWNfJZzEH1/YeZ03692PZGQLvZ4xnIIufgregIyJ0Z4uy
X88wXwtmtU9b3cfXvXzZSFGff1bHd5FX6yw+8avIUEoe30HWXXPdV9RdxVUZ
/j93rbHvZQ/KYtv10oWPUv4+3edj7h0DvZPgVZYY+6fKGuP4yAH2YaWw0hQX
ZA3m47WQ1fruBk/K53Pof+nfMXU0hZ6b5e0fakiYfURl1b2spn7vKfJ9THhN
hn1dyYeVfFm9CbwFrM3wGV3Nw6ep4D54Mrx8u6nhkOyiJPp+os7fhzDW1/HO
+gzv4c9EPmpT0e/Uu7G47R6tYizl0BlPxk5OcLzGlf4ZUt4xijgaYrtNukdX
FV1SDXhJ5z4pY1dZ2+KWHe5f6Md5jNcMdOx8cH3KfT7C5xNT4X2o/rEzBjcx
djZ2MO0T0FHLoWsiuJzOh1XxXDyzqelXO+QDUf6A5QtYfq/k8+o3dOP7kiHq
f6+s9UXlNtYfRZvYB5bynqG+DbT9TSCioOdHzS1vZZherdV6osuTgY361qKv
IpD3+TpPkNVlqC7dJ9C9gtwDnL6JvD2YR1Z0sr+ugcC6mp6rr5ewH6KGMfbV
VJD4i7pfw3s9i9lGvGzCDwL3Jd6nmH1rXYZPazv5vKTOUcaA36aezUCDGIeF
3wEn6vwWNH5F2beos0Je2wydyZp6Rkn7Fs4falt9stlXgH6vha6sCXwFvxYB
b8TYL/ftTvbN/Vq47z1mwqOvC3ic6Cx2OLQMJT0evbuR/snG/Puk9Bjyu0b6
u5jt4Q5CrgcCUVG2oShbiu9SRhn4fY/v7vf0TQM/v+vj8PyyjqfQ32cZj5G6
r0T6VuB9YBswFLqH93Z4cAnHt2fY9sUO8AcaD4z/82m2S1Szk20TrWKMLEWe
J6Abu8LHXpQ/X3dmaUMsfdUYyAbtWYHD3d1X8iN1tqz9tclX207NK6wpWlJX
C52joKwx6MQPSY+jfRXhZXfK+4G+TqWuXVrvMJ9kacUci374i3FRjD7Y28Jy
Moy6VoIX9/JdMd0Zi0Y+d2fYX9eLyNaV7PbVI99E8ls0h7QT8CVvae9xqe0f
AZfL+Ptb33P6Bld4T4bjAxkHmUBHaIrM4vOQOhf5e1AfSReFgW8jJ8Wodzxt
qcx4/Jj3b5PvE/Df4NfQZeOQrc4t7AtA+ZRHMiOf7o/G2AZYOXgzrL79iMv+
lPyKJ8C3veRd0s39vE9r27L2wbW/pv1wPYNcFIRP08DZkP0KyNl+zXlVbGOx
JXgMdYTDk5Zh9hEXgYw/bOFwUln7jHsOfV0AXldV38bYf1e+Ej5/qLOHn1Lm
Y/TtSN3JRG6HFAz6DCP8bnX/496s8njvAHl39LJ/voOaU4AVfe0nro/OPiC7
Ucj4c41sm0526YpqXzLc9cdA3zjGz3qd4WMeqtjSfmW2pdnGlOxLyR5XOPwr
3dxnjv/t7XVZTsqdQfoh6pwJXkW+GTon1NI277X39TnP3oBX12l3R2QrHvwF
aYczHB4R6/gs6Rp48iw4Fv68Td9tArqRJx98LgkUD2LFw+mPk/pmhZbqvFMz
q/fWjmTYD9P/haNbOq5y9K7iR0mfQZ9PB/qiRwfQrmOseTuRpznr22aFHT6W
4fhweHNY/x+Qm8nI+gT6bGdZ+4iTPyjFlf508Jmwnil8D+gGX46DZwKzgMJ1
7QusJHWUyO7wzGB8ZvC5ws81tK2ftdoPhHfdKDc81H61FmjtEOPw/DqOy6+W
fKmmDnBYvsUUV3hlMC4/ZfIJVo5yitG33UN9dusScFz7NeBtjJ2S2v8qbSwf
WAov5/1neF4Ffo4v7bNCp+FDV/33hOaoCt7zlg7Vvvcl3R9CXv4oZR9gt0Ls
H+wFZOVFIIxyVkDLXOR1Gbgh8Reh80XkMA6+x9NXtVvar6Lmv491LiGX7e0+
o/NhzIV30V1zGtr+w4gU24Aoyni4SngVMno8w2d191Huj8jVl8Qv9bQOky4L
Q14raO9I5/YZg/3QcdXL2cfgLtknkmxCz3eEpzPnb4fWJT3su0V+gpJ4Lxe0
5xTAj4XI1AvFbBe/F7RNRbbSyPcFdE2vaZthn6BztlLWN+G2zdZS53bj7Zfv
O/g1k/KnlLW/nJq97SNc+0u6bzqgnO+cVofnX2lOp51HmPMm8H4iffNMW/se
lQ/SGHRQPaB2eYeFt5LnZIb9bMnHlsKVszuu8Nxsjius573qOizcvbzDwsq3
BHoHkJ6zj8OXujguf2GTgNLxDgvLf5h85pzi/cW6Z0cbf4UnPeo6LNwd6FXK
c1Nz6viK+EV03Hfw8t1I75fIb87XlHGfMhayRtuQZr9djbRGRS5Wka8yuDT4
dEnzM6yP7S0Ured/XAWA34BvMmy/9R36YgG6cqHOA5PWT3Vm2MbyzCR/59+A
72OQtyeA16FhW/b/7yNL+4mnM7y/qHSlVQaeJvxNOfvMkv+sqcF4us4ZUsdR
+u0ka4DvefdMhn0ryK/Cz/2Rqyr+Ryr7D7rXdTbDd7v6My7OER4f4rnoB/i6
NdLneHSe51/Szmv9qDtoGf4+aKjz1PrHBd0/oie79rIvrL7UVwA6R9XwWrQS
sIn54CLv/ZBhn6vyvfoscEjn1Gnn5PLe20lr47PEv9GG3dLN5NkVxIrr/9+c
IrZHpH8a+u9F80Mu0OfrdBcS/CN1NEbGyuqfNd9gHYF90P8vfdaDufwZvqHy
096XdMeH/JfIf575uwvl/0T4Ic8X6pwN/TeVvjqT0z7BXofG7LpXldNrTq09
Za/wVfTTKxXs31f/1+bBi/208T4y8HOGfXldBh8F/wLOjzzfhreV0B83E21v
MIzxuwldEN7A3wql4N8g6Olb3ra+LrS2T7X+QGKK1xLzgN+p/wnk+Afq24gM
zKE9c+iPvhUdfr6p49JXuhfQmzX8FcKP6y4rZU/KY98vDXTmDvoiWZ//muFw
v86OZ6f/SxP/vZP9Z9VsZh9ap2raj+qH1J8fPZANHgwC54+3/yv5vVJYvrIU
F1ZcsrFNa2X0zR7pHNr9W4b/dYvH8kml/YSdwH+UfTXDYeF13e0X7/cM+8xT
WP7xFN9OmR8Ac5HRr5D1+bT9bG+ft1xJmRn05SDSO/BOT/p7P+uQAzr3n2Gb
WPKdOwAaQmnvOuLbezis8a14NuA874+gX6/xTkPk4Gwu0/R6kObp4Im6e6Nv
6yBWvAPy0hg57FHC40VjpSZ8mMHcU55xNA2clN3zW/2OLltnK/Pw3hvo+nzw
/k/Kut7Sdgc150ygTzqQPrWe/3W8yDg+VN7PZb9Kc9IHff3+TnBVxmWn6l4H
10DOCiEDe+n7tPb+hv4OWMB4nAIfpua3PwH5FfhrgP/vFdcaLMU2ImUrcm4B
+wJ8bYD9Bz7exH6cnwDPYUzOQsdM071FxtJu8m6kzcMYuyt1Xknn0KAvkvpv
gpvoDE8P+3i+RXyp5sO+9v9TPNr+AcpG2neIzlB+TpnlIp3WFD1WFtl7Ez78
pbWq9gTg7VvI+5uh9h+XXf9jgay057bW9cDseIfvBOO5KHcWOiuys9f5WuPv
593d8LUB9D0IMy7ax+ER0HeQ8ptS74EgVlzpyfEO382wvyz50VL47XqOPxNh
rPhw/U+AH1HF/f3RU+e/2rmee7yzB57s7mGs+FTK7sPzpuiwf6irdAW3/36G
/dU80PzDPNSA8D3KDwd+oz9+DbH/oRbx9g90JRheBx0Nqbsgde+BdytIK8+4
HlLf/ol0zqJzvHWEviv1fdkIPjQEplJ/Tcks9AyHf2sZc5u19s7m+e0htFwF
d2HsdwU6spb5Ejl6nzaeAP/D833UVRGZj0RnfUQbt8PvuA7eVz/M+CqA7i5L
/R+Xtz8t+fGWP60zjO3FtLsa6Tuh/wOgLrRcRB7q0aa6EfZxpTmxJfgZ5O9Z
1v4l0FvP5rL/sgedHZYfM8UFR4Lp8nt1doB9YR0InlfRuZV/oXkDYyON9LKU
+Z++0+HVH7QzK/R9Q1khAda/tGG37rPCp+cZ3/OBH9F3y/U/A/w9MnRR7Qjz
XZpX0fGbqCML716h7l/SHBZ+JtV2j2Xz+DHmmOGMswph9ol1Kbj+lH0U+WmX
v/Y9tDcPOmQ9dOUC36Tdo8g3pLNt2IzKZzs2IfTJFnieBbwbfnXlWU30yi3W
Izcr276F/COPqGub3vr3rzMAFyJtd1ljXuda/9W9Rn0HoQu38l55+rkRdCZQ
R4Vw+1L4oq59G/0VYZ9NORM89ntor4B+TIbXF8EXgFR4cQf8L2W1z2afRIN6
2+5wMjo+Rfev4MFJyv4KqMC4PcC8e4Z8B8ErWLe8zbtt0UFZ4WE2IJ22belt
Xw9ZtMbu72dK/66jfZa0553D5e3T6SzwGrSuAN6qYx9U07TeCDgsLP9U2ROC
OOC9Ie3Ja2++FuPkzQ72tXERvhSQDOpfMXVdh2fXwtz+UsnmR44w/7tW/GZQ
N+YM5hEuFcwjrHhhxltJ6Aql3qy89xq8DQHH0/8laX+rIM6W7nAY+Y6Tp3qC
w1/GO651mtZoo8FRyGZ9ZCh7unGDYFi+vD4EZsZ530Z7NuEB+yaK7Or/T8KK
DypiX1TxvJsj4HDlio7nDJimEq0cPhDhuMJKyxVwWLheML/w/giHhfVObsKf
ZjWNwgeDYaX3auG0B+Srx/j6N8LhS7Q1ppzDwnr2Y7x9d6m/TyNbFZC57+s5
nCfd8eH05cfa5+nsdPnm0rMXdIeaeTCaMdmPeTW71ii0IYH4WXiRKX7wTgvN
o5rLoe0Oa7/jrBtj0Dmdkb8EdNa1CNsUucU4/AX+PomMjOltX111y9k/l3x1
CUfR97OQ0a/Jn5fy8gH3yDuH8lYA+aUvyJvA8xcYC4mdvecrn6vT0C23id/X
eO9j35DZg3J7KCjP8hspUFiyfoG8BQj/Xsa+vYpqLouwf6/wdKf1oMzfq9hu
2HnSJlH2y4Tr5fB/v/rg2fT/GPTfQdp0hTYOjLe9Sa037qOXonR2k+/mv8mX
rn1IjTndkwJvb2tfF/JdId8m8nFyFSgIXUPg7Y+8c7GZ1/Na15+AnqwVrFeG
17e9xvXoq6r57VepSn77tRlLO7+ItT8wfbfrm10+ueSPK5ZngxKMFV+gdbnW
TAH7j5IfqUrpvp+qe6qQE5Kd9V2Yvk2p/2d4PVhzE3XN0J4g+Z8Ps33Nn3ge
DU9K8n4h5GVcgsPC8v81NogVj0K/RgO7kL8j8GUTbXwTXb2pnNf78TGmWXQ2
BgpDXynoTIav71B/Jcp/t4LDRQKOK7yxvuMntR+tfwWEF/CsN+m96jv8QjC+
uIN9eMmX11loKEbeMzoHR911oCEm3n675AvthwjnV1g+0Z4PtS+v7VmdrjL0
TFh5Fb5H+OkK9gmmcGaI4/qfov0Z7dMEgml6doKyipNwQnfvGhsrfk//Znn2
ufik/xiV3Me6162w7nn3hNYq8PKxZk4vwXsDkn23dku0/7U/hzzNB7ayHj8Y
7rtfowtZdt4raflJpm/aM6+203lk0gP0/S7WQkOL+Rz+MHAMdX7S3bboS6pf
AvalNoZxWZVxX4jvt0qMq4pAaZ6Noqwm0PSU9hJIe4I1whDdDSL/SWj+Fh0b
jyyUIW9TxsPXPK9DOTHF7dPydpr9Ws4kz9u6b0B5mQWd72hX+26T3zbJZ1nK
qI2c7Ezwnupe1tXlSJuivSWgPOHXkOE3gIX1HY8AXiJcEd0/EB4MBnZRXgXp
Ieo6Ws/+J/OFO6x1muLy5fRsgv05xaGbUyjjju6aoK/SgPKM+2fgVwXomQZ+
k3lzBP1cmzXASvj+Xk7va60oZKx9rtGig3pX6L8x47cAbWiK3k1FHpbAm8qy
P8H7B4HRibYntrynbYr10bco7z5VwX2foP2PZMuCwkqrTHi27v5S1+ex9uch
Xx5vQFc6srEK3Fo6ooLfqZnuM56dCto3n3z8TQMWsg56GlpLpxs3yeFwI9oc
SR3fpLkto4AqAZ+5rwrO5N0ocDUgOoivVnZYfuHqsX7rUtp+P7bQX88k2jeg
xml18jRDbkr3sM3qgZRZI+C7WS/y7l993Y8ddL5aZ0zJVx9+1QMuhTtNz17X
WRV0aE3erRXwnYJXgvcKItHvlbXG1Dla3k9jzu8HEPzff/RSzI2/Mha7Q1ty
K4fvhDoexngIBSqxJmkNTcW1V8k8UZO0TdBaK4g3B8M6g3Mkl78HdLdL97p+
DqaX0d1s3cOFvk2sN6fQVzcT7NNOY1V+uB4wz9YJOCy/eYrLhsAN2vin7goz
NxSFjibw7niU7QPlKWTfOPKRsxDI4HkMZdTVXEk/1AOvp67+nXyWRedYrtOO
UPLNgrf1ed5I66Ji/ufZIGB70i/ldlzhgfTZq7Rrl/RPuP2a/QKUJG2WzqkV
tr7QuJVvsitaq+ieJf3ybiv7DkzS/T5k4UE9r5V3S38iU2/H245TEWAffK7G
OHmadVt0Hfv3G55sH39jUh1+X+OV+akF/fszc/R5+qMhNFeva5/v2s+S33et
j7VOlp8/QVXqP6t1ZxPf8dOdv0a8N5y8S+Fb2Wj7E9E/n0N5GZNAD8bg9/Ap
H/rvTcooDM2FgBqt/I/riRj/z1Jfq59nMhaaMK7zUseWbNZdssEl/dUJWouh
h8Jpw7p02+hMAGZT/7O6NwyfZ5f3v1n9o5WstaLuEuDGAdvL0hmJdbzflrLr
dPLZFp1x6YSueo86Y8mXzHh9lbkuERpfLuf0rcFnTYA06HmPdcAGdFcK5UyE
hjat7Ct6XW3bg5ItqF3Aykj7UpIfpaa8ex9ZvAeMYsxURj9cRQY76H8I8vG4
vpuZ8zsiE4nw/jhlLtLaqYn/BbzTy/8D5sCLIbw7DEhKsB+gQvD5He1jMTe9
C64nvUfa+3z/vlzJfrfkX+0G8/DOePtPjoZnbeHBEuprjSy2IRwPfiH4X7Mu
ZTWD5o7FfV+qt87cMf+939n3BJvzLA74Gn4epR0fooeORPnuzooU256bqn0G
cD9oSAcK698I/RGt87+U86W+o9FtWYB59FudurYLfaSifXF1oN7h0e6riQ3t
U0z+xORj6/0gVlx+kvLzPAY+Fo22XYrXmQvjKvsM3N/w6TX0V1fgFnzb08tn
pOSfpiDvroy3n52+6J036b+VyFkL2jZf45G+7k29bcj/MNnpSmupeZyyTlP2
j6Qv0niHly8D8QHbTe/M+K0CDVHAAd5P0nkw+NEC6EtffgptvSjronRcRftA
EyhciHcyy3tcFwbGkudf0qtoPmEsT2zg89MXEsybDYzp6dCZTB098tlXzUfo
4t3Ap/B5JvPpAemDin6m9IK80y/VNi43MGZaQXc3nTuk/cWBYsU93rJSfhZg
BrS1Js/InNZfKejFnozfTvR3G9LH0V/5kLV5eXzm9BHybKEf2/IsN/gM/d6/
gv37yfdpgyz27TOAdmwHh0HTMcZjC+TzaGv70ZTvrBk6Z8U42YWMjWhlWZLf
K4WF5QdL4VHBZ+ehtR11riP+dU3vn7YKt4+FnZWDfhYa2HecfMj1RQc/jswn
xjrtMebHnKS/q/8y9FE76H1Rd35pd7GcDgtvTDQoXBTg9ZCG2itCr9Xm3Tb0
xxj0wE6dTafchbz3PbK+sQRrFMbTb+jI3/P6Xum9Nv7PPR/+b0F22kN/GHLy
ObqzMuWNhW9/5LQcSAbOQVciPHsZfV2WtC9p01We/0AdW+jjmbRpgfa7dEY+
l3Wq+mNuHv+j1//5KtSdTDlbGNfdoPsF+vtBms9V3dTYo90dpAOATkDngM8R
q38v8I1Wkv46z/tTOtl31BXGQE/wI8THMf8E+tuPVELAfqVGBsOdK3u87GDN
UZK2VAf3oc73dD+9lX3jjUs0ln+8ccF04bHAt/A5qa/fGUeeu8joePBa5Dg7
OngbPC5LvAxwMogTAw7rufLJrtn4RL9btaHDwgtyOiw8AdwSng1Nt45UuBXQ
SPqSZ+cq2Z+b/FgVBTfM7fCOSo4rrDT5uMpR3z6t5NvqVg1oYT2Tznr2H3TO
f/18byWV572Bfuin+sjBJGhbTP91gfai0Huqj+/Q6y79kT72VSe/dTeB54P0
iu6FOY3VnvBGvv9xSXe6qW8KkER52aBpD/2XHdyIZ6HZfEajK8/u5LJt1G6E
c5bi2ws+J0HTdfp6JDr9Fs9ulvP+qPYitSdZJIfn+3rIcRIytJJwd94/Il2D
3n+admewJvtTawmdVdZZlTy+k9oj4PMvbRv7DMxQ2tOXMpJJ7wmE6p4BkItx
kyef/8//pfum2e3nSP6h5Kvqah+H5SdKcX2XtUG/PUSPlkBeigMdezosXBKc
QvkXaPcc+PyIzul2s4/QUN1LpeyDjMkIeFYeKAovxnS1HTDd3b0UbTslslfS
LN1nB3SG4Ndo2xLqzpianWh+iC/ybzU1j31eiYbrfUyTwmN7Oq5w/gTHVzFm
VwOF0HvLKedX0lMDDt9p4bj8Ww0hPizR4V4Bx+V3rIe+r1o7PDW34wrLL5ni
88m3E7yoocMf5nZ8G/Rn05oR+v9Gxoai2HpTbh8gHv60g/9L8tjf0/o89o9T
CN7lj7QtftkFmkebFxJ+AXgWWenLu3fp334B81z8rp3Vvr5qASXg4VPp9oU1
KTHoFyvRcfnJSuOdDWUcVtrrvY1l91bhjxgT/9DfD4HZ1LefMueU85013VcL
gCuQtpfnt5gLwhLsz0a+bM6iW4+iF47Xts1s2c6WTex06uwPDAAmy+YcMjG0
mmUwhvYVEx8Szc8d8OI2svIqZf4d4XH3M3U8ErCPmH3MA1vibdNimWys60wo
7WlJGZvAeci7kTZcSXf/S799E2J/WGcp7xB4Jn1zLLfXoXmlP9HBWai7veY7
IIKx8yQ8DiMtNI/zHc39//f3hRVXWPh4sCyVqXj7XF6Dfscc3ktnJuDfk8hx
L+aHDK1pWgd9LjIOX9JY5J1HEkxLHeqvDWxn7jnX1D5w5AsnBNrToSlLhM+/
vwwN57U+572RjKnGFey3K0D5mQGHheXHS3hhosN/814neHoP3BEcq/vupD9F
HamEhxKe2NOyrzGg8FPB+JBgPuWRz6+nc3tNJn9VAwP2WVWN9W5neB6gDxqi
f06xNtpHe8ORnRLQOgy4rXOM+j8R8F0B3Rl4K87/RwpV8T8S2fu+ojbybtOa
xueA8eiJGaz7n8zutErVnfck8vcOcvF1PfsDi2tk/2DCgwP/P7y4iuM10E3f
Qv8gyhuFXvuLeDvk+TPad7CnfV7t0XlzvkfW8+yxHtZp0m17kmy7pY/GBHyI
ok2LyFdKd93qOK6zpUu0bwo/hmg9yNx0D70XS1lrWcdkQ24/Rfar0p+h9N0o
nvVDXwwl72jaOwqIp51vQcuT5BsWcHhhJcdfpR2l4feiKg4fS3Rc4RaNHA+D
vuEBn8c9xbvR+hYgT7Mo+wR7jj4Zz3fVKmidAE6nzpnonmeBj/R/C0hmDfCo
6mZMN6fuxwi3gNcjgljxktU9x4zUWj7g/4a606y7/DMIH+J5U/r4I/q3PXza
Bd6L3FdjPRYVY59qzdC5owP2kSr/qPK1JqxnCv/AmJpOf00DHtc3E215Iljn
Jzxv3tcwKpimcItgfEhL26zqBSym3/rRJwcZj3/D81r0yx1wa9rajeehjKWC
jLnF6IQxPBvD+9Og9etStiPVg/n2ffJsZ01xkn7oiCy8Sf5PyX8A3duHcpeX
8XdJh162W/MkZcxrZvtxp6Ltc29swH73/gza95BNOMQnpH6SbQg2QQfc113k
ct7rKUZ9z/fz/6IU6BlH/61uaDuE3wKnmnpcf0O/d9fZUp6FRHnva0NF+yYb
3tM+1eVb/TrzxrUW9ue2AHqfQtZfKON0pcm/W5e+Hg+6j7sDfb2Gcfk8sIjn
XaVnactD+uNBbvvx0/wl327y/5ifuvMBEdC0B3lfo/NFTeyfaFBt+yg6zpj6
Mr/P9DRBVpJpew9gHWuUVN6tkdswDl4Vhw/jtb5pbPuwE/UfDJqeAt9FDo8j
y1e0RwA8Al0fkZanhG3CFqxnf9ynI+2Te4L0GvBUwH4GZGO2Zw7PO//18dxT
l/Yf0v2LePsWewMohj7bSB+f620/KpMC9iFXmzHXHYhmfu8BLgx/JvNsSsDh
7xIdL0ebu6p/gCn0/VTdY9Z51YBtKE8Fr4E3r0H7M9Lh6JIx5EkDz9A3Nn06
E5xGHf2A/T3Ml5pBPpWHBxHANN79lf48Cj3TCU9CDn9v4DvCV5CHX4As8Gm/
zg5T117wDK2NtXdF+kzCB+mPA938THlGd/Fdtg/prw1t/J94lvLR19uJN85n
32ApyMWzpEfTz/ngWUYr+4FcRxkfwcto8n5I/7zEWArAw9FFkJsE+yFWfZoH
48jzbiX7mJav6R9aGz/U/JngOyG6D6J7B7pzoHv1lZAFujZkSILvzU2u5Ltz
MbR7BG2IYJzN1npJ303w8Gd9j/DCkEjfAZ8b8D3waObsnpT9XMDriML5vZa4
QT/v0X/mVMNHhPcCg2lnX2RyiNqbYlutx9FVp9AnxUUDeb5iDC1Fvn6nXQ/o
z5Zd7M9OaS/Rj8uC+L98DveHpp9pWzfqPUk5ebq4vPGt/M9D+wbzoO879Oq3
wHzCCYzR5l18R0R3RfTP/3nSFwC54Ek7eNEBeCFgPL+nw+2CaQuBtym/dpLb
rW/YBcHv2JcYIy/y/O98DifEOf4QOh4AL0lukYO+9MPLWp/C7x3knVzZ4Yi8
jiustPvg5ejk04zjdxv43NHjCf4XU66Z/8Wehu9/8fwma8ib4FcCHhMaG98i
193h5aPI8deEj/b095HC3wbjAoWVZxH1LwFOM8aWghfrLH2603ekO95NY6WQ
59Zk5CCedp1gLB5Gvm638Xnx5dD9KjSs0B0Myj/Fe8sK+rtHa/Fz4Meg9Qfy
Hq9vrPijop9npRlfr4KPUN5W0QgejC5ZTvtXhjp8q4Xji6QTgFfQqz2QpwBj
ISPRWPGMFvZZoj0O+TCZks/jcw/8W8J7lWhLJPA7MjERGv/oYluZspmp89Rd
kY8Tupuh83jI71rgfGHbgvqFspZq7YhMLgB6kqdxAcYIfR/fyXaSl+n7Cain
u0zSVY2MVwbDj0da7/yfbYJDje13L534b7RhBHW8Rt7XgbWsCd4A9+D5gPy2
k9pfd1/z23a7bFt2Zcw90DjSviv5xva1nz353nuS8JfUdzzSYeE6SfbP+ckA
++gcwHzSuYJ9s0j3hQAnehqvCjjcq6/DSsuPnBUAXkYW59DuvG2dtprnY5D1
NaI74H2ddUH8WGOHbzCRH6Ke6+DP8rm8rAUdVh2Kp+isOOHUAg73AuroziQ6
Iw9jvQJy+Ghj7x2tDzgsvCFgW4iRwFVou8bc/yZpdenfrpTbGr2fpTvy0di6
KUPf+fRZE9lEaWMbnusp/yfG9rIq9uMjfz4PWRONIG10FuYS3q0O3OK9RujV
9ZA8XHu7hbwXor0ejfv4ZI/9EsjNW9IhlH+TNh/MZx48gPejkceNAd+zOgds
Cvg8tWxPNaSfouqZ1j9oxwrm29dka4U8D2qZJt2l13flGaAFc8RmnnVhHC+j
/MXIxwXmkHdIK0JdJVlflAA29LSfwCf6GuQncHpf15GZzzy7FgyLd9Kzs+Bf
FcbrR/BjDe9+x1x0kjyre9qm5LvkSydfms64MEZeh1evFbff5Sa05yzpryXY
32E+4B1k5Sa8+7C1z7S8x/v54NfcDt4DepHw5619Hqk3PEqLsq+3ivB4PevB
k9CxJWAonuI0/Q//Ah7H9rH/QtmMiuQboR7vtKKun+FHYcbEVvK9r7VNX9uj
SQMaIRtvE28MPljFWHH5n5K9tZbgCa19D/8x4Hvas40yLpd2WHgePBmErDTi
ecO2DgsPBndE7nJSf3vwD+S9BASqOiycEQwL/1Ta/gEvpttHoMKlUhxXuHSK
4wrLl6DiC6hjJe0tFwzfyO+4sOILgdHQvwT57JXba6CIJK+JtgeCayPiXRk3
i+rZFq/at4b3VhfwOci1PHtT61rg7QTvEf4n+1wt7UNR4Topjk9oaV+E8qco
v4TCih+uYt+A8hGYhI6diO4My2X7tqvp61VB+3bfZrONO9Ehe8APqf8d6nwX
mNTVPh0vJdrHY1PWnTug9WnqfK2abWbLdvZcniXI3gkyMYo6vqN9Q5DpZpQ3
A5q2Q8t3zOUf8O434JZ5bVs7Lq/9DxYHBlNOKcZySWAn+fIzh19hbfYLcCnd
Pgnls6xeMduQ35Fg+ZjY2vLyYcD+sCgyZBpz5XTgHnScYWx8D/Qo5rRW6U7f
Rf7VxCfIDi9j4Wte/Dav/y1FUFcF4EXmqN0B+wFRuvwB6tkC8Eekr4Jvv1Le
HsIfBxxuneL4AurYx3i4QJntaUNvdMzL8HMVdd6CR2uQ+dqs/6az1p8BPEu7
fyL/5UK2876X+hrqrAVt7AdcLm4sm0v/Fz5A/y7qaRtMiiv8SYLfl734EZQ1
BT30N7L+CTTl1Xly3ilFvCTwBeGbFY0VH8l33YactjUr/4Yb+toPovwMygem
fA1qLdOjjdc9Cn8TjHcGD0H/3kamssGvrJXsO+oBZT8Pz/YGDArv0/qX9eV+
8LM5fK7/nTif7T+lO9T04c+MndXIwAT08Bz94yFvz7rOqzvRF5g7QvXfh/Rd
tPUtaLiNrK0F72HdUpV+aEmeFkAMZbaG9mykvQXve0NDIf2To3+LCOijmEK+
96r7r2OZ41/Qv4OG9gf/J/23LdHflvoGlZ/4L9AXqzXHUH8Y74YCnxEeCq2z
qGdYEB/v7PAlyvqxoe9fqr+aB/vs6y72IZmUYlBYfiU/gYZp9ENW5pOppB+i
7MrMQ69ksS/ilbTz84D9Ccq/kXyPyAeJzvJtgpdRqf4X9AV5Dus7qK3Dp/s6
3jSXv3d6B/egtfe8QOco6MNjQA/mgsWsFxcB4+jLI+SJY5yVaOB/sLJB8r/x
AG+zAkd5Pr69z3FMBi5Vto0wtbVLF/ssXNvW6zzpIq375J9LvrkeaeixqDGp
saGziJVpwzmeFeb9efRLEXBnvjHjdG6nnH0KyH+B/BgcC9ivoPwLTtW+r8Ym
Y+FP2nRa53h51quR9zK1p5mP+bsjc9/DqvblM62qfft8Ag25WXP/1NG+D1Vn
dnAx3v1S818j2xQLpZ7CVR1W3Ypno+ysFX0O6wRpXdGzSUBEfvtf6t3ONjND
0e3h+rdOP73D2vyo7gZF2bdh3yj7OUjWeRygF+08AJ0p4K+C31DNoOFARd/j
aAocKe/zzj+GGSuuc9DSEQvyWH+8Svor+lcrmUbXLNQ/kFj/t/yijm1Tqo/U
P0vRU3UZ+y0ZhC3Kel6WT0jNE/eQ+ZPIz31wDvp6ILJan3Fxlvb1gaYf4Ef+
PL432T7K/xr0n+FJ2jK6jeMKnyTtI8lII0N33p9Dv91PcbuXaL4ifz/asbml
w6cCjh+DX2/JtgLwZTCstB5lrD9GkfduD/pD5731P5A1R1toeSLWYeGiUX6u
fHeATMbPDfgXgJaZjJsTjPEerDEus36dnZU5CJzU0Gftvw7YB6b8iWnsLQSi
aW+NEt5z+UbrOOkb6mkL5Ktm34lvxtp/ovDFgg7L76F8Hh4M4j3B8FV9JwF3
0IHPQOvUKJ9vkh+rqHT7+Iql39rBzyjCiREeexp3ldB9e3SODjyLMXCV8fSV
vlX1nR6w/ZTL5AvVPzz0yWnS+pO2Tvaq6M+5wEj91w54H0w+DgXaF2sJfgd+
bAb+hL66yMSO4v7vHd/cNmLGkueW9pCo4w70ZSdeFNnfk8/zguaEtcAg6L2d
1XeotV91JmD+KXw24PhK5CI/4zc38CPjrQ8ycgk8DLqGwY+h4g39PTzJ4WFB
rLjSnwk+a17WPh2vM55nQ0tu9Nsu9Ft16I8GDpa1z0T5TxT/M4NYcdmh1h7E
yDT31/89H9nMz5SuM8ryL984wefddK5tREHfBWsQvA+WjTnnHG3amOJwpwGO
v07ftMzm89BPwItr8PGP5rYx+2ac7d9OpR/P69sw+P1cBzm/oDVSSdvgld+h
ovRfHmT6Iu/+xbrrIs9vgxvAj0ZRDssHqnwyyyeq7LRMAj6hr17mm+oz7UUD
i6D3lGwHoMf+ZuyN5Jv+B8oqSdlPUF8pcAHG+HuF7P8lu/Qc+ZbxjXaM8FT0
wBvqL32Pwdc11NcJekMorxLte1Hf9kA2xvL31BdN+15F3x5GNhaQXhjaxlS1
/9E9hRwWvhSwDcznobkWfK8EHbWZu6fUsE3SNMbZLMbHrEjbXtQZrF+ZK+Lh
dbtstl89tpl9nchmUsWetpt0gfI/RX73A7Pg5Z/0TyPKOdLXc/oKyhsO3aVZ
iw1hfrhP/R3R3zfIP4H83ZCr4tXsEzC0q/0C6vkD8hWm3acpf1m67S/ORG6W
JjmPbFj1RHbmgbvrXCz0LKa+T5HRALpoIFCffBPhywSgk+xu0Dc1tG+LTu6s
++PMx2nI3RXG1mOy70I/Toq3vasp0Fy+rP1E7Kb8we1sz0y+FktE29/iFzp/
rHvjtPmTwvbvKN+O68jTQt+vUT5DuQN4MYh/CjgsX4QKt2vnsLB8E2am2v9i
duCXoP7LW81hYaUrj7Div2lvCPhG939ijRWXvWLZKh6OPupC3pPQeCzFWL4l
FL4FvEt4M5AV3v+svSDC11OMFT9FuCvvJxV2WH2leK5+9kcpv5Qt4NH8ePvX
UrrS3osyvhxwuDljYhEyUSDFPgQvgsOaOBzV33GF5VdQcd111J3HP9DDicwf
45Hz/XH2Yygfho3b2b9heEH7NVRYz7JA22pozAEda8Cr6eNftC5qa/+jwoo3
QyaaVrL8faa9uiTPDTdo961C1nOyFTevttdq9Rn/TaHrbiGHr0Q5/n4j30cc
w7pjI2XMi/J319/kuw3s03+SLl6r3WlprLWEwqeZd9ahp36FLwcqW3bPU+eY
tk7fUMr2rKuxzrkCzQmMgfbIb0RH/3epQ/2HyHMaXl1HH7yp8zPolodAv67+
Jq8KjNe/0vq+23hf+2Douuusi+aCb0DbOGgfC4RT5mraEJrq/0ibkfOJunuI
jigj+wLQ8Av6eaHsPwG5i3jf/ZsqtkO6hv4ZA7/+TnE5davZT1JnnneqYvt1
sl1XmTqvMAb1o+wsY30j4+YtIK/2lHVvI8x+GJdoHxDefk4/1YBH1YP7g68z
T9QnvKaR99t2RnrPTX7UIpvYx+JvAWPFd7EeSqBNf1WzX8UfC9u34mZoXAE8
q7sl2qdmLN8CBsPXRuiHBjpn2dW4PrAHWXpd52Hb2E+i/CV2THW4M/izCIeV
pvjH8Dwa2j+hXVvJm5+095IcXtDc8XcI/wrfKzRxWPjdJJ+nOdna52vk020k
NC1KMii8OMl7gdoTbAPf98Xa/+LVgOF//hgf8XdXCOuTrYm+PyGfdPJR14Xx
kRsco3+dPPudZxNZL/XmeTHGQ/EW9rcoP4vDaO8Q1mnnWG/8SP8OYe5N552a
5NmIHM/tbZ/CurugOwyF4dFF+nUB7eqoOZeyrwHXgT8D9n1XmLmkG/LTFDl8
l7HbFB6F8+5e+j4HvPkNedzJt9NnSX5H+bXPpjt/2mv7gDLOyEYk/PoO+L6J
/TIKyzejwl+h72+Q/02+o25q/cb7k3gninmlB3l6Ak9E2q7T+znt3033UdWm
ydWc/zrtzAJ/W9PuVsA4yr+lvRL4lh9+/crcWAA8Hd5sgUeDsnqf+14x73Xn
ov15gJLU9Tvl/MP7vajrIfhBE+9RzKL+xfrWYnz8FbDdLO37vUgbrsY5v0Bh
ldGT5wfauewfyti/uv5/prIe+KKP/dnPqei7Z7uQ65PwMAnZ7AaMhM/TGJOD
0CW3te/C2H4vt+/MNAemQ1Nyf9+x0127z+BzB8qvWsRh4Z6p9htdoaFtVo5l
DK5grdAw3X49r5GnKPL1N2XMho9b6dd3oHdsNf+7lj+ceYTHwNvVvDdRewMV
7U8wjPaFxvks8gzK/h18J2CfljeT7Nta/jPlz1p+M4W/BP+FPlrKuul2uPtp
MDRmFb955z/gIXC0nbHiCejpy51tI+NGYfvDvQmeAO3jgReo9y7572rfJNZh
+dpT/AR8+oc56b/ulq+vgvYQZF9OtuXqV7M/0ib97AN0RXAv/B6QonzUdQbZ
qkBfdSxqOwaP9LQfwwxweWThPjJUU+df0e870cE9yvqZ8vwKdIL2MejRzuAS
svUJfePpu0lNjBWf3sl5plDfKfTzUtq3HPiA/t7F2ErI6/MKWtPdD9imUSz5
GwPz9F+asp8DFwiOKY0tlTGS9nUhflS2JZH3MNqXgg5tjSwPLmLbcq8CrzO/
vESfPKDslzv4LrDuARdX2+mfCCCJstJpV1PksTnwMW1+SP7RpNfgeXXG50tF
7RNufnH71OtD3e9S907oOYiOnVPedx101vAf3v2in30k/kv4PyCc9sSkeo9y
OvgY47spuiuV/vqxHHIbbR+QS3TnD8idg/qZ73bof67uDgEf8LwD73cCfmSc
P8W4X8M8XB/deDrOfhKOw+NJjIUsjJ9b9G1F4rq4l5vv6+XQt1J3CRLNw5yU
P4X0LDy/ioz8BpRD5/WmrPLgkRV9D6ai/mMjXyXgcfES9hsuP5DyHZ4HXt1g
/OYFb9FdH6pLpE0DO/v8u+5q7uHZNcr4o7D/12fN9D/79bQtHh7doN6eQDbS
swOPFbNvz1OF7CNYz5RenLKOMWeXAK+groXo9xeAveXt/6QaeiU003vQ2n+W
bY0RyFVb5ooCzW0PWv9TJjOmL5P/6xxOrwGPqgNhvNsOufgEua9Om5KQpxo1
HN5e2v+R/uDdRMpd199h4eXQ+xF0ZEPultFHM5lLhkpHUM6aRPs+fag7NLyf
p5Z9A8TCx8ZA62Y+CyS/O/K5Ew4NOYCcQK4gVnxOddvqPtneefWOfED0I57C
N9V+6syFPolEpr6DRzuoMzfvvYd87K1vW6c7uvjcai+dUYy2zfErxWyDXN+r
8pEm/2jyS3K0mn2T1EOWqtPfNfPZfk/3ivbvt5b3PyximyIN4HEG4yKzuH1q
aj+vDoKQB5pywrt98GiSbDx0tY/5Zyhrej6nj0a3PAGUoE0NKHsd5T4F33OT
fwt6tBHhw+iRTvA1AThCOBtycTPaYeHj5MlDW/fB6/vljBUPgbajTW0TunJR
n9v9lj4fU8Nh4eeK2heisOLaHztbxHtkF8l7AegG3f30H5Zy03RWGNkZRN3x
2lMl7St4daqabWNv178Cym4E7xoD17pZJ2mdJ730Ge+vo458bXzmX7b4dEdr
LuNwTl2v8Zrz/JTua4K3oI9K8V4ZIG+m58u2lJFPct7V37QaI/KhrXHyPOXu
rOt97/yl/f1aSPaVoCMR+BmdsQDaI6C1CHy8oXNe1LFf3+nwqjNQv7rDwvWA
Ve3se7VypPdCyifaltRbyNmbwBbq3DjAvtYuQ8O/yMzH0PRfAc9NmpdkSycL
+n5DFvvL/Km998Z3FTX+lnZcjHZYWOm7ixorvob089R7AnnNT9v/5P0jGm9N
/U94IfECpBcEduj+VRArXjjTcYXr0d430b97+xsPru6w5Gt/f/tsFC5Q3f4a
9zGm9gLnmH9/6WQ7jf/zIdrDdu1k366Q7sMDFRnvW2jHfN59v6t9d92m3Pvt
HRbWc2HlUfgGffyAvr4Jjkq0/86h7Q0KTwnGhYe1dx7FtZ8hP48bSb+Y6vCm
6o7/2NU+CS+Bf0m1n0KlCRTWs1+CaT8BO1j/XGG+/wUoAo9ioPkgY6FVO+/z
/kefVkHHfKH/gozx6TxrBO9T6Ytp0DEDaMLc+ht4ULTlUj5WxadNWgP1sn+1
ycBG3mnM+5vAR+HvU4yLyUmWrUh43EV8buz/t1fA8fqHjczdq+U0PatW0Hvd
8brD+Ij3VbW/mpPyc1B2Ud2pz7Qd+SrAz83tO/R48J+I9ty039ZFOgG5WgUU
y7RfPPnEy0pf7aeOfcDryHa2OOvOTwk3oF1rkOMzyME0aO1EecV5twTwE7JY
MtN7WvKJJ9948pcnP3kxNYyVXh/cnTGQXML+UOST/Pd0+yXXmZa04LmWRc3t
l3Ex+E1oHEEbHmtn+1Wy+fZTVtvFOkOebvCwgPQ4702lv6qTlpN87Zs5/Ect
x+XfUP7qHqY6XCsYl0/Da/Tbn10dLpXpuHwalmBs5+ngsLD2c+XTcAt9+HcN
h7cWc7xaI9uTaKEz38xBqUClDg4Ll87098y1RH/fHK7ss9AjGEdlePYcfTgX
KEneJtB+GDxA96l4lpdwkQ7GiieiX8rQ1hNFnK60hd1C/meU7hPiz9HfY/X9
DkwHulLeKGgcWcxh+fdT/DQytQm+luP9vTonhq67ATSDp0tpe3NwY/IPQ67K
k+czyjoInNVYRL5a6/8XfVEXnVuB9Ajy3KNtd6v5fvgixlVj6GnUwXsQCcDA
fL6jI1thuqfzKv1zXXfbgLzU9RN05QPXQ1ZzMU4qUGY33UVFZjoDF5k3aoN/
yOv7nd81t6+2bsF7JDpP31L6JMLfiH/zrCltWY5sr4HnQyU3XXxHtgGy9z7t
LgsfJyOzTxe1bb0H3X1v6gAy+k+i54idrCUuwJvptGsS/V4Ruj5Ks93cbNR1
Armqy7PdjKXSlDcDfT8dGF/Y/hFln6EptHbv4Hjz5sZKU7g7ZV2rZnu28msX
0tB3HYXz66xiH9vUkJ2NksAteNMH/j2e1T4W5V8xmrqrdTJWXOkKh8DrtdRV
h3GwDly1hLHiSt+nc/TAQNq1pql94O2DF8N4fizN6/rD/by2J0tINdIq0X7Y
GNKZej5r7HDXYFz3dIUVzxdqf4Z6novxfiuv72/nQnbqQ1cd3r1P+3rQDxl8
i51hTfA9UJnyjzWz78XFzRxe1MxrrmPBNMW1p6m9zRX0TzlkMpL3XoefxVvZ
5kCVTJ/DvUJ9vwCnyHdXd87pt8+kq5CPAt0MCtcGrvL8D6BjSfsw6kwfhEbb
j5HugypNvnlkd+cPoC5lZmVM1pOtBd1PAA7SN1W1jqWMX5o5HF7S8SjCZ6k7
opd1mLDiSl/fzOFABz87B9TQ/2DG13nCMeBZ8LQaed9E/g+xrjlBfyaUdXg0
unsSvH4KWE76UmAtvP0P2TrN98Iy4t+X955kGnqzHzCRciZF2WdGZqTtjDYc
YL9R0Zn2HRWAzwm0OXu870PIhr/uRFSDT33gdzQ4CV3WC+gK3IdPB3Lah6/O
GuvMcS94Mpj5oxqy0Ri8FJpXQ88qYF6kfUzOB3/dwb7/NH/Kv/Xb2qfhnVjG
0jq1B9hc1Dz5HJn5Er1ZXWtE6snHd+9u+rk17S3cwX5UR9SwHXD9P7yt7w7W
K08xt12kDff47qkKjV8znq7RzzUoZyx6/CbteZGxdQu8ral9lr/EWFpOviG0
rSVl7Gc87ANq8k7J3vYbLP/B+9Fzy9E1xZCZWpoXgTpaX0h3Q+MP9GcEbWhJ
X/2cw76tNoTYv9WP8K4u+RrBi1nwuiZj5Y0q/qem/2nyI6l/a4rvLuU7uvnI
W493ikFLffC/0JhHd034johHPueiz07y7CugQhf7CapJ2/OXt09H+ddpDt3b
dN6ath6h3Q0op6HWjwP8najvxee6//8ylsP/Y/TLiqJB23bIzyxgXwHf9Wik
bzfyvgxvX6rgdPnfkZ/Zb9EfUxlvjaVD0LNPQ28s4dRI+4/sCT5Q1vZ/y5X1
fst/VbyXojEgv43V4WHRR+zHUv4sv9UdhG72rf61bPhQd5juvEPrDd7vzxrm
KmUtRT4uQsdufbNJV9D/JUv4G/8/ePUvenw3srOwg30GNSXPN5Q3jn6bTp21
c9h+/MNG3ivtpbmU513ADeJsY+0AfBylPSp02+vgvshLH6BZpv9B6J/EUObB
b6CvOWlxwFe0qRayWjMIJ2s7bSt0HdX5G/jyFOukiUAL8jfrZRvmLbV3QFuy
ASGUNwc6WlDvSsb8i8j9QiCePJPow0HQNRBoIns26L+mujfOuCjLu2PQB2H0
dSvyttY8XttY8RPIYBfmtBT4c0hnMpHRDzQRoF/b8LwtsIwy7lH/VdaJUxh/
k4F2pB+Cxs+Bn+kPWBfyB/xfwfduON9MpbTWpa/ToXVIuve+XoGXeeHtGHj9
ajPfh9O9uMaswXtITmsaP1XfYe35zInyvs8iylzcxHsB1XnvDrL8F/FE9Fdr
8lbIZ/9j/+q/fTn7spQfy7915lXrSubrO8hRH3h+gPS+4G0lbDfyL/okL/kX
dfSd5RdpzwPCS3P6HncV6A0NYsVr8yxSZ62RybNZfDbrBWStKO3dVtM2MeQP
8xDh6cjxU8E18WPpXiOPYWzmRof8Dp4Av1pB+zjwp/T/d6Tv4L328LdDpv39
fdDcfizlz3I97XuW+mZp7mKMVkEPre1jv5S1GAvjtBdJny4DfoJvj9GWbcj9
+0BHytsE/3bqXgLv3Khg/5PD4U805TwKfl57jt39fBD9/iUTfLL+Z8Pbjfqm
1LiGvuzISllk5nfSf2du6kzfR0B/UdpdHAjApxbookxwU+SxVAfbpnwI1Cc8
oYv3jrRvJB+TMzXGy3jfQf/dJsPXpdD3h/5RxdrG1WvUt471U3vkfRfPO0PL
bnA/4gnaUxrgZ+v1nQGtvyHH5eFfuZ4+l6TzSc8hU4nk7cSctSzGYWH5I4iF
ruHQM4/+/QN+hUDPVfAo3ssDLV0opx96oDN93WCA55GCtLUAUAodMAL+/9DN
6Tq78zJzyq/w7gowAR1XLo99sgzUHl1H99mj0Fi2ou28TKD+/fCwQKJlYXYD
p8n2yzLqn8v4PoN8VCJvF+iukMd2uWSfK4Z+/YO++hD52KUzN8RfYT3WuYvn
evmHzFbbtlKygrPUNha9SpffRvlrlK/GatrPb+bwUOaZ4UAT6m9E+Q2B4/Ag
J+MvjPeOQNNo6hsFVNccQvxCKfvKaEZ5TYFl6JTb9MsEaG3H+uYQ8pekOV13
NRraFo7s3iyMs/9M/feXP81z8Gc1dBxB1mbD7+fhf1fpbH0r0rYzlDkN/j0D
XKefStGGbjzv28V37XRPfC90hqtc4F++Gf6Cr4ehMYQ+yU95hemPZOjtzns9
Mh3+qLbjs0PsE00+wkqQrw/rgpKdbCdH9vInN7ddJtlk6gYM5t1LvPMTMJDw
DyGOz9ccnWz+RZDeH5luBj3RA4wVV3hJnOPNoK868cju9iH8eCX7EX5bcxNj
9AFQh2cVdT8WHhxnfH2V5HNn2mdMzvS+o2xmyXaW/E/Jr+WJRvZtKVv9stNf
Oc17ybL/uj3F9+d1l11z2O5epntyKYcnM/56av1B3qSStr87kXGZDK/OJdoP
YwyQu7bDwrmA7+DLj5Rzl7Xo2Ud8lnGU/vWT55jWnskOH+/leCPqS6GeSOgd
iS4bATxJXz0JTamkv01ff8o7O5GNKbI9pTMVvHOI8bRC/7e1ZqSP3kEnbaTe
XryTD13Qhr5qDVzoZ1+I8olYS//idd65rOv+MkjP+m72AS1f0KHohsdZq40G
tjJub5BnOjwt28m+D8uBP6PO2TqzD3Tsan/Aqyk3N/J1kfZPZXxehN4F0PhA
+7pVfFdLd7Z6Q19Znm2kzE7U1THGd5Oq0t5izPVFgWeqe29U+6Ld6MuP9C+d
tlyuZVq7ib+08Ufq7VLK/tvlZ7ydzsbr/iDvZqX/nqHMNvD/cJzv5n2V3Xf1
YqHrLnT9CT9vUmY/eFyQMkO19qvuffq+lPGtxhnlP4SH4dQbBvTL9N2CydR1
A/n7E3ihs+8d6Nl18HV41I16uwLPak+8tm0bphFPI89I+Pc443lTsu8jjaVt
U5GpZ6H3cCf7jJ6FfPRj3G3QHh2yVxN670LPffClKOvNH8CfFbO96APgezyv
wfP0TOtU5VHePbS/CnXsgP4y8L40kI32pjLO0nUHGTqGE75Cf2bVv2907njy
Ly/tb3rZZJwDbRslCzo3g44K0ZkpnQ+Hn+ea2c5DK/L2paw+0B6axWfaVkH7
mpLWJcvRi6vpy7rQFQP8y3tLeSeGufcKPN6sdafO44LXF7e/EvkteQF99Elf
+3F9CH33GSP/gFtD31Pd7KMzg/pvUGbJZsaVujmsdOHSwGVoDtDeDKAe798B
94dXd4NY8RWkR1BPtP5dtvWdhhvIYfgA+zWXX5oonv/W0T4o1xR3m5bB55KF
fddTdz6vQ/M1oDV0TNA9fuR6YrTPX8knmM6lnmZ+H0C937fy/TqdC9F9u7WM
6zXAIzyryFyRoTUvY7EKfM2luzDVbLftJm3qXN7PlCcUfbeaeTmVd1PCbFPn
+Q62q5OHsTkOuQtket9X+7/l4N8bjIlM0lZl97/iU+SpRRn3ku0/KIvOldGX
U/m+Ow9+FBhI/oRsDi9r4fgFwm3p5/gWDgvLv57C54PPZCsuEdk+Bn8WI2M7
dQaIeTa9jMufBgyirBR4cAZ5WEgdhWvZJ83LjM3BPOtFmft0n5b3igKHY+1H
4cOW9kk3o5z90tXMZqz4EMpfk9V+VStQ/3x4WBG8lj7+ta3P8IYhd8/F2O9P
UhbbdpaN5zBo2oY+yw7+gL4YAg3bwXPQ0SM0vovaH9Qo4HSMw8LyDzU4q/2w
XaH8vYXsm03xHxh7u+H/zWT7spJPK4VV1mOUuQP+J5a1H58u4L91Rlf/E/Tt
TZuno3+GER6mvR8gDvgFGW2LPNSmrMO8cxR4tJxtozz+iG2lPEnaQHiSCbRH
ZxXlvSLATXhxkrX6Et2x49mn6LB/wP8iT11Zu3TPaT8Yw6lzQVPfaXw00/cd
U+H/jly+I92ROkZDf8W6tqc6nroPQ+trOoektTa64gby+k+0/bbItr1s3MuX
yz3WftHorKdreC9GPhXlM24L5T9GXVtj7XenN++/w1ic1Mk+vU/GeZ9Hezxx
6LVU2eagrrINvQ+i/ZBqwC6ef0xbpyFbHxIeQZkfgPMjE1+if2KRn0fjjTcy
bvfS5pmMy4/BbeFf5Tr2NzKIdd7zrDVeof60Lr5fubORbTiU51l7naHWPQz6
e3k92yJJZd06jLqG0f8jJUOt/Y3evKG/04dR51p4t62tbT3vop1NKPM65f3C
+rEfdE2knge0/T7QFBkdqe9m8CjwaH0XwO8/ebcs7XsLfLq+bVMfot5XG9hX
5yLwbvj1nvZgwI9n2s5xnVYOy/ax4h3og07QdwuZqg/vFktfVLBtYdkY/gk4
jo6uKlsr+sdUwDY7ZW/+Ca3FOtovrM6M6uxol1a2h7wcGQ+Nd1g25BWfCCRA
5/hkg8JTwC/T/+NpfxHKfpT1+LPai09wWLg8ffIE7XwUGJ7D4TbJjv8CX+cj
z2Og5R94PYP+HNnT52We1PyrM4fau6hku5hjSRuX6Tv9+o/6CPPUt1Vtu042
7PoUsJ23jNa29aY93dPA32m2GSl7lT2BP3v4jkRe5qpHmd9fpd/bEs5LXduQ
mXzgvql+T++r/DKklwaGVrQNQdkPXARdjalnsTCy3SjSdlm6gOfRxiTwq/A2
XHe9dIcbfram7HuU103rWuLDqWNFom1a6V7Rc8j+04y7QF3bP5Htk1+Q2XP6
b6i9iga+y6q5uC7wFeWdAHIhh4OQy5RHbBOsJXK2WWeE4NdN0lIZHynAQeg7
AEzItJ/VifpeA3+DHH0NxFHGRZ1dgOaCQDfmg6fIUxPdcQ19OCnT5+bnIk9z
gMmZttWwK9H2GqZojYwsVQYeo51PZ/qMpcK6A6f4OPqsP/Pd+Ko+g6l/Rrf1
r5N5M0x3n7rYhl9tytwKPkbfbWG8VIq3fT/1hZ6XCd5zl89a2ciUXVOdg5nJ
GFxI2ixwOd6NpX1Ngcvw84Nk2y1+rbPP3crGbd3sDivtKO/F5WPMA/XQ5RfJ
P4a0QeQZFGPbBzovPQHev4NMTs30XKh58GfasKq4/QrO41kBrW159h/jbDe8
/JzyX9BZ6gE+03+Id/aX9b6jzlbJT2JXdNE03pnAHPE0/fUu+VaqPvTUdNL3
MD7mQv9FxsoF4FH6uDPzTyIwI9P/kfUPuXU7z5tt2zk8k2fn9P2KXD+uvRVk
/k36Lz/j/3HCFdAhBYFE+Dwxv239FKfM3WH2R3yijv0W36fMGTl9dvEL9E0j
yjoMnpVpW0qyofQx8lCGcTiBev+INVZc6bIlo7D+T2tvVvudq8AzaGcs/J5I
3kmyA0PenJW9T6E9ijT9P4/zuULhd9s5fJs2vdfO8RsNvfesPehfCvl8rc7f
KvxrML41mKYzt8MpOwtjaYC+E5N9jjYm2aBwP8buf/Thy5T9ajuHhbOh4xYH
z6rrzPpA/bODL4PA/dELr6AzO8KvB/BlJHRPhedXoSkfY6gAUAnZ+QT5OKD/
7JRXlrl6MWXmJP9l2tMWnZAPOfqOtPzFvV+4XN88mT7P+l+iz7fO1nqQeONC
wXIDtvk9m7x1GV9zatqOmWyYaa0hO72tgeS+vg96Tn0KpJWzvc5o6PoW2VlD
fHU5n+96uanPeOmco3zpym78G5S3qpnn7NlNfZ5a56rH65tMsgvuyXjsTT1X
0Alv8KwaY30VOL67zyzouzFfY9vDzQ9eCz1xjJt14MKM49laIyE7q1mXHy1u
n/YvoyfqS47K2ZbTZMboVb5tSlP2m8jKBuCO9LbuSyDXhWraVqL8GOrbUt+Y
raPtmzBAP8VCdzVkNovqKWlfi7+WtL/FQvClCnV/gyz0593FhAe3tO0q2bCa
m2lf7j8X9jnWXIzxwrTrJcpbRjw34/hsX9sFln1g2QbuSX9fhZ5m6MGR0Y7v
oa4o+ntDN38z686l7l4+gLdTGH+TS/suxAHqfJDquUC+ZTNj7Ie4gM6Ik7cy
st8BmIwcbKxqmsN5ths+DaQtHaSzeX4t1fYQZBdBe0nPBfeXFE6KdVx+04/Q
7kR9l9CueaTNz/T5pZzQl0NzYG7bYv4NXXEPuu8CncJtV2lmiG0rnWL8bKa9
/xKvDB/+0HkQaC4OPdWgs0Qd39HZgcy2Q/ZuM/8URT6LAK2AzbSrZWP7ut9M
niXwdAHrqijmgapAQXg9BvqeBJ7P9B0t+dGeiQ5aV9Y+HB5q3R7tO10lWAtF
wpOS4MpJjp8nbyi0/KNzfA1chspaoH1AZK1OLf+r+I21fhXeuQoOR2/+iwzu
0v46+d6hDzeXcnhhI8eLBuOF/y89GNbe/OV23p9PR96L6TxeKYdXxDmuPTea
9L99t7/Itwp4I4vD2q9TXP6d5dv5lbIeNxo/oq0l9Dan3Xsp4DLy/ytrk8Q4
f7OlUe6eMv7vPx7ejgPSeHail//jZA/+z1E8Ez70oz/SS3hf5V9k7h/gInrl
QgfPNw3A38OL00Ai9fTTmTZwC+rPB035gbK0dRv66f1C9m+xiDK+Z+4Yhnx0
o++Xaf8t1uucJsjbi/DpJe3n0bZz0qnQ+zLxlZDWS+0l/KzGFeXuBGLQV1Og
+Z+avk+nu3Q6l1skv21A/c8uUgv/axpb3758WjCHFkRvPwXPmgOl4cerlPsK
8lCEMd5KZ2WBoT28/tA65BL6cRF8GahzjeiZr4nfYW4s1sRz3x81Pf/Vo38u
hNuXWDPG0T+t/P0wgHrC6NsJ2s/v7n/B+idcNcH+rofRn/vFH8pqTb2LwU1r
eZ9L4aw9HN/Bux+gu6qXsX3lh3XtV7Iv+daTpzf4G+bRJ+B9Qej4vK59Uckn
VT/avLyP18nt6IMj0BwLf1qij56EvkPQs4S6xjNOt2l9xrhbSrw842cZeChy
sBX5XZ5p35HyIVmyn99RfvmMlb79Dfw9ZZ8BVvCsC/12FdrmaN+W9yYBV4in
wetQeH8Cuf0Cmj4HltEHK6VveHclNE5CJg4gX6Ph4xRovQ+dK2jba+R5Hahd
0PtjyRkeo7JDVSPFtqi6dvOZIp0tukP4DfLPo03Lac8+5o69umM7wOcgdUby
IO3view8QV0zyDMLeJ7yZpOenXqzAau0fqUfxgLN6LcPofOazrLSfw/a+Uzs
W7H+h65/6anI9Qxkdx8y97CK7/nPgOZezPWv0lenm9nP/Kcl7Ktb+13foUMP
s848Sn2x+W0nWe/o3Yno9uU6Xw2shpZY9PAk9GJImN/LBj2LKXcNzy6iJ9Zm
OpxW2HHZ34Hs/9nj0R6N9mq6MN8WB6IZJ++QZzt6eRV6JZWxOhj+VKZN9bL6
jEHdVJ8zOEi+xdC7jvcbI4stkLX9fGesJ36NZ/9kcVj4IdCRvpxZx+fptb/w
JeFw/dujjjDG8GL6b0Nb23H9gvEdS39t1ryF3EZmsy8b+bQJaA8NmIOc7dOa
GdhAPe3h73DoerWS1z7TWnj907+F19njaPTjyEQrZH0RPA3RWXwgAjm8xjrw
DyC9vs8bbk7zmcM91P9xHfuv3w1+k3qWZnV4TzAu2BPMc0znvEv5G+MeMvQW
z/KXMF4b4/AinaHV2kG8Iu0S70V3tp9z+YN4EvgJuhLL22+vwhWzO67/6i8B
K0s4Xc/l31dh4QtAH+jrDUxErwzLYn+L8rtYrKz/gV5F5z+X6DPjdYEJlPs+
PBwHrszYWA0fCqbZpuvqMP8P1r7jJo0dZO4usnAHiC7rs0KB4HlI/Qcboj0S
4G3yxkHnZnAo8hwOfEP+/yjvHHA2zH5ZR2ezb1bZCpCdgNXBMvLTV0Nb+ayb
zrzJV+Mn0P2OdBG0Tuf5u4Sn9XFYuCXps+HTXOA16nqb9epkeDmN50+hd9og
O+/xTi9oPUs/9Qbfpf5O4I7IYAr6eAn5skNrduadl5CRF/P7LMa3zXweQ2dt
vqVv89H+l5DjKYylduicaOS1T7rvK57ROSbeT6PcROS8IbRP0P5WOft3DEl2
WFi+Hbdozwx4H/iZfgyQVgOenEMWz9S3f6cY5qCfac8DxtgVdFt5xvIG+j6x
gX3rzGMO+o98PZGjbZTTUba50E+P1LLNysHQsl3jFPkYSpkZmg+gewdpl2nv
Y9B4F9pHgPPSjg9I36m1v/qJOfrlJPs5OhliX0cjdG8rm22may9Se5JLwfND
7R/rQoTDwvKLNa+p15KHafNF0tIr2EfQEtpUhmcfUtd54heBOOR2VQf/z+4b
5/1w3ac8hZ4bS711mTtigAnJ9gPWJNnpTwaf6V//Ln1zox+mMf6fAWbW8v0z
3UOT7xb5Y3vyEftnk5/i3Zn2Vax9pfWUFwaPPyLtUfj+H7o8Hj7nALeDP0vR
FzmQzXBgD3n25rYf3l369te5Hn2v9bWdyazhjiv9DvKTC15/zDv1oe0N5rnV
wDrSdpN3mPbi4nzP8pNM66lhvFseqAB8QT98w/g4rDs+pe1jviG4FLx5sYvt
h1/sY1vgq3o7LJvhiutcl+bmH6TravveyfVQ7yNoL0L7CrHMvUUo59+CPjfy
fGufHWnTxjYEfwV3Rrbr0I4E8Mfw43XKCYX2vZm2Q3q5oMPCKYzBEfT1PuJL
oHMdsl0+t20zl2IeqaczhYzVZ9BBu5Gjp8Gn4PM4aLjG2GpVxOezZW/wz3L2
D6c96e6M0YaMy0eBbaSfga7t5Rw+28ZxhWWvU/G+tCEb4zsrsB9aztK2vhVs
r/DTTNsvVLh/ML6MNn1CP3wMPKs9be1rAoPos+dJu6T9DHTNb8hKKHJ1gHdq
wd9iyECDsr5D1xA8lH4qgTzfpz9zM69F0N4cyPo5xsdY1gnRjf3NrLuPK8Fb
kMOD0m/0x2fgcOjZ29Nh2cFT/JD6CV7upd4yjOGxyNf79GkL3k+FL5e72S5f
Pdp+OY/t5n7OO9+DV8PX7rzXDajAGqKS7FllOtwC3lSs6rDSFJcfJPn0zkZ5
LzXyWQedc/iP8VQVqAY8pMyL9OXjKcYTCjjch/FbCFoqI7d3KfM0euMxvr+K
M7cUA0KQ5UroxPfoz73k/xs5WE99d8HLdH8S+YlJsv0E2VOQb6q3kKWiyEIR
YDl9Wpb8K6RTMm2b4UgQ1yvssOwZyrbqUemCFN/5z44M/cX7kfTXh1qj0wf9
6Kd04D3k+Jj6sonDh/M43kfrpTy+m70JPm4EjpP+JbCdvtsGrAi3Tds+9MEt
+nY289mzwJe8s4jxOTSPfSloX6sb4+d9nVdBBgvBh83UN5Q2P874CIFfteBh
G3RVHmSoJDo+L7h9Nd8Dj+pnvCQYVnrHar4vrvtSyxgzF2lbq2jb132siP+T
LgdO6BsKnfVNId/3+yrTZyx11vIp2UajvAW8s5m2zwfPJu0MbesO/Wf1/0bn
/9GtJzN9V3RnSd/hGE17Y9E9P1DvWeh6Cr1yLslyJ1keQl3z0bfvw+PtQCTl
VQaadPY9mkBT36V5kXG1ijr/H1HnAV1V0bXhJHRCbyGh95aE3iH0XpPQIRDK
Db0IimCjSRUpghTpUpReBRQBKYogoIiAihRBkaKIiBQb//P63m/9a9299sy5
58zZs2dPOTO7fNXPfh3lR1e+HUd0937xaCCBPnhZurpq6362aVmL/H+OLBSl
jGTavyl1mke7zuHeZ3jfOcp8HrmKbWwbzVeh6RRlDKcOp8EbdKae1Xue2RmD
21OX88h7Nsq6gox3a2mdoK9op7O1HEs8OzCIsiIyeszOC+5NXZKBnayRTtLG
12V/QpO2RyYu9LNuxMokx/VUTM/X6IczYq1/8B7v3A183c9zVhL1mRTjuUzz
mL6LBlLuIGAra5ru9P1ewDeap+H3Uej5ALyAPpeL574Nfqvpm22S9HCow0XS
L/WwTWT+jta1zEdZG5Gv/BUNSv/Q2Wf4OsufHe7ruvYFfXUoMpYPnv9ZxHG+
foFfPwNzePc+ZLwg7/6O91wCmha1Xse00j6DygDfp9Aex7THFm89qnQR9hfY
PKd9Bs7lv8vwYTY4E89Nl22i9Ht59nVomA20YhwYQpuFw5tHslPjXVf0vUgZ
M4HJ0kGGnnT0i9Gki8S6vL2MZa8AL7I+39rC6ZeinL/K83NZU8+RjYfGC2T5
dILTy1o4r+93fbv3BBdhLCkMdEjnGEUz4VtaybPWXpSXHXnIHWN9pnPIx1rZ
XXLvdf7/Vf21je0uaspOBJhZzfoXByh/E+39KXL2A/d27m0/Qe3qey9KsTkV
o7MJtM3sZN4f6+540q/y/5V2ji+ttK5VQUYqA+8BV+BXB2R+NO95qO9RePMg
xLpRb3WxXlTDKONGUQal9V8k6SvIUc0Y+xGTjUJz4DH5d6GhsuYe8tV7ON8g
1ntO2ntSemGc8/eC3ybdgfxlrDtSoIx9iEhvTD5F8tJf0yRYH3t4hH3bNkUG
X+b5l5GNcUCK9H3a2X/yW1kds0Fyc5xrJ/StH2HbGtnYnJeuC+X/CD+PQON4
6nKD9ATwJMbfiRkcq/0Kc3oo/T5Za3LyH3DvJmibQ3pKpG1xZ8GL2UAT2mEG
PC5b2/42ta+n/b1cUd7/U6ycN8AzmWvW04feBcpz71x4EwAasS6oSptvYww5
Gm9bpO68ayj86qc9YurfHHrOI2N1db7FOzpVsk9H+Q3vRd3uUM4QrmVC1hsw
Bg7sbf1I6UY+5XvvOjITEua4GxoDf4K+EchGAcbZ/EC09mC4lp+xZQ60LpfN
mvgOr5/Ctxj4fZkiZvHfiVqO17e7i2P25dD3uc6RmtmmcwPpNYxpSR0cd1Lx
J//mvlv9fF57G+iR5f993eZlfo8CNjDObwRE6h3u+Ztre6jbFNrgXeT+Hfkz
4P+HjD1/AJfpVwO1JwFMgcdnqef7QEqS9xH6AhNZR1ak371XwfsWh6CnInwY
KZvsCt7b0PWSwM+88xfgNcp4Ib/18/MjRyvoW5/D963RPg+UzkvTSOvH1OS+
2vlNT3RXxw4tLRsP7vkQuUiB/r0V/P49QVw4zGntpWifRXssqkMK196ivV4A
J5LvAtyFnq7gObTpPp47jXyMDnXfmYosdqb8FOnpssZKYH3xAL5Py2EfJb/y
bCpoOU77/SC9Ksale1zro/FL+yBcL97bsdhGw9dL8Oay9mrh354M1r+eI/0B
2q6yzlLDjKsG01Vye8/lt37ecxFWvlgq79GozRQj+buWjpksUDoveAj/F4eO
oeDfZesCZGdOXlvGfptqMA++hSwmI6tLstlviXyWjADf5z2naa9FTXyeKT0g
+fG7RT/qW9x6eZ2pwy7etauA8e/9nH4PPgyGbye5lp98RdYCFYD7snVinfwp
tIVTrxK052/I71D6QX9oHAZ+QBkPeFcreBbe3noKs3jvFZ0rF7Qup9JbwHsK
OK1ryg+WXixt+0c/43z1nd4UalwEGgqlNla+UBBfg5591PtN2utX0rVpj3jq
VhOci768HZovQe8S+H4RPi0Gl6HsCdpHAm+gXpuAh5rHaM9/gejUjruqM8jc
8puic0t9l9PH01LnptD6CnP07Y6O1bdXugrI2CPm2vbSLc7kOXh5VcfNG8Q3
wRAgvpH9+sq/7wna70Fj+92fBB0V4Oejfk5HpXH+5YLWPX8F3E97J9DVBPi7
me0jvmMc70Ed7/COpFa2l9D1ZeAa8DaaMfN+De/vrGAsmgmfQxlbB5P/HD6s
Iv+Yd34uvQ/qPVhrHe3Ncm2pdG3oUxm1N4eMZgAXhBe3aJtC4BLI0tvSe0y0
Lsa+qo4x9i90/Mnzf/Vz+tk+zvfJZf2ZvuA45r0xPN+oh/VwXgXmkw5h3H6P
9VI+eNuYcW8StDcBpwXqsBbKiizFFPCZu87e/9Y3BTx4D5gC7WXDvHcxtqF1
fqT7c4n7Wuu8g3QG7cXw/mrI1GyemQX8Ivs+6d/nd1wtxfDKTZ2KUZe2tME1
+BlGe8xFjuZktl9l+e5rL18ClJm2o+PFfUe/SazsNW43aNxNH81M2xah/12A
9q3w7GtwMeh5ynO3uH4ceQnjfSV4X+Oing9KB7Hyxxhr3oa+rynzW6AD7XVW
thX5pZgOIMOh4H8aOP8vOBXwbBrPZY8Yl8K4vox3DpWNGtdWA/d570+ymWMs
SMX/h3nXCmToK95xnnZZRrmDkbPIeo7pkIV1aWXqEpXF1/t29X+peTYNkDbg
9n8r3DJQjfvSca1KFqerB/O7kP+h1Oc98HLm7mVAIfkD0FoOkj8DohNsf5A+
YHsEpetBT0/Gvy3Mm72q23bmYZjPO3axVtkJfAh9LWnHtxh/FgPpKTsdcIr+
kwr6w6THhly8Dy17gTo8s4M2WMkzF3vbDkf2ODU13krXopH9eB1RvYr77GYZ
8twXWVoOvgCf3kzrPT+lMwScD+F9X/HeHyijSh77EZ+mM94+tuvqB3zQ0TEB
bmRxWvjHLN5PUl5prWm0tlH8ePnn/zKffQ9rzR6ic3/1Td7ZW2dT3R3jSmtc
rW+7Ma6coh+fZJ6L72Wf1SNo8xJx3qvVPm1F+kA4zyfS764xZ9ennGh9V/Pf
IGi8Qb0z8X8FysgMPsh7B1D2AXAWeJYZmIqctqePtgOyBAxKp0OObsCnQfLp
Aa5E3SfwnvE93A+zBtwvv0fuoim/HFCEb8Bu9JH7rJ3mMJ5Pp413UYds3Ps8
a8GxQPaAYx4lA7/Chrshtn29TDtdAnIEvLadHfwueig9A+5tCP9XtHHMPel/
KV7lw4yOWfkePDuS0/4p5Zs5I5AZujohG+9onwg8C7l5zJj9pKbTuqa8/hdW
vg38/F46++CKCaZVdN6k7jtoq5zkcwG5gUjalEf+8wkp35Cy+2ojewOuhVJG
Jf6sAuTh3gHwYhBwmnZJruvvbdndvgzPxgG36eNx9N0rjD1ZuK8i/2UtZagL
vwfQ/iN05trb+ZLI5Gtxns/O0j7n4h0jfYr2qOhTpXVeA78Ww/sIjR3Bc2Sd
J6fhXUuRlVC++xLh93Xqf62d/SNel28PYCRrwv3U+4ec9od2IugfLQvvXAlv
X0J2B8GzZvITUtO+kCK0V0ifSSsbYOT8I2AN78vL+1+HV9cbWofqf7pUyk+C
T7Hl7Zf/I62/6fOZGJumUMcbvL8F8jIO+Twiuw3NyZS1pZz9rLxQyWn5XlE+
hfpF8f9Q+PsX7/0TqI4MZWRdsJ7xoKts+SlnEPc9AOfj3vwqj/sy5bM9l+y6
dsPrn6jXDaBAwD7S5Std45u+I/U9uZW5YZz8ppAvyD2F1GeoyzNaR2e2z+Ka
pW338JdogKYStNHhVN6bn9HBc510vaTndQ0eToZvU4HPmXM2wMf1QGHK7VzO
WPkiAfupLAqObW09gErADuaSAfCxJu/9CdndprET2bsl/Vfacmodp4ULdnFa
WH5xFTMvqahj6GnvXnv4qcDFeMdC+tZi4B5lDIGPxQNOv9nW+RLkSwKlArYz
aU5fOF7CNqBFs9gO9Dz1vhDv/PkgLg4/npftMvy6SL8pzfOvtPe3rtJpkp0/
0dL7QrI7+QOZyRrj+FIZoTU3/aEd9S2lc0v+q8H4+Bzr+6+0BkmyzbG+bfRd
I7v2re1t255EnZuzxmxW0ePkY8oYBf4Ymo4CX9MHf1SbwYNJyGQZ6CkLlAs4
rTFK+SW0XxTvyQgezyvHAVng/Qn48hG8LRdjORSP/gbvlq1rH+tJfs07J0HP
Zu5ZAR0fy8YQKMR4/CyyFh3472g7JAb8K+udpfT7ibRTLPkLyFkZ6PsavBqZ
WEGbrgG/D28LU94+xuow6jC9lb+HJ/Ce8jxXQ7Yu0gGmTi8BFVQ28lkx4PT0
Js6HU79m1Otcdtu+ygb2Ate/hq/NuVZctt+pbYMq+9NKPPuItqgcsJ6B9A2e
Mi6Vox6hjIsZejkt/DG4imSGsfUA5VQl/TF8Ts28th4ZHAFfPkJ+jukMWmcl
yHis9hoT7FfkEWNGD+4ZCJ+rqa8jq19kcfpo7WAeGqoH/N1QjvbOR/8pAKyN
s+/WbMDvlPVHC+uXTI+0HeeMoK5KdLL3vIRjg2npyczLY12Zq/CzBuUn0Y77
8loGDsierIf1M6SbERHveJGH4j2ux7MeqKm1ELJXDDkt2thtqzbW2PFqT+97
TdY5ItemUtYmnt+JHO0AagWMawecFihdJ2B7QNkCrg51WnpSshVUenVQj6oO
+fNBHSml5ZdNee1lrYMP7wDf0YeqUY9HXMvAGPYkxunJtE9z+HKB8opR58It
nY9mfCsHzIAf4dA6GRnMBL7H3DyZcgbSFl/m8NphQAfb9j0Jc3+rG3D7xwW8
P6R9orKUXZZ2H9fF58KK6ykdJ41xv7Cmu1vdfsS1XrgHLKPdG0jHlPHhDPct
gNZ+/N83n/9/Gm7b0gfQV4/31Ne4wn9zqX9acAPyDYFvGfPLQ/dR6QJB+3Ge
XQA04r93kZvG4BVa28KvesxJTQK272gCzVPEM+RpGOPGQt6TFjlulGR5nqdv
Ce4ZyD0pvG8aNPYHv5vefgnlk1B7p2cibZ/blHLnx3pfUOmcrZxfXsd7qAug
uy/vSZY9Ec8eTec9X+33FlSflSwwVk+lbWq0t5/kaVHeo/5APuF4Rz7+LwDs
pF/uByNuIbM72l5c9o41qEt14EdkcSR4C2VsjnL9tE+tOp6ibe/z/s/AP0LL
h/SJn4rZR4V8VRyV3hd8+7OF7yvNsxV4dxntSdKXzmqtDs4W5bzSx+mHQ4Bc
Onuh3TsAtekrtbWnwLOPwrymvyCbH+a1ucyXQ6RzzvuaU+/f+f/POm5H+YRQ
W+p7fS9rhMHgE9D3rNa8kdafaxGwPt3PMe633Wr4W2YnNO2I8hyubxPN47u5
5zfuPUydPqBNx/POxCjrU71X3t8uidzXhbaO1/3kE+raj0I22qU6uBrQknfe
1Zl0IfM+nPZ8QH4Fg8BNxr778nfFO3aVs41CK+6/LpsT8PFyjks7uYttYmUb
2w+cAXmaA//bBIzbBpxW/Pid1HUxeD5rldmU/zdrhN+59oP2eCJ9DtMu4LOY
L6AnMzIdDiymX70eav2m9vyfnvVIfMDfXLXL26Z8AP00QWseyn+ug/WvX0Wm
e1LfRK4P43q2MO9Tvks9OwRsp9eGNhweat0r6WDVT2cdKr1rNPcX4vrzYd4b
bBvt/UH5vZTvkyqs+7uCuwCNkq1TWhzZnQCveksnmftakO7Iu76jDzYGttcy
Vl5xgzvx32rwGdmXqu6U/1uYdbEGk96HDO8HuvBfJ9r9VegYBGzUGQTzXTfW
aqub2lehfBZqHTmY++/SLlXz2WdfRebcFqwBmiDX85jz3oVn75S3j5VE5Dq/
dC+B4aS7IVcnkOmVzGurmP8f0O+68u48PLeY9Gzabi3ttAaoTV/vntO+T9rw
ngDltwW/SNtlhP8vSKbAIYnOF6P8LdGmU/ErooH0rIHfp49soP7dAk4Ldwd2
863xHlALPpSRXiNteDsInwE9Ao7ncl/7IpSZRH40z48t4HTPYF6g9DSu/ysd
K+2tg3tx7SfGwtF9/n9PUPuF0rOV7XIy/2eA7rb0121pnN5R0HmldxZ0Xnp/
0v/THFuDteOpnp5n1UeOq82Rj8v1vQYKrexv1DYtvH80HppqUtYEcNmK9sOz
C1iRx3pQK/PYBm1rSduh9YamncjLWuaZysjfa9x7Jtrl6bzlIbAAfrcFtwfW
0LffY8zpEzAovaeSr68O/vcMtPblv+HxBqU7VLKuV7+A9b3Sl/ae9ohkj233
gVPwZCvXVkFnGGPitq7Ob6fOWemD05HPLV0NSv9Ke5+HTyehbw18CFB2SsDf
sErf7er8gk4+M65A3fp2dkwPxfbQmDw4OC7311zJ+LhdOteMJcc1BnAtsgrr
YGiJqOJr+u+dovZ/1UV6pdB/nGfOyW8FZZ6jLWKQ5QbgnownL9D2m+F5Ue57
lnvWMK4ekA0B7fd6otPCeWjni12MlRf9H3d1HQaS3st9gwJOl67v/L3GtlEc
nMa0iKaLQDPe00I6+/ThD5inB/PMPvB3yP4oxrpu2X02pTOqb+D7K9A2Ltny
+0oQS4blkyw1+TzIxyKeXQikoQ+n6GyLsu9SZjvua0+9V8VZh3uI+hl1XEQ3
XQhkpP+3Qc7alnSsoWV1vdc1VGtD5Phdno2uYj24HzJbF26o7M11vkN7TKM/
3tO5NTQcg+YxvPP5wk5/EszHSveG+edoFaffaeT8Kej9TGd7svupbHvXs9Rn
g9T0etsXQn7paGrPDShKfWvT/1IxhpQjnYy81iE/DFpz17Y9hfwh52hlPxbv
0+73kx3DajHj54vMDy8Dw7l/BLCYPrSvi/NKn2BdMJt3fwo+EOn9t/mUsSre
WHtyqxn/1ua0z1DFGlOcsa3clyGT/b8qhs7byMhOru0o5nSmRs5LV1ExgBUD
9B/kb1Wk9e6fUR9nDJ7XxWnheW39v87ZdU8SMvqxbEjAKyNtozYBOJ7Pe17a
76pFXT/UPllp++jtLz1o2m0kZS5nTbQMeIV1xoc8Mw68kfY9z7VMyGiaePtw
yFrbuvajeOYc73pJ9iiMU7+w1roMb49Qh2f57wQ0dJcdRrTXDbfpcy/rPJn+
lBpZag7OhVxcqOZ36F25uzudK4iVl3+7bl3t424JPPqNPvmU/tmdfnIFvmWi
HkeYY5/jnVc62pfMZaAfNEfL3go5jKhrPy7Ls3i9re/njPJvUtl+OZ4wLtaI
sm+0BNJl+S8eWd9F2VWl68R7n2r8ZE13pIX1DhXf82Qzz+WX+VZdRXuEM079
Ag3fUb/LJR3fUvFzX+rt2LpKCyvWrtKKqav/ND9oztAcUQOaP9a3YAd/H2j/
8RL5bws7LmFsVscdKdTCcUgSsjgWr+LwFpMKF/de4N6TlPUvPH4qv2sNHddx
aUeD0vvgTyz0XZAcZnQMpa6Msfu1ZqYuP8ieCdoe5Pb++Bfw7VJJ1+2O9pL5
PwvrjqXgM9zThHGocZjjZCpeZg7wGebo0fDneWADdL2U2d8kOrMuCayiHT/T
njLvPo0sRVC/KSUd/1Z7yNo/LhbnOGIP4cXx3k4rnpjyWgNrP2tMwPGVFFup
o/YGSzm/qLSxrildHZ5s5zt6p/a0eOYFIHNOp0t0dz4GOqbSv6bSvqUZF8Ki
vac1l7XR8uzWg1Nco6rUsV9a+9tVn5f/3VGMcemgaxL49aLWV12HzP9RxnFP
ZMuo9INg/iudU8O/VtD1GvfvZE6cCb6CnP2D3NWSPVCU++zz0omBjif05fzI
yi/I7UvkbyKz5Xs5FtxzNf0tN0C6wbL94tpY6jMGuAHvPiljH3Ha51sB3UPl
94kyfqNtT8Kn8+CujN8X4enPrLkrIzuVgBG0bxhlvMK9MmlgmA553Nsy2KaU
5VD3tSz2n/r+f6D0OK0vmOt+Ytw72c5+xsYHrA/9OfecCXGMixKMjcUBbVZP
0JqvuW19jlOfSPiZVXxEvs/KN6D8n9AOmWmXSnlsbzQxYB8Dk6EbkQqZRP48
Y8MT5PpCI9vUy55esarkt36ydFwoq4b2pqRHQr4Zc0UF6lweaN3evt3l1/0M
eJ30jzs7fTaYn1DbWPmhyNd3yMVG5KFFjPX6pLu3meuvQsvkgNPC5aAjbWbr
o0ovdTRt1ayRfe6Plr0gY2n69vbvV4b+9T3l187t9+t9SgtvoO5rka1w+ksZ
2uGc7CyyMa4x300J2OfAW8A8+L9J36003FTNY83s01L2OrLlkc2ObC6/4L35
kL+tPFO+of1byMe4/ItPCzgtPD1gHyAzAvYDMhI6BsTaj3Ac/bU+sIox+xXk
9zh05qZv30BmKzWz31OB0q/xfBXu7cq6u0mW/8KqhcxUmUAEbdMH+gp39HmB
fCN1Dtpw3mprm864eMeOiKMdSlDHKTqTBWbxfKlo+7mTfx3ts2q/Vd+x8gOi
/YTuyHj+OMt6ZIL9gsg38SfAwHj7zNI6/BF9bBWEVZI+OuNlo6DOofyRtaSt
esKbJNlaI5Nn6Z/ngDxlfJ6kc6UD+tZHJr7ipYWkxwlte8rb75D0AV9v633T
lVHWkzsFr/LAy0yUEQ4Upk+8o/bO7f2RMuW9b9Iqne06ayG73VhD9wAS9G3H
+DehnnUAjiHbUdTtU/BAraFoz6gS1jna0Mp6R/KBXh1aawLFqftkxsWDyGdL
aCgJX0sDs5p4f0p7U9IRnJzW7TNHYyLwRsDnYRl4JjzWNtGyh46A721IvyYf
bDwzT2sC3nc9wd9B2idI4L9aqbzXtA442sPnqbA6ZD9t/KtkgHJ+jDXe0sJp
/ae8/ELtjLNvqKwtrSMl/SjFJ34Y73jF8iE1P2A9TumHSzc8E3J0l/VDJukJ
I6sTeWFr2bU0ts3hC5G2QVRaPtWUHwFNS7k/PflhjCtvUmZ/2u/roD6D9Bou
yu4D3ufjPVmlvwP04RtyIu3XMcr7MgsC3sfQfoZ8En6WaL+EC7nenjZYBN5Y
0Xurs6MMSs8BV6bdR0Y5XoT8xaUAH8QZx3Z1WnqTiyljGzz6MMTn3fL7pL0y
2b/qnE1p7Zkpf5b7WkHnV+ACSf8tYUMWxTnd3Eva/9L7Yp1/rHMz7n0Cbi37
iXxOH27gmFCKDSX/pC1l1yM/WfSlt6Dn6xjHbmiGHL8mPXaeyca1t4AKvG8H
5W+XPQjv+pRxaDbPz2GiGQiNEfIvWtt7J9pD+YH8Eq2D6S+bGFt6Qf88xqKT
jANv0u5jZJvAc9vog6uAi8jAGProUs0TjL3NgOXtfUbTNsy+GufQbs/l8Ngw
m/RY+ujfkdZFlB7ibmRsOs90YMz6kvXvMOgpKB0YyjyjPUbq3Yh+0R6ZaAds
gJ4JvGcqpE8Pse3nEvrX2WLWM5eOeXagFHUuA0xGpkpBc0ngfenHM/bnQjZP
g2/Cz2XU65Z0GtJ5n/6o7HAoZznpcdAyvrax8vL9nyvJ/v8X0deP0MdmQ1OA
cagg70+EP5VpzEnUcTKwlvmgG/38Z+lIsnZ8Ted64BWU1bWtbcfmcN9K8rPA
0bRzQGtG5H2WbHu5/gE864TcdwGWItenqzufAP3xlPE4k33cvw5P65Z3fIGu
yGU34MtQ69t9SX0/T+P04mB+P2VkzmYfV9vhczl4ULaL9+i0P/d9qNPCQ4HO
Ybaf1D5eftr9OuW8DX3Z4H1WoB1jziXkpBn9Px38X631exZ/A6/R/hHPbqGc
88jUSWj/DGjNf22AJboe5n3SwzovoD5bgbUB+5p9TTZz3P8IuX0duVwXsL6p
9E4P0f5lKKM6/bQ3bTO8gtO6tlkyS7mtom3rKV3Ec/SRF8p77/DF8r6nTbT3
ILX32Dra+4+ioST95Yts9oUg/wI9gWdo9xvMyY+BhdBVlnXlokK+pv9e5NnD
eW3fqnO03NRnI235Ne+NJL9N42cXfx9sy+hvhMws7IYybkWAcyCzA7nvB949
D5noKv0w6O6E/HYBRtJ2Q/I4jlET+tc86aPQB98HUsP/tMC2VPZV80JLx6bu
x/tyaX8Gvn1G/18Kz8pG2CZV/q/OAu/yX0Il70kpLRwNrxckW2fu5TyO47Sa
dWNR+mqpeub3SuSgOWulZTy7FOjInDQEflwoaF+yisE3BbyM8TiNbFA6ON2+
mvO9KO8I3+rJ2tuA9lLgv8GfUs5f4EeUmZ1ndjLHTizje/4BprVy+u9g/qPg
tUP1bcMjW55vKKM79OeVbY/O0Bg7xnHPbcosAJ6lOQfaZpF/HZhdyen+0Fef
OvwCD2/C85+Au8DztH+l8k4vR/Z2xzvutmJuf8pzW6s57uEWcCvWHauQgTbg
RHjeASgJPUfTOP97QeuxVQUyMkffgpfXNScnOX2ogfO/MV5cl66G9PSQ/2Fc
vyQ9NcqZTxvcK2BdRdkKSF+xAeU1Av7l2W+49zZjzIM+Tn8dzIfSp/bz7OU8
jtuwpIXPWFuyTlgfcLwVpc+2d36D9m8ZZyox7o5BpnJqbxg5XQRtCws7vsA+
6Qmz5tqoNS08WYZcLwVGaq0Z5fjoZRgPejNWdKacYcjQCCAV5SyF1rqM8Zu0
jmbdlw15CMC3j+MdT6A3332b+e8f6r8l4G8dffP8yDMdkaGD1GMkY1idzPZF
mIf3JFJmMeqaq6/THYJ5xXYQVj5rfq/JtTYvwlrgJHUuWtHfm/rW3Kr5PuD/
FtGnTkHPacaDDTns50v+viKC+FEwvZ37B3V2em0j77v9by9ubGGn+6g/cf84
YAf3D4aOQfmt+ywdaJ03lIauIsC81v5/NvIyELwafv4J3zLQNm/rDAhZWw2+
CL926juCMrIx/i7tbrtM+RPbg9zNgA9vS/+NtvuI9tjFvVV513XZAXHPS8hX
NvC3jAkDuL8J8lyZeW82/M8CDX9Tn+aMGR9R/zWMH4m02wvId17qkkCdEoE/
dR/waqzT3wbzSr8XcH46ctussm2kpMe4G3m4A50HkdlDwC6gMfxr2cg6mZmh
904beK7zGca7L5Gp37PaH4t8sQwB5+zo9KD07ttVGVvvVHL8+WeQ6yLwpjHP
NiriWKAZeWdX6rYHuXkVefgYubrEPY9oo93QGdvO6T0B5zfQDjco/yZwWPtf
jKWToa8wZY2l/xQEP5/demfyizYJuicCDeBTCnzvwjjekjpX07jAvUn02dbQ
mgI9bcBlGzmOQblG1lGXfvoftHUlxtWvob8Z9C6hnonaawLv1TcDfXkR5WWV
vhL0lupiv2rvaw7leknoLK4zfWhams6yK7mdBZ3N5C+I9V56xoEF8C4DeHSC
47korov8St6kD35AWQvgwyu8903wPOBl0l+3cfrNYP7l4P+671PKO81Y8Si7
058Ud15jw2zqNBcYQZ1mhPj7MSPy0IY5LBxcN7V9BzagH0dmsF6Z9MsG0UbL
yCdR50aylQXKFrdOaTJwBB7sg9ZqYZbpGMqKBvLTbmWKep6WDZ6gWHFfU0zQ
jxjfmyBPzxX3um8k73oM376UHRyy8wLrq9LI3QxwEm31ofpMDaf79XB+AHLc
X/24m30Haw9d++eDeGYgMIa2aZzNdsJNsjndpITzRZlP91PGsCZOT+7ufLG8
9jfyn98ReDhRenNtnX6lu/NKtyzg/APobYuM/QHuTTt2op92BIYzZnwIP4eB
rzLGHYLuPPnt77htKfs/nsq1YsjgNPBC9Vt98yArtyv4XFvn21N5tmkZx2XN
g4z+zBwQhUx9yPOboKUUtJ+U7nIp23grnucvXPsGPk/nmSvw9DIwGrl6DjgQ
8PilcezvrF7XFKMuhdOYvhm0RwT4fcq7rD1X3jOXcnbyrnjquQx5eJ12P0g5
H6l/0pYl+K8g953juUMB+6h/u43PV6XbmdDJ+p1Joc631lk0bVMZyN/L+5/a
B70L/pP6Z+Qd25C5F2nXF2uGhFSpbftb2eHuLeXYPYHejt9zmPeVpj/V6WU9
E9mwvc27WjLv5uS9rbg/PeNLUepeF778gAw1pF4NgE9JR8KbOlz/qq99Nf6a
6NgjikOiuBtHKP8SbfQdsIl2Oqp9L/D70NSKNvs4YB0e6cNJj+dfaK9VzHFc
ekP/JxovgKbweA3z2GpgW2WfHeosUXsinwb8/XWNNd9x0tfBfXj3m8jTfGAs
8vgl135qbqz8GGChzi9p7zzI23s6A0dWdiY6XV/7frkcv1UxW1+o5XilkoMT
AWPJgtKfBfxNPgvYCz25eS4CSGjvmNPHCv+nEh9SEbl7mzq/j5z9zn05GMtW
80x+3l8QyE7bfYaMlGzjePbXqju+/TDGoCfI1+M09m+/lHvTAtuhMQP8+Ehj
CH06q/RwgZPQ80mMY1S0oq+dCjgO4pFc9tXcF3l7Vj6YuP450Jhn+/G+v6U7
AF0DuO9kTqcH5nL+OdprMvK1C9n5Qt/ZsdZXOyPeB7xXl6W5/b7J55vOgnQm
JD9Msk+WnbJslqVj/7iLvykHBn01HIu3b7j36tpXXDqd6fH8VwGn53Zyfgzl
P5KNp3wi1LK+qXRMxzdlPQK057+BtNdD/r+N/HyJTD1hzHqczXun8t+j/VPF
38wY7Ricu5D5qay5pmdxfL/K0gWK9v6E9inCNIZQ3hfQtYIy9/GeLdLPpLyu
yM857rtRxmtArQVfKemYeoqnV4xy6oA/hXfHanu/VHul54ELWhMiD+24Zzj1
GgF8zbVc8OSbgPW4d8n+jTYpxPtH0dezQ8PfrYwHQ8sgYAz9+gUgWz7vfX0X
6f2vcMbO+swP9YDhXB8GjNB5JH3tRG7b999p5tiE2n9RTLJqvR1PczXfIV/A
3+VlrauzkXfORWYLQUtClM9M1zJ2R7G2zE5bloeeUOoXBqyBL/8wLizh3rOU
9ZR+Wo77rvJfc9mwgd/kv3v892suxyOqQz/5ljo/Rr5m1XCsUdk7D29hO2fF
A5Q9p+KfyJ+k/Ev2AL7RGgMYCL8v8nzqJMd/S6GftEB++6Wx7qp0V6SfVYM6
VI21DzrhZ/o4Ld8a8tX5Gvhf6hLCO76jvHbQeyngMxTpe8qe9xPwOclkT+sQ
buL2W/Boc4h1ulJirPvQP6g7d5lrZ+lvi+DXYDpJbEbrlkdn9FmtzmVlEy2d
Penr6Yz3aXvnlb4ScHybqwH7c/0M2WurfTHk5gR8OZ7Xe2DaCzscab+vukf3
KqaJbLm1R6v7dwafSc09H0j3tphjlQwq73glIyjnKO3+C2P1+7KF5P4htH19
xqmjjMV1mKuaITdPKa8M966j/OPc/w74PdptA7z7lfF0JfS1qmEbVKU7VXS+
QJx1Q6UH+hblfg9eAh7J+3sUtb7de/y/WTqetOVEaNou3X7uG0n9uiY4xmDV
stZpux7wWPQD8CPQg3LmwrOv5duMMWgJZb4FvNjSOo+vhDgmtPJKa965GJx7
GsdaL1B++CrQxuWBtuU9rmt8LyebYGi7Qfov5odDyNa7PPMT+S6sA25Q7s2A
9yr0Xan9Cq1nqpV0fJspvO83eD+J9e0weHiDMX4E/JwGT6YDt7j3VsD7sNui
nK4S4/xY+B2THNTxjTT+zz9dUPf3Nvf205ko+GAvp7+Odf5PZPcvoEayQWnp
Ligt/HMwLXygl2PW/xJwzIcjsY73cRT8T6z3dKXnoLTi1yivtK4tiLRdufRz
ZVuu9M1gXrq40sGV/q3iIig+guI23OU9SYydvehPl7s5dtbVavaH1aeXYwl9
D88rdHO8sBYNnNcecv8u9v95B/iVcu4BvwWcPpDH+Xrwtyp0RgH3yS+E3t/F
qwRfD4DH8I02ivZ5nXm0eLLXJVqT6LxzRHDc7E07PODaHwHPecLKb2Bt9BAc
Ln0lxo7PgA6MI6nT2RbhZfrQQvrieN47kzGgAvJcVLaz0PcC717BXJ2Z648o
4yjjybfw4aC+rRr6f9lfyPbiEHBVZxCMIYUa+CygHnyNi3UsoyTa9GZ9++Oq
U9o+uerAu9ph1r9cxZj4mHe8Dc5F/zyhPcJKPpO539PnMooxMbKF40k8CTje
qOKOPi7imBFPijhuj3xt/hlwv/9LdYf/H8GjTym3B30ivrr9GfwdsG8D+Th4
DrjEPX/C878aOVbSzHqOlyS/b5vg01Tp7IOf0DePU/d/9G3B3Dm0jvUutXer
PdyW8K4F0L2lQeksXK8A/XV7eq5vkOx9c+2ZZ4bHEyhvmnRwkO1zpMtCYxLP
zuV9DXn2eXBv8tv5/y3K2SEbw77WYf43YFsF2Vsr7pVsrvtz/w7Z+rHW78dz
T7nnCuVODXVMryqykUyxTujgCtYPLRjUEZUd+br83s8+rT1aYBJtGJriPV3p
hio9oZ3z0kG9mt96qLIplx6p7Mo/kY6n9IyB9YyhMbR9NPBNVettrgdC+e8K
NIfIjgg8TPYH1C2io+N2XaWfzkI+i+n7FvyM5lzZlwCvJdo+R3wZCa03kL2h
8K0064WmjK3NgZyh/pbRN00YND+CpocVnBZ+DCTR3j0bOUZGOer5AXxKlWJQ
+lQd06vY7PnhT13keHBB7yt3hdYuQFwQlJZu2lbatRuydT217Wlep26Z9R1J
e/SGzpb0qTncu4KxuBL4S+T9K+B0H+/hz6T81Lx/PM/NS20d1DepawvueREe
X6bu46FjYn37C70bY5+haVK896ozgUs8G5Pa9tpPg3bb5YBXWUdOAdZRZjrp
alKvemXsT1N2dvKvORb6h7Cu6VzR6aEFnP+Vcu4CR+tZ70ixFBVTUfn2tOGL
1KUv7z9Zz3quStcIdV6g9AlwrSBW/hJjxGzauinz0Mvh9o0ztLZ1Wm8F9Vrl
h+MlzY/AcuhYBpShLhdYh82gL51jbkub4nQ6cPoU2wfJTmgW/euU1oFlfb6s
s3OdMWfgnkbw73QG21ZK30znacdiHMvuIJC+nf0eZ+Te5vDlPtceAOEqn7Ve
8RxeTyoO3wbmhBmU8YVszYAvKLc783xxnTcx36YgLzMLW39VuquR2gdMdJzF
InWNlX9G+lzQlQg8A2+6JVqfVbqsk8HfMW6MZm7JBA234NP0vr6mOI2K1ziV
8SY181Gqbrap1n699uon6fsYmjKn2K5de/KybZ/VyraFsivcmd32Srt0RoKM
XAfq69sTvt5m3P8Z+FzfKfTvE/Szm7TfbeAy7zhK/mNgJDx4LY33IbUfWRU6
ooEYAfKeKo33ptelc6zmd9I5bnN5/s/d2umv4NO5wtbTWgbkYv54i/eGxtgn
6Rp941On+Cr2N5cR+p6Bhznk77WMdVN+gu+JwC3e2Zq2r8kzN7gnC/Ufirxk
BTfj+bKMu2WA3NRtL5AH+IX1yQ3G6dzSAdEZJ2V8x9xzPMrx3hX3PQdlZEux
/4mh1GEz43J28rOqWk80R1+nP67kfIC61RZ0cLpWVefPMKasgraIvsarg+mG
tMNq+DmdMeMIdOTm/jxVrbvVnHZpCSxgfk/FevMN5Pqy9rCRgXieT6zhs49D
shujr8yA/vZALvhTTWsLYBByvRWcA5oLa4+MfH/aZSL4TeT6D+qfFpn5t5N9
nQlfAX7vaZvbpsm2wc3J87mA3EAl6ChKH+7VyDhPitMntTZn7I8g35/1U32e
ryedb51dAHm5Hgk8qOc+34b2zs5YkjmzffdFpdh/X0vevRAaMjBW/JZsXUT5
ZJaOsHghPsjm/Fol2+pv5l19KzqehGhJbmR6ZAv/Ywbbw2t/Pmdm79FrH79M
G+/rn9P6FNoWwOe53D+TdngD/A3zTT7Kyg/Uoo4FwLXBh6p5jXgQ3Bier4ee
Enz3paXN+sLPv6C5IbTHUI9GneyPrwX0nqT9nlK2AkyvzGjIhEy9DW7C9cbA
/J7GBVOczsAz/WTjDG2XmliPS/pct+Df1/Bub0/79pRfzeHwZ4jskEi30Byv
9TLvXt/R6Q9KO3+Y+meinEPgqowJsfTf1chqId5ZAbnYw39VqP/fyPp5ZL8i
9AyDjpe1j1zJtt2FUwxKX43ydeVnV/M3x+Lgd8fJFvabIJ8JzRn7o2mL27IR
Yky/Xtl+fxTT4InoAd+iz90EblO3XJndXvp2mpEl6BcJPqemnkV4VyhlhRR1
+ib9qzHysFL+WpCHOHiyqznjHFCJcWYr64oNjG9FuXc6dWxPeyyG9oPw4CB9
7jvo38d4tT+N/cQLlwEXhgc709q3yGPuf0Hf3DEuS2W+LdsE+k8xyl2XzbGQ
5KdYfscSuX9IrH3CdEpnv4XyX/iD7FSbeI86T01j5TfSZsMKeN69zDpkTZJ9
8z6AV2Op32p9lyF3TcFDmCt3NrUtu2zalZaNu/K/w+9U/N+KfpOqoufLuZRV
HV410jwN/jSvv7+lr1+Ya2elYwMcoN3b9rRvG+nGrqfsBtAUCf3VacuIdNZJ
SYTujdIFhw9vRPi8RevOcHhQVjqO0FG6ns+3f+zptel66XmztomHt4nAa/Ud
A0uxsBYzXu0j/yftdp53t9XZPvhbym6D/F3h+YxdbfMge4fLee1PS361EuFd
RnidSToW1PsObVCcOp8Nt//XAuHWBa/CfefBP0PjXaBEiv1Rfo+MSTFTMWzy
wcd64JIav6hrqRTHf5BPuhWtvW9ctK73jhUnWt+C6xmPK0BPae5NjPQ36nPI
eBr6TAXGtI1R3s8tw/99mG9uw6fBOeyPYAj4DZ6dVs4+2+XrQv68qjX1GmQ+
8vk7+GfmreVcuw0uSzkHZTsaxLd6Oy3dgXDes6SS998UmzA6xfZpslNLADdg
TPoFfv6lcaiM9X0vZnf692C+h87ZGJNmt7Se2EjyMZRznPbYLn2rFtbXl+30
20B56fDy38usUZbUsQ/0h1W8f6d9vEOMh+PqWOe7ULRtPtLQBwvCzxN5vE/6
WR7r6EtX/w64cSP7NZEOaF3wOvg2GDrjkYHV/NeuiL8dFO9X3w9vcF8sNA7n
fVm0Dwgv32BO7dTRvhHkI6E59FUoZ58I4XV8n+75SbxH9m6CU6D1B9rrBjCf
dEfkqbzGRWANY0nFIFb+SHfftxaZXJPFsX0V13cUkAW5XgCPajPvrA13Wteq
8t4qwOU2xmfyOC19lzHR/v+u9pxYg1Zs7nQF8M+xTuua8oNoh+u8uzC8rAQt
Q6jHB/RJhvmQxrQdU1FIf/pg5tT2B7Es6MtTsQ/T8I7W3F9QetjgrNCVPZ/1
ZaQ3kz3W+8VFo71//LP8OfDMOcprGOv40o3Affk/ALyU7LmuMnQsYgyvQV1X
0r9XpDGOC+rcZqd/Zgt17O2W0FNRZwLg98F7Y3z/AGQkHJ790cswmLaeHGGf
U/LnJx9UwlVS7H/gNLydCmxBRn5v5vMSnZvkgt736CuFuRagblHweDo0j0Hu
32EcHkd7X6SdmtWzn+T89O8YaNsivXzyp+kHt5jDEpCBDdAwJ7vtBKqm2G5g
HvSGSS8XOa/GtZRmjiugWJ1rka8nkV7XXeE9HxexzpX0rXbGOC2s2Nql6P9l
cni/M1x2sup/VXwGo/gT64L72PrmWAueRVlLqRtiHfIKfI3juXHgY/Dgk3D7
RewiXQxkuzO4OrRlp+41gvinnvZHsIT6LAXCG/t8tRnzds0Uj/VtydcDj6f/
76buHcAFobEA0LGtv40Vt7wAuHgf+yC4VtVp7U0rf5fnq7G+jofe9/LbV3z+
1Lb30dihceMu41QvZPUk40Ut3l0PmQ/TuStl3daeEdeuaH6nPeuQLgaeSns0
h09F4Uv/DLYneJ16nqOcGp3s10H+HcqCT1POUubw/NINQq7WyQZG+nA8U475
cB24LuUehddxKU5vbOF8D/XZlo4FWI/re6XDmMp+CgrI3quu0/JdoLzsUi4n
25+BQLrG+m9f8Lrys5H1+syvc3J5bJ4Wa9+tmehDLzOvV2AsyKT74fNVoDy8
ekP6wnHer9ZedbEE4zrBtEDpj+grf3L/J9z3F/gefAqj7T5ClrI3te7tEPgy
ibn+TFrHTNQ+XH21ObCQ65/KXgZaV8HfzTrXqua8rm+WXyLpRDKn7aXtGqa2
bkAjcEN9X6d4/N0PPdnge1YgI+8MY15IDZxBXlZI75g2T087vsU4/qSC/Ws2
5rkmQEfK3YgMNU2xj7/88PuJ1i2NHSs6HWVfBPIwnjfTOAw9a1t4H70/fbIT
NMcmGWqW9LVj0N1ctFHf/bHGheDDGdrhGdafX4LrxdnPaP0g7h9M74d/q5rY
bqoE7VMKWAd9q6rZjn8OMtaCsnfAu8M9DUq31LXe9jXaDFrT0d/SAj8ii7Pg
wwjo6FLW/lh1jvMDvLpe1Xmlj1GPRdTrldJOfxrM38xj3xNxCU7LB4XyHyLT
pcAHwXepcyve/1wf49bB9KkW3sc/18z4bLP/T2uPX/kOMbbZzkD9joVYd3pd
hNNjY52f39a2feOkx0Y+lvpU0H4CcrsD+CKv41IpJpXiOUvfU7GkynR07O8q
/L8f/Gte+8VaF+N4yYqbPKKyfXMORC7OhDqGjGLJtKEOy5GZw/TJo+FOC68A
561rHAmeA39rUMbEQo7Xq7i92kPuBT3f0j/G0Z+XMy72BNqm+ExpDePG6oyO
N7MY2ehNm47OZz9No5g/ijNm3oaGYuB2PHOdeeYDZGsFZa+KsB7jC3183qU4
TNrX0R6P/j/f3P9L33Gmvr/TWX8+gjq34L7ssnGCt+WRs2Hg0Fj7jJ2dz/+P
RcauaY+HsfQPrUko7xV4Px7Iw7MTE+wvRH5DpHtdife2h5Z1yOs7QPsU+wG6
FdTP/gqex6c41vZxyo6jzPVciyjgOB+Khab/dZ/iOp5hXD0rW4OiQf1OfXfk
d7xH+XLXelnxu/VMXuam0cE9xZKt7DNX54BzyDcWv1gjL5dNAXJfqb391Gm/
diZwWPNsiuOmyzfDKui7Rz1WaA+HNtvL2uIWdQ+jXdsy3rQHErm/JXPrh1yP
inE+Lzgt/C7BvFOLOfEr5rfzwHxkYgg0D1P9IasD9+6kX75O/kpef0voO0L+
HN6ljO06z0tl/b2iwGL4O4Q+0THFaeEU2uwY48Gljo73Kp8pWl/IP/cZaN8n
OcnsGNOv8J0wWN/u0pOkv1wEr2c+f8g82CnFvhsUA0dxcQbH2O9WQZ256Ays
qWOhZe5rW7QTOk+oGLTdpw/Ecr0KZXamjFul7QftKvX9vLr9S0yta3v9GW1s
sy/9Ne2nV01rv7IlCtqvrXS25Uf2RfAuzTXyN5Bs/xHyKav/rhXx/0Nb2j+F
zhZ0xvB8qHXDWwKD8vncdBPvb0775G9n/8N6Tv5p9ex/5xGhvv8w38nv0oaz
65sm7fH3pZ6n6Hvd4UUSEIOc7oMfsUGsGD1K/yz7M+AacA9arkLvb/mtpycd
va7IXV3WEfWAI8jMoWzWuywIPTt5ZjDX77f3mYm+UTtDV2f6QBcgBfmZk+B4
mh/x3xTo7cL/XVMcE3tCdsfF1vfaEebEgNpe91LeTPA13vcu9GyRjia0Fmdd
/D19cmJt3zcJ3L6g9+jbgjNBUxL94FFb+4vvxnvm0Wa9e1j35u1SPo84WM9n
EpWCZwqtyKdLdF7pz6hTNfLzmUemSneIZxpItzu1zyHeZD3wb2rndRYxBRkN
5/9x9ZyeF+b8G0Gs/Hv81412TEWfLY08dtf+n3SstU7nvxvgncjkhoq+pnt6
lfV9A2i/NrTnQPBBnREhi/OA0s3tF6NHShAHnB7CfcOAlZTREJ69QV1j6f+L
whwzSfGSlH4rmFda116lLkk835c6d+xhrLx006Ikh0BP8uHwsRf4LfpbPtkV
cG9jZHYCc8Bx2msM7TCAdoqExt0lnO5e33ndu4Z6BSi7UKJjQM2Dvj2MWc8j
x8/B84LB/+Sj9nd9i6X2PcrreuMg1jWlxwXX8D06+ky+L3Xu2dZzSkuuNwOm
QPNZaJ0KjmDeXQQ/9yJnWeIdQyI78pSEjBxAXirrTJ26JFPHoeDeKSH/Gaxp
/0jp0MbOK/0a5VUr5LTwu7Tp94wRfcj/UNDp5DTOK907jfOltEcGPEs97lKH
34CW5Fchvy3AWZCxifTfy3yLHGNdsYX7tpfyGeOxLs4/RRbnc89XyMwwntnT
wrYwsonJx3Nf5rTdRhXomsmzUcjIUJ57Tjpo+saT3GrNy7jctoj3BbQn0Ff9
hrH2UZJ1JNrBl7bVfe4qXx06exXenej0O/BzC+N3HO13gmsnCtlnxz3a/Ffg
Gu2SjnYfRZ0etPBeYs9w7/19IX+aWo8AV6WPQ3tMRn76ibe8cwbwMbze2MHr
4anU9ZWKji+1gnFuTKL3Kw/J/w/fBGfhz+7K9r/xcWXbLvwUtGcQKP1D0KZh
Qmfn+0vHKLP11M9T7gHk4UJFp8t0c34K8+HIRPsZEj1jGDeeB54m2b4hbV+D
0rJ5KNLa5zjFwJUZn9rRP9rms77fl/SH1joPgddhjKWV4Mts2vgX1vU/A5my
eR/wOcaBZSX93qfcW6CZn9H9maFnTgfHpRcPxIuf6F8bwOfCHQc9H2UE4OOH
sY7JNTXIt348f1u6F9QrHppWVnFMedkqVwH2d3aseV3Tf4+Yr9v1tk3pDORh
POkylRy/vR7tXx94ppLlUPJ4uai/NSv2cRzwncjSj/B2BOlzOnsC79eanXnm
Rn6nU1KcXyKadQ4PrOC+wvD0rx7uK4qTq/5yoYe/tWT3dolrIwt437kP48C3
XGuodXKieS7e64y7FNBfe4eZrBMvffjFrM1GUc9nqzotfKC1x3+N/SfBaanT
u/DjV9qiJDztIx2pdJYByWOWqo7Dta6R20I+cPvKVh4Z6N7KPqkkMwsZq8tR
l0Xgv9rZn+wnjM+J2gfkmTaNva7QvKu1hfhcjfs/LuixTHpGGtvqtHasLsWE
VzoumD8Pv67yLX5NZ5b0mTe1Nwd+XvbivR3vtSDvzgPuA03bOvkMqCzj21vM
KfsK2K5kMM/NTLQ////WPxW8BuqvM3rGj0CycVIwXZ7/R/HMNuj8pIBt1WQr
N76OdXK19/oSvP4T+Uvm/hnUeQTrqZHAIp2N0PbzufdOep+Zju9qHyLyJdIR
3u6mPtPhbfFiXgP3aOF18FH+K0u9Dlf1OK8xXt8P2m+XrqX2mRbF+HtA3wKx
jP33+P+lYv5++b6av2Fu8L57XPupq33kyy5ffvL1zTOqhb+BLjFGpqY9y8f6
W0vfXIPg/wDk6VX6eNk0/oY+1cG6aBq3NH6VhbZR8DqZNrqc07pQB4PnXito
s4pZLJ9Lg/YUA9VnqNMw2Q7Bp63hzpdqaqxrSo+irb+XT5pEn5d1ofzPpYcm
HXDtQ7DW+oBxcLC+U+h7m9IbK7+D/rILyMwclwp5egaeHilve2rtS2h/QvsQ
e2t4L2JTee9lrJQuMfUekuJz9V3QthOI0H5avG1iPmngNusA/FPb88ynyEnH
zJ5vlFda85fmrmZtvY92tJz31YZzTwQyWhT6p3PfnhK2v67FfPaaxucs3nvT
vdqT0z7NCrWvzpTJr4OHJ3o6PaSf80lJ9smdP6vTzZHRbxs7rWvKD89n353y
4ZmTd/7CuJadPl9fNhA6t9OeODAixT4NCuZyfJNxub1G0FpheV/rDer89Qj4
Ga5/zVhzIZP3WbXfqv1XxYPO2cgxoTdoj4h16iPo+Yz+0DPafmG1f6t9W+3Z
Hkhjv9sF0huULggeQHufln0A9Z0vXwI666ZNTyNvg6D581ben9Y+deo63qdW
vlke+1ZV3NNE6B9G/iZyMFw+UdTXgK/geRN9E8Lb+9DSW3LK+3qBe8KfJGBG
CdtCbkQGbha2DfbKZrbJlg1KRITtUJZxLSP8qU//2Uc6HfJWn344inLbw/t0
BexfWr6mh8H3T/n/BCCVK53vrKJuw2V329V709qXzi17f2h/qDGHsfMgfDwG
7ozMFufZddKpq+mYaZvA4yl/WzWvOXdB8wvw7WftwaZ3vNqMPN+IesxGxuY3
8FmmzjTTIbsHufcI11sn+MxTZ58jU3y2rzN+nfm/AJ3TZJ8h+oM6D9J9yMBc
nV52YvDyVf5rCs8OVne6UQnnH5a2Dxf5bxlFuY1p3+8odzj99Q60rISX70PP
PiCcMSSCOp+Gnhjord3IOovpqOe3tX3tWcqI4h3buJYP3CC3/YPLN/hixrXo
ih7vG9EXy1byPC5b0QTe+y43XmXc2FrZsaIX0fczaWzkmTH8f1l7oLTHa8hL
KHJ3njE6FB6F0VhjM/q6rs3Ma9uKI01tb6G07CqUP9zUWHnZWxwOpp+vZRsM
3TuROj9HPRKQmTe4Ng/4mXa82tGx1osBo/n/DteeTzEo/UtN62/8Vdo6HP3o
92P4byxwg/E2k2yBGjotfEvrPNr+Bf6vn8Gg9BflHd/+5xDbMZyizF61rDel
/y939T0vkn5J43xn6/RJt0/fs0vg4QzGjizI/8sptquUTaX8kX0B7U2S/T2o
b8Ew4A+uDZIOs8bdtLaRzMi1vyWHjAvR2run/dogV22B7xkjGkL3tWj//1cd
+xRfpH0l2ut3+sAoyrujNSHt9ZD2nMn4/Ag8gnuqUH61tNbJVLxe6WVu7Wxd
TelsvsZ42Ar8LOufjTl9DqhzPqU3BPMj4d84tREytgrenKRvfKb+QRsdLWk7
wpvIYy7GuRvgQowlC+mfPyKn+yId4+nNCva3KL+Lin+bHp5e0Vl8H+sCSyf4
YXPrFEu3+EvVlX7xZxPr7L/LvT1ivMeh87PS8T5PSxfpcVrjtWxQdC4q+5EI
6a3Srv3hw1N9w1HO342991ktj+0J6mlOYOzM0sHXIqlPdfB47ZVD+wTwm/JN
ofktwumNfZ3XPsxytQl4Kvkt0BXIZT9+Pco4zpRiUYxgHFtEfc9I/62OfXOG
RNlXv3z2p0qwf4YMyN0w6vlAul7U70/qcFbrR3AVnafntu78Rt65IdoxATYG
seICyN6kNjJeNMZpYdmfKBbptUTHJn1AuS0ovy6wNsLxX59t5z0o6e1rH+oT
aJiYYv1e7Unpmvxh5+RdFxgXSkPvIuapcuRj5LMA2Uqh7y7mvwr0h/LAJJ5f
wLW98HM++FXtPfayT65F1Pk3+l6+bPZTLfuUkjW8N6c9OvnZVOzlQXGOvyw7
qPi8tosSb2QnNYfnatGvawJro73vpz2/Iry7P2PT3Wr2iaQzJvlA6w6sibSN
l/yuXKU9ytC3Sme3v37tH2ofUWcmf4X53GQTa6NStGsN5Jvi//MzJH9DOnOT
H77xwELp1MG7ReBJOnelnnvK2d+k/LwrFsZl5ONKZ++JXYDW81H2o15cegji
CbgU43oZ4B/G+xGlrT+QLcFrHcUFm0K5PZhHuiA7neUjKp3Pse4Ez7R0lqW0
rgvLfkDXDgavT2WNkJryC1f1WVdyqH3ZTKMuRWrbz61swbI1tT2Y4q8o3ori
rpSr6rXtJdpuWEnbn8oOtRwy1ZIyN6v9obE3/Wtqim0KE9va3nA1Y/Rn4AuM
Gffhb5HMjpGSjX6wgX6yHtipcz2emw4Mot26lLCfH9kByx44LW10gefOAz2B
72nTt7V3Bn4tg/1Qz8xg/9Xytb46zmlh+bOWrZt8WistG+NxVW1zrPZV234c
4X1u7ZVrr1tnXzoD6xHrc65ScbYr+SuT1+2yh/6bdhrb1rY48tUte593gPXl
nJYNkGTon3ifxSn9V7zzzXlXM6BDHfuk11mU/JIrXSqYl11JDtIz4nw+lZGx
ekaKQTox0oeRb53n6aO/Jf0XzvS/OHv8/osD+GUHxwLU/kv3KPudL0q/ONHB
ejayZz9V1Dbtr1HeuNI+H+tBn7yP3C7t5rMCnRHorGAmctRH+4fw+dm+9ou1
iXVLrQT7GzrXwuniSc7PVD/l3ofkf2a9WAw6O8leiTl6JmW+DuyG6LrQczed
z0N0LqJzFp2R6KxE8W9lWzIFGZgGfpa2G1DMsaVX5nNMo04CxrpWtN39Oj7P
0dlNmmSPdfI1ID8DOgvSmdDDKJ8T6TxpTHv7JViADI6tZjykrNOyfb0K33ND
73bNO7TJrBSfUel8SudU8sEhXxyPmrscPScfB6mDdriyx5UfBvlELUk/aAOP
H9A2f+SzH8HR/RwH+6i+dbXvDD1ftPI8+w5rotnq8/CuP+/rxBg9SWsG6DnN
OHCxpH1cTKlu/+SKP1SefArvuK+9avhylHp/Amzl+YH8twW8vbLtb8/S/vXh
a6FcjguqfSj55JU/3qrUoTjjQxntzfNcHdalhyvYJ4p8oxzTmoWxIJk26Q3k
4t05tc7luTo6+4Dula1sM9YyaEemmETylyO/ObKjnMs995o5LXtK5W/Aixju
Lw9cki4N/esyeDJrkJHwrB1tM6Oav6XysCZLHe7Y8E3hURMgLNzXtlNOHfrq
uFz2BXyukP3wjqVOLwILon2+qbPNd6B/M3PZBspfD6yp4P0M+QBaSLv0gpc1
GtnOV/oldaL97bsJOApf+rT2mesb0N8CWu4hK5Mp4x2Nray9xvG+xwXsa+gJ
+NW89pElX1lvk5/Hc52lM8J9D6BxT6hjMO4J5v/knjcor36Y+0dSNse3VYx3
xXrfST+bn2KbmL3NPKfLh5fmdfla0n8HE4z1v9LJ1P0M/32RxukDXFse6rSu
Kf8bY+SbKbY/qwftj6jvaOkOcN8a8ZD/dgax8ndkK0X6QKjxtHpOfwM/CiCL
i1IcC6BNftu8CMsGRukW9RwjYH+o5+lLyZ63W1SynUmzIK7Tx+ne1GMhzy9O
Mdb6V+kfQ2wDolh990s6DqP+U0xGPaN75HNJ/sjll7wi955izDsJrAm2hdpE
Z1+Vgudf8v10FLpXc30JY+CbXI8Lsx6DYkUp5m1TYAlj7VvAWv5bAwyAriHU
p3Uq+7IaHkzLFkq2LrJ5qY0s/06ZOeHRz5Ip+mE1/qsaY/0H6T7cZmx8C7pW
IX+loD2W50ML+AxP/orlg0z+x3rQN4fQbq3pF3mp/zbkaysQRjkb4FsqcJkO
1sP7vrqvp5b+dB7rj+Sj3I7Q3RhZbtvYe5SnQvyfrv/KeJFa8g1eAj1LgWXA
htS2U6pDu/wbZh0V6apIH0XPqoxp1H0G8H0P++bUekn+OstWc5zB6gWsP9dU
dlDU46WCxspLt07+qP4G3pDuXzfrw3D5P9+gcXkcH3JTguNBTsvsvM7llO/S
zz6p0nJvc9mz04c2IeO/UfdNXM+Z6PSWNI5LpfsUm2ob7bOfsa8/9VlDG6wG
9vHOHIm+twq4Hs/fpR3e59440j1Zp2SvZD+rd8ra16piQSsmdD7qswW5S9vd
/hHSNLE+0Gey3wGG0c+Ww7M3tKde0df/l9f/b1T8/3t1fV5FX5uV2v7356Vy
Wn74lZdvrfka+8D9fXwc8rSq/aPJF4d8csjfhdLZoCdnafubld/ZvYyhe4Bv
tPeU07HXh+o8soDjESsuseyM3tS+dhPHn5WvW32Dl0K2ygB1eebdVvZRGo0c
x9PXRiOr5dt7P1/6UdrTX0t/7w2PCsregbbpBv/aM5b/W8L+L+T/Jy9r0TvM
XYfa2g9xtqz2RSz/H7PBc4FC8n/Bu6qDJ2hc47vgVCr7TqZ6ITOSrMetMzOd
l10o7P++LmzaNRfLv28d7qkN3OP+3PTHHdJ5C4LSOgtMp/1I5rEadR3bvCLz
VdEM9hsSCVTk/Z3a2t90+zaOEaX41FobVdN6hXT1VD6P2wFEtbWNjOxh5lR1
+n+2Mn9RbknauT71/oU+NJI2fQFcUXt29e2/5st21nf7At5Vh/aL8LcTtC3k
3YuRiWrI9wHZyDGfzC/kdFik808qOYZAuwjHFHgz0XEFpHfzadB3ZTX66nrp
7nD/QeaWVyn7b8o+JF05YAW0bqfN88oXUlXbk85Jj3wCo6A3IYd9nI/PZB2o
71nDpKLNrsOXnFldvsqem8s+25fksN/2W9TpJvBcb+skfiHfIrTXWX0Pgzcg
d3+mtV2t7GufBs/lyiEz13n+YBXbLkbQ3snkS1ayT/DqQIl89nMvf/dpgJbI
203qVIey6lKPHynjB+AT2udT4C/4mIZ2DUFOiuoMTWMyMIV0hQa2yX050TGb
teb5ubTpfIRMF+W5t7l3NVA7vf30y19/Ecau2Ia2/VzDf9eoU0D/AZH5rN+y
uoLXalqzyV/KP9RxbYrPHYXlc03pavSVJNq5B7Cbvtsamltltr88+c3LBp9+
hX+rGEOP1PD5vsYmjUsHeNd+6aDAg2nIZUHG5Ckaz2obK78eGt4FnqGMZtId
BZr1dLprGuelgyr903UpjpWrefctcDeuH4b+jyo7/onioLzDPTUZxEcxZi5n
jPqTOaszbd2PPtiJ93QE0pEOg9Z+PPcZz+zTuSqd+QVk/I70jijjFngvfeNV
+v1p2rkZMtsfXqxPMShdBtpeRL4mQMt44Eve15x+lZ6652GMzw18n8F4Yzen
5StfusEfh3uNrtjaB3jPdfj4k85S0/qcqzfyfSbZcXEUH+cU17qlta31q0mO
vVpPel9ACvd0hxel6D8t4ffEKPu5kQ/78HyOLaXvkknIzYYUY+W1ZqzLO1pR
1o3yjm2lGFdngFm0QV9kfjZ4LvLbj/Tjer6m//6X7xfM76vmmAAbU5xWnADl
FTdL8bO0Ls2KHORAds6WcFp4ayPjc8H0gjYeX0q39P6c4pQpXll55O++bNz6
2tZhWR3bXysubi6geD3Hx80dTMt2TDEBFCvgT2T9FZ3tU89XGU+ioGFyddvy
y45/KJCvgmO0LgLywN8szIdjajvu3iZ9d0DbbwnWlVZ8uvw5rIe9mbqvQwbq
MJbGVXQswGJ1HRvwCfX4vRR0y8enfEYAM7h3KHw+xFg6DFyhguNO1tLeA7K6
CpiU0zH2CiR4/2gA/TcLbZgNyK6zBeq2OcXpNzM5f0j+F5Dr7MWcblzN+bcZ
zxOQn9Xgl6FrXF3Hsyve135d5dN1S0rQlxdtsImxczTjw4mOTh/v6Hw86Qj+
jwRKVHf8hB8a2f/TIPg6JKPTwvL7JB9QwspX4vuvG7yans0+9vbQn/5hnt+q
PQfoeruB09uC+cVNbav2GbCQOs8BDsLL642c/4h0dvi1XeuYcPefvq3tW6FI
A+sVVWpk3+atmItbAt0ZZ7vy7otaj1HnDsCL9JlI6Bwe53PshfSJK6QvA99T
36c9Hb9AaWHFM6hPH4wPdXzxy4Xtz+sSeBjy+Xp2xzyfmtk6XDWYD8/RlgXo
s8mswxpS7yHMRSOk58bYc5wxIS10L6K+WXNZ320V6e7IRiPe15S6HoauzbRT
W+kewcP4mj4Hki2YzqjT61xefNX3hs7DqePL9Iu3uC+Pvo/AKToLBL5J8FpP
68MGqW1PIVuKstwzDH4MAXb2drqL2qyT07rWJZjWteGlfZ6ncz2d+4Uxf+yg
LYrDm47w4h7t0Ak8BZqXae+edD1oawPdZbl3LXVeA+SOs65Qubq2I3qDtouu
62tD6K8p9MMVHayfMhJ5Pkt7/Mr758CHpTl8/qBziM+pf+tijiGgWAL1pU8C
DOf5DPB5iXQkaI/hjP2/Q/cY6ajBo3j6d6u8jpmoeG+K9aYzwce029aWtluR
zcolnv+NNv891L6ae9G/TiJTn5Wzn2bFYta3kmzLdmp+AHfVXibl9wCereVz
qSy84yT9YRg8PwF+HjkZDWTiv470qzSytwAX4d3p4e3PXTyW/zemZ7D/pVPQ
N4n1xnTq15lrsdCwC5mJpK/PQoYuUcfvgM+l+wAvG/LOMtqvgq4lpN8Tfcxp
S2m3db0c7y5Te88pOj7QuRBDUshqytqex7ENtoGnZHc+H+PGbtLvZbd/6VZR
jvPbFz7t4plCZey3SLFm5MdoK2PiFmAgtKwBPkUO07T0d+Na5DOZ/A7KWtDZ
dvC9on1+vaOidQTW0/ZpKaeX2ovxYBS07uZ6sr7d4M8S7i3Ux7GBn9O+JZCa
Pp0G2NTB6b/q2gb97Wo+d/oSOdpDGRORuVHwdkuk7bMOU78GQXw0mG7Kc3u5
9w71SYDmi8hse/D7XDsKw7bwjp872B9Odv4bDb9WkF6ufTPGk1ggK7Q3Yp3b
Cdm7FWM7tFy8MyfQB7ncpT4J/wcjV0OBi7zzY64fA54ib+OQv3Eqi353GZ7d
oD9d0fc+c9tWaLwHTz7QvAu0513P5DFW/oPgNZ3Lz4buXvJZxTty1rUP9lbI
2wTWcpOAnMhwX9qwKnz+kOd6tnG88Y/6mcZPwDvA39FnVkinX/ZzlPGol+Pe
yu5PNn/SG1nBu5YDH9DP97d03DfFf5NPjE+huWc9+wxTjFfFeq2lPg9f9qf4
LDJ9F59XPoy0H9+IBJ9rPQuuDH4MDU+AAymOS61rg3muCvfmg54dPPdzXsdD
ky2j7B3lS2KB1qPA7BbWN69JvU9FWkd9SCa3wQzaqlqkY7oonst25CSS8j/g
uW28Ywm87KS9hhjHplY8Mdk8PEuZUXUNV3lfPPzKjVym0h5jJsf0/A1ebIIX
P7VwPIQU1u31mV8+RYYaNHZcSu0ByaZFfsMOpth3mOIRf0Zb/QZNORk7bjKW
Nqxjn39Lgn7/ipdwnDzFyBvAO+8UdKxO7e0lNLWffcWveERfrcnzaxg/o4GP
eEetaH8LXEvjeKDSQTqDPI9l7bKR+jTl+iTGhd+gfUKI10eKf641kuIW9A71
uRKiGfIVdJ3VmE0bH6LsC8hQOer7N+0dDf4cusrmto6R0uVyO6/4C7KLVQwG
2crKLkuxGHROofOJVsFzCp1R/M+uRjY1L2v/IsSxThXnNEOC4wUpbtBh/p9A
v58oPRetQ3XuUN6yJ7lT7EvFWxBWzAWdfRxN8fmH8MEW/5/Wf9tibQ8su+Dh
xbzv/HEt5+8gsx35fzh1GCB9OPhcmz70ZnnbcEkHSmdFOj/amtlnSYqPqrMl
+b/qD99O0a8ikMWWrBNbF/KZYdoEn/P0oI2WI9vddNaY17bKH+t7nudLUpcc
9J9PIh0z9BJ072PuvScdbWjI1dlxNBfWs83FbJ59sbLjAOqsTud0Oh9VvOPq
4QalH1HuL1E+R9eZhOJnSL/+MHK2DFraUM+55exzsD14AWVmiLdtX2PZB6Sy
Ld/4IFYcEKVvyJ8EY016YD7lB+IcP+1X5DU/Y0qNzrah0pnU/niD2l7nVfuD
15VXzF3ldf0+NH5LOzyb1+mxUc4r/SCY3xJsX7Wj0orTprzSs0OcD1DPOtwf
F+l0uWTnHxd2XtdpmhCm2ZD6PBfo4O80nak1qGXaVYeCzGeFgbnIy3vy5QBM
jbRPwWYR9j29DXlYT73fbeF4uPpuU0zcVchQF/keZLye0MX2NDozk+2QYjws
Bw+Hno7MZ8n5fA4rnyV7mUd+pb+H8FxXeHwVujYjh/9Wti/P4fTnWxBfiLYN
454ass3l/mOsu18E16U/1wOOMr8WQDY/ZyzfrffQzh2AOawZf6TMT1Icz1Xp
YynOy3fHV0AexrHTxY2VV8yy0z3tY022Tv9E295J38L6Dr6OLE3S2oAyLna0
b4FMQf8CxZgrfqcNF1BeN+4tKB0Q8iOy+SzjBdZ/v/QzVv4d2moBff14cE9e
+/GKhaC99c2hjpkQKftBxr0T3BPLc9Mkp9WNdZai9DXS0dD4mDbrSR2ioWds
eZ+36NylXRArdqzSr8ieMsznM3dD7Y/s11DbBMkeSDEumnDfFa7lCHNavruU
/4e+N5x6/8q1cO4vTbt9yLueaekzE52d3OG+lcCKUKeFM4c5boZiaCRWMCit
2BOKraH36mxGoLRsk0TPv6FOv8vzVeHPBu3Dw8NptNHUnj5z+SzF5y2KNau4
ddqXWhs8l2nQ1Wc0wsqfBBqTPpViUPoe7TANHpSgk9xMdNya0/z3YahBZzM6
l2kjH1PI/ovAJ6wVjiJPJXi2AOvZnLTju/THz3luPvK/rp/3rXSO9r/zNOWP
FfB5is5SCoXZFko2UbIhql/PMXx7UuY+4F/WrAfT2ieG/GEo1kPL5s4r/Zhn
qwFPgAUVvMEtX22XE+xbYy5wnf9eAuYz3rWl3cKp48NUjg2jtK7pDEZnMTlZ
s68rZv3vVPSrvPCiBpCT/lWUua8EfbFJRZ9NLEjt84n9Qb8f8v+RIbf9fyg/
gXsmwNsKifZ/p+8bfefUD37rnEyw3xD5QdsCtOT+N/jGfYNnptO/3qB+Myk/
pY/j7a7hfZ+Cn2iPBvrPMUZ8BfzZwX7RZLPUoL7TwnUZa+JyGiufiW/f53ju
O+kC9rVfrgPI8jOMd98jc1eBcrJHZfxYwhx0M4P9iym+rvzyzQl3vKEcTe2/
azp1qkVZy5D3U9rLg/YNPPt7Jp8baP8xgTH2ZB/XISbMaeH41E4Ll4W2UPmj
kH17PvsBOIYslmes3QdfyiB3pUOd/oL2bVHQaWH9VyTJ8bVlc/oW9P6FbO5h
3NqZ3/bzixnfVzIGp+YdqYBFtM+1GrZZkr+ZdIzdaZnX1jHWvs0aZJHkAzqa
U6+RkfZZI981Y4FQ5vuauexXU2s0ncXKfvN76L0qHVvKH8+ckpnxILKX9yzl
h0/7lnul3y8734bIIs+X0H4Nsv0sdJzQt3SE46fL/2oCsrexsf2eToL224yf
EdrvzObzi1vZ7ItmH+vLOpRbO9FxeXUuofOJv2JNg2gZzvva0VfbAs3TOn6t
4vAqrTi2ymfsaNpF8wOu9c1qu4pJtF8B2eP3sl+f+0n27VOdNt7PXPmhIML7
bW8DW4s6hlCXLPYltDJoq7MJPmyWbWWyQemT4Md9jJXPT5kTqFfFTI7p+S/y
8yXXd9KXDmrPHpl8RHu/jpz9AT4Ej/ak8Rq7XBrr8kfSd6+SP4OcDKCvFmds
Pop8lejkb4iM0r/RNz7vfQofQ+FJpdZO56b+a2n3DLXtE3dUH+ti6rtGvun/
oQ9MB9+GJ0+RhRPIelZk4w9k7lEG+1SSPyX5VTpLeRNZM66CV+Nkf6u2AFdF
vmKL2r/DCtr1ArTNTGW/AvIv8CV4CPNdUep3Q/TDvwLQlTbWcUwUw0TxdOK4
Xpp7y6a1/7Jk5Lk5z32pvU/kp0Q/+4ySvyjFd7hNfy3I83fAQ/j/rOYK2i0j
9wygrb6WX7MYf7/cpq1jabsu/DeUZ88wl48Ef1Xc6Vc7OL8gwX415V/zeY0x
yHZ9IDV97k2tOyTrYd5fl+/Q80E/QlrbbkZW5msfAUhmHGrMOrVXceu0z+1u
vfYjCfantRsYSh2/graEvI6jqXia8oO1lzpUZB4p1tF+c/6oYj868rmp+Ery
w/kY2h4BdzvaN8XLyNQrlR3HuHi4/bG9A+8a8S38Rjr7QPuJtdM80tm41g1e
t+P//rwnt84BkKOB+fxdKH3JxcjbW8Ao1kX74M0Cnm2ss17e9yxrmqm8Z5z2
HuDLNqAwc1dOxo273YIxf9v6fOxlxqyXofmlOKf7857S/D8UXqyGjxcQrVTk
V9AHz4lG2r427X4uldu7IO+40cX+BBSnTf51z3Pfefr/hRT7PZTfxIOUXx/a
+uSw/+KvUxx3/kNgHn3vD8133Z0Wzh1MC2ufPhbav+Rdh7vYN5Xsf2UHfAC5
Ws94U5qyd8Q4pldt6PqX9v5He1dlvObM29g+47J18bih/fpttNkI8p3hYZ3e
9hHdqafTwumZn2/AtyGMD+Hc9y11ygsdY5nra0p/D3gu2b7q5LPuByBNC+/J
HeBd32jPHFk5AmRhrEgDboZcxTCHvE75Nyj/Q8o+AKSDP4PgzRH62QDw2R72
47mnuefIJbnsE0jrhM28Jyt1rs4YnwmeNGjoGMCfUOa3Wq9Sf4ay/3RhP4Iv
EfBrMO39LDJck/t3ISv3qPMW5qTfwCVp2+fgz4/ZDUof4P5/4O3zjf2//Gkp
rq58akmXYrP0UOFfCe2bU8ahuo450bOmfQpfg++tGMsuam3E+2oz3/VgbKom
2z+gOnSthBcrGVtWAGV4B5dDMiCrY3jHNfh8valtbeU3Zzb/96cdGzd3fNDl
jHHzZNsELsIaKgdy15G6xdOfh8s+SHqsjL8fQP/f0P4ddOzO5u+YF4PfMv/7
X1h5+UQ60Nc+AJVWTGPlBUorzvFCaH4Inxc0sf1LEjh1DqeFZQ8jnDaYbgaP
Tsoer7njnMiXnPzH/U0ZDxmvslO32shFfeSotnT+6NuPdR4lexnqvx5e56Ju
+WjLktSvNHCGfGvGhS/BjZg3TpO+KBuT7LaNzs2aaxLj60SdB8HPDNBxjTbZ
zthyhn57FhhJ+Qf5/x/e3zu744s3bOrYw7rWJ7uvb6QdL8G7yylOa49R+eI8
X5SyT9X29+RYaBmT12l9YyrfEXntAHyOrN6s5bzSsnEp2sx2Lg/ibL/yDTzv
19Q+sW7n9trwdfr9FfAVfT9Q/xulnc5Tx3n5AFU+NqfTeYL5H5H3q+Ab4PU8
n4Hrg8CXmT9+YZwZSPnH9H0KjEJmd0jnBvg+xemK8DzQzWldU15pXZuDnB9g
bAnn/Xtovx+0Xu9nWwPt5euMoRWwi3rEF3acB6W/aue80m3yOi+Zls6KZLwV
z74IZKrjPXfFFVZM4Wu8/33ofYO++xMytZ82uJnD6W+aOq/09nbOd0Qem9En
U/Wz3wv5wUhE5gZqDoOfWeBVHtmBMY4/Sev97uz5vf8tH+OFy9rP+AzGtLvc
ewCaKzKPfgM9S6WjCc5Bv14pfyDhjnk3Czw6l88A5FtOtiOyIYkDViHTT3nf
YOakich5d/r96Tj7B5SfwHX0iSjpwCELTxkAHlOP6dw/saz91X4u+a5tey3Z
bb3Mf4sz2G8apIfsoi2+i7au5uWg3uZO+tJ16l6N928CZkJbkux5qMfHPXyW
ID+696jzD4yhtUvZHn7j/zF13nE+Hd//38XqvVvdYrF29V5WX6uuvvou1kaI
HhLRiS5qgggiQZRIEIQkImrUIBGCNIleguhS/J6vvN6fx/f3x3nM3DZz5pwz
Z+bOnDkn2Ofh5YNuI23PQn1f8e3unPZHJ1D+wxxOT/Vwfk8gr3uR2vOCPitq
OZ2g9WhoEAzdSjfzvlYoba5Cf8tPmqiz/8CFfI45kZX2zQDSI6fpgNP5Ha9p
N1BA4ybjaTxtWE+5hdBjUch04ayOy6H4HEdJs1Lvad59Qh2T4N8zylvJs+vw
75LWLfm2hc6p0Jcv93Ve6aOGPr98ReM8cA3oyLOrRXw2rneEz8dtQm7HIJtt
aW9qeJkBnqWmzv7aB+a9l4F0yNtwykqV2/kc1FUin/NK9UznXMYk+KzLEPR4
TfT2U8rsC08bQOtGQB/afZ333q/ltE1v52+QP4k8bc5hUH5LDt8fUtvX8r2s
86MrkK128oWBnIcDl6HDRXD8FbjdxGcj/iBdDs2+QR+URC9e0BksaF+fd6aR
HqzkONFRQCqtx0Ln2vTlWshIG3B+AJ73tS+FTL0ZZ580i2lnRuQsA/AHY/4Z
7fEyjlwEvxBo+C10PVXEsSJbwdOMZWwLcJ1+ep855ejsPuf3DuPrlCjvI5RJ
Yfwbd/f6aB3eb0d9N7XuR/kfARmBu3SQO8Ba2nECPE7m8zpzSE37DC5Fm/tV
sz8i+SVKoJxEeLVd+yPtHY/+WinH0xrQ3fEoQD1oWR2f1bgmmxHgHehwi7oz
o/OqoOvm8tJaeHkss9fs8wJLaVcoaT5gQG/HjFLsqNKkXzBPvxM4lziJeVcn
aDM6r691X/HmXwzsCWqfsCdyc42yu/NuN80J+b5PJ88pNbccgi5qAu1PQc8l
lHWH/vKW7mvNkP52VvRjrA5Fbvsl2p+Szl93ae84BrqnMx66L9+E78L/9Mh2
GPr0PPJ0R2dHoN+HwD34quBF46F3WIz9zmntem5g/Vp53dN1dKjz4eAwUusO
7Z3+Cj0ekO8ILbaD51bqiy5m30vv0+6UhV1HLHJ7gL6SDdmoX96pro9C90no
/BnI5HTZKUKv8lrvbGUbmDP5bAfzM/WMp75pGheo61Rj1yn/eVpz1xr8u7T9
NvnOlHOoo/O70S1vlrF98UfVvGek+DQHKXsm9D9PuZM7+Ay9fHrrTPaVGj63
ENLa55Tkk0e+eRLzO1b2n8jJilDbFutacbSV6rq6dId0CnBTZwwo+zrpRMrM
A+7jtdZdw+l99MBK7UvIfiOQr5/e12+AWyPeaVjDe0qK26V9pchAWiCrY2br
HLtiaP+hfxba0o4xfXM579tpz+4O99uDXzugITQNoy/UJL1HXa82dAwl+fF7
rrkO8jmYMe0uOmEWPJukdbVGjrWYFRwG815XZGlXDc+3VqOvblJP2T4+M/Z7
NT9r281nkkpE+lyS9uTl00T78vI/MD7UvmZ66N+rj6+VV6rnyvcMPLvb1zFu
ikHfn3o5XRXq2DeKQ6JnrTs71bVioSlmvGKj3etrH3fydVeuqON4M4T9t7+R
NpP3PEZrPkS57yFn75O+QZ31tDZA/cfhw5QsPrPZgDKayK5Vtkz036OMtdmS
bJ8iH5ZTA/sSnenzJQN7ufsDem9Ge/Mib1vf115v5aY+B/UvkLe6z1/rHHY/
nXOij/8NVMjrvTFdy5ek/Edqz0mprouDf3Zo8QZtmh3kvNIidZzPGXj2ax/H
QZ+X13nFQ9e1zjnpvJP2d/JxnR+oFGmfeZ+H2W9eHdpzTDZq8La9bBWRuw4h
PhtfOJ3Pyl9Hh90EvkEmCiB/+YEm0DAnNElJm5Kh12DZNnP/T3gylr55k/xf
8OMn9HZx0jDgFrplPM+WNbZPUNn/6Ez4ZOZ5XeBFf2SsQyOvJXYkvU9ZD4CH
WjunXY9I48B3tuwPKf9r4Gktr10pZkxa+nEV7fMyJjSJ9l58U2hbFH5klr03
OL/MfKSR5tWkM9vbH3p6YC39Mie6Obi81+lX93GMbaW/Bju/Ftrcg2ZLmSO9
qXkiaQ/wCdU+Bv15MW0KR1Zfoi8+7uu190my5S7ve3qmeNt9EuwzpGe0/diH
y0aHsiML2P9hs2jbGb1RyLZGOo+wO8xnFVZQ7xzolqOG43UobsfgZvZTongx
TYEnff/vrEwb6u4FbGxrv3vH6PtHgWbUdxCeNs/q9/VuX/CaRzkzg70fJZ87
2nfQ/oMgJp/vPeX9BeDwC3zIAz+3IBcV6G9Ty/sMzV/BTrU/o7zu3w32PtBG
eJslzOOxfKm0Dew9ad9pKu3vWt5tWRFrvys/gt9Q7g8B6nR2DJNRQGd0fhP0
Ts4SPseisy46852DvvwRfCiPDn8Gnr9TZ85a3mORzbD2WUTrb6Bfa3gWS70j
xCNoWx08SufxdXnGm4oA7P3vvu7pXe0prUvhfSWlq3s53wzcduoMYbDzSg8H
Wwbkm057MDrLpDjCnwF7wOsWNP6L+2mpZAi0T0d6Ff5eAW41sj3uRGBVB+fz
wKPcQCudp4bmLUhvQ4te8KFXZu+7lK3n8yLxWm/hXslE7318F9gL0b6KYsuc
Aa/t9Lm2VXw2twq4vCWbEdIDPG9PPe2AHuB+EjnvSVoFuqZGz4+SDSXP8jI+
TNGaZir7ej5b3vFzNEfX/FyxdRRXJ7f2DJkP7OD/9AXKv0Z+NH09Gbmug7x+
rDUt0vvR3jd5B/giva91xkR7Ldpz6ZnkvNIeWqPo67RnID+toK9X8V0p2rSa
dGNGX7+v/c0En1vJ1Nn5z9P7WqmuFS9mBDQqEWKfZNWRk1HQZwa0r8vzqfDh
tOY3zXxvOpC+hu3zZJtXhLYP6Ow9sTDmSkvgUTPG3KHM/VpRdieeNYFGjYH1
dX0mRWdTZpEuo9yqjEXtkIu34NmbwGfoqH9o179ATvAZgV4ahr5cpHFb+46U
U66c95Rkz659pXGUtVG2f8C74LVdczLK+QTcjyFTW0kzM+8JRjZSAjPg4XQg
TRefe2gFX9bUc16pzkEoXVDY+Ud8cwBYQNtHQqtClV2PUtWlvO5X7uZ7z2lH
ZnREHv3X06c7g2OXuo5htYD3xrZ1Xukavq+iswr6ByT/tc4lMjZkoK6ZOnfD
vVmk/WRXgizOpi3L0zBm0+YVabwfpD2gZ9JvzX0edDjvPaD994GD1J+O69Ho
2/StbMcse+YavNcbmtSgP/Xo6fh68i0yEv5VBbe+0DsE+buNvqmu/zuu68PX
DbxzUbaftFkHiepxb5zWHcD5EmU+gKcb+H8aBZzlvarQvwqQ3MCx0PYAu9I6
7tm/lR1jvTt0f5t0lfaGaNMx+u0B2vk10EpnzHmvIbS9Ae4P4cs4jUNAV/j2
NWU1pw+MAMfdtG8q946WdVy0HEAwOJ5HL55D/3yNzFcC34ra05WNvGwVeKcg
clAN/GsAKXg/A3Uepm+/SLl7oWl/0m/gRz/kPVh2D/DwGny5W8mgfI36vq/r
e0C47Msr2S/uYfp8b3R/L6ABspwxteN/K47JCp4HoVvuoJe/pF/sAnLwLDtQ
iee9KHcftOxNmp0296O966Hx5+inQeiy/bH+LmWyfUM2gVapkh2rZxIysgq8
VwKvwevj8PkMuqgK/aYpPIkAx8jUtiVrJdv+3j7HoPMMl6jzTfC/io56lb4/
Et5+wDtX0DFZaWc2oC598Q3mE3+nNSj/T1rf1/Vu5KcrtH0D6AaUp74egbzO
QX/Q0LHocyc6hr3i1Ct2veLWK6/7Fxr6WWXkox202oluHcr3ubX2Bj674PWw
9L63FBpWpbxqOgMB7ivBIZF0QRGn76a1j0L5KiwLL2cjK7Wg6SthPuut2MGK
IdxQNuvp7E/tV/rW28hLOO0tTR/4vap9H3xKGSt0ngooRn4kZawmHyH7MeZ6
PeTfAToPgYcXwfNH+k1/2rapgX12yV/Xh5kcv0axbBTDph+83IlMdkUfDMrl
taYMwFzkb0W0fZ8WRjbToovSZHaswuUVHa9Qsa0kz4pvdZ759GqdmUZOXkc2
M4BbeiARmeiVxnEStZ+ivZRvA/ssB0o4Fqfyuqfr0wUcVzEEefq2gK+V3wXK
u5irvanzacjYdWTmWmr7CDzZy/4er+v/U2tPPfxOhSyOi6O4cSPhRSy0Gots
NenouF+TGjl2jvb50tGeR8hS+gzeH7rAu19AxzDZMQFFGf/XQMdfwP9nYCa8
3wk+E5J8BugxdHgEzC7u8zs6x6M9vrnQOZT3QxirR0GXSV3si3sCdCrLu2Po
86lpX5pkp0erOn+A9AP6xEHSv3nvjeIue1agfOVng280tP+GfntSfYR77Yo7
tujcePvRzAseL8Lji8jB8Sp+9ziQljrSJduf3SjKuIcc3wVSyo8fda6WzMHv
c7SptM5VIPvZKXteMeus6kBuYB/lHwBO0ra/A+endI6qHOPQQvj/DjQbpb0a
+sF06v8wo/eftPek+OmKnV4SeAxfboJjYXTfO7zzLrBF65N8UwL8WpKmgmcJ
lHmZ7zcxnkR28/+59uuGIIuTmI+lp02H0Dk/Rdi/wVD+X9fwbgjtSSXacq8R
MvU2MllSa7G0KQX3c2dxXmmuLPaFtAXdthm4DC51kM1vwTdjV59x2V3c+SOB
My/Kf9TB1/J7KP+H8nuYO5CX/8N+1LkR3r2os5X0lQzguq+xU13/DO3zpHV8
s1Etfc6lBbS/3MH5VfV9Lf8n3eDhB+R7QYsMlF8BGrXh+W2e3dI/G31gHPfP
dXAals153Z+Q6HvZOjqdEMhnD1yH0ZaJQMZk54sFrpXPxL3igfw/XXwdFnhX
1wOgXX+gLTz5R3Ns6SHZjfJ/eryFz/ZUg5ftSdsBj2kHXSioNm1Jjb7KBw5p
SI9pTRGefsc4sEk2eTw/XtLrHy1T2K/rNN79BJgOZKb+JtyPAba193mc9zRe
Q9834N/dDk6/beX8Lu3xAVuBVYlOdR3GfC8EGcui/sE/zltqA7otB/wZBQ6v
Znb+41K+zsy89AL1x8qvDbyOy+Tr12j3aGBjdef17H/3leo75ZW+ktl5vVuo
vPNK9c0C2vkAvLKCz4ZWbmN0uP0F3gHm6X+KthZjvKnZw7ESImrYd0xRZCIb
32VmTJHzoDL0yzWJzjdGHtZ1dV73dC079NCAbfofyH1nnndoZjuONp1sy6Hz
UopBpTNT63SGnzH+AHXuC3d86rPMn1NDv3d1noJ0vGhE2TuQiZvw9AZwEp70
z+y42IqPXRO5GQyONbr4vLPOOa8GPqCef+D5ap3f0n6J7CNJq4LzSXDOTtuG
FbHdj2x+mpLGAhHg/Bntv5fdPuzUr3S/EDqnCe1qCtxA7n4q6DIm6CwYbasD
72sH2++1fASmBkqjPz6F1ycZQxqSxsG7BqTngbG0+wfqOMy9W8jlUmgSwb1c
jN1lSc8xvvwAPEM3roNPWXs7LqjO3/yNfgklXcB3k8HlMnON6+TjgB+0zwR8
ifx9ARxBD5bN6XzZwDPlU6NXD9A3zsf5HNHr6Or1oZ4vBmXwXLI2ZX/JWPhV
KtuMynZ0PrSaQ7ueQMO5pW1D+lk525Hmoexs3NsBzK1pH3fye6f8/MC1UvnG
U14+fcvw/XuV7MtPPv0yIyvXkKM92pMMpPtqOL8aPRjLnCdfC8d8V7z3HPBg
Lbp4DDr7fdryLfrhFFCXb6IouxzQTOe7yjimfJMyvl8CmfsSnFcgA+voKzXh
88Z89tUyNYfjtsUgn3u0FoZ8/QsPute3HbPsmY8x35nSzfHt34sz6LtxjR33
PgM0W1vWz7WerHXlSuD4smy4gGG1vF+r/DTKPQP9H1LHFuQpA/lNpIW4RiUE
tYQGY8DvOny/BrQo7ZhOuj8OmsXQhpzQIS0ydI42zIFOp7gfTB/ZhGxegb6X
kJ2aHY3z60BbtaWtv1UZm7RHCn4nI5w/HeHrogWd170y1LmbduyJc/5CjK+V
171dXPegr3YHUkPnvZRblv6UCfpvQi/1AYdI6p1PmfWo9zXa2AE+bpEfItkk
d/G/2jD+mf7U3jzt+QZ93gT8V8j+Tv+25Rw77GpP26zcq+pzxGe47kG7H/BN
ReYuWSmzHLTo29TXyn8iG3QgP+N+OHqhPPf3QYs6+r/i2zatfeZSMfwUv+8c
OnMhevUddN9nzFfelm8g8ElJv8jC9Sna9Y1sC9GrS7n/GXX/jiwVpo4g7k2n
zJS0dypz3h7Aa7LVg0/BPGsFL35HD/wG1IGP82lHDsocU8Q+4bK2tF+4k9Sx
im+PArPT+fx9kbr2P7cMnf1nOttftutonw+zoNsbsd4rm04/ngY8h3e5qbch
uJVAPqejR2tH2sdKdWiaib6cP8RxqW7rfD/QC5mdBk1/DfJ5G8WE0/kbnR8a
rvNkwN+RtvW/HWNfro/owz9Do1bpLAd9mZdN1jkL8Cmk9fhk81rX9bifN9kx
m/6hjsvQ/mkbn1XSntf/YjPVDeyHnetlf+ONoGE+vmvFeBzB/VDyLcGpBTAB
GXxOWfm595bWRYCs0KiszqpR9ljk7Tr41dd/Cu1dDI5vA7/E2RZ1LbJXVzap
3e2j73Nk4yz4lYSHP2jvk+uetLlAstO8ic5rj0NnULTPob0w+TGXb7ZvkO0Z
0OITePE65Rbk3bEFfYZKZ6bSkP4JvveAKeis72r7jJj2fw9Ay6mNve/bkbJ+
oIznKe3TS7695CdMvsi1/7od2myCB3e62q+tfPTJP59828rH7bvw8R75ZGSk
KO0uFOI9ofWx9l2ndV75UPk4t+M2jePdtUHeP9O18mqDfNTtKmR/SD0T7BNJ
sZQUU+keeO+W/Ql4fVXLefkrlK9C+XL/uLT9uYdRZwV4uLSp4yYNjAnETmru
uEpt6QfDeK8IfekvdMJ78GslUCjZe2MdK9iH8jXkPDSr9+C0L3e1qe/JJ+Pd
dL7fC34mAg0oOynU8bD+Fxcrivufk06iLcPh92TSwtTxGJk638v39OxIBfvg
SVXPfniK8M4LvNMFmZnDsxfRD8vAbyly9j50OoScVaHcrjkcc0zpwTTOP6R/
r9G/XS+f8SkCTu9E2UffTtJCsl+Dbk/hXyRpZ949ynePgH6MJ2mQ/9TAz0Hu
l9Ph6zXuz4cXV0gX0qaW4LkHvLJpv6GHz+HnodxK4Py4pvN/9vB1Bvg9hH64
L8g+xMP4biDpSOSkKvlb0Y7DoXgcdWRTmcZ7Y5cTve+l/a+dtbwvXT+wNz2y
gtd4ZwATUjqG2qMIP1de7+gc1jHa/Gao8zqPpWvF9NiNjtqs8QQ935t7e0lb
lXPfaBnhvbPd8d4/S4fOGBhq283K4BNHW0/EO67Q0JK+dxI83ub5KdK+6Ld/
WvlseRoG1nTAY/mqYizYS5qatACyPElzbe1rwtt3KaMBvJoufydaP4yxrVax
ZNtr1WxkO98p8q2AHPYFh/v0ywXNnCr2aU7onUSZfTval4Rsj2syf5vOODAN
uIK+WAKORShrP3r/rTL2uZiEjBUpYt+q8rGqvZO3gDNhPtOss81Xdf5atgTQ
LI6yYsHtHlAppdPKKZ1/gh55Bows6HgG39OuMNoQFG0byB30iw3ot+Lcy45c
zdN6E/jOEK7NfT2JekvwfH9521duob7N2icFp8Gk62nTENJdlF2S98KB+dRZ
inSBzqdls99++XOORJ7aQtN18g3Z0n6BjsDL/rLHAUYxBpXWnIYxZ10++/Hb
C7yE/G9v4XXDZejlB/D7IdBXey3MP1/g/cHgeZA+M4MyviYtLZt1+sc6vglP
6+stRe13+Xof+39aAP2m6FxQW/tfW0qbzpN21Fo5fOhEel5nSsE5fxvHilWc
2PeZD5eHV91o+0rImQp6NdW+WxfnUweulde9vei3DPDtfXRBJ755SP4ONJnC
s1uMxfEqBzyL8N5ZxrR9tKco8+4w9Hz6JMf53IA8NU5v21fZvXYGz4+K+X9m
KHAanH7jugF03gdutSgjFTr/OW38Cp5upfwKpOdoR5lkx8Q+Sd9Ihm5pyjpe
/Dr0UatmPmP+subO6IkTQGNoMZt6K0G3ROTkm/x+Jj/R35FmRo4ikh0/fFdq
xxDfrnUPyn8ZGAOuo4E/u9gHunyhfxnp+7N7OWZWdmTjM3TNTuAVeF8CnlTJ
ax4lICNflw/YjCJPSzRPRV5m8exEHscC6YZMlaCfpU6wTbqeRYJbZfRjGni4
SvQHprR1vOu/pJ91Bot/gufojbJaU6GMKMooD9yl7t/B9TY4h8Crs/TxH+rY
T2iszgi3dV52HbouSV1bkbERoT4PpvNe9aOdrx/Yp9U9XetMmMpTufLvqbhc
2nPU3mMY1yW0Fxric4GlAmcDFbtRMRxbg9e3zLvugXtJ3juCPnwCDR7nsT/L
c8jA7cb20StfvZfoJwXRz1XpN4VI54PHGwUdpyqYfvWce1WYp+xEDmeF+tsJ
+RyDbiLpKni7S+vx1JNI/0gAIqHVG6SzC3jPpQk8bwz8wveHka847YnBo78Z
a+pA239If0T/DIbmQ4HUyOZe2dZAex12HUX9rwHZY3ytfFPkNYp6CiP3W5gX
vM77L8n2rZr1yCLa2Q8+P+STB0AQtGtNezIjw59RxmD6X/nijs2oM29faJ+z
sdduKzL/y9PT81rNaeWzZS106kgf+o5nWZDZZZ191uBVyjiD3P1AW88Cv8vn
GDLxvIv3jPbWsQ37r1oXT3KfV39XPuT/u/4KWEafu8N3C6B9Y+2Xg2e5ZPt4
atLVfV79fTJtGdTL8a1Xy9akmPu8/Gzr2aS2TvVccbCfBM6LZKR/76A9s6F5
MOWV51+pAjAU/r0o22B4uZp39mhvAh7kAlrApzuJ9mMzC12QAdlID7wvW/v0
9oEgn6mDYu03tTC0OA5/itSyr//0Oez7/3Vo/1Kk43rJZ0eNJPvwKK09VMor
n+yzLp06Oa7tH/SVDVE+lycbmDfBOzTU+X+jfK18jUhfyzfKIcr9GqhJ+8Yw
jh+HZx+i+/qB11/I62far4Zeb8VbD0zu43MpfyCT1dXONrbdeJF295P8Ij/7
ePdbyg/i/WDyv0OnTtDhe2SjPeX2gw77wPlF0oupHHvgK57vlu8QaJsWWEmZ
HyI7G4At6IwKyda7fZD77+mnEfS9UHBLAa77uN8IPNpTZ0fJanrbNAyI9vj5
TozHUPm2+jneMVyWRPpafq4Oa64NzQomeM80LLBv2gB6leF5Q9JU0K0Rch6e
2/+CBeBXcFnfy6R97sY+h6gziN3RJ2koM7mN/bBr/jOC/vtyiGNMRvLeDfD4
WeurlFsdXHpT7gyerYp03IFjBR17oC0yuhw5XNbBMeEUG64ibXmS2nbj0chI
C+puCZzo6XW08Wm8rjY6wTa9OflnKAwue/P4DEx75iHtgA/hVQPuTwPfqXkd
Ozp9eccgqZTsvT+N+4c0527pucBpaH4gtc/Bbdd+K++foq2l6Yv9eFaKtDLf
VgHO0Cfaw8dH8KN3Rq8XaN2ggPxwUN9onY1Cxt4vQXmUWQyctyJbuUobZ8Xn
uQM8TO97evZDkv0Iy7eefOyVa+NzQXmKBfx7ohNnUNanZY1XXq3vUcd8oBz/
XpXAozXPKpNGMgY8Q4YjOtg3qc7SFGRcbgAfelNf2kjHTNFYL/l7mfYFwbuN
4JkUbx2SE7iGvk6H3F3SfJZ5W/EUthlbSToIvfceaTrKTMk4e5V6d1PMHqAq
Zc6ivC9lTwP/lvF8Kely0umtfFbpa+o+CZ8+hF+Zod3HtK0q86teTRzHRfEq
ttZxH0sJTuOyO680N/ffoU0X+T4n7XuHttWkvl7wMYZ3mgDVwOFf2b0ybtwn
jZC/C+A+fXIqemE3+J7q6vHpN+T+ks4A068a0O5zsvUCj6PgeKSjU10PauJ1
N62/PY7ys7ro1TpaF4Ku/ei7LwCp0FeDwW8t+LwOXz9EJ0RAp6Hg9Sb3s+aW
QRKynej+9iG8+oM+dB+YrX0G6FSxh+NqdKSPdqefrwqcodBZigq06W2dO6P8
OHg8G1n6lTqr6N++o+8d0zkZ6HOc9CL0HM+ze6QTGjqOqWKYan2lcZTXWF6j
/+2C36Nlhyv7n3xeuxrB89+QsfeQgYnIc07kMFMvxwlNl8KxQnUufXLATq40
tPkanpSEjkuKW2fJpmos9RdBvgoDj+HhdMlCDeN1jfHhMDJRgvR78DodgKqx
vnepjf8rdFbrITTIDK/zUfdb6Lnc0GFRWZ/ryS/5Jp0lf0F8N55nq+mrJWWX
D0yAv9WQheqUVQyZGoaO+SzSfuOLAjX0D8VcIln7WeiwSHDNhmwVgFdTuB9S
zL4btW6ZjjonIKP5kKO8wJjctvN5o7vPZ2u9cVA9rzlOkm0xMKCe19szxXit
PRk+1ZB9BnjH0+eLMceNo/xz1X0G47/zF/SJpdqfhN4NtbbZyWcWlOp6eE/H
Ve5EGW3aen/w5ayOk5ZT9iu0t2ay06V1nI9E3tLyfi3yzZCH8eD2I2WkgS8L
kY33ZWuObP0D/A1s5LoV49EMxq/byNd6aPkXfA+izVsZF/7N5XX9f6nvXn7b
PS0Eaif77PLdgK6rk2w9VREYCd6baV/zjj7veZp6tyEvP3LvEfd+Ij0O7yZW
sW3zQ3B7AHSk/5yGJgOKea65t7ifXWrsfZpOmf2fMx+cL2sdPnDOQb4Pde6h
Fm0YS5vHAF3A/QdwO1nLfrpepV2vAHXBcyWy1w5535DeOvE+8Jn4p7P7pB/x
3mfw+QvgIXUfpb3XkZupyMw0aP86aYzmwFpnAh6haxbLTwVwG13TlLpjgETq
aQlehUnL07YLtPssUAz6RIPHF4n2y1+PfH39d/BORdmPAOWQmQOkobR/b4Jl
UTYI3Wr47MJLOhOi8x31vZ83hOfDgL+h7z9ZfaZAdv+t0b8bavrMwd9815f7
64Gd5PtQ1meJvp8yws/iqzs21V3K3MD9rNA2S2WfLSkq+SY9wXezyvlsRAPw
zoe81s3qMWED/P6xseECEIx+aYHcPodm+XmvPGX0hN4Vmji/q7qve9H2NxJt
M1xO6+fR1tl10FVR/JscquoYn0tLOObnQWTkADABWV8bbp8x8h2zFFqXq+uY
L9e51xwcbpC+Sj2tdb5Re1uUW5c+8Ucf67cXAzpO8Yr1/1US+R+Bnnsl2Lag
E8F7kuar1FUXearF998gJ7tDHOdMsbnGIgPNJBcFfT2tq+N1aW/89wjvoyu2
yC3k/Y8q//2m/BevQ3E7SlD2CNmctDJOwkG4fIz8vwpNKqFT6sDLVNDhK/Dp
TXt6AaPgRUPofxRdU5kyiqHzjvFOLPz6LNY+ez+Pte/VbsjTZXhWkz5UA4iG
14v57iZILCEtWsExtxRX8RrtGwKdr2sNNsHzk/sVnC/ZznMV5ZXqmezvUqez
DZ78aMifhmzrptHHf6bsXL0cZ1f/AJr/N+Pf7bTWi2lfEm3ezLtPwOm07E8b
eWx9As0OoG/ulHH+SE9fd2a+P5ryupDGM9a/wr1z0LwkZc6SXY58UtOPM4JX
Y/j4MvKzBBgGNNaaDu92ANYjqxOhwUPurQPH29DsFlBO+1WMz8nQfRC4lYGX
ZdP6rFAvcD7PmDsZfuyEHx/SH1eXsH+EqdBiNG08TDt2wovBfFuvqP0/Z0YW
1tPWRrS9JPl43gvXfj065D70jm1l2+FdJW3b8gt973vNWzUHYCy6QPk/ATXA
rTS0rdbdeyvaU9F+iua6mvPGUt+3jD2NuR9X17ZhC6n3J2S/Dc+aVfIYNEvn
Umnj7EB6BH25JpPHwQbQ4w7zoH+h56fosDjK7ZxoGzTZom2pZn/Zp7XGRB1p
oXkaYI98pGp9ljSGOhPhQVPSneD9uWwp0cVz0AWH0Ff7tV9PBziNLP3EGL2B
++uBEeDWm3KT0Fm7eK8YtCkKvAZNZvN8H98d0z8X/X0PkFTAevgHePE9+KXM
4Dgaj6i7kXQN79aval9O8ulUhPRN+LcQ6I4MFOVZMN+nBFJT3l/w4bLGGyBt
uPPVxT/kYw9tbAJdUyHrx7S2Insm6r1JGo78bkbeKsgXL7IZw3vbwfVznWOK
9VnfPdA3hnJOwL8r0PcykIjstOf7wdDnzw6OSde4tePVFeH+RqAoEKl/HGgS
Vd5nWx7ns89C+S76gnnSQPTID9DnVcbpPbwXTz+7S/v202eDtX4c5vPTilX7
gG/6ij/IVTP4e11jCHSfnNbxX/9Ezpsm26arMvPbF+o6to9A+Z2xvt8/1Nda
8yqGPDZTCg1igDAgA3zLBKzsYugHDmcY20eDdzD6KBv0XQ3dl0CvNQWcV5wP
XSuvmCC6lq8w+QnTmlielJ6bVkph2yDZrnSirOLIaEmgVyfbSG1mLtSf9Ah6
4xX61UigXlnb76WGXlXhc1bK6gpPbmgdDrkfGWs/kjuBq8BceJsGGQyjn+3n
+T4gNtl+OE6ik2LSepzsDCxhjElA1wSDcyLpKmQlCh1xQLb00LE3ZcWksq+C
Zsley9E6VvNkr2Utha/Ndb6zaMB/SrDj2IwqZV/hr8kXAW0bLr0C//6k/DD6
zqY8/sd91NL/uLI3u9vQNmfH0PVH6cvHgf5a3wLG0a4K0fZtIh/ig7WOTt19
wO8Yz6KR7Y/Jb+T+h0B0Osc5b8+3mXj2iHJnQ/PttOUf8PyT/E302Sud/F4L
2nOSb04ALckXAq+LWisi3Qney2nrXuR5MvQqA28ydbP+aMW7nZGHRbLVgc/V
pQ+QsYrwZxiy00b7zi0cc2l3GdskT4I3FamzMN8tQ55bS+clW1dMaOH43B9C
i1L0gX8YS/fQtx7Stx4AUY3d9xJkm1fZfWof+fBYr1X+m9vrcB9C0xo1HZcy
IrV9WMr+uAVjeWnG/nnQZB3y1woc3oS3N/juoeyVSG+RlkE2bpOWRJ5LAIVi
/P8QV9EymYZvfwLftKRr4UMq8D4HPmHIfDI0LEZ6gvoepbFNxxT6+VnePyN7
Nu4P4v36pEd5vh24hmy2gQYpKSMF0If+3ZbrXqRVeF4MOarLO5eRv0tAO569
GOk1u/bk/0Z+v0TfDYUnC2lDH9I3ST+C1heQt61d7GdzDHQfhhxdR19s4Nkz
aP1iFdvIdAKfLvBjHLTvqvl7c/v2bwRtt/NsG9AIHPJBwxjmfaHZvAal9adM
6IgO4PEDcjEw4f98LR0nbQoPi1L/+Er2aaW0AWkdvu3INwcTDF9Bxz3Acur5
Ht6tIM1Gf08LrcaCdyTlPOa7p8BReJyljn2SKJ0o27AEx+3q0ctxHPvB53jq
uIN8ZIJ3bdB5g9Ctg4FO1DuPfhyHTFdM73ieR3g3nvtzkdNynT2X1H+0znDp
zJbOfZVM5djT4aQjUth3YAtgfjXHmeosPaMtCfj1WpDjhncNcezwFLXtpyyI
tBb9/Xe+/y2F41Z1SXbsqm+QneJa3+FeDr7LFeKYG1Pg4as8LwFv+tIvNvHO
OXCIpu6j9a0jjwOjoNF0rTeltW2UbKS0N6g9wo3dvI45g7K+5tvZPN+LHtgN
rarxXs7u3iPtDn33yrac9BiQBA2uQNMm9OWS0OAy8pylgW34ZcsfpjkU+m+/
1tQC/o3k56glOrsDda2nLx1Fjo4Beyk/H+NINfiWJqVjteSq5Hgtc+Fxh0re
sxtIv/0NvXMJyN/OzxZpvSbefn7Wym4HmTpNe74DVkLnJ9B0LXj/js76Bfmf
jkx0Ro4a0bYT4D8P/bQO3oUl+f9xfeAfUn6xHqGvytX33P/dJM//L6i/QKcy
jLNz0bu/g/c80qdNbO8T1NLf/FDPfrU6gE/hbPbr+UsNr339StqfcaCgfDgA
6SgvLdAffAsAxeFnGBAjW3PK+6Cl21kHHVs7wnFNLrSxrX0D3q8PVKzl+Dry
M7cY2IWsjqRP/6NzM7JhgN9VkesZ4H8WXNIgS0Pgzx2ef8Hzg9BuCc9zNTe/
xXfti/cPjL+9KTMvOM7i/Uk6dwM0qWebhXjmqJ2A3H1suyAbhkvQ911gRXm/
PyCV710kH4LMJUKvbpQdzbt32zpOQlHyKeHxCXTLeXApBp0y00fGw6exwMfc
v0afXQ4uy0QPvjkDHffE+p6eXQX+pt0D0PUZdQ6N+5e0FtfJ+csFfJ2NchfS
L8YUckw/xXkdxHi0UOcuudehs/fvKqTw/CQe3NvwXWfSVmUD/kHBfyLvPG1k
2xT1+VFqY1Hnt0LXwimd1z1dJ5N+hEyUZhz5F1lLAR2ekxam76SgT7eHNwML
Od6R9MJL+heWvT1QmHGiELAHWeyGXH8ZR59FNm6T7wav/shoUL47cKCUn90C
SqLXtkLfnfB1EX3n0+6+LsX9xe2cXxRIda33SwW+0X7+RmhXU/sN5J/R7h7a
38pk/3LyM6fnek/7//O15gQdFhY0LCjoezpjprXjj4DSyPdz6NmTcpKDHbNV
sVu1J9wzsC+8mO8SQ30vFd/fRt5CSO8y1m6TThLuUY4TMzWlY6K9lcJx0bYi
G725Hkk53ah3s+Yhna3T8mnfs7xjlCjufT1oG1TBMYgVi3ghtFkCbRcDy/Rv
wLPlpG/S346Bw1HgBeouxvd54e1CdPcZ5PMj9PQA7h/hvQWy0eHeOPTW8rT+
j1fMOv3La++uOnIwiH5Vi/drAm3p678wl5mELGYCp2TtJWb22fiqRb3n1w68
CkHvKO6909PpC0WcP4NO2AHusfSZqrybuZBtQRS/QHOGS+C4uZhjpUxr4xho
JZGPj2hjD+R+uLYVAmnXPM4PYSx4BToNreb1QvlZ1pphceYfMxvYr4tSXU8n
7c7cojJ1PMthX1PyKTUM6Er/KActltPvF6G/QmhDAjh1gCftgYLQfT545kNP
Lwikx6Kc76N5qv77KjmeYRfKKYvctAe/v6kjkXKWVfF4NRGdXKes4yKuqeX9
vV5tvcdXgjloL97dCA+KpPNZ+8M8TwUP1mn9AGgJHx7y3hPo2SefY0ArHvRR
6NWEshtnty9i5XXv/Qr2Byi/gF9Bl3U6Q53smIqbKedt0rcZMzbwbh/uH6Id
b8hWnH70HXXv4J3TpLlo52kgN1ANWS3AO/lls6H1Idq4F/gVXOogt2eoY7zW
QkgnkK5m/P06wnupymtfVXt569Adg5njrM/gPnkovftoQ9qbppzjRshPcWv6
4VPS2aE+4/U0rW2EZB8Uxzj2RZh9F5yi/AnwpQB9q1BBr8FPDLJf98nQ6m6s
4wrrPNW7yHE30he0zxnvWOhJtH+A9A/0vMx7p+jDJ4H+4PETfM2v+SE8PQq0
RF7aa0031vnD5R2j7UaQn7cP3Ne9I8DG2t631Z6t9vE+Br8/oNk46JIdfd6G
Nt2I8npJbCXbF3XJa98yiuc8AFkZCCxDhrKQpmnj/wzZ8jxAN/QF91q0uyaw
qat1T49Q65+Z4PRcZw/pryXQs2mR95Kkycn24Sj/jcorlV/HlPThR9AkSGvR
tPk9+sIT6l2Wy/FE5Fv9OPw4ATQAx37QZhKydQua1eCdQZpPMv9ZQ50N0XmN
gd9r2N/6LeAqc4ErwHjtScbanlp21S9o71n/B0BL2be2c9zYmR0YC2s7BnJ/
nnUsbhsn5ZXK5knv6pslyM0A7UMh7y+RZmpjv4r3mv63zR40Gp60bOV8bFdf
K697id6KD4L9QQOTnVc6s4fLUFnyz9id8e4I88A6UbZpUhwgxQDSf9egIvZb
rvqe8005ZKE57zQDTnc2PycnOj73pGJeq9ea/Uj03CtAOLLxRSqPrRpj9X+n
MleDZwrwHYtuThNv2xb9NzYt4PuddLaMMjdSx6Bkn93ajE45zL32Ne2DQ3sG
23mehO7LyvM47SfDrzXI30DGrMHau6W84UABeF45q/cz5P9fz/WeYiIOUfmk
JelDJaBB3XL2o63YbvKZnRF5TwmfN0GDRchKU2R8QYzv6ZnsALSWrvnYftKB
0C0T/XgQaQh9/1PZDDU0KK/YXer3shvSWc/eAX0pval8Bd7pz3V12Y1ojQl5
XA39DtOPynZwquuhml9y3UJ7dcnei9aedPoo//8Vb+N/wCfgua2s/WdWaOiY
21fhRXnuPdW6eB7r6R70oQRgJ/JRH70zjTIqwasPmENNS+NU179Us/5+gjw9
DnJ6Dfo+Jc3LNysb2sfn1kj7Z91GOg2cckv/dbevmi/gY3iC84r1quvXmYcd
hZfLgOXo5ZmMdcfRi4917gDaZwp1LKCclJ0j3nnFB9J1OdoSpf+tsp6fT4G3
DUlv0Jbi6OKJWg/t5v3+z2nvIOTvNWRhFJARvZVe/86kuSlrOLS40dFrDFr/
0jrDReh9BL6VAIcK+p/o6Xd/odxKlFcRyAi934NOK4F8+i8Hl6HQ4gvK+Fx7
2DVt+9w5zvbPyh/O5+vSyNxYcKtOvmoh+4gcqTlLHvumlF/KsFyOvSq/jy9r
vgm+N9CL/cCpIvQt19Txvl5Ocsyv1W0dH6gF8lSYMl5FJ/dB5hZzbwTfT4LG
m3s6jtAW0g2UtQiavs33YzQPrmU9/Q88qCVb3Voe+zUH+Cuzz14vo4z36bsv
VvQ/hv4vVqIDJtAPxgN1qng//q1ajuGjM0KK49Oee+GMZyXTe8zSePWq1i4Z
X4drDxP5upTLfiN/Iy3Fe5/U8vtV4Vl1YAry8RM0+hGIRzdNSO89Eu2PfIP+
Ows9Z/f0+p7W9mTHUpO6FvPdi8j3UPro+E6O9TUSen8ZbT/pV5GNisj6SMqZ
Xs0+8YbxbnrkeCF6PwPpQHi9vaPtNrV/Hg6vw2UjgA67C/2+JH2EPmlA+VO0
H86zFuj5c/DhXpLPYNwhrVXW86d8zXzuQucvLvJ/8kqybbNkl6V1uGvQ6yB1
dq5gfxCZ2zhGzMMYx4npyr0uwFytC7X972jhf8+1bvYiOrYfUIqyGoPPvzUd
j0Mx5xWTQ34Ey5exL8Ff4OdRdGk88nOW9+7ShpU1HP+jCt+/Kp1DWkz7bdCk
D7I3FrhGG0LLOLbqe5S9sqd5KT4q/1eYr+Oll5HVQcB7Pf38O6A+9QYhn9FF
Hb/rT2CU1iKBvNBhCPxoimyvBp+C6P1wZOQU+e9ld4LuGQjc0ty9ls/uZYVn
aerZ118L+vbL2uuCVyf0XwT/G4L/AtImyEaLcK8/ls3sOLU10T9/UfZNypmI
nKyk/tHg8V5Jz1/HogdKdnbMrRbU0wF9UEJr6MBj7elAn8uSX2AM341Ntl2W
Yr1uzeS4sD8Hnun+X4E1eq3P3wTfG0BH9PAqZLEJz2vQQbMjN9mArvA/pqPX
muQ7fhbjSwTt+5Hx+23qf4KMt6IvXYDe45Lt1+wB7Xlb+3SkzehP45MDftxI
Y7luxbNk/gOjZL9EP/5QUyWtTdJfG6C3JvBeSXi1n7aWkO2jdJv2v6HvEuQ8
GL592se+0f/WPqb2anWerLZjgSkm2DTacwkZ+oQ2vYc++QqZ2Q0EyX4dumYE
ukOHdNB3k3w5IpcZaOdK+vFD2cSIftw/yxi/Bp7/UMK2KLJDaYR+WEX//jmr
/VVpfW8iOFcCz0I9vc9/A96OgpeFkOv7BR23UnFxP0AmfpJNRzPH7JI/O9X1
AMjD/KU79O6mMxnyW0N57YHZnTzfXgF01HkJ+sccaLtIcy140QP9cKaRbaPr
0jcT+f4EMlsGXF7I7diRfWjbbJ7PAmbQnrdIe4JLp3ifs7jHO8mkd7M6TkxO
vo1g/vk7evkQdJ/KGDFXYzRpZZ0LAYf6QJG0tqXU3DwPtA/SmfhY6/6mkdb/
E5Dxb5GPC9DuCXWGo18Kqd/Qni7M1ToDQ5C1DtxLDQ3qw7vS9IW5sqGBlqMb
26/WyRq2Y5ANQ7XMtk/4F2iEnDyiztH08Zmyb8xtX2KywZddbhedv6QPVEZW
J8GnU9CqNvSoRx/MjvwFIx8Jmex3KzfwAXIyr7Ft5KZDz2l8dyW7/XKu0V68
zjwgd6W4jkT3FAK+A98F1PEmsCzGPqXyah8LPragv75CmkR9vyA3MyrY99Yw
YDf3/xbP6VcL69ln0Uh4spx0MrjWl86mfSOQ1xLwbR1lvExaBNyS+TYnbT4v
PQ+U1fo3NJ1c3XpSOlL2i9rzDafN75Ww7HVkzGrZxnV8T3s+Ahbw/GPgM95Z
Aa+eyidOVY8LGhPu0l/D4M2LIcg810no/Sn6vyvmfXytWZyQfwjk5nW+KdDF
67KPA2uzikt1P8rngaYk+7x5XvraS9T3DDr0J70P7dLJxjer/1f131oPHTWR
OeBpePSUbzdqLgY/NoDfXOiQEx7kAHrF29ZVNq+DKGsg0EX/J9wbSr4mZVYo
brvyrl1tw/pdgm1aL2TxWdBzpFXRZXu1/lbS5yl0luIaePeVXzhokCq1fRbK
73UerSNVs58/+SP8lzZPpW0DwXc89famruuy49W6HvLSgLpKaR2iu/83r6Lz
diAPOxs5TojmEocTHFv4cj2vH+qcms6oDYefI6DTV8jJWGTiQG/bkMiWZCF6
eQ70z17IuqkhsER+opj3VKKfl4b/XeiPi5v53I/efQ5N3kSW5pW0bdQOrnMX
chwQxQORHd/isrblGx/i9cU5/CPmLOp2qo1T6AfTqH8qaT++3ws+k1EBUfTj
tOA7kDFzOs/nk84gDeGbl5l3zurtGANngNbw4gnjzWjadBv8foFPF7P+X17p
NWQgHFk7qnk+72+GbsngtSXafnplVy5fvTOTPSeTfV8a9OMsrmcDH1N2Lvr1
sBb2y9acMssia9FtbDf7Kjrme76ZjR47Q/qUtv6V0f/6F9F/A/nmHm17pj0J
2tKqj+0ptEYvm4ol8PopuFSWT2z4GMJ3RZDteOrYRF/aDHzRx/PNV/r6fHpt
8D0AXQvRX8O1N5nN8ej6aayBJyGa3zD+pNQ6NDLQkbL/oq4ROlstOUX2+lDu
5ar2+5SirOMS/gvtX6jhfY0a4iW49IF+fbUXT73zWtjPyin05W3aeiu9z0IN
gy/dSR+B001k5BV00g3SlfGOsa30jWTnP0X2e/awTxz55NrN3GQ8/eSW9vDR
VS8CHSk3HniZdn+CPPXQuRn5y2CsHgL+t8F3Ovnv0JXtoW8o7d6itWigGd/d
oM/M0Zk8nWFF3t4gTdIcEZntjSzMSXasti3AHO0tSz8GO46Z/HgpltmX8OgS
fSAv/a19K5+vli/LCcjbeOBr3l2M7lsCVKdvzUtlH0Jzk+3HJbyKfbmsAO/l
tGM56VcpHT9oD+lB+nZ1dOJzcJ4Br2vwbg7NV+Js5yob1ynQrRv0SQ0Oaejb
RWRAlt8xAOWjWf6ZsxTyeu7qBraB0r7dPM2ZatteWnbT2cBlC7h/qL0meFoI
GE6/Tk+/nkl9GUhb895Y3skEr3Mh87W1loUuWEfdoyvY94biwMqvkvwrpS7n
GDSKRdMZGs7p41jiOssqH6ARwNEkn3FVfhvfzkXOh1Fvo5ROdT0fXFcjg8Hw
JxIafwHew/s6vmUKIIj3ntfxtfK34ctt2n5La4rcuqP1tQw+U15Lc4Q2jq2r
GLs/t/Y5cT3Tv0qxto7Zdwm+x1DWZfBrWtd+SBNi7Ze0HuNg5eZeD9hCvz8Q
4fVS/QfK54N8P5SA7sngO0NzRq1xQKPDvPdBCvuglE9K2ak0qWI53gofs5Bm
BlLy7Djf1aaeYS3ti1B+CD+ARgugxVrS+2lsP5U2o8+uHe/k82vHA+eDdU74
ALg3i/IYm573MwKT6PNVtW8Hjn1p/z7K+lQ2PAHbcdmQJ4JnPDo7nDZ9z70p
aXw9lfQU+iF9fsc1+qWez7Fmpcw80L9iW8cUzA2+QbQruoHjJyuO8hzgdfK7
eN6IfjFZcyXgHDLfFTmZBz7dSB9qjRW8bxa2b+2J3P8Beh3gu67Sw6SjpG8o
OwJ5K8PzCPrIGa1fk1+AjEXz/U/kD7f22TfZLPwcarsFxR8fwv1pNXyWOw/1
/yk7KVCO4bue8K8aOnsk1yOAhRpX+K5D7/+OTAStgD7L69q3gnwsbOzutslH
q+xxFHtFcVc2cB0MHaaj7+agE7ukd3yljOiJcVp/0PlfeDogMN/RvGcg9Hyp
nn3j7W1vOogesgesDg2qaU8K/b+9uu1BjqO/0iADC+j3eaDFGb79ibIuVXJM
oa1ALP2zLf2/KWm/gC+U5Cq2qV4FHz+CjlVp72ro8zu028C3HXn/MukD2cQ3
dywz/X8NzesYl/J3HNHdPg4SmRskAAvhweuMv7Po3zOBN6Hbh7z7TTuvbWuN
OwJ6r+X6Lc2RCzjVdQzfr4ZfS0L9f1w6u/+PBwOLQn1fzxVDdxHwJ3Sp293n
yHSe7GkO7xtpz+gzcJ8fal+oM2hPnR6O+fZ5Id+TfUIYY8GAit4r137wJmAv
dM4DfQeBV17SrzU3Q9+XKWBQfhPwVVH7jZD/iE/b+t43QFb167YuYxFteETZ
i5N9PkLfqrxy4BUFLKdfT4p2qutr0K0w+untVPYnOwR+fkZZO9s61bXWbxXj
UHERlW6p6bz86H4Pb+6VtI6Qz9L4QNo6kH8a73nlW9D6Z/pqI+1NJhuUby/7
P+QzPfW3pm1T6HcDeDdU/+C801A+Ezo7vyBwLV2kVNc6q6Hz3zqvoe/0fU54
l0VnN4ByyFhD6inM85XUdRMc9iDvV5Psc1tni9fqnF2y/XIuJe3E+DgZ3n1N
O9fA+3cCayfy0XcHOV+PXP7AuDqP7z6Jdf5s4DoBObiMPkgknQ39rpb1mk4h
aP6IseETtZm+WAdcOpAuQjby69xNlHVtKvrbXu5/Qbk1td5Mvz5RyWNKas0H
E/wPOYd2vAJd/4W+p+DvbzG+Hgn0Vh9CBm7LjxI8rQyPl4H/SOjWItbxi6tF
2tfJdcpLoq9Uop1BOrfBmDwV/XAH2s0C/7RtHYv3qfZPwH2H9s7AdUcv+1Hf
D89GlPPctzO0GaAzOoWsG6UXI0gn8M1EcIlsZz+08kH7rILX1LS29gjc++R1
fGfFeY6Bn/Np97xOpqPGQPl9/4BvV9OPoqHR0FDP//Uf8IA65vD/MUl22ZqT
akyEVufB+azsRDvb9/x5+k8D+J4CPGdTf59qji04uILjC1bL7+/17Wl0dE/m
UWX1D8/8fyf3dwCDeG8gcIRyP6A94fpnBb+3W9jft3x9f0n5I/UfBXwebhuV
P4D7uTyX13nRneIhsjEX2AVP7tKOO8BgzYO0fgzkQ2auprJNyo+MFfeb2sfC
Vtr3CVAnybGFdsqHFWlt5klp0Q1F4W8F+DcFuagHvMj8OwH57MPzVRpfGd//
RY8f1p4N+m9mtPWcZF1yTvcIGgVc5v3vKSeCeeMy8O+rfUvkKi7S3+jbg8jB
BvrDDeRsXuD8pc5hJgHr83qPWfvLjRIc80v2HgcDdiiyR7nRzDpMumx7W+uq
88HWbxEFfP8xaW/eT9TeEfUnwc8s0Ph15KyL/tVI66K3P+DbDuDUBj04hn5f
VvN8vmnH9Qryh6k/MdpxXwXKK/7r8oBukY5Rvn5AtyhdG5j3rEnhc+irSDsn
2Y9Eis72t66zu7MD9gqyW5D/in7NfbZf86Jp0HI5OnZZBq+faz1FaymKWX0n
teNWy0/LqnS+ztrEvmG+pZ7NtL15Z/sIV7z4UOpYQd3vAuF17a9lrM4tVrVv
yJ/0X4yMrC7m/I+B6zx8exU8GoL/UtrdHX5M0BmiPrbNlx+WTdDqKvS+Iprz
3iNgitad+a4I9RYCXonwvtx0vutEGangR0ba/AK8PqxzMcDlSK/dfwF0jTKu
Tem/Dcg3ijLeb1Hm4iDHLv9Eeybaf9V+MNfjyWcGhy9498so34su4/vK6z35
q9F3sfC0OdAAvZBIH1jE88Vat0KXfZXVMaflJ1n7mt0DZ3dSl6avIOQrtQ6d
bN9BJ+rYR9IWyvgI+rSkf4zkf1jHVeVn6EGMdVFsXesj6XnN2aY0chwKzd30
/HP6WVv00h369w5kIA/6uSJ6JxZd8LC946OsRzYTkIXuyECtKMczV1zzbNCt
MXUeoG2/JVmPZQLn7+OcZgRGaz8VGfkTvXEfuUmBDqqX1rEU+wN3c3ou+g8w
Hx6V4f1ytbxucZvyomSDg0wW72IfDNrH24w+KCO7b67baV+V+pfFWoa0ryY5
ioGWlSmrSjnHr2gQ5hgWTeRLIc7xHxRTRnHvFFdG+4vngMxab4y1nkuK9TeK
+6M4GAfpB7+Tvg8PBoH7t5kdU0T/Ay9Rx/5aPlt6KL+vc9RzfOFOyEIT2pBP
tg/ou5bgMhX57sb7o8l3gXdRyHZXaFMbHsSQboOPq5GF7UG2A1D8RsVxHEt6
jH5TArwPQZNV4DIHmjyjTw1GT3enTV+BYzpkZjL0uxXp8jUfzUPbvqdNp2Pt
w2ljfvt9qBtm32f/xQiCbnmBj3m2Rf+kPNtP+WPh2XigM/VehDa/at+qu+ep
mq/mqWVbilNlHat+CbgWps53oXNB2l8YWA2u+ymvHs/Xw7s1XI/q4/FB96KB
mshWYe1h6h9atlrgcE3nbBhL9kP/PMzdeibaX4jiwWzhvVs8L97XfhzaMK5m
0nk7oAPvfg69RyIPr0c5dlNL0sLgWJEx/s+2/i8/RP2bc9meYyU07wtuHyQ7
JnIr9PObsf4fPB+Y82i+8z441pAdMbK9kjaki/W7d6K8xteY8mJyOU0DLVvy
/q/wZy3lXi9lWwLZERSkLSd4/xnPURP/5au29vXGCo65tIp+Hkm5H2l9Dny/
yWefTvLt9D5j6TZ07z3aUwl9GM97IdHu8/of1zxEcYzeq2OfFVpLUCyRDRXs
Z2wqvP2L90qmDcTBhSa9Qr1m3by680rlO0wydo/3n/b02PffeWbGsISavu6D
7p8f5fm95vZ9ofO5tvYbMgiZOhDs888ZExyLSDGIToDTKJ2T0pjQ2ePc4ITA
eJfo/I/0s3YaK0jXiS+k3Xo51rnGPI2B82lnvHzvyaYZ+vWU7Wc928fLTr4y
42073k1GNyZrzQzc2nM9E/nIqDkvfWlMF8fe0fiWkf7zAnO7Ecy5lsCn9dSx
AcjezGmOZs5vgi5bgDG1PV5oXlxQZ+XAJ4T2pZGNGzR7VWf70eFfkH7eynYs
1Vqb35pzb0TnxoPXBtJdyOBZ2v8h9WwEfmMuVYp+XAU+dafdxaijG3W8BE1n
MdcrE9hz1p6y8j918rWe672BWW2vvS+rbbY11mlcaxjlvMY/Xcvn2L/IyY+U
8RTZKqA17T72/SEfIC3zmy6izx/IfaZg+wnU2Cc/jqvi7ctxF3WegWZfkibI
tgvoBp7XeL4f3Ja3cV57BL21L01fuAb9btT2WBjX1HP5TMjxG7zbq4H9MChG
2mloWTXJ+vejZNs1bgG3cZQzIY/XBHbAj1rgvxM5qU36k3xAwMuTPRxr6WX6
8nBgewW/q7WE9fBrMt9PAlbTD2dDj1lRvqdnk6TLaM+KfN4Dku3hx8m2P9Sa
YtfOjifXNdTj48NYx4vSmKfxrity9EEx24O0Bv8ZUY5Rp7xSxayTnEhG9gI/
5/M5Bp1nUF6+83St8U15jXFh8K4EsFBjaYJt/WTzVwGdcJL7V8o6LvqzWMdG
3xTns7064/sNz+7Q555ltm858V4x0xTnugTjzzXS2ZFea10GDd9Isq1Dc8o4
QNlPqf+vfI5hm9TAcWxlh7QJ2AycpC1J0K6K/OnQT1ZS1h368B/weAvPsyAz
7enf66H1RxrfutmOZ6HWptV34Vc/rYnT/mtaf6PuGchvbfrxTNKN5RyzS2WO
ha9DoPVZ9MzMfLbrm066OPCPoH+FLG1sK3QD+mcGr9epZ7LORLbxv8kW4L2+
9hFaJ63XULSuovWV1YH/DF1rHSk71y9Bj9d7Wr9LtwtaBe4JlJd/UY0dk3N6
LVE6XfG5FKdLea3x6lrj9Fb9m1NHn56OIbODdmUt57037btp//B93rlVymf4
dZZ/OGnWCPvD2M93aaHRh8jOhyl9NvZX7eXoXGCEU10/At+HwDbwqkj7/0ny
+orGNY1pWgsRKB/H/cOM1y+jn4cDbzHm5oBP91VXnM+d6szpUfr8ESA2g31j
yUfWVq1ByI4DqMZ1Da0z1XP8jpLos22UNYDx8BNkdypt2ZrfMS4GRjjOhWJ2
yu5oKOlB2tlWtvekv0L/V8ChQzavrYvOi2Ktyx4wDj5sYp2ma9niCJTX/cWF
vH4hHa19L60BjCzneXhqyr5JOReh/foozye3JTvV9T/Q5CllbU92vlisrz/l
egeQDrwO6/+hrNdXioP7CHTCTp4l17FOlz4fgFy2Q4/1Jy2MDi0KnEfeyqFf
fpVtv2zvoc3pUF+/pP9P6Pp5fn+n71/WWf+2PkOvs/XZpfPp96WTHKtuSQn7
aq9X23siNYGsfJdStqekr3a2DeCVQrZFki/Y/40dSiMCY4j+hzSObAW3ky1N
w0P01/Xw6DDpVvrmLN7bRtqbd3ZpPpvO69F/xHjf5zT95zqyfw1YVM++ZeXf
dQzv9YTuv0CvVeB5BPp829H8SMMYMy7Wqa61XqP11mFpHH9e8Q+/DnMMRMXM
Uyy9asBgjVmaJ5OuAMeNlPluhHV53iTbgg+Cdmcppy51xkX5W82TPku2rfxb
gbloI3RgXdIyyN89+HAXSF/a82rNr7UuI3sA2QUoJu5nwFjgK95fCl7PZY/J
uNYd3fg26VB4EIKuiUTHxNJP/+bdZqRNsziOqWKYbmrpmOyx6MUNpA9IV7Z0
HNNHfLswzrpf44H0v+zbdd5T41RcTpf1XznQMSUy8JbWeuDLqcz+J3kRHXCC
/jgGHJ5D+27QYhs4TIdvCbw3m/KP5vU3en8k6fku/j66m/9Z9O+SiDyfZTw7
A1yp6T2Cz5O9T3C1pn3XyA5D83f1jy+ALsj0LtIVfbyn8i5pRmRkBfg+bu1/
QO1FaG1sAbhtQU7KIluVa3jfSftPXyY7pnRF5sGtwecS8lib7yvHOZZwP9qy
DbqUqeD/Ea0v7Yj1GpP8JO7m+/t8N0RrU7LXJ/29guMPKw7xOf0j1PU8v3Y3
n69VjFS66H9rTPov0f5U2w5eT9cZp760JQ08mqd15NqOjfo++K8G5jDeHJNN
dw7HSVUM0VSFHVO0KLQdARQDxiIbY4CvkduhtCM9fXku3+xI4XWlbqQ74NsU
nu0kjUOPbyfdSl3bgn0mcnBWg+bZmhtXhBYFM9l/yTKuizMmhAElUzq/gnt5
keVT2RybVP80WuOW3leqObfyOhe0jnnLV8jTi5T5UyPoTFs6av9VfKV9vcVv
6BZKG/LrrAhyUaCAz+EpXZ3TvkZqZbe/kdnwLSXtG5TXsSsUw2IPcBHZaUwZ
TyrYdm1qkuffRQr4fHimutZB9wJ6/VlJx1rPCcynn5Wo61iMmudpvlclvW1u
NHZq3PwNWj4D1zfh2Q/I1GCeD01vO8qMPBtQzuky7QuRfwQtJ9OGx6RtS9he
81PZZCJvf/GfWR0cfk6w/s2gMQb8W0ObCuTb8/77oT4b0wz8ItAnq2TjDB7H
21N3Pq8XaX1or+aQORwztUgp21Jsga4x8GWBbCCg9aFWzr/S1tdR0Gef9kx0
LhHefQVeR9A9B2jvKd49WN3z89cy2Y/3oaYe4zS/lq3Ix3G2F5Fts+yaO+uM
QTnvb0nXntL5X56VZnxvjz7JAd86kobQ3lLaS2pqvXkp8I+p/V/pU93TupLu
aZ3pZXD5EBo0b24fpj9ksk/TMbz/fhv7HZWu1brAPp3Xga71KGNulOfSy3t6
Pq19C42vGlsfkO8c6ueyZdI7smc6gZyV1xlSYC2y8QFwgPo/jrF/b/n53g5N
28PP78Id16QO5X1Deg+90hudNzPKZeeFFmdkN0jfmyvbEPTHCnTAUPBeRnoX
uf0WvR7VwfP3tZH2k6IzyJqnx8c5lb7eDxzh/cPAQfDIX8I+0fuQboNPdzRe
Ah2Y822HxzPB8bH0ofzsRNtefECSy9F6jtZ9tObzN++GIccL4fP9RO9hlNb8
nPdOgNtS5GI27/1BXR9A2/miQXH4UNJrYhMo6yDvHoZe30KPU0BG6P9M5+wq
Q99UQUEXQmwTKBuyJrT9oNaZeGcQcC/a/u220KeeVaFPQIsV0GwM9QyO8f7B
4h72H6414ovQ7WvqOwQUqoi+0PwD+Lyzz/HpDJ/WkXshp1N5dzjlV6c/VZO9
ITJwO6Xt1BQjRfNw7eVqLq69J+07jaSMFKQpdfY01r6YK9WxHchOdEhjaP0b
+msSdF8En3q1sn1xnoCN8ax4j1saszIhC+1p4wlktzB0ylXLcTaPBP4X9N/w
EnI+iroK0v6oTraNfrm+5/paL9Lc/yvkszq028P7Idw/w/z3KTr1N/AqE+V4
JcXBpVplx7yRz3H5Hn8O3Qsm2V/j/Kz+FzgMXs3pK+eh8bnM/s87IttM/Vvm
d/6Nar7WGk/6to5FILsA2afKNvVoXMBvZ7DXx7TvqzWypuTfgSexJb1/cSnY
exha29E6j9Z3WhfwnoZiriqvNK6AxyCNORqTtgXGIl2P4dkOZDBNbeeVan/+
EPLWjrZmL+F9Xu3tLgvs82pc0vUY+DQD+nelnYd5d6PONHZ1/1E/es6/w2Hw
yglPi5Z0Wqyk82eYB53m/R3gvJl35uiMAPRNhN8zeTYDeAXavQqEgNcR6HoJ
eTpKegwcl0L33+F7EXTcXO1PNXWsasVPP1XIa3jrA+t4awPrQrqeG2fbDNlo
KD8Img8BtoXarmoTaQnG0D/I327o9YOJyFIxeJwHuf8RvBrSjh7dHQ9R8UWr
VHP8vQOlrRcVm1v7tsorlZ7UeKex7mGSQfnPGnuPRns2tUIcy0/lqDzFkY4q
ap/5q/n2j3jbioWBW2f0dHHSDvxLd8rouI5HkdmXa9s/qdbYtT+zppjjUSkO
Vf+u9oHUJrv9IH0HrY+0tG/fUrVsUyPbmnod7EtAsfXqUXcD4Fiy1yy7AKnh
f8Eq9pvSMJ33frUH/Cb9vAPfPqK838H1a+gYFuoznz9Dr/Pg+CNpqmi/9y46
bmIqx0NUXMQ+cfYH3wJdWAx9VRSYi3y8EmRbFu2FTEwXsLMJ9TmKV+HtHNLs
Tbw/qTXtngmO36Bz5fJzVSmLfV1pHq4zpvof0TglHimOumx7jtO+XKS/0vei
qedipPdDMvPOCPrsMnCO534n4EWdjaniOO5a97mpM2FR9pcuX+nvAdtDPRb0
kL85+PEzfPwVmKx/xtr+Z9tOO76h3unw5Ev6YnyE7Wze7ONxSeOIytC18qmZ
J4cAheULKcz7HNrjyAYt6/X2nOMTaN+K8loClbnXhnpOJHutZhj0HgoUj3Vs
Cune4rQ/DDjJOxXq+j+iAOUcC/fecXl4kBdZbAV/7tCuU7z3rf6tW6B/GzjV
tdqxjjZ0b+h/bsVxv0C/qARfGqNb+6Mvl4PPINlOUl4wzys3sT1OB2T0LrLx
HWXMgu7P8nndqjwymKmqZa5wRfun2tLFZxnlF1znGRXzRfFeTmtuVtbzC80z
FqPfL0Dr4tDoLfrBYuCq9uKD7FtePuYXBWxwVgEDweF5DftkbATfGwLvomsW
gkdPnYWmnaeAabR5KhCFjJUDXqWN+6n/e+r/iOffoVfXtvX8/0vw+BV8foly
rHetIa2SHb/aH+T1pYLMJ27W9zjdVev2lLmxge1uZLej9Xnpdel3rcnnQB62
IMNB4JWfZ1N1pqK57Z93IBdXGIN7IZNLkMWEaNvSKNX1bca6bczj/iAdRBmn
6BcnBfSVU/Dmm5TOx+X39Rp4WRKa/NnZ8V/StbF91G/ky1PHTvRsSvpAJ9rQ
ERgK3n+DR1t49BL/bYMyOL7jWvTNH5R3GzjIOwca2L5S/ozk1+gMdVambYno
hoTqjuH5LXxPD52uay2ZPv6dfIvq7BrlD2/i+D06R6B4Pse4FwwNu8iGlT7W
HD1XH1k8T1/9UT6BqngtQzFrtLahtXDN5bUernvK6/4A8BsOTu+28xqN1lfO
JBuUVzye7sjR5T4eO/bBg71AUC3n5wbGlE8D60yap2hMUf+VPlge5Lzu9UbX
PyG/MqX7y4XAupXsb2fGB9ap4Hl0D+/7ZKd9OYHr0O4r6HOWOn5v6P9x/YvL
RkW2KnuivO6xnndLdbHfItn9yuZX/VrjTWKkxx/5BpqsuTF1/Y3cDYu3XfU5
7fPU8lm4LJRRHT1VDXgdXOKgwQ+UN6mHr5XvSl/JGOe1rZfhwfDCjt37B23p
JLtdeBdXz9fKj4I/bxdxvOEQZKiG7JV4fw3lfYCsRoLXCHAdB9/GVvEef7co
7/nrud5rgly9gA4L13nDWt7zl23lZfrCcfllQGb3t7Gd0A8RXqfSfEHzhpWM
Kd2DvbapuOKyG5AtgcpfFJANychY9E0DyjynsY/5RLdKttnMRrlTmBO9DjwF
v3flNw25ndfDsQnKlrJNmPaAZCMme6UfAjZLj6nvEXARWh2jzLnI8TzolSXJ
tp2y8cwKj2vx7eCUPguvc/CKh6A5SuumnrvMC9hV/dDRNgM9A3YD92l3b/r0
A9JD1D2GskcX9j/eqlCPpQdp108839Te5/l1rl++w74Dn3ElfRZI9F2tORT0
rh9nuwHZCmitbUI67wH37uXzIH/38j+Y1lS7UEdd9HI65CY6r/dVtL+iuJRr
mIf+rrUOrq9CtytVPJYqVlNNxpcXOnpdTmtys3I4Ttpl2WVV8FkInYl4O511
kGw1h9D334y0jYLsE+SPRHHJX4l0qmv58mlGO05oHxS6f0CZTanzCfU1gsfX
aHdj2fz0sm8L+bU4rX9ccLsUaR+E8ptWKtbrGpvh9bg0juus+M4DkLcj4R4v
NVYqHsC76KdSpX2tMVQ2AwNpzwidCQbeAYcXdN4OOZ2V9J/72v9scmTrLrv4
zmE+8xIeOPfyAjQIpn/8WtH/Xs/6+rtyyNgm+tE5rdnRvvP05QnwbkF2xwbs
2MA2Anmyeow8Dx3OAd9Q3hfgkBEepe7iVNfyiRTR1v+EabU+oPNp4JI7zPs8
2h/SPk5O6hwMXbPRf3f0sd+enTpbqL0T2avTxuah3keXLetd+LsH3O+F2MdS
5i72s6TnB+p6bq40XU/nBcpvCKQqT3nFflLcp32Me6Poe6mRh7mdbbcvm/18
yE1vaHo+2TZ4N+Hxaer8DshGnTmAceoXNX0GXz7hpV/XgHP6Wt5nVywv7bXr
vsZq6V6leqb8Mmgxlr7eiP48BVweokty0LYn8q+iNiPzWzQ2g/dnlFuX94aD
7zDgO2iL6AQhwkGbg22jNjzYezGKf164gv0p/ffPVsD5xMC18l0C14mBvP7/
Jkc7hsktIDfj1gr+bxfD31ZaAwYe8M4ZndHRvlsD/9Nlg3ZrqtqW821kfyVy
Nw1+3oUm+dFfKbmXE1q9nMJ+u0MYB3Jrvx5c45kLraV96cgv4/mcYl7XXYPM
9Qt37IF/2vscd33toza2P/rfGBeT5WOkksfX9eU83upfLW/gf2055b5FP9ua
xvH9dF+2Lpe5v6ua7f2V13+7bDbkF03+0eRvvyltDoUWs8DhWflALCX9F+fz
3n7qwB6/rnsG7mkc1/6/xvRGfX0tGyWN1c9j/C+osVr3FPdJ5Sn209423oeU
7+E2obaP0d6SUp3ZVl7/+Bq/M+RzKhmTTJWq67UkrSNpvNZYrX1FzdE1l3/c
87+pXdCCwJ6HxmrthWv/JDd8ucA7DWnnYK7/oo+PY6xZAB5FeKcwUApdkAoe
rgXHNvDqQqhj+B2hrneoc2lhnw9Yk9J2nwP59pb0g3QKPDiDjB6lnfWYuxWG
xkVz2fdxCLCRb9bRl37UXBeZuYu8DuKbUsjCQ2SqckX7ztyDDB7oZPt1+TuQ
34O7/Kv+jCxWg45ZaWNHaF0N3A4xngYhawpy/E993/srj+/vQoae0qbMyEkp
2rqUsWkcuI6XfStl/IYs/Qw950C/efo/p80XqTODxjdwfBv9+Z72Sbh/EPkc
QfoY/IrRn6/Kzpjr3wQJTneD65fAp3w3kvoWpnDcrBHgOhO8ryNnz8k3ZAz4
Odlr3zq/fRbaTIc2s4BvwSMv+H8XYX+e2bRvQ/v6IUu/8O6LpIOQ4wFAYfiy
nXrHag+nrv+l36P/rAQuAPWQ82hgDLi2gD/T6zpGiuKjHCF9Bq5N4NWvyfbJ
/SJzlfPooz+p4xNoeQ65zt3c/uuWIhd/Qb/e0CELNJxQwnMVzVm2wus84Jsb
mMW3T9AT5zM6DrtisOelfz/TGh+4FpY9HfKzgf6YR7REP6woah8gU+hza/Xv
QH4qY8QG2THTzuyxjoOcEjimtXXgCn3gL2Apc5U3sro9h2XPFel2qr3X5RsD
WiehxysBSVH2X7oXSIlsl+e6XJTn+ZXB46LW2SkzmQ70ABmpBy3ezmff2Dq7
skdns0r4PPgB8Vxz++KON3tD/5qynQ2zzZvivI7XeesY28tsRc5Xx3uPRHsl
a0jHg2sqrWNwv4v2QkSn1vYpIt8id7UnJTsv4EYnx+5WDO/S9MVW4FYfurRo
5DWFqeD4KbQ4ynfH0WEngPO06QLy+1Ne2wjLB5XshOX/PgsyUUY2NrJ9572F
QM06jo3SULJN2xqDR1P6z0HSCvTj/WUd90a2MrXTONX166RjaP9b4H8F3taT
nTA4Lqfs5bT/GTSpgw5rwPf7gIayV6G8cNp6rqztPC/SlnFt7MvueV/7sxsV
6nNnOn+mWHAftXM8uEP00TF57WtqG9/cy+n5m/zU1aV9dVL4np7pLOAtcGpM
m96mjqrI4UvI/CbKLAAteyV4n61+B895e2Xx+QvFeNMZjGaMEcfplwnI0e9a
19IaIuniCvaVKb+RM5CJ6UCS9gforzlo/zrSF+i/TagzD/1oJmXm534B2UGg
E67xbjjfflvH/lM3oaNudrIPqyHxnuNpfteI/tQaHLJT53r4doHyylLejgin
ulbMvWdN/C/YHpx6g8tqaLqxkNfftQ4/DFwad7HvI9nwaO6lOVgB9NRp3nlI
/z5KeSmoe4zOuIHvY8p7pHlqLftEk2+0y5R1n/cHMw5cI70pvz3o0Tbxjme7
p7lj2t7X+k1m37/CN8+h86KMjqWkOETDKtnfzyt8PxJoCX8/QR6van2V/vsE
XI/UtZ2W5Ku/1h3BsRY4j0YPPdB8jDJzAcfRN8eA9PqXRac2Ry9eo5y26J8O
sr+njzxER83nOpT+mgjtbzS3TfDXTR27qKBsnMH141z2ufSNxv/u9pVfj/Zf
51590onF7PfmjV6Of3algm10YsApDJqUgGcltScDfZPQp2nAaSc0fAl5ukEZ
N7X2Ba8Hg0df+ugd6szCO7e4X6m784o/ruvq9LE66KMapOdKOR664qLfqmm/
JdpXD0HmF8DDNBoT6Q9tkaH2QALysIfy1oDD3xntJ7UbZQfTT2dBu7TIw1DK
6wlfO3F9nXY2BhoB15G14tDwjNY++a6iAJ6GFvEa8kBot4P+8C8yvp10L/qn
MLz/ijQVvHxM/c3BbTD5VLwfEu+z08O1V6b/f3A7i545o7VT+sNajQWyr9Y/
GzohopvHvFOdPAbKniiaMnLAv3UxjmWeHZ1SAfmrBGxFJu6B337odgwct/Fd
Fa7HUt5NdEkP2lMn3OtOwdzPTR1jwGER5dyGzle6eg1ea/HpkYfO6MKC8vmE
7KyFp69RxxZ4n4Lr5sjHBHBdksf2ugng+S68SKBtjbneQR1N6tje7kGofSh9
Tj310GPh6O+d0GyHbJDRxT/R/kM8+5k0s3xHgUt6ZGs7dR/UuUKtl/NdbXiy
DryH8F06+vcg0rTwYBM4P6HtKXReGvlaWdaxgnpBhz45HUdI17JRkl/pql3c
hzUnGdnH85KJtK2+bLV1Pgl8v0A2C+e0f8OvZCckuUcvxNLGcOiZjjHuQ8rb
WMu2Ijdpz8fw526Cz7+NR/c2gQaHZP9FfcmUMxXavECahjZE0Tf2QMdSjMdl
gBLUP5D37lJ+T8qLKeP484pDr38i/Q89k70RNPpHew0tHZtHMXrE/9P0vzbw
qCV9pAD/Q3e158icZAHvbOT6S3i5iW83l7afkxLQcj/pYWizn7Z2pIwOQFPq
y9vJ7TxHG85x7w6QDdmoIdsr0tx8N5N7LWvaT4rOzujM237tT7ay/+wIdGtE
J9v6/Mx7W5G7T4D+8Kgo7VlA+k85+ywapm94NyvQFH1TLsY+8d8HhkOTGlx3
pIxu8KO69ml0jpA+eUn/YrRvN7KeG5r+TTse0UfrowNehUfZ0IUN5MewvfM5
AteKOfJQ57vgQWroWAZd8E209y3kq+GP0o6nrDO5Ops7ijJHyy6CZ9v4rh33
X0trf//y+x9COg887kHzOa2dv1TK10t6eE31W8ax8+iS68jDpN7283wY2u3J
6njfUzvZ3/a/9L2u6LokxuovNT9GP/7V0raTspPXGfneVRynMpF0MzzfBDTh
WR/q7Cd+g+ef1L2V+58AZxhrekOvYGgyHhpuRo6S6DvvoqunJtjnk/bce0Z4
n6QleKUh35Oy4uFRN+R0ZUfvB8j+QPYJyygzjD5dIrPz4zv6+iq4XwemItPp
afcJ+Hc/2fluhXz9GtAc3F9DNlaC85/QdlYTxzXRfqnOMssXfW+gJnzfB855
wblonNfUtLYmHzsPKLcj/1Hh8OPXFq53N8+mk37O8xmkC9HHC7L4Wmf0v81m
n43yGVNEthOy+wl3nJ9m8OIHxtrb6IBh4HVVsgeO9/m2F20M0XkCeJSSdCHy
m7Wx/UpnqmU/0725XkO7ziFX/WVzwXchyFt17WMhywVp38Nkn6Ua29hnhXRO
aIzO7YBDZeASNF/NOFCZfhbPO1coYwq4fUv6M/OFEd19dlBxty9w/0eg5f+j
6TzAe76+P25vYsZKECOEmBGEIIhYidiEiC2p0WqrFK29V6u1arRGW1sVtVuK
oi21a1etTm2NDkr5v96/t//z5Dw338+499xzzj33fu49g/abU3c84/BtnZei
N/PJ/oR+B1LnCOpqyXg9gCzsB2aEOOeT7LL2Admo63PKerT7N/g95vmX6c/b
1PkPvxdyPY9igTBO9qJfasLLc7Ijp6+X5XOLnL4D/76GrmeR80vgM4R+XKY8
RV/bcz8/MIc+vEBdecMdm6NUL8fqKBvguC5PZEvEc5VppyrlYfC4TZ1foL9+
Ri5+BYpT/0rN3U2dBy8Uuo4Fl7LI5e1Mtpm4DQSpX3V9JtSZeagT0L+v43HI
TlpnVmfAvw54Dqefm6HPIP7fQpk7m78dFJtgPnL1ABr8Aj4PGIvTaHMq8DY8
/R4+v6a1MLruLfB/yHM9+f0v5fc5nFNMsTj/F4eT/39RrDXuDWEMX+addszl
G6DbMPTNR5SDIx2bpqvOkGU/Ah93I8O9ithecTrX18v2gucqaz8fnTGK8nXt
AYNTFcZX5RKOG7qol30uPkC2wqDhSsp3GznWh/wgz0KP7dGeYwcxjz8PHGPt
N5iyqc60Szov31TgsuQnxDESE6FhA51Paf2mvUR085NU+/YonqXiWr7Cc+HI
aiUgHzQ6AB3bIk974dVoaPFjgGOrzGxoP9XD6Jun1DGNOf8hUAacSgPp0tDF
2k8Lca7m9Pw+p31T8GmArAdTdy/4UpT+vs31wkVsT6JYJMppfwoenAGW0t/d
6LUMvF8L3TKAd0+AUx7t4SFzu/g/P+Ve5KgOfXgRnC5q70L2UVwPBfcaeXwu
2T+TcyCcB9oDfVi/9waC0zO38H5G2sgELKfOZR187ncImfoCqIFuaqE9QPi1
uKL35bQ/dxB57c2Y+CKj8yBd1v4NOv92WceoGgTMg0b9eC+svc8C97Xz2WCc
ziBL+jtkBXL1IjxfB76ndZYKXv+Cw5qujgV0DXr9Qb3DmJN+0TyjvQ34GUS/
XoG+WxQbAmjPOzkjncOlDM8cgP7HszlXjmLAKF7/H5JB+rMcPl3W2bNs3prb
d2VOHo+PJOR6FPA7bV6h/Z2881a8420q1mYe8PhRMR7gWxwwlmcygFdBygvI
SmHm9TDocY3384oGyM26eMdtlB1AV9oujowt1D5bvNcqz4PvXd69r/UDumJO
F+dNTtR+Nm1dAD6iD/9A24fAJebzCvD4CjhdBnoybkoz94UAmeHjYXhyCFiq
WA/090x6X9O9LGnOzaTcMCeRwxRkqzvQR3aDNW2fLDtlfVsWB5aBW1V4dwx8
djG/fES5EThBn1PRN7Po0zYgF/3+S98i5ZxD5XSEedkYmsYCwxkjI8H7NSAS
fmct5f9PgktHfm9Hd7SkPKH9X/rbnHfjuvrMfiHjrj84dYL+qZQPoNHuzs7d
8SE45EY/hrf0vqZ82bW3GaRYScwXp/I6n8vnsielXIGuuYrclaZfZ3q73MP1
zeCyAdmOhfbh2udCxkJa236sS5RtyGrxXCjP75cuYk4/J590cN6DDn4XWVoq
Xzqea6dYAcj6R/QjB/J7FrpuS3R+ge2UAbyzgT79B38SGbMDGfuZGZf5mQcv
07dZ+g7QGT7rhHXQek9Gx2Aqy/fEdWASdfzHWGzC/V+k7+HLGP6fh9yVQIZm
xTj/hr7zZLdwAhiOHE+CmMW0hmBt9D645CjlmLCyHdyb6PiC/cA7EpwbIlc7
tAaEJj/R/3y0M4jf67j+BFkvhRw+psya5vXRia7+P9uz352pOz3td6E8De4j
o53f4iJ9qUX/L1E2fzbfbqPuMZm896F9jxRw7BPrOFjSWRtL+HoiOLfubps0
xfdoUdQxPmrrG4jf7dDn0dAtBLpnB4/0lZzvcU2Y1zg5ynmdU4wxMRuI4HcV
5KMJ92OBjbLtQq43ca2y/AigaVbkrQBtz0K+ClIG5bM9s+yaVzL3lGnp2ASK
xbjp2XfKWsrx+gbKaTvYl2vaXvU6dH8EHlEtnRtTOTI/TPTewFjgvGyvaePr
nM6hkZ614xHGw2FgOt+sL8Gb9fRxDbq+tmzmA32gFAiPnjAWguFvAM+lcD2m
nPMGKn9gv1yOT9Gfcid66WXqeAm4rVgcPJcDWuVvi25SrIy2zlV/EHyHgfe9
Vo7P8f9xOvQ7INh7X9r3qgGvfwhyDpEM6LKc1JXMvJWL8jL3LgC5n/3/QzX/
Po0+yMe719EJW2gzD/ffq+N914A0770q77jyj39WxuvRZYzr5+DLKHTuBPTd
azpnhg5B8mNq7z5OjHcMDumXTa2dA2k6dJmZzbkD4xtZz0nfLebeIuBgkOMK
babuMz1tH6k9xT/REYWYF/6inazUd7aw88p9W9j7WHWB+dTZhfkgJ/U2aOE5
+16A53DlZ92J7OwoaLvwB8j0H8hMf2SyH/AuPOrB9RSgj74/pOsa2wd9MTqk
ALzMX9u0Ep3O6Iydunfx/HXaXMn7Gcp7L7o3MjSOsdKTcjNtpCBjWyibwb9M
+t7QOgs9dpWx8QPy+VtX73PeoW/r0Xdh9HslY2lTjPel5OuxgT7Pzu3cwXWh
7UxoNgO4RTt94VkfoGs5+4y+xvuLn/m/yw++FXKXjXEfT9kaGV6PvIciNx0Z
Ty+W9/ePYs0rl4tiwX4b7T1L7V3Wl09Pe+sm6bi7JR1PaQTPDwMa1LCujmts
fR0X7r1u7Xn/lsU5g6QTlsHnJPp2ADleqrNZcBnVwN+rH4Fv1/KOXRAsXyX5
JNOP1pm993qxhudl7SWUlL2J5kUgb4T3Lp9n3hir8yVwqEO/ikY4NpRiRNVv
7filimMqP+Fa0GMZMnMB+Tje1vu9+6hrr/aks/lbRd8s2t/Mi+yPg+7vsg4K
of+lgBjaGwsPDjPeQtE9Uchpnbze6/sXHB8BT+Q/wvvvAm+wzjyvuBPwuT/X
mzKPxQL30PPHwfEbYKTOMuB3CvT4lTY2IRsj0D0FKnhfYxD663n5Vsc5vqLi
LC4E91W8UzPe+SGUV0A2eLKdvlTb9tOK31EXuYwCpiBLB3nmY8bjGw2cL0D7
wvno4zZo2ijR/+d/9ls+p7/1sN+pntU7ol1G6HyaMhP9Ol3FvzMD1+jDUHTI
S+iHbkW916Z9tiPQrpJiT4iP6KHi8L2Y9imbO+Zpa+4Ppp5BQLpg5x1VTmfl
dlbsmsblHINmGTqoBrSZntXP69mryMPkCo4PoTgRg5Gz4/CxAH04Rj3jkb8J
QEHo8Brjf1QT52z/oJXztqssGu//P0enLaVPXeUTVtUxchVLXvkIlH8lP5At
yL7Z2SnfBf/bijUFfB3tPccUZOAWst9YZxeMs5Hw4rHsfyvY5kO2HyW49jW0
joKP9xgHjxWzhPeeIP+ZWWv8zfsl2hqC2/paNXifoa1j5Rekb8X5vxgQ84xn
4p3aFx7a99QZxTXG+O+0OU/nQ4yvdfCmHWNrIONgLX1FHNJB3nRr5QfL2Myj
Mw7oURU6BkT7mmzNvmEs5aHdMPltaU0KnnkLO772PWR0IWO0ILR5h3IOsvoH
9CwGTSbQzvgAx6PXfp9y1K+gvvlcm6q4dcBm6v0YuB7lXCDnGKeF6M8e2rxe
2+vffei/7KxNsgFXkYXXGXtT4W1LeFCGe63CrHfTA4G8O1G2oNCzCrAXvueA
n9kLOodB0cKOiVKJMV0M+QwC737IVmHe6wZ+9bj+PXIeTfkdsl+E60Pg8yXa
uc+1fIGO56996O/Qhf24NwEdPjfcOZuUk0x5m1rw/BbwKA09tkHP7cCsbvZf
+kC+sUUdw7dvqGP86oyuVrzP6S4wV5wHViGD4c/2q5V/4zaQDbkfXNH4/UK/
c1PXiQjHDlOOOPmgqy/qk+ymTj+zncoAPjORj6L6pkTvLAMSwe8IeB8GMrf0
Gqof72+Cd3m4n6D5AsjF+usM88LwCK+phhT2ul9+LfJvqRvls9Yp0HgykI4+
/Y6cr8trmoveij/Thrr6gPdJ5P5+W+d8Ur6naozJ7FmdZ0P7sgWQgSjKbwLt
jy+fDeXD5LX/5cSsjJwVox8RlG1r2XdFttOfl/XZjXK6/814y4Cu+aeC905q
5HUuk9PQ8ywwkvm7OHU8pu+LgECu3Yf+hSnTs94Ikc8Edf2quRkYQuNj4c0Y
oCj9jqRftYHuijVFf09B45XUeRyZ3ko9aYUdV07x5YLSHHtC9oeyQ+xIfe/R
j5zcTwHvavyeR1tdkKXv6cs6+JSJMf9+Hsfo1prvlZpeA/7DeO6e33upynmQ
AxkNpv4neb0Xpz25Kxls2yMbn/z8nw/IFue5RHNKQcr9+o5lLB2o7Xh4w+jX
CWRgts49GJ895NsEPsOg4cnmzpkm33T5pVdG12TWNwH8TODZeKC9bAC5Hg4k
AmXRI1WQpTKU9VA0kYyJo+DRETnow/W/8nv/Ywn3zunsgnfCgI/RL5uhbwXo
UB6ogNymMjZKpPma7nWgzhyJjh3eP8C2jdmAd7SGqO845BXpT+uCjkWpmJTL
6eNw2l1GmbXZs/OKCj5jbY1OSg5wbu6H6JaFrGUboxj3I5OfA5/y3iP0zTbg
M3j7abzz/s7k2XH0qx196sC1OK6VTPNa/wJjswdlKjqqP3AFPXAu1jHuFd8+
LYO/OfW9uRH5KcD/yxlnucHvCrj9BH1HyG8ROAWfaqV3nNzswJgg5yl+i7I+
fYgGjiIXM6DjHXTkHxkdx2ee9mqh70J434/+3aPdUHRURt7NBExnPrjIGApD
Ztc19Z53AcrTtDGC8T4SGAoMA96gr8uppyH8WUNfZkLrull9lvqY8dqf9v7j
WgF0U6l89mFd1M65l+8h82llfR6hc4l/4dUM2r/B9fuMmcPcu0s5kTE3mbon
hTov+fsdnZtceevHIZvtuZdY1b6ktxhfEzPZT6VeOdvzXOH5vvSvN//3Q+/1
oWzQy7HacgPVqX8hdNwU6//3tvdv7c+eTrFd/SD60Y77g2s6dvFTaFSEMpkx
8IRx+R/QgvXTPJ5ZVsv8Ft9PUscA8RyIADYwFt/Ut4H2MaHPBOS9SmvDJP4P
pyyl/QxwL1XO+eF/5NnOlDvhf3Xo+GJ75xytBa3eYb1UBD6Fg29B+NAN/Tlb
dtht/Yzyk+q553i/rewIqKN7bucGOEH5PmuMD6DFB5SVyvpMSOdBB3n+ALAe
eewHrVNDvd7oT3/LMn5qdHGM887U3Um+67KXRlcls86+im6YD2369TE0g/YB
sT7LT43z2f4XzAubtX+nPRtwOou8dKLM2trxtCt0cz6kh8APtJ2VebIx72ej
nM847sBaqT0wS3v1QAp9GEPdL1FvG3TneGjbSH5U9OkoemEhdSwIdazFl4s4
TtjeIrZv0ZpY30hXgA+jfeb8cynHi8qWYL8a+dQMQ1en0JefmYM+b2B7vSus
0w42tv257ND/ki0lv0vB/97I5GzG+l1kYzh1jgC6MI/8zthaz7U+9ewXqPF6
ljERSx0L6EsPcK4HvSYzbuYin5PBYW1u+2RVk/8C4/WNZh4/yqGu8RRCewdK
O591rPYueSciwXuZyj/TGWiayd/d+v7uA1+L8zsKHFbSfgzP5mM8hyA3E+T0
glwVhT+/oDNGQYvNjLPm8nelfMIYfJ5nH5e0nbxs5HtCu3PQ+Wd+/wSMQ0bH
AueRmfzQfRjPXqrhvMzHpFNqOM/Lm/K5BT7U9zSysqqxvx/aAVXQn/+A7xTw
KJ3mfdeqjKcp1PcHen5PLvt0H2dMVIcP1YD36W8m+PSB1hDUFU89ZXi3DTjV
QrYvsv4pAp4tE50L9BD1PwLHJui2eoyzukA4unYe/a8e65hACdRxspuf08I4
A/RK39Cxi5YXday9jtyvynvVgQ7IylN40pFyBn1rqnkPHMoBX8CHw0Cexs6f
2Zb5fnw2xzpV/ofm8OQEvGlBWZd+TEcnfoDcZ2R89NHeNvL3B33Yhv7+rZRz
kPSv45xU2VPcP/Xzc/nPIbdHavt/+SHr92JkdhdtLodmFamvCHT6CVxC4+3r
IZ+Pa/RhpHz1VD/jKIw671Eeb+lvqOvVnY/j3W7OyTGS9ccN5PAWMIhrkbxb
GxjM//Uo60c4V4nymI8P8nmhzg07owvL6rucuqfQzwrS7+AZRtkZ2t+lzzti
fGaos8PdyNhbz2xwtJ5TDOuC8KFhhOONfYu++4C+DtR3H/QYG+vcrqeA1ryz
F5wngeNE4AfGYECKbVeLM5aSZCsEjl8i/6mZvL/wUknTRTRZxnNfN3VcuNk8
m4PrZ+jDUvBbgE6Kou0Y9PpO/l/Ou4+1DwJ/l+g8D5nNiJz8AO1vgXP3CPuo
7IWe98EtO3XkgR+RyMxX6Nbq0P0Lrq+jH9NzOrZ/EnprFm02472t6MmjjJ97
yO+f2s+BJ53o258RLvU7VPMPsrePdVtQguNjKzb2DfTrefpyTv3m+RXIWD/Z
3KRzTrYvgbKMo5XwZJL81Vp5D+a1Gt6H0beyvpllq7iHemcwR80CqvH8H9HO
5fYJ9CsrGaU8TH/nQ8dXoUkyfegOlAe3KbTRTn6glL+2997TMOAMMvEyeFbg
maboyChoWgfoidxchw6VkYUi+kYDwvQMengD/JwMT2KRlz/BcxtQVedotPkT
bcfK/giZ/wPYj1z8xVg7zHplAXXM1Hk18CI8SKGvL1D+B927VHCezVYRPt8Q
3X+HDj/TrxX8/x/0fAxEh/hcTedrS8B7IP0tH+/c0p+AcxzykA/ZfdrYMZ//
owzh/UzUszqz/1dZmnKjzqy1V9bXclgxzbJ4nfqzcv97ynkNPJevhXY1kasR
jKlIymJlvMYpQjkLOqWHFpeyOI+08kkHMRbqgNfxptYTyvc8vb73rn8p77NL
nWE20HqKtvPw7iPeu9fS5x7t6UMG+ppewBwzHxlbGOlYxwPRBy0y+txO53fK
5VCJ+sL1zQ2dN1LHVzx/FPiaOr8C9mkvnmcPyXa+q+d8nSH0oJzG/VvQtgh9
+FVnWOB8pqRzZ8QDP8PvosGO+f0i/Y3ua5uObrzTgt/ZkZcW3O+B/q2c5tjH
0lVak0ZTX4nOPleYDG0fM0efZn45BUQiHzuz28f+JuuSjjx3S7ZyPLuM96/r
m1y2UtD7SYRlt309x7IoCE4z4d0ddPhF5uoFOh+ubp8rnQGtirB/2AbtE7I+
C2BuqwJuQxlvh5hzRtCHrPCvmtb49LeC/OvAuyrPbGFMTEV3lOG9Kb0cxzYV
vF4Hj2ppjuHzfX/HP+lHWQnduCvFuSeVdzKA61ekx+Mdl0TrqXBoFw/+1dOc
N1jfpjH6Hta3L2O0TBHHuZPvlny4PoAm1cAvmuvVde4OLfMCi8s6tufWUo7v
+Tz9nIWMtoCXR8C1LH3/jrpLaG8VuZiMntvOc7UppxRyqd/bSjm/u/K8f5/Z
drnyMf5Aco5enE6dx5o5l28EOHwn32Wev8b/+Uo7rq32iNuhnzJz7Zr2H2Wn
WdX7ymHN7JuyBf4EN3A81YVAJvRtHuh4HDr9AW8/lN9XS+cgmdjbdgj1G9u/
WX7On9BWcEfHcsxFG7X1zUwf/tSZtuJRQNuzoc6fMYd6mqGLnrKWSGri3Llj
+L9rE1+LAb+89CMA+JtnByAvEToLg7+JtNUa+JFndkC3JM0r6MlrVR1T9i7j
bXk7f9PdQ3dPZizOqubnpGdjQx13VfFXtTcbSr/+Q84i4L+U/Q35QqDv2vP7
He3jNXKOmDczOU9MXFPbDremrufQB3Wg2S342Uq2y4zBEOGIrk9hXPYEMubw
9SG03wEZnAXebwCFwD0avR6Y7P+V80/xgu9R3w7kYle8Y4crhrjyKogmX9On
KvyeBKo7ef4u12agRw5BowDkYjD9fp01Uxb4uZ1xuROoCd2OwoPJ8rXr6rxh
yruqMfAF1yrwewx6MQy6J9DX7eiZlmXt8y9//7aKoQEsR+c/LGzfFvm4FJM/
qPwd0JOvob/qwrs93RwrNqGqY8e2oV+ROkvt4pgoS5DZo7STnefWycYT+BP8
C0HHgvou6+bfk5gvr9NOW+bPG5QN9Z0N7W8wdlroDBKd0C/W+ZFvAr/QVlKQ
z4vi8jiHbmVkdhA49dYZAHVnBZdF4JAjxDGZpH97QIcU2Ze1dkynucjzp4y3
wbzXIs6lfmvu3wu9qoN/Ff5f28A+K/Jd2cz4GQgOz3HvoPYnw+zHMAKa/EVf
/6zivT+d/TePt21db+D5EOtR6dPDQBrv1UBetsnfhvm3GvKyHxm7wXjZ3sK+
R5G0lZm+7+zjfqlPpaD1VekK+LEHWc4tm0zwiEcevkJeNoJbVWSmPP+HAaHI
91Vk+Q1oMqqHbUca036jAo5FIh/jm5S9qXsu8tSzsu2FB3W2zbBy2BaCn/m5
XpI5dhGy2Qm6Z4Omn/LOHtmooKduUP5GOUN7U4G2ewqu5vi4ipMrX2vF/lMs
wILaI+J3LWSlBP/f7GG/vTKM61dpc1NhxyZUjMJg+l2BeXmF9r/Ke+9ae6Ha
vw6HPuegxX749qVseaivLu8toK59zBuB4DNAZz5888Qwn4xHlyUw/kpCu2pc
rxptO8SztDGxgONAlodPK7heIcT2sLq3kHvr0bfDGFdXdAZW1LboslX4JIvz
HcRqLQNOS5/tE1ZB3lpCq1bdndtcuc+1dpkJbtmpdyw65E3aiQKXgcnO96mc
usr/KTvebuiGq5Sf6FwRmYjh+qE4x7VTHtG3+L8111ZRTpMvIbLcuYNtDJUD
8/Ni/pbQN0VtYD3PrQM+Qve9Ab2/QWY+YZwPQB5ikI2BlPm6O8bcbPgViG5M
bum4y12RuRO8d6O839+Yz/VlpbzezfksX4HebeHDbORvMPwrhOwVBHbpvIdx
mAJdejOmfoY/L5ZyPk/l9ZT9azroO1V73shKUlPb7XSlbMg7PdEJgYyHRjwb
B36NIx1L9ucGzg36AbqrLHh8GeM9nJWyGZd/BXR4LqvPvMsgd0/hUQd4WQDZ
7Un7XXs6H2DJaOcEfIROyEL/Oso/nXFQB1n6jXF8izp+BO6Xs5244isqzuKu
7o4dtbu7zz72AJXoa1BTxws7CRyAlqk8f5AyhvKtQrYbGs94LkU77zF3ngeX
D+HVBcqJsjdgHFfUWTPykp2xcg4Zywh/niAjsfTtKPxYFu34+LXQDfOhdW/4
9HqMbXmWhDsWnHz+T8rGlvfz0OfcQEP4vgief5JiPx/5+6wC7+20eQE+7uba
K/Udx2hagPMOPcfvjfI94v+p4PUGfbyHzr0DTyYyDqbRh+HgtAJc1ioGDOPw
UCPnAxnWwDlBLtPvPfDte9pZrzVijHNBRYPHV/RjE/2sIb9gcOkIDoPBaxBQ
mWt95ddJm8VoZyX64DHj4R51hNHvf5D5gYztKzy3SvEX+H9NIfvIXWed9p3W
ulrHJfj/s+n9+xi6tQ1jcREy/muC42EqLuYe+ne/u7/xM8PHTPJ7o60cyGZ2
YAg8G4fcVGMOrAlNtjezXdF/QFv51fN+CvgtB69/dFYADzMgy7+CX1hz28XK
ruqM1v/w6YR8oGr4fERnI9qLLs3YPhTiveilPLcAvCeynoiGxtXh6dfcm6Dv
UIbN2ZLOHdWwie3VVjNemjLm1lDO4Z0Y6X3Kgik+l2zBuOYv3UbkT1s4B2m3
tOxqa3vPuU1+x1p6J8ExTVbBx3rUV1eQZptC5RZUjsF6abYN7Me6oT7jIxc6
onRl+ycpbk0Z5Pzf0t73qR/gUr9nUl6P977Zr/StmGx7ijrOnfzlGKLpPoJu
nZHh4eAZntN+AKVZu7zG3DAKGrYtat/H/e0dU057Ohfg4X1k7QL93Aa9v0Ae
2sjuCn30PWM7Gnw3QpdNwL/QrAXPjYRfI4CIzj7TqFjKdvLK61sizvvu2n+P
6GNbtTmlbK8mW6gA7t+AVgMYkwtA+jnKzNLL0GxMFX/L/Eq7h/PZjl027NWh
9zrqm0Rd78G7kkAI0D2Hv1crcb0o5VrGacu+zn2TIn0E1Af/wY28p6H9Dflz
9Ip1Hmpdv8+1htD1IDS6VNPz1OvUMQ05KwR/Z8DwtYy5SUn2u5HPTWX02Eb6
EVPVvjaPeK4/NEyGbt9B27z0+yplU/B+hb7FhXo/ejhjewjlT4yjBuDVMM3n
Tyr1uy968xo0jWEdcIC5K0T+e7SVEOg8wUmUy+HpSiA3snFNe3Dw/HpFx0iI
bP2/tN3pHtDGYmjzvOalDt4je44+dgenV+DDnFre+1Nci8+Q0Qzaj4Uev8G/
wvTlIe9vBe/uKbb5ku3XSuhUFnlt1cj7fOWobzFlXuToBrz/APxegGeNeb+R
zpDQTXk1dkFoNX25RJuZwWNPPeeLUkwT7cnJlj84xDFvcsO32eia01ntg/Nh
hGOP1KX8jj5P4JlcyGHOLL6ub2LdO5rFcWC+opxN/aW4NhAeXqZv/bmWKcQ2
i/Lv6AbUZuyFg08dyi8CbBcpG6TvmevKt3eO1U3ouOHokh6Z3cab6Jg6EbYP
TIcOPcFYmQd9l0H/PDzXjzrGyw9StuTI3UB9i8DT0dDkNrpsDOVf4FQ8xvuf
8tNRHi+N0Tu0eQZ6jEQu71BvgQa2D90mmzDmnVbohJ6MqcqyV2Q8HGXMT0Wn
RcGjHtS1DvlaC3Skr98hMwPh5yzZLtey3f0FxXYBl/cj/f/5Z79L024J9P76
xrZv64PsnZFdDPf2M1abpDkP1d4Y56z6NqvPWWoBq7WnzXhIlH5nPO9DBm+i
h0J4vwP322f1Gear4DyNcRJLXbllA675RLbw4H6aMi/4VgOPcUk+X9DZQl/g
bCbnEVM+sQedHP/3Z/rO3//iQs1CFrpT90zGY3fo84i5fS9z7mPK1vCuDdAe
HdaGe4d0dky5Apk5C2+zyI4Uuh5DJtL6O6ZAAuMlEVjB9TrooT3QOAOymwlY
BW2aQs/i0PgidLmJzCQzVnIl+bs0sL6/TbvL7gH5/YzxHcZztbj2AeOkqfYZ
c9gepgVy3Qt5eSfIdhhB4DmOTrXN6Bgd7Sin0P7ubvZ/f5c26jCuF8GbXtzr
CdSBzrvo/5spzrm7h7Zq93J+5iB+3+tqGxXlClXO0LrFHd9S/u6KcTkW+R1S
yfHdR0LPXOBcijG5vLTjkSyjbAkf5yLbc6FZHPi3lw19cec5Vr7j9+nrdvC/
zti/BiyFpr/Lpx+8N6NDZyFXKfRzL/pmHLjvA99m1LMB/Eq3tO3P2mbOC3UY
vOLRFV1oN4Y2KjJPnSvmNb/Ohx7S58s6C0IWr1AOr+nvRn0zftDEPgyKYdZe
8w/zwATqXMX4uVrbNmCrG/i3bMIGaF+Va1uBBcheKvyBzOmG8O5oxk8dzXMh
jutSEzp/jH4rSp/G6Hwdec4nfxVw640st2dMrkf2J8h3q7bXaSPA6TD19Wrg
PKzjqvj/jMhpR8pOwFRwzwfvplE2QQclav+ujmNsKe6W8sEq3sWDaMe8UFwv
xfRSzJAExmrdWJ/rKSbPgX6Oy6PzwVW0cQ6eX4IP79CHpX1tp1+hkG3194D3
VMblGtk6gNc02eNTToWXA6g3CTk7Qtujof9e2t1Kn8KhSz3muAP83g+8qf0h
2p8KbgXgSzrmpC3wc2sBX9O95lor0rfTXK8GnbMiUwUDfT5REH7Gym6LMlM7
58XTejeYZ/8t7L2T72vbHi8MXXoK+m6v7twgB9vbTk6xlhW752o6x10ZCn0C
u/jsQDZVsq063882grJxkq1TW+ptD3yDLLZGH2yCVmNTrdek35SPr4XOPOBv
y2elfjdC/i/QZm6di0Obi7wXL/9+ylegxT768iXXc9ZzbHTFRZdtzT/htrX5
lT48RIdNDfQ+7t0StnVVHAXtyWzjubyye4U3rcFhK8+PymefTsVQUCwFjY8t
4F6A8fhtB+dyLg/8wXifQh2TgWbQozo8X9LJ+cLerGTZ+QH5Kkn/69NuNHAl
v31PL1Pmo94g+n9CPhKMhRcrer2hWF2KeanYXRpX7yAjqygfgE8b2T5kcj6B
vr2dUyAEOtxjHD2Ejy1jHEda8aTlq5EL2A9fhvNeB9kwQZPs9e3HpX35wujf
6MbOrXuons+vLiKXwcAWxmIpykHUHSbbiXjHLikENEBmb6NbgirbXk4+IROQ
1bxB3mcaUM97TXnlG8i7uxmrGZC19EDNCraVk82cYn/3Yny/jr5rhfxfBu8l
gbbZ/og5Y6PswWlnKW2c5P/ajKWG1PGI/5tz7R74b6NPV3vZjk9rM9nyRSCH
2dFxOcDlVWi7rrPvP4Kv5ajjbd7NB0//45lu1R2n/wE8+Qc4ybr4C32PM1cV
o1+9szn3osZZszYea+cUO1HfdTxbDX4P6Gv+t4Vn8S2dx70sdH+Zvm/Tviuy
XB1535xs+yLZFu0Btwf5HA98Ntfqw5da8LRdc9titoWeO8JtZ6tyZ7ivvdjc
/xcv6LlH84725k9Bi+WUvYs6r0W34s7FpYD9ip8ck885yBrlc4z0y9mfxUnv
4lg3pRkDOaljEWuhNsy1P9PWWuhyn+c7woOxjOlPqO9v6BaIXCW0cDxp5RdX
TGn5VbSGBgkhXit80NprB/nMy199AnyYgq5+yPNndPYPTU9UdHzrvvKdg1bz
Wtr/9wn6smlO+99dUH+Rk2PaI6f8hvqT4WdmZHq0fJzAeUPUM3s2ZO47nhlC
mb+I10HNKjiOmGLWPI32WJD/qHzJLkHnX2jjtcK2be0ETYtrXUR9k7gXn+bY
9Ypbr3j3KU1sTy7byVT0STv6EonMjAT+lf0qNN3M+0HgVR04Ab0m0+8w+eXz
7nj6NBG4AG2WIF8J1F8IvAsDQ9A1D+nLPtrdC1yBDrG0vU5+3DzbmnYTZccE
bf9p4Dj/9/T9Bfwj+rDGOQ4URT6D4dlDeJgdWr3H+O6uORpcl6I3iqAzxtfx
ffnYyL8mgfobUbbWmX467+v8rHlXNlg82xo8P4SGiZSr4dEl1mB3gD8CHK97
BM9dhSYfUwbpLJq6ekGHLshWj1r2MfmYtjMhMxlZPzaDdnVaen9KdmGyD3uC
XssCDd5iXruPDE6BpnkYb4cKeDxqXE4Bv2nAPcZtCfm48GxJyj7I0bfIe5/W
HlPDgx1jf1oXj98E2ngDHGaXcV7Hvc1sdzyts2OfzKGPnSg7l7XtoezqVjOu
ikPvVb2cX1Ox0ZVL+BJ0acFY2Ek/bmnvif+fK+fc24NjvK5LAZ/OtNUJeAHZ
ikPHTJaOAZ/yjJldwDbe/Q3e1qU/G/gdxJw3H76+pvErW2wgurJzDn5M3yLo
Rw2gDbiXB8/Y2j4XeS+H45RqIbWd3znRpTsof4Oeh2IdI3437+3P4rzvcyL9
3d4PukXR3jD6cYX+jahkvwL5FGieqFbT46QN82IPcPyB8X0dWV4iWw2uD9K+
H7I0t5TjsCseezXmhSDNX+WcI2Kv/FeR6a8YC01od6jspCgHMTbvIJPVGJ/l
kJvLzKfPg3c41/9AvufwOxT9843O7ujDTvTXwdo+p58D/SeBay7qWSNfOeqf
qHhL0KgKvBhPuYX+REfYTmk/snYhxHva4f2dC1N5MPPx/gvgnJ+yf4JtgyvD
h7/RZQtYLx+n7Y7I6E+1baf4EPwiGbs1gfzca8NYGF/TccoUr2wAbT7k/+XQ
9l/Z9vLMUKBtms82Dst+RnaKsneV3EGr2fClFzopFHmfA17J1HMX2XsATRtA
x62wtbb2Gnl/tWyhkaV2afYf0Lm5YiLo7Fxx7RSrWrHtPstuuxjFcxsDfzWg
z5bweHxeeyCy3aH9CMZICeh5DuhGXV8zvp7Q7x15bf9SV98YvB5F+Q90G8zA
zkVb/aHDC8hOQWgyAv73QP5+1/olwPG6tX4ZBC4ZCvp89kf6fRP8b9KnAtDu
gPYTKBsjCz9qbQwUkw8APJ3E8/dCfP64Bfy/oL9RjLtDlEPbOr7Xq+BxRmsC
aPcQvLtz/0B7x2EbIx+yOOfCnU471RjXNRkvuRmXuYA50KcZ+C9jrL8HbGNM
rAf32Yzd3dp3SnUMVOX5Vr7vpT2dI1DnhzpHlB2cYu+uoC+j5b/DfD2G8hJ1
fsQ739JuMdnSlbAdR1no0Y05MK6TfV/lDzsNPIIburzG7+O0P4z/XwF2NHEu
4EbIUrvujjfyETL9n/yM6MvwWOffrg5E0uciTRwfcD70awIdimoNjoy9JJ+5
SMdnbVXNMSYVH1M+9Yt5fhFwijH1DvjP7e84AOOgd65Qn/nJhv/Vrl6fRzR2
LI0mXHtXNkBdvOcyP5v3YKKALNwLgyYvIVuzGNep8PRL+ta4o/O6nwSnJNo6
Rdke+T1Lnb91cL445YeLo8wDT/uja/v1cpxW5b5QHNZwrt9Dl/VnHi+d2fZA
ZSiryi6ea6k8vwl6d4F+w7WPTH1LA72OLE775bQWAw50tJ6Wvv4JaIysdUFm
eyGHreQ7xf1FjMVJ6O6JwCjkZ5pswME3s76XRFf6HwMf6yGPd8HrWBWfbehc
IxFd3aSF82srZpp8GzfIjxRYJx/ljI69qTwYir8pmS8KdAh1rsKOtDOIPgRA
m6PQ7loW+4WEtPS88FUH+9a9Itsr+jbhmQ1HI+jfJ8H5A17S/p3s1qTHtGdA
/xKg0TT+b6IxQRnH+6WocxB1ZoWXjcB3ZzOvQbUW3Qj8zDMXGY8XKjkmxlLk
8S46ZSBy8k8z5wZSzMthvH+Zcj28L9nR9jH6/l0U4m/gj2TvwjhYiYx30h6Y
9ABytYWxPACabaVcwnOLgXnU9Qv9bsL1V2vaX0++eopJpmSwp2S7msG2EZmC
bFtxhHG7Ef2zIYdzISkvm/Ih6Sz86/w+Gz/NuK4E7Y7EeA+/t9aoVFkFHlYu
7DyjOs4D7XRVefYisrgLflxDvrfL1pR2O6d5L2cc65E68LBEQftGbs3lM2Od
Hd9Ef35aznYTs4ECfK8tgB4FKR/RwL9qBHzWsz4ZyFogG/LbDt3cVnN4c/vZ
dIReUynHU18I47cL7f78zK/nPeCb3Ky9ka2juf1Nr2/7LNKHdCiJZ7vqLBn8
o4Bu/F8c3FbT7xj69TP4bQlxHLBQ8KxQzn7UOi/TWdk9+teG3x1lJ9DIPkuK
+aqzhxphfu8a67C7yNMdYAX9aKvv3/y2g99ewfGYd1DGc30VkAJ982lPFRje
0t8SOqvQOcX7Oh9tYJ8p2f5rfV20pXPc6IxSZ5U3kY874F4w2faJd57ZKHaV
bSUwNd7xz4ojI8WADjw7irX/yHqeuzSH1ajgPMiPYPDqOo75WrCVc+QpbpDi
B2nd2A48zqO/FlBHeeiXDP0qgedXyHc2xlUY8hjPOG4vGgG/Ut+lMo5P+it4
v9zSueTUh64d7MswkDXMC+U9705L5xzykxs4n3kb6N+f8n3G1jH6MZVnAsHp
U9GbupdBvxnwejrwOXzsVs5+wKuoc43qlR0Y/VmKvoilzm8ZGxsq+ywyJtV5
ALrr/IvnnirmBuX1LrYbO4G8lWZ+a8C1GNmjQIcxskPK7pjFHwA1mGvWwZMi
0Ks49a+r6njCyoOtODPat9Kelc5GJjw7H3mhsm2JZEekeF2/aW3d27GjlKND
8aOEx6Jsjln0GfV8GmX/hS7IV5WajqnzLuNnAG1Oqer4Jr9wLwkI5/+feK9y
Oe+ZD8zqfXPZ3cj+5ift8Ta0/i0O/IkcvwyvLkPbeemdH2oj422hfMOQoyTw
aUj7Vxg/G8FhBOPvo7J+JoIxcYi+lEXf/UfbzRiP2xnLp2r6/E4xPRK7eX9S
+5TKAaBcAI/o750Ex1LZwTsbajqHS4PsjnWiexvkZ4BMf0m9R4A8sj1hzrkI
yEY9Y5Dt1H/m2RXomOVA/7L2i5d//FTqHSlbS8rb9HMC/6ekOY7lUGQvqIZz
MSo3b2w/6wnt/8lOWfYJy2mjfhbH7VTMTq0J5At+KMBnMX+28lna98Dfstei
vmnMHynIwlzZbwPPF7Tf0l9JjrueXv5U0OBTeNIZfd2cMhyYzliaqfNtnlks
+wXm7vT0pRNtPGX8dEfv9ADOhzjWsOzW8wFreDc94+U5cJ1DWxmR6yPgOpX3
xmtfGxhA229HOjar5vQfkNn/kPXSjMM21J0IxDf1eZXOsBSvY0JJx+zoAb2+
0ndLe//W9fHARe1R8l5reH++seN5nwWH40BUsG1h9b/OsfRb35faJ2qN/B3h
/beyOU6qcvgqf++jPt5T0d5KWcbDdxnsyxdf0OfX12v5DLs+tPmhquMmnUQX
7crjnM3yAfxM9XV0zEbFa9xG+VyQc1cph1USY6UHY6JtiteLE+JtS7Ktjc8z
zvd1fJgRyN07kY6ho287xdKqy/iIZnwUgAej0blLqP9t9F6jMP+va7ngV0C4
43xtDLY/ze/Ay+BxtIv9LhfB123F7TecjudmSN9Ci2706xbPvIwsd6ftZCAR
vfEzeK2GJpOa2B5Ta7RQ4ENgtfgPvAs979DORWTjAXprdaDj3+bm3VR42oc2
3mMufLWfczO/lMF5eZWTt2ea7WtlW5upiPOhybZ0C7ht1n4av/eA78dNHEP+
Bu08ALfr8C0f9DyJftzbxT778rGMQU/cYxwkyiYUHAYV8j6U9qB+a2771D21
bZ+3pKPt9c6jV88Bi/g9j7lrKOVc2hkQ4bwYyo9Rrqd9VOTLcoG2S2R0XiXF
yWwGNET/3Ae/DGHO46M92WRkvwTl34y38/KLAd6Hp+/RRl14sVr2beDUi/6n
IRMprJ+7A8vA+1do+Zv0aVH7M8mvqQ48e5m2oyiH0b95yOYCoCFjpyh6+1vo
9gXtlYXm5YCdmi+RkSLc+waZPQZcoe3c9C8b/2et6rbSwcsblZ2LVDlJ60U5
96dygPbt7LiYyqEakWzfMvmHT4B3HcCrKXT5qYXj1+gcWefJH0HbTUAifPov
2ueNYbw3Bfm9nNdzaad2/n68q3PnVo6XrVjZifJPhO/Tw2232bCqY1vI/nT5
s/1T2VNXbWebasU9aAF9q3X1mdRDoDttVeXdxpW9dmzLu4P7OudfI37HFLb8
ZH5mg9MYmlfX+IHnOfM474zk5Cb96w9txjPWb9Nuc9raiJy8Au0LQ+dAdHgM
uu0/6lgPbk8q+/tgQg5/I4yCtk2Kex0/E/l7jv4OLOKY+0sbOF+OciTpe0t5
kjoVN9831fe6VTar6rvOcnSmo6WpbAN1NqJYtYpjqHiGDbSPCa8TqK9AZsd7
utfcse1HMp5XUmdhxnjGbo4dURn6RFBZrTKO89aBdyNpMxt8ioaXC9Cb7wBx
HXyGEgqM470JQG/6t62Q9+i1P7+c/5cBH9HHxuixPtyv0NO+A/IbKEbZAH7X
T3HevuGFbFtZDB0xGtzHdHJux8GyZ0y1XYbktW1/y7T8hm7ks+9QxmR/V8rH
5Af+L8IYKgzMRha309dOYbav65tmGzvt/59+dgawEbpvAtaiI1ujsy6G2b8+
XnOb7C14PrmU/RtS6eeP9KE/14bS1l7mpGjm1QbAVGR8CvAb/WoBj79XDEX6
Ppy5YTbj5VXZ7SCPH8KrI239/6p0/r2e74kXeWYIsEH2DrW9P9ofeewJXAq3
ji/Z2TF+u8LfDshaw1a2YfwC+T0YZT+XJ0BwguN8RmlfGygjPxr4/E5zf/eG
tvZ3cGZ4WqiXv1F/Rm5/493bwF/Q6k/FPEKuH+msT/v19Cc39N7JGmMHkFV+
JOARof1hru/N5/X12Jbed9Oe2xpwKxPqXIaK/Z5U3TEJmsLPolxr08Dzg2z7
ZNenuGxlgLqMl6O8vx46VOWZmkmOMXYK3rbu5pyCJSgbIpuN9P2msUzf2gAL
tEaF559msG5XPueyyMgk5oDJOkfj2hHqbK71E/BFkvciFRNPe5O5ebddiuMH
Kq/jlzwbobMN5LE05XDwH0dfv2fc9evr/bQh1byn1hkedIYe3zXyOcnZXD4r
mQZMBbagA9vxXu//txOQryGwAF410r5Wb8cFUIwzxTqTrcVLyN3QUs7TNhcZ
fbus8wSmIoNNwG05uuBF+HMP/r4GfRvSThg64CVodwAaB8rOqYl9LOVD2Zkx
+6Ycznj2KTi/yby1BNoH61tTZ+Lg9jYy/Dy4luGZEtAlhvGeBg6NKD+HP+WQ
71LgNppnXge6tbPvvPzm9yFvZxgnk3jvLOVjxmsPeDIGecvEeNmLDmxPm4My
uo0vZStU37n1lDevF7Ia18txF5UnrRp0eNTDtnWzWti+Tt9W/1L3EPnBaT+7
vX0ldyDDN4Ey0HYI9S5s6VzPBygf8P5o+tOSPh/n3jcZvO9WnHHUmv5E0Z86
QBPW40+BNOibjvVLOeq62MDxBuRDqG9x+RS+CT2e45nCEbbhHM/vHj0M+l97
m0m836WkffjKZfe8NwsehHOtD21ULul4L8q1pxh+F8Dzz0TPSQOo+6LomuTY
Goqr0QT8TlH/tPaOfaf/k0r790loPx/67dZeYinbmjR6ZjsoXCciIwnU0Z77
rSgLwIP91H0TBCZBkzuMrfiGzv10AJocBD5o5Dxh3dCJZeFRacZpE8ZmLLhW
5X4P7WUwb38NjGjkc/lPwr3Gqy/7UeAFraHyO6a74rYpNp5i5Cn2w1TGW0fe
XYZ83JPuYJ4ZA8zj/twYx4yQr57ikX0Izkd0xtbEuZx13lUYXdiYskZN+6wG
yzYWnZWZ/09qvwlZ2A3tdwAXofVi9PzTMMdmrlbP/hZLuDYKHiwqYtvr5pGe
KxRrQnEmlEcmT4jXV5HQ7D3eX4aefg/oDk7Fczs/eS/+z6A9l8wekxqbKygf
Z7HsSIbyoxv20LcClG+BX150WjH6dhS6HAt3Ps2Bac5/ojwoR2nva6BhpPfe
BqU5NpLsa3YX97q3Ovz/DzzPQcN6yGdd2RXz/0t17ftdqKH3V9/Snit8XlLX
/t6rgQrQaVx1x9h9jfY/ZQy1RBfUAq9u9CtZskibM7RH38rxExVHUTlLnud6
tjb+vpZP4+py9nFcor0h3l0a5xyrQ+FnWWSvQoBjSCl+VEPk8Rvk9XiQbSof
NLddpewEtG6dX9D7/615ZxB0/hf+ZaWNQry3t6lL/S6p81vGVc3sjmlWNs5x
zeRzI98b+UCm0s/Pabc8z+dHlxxGbofz/vlizqF9h3Ikc3kG7cWH+hz2uZ7O
jZC3k+2hlRcolmfOQ+/GlLW0F9Db7baWbRlt9gTmIiN5GRs1Qxx/v0ozx+PP
R58ngscq6uoKL3ryzn/ZHAtDMTFWQNMXwLUI8jyjl+PpxMi2MMVxkZXHthjj
8h3aC09wnM/i8OgY+OVEFlbKJyGrbY2HUM+LwKeVvXdRHf5vpGxMf76izS+B
dLWcH0F5EuSroH0Y7cforHvSs/NuxUnXGcZw7r9ImY72njL37IcvXSOtp1vK
Bpy+NKKe3sw7jehvMjxvDl8fs46LY3y/Ce3eoF8R8l2izSPIe3RO++JGQqOr
gY5pcruPY5ykgWuE1gzZHDfmK9p+s6L3rGZ39L5VfKTzNpTjnYPQ7jBy1wNa
zW5rPwDFqO3GmDoe73jiL0Czl6DJ85Q1kNNZfRx/bkKqYwUoZsAuZLZAM8eq
U9xs+bPIr6VSksfUKXj/MnWcrOB4D/IFeYXrDaFPtbKO2f4qeD5hPCbRz1Bo
MhH8j8D/CZRj6vh7VeP2FvJ9GL13CKhNX9qD6y+ye0QWSkCLYOCq/Ljg3Ujq
GZ3TcXUVU/cO81Y3YFJx+8895HoqZVb4lSXMORyvQPeK1NuXtrMyxrMAr4Jf
IuPpHZ11pHqNqLWi9rAWwssm9H1OB8d3UayA89AyXra79K0gvG2PXt2Xzr7w
N5CVQOTpWnbHH6rVyDGI+tJmE+0BwbuD6IYExSkp5FjWxxMdz1oxTFskOqZp
TWg4FFrWUNnXdrftwDGENkrJNxNeT0Z2CrHeOp3P8QnS8fsV3jkE/sMoLyQ4
dm94qOP3fkJdw9Nsu6F4g0WADej2pBIec7M72G5V/i6yY10JnWvSh2/lO01f
PwYyIauvQoNX9b0gmwv6Px9cXufaTvrVit+VOzjnSXvovz2jZV7y3hOeNpYt
CX1/izaHNrKd31Po8F5ry5JkSu8qb0q7nM4Lppxbyrd1HZ6Mk51nivehtB81
BxgMPapz/3Odr9Sx7aPsHkfTtx/DfHb6CXUuRC62UX4FHY8Cf/LuFPq3Vn4c
ZR17PgdzQCRlV3DZx70RafYNytjU/kGKH3oXug6gXIEMdoWm8bLNQafc7eh1
9O1Grkf1Kbej8jgug+Y/INtH0K9fAcdkUx9lP6rRsr9gzJ5pbj1ZOYt15Wqe
OQi8Rx3NZAfG+vJD8E6i7XmM0/eaOpb/g9qO5/9ANOHdfzpa/0sHl6IcDH86
6hydMh2yOQAaPOHevQTn7z0FjINHVXmmK/Tq0cyxsXo2s13OmVDb6SgPc2wR
52KW/0sKeHUHdoLDbuBz+MgwTXeLeqd3d3xZfe/ru//NKMe+mEN5DN6e5dlz
mi9inX/8B+hfQXsc2vNI9POKRaqYpMr7tYY+bpVvDbxdjDzU4Fo5cF7KfF4C
PAuA32Fwyo9cjUzz/NYLOfs1wjlGT/W0DpIuyoxsBChWivZ1gpwbaVSa95cf
Io+PAh1PTuvNLVFecyr/ziau/cDvcchLZni+lrk+H/WtgW9X4f9irifrfCKX
Y6j2iHQc1TbhXoMkap9Rfp6sb5aGOQb1ruaOQ90NXt6Bb1+A22vgco967wJD
tb8Iji9qP573R6CTlyIHzZCzAuCZP9C+dNpDlT/dt+A1AlqeoUzjXj/49wNt
bpUeBYLjfJ6qc9XessmHYbHAXtrKmORYfmv4ftiNfI1Apua19d7AIOjXj751
LuI8Q8oxlBznva68YY5tLB+GyRnsz9K8gHPJ9JL9v+w2WLM2YBycpR93oWFC
Ra9l/oVnCam2JTiR3TFX5Re/H3iIfh8Hb6vU8TqpR12vmxbqDB58gqH/DdoM
Y56Prep9BuU7Vd7TfdTztLdtEz+g7Td4txntNaPcltu+lop5VrO0456tqOv8
ZcpjVgHcW0KHP6H9JGh/FFpV5148a41w6n0TWfin1/8+E9NFpLNsSC4Ug/lJ
jHM6FGTuGE97BWSXBC9yaL5BnqYn22dcOR7kNx6EXB/WmTnlr8hCW2T8cIjX
29qPqU19g8BtODJVCt7f5PoC2UvobAzo0M0xh/8X+xT4BVoMyuu9HtnvzgX3
v4F5CbY3kK1BPyAjMpShkmNbf8rvPczru4FPeW55PcdQyYk81K5nv4R20Y6D
U17fFNSbhIxVo6yUxfpKekt7+BGBzr3UtJ/zYysXss5HXwVyoxd/5J0mQB75
EdNGGnKQWtE24YonobgSn9Dm2zy/jXJUqOdmzcsRPLcCmSym/fliPrvTGd4D
6FcROfmb8nlk7K1W9hlSLJYVXP8dGs2AD2u0p0h5HZm5BtSivg6Uo+lLG2R1
DfpnfUH7xjcMtN+UfKb0f7lI/1bs1RYlnS80CPmPhi6HuV5aa2xgs85neHYy
vDoGPQ6lc/462ezLJkf2OIqX85h7r6E7w5s7L0dx+r6qjeOPKw75asZ6Znj+
uuYf5oD80LMLMpeder6mH93hTXKSbdll094qzmcOIyWbmkObe92n9d962tkI
VIYfRbneXbb22kfq77VSY57fh05/BVnfyvvRpb3nrv32jT3sE/My9c/W2O3m
+KBVqCeO8bU02XlM/tbeK3jOLuXvN3271WSc3pUtF/AFeqQBurw+8Cs0fwiv
prZwvjDlCosHniIX6eHZFeidoDNnfT8lO3/g7DbOIai1iXxy5Zs3kfd3a04s
7fPA8bQzJrttUbYw5xRhnrtC/xObOdbHJGh6HLn7JsxxDiZHO9aB8BEu/aFF
LGuOUujFkvKfhuY5eHY892aDRyH6uIt23o21f+57lMdovwfl15Xsm6D4CvJP
GK09qEbO4ZKgc0quZwceQpO+tP0v5WToNgC5nxLgnGpDgIxVPVZ+qeJzpFqs
UX4P9t5pd9mEIbPJFZ0X/f3CzoeeTH370QGjA2X8gWyj26qgo9+X3xM82ohO
rE4fDonn4NI1v8/l9R2guNyKXTq0sOOOyL5Ntm0lS9mmU2OmTn/740XVtP3I
GPp2PZvpLBpP5PnVlFXhXxdkfyz3q3MvQmcdwHfIXVxRx31VzNcy4LAIWMC4
OV/ZPsfyPX6efsxCp0UpJgXPvdzK8tITXL+iPMS9NfRlsWyGtFcBBPH/EGiW
lNWxnzPUd/znq/D8CDh/T7mTZ3YAR4vY3kdnFLLLUpzxBNpZRJkH3MaB98fd
vB5qylgrU43xRN+OaY8NnIY1856G9jaeyB8HnrdiHv6jgOcVzSmj6evrQJ02
treq1MwxZpIZ47f0LuVGeBFL2RR4lT7+KNvIGPt5yt/zPegdj066CE8uAFu7
OxdB1pbOK9iQcfZOI/+vXIP6Hcj47AQfOwJBYc4Nt4p3ZzEXPUaHZpRNCTrm
IeuEC/Jfh18zwHtZMcddGE/9DbU24n5ycdvYvx7k2EOKO1Qc2hUDgnXOCM1K
ah8OvP5DJjbAy6UdHAfgy1KO6bursPestHeVmzGVHrzyUA7VWQp1VON6f3i/
l76mUk6g/cs6R0MWPmVOGtvEOTFCkcGC6PtAYApt5EbO/4OH92N8tqFzjYrw
rpz2r6DDnxmdSysrbXdgPGRjHOcAxpT1N/hEyS78aQkvblDOZfx9BByFRiOg
b0meacH8GwNtKiHji6n7LeSgEeuaGCC3bAcon0KbjrTznL7LgYRgx6T6vp1j
TirepL655Ot4S/ag7RwfT/6xvwNzoM9Orn2nvdeWzjndq5htBD9/ZjPYFD1X
Erw+h74VmRMWosMrUVZGPidRbxXKLoyLgzoLTLN/fAT4BdN2e8bxReR2OnX/
Af+yIYvrwDceOV4D7X5BPgbR1gvI8QLmorehwbzajs+ahp7ch4wc4d0ajKH1
8KIE5Rh+l0OePtT+Dv2tFewYo/JtLQDklw9fNdvvTpIfWWbbRDyCX+MLON6b
ch0GQt9E6liOvOyGJlPAfQ/lbvTVp8AZ8BiOTAwDStC3UuBdGpiV6jwRyhHx
HM+cgz5Pwecr6k3s7P0m7TV9BN/z0v/PaSeN53JV9/MvAmt59lVwXIM8VqVf
y5DzP+ETLEl3uoNjCytmyOJUf7vKLn8H5SfI4QPkvQj8OoOcXgavRawBvpG9
cGafIQaId+A0Glrn4Z2L6JkAyt41HPO3Zw3Hdz1Ae+doayW4viY6UE4Kdns7
yvkMcG8GnwPuAo/50LgLeigSqAnsoh8DeG6i7JqASqU9Z2i++AC5vgON7wGD
Wcum0ccXatm/Y01e5wvQGvqVaO8/KkfcVNGfcV8cPZvUyPmRYpkbpnF9OvA1
v5vJ3wW5WARvExizb/W3vXcX+vGOfMGQqRnae0h+Fluilv0Wd/a1H2EqvDhN
P7vJtwddnT3esQrv9va3mc4NdX7YgmvlqXN8gvfYx0DnWGSyPHqmj/Sd7AEY
E617+SwkvfYHqffFTN7/7AdP9jV1bIDR8KQUc1J36uqJ7okB3/NNXfevPZ3z
MxDdkB3dUhbaTAbP0nmtj/+IsU5WLIKK1BWuc4tGzqFeCOjL7+uMxdzZzeee
/P9qScer0DmH8i01y+44y5vpe4VStn0Oe4bX2Mw+i/hb9gfw5B/K93j3XeAs
tI1q6PlONmDKEzse+velXAne3VMdh+sV6Dy8s/NVtejp3K/lmHe6In9j0LOb
gvw92552/qUsxJjMj25ZjLwUZb37JbqjGOWPOusGt6rZvb+kvaU8wFDoNBM5
mgG0h9btgO3wLyHKZ4GFKYfR5hvgUgqcZ8LD3eC8q7H/n9LHvz+lnVOU4ylH
Mn4qQeelEY6FF4T8FQdele9EacfP6EA7J6Dpi+ji95nXVjBGz0DHvvLZgN8V
OznWfq9kx9tXDq4sLRxLKYjyS/oY3MIx4pWrVXlat1L3JXgU8Gx8zNLZNe/e
YMyNY2zcpPwXWasCbTNBv/vg8TdQEbkZQD/WMT7WdvRaNoJnHyKTs6njNrj/
HmB/30B0emGgIt9nbWWvDt1vxztHXyjwnb5b5dfawr6PA7Pb/3EBbRSFhgsp
J6V4nf8Gdf8AD65mdWyEXZHOI6Z8YtXyOjfFy/Diq0qOn5wXeZlB2zO0j4tO
ypvTuQPfTPNeimKOav9Fc5vy2AzvZX+yy1ojRTpP2oKuzpXWVd9h2heGPksi
7SO3iJJupWOZky4ZHo7o6b1h+URfkc0Gsp8F+pzn/XvQ61ud05R2LqXvSjs3
4hUgHPrfbGJbdfkY6dxSMemO0Z9S0c67VIO2djGed2ZyjAPtGVZhXdakjnNj
K0d2Bp3H0F55YHSs82AqDsAk3tkM3x5oDVTUuaeVd3ocfcqbyz5zc6DJJd7b
Ib+b/J7frvX2HLcfnvXi3b39HOdiIvyqCJ12UH4G76ezJrmDTDan3hrwc7bO
q6ivKXRdg3zFUUdrxmlGnh9SyLl6/6aeLeidizFee/1L2xVTvXetfeuvGKfv
U282+pHEu7U1F8tvsrb9v5M7WJe2pv0y9OFf2lwi/2nktK7sHnlvJnQeqDMu
nd3re4jyM8bJF3wHb+f6FhmGU8cxysLyRwKS9D1JfTmBXPSpQRbbTg4o5ef0
/DcJzpcgO1zlTxAPFftHMYBW1LAdvGzgtV/Ynf+To7xO1Xq1JTxbw9i4j9yt
VfwiaDwj1bY+OaDvMcZmL+3193Ddipn6fm3vmyoX6GloVRVZGk2dZ3mnNe/W
oU/FoE0+9NxhcB4dYX/LuGyO7f827bYK8PeYvstk07GO37nL2tYvnrkjs+xp
welH7t1H3n6iDGM89kFufqLOn7lWDn4eZJxMp4786JXNrW271emZ/ZZsGwcX
sn2j/HRuwd+UUJ8Z6jxBsc/2IFcnWcOcBorXcT4k5UIKkD0S9HoMdKKuF+Br
PeR2MnNCdeb1KZSD6HdR6h8KzlORkQEar+C5RPUx7k8BKxgnv0GHlZTV2zn3
QT7gtRb2D/+JfsxADlMqOFa/8nxo/+gkeuGDcrbJmQaE0/dC4P09evIC9b4D
P/qzRtmmfYq+zl0kHimW7dw0rwXinq0Hvqc/X4f6zLk4MngOCAIew6/54PtG
ZftbKqbW0Kben/sDvd8fXg5gvI5GDhOgbXGdv9HvLjwfh/yU7utz10aptvmW
vbfOW9eH+cx1HnqxZy37YI5v63W91vdtkddO1LcZPTOqj/Pn6LsmuovtEw7x
fi7GxO/Mhb/pu59+nJZtE+80hU4XEfuhUc4dc082PMjOur7+Xs3Amuwg+BWh
z+u0Dyw/e2AHsJixch/a/gm0KG+5yRNln4BJHR3DSGv9XuBSLIPjqD2XxTbX
ivM3X9+79KkedK8P5GJMFWNcvgtvM8OTecjKSPDN0cp2ibJJ/AmcP45zzCDl
U40LdExLxbE8D43SI5vjazn/ifKgvEg5DLocD3ZOD+XVGQxMoZ3SFW1Lt4g6
HtLOWn5/H2a/F8WHXc57U6NsM/QDcjygruOpHSpkX/P73EtGhl5oY7+PNkBQ
qHPkKabtSJ4fAfRmXBaqYb+vm/ChOm383cl+GMoZpdxRym0dAj3LAHnpbz/t
t4PX3FTbv69CXwZTxsDvEJ2xFfb+ZEfo9xL8OcO3xkhk7T79DBHfkKP0QBSy
0bS7+1WT/0N4LpLyL50jIrMNczu23zLu7wbXzPAsE3AVGq2nrp3yQQeP3Cle
10p3/1zJsTODgALqG7wrnN57udrH1RnikDDbmBfg+W70/QS8qkK7o56df+kc
TPt6mvdvUu+EJj7LntTffrnyzx1FmY41RDvGZDp4l6uF8+ncBvrB59T8tjX7
DvyvAvMYD/MZs0eQxcPAr8jjRfRbT+r/Wn4krJ1S6NvfmZ0DVflPZ5T1npv2
3srCxxO0s413P6zqPWblt3s9r+PAzJcNEPjOLOx1R3PgMb/XwrvNTWybqHlT
Z2X3n52XKW/SGd7NRjtTaGcy0Ip7a8HjTXTBG7IHgg43gEOKTUTf5kCrmtor
BufywHzm0L8Z11tkOwY9fkDPFIM2NymLg/NA6lxY0XnmFFNWsWXboVvaAvnl
f4CcZGM8Xi3svTydVYYDl3I7PrJiIyt3lfJW5dJcjYw8Zvw9kk0Lv4fxfgpl
aqRz6HzcwHb69cBrLmVx5t58SV4jp0DTFPBvkcP7nXnTe59ROqUq9KlJWbC3
80IkAvXDHPfmfX1/Bzk22RTkYw2/B9LfS8hfGLhc0P5CM88J95CNu8AlZKVV
b8fHfY229UH7FHp+Bc8/gfdjkfHPm3rvP7WC8zQ01bdVK9vNyH5G+9pl4Mcv
0O1t5PcT4B/6WxRZqYbcLOCZA9A6H3L1gP7+q7MJ2iqE/AygXIb835AvOHhW
Rl5GMFe+CkyFDj/z/qMK9iWsVNT+hIpx9IS6CstGmnE/j7G6kDZKQ78fgzz+
FYuuKDgNpVyQ3d9E+m7RnmS+BO9L1oWO5bI5HvsBZGSfvlPgy0/w8zGy9bPK
yrY1bkBb/aDrNt7rR9+2y7YfuMO4rNLUcWWaFLT8zHomQ/sL2g9f/lRX4MNV
IJbr76O/FRitF32bjB58Q3Z54PkG7y1C1jand1w8xUdSnCTl/tyK7KdH9tLJ
1hJaPcnpOXhlOc/J2sfUfuYlZPNr7TEz3mfUt1/zYvD9i/kiChr8Rh82sGZP
6e2cFLJT/gXcS8tGIMA+6/Kvlt/6aeTyZmXn1RpV0DnTimktS7mH8Z0HmR9D
f06Cx4ksPkMZApwHz3uMxU3QLwB6ZgGnBcjzsHDHThzb1/ET54Ta50n52hdo
zxFeLixsnxzFXmmNrL1bwLZhf4HzDGg0HcjNfPMZ4yAfctaK371p8z9w/wRZ
+gzeX6Y/6bn3DjKRDdnMCszT/kkW+/2Plq2y/CYoK2sfGvo2QA+mB59VyMg5
dE4lrjeEpg2y+nywaXrTOwt1N6TthdDvss5P6OMR5GARv49Tprb0umYRbS/W
mgf8UpDJoejxBcAEYAcwBJoMemYHnMTzbyOXoc08T8lHVnPVXdYL94G/ofNg
ni2cyXNwOvo2Vn5JobapkW3NCniyXLaQvHepnc9oJhf3OY3iL+r7Xd/xH/J+
Rd69zDNVkLcEdFKnPt5L1DpRukHnvzpv0BmwvmuVf/J32XNC2/M8+xfy1CDc
9huK8b+WvteLdv7jccjy34mObVtK32vg/pu+G9r5bCAECNXeKmM6ewXnnFW8
te7wsBcyczvGbfVAvo/C8wPo/Rb6ToBXGXVGhq4YUMTn4PdD7HOjOIHSd5OB
TF39bavv2mW01T3I8RuzVHMOhR+hVVGuV4Vuv9N+ZcpTDe2fsAVcZkoHo1vS
kPtpSc7tVRXYyzOf6dsH3LKF+XxH5zzT6PtAZCAn9MgAjiMZcxW5lwaPUoE6
8Oga73QtbbtS2UG2iPS5eGBu+w1MyGhflrLothVANuh2Drm5UNQ+aKuT7IdW
n373Zaw3KGLZk22H7DqWwMN1XMsC7W8xHmvS587QKpG+tQW2w8NVzFX3kLVT
0OCyzpIjjNNJxsxdaHOK8kw1t9EQyIXcn4cfF6v4nEa+2YpF8DXjfhBj5HX6
HoksvAWfPqatDL28zs0ElGSMRcheDxlfkmY7pVfp32zt+/PssWren9TeZOCz
9ZDWRfqeVX6R/xo53oLOdnWuq5hfecrYL2RDQef+Vown5f+Wr3dMd3//aG/v
3+y2c46vYF/vDrKt7+Nvi28bO3fNDPo3HRgDPQ7Ch3zIx1LZfVD3bvTUVeQ9
Fv15Td8v0P4L+FeWtebytvYTOgwt28GX5PaOYfmE663hVR94/3GI9++eiK+M
qU60926az8t0VqZctv1kZ1nGseGGZXfbavdQN+dh2NDMdgQV0XszwP2jms6P
Uh/Z3gWNNsoXP9jf0/1yOrbuHdn6IjtfMd7nM3bzMwZWMk+sop77tD0bmfoT
XZILPm+tYfoqrsV24Lr0fKR9mZbTRm6dT5Sxn7hymYfCq3LQsx60qNbL602d
K2uvSbE1FFejOjiEJNj3OCOyGRfivY1R0D19dh1mIx/6LmZsVahjHaw8xcpR
XAY5yRbu/ZNC8DInfHqLeprBg1Hoj+w6h8juWJuKt6C4C4+ABuirxyHO2X6R
8XuhqXmv/V3JwlTa3AP/dwd4f/t6Xu/htYZPG+hLB/r6Hn3IhbwuS7NN78vR
3uNey9orP+/3Yw4+Lft8YL/iCED3atBjKWVB+Jmd8b2fuaGizuXp6/I0x9hV
rN0PNcfXdF5z5TRfCA0XVHBMCMVlGJbRNsSyU+7a0rbKOg9bof1BdEdn8OkE
rIvwHrH0mfaMFXdIMYcml3B+5Y61LCvnGVd7oMFH4FKMvr3B/ffAdXUm+858
RPkLNC0MrxtA+0zQ+TLvHALH15GHm8hO2aa2tZTNZSz1FuLZ89C8RqjjwCgG
TC5kYzc864IMjO7rmMvL4ecVaHqD+m8BWRm7lSJtN6m4zV+h3w8hJ0cUkxVc
mgAZ6WdJ7n/C/a3ABPCuq3gcyOFE2p8M5G7lfHGfKbYI/Q9int7A+FmpfU6u
T+zj70HFslVMW+VdmQk9z8Lv6p29n/RmR+8p5Qx1XA/F9JgJjk1lr8D9q+iA
YVmdzzutvH3O5W/+BXWv1fmx/ESgfwvtjUHTk8jTrjif9X5HXduh/VP62wh+
xgDv08bn+o6n3b2UA2r6fFDnhJPpQ5dU2+Aqx3XlYO/tzOT37qZev3wAToWh
eVEgnLFcSXvvjPmZ4HMO3v+qbwJoMIr369L+HvmW6hyxg/XcuWe6TrFiR4Lj
xgzW29LZRynT04czjKeFyEBf5oc+wGjF+4PWDdBzF+nfMOpr2cpxo6RLpUen
wecz9OM1PQ+PLgKn0S0lU51f4RFQFXif8fga4/oF5GglbV7WHob886HLbWSs
Ns+UYl1Yj/Gxsr9jzSnO3DTZ+NDWZyWde3NkSes62Rc27+i9Me2RFYevT8Er
kjrfb+bcwyOAsYmOEV+6mf2pFedH8X6eIIdR8EifwrJxCIO31ylfhkZzq1qv
v1LFufCUE69UkPM3tEZPtkQu4rWXXsV2aYr9rhjwbdERr4HbHuQoJ+3lABrD
k9vI6a72jptYD34G8c76io6LvJWxkhMd8gl4Fqrlb/LXkaNRwIJm9jOtRf0f
Sn+AU3ueuw7Sc5Kdw+YR8FKY7bf0ba0cN8pv81xh53ZQzMlf4B9NpfuYsToB
2n+J7pkD/ycAI5CVkCDnIE5Ltu2WbLg6olOeUl+s7IgY27fAZYzsVpDFQKC5
znB72Af8AvQ9B1/zBDjm841CjvF4q5C/k2V/otgWslVVXP/tfW0L3VJreeBW
efs1yqfh70j7F8vPWPZHskP6lfd3KN4kuE6SfSb83goNC1LeCrBNWZF8Pu/e
X8hn3pXg/az6jpWVHb1SSWtc5G82eK+ire/Qe+uR5d/b+PtF34FfPTvD0n6o
fOamcH0lfV7N81uQ0SrohqzQrK3OuKgnK2OmKP0cBD/iUhx/ty/vzNSZbrx9
SGO7eH+hPPSsQ71Um25nK59jy69pCPw7Qxs9y9vfIwH+lodGU9BZKYzHqZTj
kJ/jgf52U1wPxfdQPFHlmZgV6Ri0d8o4x8DvlDllh4R+CZC9J/X2hx578jvX
ktZNWj8to51ZnW3vI96egfZfa/2JzhqJTnqpo+OQKh7pccr8tDUXHN4G5jFn
zpWNLPwom8P+N+Wh3foQ55YPAc/mQAp9/J13m/BuLFAQXu7nuWjmxgOxjjej
9cSntDsql32OXqN8AO5vwZ9Q+Nq8jX2V7sHHGvK51tZVB9vyhaBX22jfo6fz
pRXq6T1z6QTlDNFe1ZfA8rr+XpMtp77Z0snvG7qnp1zfx3mjajH+94DTGfr+
TlbHq1LcqjjGygJ4ORMZLMb/idTbnffaUP4K7WpDuxW17c+yr7R9WpSjSTHF
ladJvgsxIfZf0Ppca/MPgLLwrxhykF97FvTlIDgOkS8T37i94fka+lARWi6R
nRD1RSML9bI7X9rz2h+r4jgC0pnSl7taON/zHtalDyhDNSdQfy90Rkbk4jb9
WkaZrP00eJsIPc5S91idl7Xwe72e2dYG8OwR+RoX8z7Q9TDH7ZGN60u0ObS4
zwSaZHbcWNlgnH1mhyH/a8VpGggdanO/r74JKE9xrRJ4B1ey3Xg39MHXyHtN
8DgGjpFZ/F0c09B2XqHwfx0yewI56wY+eWQvk8F5ZXrUc56ZIbQ5GB0eHGX7
/LHAx+3sr/gI/MvCz3bw+xXosxDZucX/PwK10V//Uo6Ezw8oXwXXrbw3vJrz
KGhP7XF5xz9R7JMMST5rkN2czhu6QqdttP0ytC+E/Bbs7vznhdCdi8DrHeCS
9tWBqOr20ZRNu/JX/U3/G0HXbxh/a+lLlM5CgS3a4wGyyBaD/nyJbC3imUGQ
6/l09mfTXq/2fLsCLzFXvMTYGlLLds+yf1Y8gmPopIXMMd+UsG2xbIzl9xfL
Mz8g4+XB+VxDx1ivTT2vg9848B9PHz+h7W1AUZ1zgdsa+BaIXBYr5DOk+lrj
yd6V967BgwY1HGsqm753ZMDM7xL8v17nJ7JXgKdzinhtMJV+P0D3nGD+7cfY
WgRPbyrGCPWNgHZF4nwue48x/Se8Xwk/7vFsd2hZl7YzMSb6Qad5yNFPwHre
3UxbdZHdZPRDN+1n0Y914LwWSKLtUYzTN+BPQIBzEmhuikrxfv8N8J+S0efm
Oj8vwXheU8H5KM/3t+37p2387bn42ffnJeasJeimKxE+38/CHN49wLYnb2je
6GPfvFx9nIMwPc9lBM6Dy9fge4Pxf0W6hbk6A7oigHGQh7aeR04HA+8yPk7B
n97Q7CFyOJ/+fdrKsS4GQKPh0Dpfduc/UO6DIfz/qtbeQGfWix+C4x3GzB3G
9Q/IxtGCzsOnc5dE6nwTnbQeGv6AHujV2Pm4lVM2DvzqIas/JzoPUkAn55g4
zhj4prxjPyrn8+8Z7XN+H3n6Bjre6+fYDIpBFdHFORZvl3eexU3IWmedJ8rG
N4f9kfXdOqa39Y7WjPp/7LPf0xLt9yWfr7Jh9lPuibwdhE6dtc+oPYM6zrml
2HuR8P1leLuH/uVnzngTPVuAcha6aTl4zabsoBgL8LEd5evaj+L6ZvAsSj0l
kKdvyjiu7Fu8G0g5q7n3l2qjIy8yzmfKz4D3Yjo597fmvUeSyTrOubyc+8uA
q9B9X5x9uAaXt21yLr7tvgOfjND2BnU9zWJ7V9m6KmZaC+rYDD7J6J5W9CMV
Gn5DXw7Sdlbw2ce1h0nO3/ov5XFk9nnZspRwLFP5CC7T3FvTa5GVlGOh03fa
PyvovGx9GROfc690B8dKVcyplDrGX/0IyOm8x7LtmMHw/U/fHJSjqvhM4AA4
hcCLdOBdOsxnmLIV2SQbPOSlZGvHpGiMzvgSfRJDeQZd8RP661Qh5zJVTtNm
yGsO8MsOvI3cXazlvAfrqXc6be5mPppNXUHgWLy895jfgYZtodt09GYT5siN
2sunT615PoR62iU5vtfn+s6ALufR4yXoe/5W9smUb+ZnlHN13ia7CsotvD8P
XuWOcv6XQHiaCE/zUMd+ZDOO8RWmb2XNvZTToGMY9Z0J9LygPDs6y9UegPym
3uOd+5o7+jlHrXLOK/d8TuAxOigYen9EfyrqDBi4zPMbqjom2u/gFBxqm8yJ
ZZyjRvZha5OcJ12x4pQrXf4Gy+HFH5QPKBtQ5+O8zs+ZxPw0lPc/5b07GhPB
jq88ijanoRsWPzvf1zm/7KAaMu6TZHPXynPDG8Ay6Lw/n+3Q8zLv5gc20f/y
vf1dou+T5bRRBZ68Bp06Uf+9Co5v14M2P0SfnYWWbcE7nOcrARmZCwpDi8El
HMf2RcbiTWj2AJrulb8odDyFXjwsGwbaagy+vaB9k/I+G30F+doQ7HNPnXnK
f7JyDucHWo88v4JIPgc9uhV2LjLZIikfsnyBcyKjX+jcM9l5RpVj9FVk6Bq0
fwF6TW3oXNPKOX0SfDqiGz7WOrynz9NlRzsBXk0CNiCXnyO/m9McryENmf6z
gdfT+v/LYv49H9mI7unYjJAx3UnkAZT/55fSh3oCKKugtyaBVyHGT4LihdL2
vjz2U8sEHQ43dN91Jqz+34Sn64JNh9vtnTd4PuukeeC7AOgJLw73sq8yopRu
PffGRNm+RWu8hcjgImApCP2h8yHaatXWPpHx8t/lWt5Y561PhX4twWF7nP3P
vq9sH7Q2zGULeGZLmnM4XM5m+8tZyFQaY3ILz19jXM3jnWjZ16kO2eRy/xX4
HQ8R5iMDw2TvAa3a8H4r6hwIXV/huSx5/M2rc/FByHNLdNFW2jojv3f5aGnu
QXb2wMdV6JAIcM+G3s8KzNV3IDwJKO5vuhzhjuOvteVTaJIMPc9xbzRjZSa0
XsMYK8Nc0LmS463lQY7HBzjeW+12jumvM3KdlQf29plCLdpYgJyG094I4Cf4
14I6fqedMeCb2uR/YePT/ZHN8ZAUF6kL7w4ItD+L/FouFPP32kXKetVtVzwC
etzVWSwysRoIqej949shtm1WTmvZN29DV53nnZqUG6HjedZF54By4FALfHrr
exY6v97e8UO196Y1y6YE55JowlhuR/kmeOyB3msb2oZb+/oPqCMa2VrJuMkc
7tjSP8DPi5TB1HGN8TMBvCvqnBh4Afqt5F5HaDBD50jQsCz07UId0dRdt6bz
K9WU3S9tpjEvbqRPB9F3H3VwnFXFWFUezWDGyVaev0i9OZDFXeDyITovjL5+
zjplXxHnpVFO8Kfc+0y+l6V9VlkKWTmJnJwADslWhHF4T9/77XyOJB2n2I4t
+znW42FoUBh6l0LmhsOrpdQ1gnIHde0EJorH0PIt+JH4zE4qZ0vbSoVy/W+9
3862JjMb2fZE56Eft/KZaDT6bRH1V0dWv+jteN6K06lz5GO8exS4zPUiyEgx
oKnsBoHc0qvUv7KYY+fLVkN76J17+QxnRm/76GpvXXvs39BWEu0e1BlJG+ss
6a4bfRyvVnFrA7nXLNQ2kc0pB0KPZNn+9bKfzxCNQeq62NZnzr+Ce0GeewFd
uoTxFQC9pgY53971/2PpvON9rr84zrVde4977b1drmtfm2vea1/XNa7ruveK
rKwQRWZGyopISWSEhGwSRYlsKaUysgr52b/nq9f94zze3/H5vN/nfc55n/c6
o7Z9I5fkdU6pWN0V17BthGwkNra1DX+XkrbjVxxIxZqZgYxto95hjMEtmX0P
ojuQL5t7T9a1gvdlb4HLLGBHUa/H8lXzmuyR/uPZvtA0dZRtJwJU0lYR2p3c
zrHeM2pt2NM5yJ9X81340M7Ot6u8ux+B6wXG6ZlA+wEoBnT7Rt5XKK+w9hkP
M9n++2Mga0PnBNoEvAw9f0DOTmZzfuKAgs5XPJ/381BvPuA08/tZYHRz51J/
AM9X0N4exsNbyNQJ6NwbGYkFbso+A16U4vmi4JcJXP4t7fzxZwONZzoUyXLJ
DWPoIfPVDJ6/Aj/qIys/M/ajoNFPRfz+j7T5uLNt7GVfH0QJWVPFQ6Nf6N/O
Vs5bVjfM+xXllVMeuQ/BbaXs6wOch/ok+ubTho4Nn57+fcWY2QK/Z0CXWZns
763YDbLNbQzutZD9JpQ5aa+ZzmmLOsZPatr5JcgxeRWbNzPriQvxnrc0Z+ms
QLllZEOYg88H4Gkw+MREexyfBA6D9yxw2gyvjmidp7sO+JJMWwWAUOj4GXTb
CL5dWFtkKPFferZUoPzf3Y3ubRTPUXE/FKdJsT8iS7hO1f0/eNaRMfov5ZvI
TSDthCOfj6H3mzz7hPIAsruVcfUKeJWl/Q9qOufTEMp4dEVrcF+G3C0FJsCP
DTReSbYb/P99e68/z6Z27KfGGR0L6mfe20d799Cl7cv7rmcx8BwZy631C1AN
nP5CX9wAKkLvE/L7A+YyjgZDq0HAEeq/o3sFaF2M56LR1UWy25ZbdtzN4FWv
Do5H1ruDz95vlfX5u+IA1wJCgVfB4SC/PeP5Icjdcsbt+0Be3lvOXPkF/Z/Z
2XeDk2hrfl/bLch+IRb+doOH25GX5YzlW9pT89xacMvGGPyDcl6QY3go/sL8
HN43rQfPXws559y2RMfpkM10I2BEJ8c5eoXyCLI5Eplcq/OvdrbHll221rta
93aD9+2g9XbqqFrSZzcxyGMP4A9kqCB0KpDBMTmuMG5nyq4f3m6RHx9wAbqc
BzL085nCJnTNFMZfLOMttc7iQmwzLfvgs5kdS35MmOPJ/w18iFxU7ez4nrID
lg2w7E2Ub1g2J/LzkL/HWupanNc+5TvANUq+BsCtNo7Tmiz7evTbSeo8B53u
Qc9eij2CHPSkHCvfOmj5DdAbfo2XjyD8DmDc/wh+J4E2rDfXyi5R8WJ4L4Nk
H7xeZTyOBeZHOdar4rwWov6y4HaJeqbS9nHG5z76v4P+1QPHBsDP8HMRc+1r
/L6Y8heeLwod+8uHnn421n4t2nkHa/L8LXRNJHVdymbfqzmMs2W0+xT+f4n+
uwWdl/f13lZnfdrfZqDet+hzYHPfidxOuRdRbEHFGHwF+QqCLv06Of/VPGAo
ctWFvu+C3yeqOP+4YgA04Pn6OR2/8O0YxzBcUMHxkBdSNmYNMYq11EigBnTf
zjgr2cV5lZVf+T1+vxVl/SM9pDNYxcrrDc47oUUq+hkAhPL8Feh4Sv5S1FkD
2Akuu/i+V+tdxQZgHp+IHsjG+FrLWP8ZyFPAcajHwac88HAGeqAdbY2X3Suf
D8nPpJV9TKdG2M9UdrSy5ZFNTyv6eBJ6tqA8o1gHQMtY32VUCvZ9Rhaeq6L1
e0/7qQchh18m2t9ubLh97nQP0LWL7wJ2IrtZ0Y/ZgVX0rRhy9CHlOJ77UTbz
8Cd1PsdSeruEcyi1ZTxe1d0/ODdBZzcG9uawfeY+ysa8cx3cP29jm+HmQOHC
9gVLC393gs/LrZzr7G2t8eH9VO0DKOvCzxUB3ospv+qmnrbRzsO65hh9aQmN
rtLGLXDbGuY88JUqORf8L9AhPXuUrLo3o51koKDOEpGvDchuIGP6IXi05dmP
4X0daFsb+Br8WvL7QuSseWHHPlQMxIF8PprGedaVh+RkQZ+J6WxMeWSGITPD
2tiO/St++xooDi16Q6tA6FgP/i/ta3u11/n8NMw5V1PBoxfUeQ59kI7+ZgCy
6MyHOlsD16O9r5Vt36/IQlHa+YN6wnRHyXgd38B5qb6Anu8pRgV8yC8/W+o4
jdyMjrBvrHxkD8LjA8DJqvYRkh+r/FknUFfpWO9N5Hf2GNiV6PwXu/nvLerK
VsUxe4ORlSn0rXEzr5uf6Pxa90BRxlH5eQ8h/5mh2XZ41RC+fsgza2lrJeXw
fo4z2oWxNAE8mkP/G/VtHyE7idfRq3VzOWam5qqVtPcCeq1lDL+T2fObfJgU
Q+58UedBlg1xHnB6hByNQucvQOZHU4YjO6flV0q5Gr1/Bf58Qlk63Dkrz4V6
ftM8t5v+fgsOB3XmUMox0hRLpQbrqxa8lwUYh/wkQP+SlC/qOm/VF/G2LdDZ
l85+lGPso9aOwzggwOf1LelzBp198f0HcJvdzXZ7st/7iD4Phc67Gpre6Wm7
AmPyD3hwhXX8KOhahzr38P5E+lcQemSu7hxQleD5E/TFEGj8MrAfObiB3jmQ
zvkIn4HnUyBbX5/Jz+hk+9oCwOJ43y3qXvEL7d/4fzDQjnFRg987SzQ1R1B2
pn+pwekN+a6A4/9CnIf2LmN7HbzYJ1sW9OBf1ZxHXjnkF1DnCHgySPYP0HYV
NC8Hr8s2dYyEI30dJ2Fkp5S5nff2U+9dcO/D92fgsRlaX+S5LbTzq/ZX8jVQ
TDHocSab8yoUKOjcCkt5fojO8ovbz3gW47UB7+zVXa7sSMC9JTQqgiy/iez2
QZ62owe6oHMvMu6LMT6+DvCZlc6r5tKnb2k7EpnrKH9L5LUs9Qynb7Na+bwk
gO83WjhOjWLUKG+afNzk6xZN/W8iT9flO6w7b+Tow8bOuai4VYpfdbyZbeBk
/6Y4Wm1yOZZWi8LONyY9pLh0A2THGupYZMrz3Z++LMvqeIiKhSg77YrylYy1
raDsBBVHR/FddVetuWkQtGgNryuDc210ymc8N6iafWqjO9uvtjO66H363oVy
WlPHPkyiLAmPSwU6p5t8zeRnprO0z5HJ4+Cxj7Y68PsJ5rrIfM7v/byoc3zP
R9/Nh2avpexT9vJeEm1fou1fCjpWdptajkE4MNi+oQuh7wLt9XI5n2A99Mwq
3i/czD5iypck2yb5wc6HD5nB4TJ4doPWN/k/CTgV4rse3fnovusUuuQf5GMJ
NF2s88bSPkeVv+UrPDOez/sYW8OZT6PA5zXG/wSgGf/9rH0LstNYdkPI8Z9A
RdZG6enLPcb6Z/AwHXLQHro+oB+L6EcfdHBW6PeMuesn8LqHPEXSxtqutgtv
1tN24jprPdjedjSK79CzoeekQ/D1DfpVUjHw4P0eIBidU152d7W8flUO2QfI
+l88syPK65AvKVdD7+vFHH9kVj77ZVWDHoHdHRd0GzAdPGZnsT/SLD7vBIeb
jPuPmNffheaPwa16Xd+p6D7lAXKzO5ftBHrQ10Afpf23DwtGf8+l3Qw8E4tu
ypjT98ftdEZIuR6c65a0Tc0McL2he5iqjleVG1nYwtgKYOykAd8F1D1LMUnQ
EY35byo0De/p3OUNWto/RmeKyh9ZnO9bczum8QL4253yAHXl0TkH/foRvqyQ
/Qbj4Rr1T+T5X5Hdg8hYW2S+TWevfRChVF/C28f8P5tx8hYQ29L+d7rn0H+w
ItV+5HxToPMgKx/ylxltIy778Jbt7I/5Kf/t4uEwaHcXuv7CbxV1H4l+CEOO
ihS2ncdh+nCL8gjlRsX8kA0b4yUEPVQTOKAzZ/RSDvlxITs96ed4xuW4lP1v
QF3TXnQvRjmPMpl2VtD2Y3j9NnJXG7k7mJjiA5DfMbNOKTYM+nUJ9U2EBx92
8V5yM3Vkkx0LZVnkpVlz3+2XhJdXoEdxyi/Qc1sL+BxLuWH/reT8sEFFnbtQ
OQyfN/XdzjZ03bBCtv9VTrI5yMhsYDnzwjfQpFVp+4yUZe0TwrPl0pi34vFj
xu0e3ulLfV+B02rwLYfuKgt0hVmfIMd/wusb9PlX8G8HP28gt9dLOOer1vbF
RRfgVfTZWGC9bGAZU6eRjTLIwzDZEIDHUWj8ATK9qZpzmSkGy6pOjsPyL3wd
i+z3lq8+fB4M/tvDHQc1P/J1Hn3Uq7rzlheNtg7YxHO9NQfCt2DG9ELN+fD+
Mr8vR3bug0ftftYVXej3IOoMz2Vf51UB9neeg/yfY3yfTLG3l619Vcp26K/D
0P511g35+P42Yz8/ZZke3htrX6xziY+hRyS0XaozR+i3THM867wp6LYh2gOD
+2/g8zcykA9av0Of8lMG8MzBaN9J63xpOjBK9x1alwXbtj2b7D+Ar6m3K/hT
XaofeeYVZKtpef8mOyrtPx4WsY3V3ea2s/oDnEahD0YCi6FNJp5d0sZxMBpB
x3CgLv0+Ci+yVbbvYrZY+zLGh3vO0ty1mucqtHGMsT6sfzpD0751PMdrrj+s
s1faGEF7Q7M5Pq7i5H4KbXpnc6z0ECC0h+d8zf0vg2c25tzqTRyb95dajs9b
grERyHjazlhpQ3/aAWeRicPUN7Ki7blmII8VZYcHn0rSz6X8Vpwydwav14/Q
7gBk5KNsHi+L6NMQ+N40zP5SbzW1z1Q23juSaL2ne17d8SYia0d5v3p9x9L6
AFpmQa8EdnVc97no5xnZnOejCXRoBiznv/FlHfOrBvqif9r/TKlTXUWupyMb
VRjfk9k3FUAeXqfcwTvZmMuudna+qRr0Y1iqlFhejMfh0GYMPH9fdh/onrJA
XWS0HpDMe3HAho6OkXO2k2OBby3vu57Z0PJTcCvE54LARHj+IsbzRyvZATEv
pI71umoFY7k0fXrK5ybyd0XOH9Dul7Ucwz0G3k6ivp6U13T2Wt/5dfX9Hd7N
yXxYG/p8yzvfAFOY0/Iwp8VIr3S3P+6R8s4p93k2+8yEyDaKtvrRbjRr2Big
BfIysrZjoQXR53al7Fv3cYzz6O6v71y6t6HjLeCbRM8Rmh/25XEuqfPgu573
KkKPQGRhFTiuR+fNBJe+1NsIqIdMZOH7SnCaJl+GRN+NH2M8bIdOf7Syb7F8
jI+gt243d/zI8wnOX6k8lmfQm4vB7RTl2WLOOSsz1r7wrDF4RvLfawnO4dER
ebsmPxntGeDZGGjyQ3fv/RQL7ed8joeWCX2UMZdtObcwPjYDw8F/KGPgSlXb
5Oou8uUI+6nWrOfzn9AUv0n5sciHZTm6eJDs0nj3DWhaI9y5tZR3dlmsY90o
Tsz39G0rz4WAY035CDKuViAXJ6n/z07Ord28pvNrt+L3YQjzCKAdOuw6dA/i
mULU/Qu0b8GYbwCNRqDrrzaxn/1A7cEYA8eBR7KRSOu48Mp9uRSI1rmu7nDA
6QdoVIU6vw9zfODU/D+/p+1+DrWxHdDLPLeOfh7jnbehzT/omhzBjr+vuBXS
4bnbO//SWfTCj8yTJ4F36cNR+HYM+C7R8TNmtXOeb/mdyefs+0TnMFL+oqdA
M2T1cSvHiJ/N54eMuQvyU+LzrOrOIdkIXH9DNs7QzwOMvdLguDLWcfEU27wn
4/hSJudwUv6mKTWdL7VPfcfDOd7bMXG20r9ZPDsTeAP65suZ6j+/sRe0eRi+
PaOcTn/P0+4MyveZMz7T2V2072V0J9NXvi/tvK/WnnomfN8BfYbCo89Yn66q
4vhrWfk/AEFtls9xpOe1dSzp0dCuEfRf0szP7wr2O7V1JwJ+GWv6c5pAfz/M
+Djc0PkhiuoOqJf9CU5Dn/h89k9qwTMvoceP0Yd/wWUfeuc1xk59mJUovSw/
MX7rS787wethyNgI2WCjR8/S1iPWdHuQo79K2r9ffv7DeP8K82dT+jeumO1k
ZC8jP9Qb4P0qZao+9jeV3+lB6P6CZ77J7DwfN7s770c3xn9t+euhv7aik4pm
9RnoD+iM79B7Wwo4tqFiweygjlLQqCTwY4R9PesytivI36q787hMoezK+3Uk
u8hsDPKwhfE2m3IxOK+v7hg1fXS2pjME+FUX2nTV/MZ8NZt+n4IOx8HlAvJx
HnhV81xOx9LtT5kR2egLP8/wXCXeu0A9ysnYVTYdyEU32f/ldM72kc3tvyQ/
psHQI5q298OTO9CzD7SpB38H0/cE+b8BoxgnFRgPM9BHOYAlOptmHTcmyP7A
yrUj/+CsWXxG+XEO5zvXPfcC+U6x1npGvbAu1Un4P5b6hlGupu1vqOs4MnmW
P3f0cx7rRPo2HPquhFZZkYHjfM5GWbi+Y3r0oX+DC9hvUD6DjVP8xsqDwxV+
v8H7k3n2Xkv78m9VLCbe7wauQ4LtSz0MmZ5B/zvT99JAc+TwkvzxgA95t1BD
519K6uvYzQktHcv5+QDbMeSEP12YlyrzuR/tpab+Q/B3m+714h3L8WWgALyc
yF7hp3Db9GjvLxv132gjAJn8lz5ezm5fgr959xl8O8icVk00Rm4200YeYAN9
+F7nktG2vz0uHa3z4ADfDeqO8HrK/Kvc9sp5WhKaXKK9rfShVG/zfhJtT4d+
HeFHX9ZN3ej7bOhbQHEQ0FkXi1mvac35O/PSJmi7GcgLbz5D76bW5R1yOw4Z
Gqo1TXPb3cnm7hxljc6OW9SV7yMYe+d5/pVA30U2y+r7yDnor9erO979Dtrs
xPiLk9+RzhWgeSS4NuC/G7TbkHJtLduDTavtfMu/FXPO5SHg0xkZG0y5EFxK
aP/Jc4PhSSD9a53gfaNsbVBn/93jP1A/wOdIf/vBnASfVnx+DN1+SHRe8cM6
R0VH1+C5lxjfxxhHy3L4rk13bopbtCzE9/Xb6f98ZObdAs59qByIxUvYl30w
/RoEDEAHVOSd7+hLSXTlkOZuYym/JzPOkrr4s2I16ftDnl3M94fUNait49Ie
5PNi+L+QchP1L+rqs6nWwFB09gHFLqCj5zs6ft896BpWzPHuFJtmOeNqfwnP
4V34LQbID53CKcvxbAOdkdHOO9qnogdeQfZO831aX8cyUfybmZQFkLEBrCv+
qpoSmx6cRzEmosFzKLK2Sb6NjMsdQMkqvhMsGOd7Qd3rfZ/RseYrwJdn4FWO
ch88GEY/RuRy3G3F39a9S3KC7SdlR7kTPfgx/9eEZw3DnX/ijs7L8jkGk3wU
25Rw7CPFQDqIrs9QyHnD9PmPeH+fB61uw9dbwEL6UCHCdk8rkNv00OYfnRGC
30b4doU6b7e0XYrsUz5TbFBksp7WF+B8hno/LGnfov9FWVfvBtddQCC4RfPs
ROoqzViaoX7TxsyM9vOfCa1C+TwEGcrFs0MpXyAfNRlzNRrZHv+d/I653Z9n
y9DvhDyOsVdUa+nezrulHOmJ9CMt4yY9sA3a9JF/PuM6Lo1jmcn3W77YXyH/
AVqnwJM58Gt6Osci7pTaNveyt7+U3nav13SWDP1LMJYvgct42npE/W/Xsh9E
lkb2hdjO+ug89DsHtA92bqYOlF3AvZvOTLo4BmeLaPvlJVAWL+e4fhd72odZ
cQSO8V79pvZnjIOOCR3tb3mP9s7kd37QMtArPX1dVdh3E7qXmAR0R85qMH/V
rOZ4cYoVt5s6T0Crk8CPQGKQczJpHai1R130bUvKq7yfT/1EHpLA7Sz/v9/Z
/rNL+Hw61Hv/NeHe/yteZPfyHuvyX1XO8B7tbOdaKsZ2r7lKOz9WB/h/t5rt
tsoEOx6+7rszIrM3dEYJzUcAA4GHjLmk1D6315n9HspHsneh7IO+nM67I1ra
J2koOqSM1gT0qzhj6JjWlawnitZ2nswy6NYCPF+N+eoM33vyTgwwGP11U7aL
FR3/W3cNDYAZ6MYtyFZ/yQO8mcazR+hDxxL2lR2OXJSgn+kZ70Wg6wbWET9C
v77ogzehazx9Pcb3/pST6P86ZONT2VkzRk6DYx9ktxW0naB6ZUeATNaUnQ//
XUK+svD/JXRD+7Sez5WD8w14OhS6TaZ8SzbtjI/rwDT0dKtEn6+FtvSaQWuH
8vDqLG3nBcfO0KQ0PDnOOFijMwlomwt+ZqGuR8jP/4A8wfYTl8+27nBSV/U9
Th3tk4Ak+rmZMd0FfA8zP14FBha0TcpRnZNqja/7m9KOT3QSGc0CvV4Cv8yU
XSm38u6NAr5/yQWcpa1gcBoIHsnAT8hZMrgmAU959g+gRDufK1yjjQPgOIe6
V9H/V3t7TlvOGqJcJZ/5BRX0uV+NzI4tWBJajgO/7+Bxn0bOLZgc6fyCl3n+
CfR8DFzivwzMa5d1H46s7KvueIZTe9me9k6840Kspyw7wPlmljV2/pnG2e3X
Kp9W+VMU7WX9onOaKHDYW8KxPhTn42Vo1IDfxtPmavh7G/rO4Pk7lPfg2zT0
+dRczrtSk2cz089W6JkN+c0b3akrXkZ8BZ8RpIH/J5Cznl3sA/wauPwBfZqA
yxfQ4jl9qCifVMonze3/Jt+3SuBzjd8qU4bncU7Pnxi75+jHKd4PZD6rr/sd
+VfVdR7GwsHOz70wwbbHskHeDJ03AecTfbalM647Cc4jsYF6Ayhf5r2ohl5n
iobpOzu+RlPGXkvGcwugCH142sd3Vxeoa7pi5vBbFLqvBjjvhjZ5qOtSB9uR
dKvnvOaK4SW/5t/hVxLl9Qq2FZDvYCboVz7E/oU6D9caR2udzLQzg77Oy+07
SN1F5oQnRZDHFfAtHFzfTPB5dh9gLrqnI/NdYjXnnOgT4RwUhfkvFJqGAbXp
QxjQB/6fhQ+R6LSxfI7s5vm7LTzMrzggvHtS9h70/T2em6gYBcjdWtpfA7wJ
fTLLloLyHdq7CC166d64su/lZY8Wl8NxH5SvWLGp28Y7PnXGuj7bXsBv6yp7
j6C9wjuy70pwfmDFYlUc1ouyl0HXDwSXZKATdCwBJMmWkL79RLvh6Kd3A3w+
PAQcDjZ2Lp9k9Er5cNuk52nt3D4J0DaP7iB5NgpoiGx9idw/LeXflQvzPWjy
FfIxAxzLMUfmiHF+pIMl7C8zIpVzyOtMr4L8r5C9nIzdsayzasP3cpHeO8v/
PlOY8zWmQz5aQNsxCc6HUwJ4wfz0jD4MHWAf5TvQ5rlszBkvi4Bg+hmCDF6k
3w/4Pg/8SgP/Aw+6m6oqeFYHyiMHIRkcp74m9Lze3z6GP8OXWsjXSJ3DyJeT
59bW81nPuiw++3nBXDKDd5Qb+Thy8T1wJNS+ZvIzGyP/F+Rwhe55qfM4dfSn
jqs8PxH5zap5nDK3/Lo6219KuZ6V57kOsjuSvi1Cbt/kt5PQ+BTwRDaBNW1L
+JBnaoFnKDApm//TM8+A7eCwA5jNXBXCw5d095zoeStrBc9jytctP3PdNyhG
0u9x9mf5nudH0K/hQARttQGG8s7mEo6NqhipiiGZEOU4kg9DfX+su+MLpexb
8B64/UJ7U3hubCffM49I47hjWgNpLaT4xm+UcYz4XkAYY+Izvm8EouBHOPV0
buQ8UsonFdbYOfx+aO1z+4GMiWL0eW5L50xXbEPlTZcflfypfmesrKeNOoyV
Nuntc7os0v6jG1nTvMTvHZlfYnVOx7tVwLEQuDZiPZEJWcrIGFgKz55EmX+/
8/sV4BVw/Yp5rAw4xukunPaGZ3XcIsUvmgXUYNx2Re/ch4cV+V4hyOueHhmd
y/qV1o7/qhyW8/jcgb78CL4P2jm/1TQgBDl4gK6/D/yFPr8MPT9B//5Q+7/w
W//dd9xGJ36APK0EikOvC5S1oEFklPNdbaPPX9CHX1kfBvN+YfDJTPshBf1d
um9OmHVhgzjvZ3/l94+o92Pg33Db8mSt5/wY2hf/CG8/Q2/EIdcR/N8q3PbY
8nudSj/n8Ux61cfnBujf76nzVCWfGf9GX+9QruXdadTbHZ4+RC7myq5dfgt8
X8a4uErZNrPzT1xHpr7W2RtyeZjyA/D4mrqjghzn4kp1zw8/wJcF1F2Atgcg
Ew/A5yGQQH+7BHneeh19eZM1QReefQ+ahDEv38/qWJprOjme5hrGXGwj2+5n
gXa3kY9bwDvNnUPwbco45Kg0bU+jrZd0rgcNdvP5EDwZXSgl/0mAfe3lc3+U
sZ0R/XmMcjL0aIB87NN9TyPvaw73dIy4Lsx3Q+Djd8BtZPZuen8uU8nfdU8z
TmfclC2g7RHkIqaAfQUUm+J3dHAOaFwZvCs0dF5XxU9Q0p7byFoW5CsQ+KCQ
z7OWy+dDax+gLWPmAHUXps6t0Owp7zSkrgrpHYdHtraZSztX9gvmvB96OraM
1sonVCJ3n+scp5XtKRSbJR39XC//D2jQJ4tzSinHtvKa5qJPeYBztAW7U21D
L3SD/pGMLR1Z/gC/CyHkQcA6oFWC5+8qyN/DKs7Tkxl4me9x0KLjAMe71Dl8
if6O+ab8FYr7FhnieNGKrSXb6d8SbT8dHewYOIqFo9j1OdI416VsaxV3V/a1
iuuk+E6K5T4F+jzn+Tcp9+eyXVUSUABdchEZugGdovlvsO4bgDbIWwDPtaUc
x/uz0VdbaWtXPecnVm7iz5GHLXHOT1UprXOUnWKcl1W8UWT0ALy5Aq4v6Mtz
+UjrjIPfdkHDUYzvsqW9TlLc2XcYz9u72F+vW5TjeqWGDqmALPG2o5ANxWjF
X2jmu6lSOf1Z91X6/lYuxxsJli8UOI0Ch9+hfWe+n6aN41R3pKvviG4l2Kek
KuPtQ+rYwzz0lPf3Us7T2p7yKpCG55vC9yLRjvumNazWspuzOc+BchzIP1P3
XMr9oxwKij2xijETAW0Owo8DwEDWRek6Ox+dzmsyp/hpHtf+EXqMB59i1NUj
0v4ny2lnEON6RXbnLxV/oylfpf/NqbsNPDoJXqORg8fQoRe6JRb4HRxGQ9Na
4PgSNOgVY9vk3pStoetj6P4ZuP+hezZ0Wb9Qx2o5LbsGIEI+7OB/QL4P8Osz
eLIR2FvHObOzASvF65bOh9CGttIhtwcaO4fB38AVxs9M1j5vo0NmUP4WZz/N
J7KxpE+3dc/fw7GEiuZybKFf5OdC3R1zO4ZEeaAFtNnB+KlXx77H30bY5kG2
D8X7OhfFl419v6R7JsU8+RO5KSufHnRAb/i4I7/vxD7SfS3v5qL/76JPXkd/
TAa+gQdDoevLwLjKPtdJg16628BnV1q37+b5Sbw/ETjH9wtAcWjXTs+2c35E
+Z0pd6p8z74C90nI5CHKj1h/TOT5/p1sx5gRmBXsPHuaHzRPKAas4r+eqOdc
FkvyO59FBtZq12X71ccxbF+q5/x5penrE9YBWfI6PrBsmgPrOo6M4sk8jHAs
qcIlnbvzW/AqBL+CgMl8bw9PbpZwzJV/KzvuyibG7vvwYVFnr+GUL1VrumyZ
nPNV+V57K1YPMJ9xMwZevczzo3I6nodyBsgXsbL8lqU/cjoOneLRNW1rX+ZJ
QOqs1iVHodd31Z1XQjkl/olzXmLZ4yn3sfKYbYb3u2rbZ2d5sP12QhvbZy9P
Z8dvV15F+QkrrsQ3qR1nQjZTsp1SDA7llFE+mT68MwRalmrrM+kd0KY7vHgF
2X+dtr8FrxPwqRZtfgOeYbLxoM3fqP8BSn08NL9X1Plb2xd1bubfwHNaMfsP
bYLvb0HTkchg+q6WL8lZnM5P4EUYtKjZz3F/lLdtD2VhndXR56s97V+Xm2cy
R9hOVPai3al7pdaH/HeZd+6Cx27+Hwfu6xmbG4BDrWzbo35EI/dpq3uODtG9
vuiLXvyH/o4qYDwuADVTfMZCM/sMNKmVYy1d0BkvdL9IOYEx+pzfl8oBSLjB
408H+D5R+Z+KU/c92avlsk7uDK06Bfu9WcjbfK2N0theRHYjj2Nt8648wtVa
2p+sUg7bVekcckxhn0WuT+nT0wDfAQ1J2Z+3hzbloP068PiT+n4HhxfwoD34
zM1n/0LZSstmOpPiJyCnK3nvMvzY292lvsvuNSd86UlZHb0xQntz8FwObZv1
d16yxX2dC/41IBPjpWtlx4ZIDz/6QotF/U070VA+d3939BpTa03lEtG9uPax
nTI4xnULeF2CtidD1y0DTG/RXfeFDXLZz17+9oopNnqAYyfrDkt5SKvm9Hyt
M8gMwNoA2/TrjOOCbDaY416k7FN11687gwyMmavQKGNt5wL+AHk4wfP56Us+
nQdDj1c6Oj9oDd7PVMoxnl9A30hkuQPwooHxlB1CGfCZKhtcoI5oAh6BwEFd
baNL3kfnjwSH+dBllvZ8wADeX0dfEikbIYt1+f9vaJU9i3M6KLfDqMK+izoP
fA49FugutaFLrQH1uXw66xLlt1UeVBlMKqbNE/gwWfaflA2gyQFk7j1o/1oh
62bp6PX0vzVzx0zt7xlPIwr594rIWQG+L2rlXM7Z2npe7Q8ePxd3LuKNyMZ4
dPsGyvrMnaebOi7e28xPfyMzcyk3IDMfIC+tqaMCdX0H/R7Lv0C287LjBefa
HX1GJlvK3+s4r/x73W0PozjTsok5B1wAzpZ3nmjpmBjKjcB93s+PHttd3et3
rePl/6AzF8XsrVjGc2iBOJ/7XtYZMc+2rOkYhYpPeB9e3abNQuCQF1qsl4zx
fmvN98Db6OtdtHOhqee6JMbGcmT7fWAFdF0OhDAPrIIWo9E9C/leppz9ZjfQ
/5d4Jyt1t412ft12rE9ageNu6HYfmTmu9ZD8kbXPBc+l0DgQXZ05tWPsDAWW
INPL6M9nPJeT30+j37vR1inKC+C/UXcPlPdEb+Q2AsgBzRuiU77O73jAivnU
kfavFbZd1DLKWuidUK0FkYkpkll4/VuE4w7KjiC8nOPFXJE9H3NEsHQ5+HSj
D99mdmxlxVUeqHNh+BHD/1eYC24yd2xCHtPRZn3mmvSUrZHFo/Axu85X8tr3
fRLQjTZy53U8YN3Vyx9cfuFXqec68JP2VD1MT/kgK7ey8t7Lv+9cylpjIfpg
KnPMeN6LLup8ynHU3YQyQw3HoP1WfhHo+/HQ+9X0PudPAC5oruzAfN/BseaL
Il9b0ZGjGQOH+jvGXmtgP8/tlv9ljPM2R/DfRT4f72c7V/kddka2XsiWmzK+
rm3UZJ8mv7dfgJshPltVzBqdrzZBNgLq+DxeNo0Zq9u/aliIz7sWAk2Rs7Tg
PJPfVqdznPNPKNfLXrGibX+TePd9+J0s+yRo9Sm4y/VH/gXyLbgmmyCevdDV
ORoHwOu05R1T+Xdo9j9wuUWfylJ3Dj6vCbH8vN3fMpRBd530I2M3x44Y19nx
IxTXdw3PT0Emj5RyTBPZ9t2C97cYBwXaOx/RPOSkMu/1i3EMFsUnqZ1iq4xI
pgqo5nMQnYHoLEdxwHSeg7ikqku7TImpFusehPFcCsic6LXihBT/d/m+N6D8
gTExXns0Kq3GuE+N7FSn3IhMbNB+v7bPXdIjpz1ouzHjqRFQOczrM92dar32
J3h+Rh//Rg+sYVyGab6BrheR+x9o/zzlQNqYoLPFROfi+AR8p/FOWsZKLDwJ
hXZ7GUv7gBrI6J/QcxI68WwD30+sC7fNzVvo0YW1vNaOb+YYdxHo4sJtHN+m
R7Tz3hbp6dy3/ehPBq0h2adkyOZ8X+vhUU3FbaAvY6HBONYO93o4t4FssWan
tz3WDXC9B26LY2zf1Bse7Qmw7/0QflsA77YF2U4zP3T4ir4eBCrAw8OM/+2a
2+FxP56JA9Ygxy3lU4dslUUGvqCurcBs5HPWgFT/OYVrD1g/rfPCZOX9JVmc
5zFaZyn0+x0gjv/uQue54Fa+ru0pJqXYVByRrgG+5rkn9PU+tLlUwTpdul37
pPWyDYQGt+WLAp+XK2Yfzw+A9r9A93L9nT8lT7xtqyomeq7Q2c9qngtGrtfT
xoclnAehYR3bQQxRjAL5vyCPFTM5Pu9T+tujh/cQmrfl16czY6pO9Yjf6oFj
EeSxTILz+86mjGEMt0QGyuWz7bvs3iOQv0jk4Qvo/r9MjhGt+MCye+qEvipQ
y/GpD8C3MeV9v6FzEp2XKJ6q8nnrvOUv+rJX6yBgFrj9Bn1fYg7Z0t/5RKbT
9qf04Si4/cLv2cFpEHLVFvnNVMJ5AweB+xho1xAaNACuVfJ5ts61h8OPq9Dp
T/m4INv74eVeoDx1bqcfc+jDIvofwFhYXNHnM4pn+Uhrm2jv4ZSbQmsYrVna
wL/d6Ie9wHxkPCvP7M5sO785xRyTcq7O6KBFBLJWq53PypfIr0lrcOiYoPUg
MnYeWbsIpKafvShnQbfelKPBay40qt/acSaVj1t5uQ/w/lfANt2xlPFdbHr6
cY/3HgBH0HvzOjneb/1wn5PpvEw+iFpXyY9Y/sTroHPPao7PehBZ/Jn3vqK8
1cix4tPx+X3G3OcJvoNTvIEmvBtAW8GMk9r0aQ/v3NRZS6Ljr1XSOSbj8C70
OtPJ+UPKIv/nOjqH9Of1HKtRdgo1oO093t8G3A9xnyPka0VbAyrZ/1Z2M9Ih
0h/KxaQ8n8r3+SvlFvh+hffqQ8e/dc8Krat1sP3aAuQuGfzSIY8twSEUfq1g
bVOSPpQAfkvr2PKf8B7VpSqEkv68kPl6SHsK6Jijt+My/BzkWAiHmjgewkVk
rRhtFQWaQp8SjIXlsjfludw8n1f2H/Q5Pf2LQuZ7Qt9F6IVYyveh6wXa/glI
Dy2zao8PjOW5d2T7TN0LY32W2gTo1cXnFPXg8ebAFL8a2fcwV5+r6LjF78LX
pbxfRHFI5D+NjOUAukuX8GzqBH9+p7e/r9T5MvgGsea5Vs1+mDorVMzeXQUd
t1c5oj8BaqZxDijlYZDfY6sA+8PVCndOqkVAfu0lyvjscQI0aQU+05DdN+s6
V1gSOCcGOifAF+2dF0A8FT+npXOeqzzVffYrG/1MtDMzm+NmKGbGmD7OHTEK
eeyouSTB9xHjAh1/r2YWx+Arxng4EOUYnvl4N5z/vhvgOTeaOXMS4yctshAM
rxciT/GxllHJ57/wJYG6HzZy3PgW8GFUJsfTXsr/HZC1yhnsLyK/kQR+65HP
68mHpR2LRLkFtMaZHuJ1zljWJEeQuTfoY840zsVcBWhR3ucXOrtQPjrl+R4f
Yhur0S1tZ6U1WYleXqNtyOq5cp18TunHycrOYSZ/AeXilc/AL/kc3+sZ8Bd1
hTJ/1gQyqD36mbGO1wv/yp88i3H+NwXv08j/fGhZiDanM7b7wKeYco5FuJN3
yzHWmyF/R5HhNjx3SL4StPc1ZVgZn0UWKeo7nVG6x6P958zjz3I7B/MrPHe6
ufMqK77xySjHOC4R5pxzJTVvIzdfUkffUN93TALWdnKeVcXqKo/MHaWuEGTg
mJyAZFMLb1+hve/43ge6lc5h/9xLtNMfPgYjq4v4rwPvJsQ593ZFfmutM5ZY
x5oYTR+PIyuJ+Z2XuSG6ugHwGDzGMS6vQauECvazuwnMpI1DJRxPUfeuOrdP
Cra/c3+gcUnnZdE5hPK06HPOlO9DmOfvoKt+kv0c9XfXeNT9ch/LuPI2ar2X
pb/XfMG0u412WtKXP8CvB/r6w/w+r9IeX2dWmgPOwou3YjxvaP6IQ84L0b9A
2s9cxX6NyjWXu67j+gyjnmDqCAHv6sATaBBKPxJaOw/EU2T1CXCCvk5uYb4p
zqvOaLT30pnNJNo/wLOlWJfsivfdt+7A51PHP7LBgC/fMn6+Ae7yeQftVqXP
PfmeHzwLApPRpQvA9ZTsVtN7b90W+JPxMKKkcwxMLWH/g8aMvaYZHJNwL/B3
ovNbKKblJNpeiTx8QV2DkJu6zW2zIduNt5CpbYzrNODdFL6ugg5T+Z4xRcdI
1yjHmnKtrQZCgqxHs6d1/m7l7s5PWZf36wA/MSZPt3XO517gfwLZ+byAff7k
sxvNezOg7cEuHhc6nx8FTbKiJyIZ64einD99Cs8cRn7/SbTPyj3K6voPfj1m
PD8CkuB7G97tCD5Roc55oXwXkyn7Q+vCOuOGT69Q11jk5U36HQOPx9Lu07Q+
fw1HTx+jzBfhfftKvheDnhu1f2jiWKH7GdP7gCzy5QPHrbJTZ62TEx0Q1942
EOWRr5+RzWjG6lH6/1T2OfS/HjCc336WrXZlx5zbQl8vMIecr+r4ZPvgy1bK
V2j7QF3zZQ267BK6bG1Wn0v/Bp82U6ZFrjLyfAagXlbbhsSD79bsPnvTfe8+
9OleIJD27qAfB9B+2nb+3D/M35WbRWeFys8S3cT5CJSXQDkVFN+tNM9+A7+f
IzcB8G5eWZ8RzaEsl90x+hTboEJax+4qhZwEw4+S0CNTe98FtoYPbYGy8Gow
fTmkuwLksSt0TksZybubGaMFkZ80/W1jcgA8/gC/cHjUEFiFbnqCXP9OX08j
xzNkI4PsZocHifI7gb695J+K7jkAzIIGRxm/DxjTAeCaT/fhtHWF72+iJ+vJ
ppp3bkHnm3Ude6ZYSvwZ7S0X1HMejUXMHdXkE1fDMQBGBDgOwA+0mYa5cQ28
G9Pc/sLv53WbNeHNHHTUN/AgD33MDeyv61gQigkxAh1WCf1UD33xMNpx57/U
2bDGJXBfdxHgVgF9k5Z6H+g78DDRdpPa25WEzu3hVyQwmjF0FZofZUz+0chx
EArQz3X5fS6nM7nXkaWR4cZBsrWF9eII+PGteAr9y2Z3DPT9tFeGsbs4yvbw
ZWjvMnR/DK2fATUYpxfp3yTa+YlyUQnnEFtA+VB2hsjX5fq+J/+qu+/K5yk+
C/B5gG0DdOYk+wD5KW/rYVu2tYzPgT0871+E3ysZq90ZSyNzed90GBqfoe7T
9OWU4jfQ78tNnINUcvg9MjpZMdzo5yp0YjkB/P4fdaejT4vA9aB8b/i+oKRL
ff8UGq1kTK2hfMxvYeyZHtHuNegfTr/GVrRdVsscts2Sn8Mk6LIHmcpI+x+V
dv4z5WZ+wvuZkJ2nlBl4Jwy9WRyZfMb3LLz3MjR7F/5/r/hH0PFKqPdUJRkP
n0CvOwNsS6UcHN1oOzNyF5Dd95XK0ztCZ/Khjv32PNHx32a2tq2c4vuVBr8Q
6hsMfSOpqy3zw1vgdbOn43sXp/1l/PYi0TFDtcf4QvZ59L+g9GMpx1OZ0NQ5
s3fkcfy9WfDkDznnJ7G/q+D4ijpwkn5Q7MchA5y3uTrQGn2Si2dzAql5PgD4
V3ds0G8/eDRALstoLFDngfLOu5KGZ3RAMJG2H/H+E+BItOPUrWLcDZTdD/1b
w29pefYmvNoCvYrzWzq+1yhoe9RUyMoL9GBZxuyhWOdq/xo8jgDjodOSdr4T
7oQsPkPP/sDv6Xn/A/hXjN8GJDo+7Nkajherc//nwDn61wF82zM/ZOD5jMBr
6KpJwBzG4auM40z81kM2i5SBQJYkx+XZAc5zme+y8n0Y9PlM+gQenQe/e+CX
Mct/1/qp8rbzeMkDn85LVtCpTylv8n5fZLwPkI06/qGO+wLqyc73b7UX5fsC
6juk+sF1OPCz4hkxR7alzi01HZckR5LjlOhz55Tv7yLD7yN/v5d03tIA9NAM
+JqLd8qzjj0Jbi2ZPy8jJzl5vjTyVBbd+yF67xfGSC5+uw0dvuGd2ujdnbS9
CfnbCb1e4vsT+pqbZ/IAeYGRyMCv9KU37+bj+y3eLcC7VWQnpLPXPL4/Catj
/6z8PFM+yjqsTYoeE85/lrSdnvIr9ivoHItB8GoxtF6ks11ka28lj4/qQAHq
KQiEI1tj0EmvAoWgVyvov5jyY3RTIckWY68wZTC8LgrMB58gvjegjoUDXOr7
FNp7HflrDO4fA8/RL8+AX7s55+bzPPYZk++YRPN4nH2TusOnbIoPpdgz4NgX
OnaGR7N1n4X+7sq4C6b+Ikn2KyxKuZt2i1HWSrAdcCgV9mNM5EVfToKfj3ju
VnfnfVP+t+I825lxWoffctCHX9H7O3mmBL+XBHLA+z/BI66CYxeX4rd06M7S
dfx5fh1//6uG/TlL6z10WdtqznuzijXuq8jmx5S9wTkz8/yryNv/wOs57R9i
HA5k3RFM3++yhvuE31a3c/700OKO96a4b4pjJD8HxTIqQxtjGYP5odE25Car
9qxt7UP1MfiGa2/Js01pb06c848f43M+7TGh58VKzinypLFjIwjn7LSZq6nz
x8RrzmGcdtQaCj33K1CthO+4yib5zEzxybIgD5A4VXHdEcLXxdRbiDnylM7j
KBOhV3xvxzPVGncdzzTo7dy5yqG7F5406e5zdp2xKx94LaB7c99B6i4yQ6Rz
M3Xh+yOeuYkMlAOHdejI1rIJog/v9rD9bqs6tud9A1mPpM9v8962Os7d/HlR
530oR59+oqwFzdfB109jvX/V+q8n47gwvCtP/UHZzLv3B5h/zZGnCuI9Y+IO
vKjI53m0VYmyMlAFqAq8VND3Fu/Q9o+8dxIo3MFn+DrL/19T54FQHtyBuZ03
Snb25Ro79v9P6Kin0PUn+tCF7x8w1xxnLurMPPg5/f2dfq+h/n+hbUm+l+WZ
B/AnlDF5X3wCh4vweiLrqMXQLqq67Rur83spaL4JerfMbT+QgfCwqGwj+S8t
8nsc2TyquwXmhUH0NxCa1+C/msAa1sUP5AsKflX5vQpQjfrWUtc2ng3VmAPC
gNpAV+SwDuWfyE3dJPuLvZDPKZ+PUc8V5Kw+n3+P9nyrsz7NuVqHaA3SpZvz
BDbgmbeg9wh+ryi/6er2RbsNz/owBlbJjqGVbfEiKlsOl+qeCbw65/Yzk+H3
d5rf+d4wyTpQulD5PcL5/j943Ej8rGa79LLI8WzqaZxk/6E6QJ5O3scoboPW
bS9D+yr0uwnPrGAM9IUW27Uf5HszoDlwnTFwDSikPTPy9T3156YsGukctkMY
g2mp+yZzW/EEnxsODHOcjxa8P11Gz/SpJZ9bAY+gQ3nG0V14eAeIgXdFwOnf
3LZp1HpXa90Inv0Sup7X+QTjuGui8/42or7MOtsGCvNOa/GK8bYyBX/1Yz1j
ryR0eau8fTama38GL0J4LjXykgaIBY/f4GebJM9HH8kknDnpZdpom+QY8MOR
j3Z8bg90EM3p99QQ7/80j5yBzsflp4JefRt6hDZyfpIWaX0vGlvR/n0daGdG
JecXfARff6HP9Wh/Pu++DVxp7b2K9izyo5Uf11mNf9o8JV9Ann+b8dKRdlrl
8Pr0KfKWi37thJdRPBefyXYNs+Q/Be4NkJcXHR1f9wT/VZF9I7K7jPoSWI99
A99aQIe74HSpvOdPnUt0pK4z8HAPbbzCc500twCJKWu1T3Qnwhit0sBn2Brv
GvddkhyTQLEJlMdtcbTPoY7pLp7/NrS2nUX+vLa1CNGdVzuf7yjvpNa3Wufu
YC7oxvNNwLcVuB6knXzyy+O57vwenWTdK727v4fPEDpSZ07mvMs644bOybyz
BZplY47NCtQPcswO2T63ot+7kMfayPNWxvUqcMzGPL6YegozpvOAx/s8W4L+
fkL9R+HrD6ltq7hENooB1qfKldBe9uDIzH36cR/Z/YuyB/itRF+GMcddYc0S
z3zTD4jh955aJ8KDPxk3e6j7KuVJdONZePAjZQKwkzp3ADXQryFAFsZULO/1
AnprPQcslA7S2Trv9eX7Msq4JN/NVUY314QOEfI9q+8+VqN/X1Ce6e39iPYl
Ouc9W872HCUbOn+F/JarxDm3tsZayWrOh/4PsBKaZQWvfrSzv4JzrSuGy6fQ
dk+871lP8vuJCrZHln6UniwqmyP4XhX6ZdcZIrjFax2L/M6FPjuYY17kd941
5V+7Bi9/os+L0SH9RUuEuS18O8NvvcD/Ac/fB3rJbhq56E05iD5lAu+1/b0e
VKyWMtAogfcHSHaTbHcjW6R5id6rNIE2v4H3RMbQ60BSkmObKsZpSXDPQh2d
wH2v7tT5LxvjKZzxNAwdUAwYAnwLzj8wxo8D1dFRm7XegIZN4Ecm6NBU/KGP
A3n/D+j/K7rhMXLVm/ofIR//A6JoZz9zxGjwvay9HeUbzKcRjPP7fN7DGuAb
9GU9xlgMdH0pybKXOcTylw099Ax65EF/lAX/WN6tmehYotPbObZoErR8Hdy/
gEZ5waO77jap8wz9H0R9r3ZwnqQO4JdPtvwDHK9kLXAsrf0IH9bwmWy9Yj6j
1R3IfMb5Re1B+vg+bhPlJN6/Q5vd5beGHA2m/nys36fT/staZ4PfOsVgy+b4
zf/S1hatJ8BtdB7fTxbm+8FAx6yslc97d91Na0+/ElpfkR5F9w9Jcpy7r9ra
LquH9oDUVxg6nUeW/mKs56TO3HkcQ1p5+bLyzMfIbu4B1mFVgb/5vkr29JSl
tKejnzVk+0U7ifR1QKhzYp1o4RxZK6hvaJLjNejz1y38fRQ0LUKfxsCTjqx9
H0P3Yfx+gz53Ri9fo7yMfA/QnSLt5mccNkVv7dfdG/q9AN+zyCYso/PyXKAc
yrhrRP13dJ5IXWN0LkD5a0vvKSaD52bwe4XfIqBzX2g7UnsI3m9OnWs1vzK+
S8L3q4oLRFtR9L227IXp03vywVSsL8q86Ps8iscATvNodz7wmLm/B3IxijoX
wd/5PLsaPEdr3xBuG8kxSc6N1JY68mRxrjPFwlFMnGr09xi8yd3K9loVgMMl
bFcxNsl2Fq8mOXbQ7nDHw1JuQ9lZP2NcjuO/UPp/Fz2wiP4NpK/DO1rXNwW3
VOiAirzTD7qHodPH8/y7DXwn0hHoxTj9B/gbyIrcT+D/v8Vj8EyU/xzvJ+nM
lrpelPWZxkb+/wXaruhtO/wfGUet+P014cueZzi86C5bYmTxNrS5huxcBZTH
SOvq2ylr61SiAzSMr+x8W8q1VaWMx90EcJnIM4e7OSeO1nRPqasEclM8q9cr
WcEhW6Tv2pXbVHfvymPXD7xqUU5KchyIxvG+ex5e1HHvNyDrYTkds1Fr8EJB
Xofflx3GAJ8nzA3xWYbOMaTfpNtyMWYHIqNNGX9JsjGCh40pp/JuDWi0Bzq8
zrPT6N8bSZ6bHiq+BjS8zPiczG9HwGM9+nUKn/vCv87892aS4xi/qtgvjIlZ
0G4mkI7/j8HXqUmOz6lzoY+zeG+ofeFw2msJT6bxfWpvf9a6Rd+na42GfhhV
2rm/80f67P5XaFQdXm+XbR9yelp2tdDlDeaJ14GbulsJdaxcxSVOkB8scjsY
GB3rfHoDFZ9Ia5A2jkkk3olvMczPkfRjNXNClwifl8zkuTro329hd1NoEIhO
mMVvk9GBbXo6nshbWrOAXzQ671l+x1qanWQ/a8lrRdrYU8c6qCL939bO+9W7
sp+g7Tnal1FvplbOVTFX63zgbb0Lfb+lD5UolyFH8/ntPd1VM8be4XOA1j/I
yLuiGfRboHUaNMnP2vYS89tPQG70Zbvs9mmen+gzhoVJPmeQ7d1xyUQn+4vk
irMN815+zwStm9OHLvLPha6zujnPfEKo8zN+Cl7fM/6vMVavIUcNy/hcdFGS
8/cpj981+rWJtUHjIN9R3IZmB2JtbylZkZwob/r2Ts6j/pfu0rs6N5UCpeg+
+w51LKbOa72dG0dnM4oXuYp+HEYvDIK3hygrgEtIpGN1BFFOS+1cNOUZ00t4
vzq/Z4U/M0raVnB6P8u65Lym7ITB6S7j6678Zjs6DoTyrb3Hu3fB60Jlr7E/
7e7cYzfQP0v5741GPs+cLNsRxlwyui0LsnOYfpaRb5riJTInfKhz9yY+d1Oe
XOXLfUV2afCyLDjNhw8P0tj37n/UVRv5eKQzXq2TmA8nQONXeC4XuuFr3v+H
sX41xucHr/D9Q9nUF/Oa6H1geZL3e9saet8k2q9IMv0V/1Kx7d+ARv/ks/3s
B6IRvF9J+WGSY6krprpsoBQvQDL9nDVJe/j2J2NhHnRYTb8/4vfb1PNGrONg
Kgam1nB9oWMsPF0KL+c0ciyhW9BwA+8sRH4y5Pa5ts6001N/NP14md/q0u9S
8COP4mtIZwAd0SUnCnpNVxt56ZvV/kPyI5J/wX3geEHnFFZ81zo81xW6dgHO
IZOrtSalH2WhXSVwOYuOTEJfTUVOP+G/jIyNqcGOPTMNWdpGP78ApvB9HXUO
ke0zdPyM8RsLT0fS9jZoOJa2tlOWpo+dkcmulTz3aA4KpBzPuF2TZB16kP/z
hdo2Svexe5o51t8yvk+h/5Wp8wB9m4QeOMpY+1h2FrH275G9x3Htq6izUhbr
kSD6PIzfCikmj9bHST4n/0pnRkmWFd0nZ2Cdl4v61vHbdegyDXk8AS925fY6
aTflfPZ+f6FXX+isGp12mn7MBbcG1PUa73YdYF9ExfvQPj47PFpPfQl8fo7c
buBzWcpu1ZwjaiT83Sj9xW+fJTkWXDH07kZkYxy8/QL8nzIWc8OT/AnOIV8J
mnUG1+7Z7B/yKm0/ZZ6oVtB+xfIpVh68W/T3t7K+1xYNRcspPH8FfC8W8RmF
zic20M9B3ZyfZRM4DAnz/kD7hJsV/nO/TDVOa0Zk4mIax4TawrNRlJt5Pi34
lQOHgPyOZ3oiynUm0fem8iWhvRbIQnOgFHzdkuT73M+T7IP6QQf7pCrfRBzw
Ahm+WMA56LbyTE548Bgdso75Yhlrm0y0mxG4LDsD6HFNd/tJXmdvo6yLDGyn
rEc5XncCwY4X+BI8mKv1I7hmph87tHZD7lczJjPQ3ieUX2r9Cv0+Yw/5NXw8
wdiNRZ7LMk98Iz1F2YznsqC/GlDOBLczyF2ebo5Xlx4dXAWCjde+oJvPO5QT
qheQBN8+jrQ/u/zad2ofK3s+xk3J1o6xp1h7Ov/fleQ7gHbIwxh0bac0zqOn
fFQnKXsxRjogM1FACPPPM9nrVHDe2tPUHU3ZAz7spo49wDn4sJdyIXTLgn4N
BM5V8f2/7AAaUKaiP5UZv6kp9/HsfqBaHn8OGeDvpVLuQXQfojXTOHi8Tvf0
8KAe66V/afsAvx8EvgLelC7u47yxT2S7R/1PtZ+GNyN1Zp7key3db/VFNldU
9h5be9U7jPMPaWej7DXivRbROkTj5Vkhjxnl4JvC/4dYDyUhS52g8df8P1h3
7NAkTWmfySoGykuM3z/62AbyPhCGXjjMs+soX85i+/Cfea8bY2MGdO9OeYz3
ViO/D5jf4pGVmtqPU65hnhtKOQQYWcIxqZYmOv7ZEer8BpiNfrgMH1JD6/KR
PnduBqTS/Tf1FAl3fMDT0O6f3M5HpHto5Q5cAt0i+zsWcyJj9xG8Ws3YuEd/
v6XuIs28h9ZeWnnnd1Lfft7PgLw1Fi7QdB592cV6Ipj+rUc2fuDzBuofqDNa
Pufg/TV8T40MjpDtPrgepe50yMqmUraRka1MTcpw8JiNrDcq4X2R9kfZaOdV
fjumtZTomM1n4joPn9LAcUl0DluV5yc19Fn2Rtr6Psnjaz2/XarlGME671oY
5TMvncVuR6aOa10P5FYcjiSf6+t8X3EFdF6uc/N1rTwG30oZh7orOZnk+5If
KctDn/eg9wWey8oYzw3fkqj7c/Bvz7PLofEpnouGx8+h011o0pO5vATvrAhy
POb0vJOujPeTRdGrwejBYpSFkd8j3bxnOQ18TRvfMP43s1apDX6J6KbbrKlG
8WxrPudBHh4Dqat5r3uokfe+65GNGantR1NEPoO6b1csC3RPJmhZEj2cIcEx
CRSbIAbaNUFGpsDv+xWca+ki8EER0198qMh4GER9fzJeCoBTduaG9vTvDHh2
hVZnKSPRi+H8toFnRkLbxsW8V5hLOw1T2+djQWPnF1Keocs5ffeh2ITf0UZm
xvD3lOeoqxJ0HKHzaGS5I2vCtfQ7sqX3I/IBPV7ZvtLymZZ93VN06x/5fK4b
Feez3VB+r8C75ZDDtMhZBGPgVfYnE/t4TtDcEI6MbIIGOeFlV3RmOj5/1N93
IOeTfA+ifYPm/e2UhaDPSv7fGO87JK05DjE3/0u91aB1CJAv0GflOievDl7/
dHfs90nwvBb65xn/D2c8tWztc6ILwMUkx1c9keAxrrH+E79dAn4GroL/VupM
y1j7TvdrGZ3jeR3jogW0/pQyT4xlWzI+AHn4hfJykv0GGiKP4e3tX6s+q7+K
0aBYDY14twzvPenk9WU89b5OO4vBN3shn6/qnDWqk3OAKBeIbP91fvRrknOJ
n5RdADL0G98HMRZekv8OunIDsnaF346ij96EHscou0C391o6FqrWS33BtSRj
sBzlNXC6Wsx2IbIPyUs75ZCPu8hGLq07MtteQ+faum/TvZvmyLLg/Tuf/wDq
o7verWL79NL04ytk8E9+34scrmAsPSlqv5Cr/PY69c4CvqS9waq/uv3iejW3
X01UDt/NXUtyLKIq/R1jUrEmWyNPfZrblutz9OS3jPHrPPeY/+pTf3l4P5ux
eiO/cyv8RXkUme/JeP+Tun+mruXI+GHWivsYF73Bdwd9zyvbCfr4k/gB7+KQ
ixx83lPDceJ/oj9KfBCd4sN/tLjPBXQmsBi6TqXeQcB86n4feg4Ch6IFbWNU
FTy6RfssQOcANyhbUO/30OQv9bGMz/hu8jkQ+lbu7jy6V4I83w7JY/+Oa/Qh
MMI+t/dq+9xGZzbKgzVItmPgVTrK8cOKQd9a1DGTsVgcGTwZ7zvtvtAplP4U
iTBdJxe2HrkFzOzhz11i/P0tdFGhHpZV+c/Ij6ajYp5Ap+yRtqf6LpXj7beg
zzPgSa463qOnp5/fI+crU9ZqymOpfJb/Q1flLWw/k6OMi9/QGfuDHa9+L3Cb
dsN5/zrtXAPGJjiW/M+K25DPawvt9e4Af4PXXco66IIA7ZUSvObXer8dsI4x
s5a21qezf6tsM2SjIXmX3L8KDbo38VpkouqKsE2IbEMuMLaKUDZvZ10inVKe
92PZp9Xu7zXAyAKObf9GBp8F/pnJ54F/a27kuU1VfT+iexTdoexjHA1CzxyU
zQay8TuyuZqyEXIwQHu7JN/LX0q5m88c63O75b0dF2Yg8Brj5Z7WZrS7EJxX
Ml7v8/0B0A9e9+D/6tU9dpRTUuNnLrp3DtAL3v8vnddIWit9zH/vQM+vFbuC
924CFfo5rswXyMp0+vgCPuVgXP8D3gvY6w9HJoYU8Rml4hzqzPLDwvY7/Yjy
CDR6D1ova+r8Zm2Qy8Faz0GbU/RrOuMmB7rjV+TkHpCRNsrIVhPoydz7rOJ/
YW7/u2e7Tz86wfd+yF5acNpH/dvRcQmsbVpQ/sz7LXU3pjUj889lyj/g279J
jm2neUx+M90rOeef1jJTGzjOmvzkFNf6V3hbkf4l8n6+6o4No/sX3cM8T7BP
jvxx0tHfh9TbWnt5dG8O9EBcFdvMyt5tSmvbH4UiB//juXvQOgzcPpNPLzR8
L5VjFH6Q4Pw5x6BLpR7Ou5BQ27F5ZwOpOnifqv2qzvQfUVdzaDCC+mtD68dJ
jneo9XvjNLZlkr+WxtNO9MOSeN8Dyjf0ADyI7en8x5sVm0N+G/DnKfR4Qj1P
tQbXXAK8AF5mvZEqmbUNMBAe1RE/451bpg71BNZzfA/F9riA7K5Bf/ZBt5zV
fj+9878E8G4aYARrhOHAOGQwL7TqVdv3kZV6+37yGfwrJ1tAyreh1VnGZV3a
eK59BO9HKs4KZXogQ7I/t47w9y3Q8E3ZrxZyLhyV+q75Uz4gmkNnam+APnmX
31fIXgxd9Da6+VRNx11OiLcul06vi2xOQQ8MY71WX7qV/x7rTCTYsR8UX+Q5
PBtNu/F9fQ4g+/dO6WwDf72s7X6ulrVub17D+v196HkTWpVj7GcE70xA5mR/
/ie/vx8D143MnTt4dx/jpTO6ZHlL66HAZNunXUZGVtKPXymz8NuDGOdjydTE
azjlL3ncxec5iin8MbwYqbNdyjmM2VAgRDavjKEzmW3DrTvO7fnsT/o9chfE
+C6JvCRmsL24bMUV7+HrFPvDW92cty9VkH0zere0T4ZiEioeYSpkrhIy1xe9
NAM52Q2dQ5C5fPR9iOzQkZW0VRz/uDuwifm3MLwqBLyBDF1jfG5DNyg5RxfZ
HNLPBGS7KHSHzKl+p7+x8OYO/99TPDjoda2MbYc2gVczaLAa+gQm+uylLlA4
r8+NslHXfni8trj5rFy02fltPeW/9Pc4dLqfwXcqU6H3qXT277xTxPlqdBeh
OwmtEf6mzf3QJLmv75Vkr9AkwXOP5qAwys8YXxuBTvS3ITLUHjq8Ar4bwLUe
ff8BnV9MMTag4UXqP0Xfumt8tncuhfLQcg3PhCObA/n/PHR+Cl47ejuGkva9
ivOtfXB3cM+h8SofXepsBQRl912B8jBv7uT91McVvafqorM33n2DPhQL8rr6
Ct830P+JzDcbxX94XwGYVddzcU7qr0nbuSgXy6ehl8+sdXY9Anrk5vfx6MQO
ujPj8yj4twbcxkK3V4Fx4HQmlX2QlJNsEH1pwrhYw3h/K6/juSqua17eXSCf
BM21so/je/5kx4rrzjgswOe/masO13Ae71rMYTlZ2+3O6f10ato6DD2+h0Z/
MDcU5PnP4GV7np8U4j3AW/DnifqWznYGofAxkvf/hD9ROW03rVj/ivOvmO05
0JcDtUaRvVtzj8208Ohb5GEz82Uh2igMnAjy5x6p/T0ICE62LbA+b+7j77/K
9x5+34Lup6n/a+T0onwlwSmGOqOYzz/tZh+qrPBxCTSOl/0e716QXSflRcoQ
+pSBcfcl/WpGG6vB6W4f2zsV45niyb43kH3nW5R5FT+CsXg1g32odJ+oe8X4
lLgC6elXZ9mMU8/Sbl7LaR2ne5Yesm3imQKtfT7SCZoc72DbkNE5U9Y22qvy
7Bz4NI96S9D+8hZeK8nXQeuljrx3CRmPpKzGWMxPvQUZl2W0F423bZnyDZVF
7ifJpxV9/W8zx52tgv6YBH8nai+d7Ng9yqu9hzaS0Qml+C0a3EqLBylnODq/
kQ1mN/TFaNqL4reuyEwydOpGuSzFNkY2MmV47xd4XDbZNtG6T5Sd1Gnw3lPB
vh2x8L8c/4/N5fO2cpr/k20vLVtp2Te/qv0xcv4Anq3l3dHIc370RAWea8P4
r0i5lN8rJdtGcTJzziV4830P2/vK7lc28eUaOu7fVuT0KTT+K975pCsn255E
diWFGFd7Axwr6A3+LyK7VOaVBYzPKjw3ge+bGSfrmMtX9rQttO5jdBej9WlV
nqnE5+zQqxqfX6/n9YVyrtUAqvNbIjQJoRwNDeIY69WQ+VLwuSu0LE2ZQb7a
OmujD5mRod3M43938JpTdlTpoEcN3s8HLj/R/ois1uHS5c2QhS+RgaaUNXkm
FKilsRToUt/zDfCY13jfQJ3DkLm10KQ2enwla542zGth0k+KUcb6oD3y/T/m
uwT0WzXkpmoXx4BRXi6dB+ksqDbPL+ruvNrKMaf8crI936azlYamdW/wTkfd
aYHzVXzOGq84CsyVdXh/NXNwXcp6QP1k2ydFIBc5gQZ8bwjsTNlPdKUM5/ub
jKFGlA+r287uEPRaA80bJzumpXI9KAe1fCcU660eONZHj1VkPL7NmJlMv5qo
XmRkC+MjPf35NsY5feOga1P+awacKWqbQK0bZBeYA3405/eFtDGzrs8921Qz
X4vwW1HgB8ZZC75/38x+6soVKl/1AjXsy9dSfQQitA6TzINDm2Tf/c/K6hgK
uuPai67eDwxAJ1xCPm7T1i2grebg9s5foLgOX/DekhjbIrXTOog11mHo0p7P
v5X355N9/T1J9EdPnKhqX8kn4PsMqAytO/D/3l6OR7iske/D7umsqLtjcZ9m
jIxAxiN5bjB4XdLelfpu8NyzfvZbKt7Uc1gQfY+inKUYafJDQlfPLOVcuh21
7mSMfy6fCOQmk+xjO9l3Q34bNWVjRf01NX/09xpW+4XD/Fe4tW0VgigXZLct
k2yadParc98R/FdZ5ybI9Ied/Tkyxt81Pj5CzrdktL2A7AZk6ziF/y+D7y9A
lnpen4+Ht7l5rh+fW8Pz2uwfdvPsrjj71qfJ6lwtipEWA72OUhZG/+QGj07g
u42x0ZmycXufizTS/XAx2w4qnoHiGqTSXW6iY+p24dnmsm3P788bi/n73+i8
0dA0V5DvRG4U8b1Id8ZBV3jSLeK/VEqpduo8nM9pCzoeSdHcnjeC6M9o5sSp
jLcg5P8D6rzey3EWFZPlzZbO+9GmnW0rZHt/lfru8E5X3h9C29Wq+t7uHOVY
8CkG/JVgu3btgZVXcRRt/lzT9sY3aOcavLpOOVvnHfx3Hvy7UV/3ZNuR3gLX
aK3JI7wnqa94RuD1T0nfgeTS+W1KzB/F/pla1TnW42m7B8/HAD2B7X0tG9pT
3mCclM3rs95q9GVyNccp035Ke6n9lKlqOvew4skN62c/J/k7RYBnL3ibBllI
x/f34OUSYBo0jylhH+Hy1F0OeKmBfdsUP0i+bgPAoRrtVwUmwL/YZOeDqi6b
4ULOgz2BMV4E+SsFnYM7+ox4API1Bxl+JlsMxnUNdPMZdFF1yup1HLcxhPIb
aFQIfnSLsw17I/TXTvAuRbsfBDq/VVn6XIJ3I/ta/iSHTYEW9GVoP/uclkIX
taS9OWV8PqJzksmSTcbnYORiEDAtwnnhV4BzfniRHfo1TOc7gXGyjQt1POTB
6JRBwEjosAX8ezGuriGI8chSdtl28z0j3zMAQ8GtAjx8U3vdUOcoOqfxTn+q
gFc6GSbH+w5ROREz0tePdNcF/IP8baG9z8FtBONzrGI80L/sCfazkg2Y1luZ
81hvjFZclfaOmyq7uB59bRunvVPV0t5L9dbal+f6UH7MOqQC9baCJ+Upf67n
z4qnt1N3bLIbhPezqbMvzw/j9+f8/wzY19zxUbR3lI6QrohAXqbHpcRrhT6L
Ep1HJ453+yU7/4Xm14HgvZTnazBOmqI74vmvhc4/GfcvwGM175xj7urHb915
bo58mXiuP8/1R4dsRwbmIoeZ4FH9yo6LOUr+KNBkNHivBY8zuo8P9HouATp2
SXAMkjTglMBvE6F1EPNgESB3oO9XDiIPY3imGXNCDfkRQO974DqVz2nB9Tf4
mS6nZW9loOVPNFqayTRLo/hZ9OFjaL0SnFPJ3ryKfe70zHtADtmRg0sY64oA
PqfRej7MNivfIcuPKQciV4viHIN6EPRoHGWed4YPc/LZVyqcZyaz9nye0Xs/
7QFfA4ZDhyrtbJMpfwXle1TeR9lWZGlh+wrtOye09t7zJeqq2dbnhyOg7QrG
8UpgdXGfY2ivq33oAGj2VXHveeU3KJ/BL8H9XflaxtsvSP5BpZGJROkm+v06
db/DOqoKOI2Bf9uQu+vQcHuM5ahLNtvjy8Y/e0vb+c9vbHtB+eDo/kd5QZ7X
85jX2L8P7stpZw5zwcAgjwH5Gj5nDr8CHaeJ5uBQhDr/1Pks9d5Hh+VkHK9q
59jYmn91Dpoa+fqnsHM7v4R+iJOtFGUC9ezjnXnQvq72vND4If2eTX/DoFUt
YCr0+wr65ZI/Ofi0gCZP4+3/NG2AbfHvIncz29t3W/dDuicK7+c7X8Xv7MU7
SdLN4HsA6ARt1oFzXepJTnb8+om0vwCcwqHBd8hGM8bjwGTH4pf/lfyw/gr1
feUXuX1nWR853sJ/DTT/owM3K3ZIpM8HfgSiodUG6n1I/z7hvxWMsXPokA59
rO+k994t5lzlylk+gTqegks16n5Ke3UZO5eLeL0+t5Zz9hRLbd+6ypH2r1tC
Gy+BZxjv1Cjpe505fN6T0Tkfq1H/Lj7X0j0CcIK2fgAeyz9WMfSAx/CgZBr7
ui2Lc1wz6TKdB8XA+9WM3UHJto/RWc1gPu9gnZYTGA9uy8B7KRDC+KgP3i/z
/wH60Q45aA/ENnX+X93L6k62H58j2vl/xbL4FlnpDZ1e5PN+djgwhDreR6Za
A2+0tD/PC9kxhdv+s4viJUH7JxpDzf1ZpXTtOMbhFPqUo5b3RzrP1VnuzUo+
6xia7Dss3V/pTkoxT74r7LgnsnORvcujyvZp0JmDYo4FMk6G8V54hOVcMj6c
7/NY+z6E3v9oDtAZE3q6RkvH6Qou6xgE3WnzPmPwJ/YQqeDRTubGN5DJr3Rn
zBh9J8j3RJVzODarchRlob1i4Nchwc/rvaHoxBF5ne8yK3RcIlsw6s+pu22d
BfN8hn6+mw7XXqmsfXTkqyPf5qCU840z4D8QOAt0QI7WMPY/AR6xHg2G//Ur
OI6X7I1ka6S4SUt1H1/OcXEUH2dCyh2+7vJzpdyt6F5F8XaVW1g5hr+RPqWN
EbSbo4Tj8MhWO51sS/lvAvU8623/Pt0fKoZeJ+j+GniMoZ4IcKiPrNys5nO2
zO181vZKsv0l5CuRExpsD3O/l8j+lzHzSQ7v98a38v4vlDHTh7r39/IepE4u
560Vj8XrxQ2dMzZbO/txjqT+UdpDA1MyOJZq8ao+09N53mNkfiJ4bGYs5+f7
Ntr+gzH+ezN/jm/l79tSzmt1bivfvjHJ9u8bS7kG/ON4rpnuOBmD/TL6Xrl7
P98zv8E88QP9Ox/hca27Wo3te/Rhk9aJ0Gy/7qZCfAb6MbIeIpuVtJ4PNS/+
l3ccuT9RyDkONLf/nDK/vwoEygZFuk33K+l8Xy/b1F35bZ+6ir6vb+1YnrI/
kx2a8hLKtlp3qeO0pqT+bshdA8rljLvy0iXogrTw7Ax9ywtuKylb0tcPKSvL
lxDaV9Q6n3fG1bduHqexhC7fl8XnbunTW1aVV0I5JdZWd+xpxaDeCqSGZ+N5
rin1TKD8XGdaifYdlt9wKcp/eP41/vugte9SJib7PqU+8tkQWKw4Uk0ds6CY
bEJ4ZyQytzyLdbfOeKXLlR9b+aiUi+oO/Dgue60G3q/obiFbG++rtb+WXf1+
cJnE51Xox9cpz9L3IbR7Fr1Qnbk9Od6+K6FpHMtL9+G6F/+mje0E+9FeH2AR
dT+CZgv7+mxjMPWtly0gcjGTNnYhq29oXwM96wH34fE9YDK/PWDeq4deGQ5/
46Bxd+BD+rwDOMaznRnn7yAqw5CTKeAWr/tM3vktwOdbyk2gM65S8OAL7YXj
HcPpnWjHcVKsI8U8UkzjL5G7GrT7FNzrgFc2ZGAY708Bj1vIal2emQLd6tHm
m/zWJ6fvx6YmO+ZEN8ZrLDI/IcD7+lrw5b1gx/hWfO9A6pum86VK3pdqf9qg
gM8P5SOhc/YEeF0JHZYRWZ5Dm1+Dy0bqnC5dH+n4sRpD4W1t8zABuTwO9KGe
j7La5m0Gz87UfhR5P4ZMdIRXFdDTHyAHs/j9rWT7+iou3NvQZBz6aw865F5P
5+O4CM/yIKu5ytiXQz4dsbIB5fna6NQllOV4bzb1zIcGQ6HHbXiQk/XACHh8
Pb/tnubw/3ntD5mTAuBBLz7HyjaskO1xZYvbAtzm8lwl6FQXuuWl3z+0t724
fPeu1/O977AitikOA89awClo1Q4eXoJW3/e1L7RyxMjOaCx8H5PbeUW15/w3
JcZKQcb5rlj7jo5sbHvV213tOya/MeUW172l7i/P0s8g6o2F5gOZg37XflTx
xZC7NHUd9/4BMJtn0sj+B/k+TPu50HGftPQaXWt12cFrHSe7nybyF+5hP5Tz
ijVTzjYz8Y3tU/lcdo4h/6m9/9YQ7elLKPVcbme7QZ3D6Tzu9bS2e5TN49yq
3r/qPKUQsCG1bZtk1zQPuk6CDuOpe3ai43rfhOah8KsA/cwheea3qcDbPFuZ
dj4pbxtQ+c3Lf16x+DVPvZzTc9VXtF8aWThEuRo5PsfYvJLf93HKOaDcA7JL
/7aCbdPn8MxOZHZuOt/jzWrvu7z08Pspz7SDFw3z+ewfsU61mva/a2G5rgOt
zyCzY/mjLLjN17olhz+/39zfO6KTasW5L1Ph1Tva71LnN3HO1bGf5y9Bu5+A
AxH295DfR4sitrv8pLvvFvYhl8H0+RTQAJ4mQduBwLvUt0BnmFrH0eeXC/o8
bxe4NoKPu2n/nmxO4fVL8KpOjP2pFzWzzdTOQNtNrUUmFlFHsR6+G1Q8Bd0P
nipon6jTBZ1vqjVQhrVX3ZrWiT9S//J4++QppsUN2SJoL9fYd9e6w54HtFc8
E2i9LMD2UvIHnolcTK/hOEyyX52Tcuelu69Y+NVde1/tz8GtNnxJ7OX8icqd
qDyf0qlX6jtOiWxAdBaZ3NSx4HTPrTvus8xfw+jLgMz241fcknK83zTUvtQj
OtqGqHp22xFN7+25ZDa0Gt7DOYLkc/rRAPsfqp+L+f91ZKYI/I8D33B0Wyae
bQa+b6FX2jezLZVsqnT2Ip/b6bWdL1g2YhWRg9fg7RLqeQ9oh07tFmP7M9me
xVDPHXRQQqRtL4+W92/bofWPjIttrbxGTdfW61TZRMke6iBy+yzO88hrGZ3r
VZ81tzwA1zd6Oe5NGPV9gAwtTfb5q2LQyF8sGnkqxzj4hD4t47+GvL8o3vEt
5e8tX+8w5OV9/luuPRvQmt9ywseStNuHvpZDF3VljI3jt6plnG9ZvlHykfqj
o8+XFQvrhtYDQEV0wVD6+gF11WQd1I85qS30Ggz9oxlXVfjcQ37crK+/590v
KJ9q3QYvnsV4PaO1zF4git/KsV6o0MDn2RoH0sXz2tuXYbF8IdHb1cN81/QH
MhAFfr/1d1z5ldRVANwOoROjeLcjMKeKbT5k73GOd3bBkwfotHeQ6Ryya+vq
ebg283HWEvbr+JB6PtK6RGdSwGogLuY/18FU45m3FhW1X/diyiXa08U7x1tN
+nY7zv784xljUYyV7fCuOLLVCjqVreG9mvZsj0vaLyRM8bRo+xPJku5JkI1b
zLGnWGPdzmq5PcL7F3o6J94E+eJUdWxkybxkX3sp7ameMEbaRtrPS/5eA6H9
v6wvlhT02mlML9sTfpcyp0sHrtG5L3wsVcE2VtEpdlZtoPUB+reW/z/VPjbF
rqVsb+9lkmlzIfNRMjprHf9/g644AvSFPp8xTtbz2x3dpzNfNIQ3jYAtne1n
+DnluiaOKbG+ie3QZINWTvMV742v4hgBsqmTf8CjvPYHSc7quBVdoq1fpWc3
ag3cwfpUvmettdbSWQL66yH4ZwSHb3l+Mb8dpfyafgyG9oOApsDX0HcTNHu5
pH+X7CWDXzJ0+zPCfhOyDZVdqMayxvSASNuaz4J37zJGPmDsrQAK6b4NfCLA
tXSk7WVkN7Mp2blUNV43J1sWZzO/zKWfnyLz67Wfh7+NGX9fw6v8/B5Mm791
tL31JsbVZxlsa3+GPkyjb1OBLcmOY6sYtg11B6g4Z6x3TvHeBvj/uXRAO/tE
vQlUa2Yfn/INrD+kRwZST3v00B36fIsyHJ2xlfcaZbQNyFPkLCjWeAk/3f9u
RUd8wTPX8ttOSPHKFDvzF+lOcCnIM5Ho4ozgHJXesXWUo6ojOuT/RJ15nM7V
+//t+76MZezrWGbshmHsY2cMsxgzxmxmu0eWUn2kEpJSUipU2pO0EYUQhShb
hciulCSk1dLye7563d/H74/zOPfyXs65znWuc861vK5a7J/rwG9TGd//wc/r
ec4o2pMum30945o/Ay02SDei8yNybxJt+LWt6ZJY2e24yDr1OTTcyHWb4d21
zInzjPU7nRzfozifpyY637ewUyIkQ2Wb4d4vaONBSgpzNY651RkenQzv5rGW
51IuDbB+TXq2HWnGLdmZa+yS+ZWNDzWPeh1r3P/kI9bKOi/pvg7DF+vg/9HQ
ZFW0x1101tgrbqIX7S7TyjZq2arlU7m9ueOvFHtVPd5YNVrjWjEv/kwy3qD8
BeU3mAtNRofb/i47/BL+6xttX9aT0C4c/n8cOs3l//LMl7nlHY/yVzAmpSRj
+YHmDPUl9t1naO8e5vGdtGUV5QXG5+9yHlf5gTWCDlugyRXGZ1gLxxko3kB4
sb2bGjNWebTkp61cWqK94rYUa/V3tu0QskEI5zC0mbEOFccoPnyxiD+r3/qu
s2Nr5E5oW6+H8hNWTI5yujYfZh/gTbR9nHQJPPM6faypMyNtbgu9N/NfGv9t
oc5mPLOEAVDBOCzS79Tkmof5vxdtPi19vHiRtSW/nTEmhC8RyhyoTzkO7T+U
3INvv8yxP6zk/NzSlgXaB2gPoHmj/OLZlI9zjWu6Gfo/Q9kNP9Tn/wbx/vwq
dEqDt9sxpls1NxnTw8zXr2hPBLzUhzYUq+9YsLHw9GSecRb++pF+5zBOdzHW
21K8NzzCf0vg5S/j7af1eLj9tm5UMKbUtgKfrXSuEhZgEcakJDzaXnvwNOsC
PipwXKpiUu/guWOQxR/zWzz108ytniOcL125/FLq20ddeOnbC5wv/pH2ztuz
sL11fNL19UiwTnFoc+elEf7sQeEGV3ZdNtGfddbXXm3+BOtTpVeVP9fkYaZT
Odr8IPJ8B899KNZnIp2Hyg0O4nV185ljGbQ8zDr7BPOsA789CD2aM0+KMX5F
xxrDIAs+HyMfcerWvG8t60IG1+yUXgS+GCDeiHBOlqLjvYcZ0dX7mHfK247X
Evn2EnJ6D+3a29d5Qz4TboLOf30d1654kk8KbKvdVeD2CzdVfciHNvVSjOsu
XCzFglzi2dvT7U8pX8r74KHdXLu+peOX5NMwLKgfUt6PI92c1+ZB5FUz6j/l
C6SzNu8pCV3CmcdthUOmeHOtQ0Mcv/Iw3/foLA0N2iCPn0h1DM178Y6j6Sm7
M/fv5Zon2I+/DT0aIgOyeccUxfMqrggZkAcdejCHHy3utVcx7jPDjA+yifvv
go/ncO1bCdZv1w+zjnsf5Rv6MlT+BDznc+jwAfXb8G2M/CkUk5Rr/fxyrjsk
TAPGoE8H211yoFlbZMCS3rY3K55xUKSxnoXzLL4Sn33GdRHQe718D6oZP104
6sKM7isdH7/3Zh3bwVh+HzyHTq7iNUdxAMLBqDfYWBjXacP+AscI9uO6AwX2
HVeudOF2CSOoIW3/nN9fgiYpre2rMBAeaIPceUT6g/HmS/lay+e6GvLnZlPv
/+6D5o1kQxljvKsfwm136pjhfN2KbxvMWvEQY3FilHFMdtPHTdCnGGU3NJxf
yfsZ7WV2Uj8oXDXeuZ11eTp9uI1SYqxtkg+GOlefYjT3ZDhOs1iy9Szv0rYF
DayXlE7yAO8rLtsM1y1RDAL3/NTSPg3ybTgPDb+gD2eQJydGGP9UOKjb0zzf
lJNF868UPJZM/QJ0n9nFccGKD5afoeL4hJM+TNhU/FY1zTgKwvT5kmd3Y3yj
Kdt53j7uP1hgfFlhTZ3hvtOUQ/yWwv/JzNMe0Gkba0deCcfciU8OU0pA35Ja
03rb3ywK+bgAeXFEOgjGcQ20OgkPzIc234y0H/9O5sgD1GVCncNa8bVnaFcn
1oBo6bVZS+MY6694fhP4ZRFteTzOvu/90+0LLx9j+Rcrr9yRAuNeC/9a+tgK
mdbJfpjhs5v8aL4U/gf8HE95s4m/l8w1xrb8sxWnncWcXNzUsaNb6PNR6b8K
fGYP7e1zu+KNFXd8CFof47+LuT6z1RxqrEDhBJaHHuXGGG9SepS9lAk8O11Y
TfK3Zn69Qoli/G5D7lfh/ak9nQdDfknSfcg36c9U406cyvaZW7pb5X0/3NQ2
XfkUH+f3Fsi58cj1x3jOVWj0M2W2fMQYg68mel+r/a3iSKULEF6pdAND6fts
6PsRNJ3LnKoNbepSlNNGflmH4N9Y3ldK/hVFrZ+fEmcMnEPc9wt7kZRqxmVt
0cjYrPdyT3XhH6ofPOMAY7mGts3n9zXMgZMFxrH7lGfcRx/ehtZPxjvf2Viu
n8dzmnB/OXjoFNfmpBs36eIYYye9xLxpwDVL4Z/T0r+wLpyh/gNa3WScKo22
/5h8x05Bwx2KcWAsh0Hns8HrdE2vysZwGELbVkPj7dDmY0pcWeNmCjNzhrBv
oP2PzOX0Nt6jrmfufsNzJsca520cdOilGP04xyFq7clhXzcIfnm+mnOr1uK+
Z3jOWq4pSb8K5INHfQ/jVb26fbXfD/E69q3WJ+iShKx4gT3FfubKPkoY/R8v
H3HeMZJ338Y9dwi7h76Nyraf77kC5wrqleLcQYuYUy8hPwZCl2+aGodNeGyS
lX/neG0XxpnGY0Gu8Vmki+ij+EyeFTbaNnnlRn6cMTrK+F9JsJ+S/JXkG/pB
rrH2bw36fTeXn7f0G/Rrdy1jfV5LdUxsjHhKeOTc/0B/x0r8NdQ4zzNpz12U
Uzx/PuM/j2vTeMYmxbHVMxbAWXjke8kE+WQnO3/oeZ39kh33VW2kxzm+j9v3
AuU3aN4YmduI8kS8MY/X8vlT5ukBxq4zz/odHpzJnuV2aLx7vP0ImtPn8zm2
Ef5QYD+wC8yNUPnx0d4L4gHankW/nkz0uUtnLuEu/KRzOXvesbR/ufQZw42H
v455OFy6MsZzW47z1uq8qnycOse82cznCp0pGvDM55GLP/L/COnfoHE8v1/U
eUw2ZOrb6fMlrf8aF2h9W47/l55C+oqmsbYBS3/xFvWbnYypJWytx8c4/89l
nvt0C8e/jKV04TkxOu8Msi1FNpWl3Yxxqlh66SFDGecNiInL0rOk2c6T19X7
18lNHHM5h3nfo4ljYLYyBz5SvHdd+0HIH+JsQ+cPPdfTOkp9Vr2Yv0uXMc5M
y86uhTvTqZljj2Wjbca8HEg5wxy5lftugw5FMrwPv0JbfqZcLfDnusn+Lh2c
dHEvZNlHcmpr62t/KbAc70/fWrRyHK5s5bJrK1ZUtu3YYfblvEbZxth9CX9+
WMo5a9rRpwnwQUt4Iwu59Hlrx61uo03FxznfinJLXaBug/xLjXU+Z8Vithzu
eMzi0LoY5VedDUKN1S3M7unMm3rM42z2JXtznWdb+bblK5TFOwuHGotQ52/F
y+uMJUyJ++RPLD0+z/uLMU9nzc6k/IU8eDvNeOTCJT+Y7DxG/erbZ6huqn2I
fi+wjfiPAut3JwV1vPIDrFzdvoD6XznInqOUoV+lKTVoZ+oIxy2ugueGF7N+
sDZzYT5z8l7ocx/lowjrZ6Sn6dbHuUUu97Dd+oNE266FfSfcux3ljb11D+3M
h15/8t5Z7H9OKD6XZ71Oe/YqTosx3YNMuVbgvUou/W0tnTfPOsKzD3d3LhLl
1aiMXLjOdSXhnWlhjuW/UeB4/lnQaB/teLabsapjGc+vqfcXdZ5uYWD2Tgnm
ZIOW97NHHEXfH4c2MWmOAxS9pH8TzpNw8GvDu7UoLaDPTd4zlt83Qs9bkTEl
eN6zYY4FrgYtn6aexm9pvPOg8DK4fgtzZ00L45oIp17YJjprSIbovNEE3rur
hXGCZPeT/a+39PvI2v7suW9A7zfbOQZWek7ZamSjkr1GcROKmdD5YFg/+38p
5qm5+gydWsmXqYexSIXPcJDzwlvIqg8Yk/d5ZxPmyN38dizXfjXyrxGuy98F
xna5KlxwzcUa9pv4rK59J2ZDj3NcP6uZc2aUp2yEVmHB+B3F8WzXORJ6juSa
53nmZMYylTlQQJ//1ZmP+lDQT1v+2qsYzwd4dhzPeiTbuPWboh1HongS5dB4
hDadZZxWVgzqrXI8d4oEmFsRxtHYQsmHD3Mp7zG+j8AP71M3QA4U5bpilOPI
2KPlnP9gG+8cy763GHUAGdGHdrSlvEl7y8Y570Fx7ukx3rYoncNmdfFZTHgZ
wpF+jLoE9C/BdStp52r69HWYMVxaZ/vcrjP7StbvklzzGnUp6uvsmSfx7kLK
9q7+Ted+2WdOyQW4g7E/7ku3rBB+qfR2ipP9D6uH75mh1jFKJ1V7rHWD0hGW
5ln7mF8HKEcm2DdPe4J3mttGL1t9cjAuT/F5xeDT7rQxN8HxrvJVVlxm4hif
C3Q+UGyiMAGFB6iYjp+bOK7jYfpXBX6qSiktvTLvLhuwDVa50WWH7a34E+TF
gmSfC0YGzwZzkRO3jHdu1y3Mwxu0o6RiuphL65hTs6t7Ln1J6QjfVoL2VSjl
Ao4tU24rxZc9yHqwind1k38dPDQROZrQynFO8rmV7+338hmnPMx7J8cbz0hY
Rq8E7fbLB9qPahw8Nox2PMNzY5AhlXj3G12NMyt7l/JvCUND68N61pg20nlR
/uC6JOj3AXP07Ur2BXmugmv5g+jzJ8yHP6Dp43zew7U74bNP6P/dyJMf+P3C
GOOfCgdVPpglmN97GxtzQGfu+KbGoHqddq6sZ/xn5ZL8CZl3sZvXRcUQaJ28
TVh8yJzp1OWh11janyQ9OutyOG2PYj4/wLsq8F90Ccc3KbZJmEIV+a0PY5SG
fKjE5146+1AWQ99IxrEb9/XubLtq50TjCrUa4rgt7dvHdfXevRx0PlPHuVee
YnxPw7+V4O+hwr+BdjfG2u+nMu84OsGf5Quk76Gce+5kP16P+h747m7Ka7S7
Cv9Vpawp5frdUv48bYDPjTozat4/TCkf4zVCWC/CG09hLVmGvEmmXY/qrEy/
T5UwbUXX7kO8d9ce/hR9f6m997EftHfs/FLGsnaof38l+F9cY8eHKzZcPqiF
vDcwwPlwenDPmnDHhkwc5BjnHax5+dAuQDnSzPr5JVxbjb50TzauYwx0HkA5
18Q4wMLVEebdgqBslIzcQt/60JflzM2PK/l35fy4ZaKv0zVPwotnkZPpipkf
6Fw5bZjnO5EZOyjVeec2aLa9h3+Tj88XzL9/eF8xePol6FEMPqmf55hMxWOG
5vp7jYCxrS4iSxPbOB+G/OblM78X+k2tZUy2I+2cg/Fl/q/JPT3h902pzgU0
J8b5gIStvpV2hgQsLyQ3hGEo3bBkp/SeoxiXk3zvEGF/l+X0uXyocUR1n7BE
JaMknxRDrbgTxZ8Mz/7/clYyVvr8F2njO6E+t+v8rhyWY5A30ayJDZOMhyJc
lAL6URRZolwts+HhrtLTUfrJthRwbLti3PU5fIK/n4EW/Vo6t15N+rR3nHHg
5O+7izUsI8p7mFJx3sfMk5+T8ArhgRq0pzqlLe+ozTMv5BhT7MXa1oVKJ3o8
xPm0FbNwB33LQnZ+GO/vwsj4Dx8j1TFCit8XnkRdeOIqY/ACe4onhcfR2vEN
5RmLC7z7MG2uw/t2wKN3wKO3U54Z6DNMXc1F9ZX5s4z9RUimfRHkkzAZmlRP
Mv6ecPiE4Z/fPogjFW3//7e5ph731w/YJtmA+j1o8AFtmlPBPgf/ljFuovAT
hWOiPHA74Y2GAfsKNUky1t0BeGUkMiyWciDDmAu/ULbCCxnQbHA1n9l1Xn+X
0ihgjMrGAcdNnRvhOKqP4dPW3N8k4DiCLeMcS6B8H8r1IV3hEOGNMSY5ikuB
Hp/RvqYB6xA+ibEe4YDO2ez5WhW1f51iCJOYgwegfzOuHUQb5keZntMpkV19
3tZZW3px6cd/pyyjbc25Pq6+c0kpp9QxymjaOiHTeTe/YJ4llzROsnCAhYkU
y7Om89536M+XtOdXvtdt5n3rg/SpamuftxX7rLjnOOH8SN5Coxa87wBj0JI6
m/F8HNqO4VlhAefYahVwni3NsR3R1iu+nuLcFHu5blcfX6/7pvaznl06dulp
5EMhXwrtaXN4fw/GYBFrxGhomsT6HE4bGiLXWwfs7yRfp3Dm+DHoulBzs6Pz
vsg/vQ3XvNnTWKzCZFXuoOa0vzrvOTfKePLClZ/CuyZT7uxrjHfhu//KvFjM
PVWlY6NeDx3baq4GrH+XHn4vdImmjU+xnj5Zz7bCf4raXijsM2GA/lXUegfl
XJIeQn6R3zS2b+SBHK8NWhdkW1LukqeaOaZNcdEf8N/gEOOIRvDeibRpNPdk
UfeCrlUZk8GMbQ36/AvtX8H6uJ75MIx5u4G6HOP4pOLJkGXxjMEqZED0MONm
SW/1CH2ISDWviE8m9nLc6tYJ9sP5vpzzYZ3kWdsZ71/lTzjIebF2IAsPjbJP
jPxhxve0Xl+4f08oXpQ+Hc8zxqVspOFDvG4Ki1w45Hfw3hGsFSO7GRtEuCAr
qefwzAjo1ZHxrB1t/G/hgM9hv/wg32vBb8MHOsbpVXjjnHCkWF/ui3A+nKLw
wPPljZsqzNTpjH0nxrwCY3JHhvey0nO16On4pokNHeM0A759hzIEvrw2wHk5
rlHaBYwdJPn4DHTaCZ3/5b3vD7QPZOskYx3Jzr67nuPZFNcmf49oaLAuwvbp
7YxjHWi4gzqvt3M4vo/svAUZclD+O72M/yQcqAaU9rz3K8Xb83+/so5nV1z7
CuRVC/k8CWOhjGOyFMfZAvnxPGM4qafxC4RjMEIYC7xnBvMnjmc3hyZdoEMH
nr0oyF/iszz56/PbfcITinSeLuXrasG95yOcZ1dx0IqB3p3jHIDy11cewBfp
5/tc914XYzjqXKV9RxPG8Wv2Vp147gA+z+Q525l/MbQ/Vzon5EMic6eS5kR7
46/IP+14qvFiB9U2Zmw8+6NK2mcV8f55YZYx6OSvpzwoT+R5L1MV2valXqL1
lXGK4blzoN0QeGk29RO8b1OCfc7ugn9X0vadQfu+bPupzPmOle0DtAF+uIs+
3025tYVx5jsHjDUvHGxhYD/P3HpP8YP9jSsg34Qm2gv0COaGg9eOQqdN1KsZ
29VcV4n515T752cYZ08Ye6+McE4B+WTLH7uAdSyfMinc/oF7eNb/kCF7deaj
3RulV4M+XWjPxnjvwbUX39TX2CHR0OBnZMiKzs4newWahtPWCMrcXtatSa8m
PVt4Y+OvdeUZW+DFzrSxDHP0t2jjRv0a7Txqkfx/CZn6GnOwPc/ZKLsO9BpB
+3rz24ZQy/yL3B/G+3+hnxuRDwnD7d8lP69u/B/IMKbGvTDYPZR3mTudaVOD
ZNudlZtBORq6pRlvR1g7Pcs6frwipTvPiAo4llYxtYO6GtO7e459S5cxttOQ
V58LXyDRdnHpfqQDks2nR8B+T/J/EuaJ8E6Ekd63kfEQz3Vz3vZKlJ5cW4fn
LmUuTaeuzFg/BN2qNDXmWWpT454d4b8Bec7TIb2QdEKVOxqnURiNG+Dd6IDP
XTpz6RykM1CPPs5DeY1x+CLdPkKSF/IT6sX1NeD7QTyzbU1jdwvDW3avm+ON
gSmskl3Qfg31bNb7EH7/o5ZjJhZLV8fYVx/huJLeAWNZ/DjAeBbjaVsu7Tyk
mChoeJIxn1XOGHvCF1pN6cM9zzBefamTmTf3UfoF7PszOej/k5tlXXhmhv1m
5tSyH81bubZNyEYh3175+G6E1vnIit9oX14HYw8Ig0BYDuf7OWemcmcqP8yv
ZZ0j5kDw/CJ5ojx0p5Kci065KZSj4in6uErnXWTG60PsRy8M2VSuWUR5m7nz
WLax+zcg9w/R/7+RM/1Zw/pJTwB/9KdPH1V3XOxx2nGaekGGcyEpJ9J3jHUz
nnGsj3EIBknXUd76d+mgpY9XPIbiMp7r5TVHeN1jKR8N9hqs9bdab+fdHM04
v8TesAzPacV7buU5H8m3hDIgYJ1kTMB6O2HYSXcn38r/NbOv5YPMjU7Iq0fh
m60ZPoPp/CWfQ/kbflHdedkUux49yFj3so0rlm1gwP4WwnddBY2HaN9b1Xhn
wj0bR9nG2a0N7/kxy59b5/i76q18v1jdewvtMdqX83UXMpwLomec8S6W5DlO
UPuwyo2cE1Y+Hnp/DPJhEPXggO21t01wHE0GvPMVcvQo5VyO83AX8r4N9Okr
6hHVjSkqPNE1lYwhpHgNxW0M4VlZ3PMM82Ayc/cWynPQfyi/r1I8HrLxf7KL
ax4wlq2a2m9c/uPvwPNR7CcfZl7MY47MRbbtGui4F+G3/BbpOJgbwViYzrxn
D2M9qIPtxNto0yPIvfqKc4EvGzPmLeGVfsjdvp2cq+aHCOdLOiobOaUcPPUa
82HFGMdLaZ//HLJ4OeVFtYFnXmDe1qSfK+CpkKDuoE5QfyDfGfnQKCZeftDy
oRQObXfWiP6040n6Mjxg3yT5KOnzLe39fQly4hdk/dLxzg+5CP47D3/2RA7E
870xa80K5vqIgH1VFbdeEhlTgvIuwvzr5rZHjAyex3Uu71DHcazCXVJM5fWi
jqtUGcd9n+k5uY41UMxBScY0AB98zFxUXmnlFFNuMeUreDTZOQuUs0n5wJUX
XPv3xUHf4suyK/O8OPg/m/e9UcG2fenJL8bYdjuGdtWAL6tp7dAZnLlQNNV7
WvmVa197NNkxZ4o9k86xKW07DN325/n7/32WXlLfpw9xzIz0B2m5xrSpPcy4
wjqXClv4v3Me/BQbsP+E/Ci617SfgeK1RgWM9SnMz1u622dXvrvKDyLbfdRg
2+9HwutDoWMP+TANNj7ZPvp6gvok5SJlP/zcGlqWYUyTodXN9P/SzRVJzbT/
jXxvWshPBZl4Epl4Jzx7XGc7xmqB9jC09d4wY3wF0o3zVTvXOVWkD3mQz7UY
o9e5Zz9tWw7P/G+09zRHE537drr21/Dk7aE+R0ZQt6NMZEz/pn1xAZe/pKeQ
nwQ8fYhShWc8ILtoqv8X7mfpEcYBLVXSfgPyGVAuKOV9kxzVOeaJ4FnmEvUX
0G8186AI/29iDt3fy23Q+3We7dLZsformztvlfJXja1rH7kWOneG2XYsnaPs
x8rTKlzH0UEd4ek845YojvG14Dwdw+83kee/j7Yvo3wax9WzL3SZhvaHnjrR
ORmUm+EK8/wdaJfFvR3ggxnwZEfqgbShYZ5jEmcxZ7NZG9YoVp72xEtGUafm
GevjVC37UsunevUo6yQnhnqd+CTJ9iutG8ovJ9855ZgTxk5uB+d+1PV1g/co
LkX2gpvaW8MDf8C7p/KM+6WcrmvD7ecjXzD5+kiX+FxwDc4N7uv1XbkGlGfg
BP2ZPdR5ZHch1xJaOL+yMEfkf/YG94d0NDaC7JsJAeP8y65/oraxj2brLBfc
K4untHdWXrKtE+07KnxQ4YT+Xt3rkNYarTl65oH+tpkKO0xYMIk8/4kof9fn
ZPi+G21P0p4gxfjUwqbWGT0iy+d02VqEmy/by5CJzi39QIrz0CmeTfHeslHL
d0YxixmRjrsSlnFl2jW1tnHfSrOGFJ1g32zlPvlytHOhRDAWdTKdG7YtMqMQ
XvmSNs+iXbcyJ08xD9bAuy2TnG/rDXhlB22ha0WioHEkJUn63WCt7y+W8L5Y
cc63BH1SpFOSL532Q8JiXamYBPjoYZ4XgexpR5ld1LFF/Ssbh+Mi707PNhZ/
ZGXHnwrPRz6f+5rb7/PPeOPVCLdGPlBPVbUf1H7272Npz3zxTlnfIx/RSj3s
c1OZ/r8HfV+uYvuJ+P2LePO8fCsWye+xu/WE8nmoJJ8znlcXfgrn87f8NqW4
4zZlS5NN7Sr92tnCse2K949kbnzIf2k1nCtoAX1vGWv7uXK5KqdrR8anBNeM
k34YGkSxHrbp6t/031+0tzX8Eg3fXW9rPAdhOUQ3D/r4Zjjn9xPym+xgubQ4
WOt7t4Y+63ZvaNybv4oY+yaF95XjXT908F5lJmVze+fdnotcSuX//bHOwa3f
PkGejOe37zpZjyJ7wnTZXJG7e6H3hjbGspZvgnwUZjTznvC3dralyo5an/fV
lA8H/PrVaOeD/jTPOaHX1zLuxUX48TzjUEn+v+wr2jM2ydIRwhuz2H/cQ1nQ
2bkv5KOXFjA+lnCyloQ6X1Hpgc5fJL9v2QxkL/i4l/USr8qeMMgYi8JXlL5o
As9QTnVhTjelX9uCtb4Li1o6zq5p1hvPhsfiSxqDR7rK18cZ10Qxu4rdnT7U
uMPK/Sq7nT4Li1jfW4tPoMdFxv5olrEo03n39qaOX1Ls0j3QcEcdx15oTdI6
pDVIvqg6R2gOyTdVtbCNpW+bAs9Na2F7wknG4UoRj8ly5tjxId6Haw+uuAON
vXDxhX0UVt164GkjjekmbGRhJMufSX5NZygRY42pK2xdYaU+lmy81DBo2pj/
MmjbZ0Mt++fQnt3w02eUX6D1M8KnRe60yLOuTHqy51ir4mn7dGTRVJ71Om0s
QVuLh9km9HxQhu9Ncxyu4nEzpaMJxu5kSacrXaP0Xm0d1xAiXTJzPI2So707
dI5iDe1OSaLNV5CJr1EmjPYeVHFg5ZifJ+WXTqmt+EH52LZxvppp8MWj0CtX
az99rct/daL8XZ+FSafz4RHqJ+TXmu18sdqv3EOZorUB2i6BB5e18mfV0mf1
ga87Q++q0OQH+OsAbf++uPslm1VX7t3DOpnH527Mk3zqBdCiQPoJymusPc1p
U98sYwgLS/h3aF2c+XNN/vnQdizz4Cf45zuuOcbYz6FeBt+W4Z3xPYw1+i5z
rDDgWB/F/CiOoNRg67ql8x5OPz+DfsPkP4fcvwLPX6ZMChg3TPhhC+nrC7S3
cazjUoXpr3yQT/L832SbiTR+3EDOdKG0aRW/f8yzR9CWlcISaOk8Jtp/PdvL
/P4jz1kQ63PYeuj7JfzyvvyymENfwwuLqRvCV6/QllsCti0eZX9ypLd9I95v
bl+JfhWNNdWG6ycHdQTSD7RElkyhbgAdZiO/LiPz2rOWhlQ3rqgwRaOS7Bsn
vzjh+ulcvZ4ym7a1Y0wietqW8nWO7SkDeM5O6H4Xc3cLbV8OX2bynqcbeH8V
xlh8Rps+pfwMD96Z7jyMyseonITNGjov4brKxlIWprLyKm1RPAplB7TsCA88
ytgP475v6UsEfa3Lc5rRj425jn+5PdkxMI8pHoh14jFKAuO8npIYb2wu4XI9
VdQ24PPCe4EWxUsa01jYxsqZOW+C82Yu7e54v2kBF8UB9uW61zs417lynt+Z
6Bx2I6H3mo62c8jGsaWi834rV7VyTyl/tPJPlaK92yLtuyKd5omgXUL5zcrF
OMdZNutfFmVDV69JWpu2tLfNTPYp2al09pkJ/RbDH9/xOQsezeziPAm/tHSu
hKghtn/KDirfwkWUh+n7BOTcYvoSwxjdyjM/HGlsM+WFeTrOuWFk02gftGs0
p03dofXYTJ/7df6/QL+nKd4z0nhEJ5G5J4oYY0++zFNjvSe7jfsL4KPpwb3I
3hrem8jnSLrTMrSnEXvigVpj450fQ3kyRlGWpNhvoWWE90TCJdO+qBXXToT2
PwobBhosEn5Vvv3TYtoF87P28rlbcYv1GS+mcRGGssgO7r1d50H6MIhxvwca
zWvuOTE1w/PiFO2vAh/8y7Wr6G8fnhGV472ccFC1n7sj4FgwxYQJF1Trh2zU
LXOcOySntHNI6BnLkf11uXZUlrGcZEOTLU37MBX5Pms/Voa23Mlzy1I3gd7n
uD8Wnh4wxn7nvUbZd0M+HDXqGHNVeJLClZR8LjPeMvpXaNqCd44aaVvMoxNt
j9lM225FBv+Pa35XfAL9v6ukMcPq1nY+OMlCxT4qb/dg2pEkf8KWzh/VuoJz
uH1U3LhdDzDP10GzNRB2RsA52d+jnetS/Vm52fVdeyRhihyOdxzktLb2y5Xd
UDbDlxj/N2IdE6Jc6AXImpq0oRrvKUv7v2b8piR6P/scfUmJ9edZPfz9zjzz
XDdkzQj5hlLqxRgLVzi49/Xwfl57eeFs7qjsWJrBkY7pasy+7FKeMUqF43wK
fqhbyn5PaciwP2hLZehRgjE9Rl978v9dAedLFabLf7mKo+wj9z/F8iTYD3lm
wDhZksOSx+8NcAyD9FLCaZAdQVgNc3nmLQPchlmMe9R455gVDrrw0Pf2cG6I
//JC9DfubKcqxp5Vvgj9d3fAsUsZlHzo8yljHQotD+Q5nl5x9YqvF/ZrPr/d
VDxcwPhk6/j8JH2bzJj8CS1ehSc6M25zWllfIqxXYb4Kc0TxYsIgUZ6/Wlwf
QinV35iTUxt5rm/sZEywu7nmXun+WMua05/ytOk++jSNcf2B58wa7bhv+VQd
ruR8g8o7OEv7HfmryY97nGM6JyfYB3tAc/sJyF9gs/zS6ctKxulp6NgT+TcM
WnSGxnupu1APhLZvcP9W+nCgq309r45zndHQn4XLLd2jdJDC2o5NMmaf8BB4
7H/5ZebzXw3mYXdoG04/OzRyPupxwXh/5TL/RrhCA42/K52SYliEAaRz5Wbm
zYeUu1sYw3pmC8f/rRzqGEBhh4v/hJVbgXe9yHh8w/trtLXvlHyoNkHb31nP
mzH2v3AOqM71Zxinn7n/U/jzNDw7Sns15uzBVs4ZI5+LCfDP4HTHaN+ndSzV
eci/kDwLcb6gxBDrslJzrM8S9r5qfX9P+/6AbarSjSkvjs5YpWjXeGg1h/92
sIY9KtnXzmtGGHLrhSGe30uqeY6Hs6YPKeN88drPax8/N9d2dvlhvcJ8+rCi
1075Pb8gewC8uL2q/Xllv5lLuVbbGI4nkHGPSx/GexZT74Cf/qAd6awrC0c4
p7bs2U8hd6cwF26Hl5vBF+24/2Bdnzl1zjw+0XnSdebReWcdv5Uaar/sv+nf
ccUWB1yfDH6+wPuvS/ZC28VBnYZ0G8rpUCXXeR3S2U/Now/ft3H+GJ1DdAbR
Plc+WtrryvYibJW88o6vU5xdX655Ft4cwzOWN7Te74Z8mSPsDyV/qsHc+x50
6cZzQrOcz1557RtQl+7r/Yz2NU/VNea1/AYUY5aQZRxQxXQptktnbPluy4f7
NPSclGK5cD/lC/hzGnvxOtnGwp/U0Hj476d7DzqPa4aUYA2GFwdRvxRhnzD5
g91VxzgCyr2Ym+OznvIPzOcdJYRfNcp+ZRHl7Fum9bku7X+Vvc4DPHcn/NKx
hz9fyvT3QeHGdyigVOOGb2S/q24fF/m6zJdMDnWMl2K9pA8SftXcMNvTlUtD
Z5CF8onnvpm0+UGdKehjI+Zmc9q+sprPGDvhn6/4/1npI3Mcg6B1vR1j9Sa8
3Uc6Ntofyj1nI3ze11l/a3n7PQjb9eVo+2UL5/xt6sP8Hiv8rGqO0/uutrEU
+ld3DgXlUqjEWH/EGH1M+Zx2fQ0PTq3iz6pH865pqcYIFj5wMr89z1r3Qozj
gB7i+k3Mgaf53JWxXJrgz8uD34XdoXhuxXWnDDLmubDPFzNW3zJ/btDXn+TT
PdY4Z8pTrvwCM+DdY9C7TLTtprJFyg6pnF/CpRU+rez3u+G7Tyk9ocOXnGeX
9XXeNOVs/JR73oWeTyGbBtH2+5kXJXjWRdrzE+Uq19zOOl1vmHP+KPdPLPQY
w1jcxhg/JH017TjBe1bRx56JxupVnKt8jZ8pZ39jYYFqb5/U1Rgel4I4Ht15
XiKyrip83BT+W8Dz/oUOYbzzoQmOA5O98WHZVqobU/p0Z+NK30L7FtHmR6R7
ZvwrQqdoZO5TI7wuaH1YqDWY9fNR6map9hcKreR8LcrbkjnUOMXCK34HOoyt
6bjJ/oqHK+o5prwTB6rYB/Ud+bmx9jQob5uY/GPfTTdW43T6tyhgeSR+0/5O
PPdHsvWo0qc+xv9daMPjAcdCKg4yn73PY5G2v9asa/8p+VFJX6bYL+XLWcN6
vTjgXCQrKzufsfIaL4Fud3R0/K5yWkgvrbwUymutnMvCjS0Za/uWcBCGDzF+
j3B8pE8rhwzqwz29KQfD7b9TgbZXhO/ui7Yv0lf0uSmfn+WafYo/5LcX6xqT
aR3z40OeGTrQeah6w/MPMebpjEHRNPv4HeW5y5AbS+jj67R9aaT1+U8ErOOc
h3xsMczYCsI8Ed7Jz/L/hB/aIWMiKGvghYqM0Rza8INswrxjB7J2CXR9ivKk
xpdnfiyfAujyEvwxDHnwO++a3d35A4ZSboOvRtD+W6lDmUt1KU8FnCOgInz8
Be3d1d97NPn+KOeTcj8pp5pig/4e6/igJdwzM985sma3M/a7MOCLQNel/LcK
mi8b61yhkdy/jN+mQNtplCvQsD57pm/lww6dlzF3Lsb5s/LP6rvm+zhoOH6s
9Q4vF7cN+BVoegJePEXZy57uK2TkBsZ4AH0bofWop/OMPs21zwR8/igXPIOE
wfdHoOuzfH4LOk9m/iwPOJeB/Czk464YtaMZjlM71MDxmYrNVA4Q+ewIg1S6
bOm0D1NnjvG++WZrxxIEqtr+qnmg+SD81gRos5vnJFZ0nhztSZQr53nakDPe
Z98qwiTinkrUMxKMranc4Ov7Oobwn/7GFRa+8O3jfZ6pBm0S6e/zAZ91R+e7
nAyeeb9O9373CPV8rl8KfT+Afj8z9/sgc672sT+p/Eq/Raauhs7HhHXDPP2L
8/AZ7h072PpP6T6FOfMD/69iHl1nD/dCwJ9fDNjvTP5nm6DP8dH2Q3mxi/Mb
K8/xMp2jMx1rsCHaeIHaswvv4Y3utrnL9r4F+bOZcj/3dxpl7PTq8Hoz6PEW
/X+Jax6TTzB0yJD/FnOnP+XKYOfBVT7c81181u4WPG+/zD0dmD+vUGem+Vwg
TPq+Wr+Zl68G7C+zqbXz3Qt//micMej/6e249aPxxo9pCi1P0b5X6VcaY1WF
egzPrMM8eXuYc+r2o4/La9mmGTnAds086QGhacWW9ucpSHZsg+wUslF8y293
0vZGtLc5/0UhF1eIHsyBN+O8F9Oe7BfZpeD9AGv01gTPtfhWzqehHIfKbyiM
XmH1fs4cGx7teC+tWS/y22Dm/WsBz4+f9TzFAEHLC9onIqdWIzf+gZ77hOkp
GZ5oLMmV0s9Bhy60+XU+v8y8e4kyizkwm/Iv7VrF729Q3qR8Dp8vpv9roO84
6JRMeY1+viXdDm2tSXvO8qxkxdgrtpD3vEC7z+oMIn6L9rn4ba4vyvPfoZ4D
7R9jjGbC3y9X8nqmtWwr82oX86QLPNVppPForkK33yg7aWMavPU1c3wF+77V
WncizY/iy5eZ4/9C76O8M4brBogXJ9hWJpvZzEyvifNCvS7eVsrtX6M1Gb7c
XNmyXpgiwhZRfNAg2jmQsjDHfpDyh5xOXaWd49wV716HtfM87/2znHNyKzd3
X2FQ0f7HeOZexundgNtbkOuzoM6E8pF6iDYtoAxiPtQc7rNLGuWBCvZHkS9K
Nd5VlVLA70UZ113Is2LUHen7Wp7VSvabEs5xH8NcrkwfK8kerLMXbW8ueyT1
FNr1Orx3N7KmIryxjnvLUyek2xdPY1KLPtce4djO92hrSd4zBnkVYHwPwasr
pMsMs+++/PYXM6f+pz1Ab/uuKn9pNPemQffxsY597co9b9C2ziXt718cHi/a
wzjBws5v3s15uZSf671E55RTbjnlxs1nDKcwN5KDNiDlNxR2q/YM1SlNkp33
UP/dTrkFuV+mmLE0Kwx17NuL4bZzdm1k/M1NPXyuuh70oWgJ7T5BXi7Nt5+t
/G33BtcdrT9Lmc9PQacGGfbJlD+mcBtvVHGOcGF/y19Pfns1ixmDqy5t2y7b
EX1eybNvpX5PZ1zK8CzXz47154PQpBP96JIc9PMe6vNtCu04r7hRyqBk7y9f
GmM/ZOnN34HGJ5BDJ4UPAJ1i4ozL+yJ9uyPdGMrCTz7MfH2HObWOPVVdZNZI
+tJL8SrI9pETvT/6Wb4E0P0kY9Mj3TYh+R28Cd2mM//v4j/FSyrOUzGTwt0T
/t74UGMKTqpjfNf1XLOLe+p38+c5Kf4u34kXaf/ZOOeOVh5gYZg+xhxK0h68
oc8p2fw+r40x687AH7eONkaYcBiExyC/DO1TN1CWMR73Mn4PMya/QN8fGccO
8uFG1hxF5twiWyp9eRJ+fIJyifW1g85ZjM9ryPnhrDO7GIP7mUdtWjgfq/IU
K8foxoDzjbeAZqsG+zfpdfW7fABk/5euV7lxlT9V+XE/4L/LrFObqDdL3ks+
BpxPZSv1NspHAWNgCf/qR3joLfixIfwdz/d4nvex1oBc40EpX2mJPsb8FPbn
xgrGZRU+69bgu/RO5QqfXd/5wiciC7YHjFP3cqTxPoT10Y2x2szcypCfAHJq
DDy1tZxzwV9GLvwLT3dVnBltGUI9WnZSnZMDrj8JflY+tarc++hIn7Mz4cuS
HY2NI1wc+ZX9iGzelGkbuHJaKLeFcpm8n2wcbOFhywYt+3OA5zRg3n9HX1Lh
t+G0tTj3loee8fR/D98/o+ziWemSR6wPzylWEtmzr5uxtgoVp8V70vnvBeRt
RkXbN57rauy4R6HxxmHWS+osdTdj3wx5dYU15r6+ziEpvCXhLq1F1pWjrbWR
o93yjW9ylfaUG+6cqsqn2rWt8Ug286x61L24fw+03S29TaZzGynHUQ/6/WnA
WPCq9T2a8k6WY6u0ly3G+M6m7Z9wXwjtmol8vocyi9/ayTbFvauYk9f47U/K
Z9LPCEegmOPDLiCbxvZ325SLTTkHpvHciox9EWg7SPGkPGMP4/t2quO/3kk1
ntUweHd9gv3x5ItXinpIlnMzCO9Re+TpXe3nLgxk4R+XHWys2arjjDerON7L
lHsTbCeXvVxxKsoBo1xr0gXpHuXKKUbfd2o/Ir9Wxd8wn/cEPKZa67XO5yNT
z/Gsc4zHBGRLpGINZN/Itk+BfAsaML+TkHnJlLfynPd5ZwPnfmZYi7zBte+W
d362gdHO0abcPMPls0DffmxpHWfTKvZ7+pJ+9OE9HSd4b7lXc58xfIo+XpGd
T+sR713D+Wr5MGPFZA1xDILir4QbvI977oVeZaR7hI7RtL8jczWkr+1NDeGR
26HTfq5bWtqyQzJE8uQu6jjFBQ+2b4D8AipIP8R8Pos8K9fB8d+fj3AM+LSe
jrtTzN0Bfj/FXC3k+eV5RjHFOTO/WkPnz5FzrdraN0U+KorFmJTlPMvCQKzH
+rIdGZDQ3rkgZUsUxrjiQhVT0UF4QTxjYWv7b2xVLAl93EL9Oc/6QrIH2n4Z
cM4p5Z46GLCtVDiBVctYl3eWuTyLZ1SmXfe0dl4T5TfpB43DGI+5ijOn/oF1
6zzl01rex/6d671sEdr6hvwjeeY8eOM3+ns+y3lI5Gf8JG09xHtDqUvAC2mU
u+HxusytG9D/k2TH81WAjnnMi3z4rW+6/fVk55SflPyldskPjDEqwzWv0vYH
NDdZ13ZC77bQYRvzsSPr0TieXx66VSznWOuMTOe82U9bDkGPl2JMD9FlNjwX
4PcoyvdNjF/Sp6YxTIQdvJS2TZe/E7SJ116D/t+EPz9Atm2iJJbw3iFJfNDS
eaqlu1oLfYowj+7qax/Nei3ts/ko8y4ry7YH2ZPWxti+9A3v2Ma8HAINV8OX
t0Pv5rKxwGuv06/3WdMfGe/81Ju458ME54lUjkjhCFwtYXt+Km16m+dzy3+y
XDL9PcpW5saP8M23WY7PjaVUS3URbl0Y/HqJ/yOQsffKt72I/SNG5ruWv4Q+
ywdcvuCJNe1HoX1hZAXrTubwnEGNjecnXL9q9LcsbZrLXmteKceyKKZFcZu3
wrtR0PJwwDmqJZslo/W5f6a//6Zxo51f8fka7dnPXPkB3riPeZbM3FhBm+pB
n1BKz7HGCH6unbGjn4PX59KJeeWcI35gsm0cx+n/Zb6PaWHfRfktPh1r/6sO
rOFr5Q/B2AVa+z3L4bEX4LcpFWzHkW/gF3leB8Rj4jXhHAnv6Dz1Wvjvpx72
bSvG/Y+yLl2ibf8bZ38U+aLs454XKHtVEh0jdITSic/HtIa0cFyO4nNukV82
PPkbv9Wgfc1b+OzeooXP+49THoIuTycZc7w1Z/hr0D4JebuK/VUF5snzmkfw
Xz6y9BXZTlv6/Kxz9Hr2BguQjzJ0KQY0mjlQa4ixhd6CBvUZ5ybIx5Pw6wlK
SD/Pi2XJnhuPQINf6NO/I5yDqEusfdWFHSo9s/K+fCnZzbvG0L/7oOd3ucYN
UMzwnhHGMhZ+h3A8jlJKBbEm5Nv9B21pLdkCfxYMsH1Ltq0hirfjuV3qOh5E
vpeKCYmS/zN0i85yTp6HGLcYPv8RZvvwN8iKP5GPJVifv4bPqw9yzq/rfZyD
XbnYu8U618OWPOd7mMI78nnG67z7cdrTi/d/zfvuoB+3yaeoun3TZNM6xu9d
kR1lkEvH+dw/xzZ1YbdvpH5CBRpnxDi31aosY3F0q2A8jj8Uo8Rv0+Hvj5EB
e7hmao7z19SkzzUaOhamcLjjYU7wjsbsDzvIZ2SAMU7XUr8bZT77mfm3pYzz
PM1AFvWCF1+hr69FmYai3yDqkwH7ZW2aYExjrWfCNZkSjLudyvvG09/vZGPk
XXXgt++RZVXyvDc8F9wfih7poabJKZ5xmjKovD8fTvD3iNrOr1k31Dng5cd1
RuPXznl1lV9XNvazAdvZZ2vvDm99Q1u+FNZVK8ePKa56nuIIkHnXejoXpOJq
hIEp/MsdYx3L+HdLxzMuo/5eWHEB42hJDyIdiPzL5Gc2hM9PKRZOdt4xzg2q
vKCNePa3/P8pMqVEf++DpPc4wH/DOzl3UX/GvAG891Hef2no/9Mzyr9GeseB
tKOrYt7yjccvfHPFDYUk2PY0CDm+gfFYLx87xva2BO8RX6ZdJeHPV5s6p0gE
a9gynlEQYqxGYTbuKGU/TuXLvtnHcqRxhvEjP4t2PMytivtjDRqAHIuDx84F
/Pyp450/tNcE5xCNKG989hUhjgVUTKBywKreVsef28IHk+WDDq26VvR/ysWt
WrGD+vxdwLZ82fFPN/N3fc7m/4dow2/IszI8Yz//HYpwvqLvA85f9B8eW6R9
zxp2MkZJaKo/C6tE3+WLI7+f83yuJOwinWkYg9dpT4GwBrs5zjEn17GOjSON
+9Qr2OYuwXafTbLeVfrXCozlROb/UEo7tVkxmc3s7yu/3++lV5N/CHx5iFKK
9k/hPT2aWuZtYQxPhjhHseJzFadbiflZkdKB0gJ6JCEvkykDw5378F7JXsY0
JsT2jFeQ4y+3dW7CXd2MWVSSdSlyrDGMhF+keGTFIv/Ty36f8v8UvvWqfOuW
pGParDgb9lLvJNnX/TvmVGqY9zna43xH2QdP3ElDQ6lXIKNXUg7T3yk84zK0
+kFnJcqPlIuSdeUt4/+hJNC2bfKlaerPHw3wd8U2Cftatp+fuKcq/+fyrt28
P4txyqR8Jh8XaHRJ+jrpVyo7J8Mlrl8CHZ4KMSb7z/FuR6eSxphfivy6HPDv
wp2WD6VwqIXjXo33ZrM+rIKep6sZe/Qw8nMXNNrFWB9hjfqyrnNdrUxxzjbl
bhN2wtxuxsidQz2R514J+D3J8PrP1Fcp7aHjbcJhbOt8EMoFMUn+b6z3DyBT
DsoOwTtWUhrmO55Vvh+KaV0KPX/mnUuo55Y0fk4y8/ID/j8vnTDPP5HttfV9
7v0HWfur9CdVjL+1rKZ9x5cwTybq/CbfHeRKDa69IR8a+OZm3aAvZqj9LJfq
XNHGefam97Y+6lvuW0Y9nvdUzfA55Cf5JjAWXya4jS9Cy0WUdObbK/BLD+ZQ
G9qWLbzgKrYByBbwe1fzlXhKcRR7k4wL+xvtfou58QzjUBHeenyo8Rz3D7Zf
jXxqhGV3caQxc4Sdo72M9jQ7wp2/6Bz/3Z/nuA9hbR2lhDHO1aFLTUqdes7j
rHzOzeCtP5jfTZsY71X5nzU265gnx1vbhrgg3WM8AD7rQh/Px9kmvkD6IeRl
9wHGO1EuFuWknB3cS2/s7Rxuf9Z3HrevocsUeHByGctx6Usk1zODfrnyz62P
HMhhTNPlc0RfrzJnNkGr16BnCjRApPyHB1B2kPO0HuO38qyFFSlpPPdP+h4i
/EPGZh/XfB7h+S0/79+hU4kQ52/VmV2Yw8L6/pf3fcDvP8BTm6gHw8N38d4t
pe2/9sgw43gpLlTX/REwNtc+eKc1dH2NfdAe2tqN/29y3X76/6f2l6wp16hf
o6//o/+JPK90e+sfelS2DkI4qMJAHUjb97Me1WO+H2hsnHfhvT/QOrgXLOq9
oXwX5bf4VJTjNUoip/bQjrXQOEl2NtnEmL9zc+wjIZ+ONYzZder9iY65U+zd
QubEIejUGz5L4rqNvKMfpRHPbsr7v6lg+2WLTo5jbQkdBsJHCfQhsod9ZmpX
Na7mhhxja/Zjbu6Srlr614bWo5WENzb3d57O/hP8m/Rqxfn9RsC+aqf7mx96
07bDtPW5DPtvyI9D+yXtlWIp51jbFtPeb6jb9nfcThvotSzO2E2/UW6tZ5ky
NcV4rdKNSEeSEvQLqAL/34Bm9zHHHpP+polxIoUXeQdt6FLSOMDCBFat79I1
TutmfaPyot7k+wM8e+dI+23Ih+4vreEB+x0Jl7RJe2OTDmUeDKfsZ4yyYmxz
lb31cb6fhSa9qEMbei+rfWw+9K3POMWPc87MPtA9hncXMNZ/DHV8eQPGfjzt
bcI82E8fYhjPAZQxjMdG6UB7O+/k4IrOPbkdnrk73fq24dxXJdX+Gd25phL9
mDvY5x6df5RvKYpzz7qh5qf369unQbi2wsb6SHaYUP++hLa8R72VubCNckeM
bQ+KtZItQriki+njq9LTd7D9dXWw6LPsRDGMa03e+VmK/cnlS34f9NsUaaxF
6eNbw09tKT9EWe+h/JHSffRKc/7v+5nDH9HGu3jPx9QpzKU20O/zvvallx/9
b8ih7ETnBb5R0/kI5Lcqf1HpG9dkWueozx9n+rswE9UOtUF42EXFt5QT7ey7
PpU2Tef9TzOPBo+1zv3HCdbBf4C82Uzp2tO4jvIZke/IPwHHsysW5ft2XgOk
/9kF7VfTlmp1/F2//xjlM4Tyolyd6Dw/skM9m2W9ojCKJ+U5B4TyPxSlhEUY
q25hJ/uXTxhou2837nmRPr2MXPxXOjL5GPPOHyZ4P3xNflD09WvGfM9w5+P5
Bd6bn2YcN/nSyKdGcWVbWjrOTP6G8jv8D9unv3EshWeZxTP/oc9dKTtpUwPK
HciFrrwjktIMXjnb0rGVirH8Psq+x/JBHs7Yz0Y2jOjndVM6Pq2dVYL2a2EB
KT9QYozzBf0w3H5P3w837suaHGO/PMO8rsY416hoHLtP4emT1B3h99W861RP
KWeYL/ShcJh9vN9nPNZTzoz3eU9nvbK0/UPma3Hm0dM881nKHMb6epb9CIWv
doj7p3FdX/mbal1gDIaMcYyQYoXky5MU6xy1ylWr/DaKpVQc5RL6f0VnRfaE
TWs6R5VyVTWCl2ogYz9Gtr3CWtSS90yPdJxOBG0JpzSHxxPgo4Fc/wf0LyYb
KN9r6gxL+4rSvxHI8d1ce2tx579QPh3l1Rnd2rgNij3+J9O+SvJT+r+YPcXr
yefojzb+LY6xGCw/Cmj/F/KqFDLvb+qp4f5Pv6voGp3FlM9b+GXCLhOe0cPs
Exb0sU1MsaWyixUrtC1Kvz0HrcZA+zuqOcZc8eXCE9O6mVTaa+cVxqFeum1P
ilGWve1e6HGCtr7CmKwYa1kqOVqnoXHtpeNRTjrtkYSRoO/Ct7wliHEpvMcb
DY35WJz21EqwP/Db0OQtSiDRe23tuefTlmOUZzNsC5sPnzzE2n9cPr48q3yq
/U/DKfOgy/2U7GCMhWItlGO8FXxxMN85KpMn2r53Gv6JSnY+8BCua6XYI2Ek
1fU+5jRn+3aMcQL3J8MPkQnO1VmC9i7rbCzct+GVzeHO16hcjcJcLVlo3NXh
zX1OElZSlQb2x4wYZZwA5aGTv7dy4v5F227KZwIej6effyMz8xmPpvSxSTHn
3e1BW1Y0NPazMD6F9al4VMWlduH/kcmWNYpbP5DkfCbSOQrXV7jgwvb9k3vP
ag3j2RPqOYYgvZ6xIRQnKawIjYF8szUm8n35g7lyL/VjPGt5bc87fVateH75
nsyMc+7f7RoDfivFvaULnds8oaXlpmz58fWd11D5DWfQ1wTmQjzlIONRh/43
4z3VeNad8M865vPt1Bfhm+S2xhC50sbYQXX5fL20dYXSEyrP5mM9nGvz1oqO
KVI8UfuKjqcIkZ8e75lHX8tT74Hmk5kbszN8Jv17tHGycgc6NkZxMWUK7W8s
v+NfePav8Mcurq/OfuZT6RCK2o6tdUVrypeM6w/Q/XPqt3Md56i4wM+Qmy3q
OC/CYsZsK898op/jqZoyjoug7/g2zvsdxed9yKoD8sVnX3GWPqTx7rKF3gut
zvZ+qBzfS9H38tST+P4Z839FltdtrZt/RDiuLa2nY9uUzzpC64xipeDDUvBC
ceZOkxTvD5XD/cNyzhMpu20b1pFXad+MNOPAX65lLPhI+tmX//uUsz1Kdqlp
oyxHZHeXXLkR6Zyv0/htJHubCvy2m+8rZMtEDrzSyHniFBcvrKQf4cUl8G59
npfIOP7AuDzd3xgByh+TUmC90iz5mVP3YN6dZcwfZzy+gabdeXbJqo4DXsH7
Khbaj1L+lAF4qGSacxfeTxlOH4bJNi5fQu5ZSjkufy3OP73h/UbQ7Rx9q8Qz
Hu5unMta+ca6PAfdMvm+lbaeGOT8KQu7GrtvC+X9TH8Whp++TwrG4ismvzLP
q4jcPFTSuWyU01S5/KRsUw4UYVHdSXtHI9fiKHfz7gXwyEOUfYpL5JqtlCeh
XWX6toI5cSu/H2Xsj3VzLgjhS85Ffn0rPz7G5KMkx28pFuyLic6/m8E6M5zr
1/D+n6r7PCWcsJ7djBX2P+3NoMlt+bYLbmO8SyBf6tCHg8Lnht7taVtrxu5Y
Jfuwnw36scvXrVsr+77pd/m4j0l3zvW/GaMbGdYz/dvduqat9KU6Y/NhI+/J
tR/XWjUfmfloJevcGgjbmHFvSP1wFeP6PaQ9CfSsShkzxJ/31fJ36UelJ42s
4ry9rzLOLXjuPwMdL/b3QOez1Rgol9AJ+vk+fVxPmSp9OeVUfeOwCo9VudXa
wx+b6O9D2dbjC2tOev2FyK8c1vu7xzg3iXKUnBvt3M3K29y8wH7Y2u83gu75
0LAG+6A86rZRtjOt1rmul/HRhI2mfGvKuyYMyCuJtrnI9tI21fnnFDcdL10E
vDiJZ55gTv/FWv8PZTT0r8VerGpv+6nLX303pSr9n877KkKb8CrGKNAeUngu
TyJHn2hrv36dTU9WMwbOJ52NgzO6lf0Gu6Y6F/vvJczDD/J7fdaodbJP0PaG
wmqEhnuhxRvQNoT525sx7EXZ0djx1Yqz7jLIdjr5HMjfQH5l0vtN4/sP8GAN
ePoCdTXG8iz83Jn+reM9J2jj+4r5nuj4BcUxyOdYMWLae74Kv93gWfX5XruP
15wkysOhwbxc1Pu03stvkNKdPl7juuoKkOpj303hGC1BDlbn3d8xDkXyHCt+
lNKeZ5xLdazn8hGOvxLe/la+f0g5LB8Z5suj0L0IbTmT57zTyj8tm4ZsG8rj
vosxa4wMvI+2vc/c/xuaf8r97cOce6ZDsB7e2J+Vp0fxQYoTqpHpnN+yOVZN
cP7oPvT9N677hXdfpfzOPJjOex7M9965Xm3vn49D1zRomd7F7Zkw2HYW+WvK
b1P5vz+lbbspM6sae08YfMIU2sjz3+dZ66njoNUJ6LyYdq8Ms8zsDq0+oQ+3
wKe7qFOgb3t+y0TeLOTZy6DB092NPQJbFKnPu5tP9P5T60XbPs7lfYR31uB7
PfaSNQv9uf5Yf+8elM+S08IDln/CIUrzks6xIvuG8Hmm86zV1P3kI0kJKXRO
t4/K2+9Pe0HF316mjZNGGeNG+DYlaV+tQvshKR76jDAVqjre8Blk2LPpjktS
TJLwquS38yW0/wyZ/Cj9HATdEsrZ56bsePvgXMwxFkkaYzWYPk/kXV3hu4LK
jmfQuVT4L/OzvPY/1MJ2wPBE59h9gDXuG3j/ecbpa9r7WZZzXin31dR6livy
n5VeYTTr0JAcx0heY19ymMl9K3JsdVvPP83D5fS7O3O0Br9fZS4PLHC837ng
uUBr+Mz6zjO3iOcfrGTdtvKcKM9wqwTnGpbfovwX5RNcijEsSalUxfiQveob
I1L5gZQn6Hnm9qFox5afGOa9sWSL9sfC3tw91Pib8bS3tvZb1HUK7Xesd+iz
fJH1vX0786OwrrT2ZSR4/aurvTa8N481ZXEb7wO1H/yXubAR2m1gjXmW8c+H
Ptd6Ozej9PvS7cvWKp3fEeoRvKcPdB6pvddI56BoxnvWRhpv6UmeeyHN60t/
xqg3v/8p/44RthEOLG874VpoUZHrT1W0TiW00HoVyTnZOfr3s4+n4scvUdcr
tK1wanN/3pbn7/Xh63P0q0Efn291ztWY/lnXuLrxyc6r8hnPq1/oXE/KXVic
8ZjDs36r5TiSKfnOLTi3ouO2tK9KpaxEXkxkDn8kW25z57f5vzw3DQqd6+aO
kbYnz1AMFPzZF9pcqGyda2R1610H5DgfRqvguaZurjHQ1qZ6/moeS74pr5Zk
22XG/HX4o1iOdVAFI62HKsv1dw8yFqbyOSgmXXgmsl10TbL9omGhc7I8HGvM
yEaFxoWoQl8uUJYx9/7qb1tfbnPjNgmDVpjHyr0bIv9h5nId+tKrwNhQFeBN
4dD1YCwe53tF6DeZ7390cC4d5dRRbL9i/BNo98MTjBW6Kd/5KRrThiaU9fDc
eWE0UJ/lOe9C+4Pw2EDWj9PM4w0NHPclrM5E7f25pxmlOeVdxuAp9v616tg+
F9Lb9jrN/0uKf6EeT1uyoM1nyMCv5HtCGcI1bw03Pl0UfFAj2zhgwgM7xftj
oGd5xuMrxuNEuG1KD3e1D1L3Oo47LVbTMU06x/zJb+t7OYa0A+tNzxzjwQsX
PkJ7Hp7XhnHaIkyUWPuvyHfl+Qxjzkp//Jz8iaHDu0Pt/7M7wv5NvTiLHIGP
e/c0H6eUtKzSWqs1d1WkMcWELfY619+kP12YU9d7++x7r+z+Db1n037t5mjr
zxXr9xztDa9nvKEIrm+Xa/+PFoW2G8k+K2wS+Ut8XNM+E3sZmxKsFZ81cQxO
jQLHxm7gva/w7Gu0+6t0x8koRkb4JHlBjJLT8MBmntGy0PY22fRkf/sZOr9D
265Sz5B+ljbdbGjMF+mgpIs6yfPe5ZpT+cYGFk7YB9AhnvG9yrvDeOZoaHM9
3vl8lfNoWDHnRJcuSTqlWXxvRF2MdrXi+uvl7e99g3ot68Y17c2oByGvxtDv
IQXGYo1FVu3v61yQ67o4H2RZxvg2+tkf+raTjy/r3t5RjmGQn0/CRNuhZY/+
Nd15k0pq3g43hu2FssaxVQ4a5fyJzDJ2onIhdlF8GH1qyhw8z7hu5/eooI4x
g7GbicyeUM0YgTmKxalrjH5h9c+jvoM+H2Xt/Cq490mpYN8r6baEs1OEd19T
/Bd9TGzlz8IA1Pf3s51XSTmVtG5oP3OW0rrQfpTyLZwmOybr0QXKeMoiaJPW
2b4V8rEI5/6fYhzbKyy6y+XtMyF/CelvFLcvHY7O9vKF3sO4l2cOtOEdHbJc
H+/rz8IMLEtbuna2z2HbQueXFN6RsI4eYPxuNvHapDUqnP8LoUl97tlN/b3s
U4z/OernkF/LKaO4/7za1tl4C5/TvgjuC4fuKYxP6nDnWDjNeE6CnrOYu88g
a8/R3uuKKZ9gzNh46DqPe27pb8wH4T3UUFzkaPvty39/PuP2EGvfJ8zFTHg5
m3KJ+VYfubWivP2gq0Ob2tAtKdF5Ci73MT7VpUbGeS4OT7SjfcXpZ8Msf1a8
ueLOtRYnNLHv08yU/0hUZGKKfZvvGmw/5/Zcn8r7OxR63iv2T3F/xZhHRSNs
O5Z9Tba1R2sa50z5U25Pd/4T5UFRnvC6fC7PPO5Y6H2W9ltboUEK73+E75mJ
jjHpjoz9fYDz1PRibKMpm9sZE3IK/LNT53v5tEKXBSON7/Y+ciyqt3NNPpNp
m8jyTraLdOJ9w5BLnaknDHOuTeXZVAyJYkleov48xzFfQ7ReDPV5SueqLlor
uPdSf+f22cg+47tk5+QVHmJN+vwT8+pH5NAFSjPo8k2W7eGyPXYtNOanch4f
7ewcD8IbWEj5jfIQdHqPdfqf6s53prysynn2UR37z0Ryf8ds+/1HDvK+sWUw
lkHYqg9mGV9V8VeKwypGaUs7i46wL+Ei6NmaenE76x6kg1AO5Qk5PnsIp3Qz
a+eH3a1/CoX2F2VHh8+j5bMkvIwqzvH1LWUY7+7KfNgRaax3+QfeLOFzoGRs
DLR9ZZx18180tX5eWIuKq19M+ZB5daqU8T260beSjFn3QudXiip0jiXpeJRL
Unoe6ZZfTrF+WbGiwqypAV+tCL53N3MmFHldv6Rx+9ZzzRLGbT3y6jB7l8fg
j0UjjUmROtEYFfLHky/eYuoehY7PVpy2Po/N83f5+UmPJXuRsEeEO7KJ3/5i
brUsb19D9VV91ppYEXm1QGsh7zrY2PG6itWVblFnjWFN7BM+Kt9+4Zv5niQ5
keW9l/ZgwiIvwfu60acDIy2DJIvkD6KYZcWzKZatJ+3sz/i8DF/Mht/2Ib/3
UlL6eK2Mgi75ir2K8Dmvcg9jOIZDgy4TjKN3hNKquuXE4M62IStuV74pd8EX
TVgXIymBXsa/CGllvdXGEMeJPVfKOLHrcnyW0JliBmNZkXF9RTKcNs+ifyHM
s2fGO99jm5bO+Xgh3bFa5ZC3q0bbpjpuomvZWPW5E+1/NtU635wc6/dW0+c0
ZFp/eDw81jyoXAPiQ/mbKlef8vQJu1u43S9QLvHOCGRrB9nweV57+vr6GPs+
yL9B+NdaQzS/huTZn/R2nYvgp4fC7R9cDzrn8Yztkc7DIvub7HCNc+x3OZz3
TIKO++nnjT7e5zzDuIVwTQn6GsM8XVPg/FnCMloKn7Zm/Ovyfz/pFKBRs072
PZAPQkXoHc0YXxpvm0w9nhlKuaWXcxsrr3Esvx/WGTM5iI+c4ZyC0u9NaWUd
n+yFxaH3WwXGbV3Vxdit8hEe2tH4eP+Xv0q2TeUEk8zNzHKMpWIth0oXAr2T
4KUk2lmL997G2vFzT8cVz2Ss8nKdF0h4n9J9KTePcvQ0phRFplUqZ8yGsCC/
ie9u8o4faWMv+jktz7YA2QSUj0fxpYotlW+Fzpfyr8iqDS/wjMoTnc9SeSu7
MpeOICObyc4lzIhC5zpWzuO1jPNw5sYxxvnOONsJDo5yHqdBg5zLSfg5p+CJ
4/R1BjRJZn+XOcGY18K+vpXxT+LeeczP8lx7H+9cCp9PgDd7ZRsHRXgwx+hL
P+j3T3fn+hROqfBKK8CP3ZGFU6BB+RHOL3FZ+Gu0qQ9tfYK6A3vQr5g3hymz
oM17jF8I7z0btKvKvvoS8qYZ43uE8R1Z1GubbP3SSckfvielb6FzGkyinZml
jRmYM9o5M5cH8Ty0B7snzvYD5RBWLuHujE1l5t1GygbKvBznqFZ+auHOCANT
2DNdBhpPQLFfk6HrIPoZYPyGwRuToEcD6HYXfN27qPUZiUOMjanzpHDWhMUs
HGZhjAtfvEC0rGydjXQ3LzO3n6dN/WhjdfjwdmTKBJ0dtEcutOxvT/8H8Lkd
vHE50bmgmtOWBtC3EaVMgjHFhS2uHEHfw+NpyNQ4+OH+ZOcdVM5B4XwK41P4
q//h4uTbj6Ea73iSMblbfqjU7+QbY0I2yK9kM6ROyDV2lzC8KmY6R4NyNXxC
f76EJ6ql264ZqGc750+xxmdrxntG8v1r2QKo19byM2XjlJ/1zVK2vx9sb6wx
2QgXlnUuKuWkag4tW8QaE0243cLvfpZ6HP3LYpzvhTZ39DCeuuzwsoUrDly2
cX1WPLi+b9aehOurh9hOL/9L+V4qXgNWKLJGtpmhzn8RSpvnwUfzKaeG2jb2
TYZtZUXob1S0Yy/OCduGfdM3ycYUWQT/XlVcAPf9BS16SQ9DG56GTq/GOC70
V9q+s4RjJRQncZox70zboylr2ziuXjbOzME+N9TN9NlB81Pz9CploPZ19Ocl
+j2G66L4/68k+ytJrshnqXac4+c61TIeQ90gJoOwQnWeUb6xM6WNt7qotHU1
0tMIZ6cxbeoHPR5hHGYjJ3vA75eSHMuqmFZeW+ShIY6Le5B6OnzfHf6PqWes
M+GclRvr/XnLnt6jKxZIMUHywdRZR77kf420XS41zpjV8gs5lmI/EeGz3h1n
jNa3eG8b6LCaurHyVtDH0zy/G+8Zmmqs+dXIj3cp7eV/Feb4UMWJKi/Re22c
pyiZNrQRdgU8UKqfc48p75gwFn/vYZw85cyVv5Ty5kq39zj3LqLOQLZFSKZA
6xcGOp+b8rop7viXso49for7akLD7yu6ngGvDi50jFaA8mCmc3lpD6+9/NfM
1+Ksr2HlvNe9CI/11XjDn/toWyP6/1uOsT+GaD8ODwylHkHfW3W1jUy2MmHZ
LIRuvZs4VkA4qooXSKM9rRnbtqWNP/E041WmlXmvu3T88GhV6Y3gqcPFjOUs
DBr5gYS2dn5K5ab8mfX0HM+7rYp1n9KBKi+lcE5+QPaHtDFWs3CaFbN2Mhj7
UpOykD49wv27GO/xtG2lMORqWDcmHVkt6sbsNfKYU2/m2i9JYyjfpOJDHIfe
qcC+OPLJKSW/zyz/LiyPbfnGyxBWRnmthbqH8iS0WgXvDRns+NAhQxwj2ifU
fgTCCZM+V3rdLEoaa20dnj1Bvl7lnUt+QYzPOXOzfO6ZC3+lQJ92tGMUbeyo
dSzaPlXyrfom1bk7UuV/EGOMvR6U7Wk+X/wI3wwrdB6Zv+l3PWiTM8o5CXVu
vqSYMJ5TJNq+Zc3aOMY7gznZlj4OTHJ9I8WftadS3nbtq+pnOo+V8lnp841Y
20Fvh0e7wWeRjNPS2rYJyDYgH2r5Ut/C8wu4phrtfpN2lR3hPMdv9jAmgXCM
llHWdXNOKOWGkn+c/OSUd3wrz4iRToF7BiLXS8C3g6ifYIwXU6KZgz8PM6Z5
y6B/jHIJKI/AMfjnI9kokB/vwVvhPO+EZAXte6+eeVN6QOkD21G/P8iYnOsG
GSto3EDLbvnjd2PfmsPepyLXPszv7aHl41Wch74+tP1EmEf0YfNE+4jJV0w5
IJRjcCztaZFhH1flje9ay/YE+ci8rPMk56AvWJ/6MS8fpw+bhCMG7Y+ybg8v
NH6AZI7kzaBYt0Fx2PGyBTWxv638bmW3SxlrO572D6ndvYc4iWyYF2+MSuUf
lp5XOl7ZSttl23YqX48ZbezvMYL/HqUtCynDKtv3Uj6YJ7imgOvnVHF+EOW7
W9DdvjmJlCsTjM9wED7dMNj+5YqVlb95P+TIgGTH2clnT7F/8tt7XX4FPK+Q
dfobxUlx7ZqmxnxTzJdw35Srtmi+89Wqrt3Ln88UWA9/sLLz5UTFOH9OFv28
hbHdxDPCB3vuKF7nCLT/mtKhsWMSpLNKYB2v29r5TZTn5As+vybsHsnyCsZZ
3TDCuc1/pJxHvrVWrBI82SbRPu0DeX8I736aNWoFvLGpuXlXfvCKUVjCu97V
eYJys5Xti39RN6HPjzM+9zHWU2nvd/Ld5V27qjo39M6q3vvNgldDqCNj7McY
ynsaQUO2DUWqFjF9pBcQbWZ1tg7tiRHeI/VOtl/bpFjHPyv2Wbklni3rvBDz
aWd5eOhyrvGfhbsnDOg4+dN1sVyX/DwCfZpQR6Y4NulYD9unHg/aqP6G7m8U
GNvtJv2phCw42c46k7ENrDf5Fhl9nbn9P9nXoP1vjPOd8M9Rntea5x6DN36J
9JlX9rQfoc+FUs75pdwvT2dYv6K4h5nI4ntyjMn3BfJnUYr9GOXDKBwK+avL
V104hPMZw7Fc99g4789uL+v9mtaN4uItyjsxzon1KmWV4puZc1ehcyzt/IvP
vxU4dqkpZVShca2U11zYVm+E2+9I/unyLRKNRJ814xzLnMxa8yj8Mgs+ac09
cdp3Q+vR0pHkO++gcg4qf6uwu2STrAw9V8KHK5r6jKzz8aeMwUzuO8p68il7
xW2VHZf4EoxwJsX+AAMY3/Gs618j8+9Axk8aa1vwLWOdK0E5mKVHXAff7O5q
jCs94540P2cx/LqWdXUX/bzEc+5nfzyCUiCZz1r1C8+5Vse+YsI+UXy0YqM3
QIfsFraXy1Y+D74Z2sayej99KSp9b5TfpRhKvW8HfWmM3FsY7vzSY2jn2lL2
q38q27712ciSxmUtVxdD343c/7Z0t4zNg5QWYc7NIV/xteWdh2r/MOei+hs6
necZ3ze3PfKH3rZJXmGNHkqbf6aemO89kPY/sRPtyyqf1sr0YVJn+yBM7mUd
QXGe8TEy7zB9OYQMuYMxf6+Xc+jOa2b8uXfoY6h0VQWO+/sAvp9DW96C1q8G
7a6yvybyrlT+q5/jsdEYTZOtFnruo++f8HnqKONiCR+rOPUV+UpVcD6edsF1
66OgLnMCfW2FMDgPT3dubr8j+RwpNuJCC/sdyufwdDnfo+uFAzc921hwK8Y5
z21ceePlCze/GmNatIZ9gA6OME7fc7ShOXwxkfe05Z6cbs5BOpu2pvHfROZ7
Mz7fZM1tCU/P4L4TQ4yDKDzETpwNjvRzDkDhl8jWJ5uf8lEJV0m5Duek+5yt
87biylbXcPzPLOZOH+bvs1zXS/E1oc5JsaCs49LCWaNfhJ+mQa9ZFWy3LA2P
bYD+S6HxA8jRpdJhc82/Bfajr9PZeW3PJznPrdp4LdjOUu0dZ1MKPu4WZ1w/
YfrJ5zYs136343nvJd5xhRKmOBjeW5JxDx3rM5LORx9C4w20t490+/BwUUoY
PPQg9X6eMxIaxUP3RMoI5kV8oddErY3yCU7ge2KhscN1BtRZUHJ+dlDWy48t
G/rtYD40zXaOK4a6SAX6lMR970Xa3i7/8tnsMb+GR49S+jC+W5hfzcI8l/6B
ln9T/klzbu5CZPOTPDscWpxVDCb1U8jlfezvlxRz/vfSPYyf34V37GTsz8jv
jrGbzJj0hya9sxyLpJikEGj1A+2vDC9kI78fQO69GWbbnWx4yhuqmK7ZyJu/
GJsGtG12P/scaK5ozoyjv5/y++Vor8uKeZSN8XqqP8cHvys/VH3kZh36uKya
7XlPV7MvpfTP0kPHse8aU9z5jHXOHU15E77spDMia0z7PI9F/TYej+Pyqw7G
zAv3VZivicOcY1K5Jh+t5RwryrUSpj29/BRpb9s018vr+PNkZFh4E+c4+Bhe
WdvCOcm1Fnw90euBsHdlp1tRzH638peTviiCMX9iuPFQlVtAOQYuVHCuor6V
jc0vTBhhHX4TlH+Sg8fhtaHVHNM7Ncv6WeUpVN7CaPl9UNJoy1We26SB/Twb
0dZHmFNty9rGe1tX23nrcc0haLiZvpcM6n9XsZeNpl09KTPiHQshG5liIzbJ
d552z6E8OMF5xaQLk+1GckH2m1vH2Udc/uFdaPtA9n3Z9OtP9iLH+P9aQ3/+
s6+/92fMUpG35zv6rLCHNvyd5ZynP7Vz3lPFI2qd/TPd9ptNBbbnKH/0GH6/
wfPrs04+mWMf+XnMoftjHIszmXaNZNzHdnXsw9oo26qPxBgz7yLPvAbN99LO
+wdZhhxjve3N/HsuyWcbnWvkcyrfU2HTCKe2Pc/+a6JjZiXjJN/O86zb2cPc
7Ov8rxmU7cEzl85b4zo4T8VYaHmUOinLPnvy3Quj5LJeneH+E9wfBu+cFI2Y
R5UZv+91buHazD7GxNXn4nn+vlJrqvDieO6J1t7jVK3lc672S9o3CTdT+JnP
hxi37lgH5wFQnpNxhc7zrZyhH45w3tCnad+ySJ+1hP+htUu4jnqH3qW85x/F
GtM6pdD41qr1PVT6SebIniL+XfjXwsRX7J/i/RTrNz7aGHbVacdbXD9UtiLG
qDO8u5TPqxiL37lnDDzxaUfjEijvsbAJhBHfGfnXENo/1s62uwjm+QHkchft
3xirXbKvRdmu2VL2gbbOT7lQNlHm0gBk+o+DvTfNSLe+SXqn63WNTyVsqhzo
thD6t5ANkXo199aEZ1Lp5/d8nkpb46rabrMsxDFptzOPegXt7u2YF7fTjzsG
2V9GfjPzOtk/Xn7y43K9n9a++qGS1tNLX1+WOV68t/UM0jcoB3Snps4D/YfO
/Mz1P6ON5SscmGSd/dkPHK9j/MHB0v3CvwP6OiZTsZnCNZffTSOuKwdvzWKO
5nNvBvP0CeRCV+qW/WwDKxlnm9jLrMvHaMtm+GF8sveRKdSLq3rtFAbdr/2c
K+136gHQKIbysvQA0Okn6Zy05x9mDDvh18kWFcV9kcWNcy2860d4Xg/aHkU5
B6+sr2I7suzJyhGjfDHSOeizauWMyc42vqXywc3o8V+qwv/2E0NH2SYq32Rh
965p5rX+O2Gg0o4jw/xZ+AP6rv2dfA/kg6B4RcUtXqd+hTFsxZzuAD2uMD6L
4IefGxh/8CjvvKnY2RzH+XzM3Lq/uP1jQioaJ+we+jmmvrHao+sYu/1yEefT
7My6eBoZsyfc+4te+Y7zy6J8mua4CcVPjIGW7UXP3o51UpyT8O/k792dMoPn
jIv6z92kSBf6UIp5Uhua1C1hX1n5l8g/UXYP2T/kFyMdrPSvw4rbpi7b+l/V
7UcmX2KdKRUvOl7ynvpfxqMTPMVUKBJDu44xz+L4bQi8F478GEq9jvnyL2NY
FJ4ai2yolmk/FJ1Rrsu2ybvmwl85lI/Yn7yc4zyIm9hP3k3/ZlJKRjp+VrGz
yj0hvB7h9qxh3hSvYV90+aT/lzOR/eCZUcYDEf5wOvVZ5u16+tAY3p4/1L4S
WdLzhxgbphj1cvg4Is5x9Qfg0f2UgczHG2GOFa5D27ZIF0SfrkDXY4zPG4zP
Htk0+zvX96JcY4kIa054H8I5EZ6QbIUfMKYbezqn1kTae5z2PhfifZ/2fw15
bwq/39/OeXA7KJ6XsT8uf40o+07Jb0p1j2b2o+oHDdL4bQD9vgcaB6DdByX8
uVOCv7es7FzkK+lnTdp8mPceovSS/RnalGUeJTPmnbnu3RbOcSQMsMPMza+H
2NajvG7KJZdEXxMpP8PDm8o7B1e3FOO+dadOlFylL1/EGc9MfjYNmZ8v5BkX
qVIZ4/Mf7GuMfu13tO9RjMBJ5ttkePQgtOvCXvNj+ckKL2SsY9pOUR6B11Yy
h/YhT94QlmCEffXWTjB+uHDEhYGnNToqxHglwi2RDW3ZKMdsPE2dku/YO8Vf
R/L/c9A9ErpPhj7XGLOm8fatlI+l8vxOKPTvyl0wHVlbhX5VK2Vceq31WvPl
F65cd/ITlxwQHqlyeCnHtXJdK8Yhh+deoz9tR9tnWbY+2fyEbSO8vxujrMdR
bKLsXspbk17onMr63DnB36t2Mi5ZqxT72ssfUn6Ryv2lHGDSi8b29RqqtfQk
7RnFPHw2zDHNim1+sYpzpSpvqvzJlV9VvuVtBtpeI1vNT0k+V8g/eF2k98Tl
4o0lNbWW8W7fFA0Zg9/TbfsbF8RCli/7m+zhdur5CKEM1rRTzM3Glf1exTBL
tl2vjWySnqGV1xzlOFUukXoljNki7BbFSilmal1fx7b2yHN8a3/2Cv0o2+j7
p9AhSXZ9nQFp5z/QPg6aPsLnJsiY0sixnfDsLsrKWvaflO+k8Pzzg3YV2alH
cf9XvDO8r329hqTZ96tVnOOqstkr5PR0vvjJnRxjrf2S9k1jgzHRio1OHOyY
wGW0rTVj0oYyrqLXDdndns43robwNWpRZoQas0Z4NcqdcXuO82coV5Hizj9N
9N5Oe7psyqQJjnFQrIP0r4qHaETZQH/yqLNzjZUpzMxXqcOg84Nat4L1a8HP
innaGeu4J+naAoxLb9pZnLl6AH6ckmo82kHQ57XKxsgZHGOcHOEjSv+r3DFq
j9qSPc4xnLuCuuI7od9rzNcRPPtl3nGY+fJKunOAKtfaqE7OpSgbXQb0fjjF
OXdlSxysPf8E5wg+w/tO17Kt+lba1YU5mz/O/HCqsXniRpb1YhMUl8Q9O/Kd
P+tD+PAEtD5FOcgzMnlPVqFxRIQn0qqS9X7CK2oSaVzP4yHG6fw12jGcl9s4
hnMJ36ch69exPvySax9q5UTaXMlrk3SH41pZf6i8IMoPsrme7X2y9YXxXx2e
myo/Ger1BcZHFjaysBUfYGzPy0bK/e1H2N9X+P6K03h+gvPMr2dsLja3HVUY
wZ/BG88I34H/ajPeaxsY72NNA8/DPs09L6ezX3yE9v5SxfGIUfD4DOE8MR6H
KtgWJ0xfYXHKRy4T2VdMPMjvOen2D7xGO8fU8vgqZvcuaNJF/gLQaxDvG0hJ
kH5lpPP/xbGnvD+4x9Neb3st5zAUfs5A2ano+788o7C6z7Y64yr3WYPm1suv
zHRc8iVoeLyec+XNovzNs/oh776h75Wh2dus65/wjinImQ95xhZKLPR8l3bu
irHtQvGzUyibSjvnzArKPvlBQ+tyPPsSbbhCqUlfrrZ0LKliSnd39HlDZ43a
mg+DPa8f5fs16th8+/u+A2++Xdb53mRjkq1JtuLwoL34HsayJv1aRBtmcE/7
2vYPe4zPjyKjFha3vWZOjm02bw4N6uLoayvWjJr0+xXWzQdYY9pmO2+ecMGV
J0fY4Mopvwq+7MPY/z+izjs+i+IL9/TeQycQSkgIndBCJ4QWCCWU0EkjCSkg
CCpKUTqCiChVUTqKNClSpEizAQooCP4UEAt2UEFQpNzv45N77x/z2d333Z2d
OXOm7JxznucOa4g56EJudCgnz6UxdxRJMq/UCxnmlpqY5DhBxQtqT/Uuc+5T
yCQVedSivZNHuswq7wJSguwugeZTl21VNtZ2/J/EmNqJb679jR0bfS7F8dHj
6A+TuU6j7r0Uj5Tk/9aRTxnm6fUtjbMovMUYxqCWlDdD3+cZfi5vmJ+dgAye
IL3GOPy/NOMD6ztM3BT5mEOrh9lfXb7qWl8Jv1YcKSXJbzp1uNTG3FUapzq0
+C9M7j9sFvk4zCG/EbwvijGvNmPBR8glVbGH5HePe2LQoXH0284N/P2mbzdh
Y0r3Nc4Jk/H2EGOWhpNXBdU3y3sn2kN5uodtJr/SBu+0tF9drjb2szuADPag
v7cTjRk5kL7SGXlupR8XoF69SfcrGGdKfsKXU8yNlsb1GO0VKX6cdKSmfavk
Y6X3FynpMgznPK6GsRT7VTI3+DBkuEQ8GKQHsvsgkx6MAxtrO454Ym/HEt9h
/NyIPC/TZtN7meNE/CbDEswlOoHjQ979oJV18gn6ypP012PILbO551Rhy0pH
Bsu/lXFhtGKUSOPoI29R1pq8K6S3sWvXol/rSD+1sN+v/H/ldynuRnE2hsTb
d6F0b48FG5M8Nih+VGssra+EsSS8auEsiZfyKHr5InNDGvJ4ljb8opIx2ITF
Vio4Gzci1Fx7q3s5Bj0s1PvBNeK9JywuA/EYiEtyjXBSkNVaju8h7yjOO0Sa
02B+CfMaRNN/9pO6lvKe9QzWJ1WQ1Uj5Xsm3v6PP9w/y9ZpCxuxbXcgy2UY7
p/P/99TlRANjFN+SjQJ9/5Pjgo7mbRJn0zvp3kfQHoIwOTKyzCH0eor3eUeg
/+3kT8XvBxI9XxWjXCVKOU5tMu9fWcznE4f4WjFsOtdvwgE+Fm3O9CHI4zbt
/3dHY2vujTDWZrXcxjDtjQzikNfP1GM3+T/X3/i/23IZw/gaaW6s8TSyyHtM
P6+ltKZSzPqhOON3yB4qzILn6xjDQFhgwgR7Br14lndupl8v4l2vKyaWurbW
N1tJxyQoHkH70NqP/jLd/bJcJ/dNYa6PouyPkJ7m/l/Jawp5XS3puNe3E41F
8Vtv41HoXXNJ09GH9+Q7Rf9Yx7OPtXHsxeMcX2D838w9m0ij5FOj/YaR5l3s
HWLuReGPTknxN+bJ9vZNbl/LfsryVx7NczuEbxJvf1Od5+zl6yltzQHbSOs/
jr2o74dx5rmqQb9dgt48IL+n5afB8R7z9SNZ5vCb2Nr+cPKFm4p+/CO8LuS5
nPuqkceFRPsbz2R82t3NGA/CelC84CH6/mFSXHXjzT5fyJiz8kGLlv2ypvGA
hde7g2eeRQ550ceqimWnb33Of3EdvT8on4yJpNXoQ3X0YityeUhbjVE5h5kv
TOOjxkZx/4gDaBapO/ePp59/jOz+YDxfojUofa0kdbtFuW4383pTa6qUwY7/
Fw7AhyXtVyDckuXkuaanY7yEDyZON9mRZU8Ol02+lGPiJIv/ZMLvu3jmbVIV
6vkaddiKjPdH2c9IcXjyyROGmPYEtDcgX781Q2zrOoiulUwxVnhtZDSfNlzE
+4rIPwgdGh7luC7hb4pzei3vXkNqW9z2T9nIZR+/JJ802qx6T69TtF55J7/H
Zo3R22LM7yCMBnE8LEcWy5qZJyan+jtl+F+42+MpUpNu5gz+jzuY/z5G94LJ
O4fkQHnGks9Uzk+ONJ6A+HYVK6yYYeH8Czc4vart1m/QH5oyht5DFl05L0m/
fDTLfEjypRLvh+ZTzaWzyeMT6j6F9EWa47sU5/VEd8fipJA2JjteX3w/4tX6
XWMu/biXfDE62t77NmlRivGHupDaIu+1Ix0rNbqqv/eOym7OO+8xp1dAnoNo
g27UqWCIeUpWDTNeyHelHTuj/daz3PNyS+PcyL9Dfh7CLZSfl+JPx1Gv+vG2
2z9Z1HYT2UyES92DvhRD6trTPifymZHvzEr66X3KOqq1MZ/EG3lmpGMyJiKf
TsxHk1J9Lb+uiTz3NnLe3MPxEvIDE17yj4wxOdHRs/3Nx3iF9jzGGLSYMrzE
OLKovX2n5Tc9Q/tq1KcY829pjqea2v7TOdg4HGuR0WPyMUEWTYoak1WcuToX
b67wfLV3voX7FfBeSXZQfn/I+vQBaTLzYgfkMQNdG5/lbybhL25VvCfl/h5d
f4zfq5DHZO75MsHrW61tFQPxDLq5srdjfoV7pH1R7Y/+mdNcyOJBLpxuXD9h
+gl/VrizPZFNW+Q1h3Espor3tSaTHs/yfKh5UTwLj1GG16oZC0j9S31LsZMt
5BdAezbn+ATPPOBd/6abhzqEZ7rmdYxqKv+n1DTWTiI6N4Pje8XMM7WI876s
p3MznqxHru1lT6BekRzfZI2ymfQFeXxI272CnC6hv8Poq0NJifx3r49jPzsk
ms9CGObCMpets1Vh+wYkRXsM0vhTirI/rrIhsy49zeG0vorjhcUhIi6RYvwf
QCpBW5Whnrnoo88gw8e0/0b+0R1sk9M4WyfGfFoTssyv9WSWMWQGDjDne7lU
877Ld1AcHIq7K5PqmDxxaei8dPb1DwHmyBNX3r/IoDJlODDUMePif3yb/LZ0
cnup3Z6STVtjI+X6lN9PJpqrIKOHOaXEmaw5Rf7NmlfELXE9ylwTDfm9Aals
TY9PE7PHqAetjVt1LtU2ZdmTdzT1/pL2lmqQPpDvF2PhhxwrRpgzakZPYwSc
RkcXcqw9wN9B6pO30KGbpAj60nPdHDs4j2M32uc4MlnAGPw7sl8/xPyLwtwT
F4Mw+QYM8Z7gpnT7wDSpZT+Yj1sYB0X48+vpQ/dpg9aUo+UAYy0rHqxsNqaM
vjvXcl2TdgsmvUO7pfL+iPaOX1IcU2ZT+3PLr1u4VfWLmFdK/FK1s/eW1tIu
3ehTL0nHc3pODuD/F5B7c+RTmnHq947GxhZ+5n84mqSfZXtN8/mvwb4WV9rg
JuZLe0L7LNQphHQ4t3l7g0k9I4xtI4ybLrk812qenURbRVFGfWjJN00+asI2
0/6iMCy0x5g+0DE/GQONDaz4T8V+VkPvq1O+PIUcbyUeW8VcKY5BsQ6KZXiW
8twn32rh9iURb5r8SRQ3qPhBYeneqWrfK/nwib9GfFGNB3tM03gmPqWCDbyf
nbeP1yPqL+o3w2VbQn5jczoGWfHHl2Ltp/8255FVjAE6hLp+TL3bUe72pFH8
15t2y8m9OUhjIr1nIDul5lPtIwh/Q/4cioOV38N+yvku7bSP4zrkXTzDPgX6
NpUf/hz5lnDdl2cmZxmH7Jx8s9CXOPJ9Wv40A+wLLJ9g4erIH1d+uZ2rG29M
9kPxE7yQ7av/fH7XXXv6qr84ABS7VY77pvCOb2iLp7Nse5c/RLPBtjcsRo9a
p1lXxNHaVusQ6vA+OvEhqTnXL9AOeTn/kj7eg/XGAfI4G2ge4zf6Gtfq3hB/
qwk/T5htxat7vVoI/ZnE8Rl+G08b7ET3Xi5oP8a5vDMo0liLwlz8Lpc5bi7w
vfT6CO8NNUy3f9F20tPoxSHkmgdd2MjabobsaJTpQ8p4hnoUGmosI60H5DOo
NYHKWLmjy6n1yvtxXr8oRq27/FGLmT9CmO/y+xqp7071x77m/tM8Lf5k7f/e
p/+37W4+Pf0mTj0dI8N9Lj7SlkGOc/y0ms+PcjxG/ZvKfs5xDzrzTpxxBK7z
jkzKepo1y1TkMy3L3JjCcpCvbxp1HsczDRh7E5FFBdZai6nD5/HG1nmCdv4N
XapO3wsmnea+Quh3Eb6JV/De/vTjavTTVSmOYemErIrJL4Nn+ggvlnZbEGc7
3Pukoj3t43iY9niNNv8gyHtoBdP9TaRvowD6+p+sf09XcMynYj9DCttfbkZz
+8zJ5/NAT/t9hqaZQ/2gfMOy96jnkqbznib8PiPLPjfPonslmQt6JBi3T+Oh
zoXlp2vhjh5IMvao1sjCf/qFsTGVYxfqEk0K4JleyCiQ9p7JPW9wfV82f9kG
6BvzSRXIo778qvn/Sjv6CHq9kXz6ofNHtWfA2HUV/UhFfyN7GPtAGAgPGLt+
qeA+lsY9Axi7d6DD65kDHuOeMeTzbYTtu/Idk713NPN6KPc8Mcx8ROIlEkZ9
EcbZoqSf6Q9DWjlu+7/4bf6bTbleSzbXz+8jzPfzEeU6SF4HGpkHrDL/rc++
R3EVc7LM/V2Z/yuRz5+0/1bOX6csFxkHvyDdbO59NO2nyW75J21zhzwG6LsO
PYuTPZ3fH8ofZ6h50FvTNw9T72MN7Scrf9k7Ha0j0hX56MhXURjO8ldUrJJi
lg7Fmi+2I7oTRbou/yGeWVTAsVz3kFUXynOb9yVIh7p4v1F7je0yjSEh7kDh
SMzlueu860qy4xPPU/9PFdtJea4jw3lZ5rN6LsucVnkq2G6RV+MpcrjBffep
QwfqNAh9So+3z6D8feQ7/whtloN2nlLV3/nxrGXqcpwqLA/657RB3svTnl59
7QdWsh1XNtxQ7S1lGHN3LGP0O8jyKP25O3q8gXy6Ivexiqcgn5oxxukQXof4
o4YwHuehT65o5xip5O6208s39NFa9hWt0dl9u0hec12mtzbfpXRPercuxFgs
Wu9qrat54Q5pHvfPamC7s+zPq9owP/DsrNqOk1a8dAXk8AbtlAddPTvQtkLZ
7zSfK65Y8cX3KMsk5NgVGXRi3C5FXzrLf2dCbDcV3/usCNtSq/ezjbVWb/O/
BNPHXuliX32BKMQji3eKGQ9X+J3CzxV2529x5lIRp8rz6bY3zldbhjnGT/F9
j6Sbf1A8hCk9jE9xr7p9mOTLpHL+IV8b5aGxI8GcH+L7EL6OfA+EsZNfvhuU
YT/yeGWQ7T27W9hWOT3D9spvGAeudrCfiLgLe5c3f2ENdDA9w3NZqOYjxucd
bc3hp1hV+cbuz/ajuNfJuBBDsjFhnqNz1kaXb3PP+BhjYmhtJPuF4iSF/9mG
slzVfidppnzaSN3THCdbWjZM+nk4945E3lUY2xdkGd9AfLOHaJe9tFNmknHJ
hElWlXHjM3TmIe/5kfl6Dc8eod6DaxpLWZzE4gR+sZ/HZY3J/YTDTD37cuxE
u3QhnZC/Z1fH3Cn2Ts+XCXN+4tHOWdRc2sLAUV0Vz1KI+lelf1WtaexSYZgu
SjNvgta44k4I0vqJ88kp5lV4EGfuklm0y07qOoj+GtDHeHHCjatP/5hGP5mR
03ZC2QsVtys+D9kvxfURS32akvdHLcyLoHgM8SSIy1F+aPJXus74lca8GEGe
Z3huegXb5mZxPpi+MIk6ZLU2B6LiJJu3cby9+kTRgcZhFeffC9TpGGuVZfz/
J32ygOJ32pj/U+f67TRz0geM7/kzzcE+EP0N5T27kM1OUmiSMSXH8Nxz9Nv5
vKMjv+dgLRXDMS/jalx7x4goVkT4EendHbcYlb1Hr7162ZFeoW329DaHaDjl
XUj5XiS9ye9fc380sjiKLKtTlpeyjJMhvAzhMMj/T36AGYyTi/ivgHB9SUsb
mydzWWPzu4hb+1/qdKWX/SO07yRfXtn05Nsr3yFOc6DqOV6TnDi5E2t+LfH2
9VKMHze0pU1CooypKDzFt0s79lUxsOIJjm1k345Fw5yvuNfFwS5f+vV6ATqy
EV1qjM41EW4PY2Qj5N0wzLjF8gt7QJ6xdYz5KLxH8eeJR28Jx9y0cy7S34yB
7RUbSPqWMWNeF8dnlqzjPYXF6svpPi9ZydeplDs4w/zqU9qZYwyV+88PSrFV
iqvSuPEraSzXO6jLcM4no1PrkM+fyHhhUfM83owy55D8A9/i/VUjfS4/QV3r
W13f6OMbm1/6mQjjAGgPUJh+wvYT34Z4N2aMdFyL4lsGIqPAXo7RUKzGe8hn
FOUbGmU8H+FoPD/I3zCygX7Pu+L1/YP+3aPdX4q0f7x84zVWacyKZZzYX8uc
pOImvUNbvsRYOonzfOR7K595yrVH1Vrr1ub2wawdbj/MvNnzsnwJ5Hukfidf
pDrMgZ+hGweo1/Ch5r0Yx32B6E1ZUkXSEsqciFxvpFqOkucp5FGFftaf/4MV
o0R9X69lHNhP0IGTyOB72fFDjeGxjjr3oWzn+e0UZV7bwFxl6zg+x7gwjDG+
MfLoQL1/UOwX7/wQuY1Nt/1QR12vQsf+5fgP8rrK+ULk+CNyiEd3orQ/im4P
7Gm/ffns72cuHkh9yiGfG8hhgXwpSb8p9jPO/BGBHLcggyplbJNZR951m3iP
aBnl+J2+P19jBGVYzXx0jPZa08J237cpy84Ic/LIxrCc+1/W9166ObqERfs3
7VqmgTm5t6SZl/pUC/v5CNNU/TC5i/kG9yCraRzbtzEm+UFkXlO2YcX4tXQf
D4y3j2AexoNNiokUdgb/vU/5X+HdQfzfLN64nr/xjgDuXZHl86E1fC0OOnHR
vd/LfBTCphWWpPAdD/DuQ6RTGY5j2EnZNpHf2DYeK5tS9mDmwCYtbNOWbfuA
7qXci0iP1DXX4o8lzLconqmxEeaa+i7O+lEhwzHQfXh+AWX6Gj061sb49ae5
p3e8bZbyq5B/xVJ0ayqyrIT8GqQYY082t6872VerUFvj14mndGe44/ViqU8M
dUvhuZnUdQX3zOpoHVkvWwjvu0V/HcsYMYZUEv1JR28b5LTdTPYzYd+XQj+j
Gpv3plq8YzAVi6lz8TD+x8eIHhxGp65oD5B+8dNAxyLru1Pfn0UUU8zc8Y/W
Jbkdkyqe5OKdjbMom8HI/i6fynmtjr8B9C2g74OhPb1np/u0ltSacmUb21Bk
P5mRZBzQTaRalKstZc6lGGTqsZY5o4P2ppDX35ThSEVjkQrfTjh307s4/llx
0H1511XmvK9JX/HuV7WeYyzZqH0F3tuK/G5zT2i2D6L8DzcMN8+1+K61vl3R
xlhAOZFjPc6r0VYzua5POeqQZtKvWnM9mP75MWUYgWxr8fxP6cZ8ko9IAPrQ
Ft0OQF4zkdWMbvbNE9eWYmuFSSp8QeEMXqcOLzUxhpj8y/bTHrcY528WMgaZ
cA6WdPK5jrcVQxdhvEFh/c4Idt9Wv34tyz5ALycYa7U296/kt07I40fK0KOC
49beJwUh66vMHzmQaZV25q5QrJG4LPTNPpHfJ3U3rrbwta/3Mjed4kAV6yj+
KK2PXuxh3CFxcG/i+AM6d41UNsAYzsKwEZaNvkP1DSrO3LnMEZ8im3MDzQ14
L9T8gJOFxUu7DeFboyTjSqkcjnd9tbgxZVuE2k/rXDn7bQnj9Dd9f0Wamy6R
On+PTIfTvu/RF+I5vh7svXTtqdfh/5N8J/0g30faOi3S2MVaM68i39gCtp8o
jlo2FPFmKhaoMeNvBZ7dTt4v9zMni+LIFE+2Fz3txn+dqFetdMehKB7lG2S7
nfXTLtkw+hoDQD76ik0QJ7J8ZFeT9xpS+0yfVw3zdTh9vi7jwi7ymsz65T30
6v14f9/qO3d1inEHF1cy9qCwfSbkNYbC5/TP86RXgz1u7mHMnzfYfLjiwr0u
PwTaYS7vbzzCvOE7Rpg7vAdtW4X2fpY6fkl99rGu2ktayj2XkUuxVOPrCWfv
D+TTExkO0nczbfAEefRQPG6CbUPXyG+j/EJ5f3HkGUR6XTgkpLpFjYEm/LNn
go1Fqe/bVsnmyBKWlDClomSDobwdtSdJWo9uLqvpcUTjjnBehRW1I92+JKOz
z1cnGztVMY+KfcyN7E9R90OU6Qbt/QFy+7224633JtrHYGaa9/sDBxuXPKu4
ccrX8p51pJoNff5HW1//gw5F0D/W0H/f0B5sT/fJ7bR1NHqzh7rlQ+br+W3b
cMenyqdqWCfvIdUjPU45v+W3r7T/GGy/FWEaCs+wOGW/nGzekO/5bS9yLNPL
MUfaf9A+xEv8Fk45G5FuMqeN4vqZOsa+/Jh0nHIMEBYMY+CI6saz3aG1dpLx
azZQtl+a+3xNEV8/Qd+9In9M+stvGfZVkM/CCvrjK6SJnRx72maA40kVHza1
hmPExAtbgfee49iB396lXtsbmCND/l/1GDOasN7Jn+IYZeFbpmntRX69h9sW
LOzPuehzPfJ/jDabwH2jyC8rzHZw+TjJ10l+ocIn2V3PdiPZj4Sl/kltc4uL
Y1wY/PKl+b88mPKtERem8DZmMH7HJBqHVhi0B+WrUN44I8IYuR5gPEHFPQyM
cezVaeq6A12JZy5ZQvl2l3X7qe2EcxVOmzUi5SDvSejBcPrS4wMcF6P4GPFq
vcF9nzK3dOXZbqR12u+kPD3Joxs69Dn6/gL5nxOGS0v7OcjfYQXPf8E9/wt2
PONS+W6QalL3aOQZrrgx+tZk8irNu3sn+jwUHezY1ZwkxWPNJavYxycjjfsl
/GXZYeXjJJ4c+TnJnr+qv236NbW/QBlPpZkz4Z+a5k04Ir86re9ow2/EJUS5
4oLtg/J+uuPtSjHWTqDuxSn7lnTHmAi/9Dpl/Yq2OMv42KyR916rRdk+G0Eq
hq42rmOeDvF1DJItnLFpAMd82bGnikHtL99TfpubaZvvvDDbffV9dYGUWd1c
4cI2EV/479ThFuWtMtw2cNnCxU3RIczfgxPDHbNxroNjOE5zHksb1W5jv9pR
ne1b2yqH51nNt2+Q5slvrLfPZyb4upn24PltNM8u1bc3ZYnPY16mb9GBY7HG
7ZZ/0mDkVyDB3/j61lc8tTDiFFMtXuw/OWbkQtboxXWeOYhO7WC8b8Q8tDOv
eSHFCbkTPd1bzHtl2jPbyFqlIXm/XsXf7/p2P9zU9knZKRW38AFzRT7Gnbwx
5stUO6mNRnMeTH99nzZY38F7Z8XJ5yFt+gRtFp9mrFhxwwg7VnZqxXbJVl29
tW1+svcJP0w4Wk9S7/ZJ9sVM4v8qg8wp9fxI4/UdZKwLR9e6xdu3UD6G3WQ7
ZiycXcAY5mNTHEcfT1vO5/mu1O1XrSuEeVDV3GQ7kePKlsZTfKW3MRW1PhHH
oTAR5Wcsvk7xeAqn+TnG4edJYwLNVSaesvml/Z1QFN05Uc3xdYqtEz60uAX/
4xjs5D097e3Jvpoqf5hsrDrxj1dKcvzvmUK2vb4XbfxZYc9qD1j4wIrnUSzB
lA7Gko0lv/68bwDpIm3UhLK8U8IxwIqNEYZcYLoxcO6E+1zHpbI7Ur6iBRxX
I/w3Yb9tzLZjKJZI/G+L5c9Am0Yzjqbx7CrGkZHp9l/XftTeDPuMd0ee37S1
D4/8d9ZwnEx95/L/UPpPC40dtNkE0nfozY+8v01/4xHeGmjc3L2VHAO1j+Mi
1rddqefy/LZXjhtg7qT72X5f/ZBdiUz7hMt+NnSY+eD6keYneJ+2VKa54cUR
P49jX+4ppfEDWV2N9d5ZRfLJjy5+RZ+9kW5+gDMdzREgP/1jjO+Pab+SuWE/
6rmW8mQir1GkgeTzDe30SKC5DzWeKf5dcfDazxyfYJzpOejC3MGOUYtId9nj
SEfoc0up+9sNzAsnP4t49K2B8tA595aJ8bXOxTUqztHTnTwGyD+xcg3H8Cp+
N4i+eRgdfIU8LqU5rvOTYubMeoLf98ififxuUc5dKca1Fkew/PPEE/xRX2P/
Cfcvnr6eizXCsCHGfS9a135uR+lTa5KNM9IH3V1K2x6rYYyb6wn2b93M/03R
k4LIuDrnMYzL3Ulv0ibDKdemLO+Rr1G8AnIOLGMMnavB9teT3542ucRNJ466
8OaOWVE8clQj484Jc24j19M5bta+I+23kvVSd+oZzpgZJHwaylC0l/FKXtXa
lVQuwfwN4m7Ynb0G0VrkBdpxAanwcGMkDxLuBfX+iqJsyTIW+sAMH3UtP7Bl
Te0XJhzofd2NBf0q5WwuXzHKnA/ZHGbN+g3lHFfC/HKxjNH5Ex13pJijr3lP
oxG2AQrjXeVRuSJ7ei3ZnDa4kmJubq1DPqFOVdHn0xx3UdadpAja7jLH3xR7
h650bW9OW3Hb/l7Ve47ab9wYbc77bbRBXu4ZIPyjyvbFFd/9Y4x5xWWLQqbP
kAJ4byppah/7O3UmbW7j364zlu7uaz5rcVkPI78s6vYj/WsY/x/gv38YzwJ5
f4jsHq1sHxN+idZxWs8V1VqNeaNOdcdQyPZbJNCxFLq+xvM10owXLdxorVe0
bplKHR5FfpU055DnXvkYyMclxngjTbj+PdJ+9oqV1pwjvpRJQeZMEcaK7Mbf
FzSn61/ZMcbJ6GoS9ySSTpAGU9+hpHL0oaH0rZOs487xvs9Jhfrat7x4H8c0
36FMV+RrxvxxrakxkSJ7O55KcVULEry/o30e4VELT0q2Ktms5GMj/xrtsb6h
b9l63sNXLGMPxpWYov6vVQvzqgSUto/eEfI5QP36IJe+qbb33mGcDBtoLG1h
ajenXWqQ9zjZxtGNqeT5AeP2W9RrCf1kEWkc18t5bhFlfMAzN4UZRN4LqFtf
8kkt75hMxawqdnVwc9vYZWvfMsJxxDdyOZZYPAPiG9hX1Da6mbRHKeaZTsX8
va4Y0Xj0Nw/lGsaxHP9/TLlzhZhDWFzCW7OMsTCdus3m+CTj52N8C46jrIuR
w1LSa1x3QJ9XsNaJjHZM8TvdbA97rYNjl7UubsoYdYNx+nueudXI8aWnmFsK
jjTfg7geKrS3D7N8meWnJkx57YNPRiZfIJNtnDeobY686fHm+BPXkjiXtMdf
vKr3+Quim2V53+J8jpVVzKzmtLWUKxb5DGxl7tR6pPZaO6Lr3zDuf01KZdxs
obGScfAzZJ8HeTQcas7ra+nmvd6cZO7u/zUzhl79xsbRe5b37qJcioOSfffO
QNt7ByumnDyii9rOqfhK2TrvMc49IF3i/c+T3zRhuHD+DHle4/cR7cwjdqG2
ucRka95f0PZm3beCfItQnx+R8SPUqTX96+s0xxoo5uCtLNs2/qFszWQr0/cB
x1roSqL8WLLcp+XPIV+OH5H9ecrbmrHkX6oRIV+PVHMu96AfzW/pfRXhq2hv
5XHqd2CIbWirkNMOfpudYBwMYQ2Ke00xtIqlvZfDGDzCT9uRag40caGJi05l
frOtfWbkRyV/qukcQ9Dxp/hvD/n37unrYU2N1yL/thacF6Cus5LsmyF5S+7y
c03hnvXULaaGz3dm+XqX9siRx81I21Ll2y576hzmzf8JdzjLXCTiIRFfbx35
U9ZxX5Yfsfhsdmf5eJxxLoZ+nJ7puHCdTyhoriNhlrWuaRwr8enI7i77eyHG
jau01yR0JDflbMI7L/F/yZHGwtQ8rTl6L210k7IdQ34f8u5/6V/PVnSMudaE
WhsKb6pZqjGnzjPvjuPexvTTJtxbj/cdJc+x9K2clOF4mPevtY9dmveN5foe
73q9s23MsjVvQAb7u5lvWn1YsS6KedHe8Bba5rj2RdCJxOYeS8TbdI86LKQu
dzl+Utw4pUNqeL2odaPsO9e4rwi6NUnrT3S8JDqzmXJuoR02kyrye03KtYSy
HqcPbkk27qV8BZSESyz/686Upz33PU9536ZfVESOnRibPo81X/0E6v0y41g+
7clQ3rEFjE0kjCLtlcn2qv0y4SMIJ0H77+JtP5Vg7vYgxqPR3Dcr0/Gxsksq
XvY+/XwXddwp/7Qy9oEQ163WtRfQt2a0+2n5wFKna7nN/6KYUcWOCnelVLa/
QjNkt4djE44LAh1T+o6OjM9R9LFMxs8H2T4N8mcQVom+eZ5Otl1VNtUA2iWw
mONG9J1eEN3/gXHhTeofSV7bGTfG5XR8teKsF9A/jtH+IeR9nOMZ9G0I5y0Z
NzrRf76jjV4jr17R5uvsiBzCyO/jhvYrm9/VvHLH0c1i8p9HBj3CjVOR2ce8
vP21h9fLvoIT0funSBOFd0R77EKO24vbz0v+Xuq7wuC5w5j5cR77SohD4zXe
vzfL+FfCwRJmpjA7UxuYN0v8WQvRoebp3vt4Dd2/1dq+RF2rGAMlEJ17ivn0
8T6OcfyLehxItd9NsnwD0dE5sg2XN1/n+i7m7FxEW/ZmDLjU07juij0Wtrvs
R1ub2oYk+5nsaFV4d4r8AKjvgl72PxSXYin+X6E5FH3/gXova2Eck8L0r8nU
byPj66FajnVqFWs+Ea3H1d/HIpsnh9sOIRvEG8KXQA7fdfSYVJ/37E7xt/dZ
1kMDOb6YxziLwlv8rKv9WI6hpxVije0sjGdxmYjT5B3NA5QvTmtK5ogq+Yzp
0DHOvC6LO5jXZSj/9eL9QbyjP+0Xo7GX492KxtIQpoZwdMYgyx85jtfejfa1
yT+so9d9l5mHTlO+3ujLgSyvo1oo3nyofRrk25CnvzGXhLe0kuOPSV7jiltC
MXCKhWvIcQHv7Mp/ZYRtwfUU+lOxzt4DWFrf+wBj0JEfmcMPhdmvWz7dsk/t
4F29kU9d+bpQpwnowijmryyuX0n0vr1izRRnVq+s1xNaV4iD91iGeeK7xDtm
fQi/BSDjD2jXj0hd2hjXvRTl/J1jBfR9Bt8VDbV/VTQb35kxci66NZlvnt2K
v0Qu7/X2b+HI7zZzY2OOG5FZHDq6iDFhA/+/TrrEu4ehK5dLmG+vOfo5DZ0d
n+z5Vv4qmnPliy2MCeFLiJ9IHI2Hejvmuyd5HqrjfZXXhOeY5HPtr+j6A+T9
CzI7SBs15L493H+d8TcfdRtJX8rL+y/QhpuQ1xP094ussy9Rhp9479f0/VYt
/WxmkONZxud1X1O8tPqbfCmEf12qjnGvtQ7ReiSQfr+bPrWasXcieUwiHeL3
QdT/D577QXZT8txE211jPI2kbe4zbt0jLUIXP6Nc52uZD1jYncLtfJfnr1Du
Oxke3+Vn8zTtuot2foo8D/P/Z0XsdyT/oyez91GFJScuz8damNtTPALiEHiG
9h5AuQ8h+6op5n4QB8Qk+tx0xr+3qNf7aY7bKYKM7jVyTIxiY55uZrxP4X6W
yvC6W/Ok5kvxwFUmTeCdIci1Uqb5It5CPxvyrrREY3RoDBSHn+xNsjUJD0v4
OsIDLdXRuN0/0q9bs6YNYM37uvasB9j3Vr5c8r/9j9sye+01MdNxqv9r4fOz
RX2tGLfE2o5za0Q6wm9HSQUUy8o7jqlfM6b2pw2qD7bPh75/v+beXMjwFPU4
zj03+nsu28Tv05DVZcryJP0wMvu6VW/v8fzVxz5SCxl3DkXbpiBfgLRy9gcQ
95R8/LRn+SNjUTXGpO2UoyJ5B9FX+w+2r8F7WfY3CGXN2V+2/NaO3ZOvs/yc
te8iv/G3SBN4/3ba8wnKupl8vkIHvixi/I3/h2fGO97XujDYHHYTk81j13iY
17G1eL42edatbP+L8nWRfVXj2l+kD58v7Zj4iciyFbrwEnXJkJ0kw+PjDfIp
T1m60jZP0I9W0wem0veeCrPPovwV5ZsoH8UV5NEXHeuFnjzN/Xepb1nauQzp
ZcaK0tRvC/2tSjdj/9xFdh3ymhskKq/Xgyupw0HybIyOT0f24bRzJfrMI/Tf
3AFeuwgD5x/SL/FeawlrXDFcwtAty7OR1Lm9/F8oS+uR5iQVN+l09DmU9ovk
fSP6GxPqFPU9RFtcZGxYwFx/nXrH0navM0dsoZxPyqcCGSRrTiaPHbx3FfJ7
UX749MFp9BkZjN+ivpPTHLsofEPhdmsdMI/jQq2Ruhgr4jF9e5JfB/pKV+Q3
FRl/kGU+wGWUpU5Lx253RS+m0V4/6PtU5WCczsdv07n/wyz7vHxLXfaGmtPj
SgvbSuXjofhq+XnIl6SsMDE4fk/6jvRRln2MhP0tfxLF6gozTvG6v1GG31iz
3CBtoQ7PIuvj1c1dpj3kUi3sN6txQd/l+tZ+Un76vOt8nI+6FnftBcpxgntz
oYvlyKtmX8dVLaEfnB5kfgPF4ysuX3aXQsj7UbVBffP2ibPvX8ba3MivRTdj
1wnDriLl7lDHmPbtOd7inS/Jtybd8Vh9yjsmawDv+4Xy7+V8MXkF09ZLOC4m
/yX1HSujPqv++lqkseOm1TN+XBvaaQ6/3U4yLqDwAk/KTo5OrqQd++U3zqC+
XQbRlg9KOW7w3BDHWSgGQzEWsU3MBb1Ovk7kdwGdO1XM8Q79Ojnm4WqK1+yv
dPf57gRfF0m2b5d8vDKHGkutFeme1tQJjhVQTJJik5qQ3kE2+0jb0KtT/Lea
Z+O170Bb/IbMvx3qtpPvs9pP3FXitRG/zTPcEyOsAcp2rbFx577TXpd8EhSX
UN1xlD9Rt4e8q355czLkUJxhtq+ufHajQ+1rPbej+X9X8P7y5FeDvnKZ/y6R
irD+aUEeEfHmNNJ3rPyBZVcV1s7iEONECC+iRpL3sLQG01oslP+vUParwjdA
r5v0sk/XvZHeE9R+YBHKeYhxb9pwx4fc47iNvKtSz99kd2AcfKOEx6GOwlps
Z57rMfWNey/M+86kg+hSR9p1LnkfTTG3+GOkL5F/Z9quZ7T3Ytf29H7sZMbn
m7m9HyOsg/B44x1sYUzZTHqphHH+x0cY678Y48Z67ktCDz/mvjkc5/L+xXwP
FKLuy7Q3wLvHo8N9eL5pkvFehPuyiDz2kFaQZynkMFj+QHXso6P1tnx2ThU3
j/nrlG9TL+PMzq/leM83kcUw+R9Sh7w8M5O+lcp1nXTjsYuXWBzdsj+f5bcA
nv0LfXiXee0BZZqX7HFNnACK/S2S6XikVvTn2ERztVbmuQY8XwadD5L/JL83
pu2H0L6Pag1PvRpWMCfBW4wll+hP/+Y1ZsAnyOM0qQp5BJGKKW5KGAoB5rOb
TRu2zS6vyr0w0njlX7DO2pFk27HsxjuTvKevvf22ZYyDKzxc7RXvLW27qeyn
TwUZA20iadYA8xGJl2gq+fbtZf4DjU2HBttWvDobq0KYFdpLF/aE9tOFtfAy
8viB30fnNwfdGe5Lz2efnfJNHFOmeLJ9yCIkzHg5V7QfgwziaYt99K1lyDiJ
+08291y/IHu+13e47FIH29oHSf5H4loWHtJC2ue3EY6nnyvbB3lt4riHvriX
9EdJ2zfPZpmHU/GYeRhzPuX6tmKzh9nXR+s1+f7oXtlEdf+OHvYVkJ/AGvRv
M+UeNdK+J/JBmc3c1LeP/cxeJd98wtHh/5no30nadTnnkZT7M2RVJM7Y9eI3
0Pe+OA7aKM4JXXiugt/TK9h+Cdo30J5B8f72f1mbXRZ9X+6N8zemvjdfF8YE
v3VjPdF8oP3rO2kMQIeDGzq++IzsUqn281+Vbl9/reu1vpf/9Pns7xBxpGo9
eb2s15TvouevUZ+/Er0/lD/Be0Tign9juPngxRUtzuiN/N+3UjbfMfkN034R
+T86yGs/5aX132/8d47j0rI+v1bF1/Lbkc/O1uHeH9U+qfZVZ2nfnusS9Ntt
yOoq6UJbx1or5roD49L7yOg90mb0uTZ6+CrPXqNdjqZ6bfIfVjzj2ZJMjzfi
m8wtP+sS5jl8d5hjAcUjnkIdR5CmtzOGgLAEbvJ7FvX8o55jl9ZmOn4pGF2v
NMAYifrGqRrs75zetH2vUNufhV2q2BRh1WusFle8xutq+h7lHeeofxr9/hxl
yWxvbllhmwjjRJjSwpMuS9l6aCyh3G+GmKs6M9F81eNps3ro327U/m+eL0n5
AuJ971+5zRG5kLq+QHoxyv5G50lnivj80FBfq4+MCbDua87T3NetpnHf9C3d
uIz3O/drviWlU9d8pYy5Io4u+TPJr+lPyh8WYtyXOz0cZ3aF94Ygq89lWxAu
iPbfOK9VzOfThvn6IukL6Uakz4VVqOtx5P84urs70fyTF5qag1I+gNGk4JHm
TNVYUIj103V0cTy/NWlrf5TPSQX7O3bhP/9p+Tl1MA6OfAVHVbU/gzA59H2u
mJIZHB+vZJ7IVaTlPP8u915kfZ+P+etQNcfzC0u6ZrqxpYWJJJy064H23xG/
wHzKV5S2nklfKcbxYYL99OSv9z+tRxlXGwQbK3RKNq5Ch/zmbhffdbHsOV1z
+1Nl7YM4k/OmtPslzq+U9TxxmPpvKGSfEa3r9D12mOfXo2N7u9k2I4wZcVvK
B2h6mn2C/lZetNds9et0cxOIo+BiP9tiZJPROkWYMtpzF7/trY7GMW6RatvT
knR/s+t7Xevsx7nuTp4H6cuP8l3UG134EV16kfc30Z4rsqjGu5fTFkFJ9nMr
x3vOyhbO9Zjafu4d+Uplek/1MDJdNfj/c2PrXBy3+qY/wbFBW/MNiWtIHFiy
yz9AFn/3M/aRcI/aMR71kc8EZT7e1t9p4id8kjwWak+KZ0dqb7EA4xvpuOIC
KeMUdL9orHnKxFG2mWc+J82nXhfKGiteOPFLYrw/I/xn7dHIj0/+fI9T5g20
+xT66evUvzL51Al3rMUa9CiqoDE6/6UMYcjxV8URMXb3J8Um+Pv7X+p7k+OX
yKIPso0l/ZxhP1/tRfyFDu3nfU2pe9FC5i14qYfzLI5ef8lvZ+ivp7Wua2pu
ReGibypinhjxxTxVwjE/iv0pQTm68P7X0ckNpK+yzC0r/F7xlZ9KNmf5m4xz
hZF1ocLGhhSHofAhhU8u7CHhDmk/aCyyHtfSfVP9Uj5It6j/HtJuUlfWdH+g
W7+TxpP/ONIl3nkSXTsTbC6TQ50dy/MY/a+gdJKyXOb4mPYL+H5/XrjO9OMy
+k7j+DPlvs9c+a10lP6QiH7loF3T+hpXUZiK8j+U72H+luZrEFeDsDcVw6j4
xcqkv0uZz+6Jsl7XhWev7eS79hSphPb5atmX/k2Nd1n2K5JPkc679vO1xhr5
Jy/r5/FHGFwagyLQuY9ou29aewzdkD0+N6xujjLtbwgPQVgIj5QzD0CjJuaC
bUCZq3PdkGMQeeWlfo141yJkMWGQ7b5v5zYn6pTmxiZ6V/sCWfafkh+V8Cq0
965990n81gRZn2D+OUmaKDxB7u/Hb0W0z17D2AfCtp3GeSfecYry585tfi2t
YbROuUr+m5ird5COKyacNV9e0s8pjnfRnq5iXqYgI4qWIz/1bM+4G8440aim
v9HELazvtAPcdyzNWGN1KWsdUjr637aJsejbNTEXojgRxe8+jt8OIN+/yKOX
7Bq0YQ+OZyjnTu7JWc8+MR8083Vd5cs76ssWXcYxuw34PV9J8/T8SBk2tvS3
WS35taALddGBAoob6mMci3Gy82aPdRq7Llc2jpP2RB6lXdpTnsrJxtpV3Oq6
uo7LLD/SsZl/0M8b9HJc0bpKxnTfxHPlw+yTLN/kf7jnc/Ttw3Tj/EzJY6wf
2axkuwrheIL2ukGfOdnYODjCw/mKYzr94CD55tL3tTCUKGdz7hlKfztCXx/f
2d9Ur5QwhtqBAR6TuyOrUPniI4N56EZRfmtYyjzvwuToyFgcRUphvvpJvjqU
4UPk/hX9q0lD496fQB7xHI+k2vYgu4Ow58XbJIz/jeS5kP8+T/H5H118/XSm
+bbFtf1doteCWgcqzkTxJs/Q7/L3cLyn4j7706Z3ZGPm+CxzyjxSLdb5NWLM
oSPflqox7ieKzd3NXDMNOcfxvvPk9zT1m9PeNj3Z9jp2s7+DfDjkvyH8lsq8
uynHzcwHDWiDkYx7VVPtbyy/Y2Hoy68uMMPfBE8M9HeBbOSylQtnQn4k4s66
PcK+JeI1EaeJbG+ywb1Rxjx7il9V7OoTvRyfuJH2P0J7tqAd3+W4qpZttLLP
HuKd3yLXA5k+T6ng6yzkclh7GpzP6Gxe2sdIHanzHa4v8b5+yLCPxifqOYf7
kzjmQc+aoB/5kV94Y+NJKDalR5ztq+JAlY21GTL7ooP51Mohg6k8O5017aOU
Px99NCbC13PJ91lSN8r1Pf1rMvW5qVgD7plJSqEtejAuH8s0f6f8MeakeC98
NnkEIcOrwoIq4f2Et9CJZch/O8ceyGcifbwW7XKffJ5mLIimTVLqGt9wLfP/
PY6VRhqDqinj1E7myRbIsDP6tYD3B4YY91w+Q/IX2kC71OY9YaQcXD/k/Yf5
7x3a4F3SYt5zkvVyM8bAWfTRmrz/e/L+IdVx7pEjbUNehU7EsL54lTaOp41P
8OyXlGUN/acF9VrLcRr1bos825M+YAysxvMhyHkNslxNGklZsuSDJKyY2vbF
G5Vqfzzh7rxAGkhbvIIezEA3ppP+h54uZuzd3MC2urK8I5H7L5NfOvU+08C8
tFM7m5tWa8O92evDDX1cR9X1X/rLFfTyWpaxlr4nrUg3/8bDSHNwiMdM46TG
y4bkH1fP31Ly8xBOjTBqFIv0YifjYmgcejd7LBIukHw6W6S7LW/KDkQ5vhe+
zDCPef15they60lKYRwZQZpE3rWo08eMTUu4P4W800ibCzh2bl2GY+n0DaRv
IX0/fUabfEr6gbp8Xd3c6uJVj+f/LyhHMXR5Am35BGmFfEGYZz6hnxfgXaH0
ma2cv6+xiLoG0H/rUu8kypBezzi4ulf31eadQ9Hbk7T/j1mO+8mvuFr6zwzq
c5Nn8+d37LPinu+TxtImfRl7PmhvPxFhmst/OHSkcVeEvyLc+PGDbVcQXr64
9VZy3FfHuAvvcNw+xJx8Ozg24F2tKOv5aGOYCcvsIXWdS76DKOf/8hp/JIg2
+SCX/afEwSMfKnG11mb8qkuqxji0Bp39KctjvXCYNPZr77A7Y/w8ynNWc0YR
4/L9IL9Kfaezbiky3HHL38nmjU4Pb2wcA/HtFiW9xfv3BjgOeB/Hn8n/Cebz
X4KMcS28BeFch/ewzUW2F/UF9YOBpKa0URNSAn3pZ637oj1PyK9ePvUf8u7B
IxwjpPggYTOfG2Z8Zu1TCoNEe5XTW+TIMbqjsd61f699/Jc5P9PJvlHykQqQ
Dwvj5sEA46ncSTCmivz8xOkjbh/FkiuOXDgU+q7+hXSnpM9PRPtacZqK0azC
vSHaR+X+RsipFuu/GtSleJo5wbWWztvafJFvlDJn5FO0RQWOlUh59H2JjJ4j
HaVePbT+1H5Gpsf9WmXMiy5+9JKV7bcq/9X/ZXrN8XW0MSaqojsxyLU2dfqG
PDvwzgjKHzzI3ELa75ePlvyz7pc3zlp8fuO9ZSjmgfGxK7L6lHw/Fd5amOM+
aw907Ody+v8rpJu8f3NF46x/Qj5D0d+bPPcnqTO/ZzE/9iS/SV3sI/E3evAr
8lpE3V4KMka+7HGyy31b2pw9v9a07eA37itZwOcvd/f1OubmzTHGp79A//qU
cewIdd7Fe2cl2pa5jjb7AB2fGuo+p74nLgFhfgv7O1RrugrGMReGuTDnnu9m
TvAZPD+ddJR+VE37sMXNmykfy9zIYgnH+xnGNBa2cXHKNoJ6J5NiRziGWfHL
w3nmCX0nyt7c3P6R1Vt4jXgo1WtG+dDdzGm/ulzyx0I2EaQZyK1ldeNI76aN
ZzMHL6X8se3NBSUeKJ2/FOBr+RF92dq+RMLkzt3NbSsu0Sv6DqReAxkLQsjz
fd7XnD5yk75wOtE+MzoKt0s4J/I/W0l7n2EO2809q0Pth6dYvKOh9qlrUcN+
dfLn/SbFPr2B5Y03WZHjgdquzzsccw/2d/5s1gf5ea41bfAT5S1Lnk2oQwf5
zMsmTv51kOkY2vE31kBB5BlN20VpfkZXc9JvTqODs+uaPzNK9mjuuYp+FYl1
nMX1LPsfyPfgJjp+UPZa8h3Y0bYH2R20H6E1sPYqxGNUm/SRMOVII/j9MGu5
8+TbALlvZcxY0cB9JnCE/S+KksdaZLCVsj1A3mHI+2FH40ILH/p5xs6z5L0a
mTfK8livcf4Pxsiu9K0upEfJsxbPFc9vHgHxekge22izpYy7A3g2L+NsflLZ
GGO7JNI2YZQhorhl04l54etMY6oKT1W8z+LN/ZOURnpPPoKkbV3NXT481ti5
n/Q0fq78SeWDKJ/SX2mnSZTzt9reL9Je0cbB1iXhvEufCiSY86qgxnxh7XXy
t78wFaelGVexSIZ5PRR//W2M48MU13KD/9+g375JWpftHyE/iUv6PkU3PqF8
G9HvFqQJ5Fe3pW3Bsgk/yrPbaMePkN9Zref5/0z28XR7n4uTYHdjcxQ8rvgM
xZlwLBpju9JD6t2psvFLO3NshcxGdDUOnHgmhRcmX61j/PZMqvk9rg41T+oW
ZH2D+mxJ9F78T429N/h1ov2n5UetWLI9ZexbJB8j8Z+LB13zbRFkXR59uV3G
vmjySdvZ33x04qVTHJ7GCY0X25KM/SEMkOe6GzdO+HG7k/3NJr2N5vgA3d/D
ePoT8jnAUvYwetq+tPH6hNWnWMg0ZNs6yns6o0K8rym8UnE6iwtdvM7iihJP
VL8anoO3RHlOlo+lYszkZ1mAcWUBfbcfejOe40/8lgc5/E5+K6l3dfn0c2/B
csbyl/3nrPzS0Zs69JtPtY4g/cS4sEt+Z+T3Ju+sz1j4BsdnWnrPTj4WDRj3
XiWv+G6OmazSy7jIlWnjysz1VRRP0dF+Q8Is0txTYKTnosg046UINyWM5ztT
nqbo71T52NMnpxXzerQkc84a8tpKWdNZc7aivq8i+xWp3it4tZL93F7hOC7K
+ybPtTXvtPinR9Mv2gwyn0zbQebvupZtH+mLXvUnlcgyL+143vl2lPfwgmnH
n6nLRfRmhsYntTfPNpc/Ojp2l/xPyy+Ndj0dbf6hyyMcP684+iry2+iTzanE
8T76ei/W+BZU5T8+toe0zzfai2Osfwmda0/qUNC8O9/S546Q/kE/l3LdkzZv
McIYTo9m4zgdDTAGSBCpUqr9eC6k2j9K+5FLKEMh2mBIpveiJmouQd5LmIPP
8Fv+Ef7ukG//3kH276+c7d8oP8do1pI9mpljvBdt8B1tUZh8BtDWy3r7+1R+
Et15rjnyL9HXe1za65K/nPb4L9e136B8Bt+WjiDXysJKJe/tjCn1yX9Qfecf
q1icSLffvLZuz8aUuTX9oE2IuTTnyP8LGS8vaHx8zRcbyOMf1tL/kv7Qeo+y
7JOtPsz4tcKxncLYPCfK/AWyuc8nlWnpeDbFtf0d6Ji/gFyO+xPWhuIShL2h
9ZTWVTmY68cyJ2+kLPOET5bldtA3XA3FdWpvhPtPohuvMN6dqu09aPn8yd/v
cWQWwv+z6hpbQLgCxVP9DSE9kb58WNU+Kx9VNd6F7JuKr0+nbhmkyO5ea8b0
99pTY1dudK8obbSmrLnhT6YZz1e4vp2rmQthIO35Bnoyraa5psU5nVrM/t57
KxqHSHhEt0nXc9lusQfZXaedhqWZs0jxriHMQwH1bLNV/KXiMPPyzj/oM2fo
mzc1p1He3F18/kNbX2uvU3js2vvckeD9me35zGf6dYI5TW/Sll35vQu/PUV7
vcv8synQfh6BtOlD3tsq0riP9ZDlW+j2HcaceerftHExfpstfCtksZW8zgQa
30/YfsJ+lS1S/lKyR6amOYZQ8YPPFrfNT/Y+8eNpn1177J/SvwoxN53h+F2q
Y/Ev9PL+jPRfHGraI9L+0Nxo4xQJoyiMsfJt+msR9K14lL/1zzbw977mIM0/
Ia3Nhysu3CPMB3HyP9T+UVfHxaTID3CAeWfFoRLGsQhtti/ePNWyxcsOLxy/
4vW8J6y94bgyjr35vLO5msXto++W2VzfRn/+ymPsamFYj0UGs6PNwyI+lgT5
9JJffEmvuWvV9Rr8NvUuQr5jO3n/ujDlbMNYXJV6nSCf5shxa2f7CspncAEy
/Jy8Zw43N9D8cPMDicc+IMD8WvKXkK9EEPIfTTutQzcqU8de/H+plH25tH/V
l7VUn6LeM9PemeI6Nc7JV7EoqTQyrU77z0eWX1Omu1p/lDdHxBrKfUI2DmSz
inyfFM4F/awSKYT7LlV1H5D+C3dW+4LCoQ0o5O+vkhzrUcZMxb1VtI+D7Jst
GTsGoUePUa5zXI+h7FMY85cjy/k83xNd7U3qg+ym01ez0IGveWYcOhhHPVbR
Tucoczva8GfqXJ57KpLSWjhOTzF633J9Abl8V877Ftq/EH6JsHjqkd4Ltq+/
fF5/o+1KFLH9bDty28ya5+4gc+JGMBa/TB7NOKZxXYc+VYfyPChnHBBh/ol/
qUF549QLN17YgsIVlJ+ZuD7lJ6o1SHue+baYffnkx3dTa3fasVGQ+bv/wxwI
Ne7AH72Ng7BOdiL+W9nQfOXCwBH+zS2efVpjhbAUk+wzrvFQfuPiLBR3Yauy
xhF6TGuZnsZ811z2YyPjVQm3SnwEBch/Pe99U3MmsonKnhuFS6S4gI+6m9dM
e/T3R5pjUfuM50gvpNi3sR3tG1XIuNPCn9Z+wwzKOivSOPaKeT+K/tdiXNyH
zoVx/HKQcco2cP9VxpQ7/H+R4aoG7XgHfZxU0liXwrmMIb+VyD4nOlS6qvF3
hMOzm/I3JR1mXI2g3Afkt80ck5M6FiSPS4xNXxU3fqxwvO9UNceQ+IWmMweU
5f5t1P058m9Ouz7f1XEn4lxZTv+vWcrjnGySipf+HZ28Uc+4gC/TB4bw+2DS
Ut6xRONgd9sDZBcYW9rYfcKVEI6D4oI0X6jPKGZCGKCKm9Cat1/2ule+zvJ5
DqU//E4750EWpXl/C8VjIcfQKsarmE/6mHfdRkY30d8vEr3fKLvKz8OMz/Zp
RWO0dVA8BvVtTdpF/tuQ29ZI24rl6yB7sWKm1zRx3PSzofa3nRDnePitQ21T
0rli5HUdUdhYi+JVUuyEYigUIxyNjO8i393UZxrzfFKi+SKSs4+6TpbvK/07
nLVJKXTuJnXJGeZvphrcs5Fx6jz98Z8e5irS92mRCv5GFZa4+LyFJ36BfvoJ
80n7iv5++qiW/WnFs1MYPbmGHEKRUW/myXn9vRaYzH0FQs2PIxkJv054wIrl
+au1sdRWdDKemnCqhZMnrOo42ikP7xzA8ck25g+uTZmrkIZR3kCO+yjPkED7
XsuWrn1j2dOFRSVeDWFTyV9CvhLxtHUTtSdlCOfYIN34D8KBSKc995P+4rkl
tO/iko47kP+VeJP+JsPYosYrEm7R47Llkc7UtP/nDHRuU2OP0cLA/gx5tB7m
vZxWHDtq3wxdHMB9I2izzehm3jT7ks1AXhP7+Fw+ZboW17NinBTf9BN98RZl
/JnjJfS4bzPHrQqTKaa5sdrPyCeFPIsVNb5UpfzGmHq3lO3Yh0rZ7iX71zba
6e3+/lbUd+Lj1HUr/ecY7xxEf1odYBvBmuyjroXBrz13fd8IN1/4+ZvamqdW
PijaPxcvu7AnX27ib/R4rd+p81SuAyj7NI5Lkc1WyrEkwfzbicLPYXw72NXf
l19y/2JSJ+T1bx/jngv/XLEf31LPh+jJZ/IXDPX3aWKM9xS1tzieOTMYnXib
e9YLp62EcQeEOVCiszn3rtK+48jvBs8tD7fvsnyYZ7IuWIyMFpH+kn8X+nKo
o7Ee9X21C30tKl9E6tRe6zLOP+b5vQ08tt5FFlnIMS/zSgzjam+ePdHfvtRN
Kfsw6nahs9c5ii++kL3e0XVe1m2jmWc+Yyyfq1iLrvav0TyVST+a0d4Y0QXy
GP+9g/yXeddftO8Hik0hNWeMuoC+3iL90cgYFR16GKdCnNUrkFk/+WsWsl1b
9m3hag/KMLZ2In29NvWo38o+t9z2H6biJ7RjR9r/T8q1Cbltp05Ns+yT8HgH
+yPoXL4JuhYmtvCwu5D28ntO6jAlyjyuvdPM5Sp7uPyUZROXX5N8msRNk0i7
pdLGC5FdT9rlu9z+xvuDek/lvm7aL6VOd5j33ytgvqUDKeZf0vn7w31dlfoX
RqdGk+/FQvaNkT+LztcM9LVwULRvJIyhb5iv2yG/G7z/09yWpWQqnCthXA2h
zQPpc/t57q0oY6t2IK+PKEM/2r0O14X570nkm6Oy8Ri0H1CBvB9lDE8kj8G0
cWfuGUTb1eD3G1orMA6Pb24M1X/RmXY1HJP2UUdj2O0Y5NibFNnx+e1Jxukf
ye8pjl20xkVGmc3MqVSWOpRHpvvQrVbcO7uLMRYUy6047o8p2inSh8LV6ebY
GX1/12NufhVZBCGLiGHmMAmRj5vWGfLJoZxj6GsbKEsi7/qYOaQT4+cpjn2R
0x3e+RpyCEIGx/Xticynoq9fyj7J8Yt8jk0XF96zyL4jzyYXsG+f8OS/5niu
t/EjZ7PGrdHUPDTioJE/+hDKtI9398qyreQ2x1PUqwn5n+znOMf68vscaTzv
uAT7VXdUzINwOOjLORsaY15Y89/xbtQox/cFjIP30whj4T1NP7+S5m/uNvw3
vbNxUh6hn71Ivd4h/33p5hx/iVSYsXku8+WjlOk8v0do/4Z+G4ZcytKP3qjt
Nex7zb2OVbx+TcbW4OL29dF6b1ec4+zVRj05HkGnzqMDRwuZS772CHPL16Wt
65AOI79ltNOrzMV3expHQX6vjZLsYzSBMk4Q1iBjzVbeF1XGfEPC3BceYVIr
205kN0nOa+5TfeMIj2s2OjKe40nmjyHo6We07ePU8zFS7WjzeGUkmNfrZd47
h3nowyHG4RYHjPhfbvNfTZ4f2t/cQf3l58Z/Y6v6Wz2Jsn6E3FqSV2vSy7Tz
Tdpx+ADbZpNJo5FjvVjv9WifR35n8gmRb8hLWk/Itt/avpTab9S+o/h2xbXb
mfY7wX91uO+fOubCu0C57vXzfKl5U7bKDH5LJ02hLw5gHI+lPpNCjGsale2L
NV1rP2E0cAzgmSfRrahk7+1oX+dz2uAD2dvkl0f6tptxqF9l/ikpfwSO75G+
0PtJ/4sx7q3y13vuUOZLyGdEqteEnWs5vi2DPpOAnO/ybDf6QBD9eDTtNpJ5
5Wyq4y5f5r7lpEERjs+pwTNdqH8E5XmVdlyRnd6gzKFFzeUYiyzP0dbHqW8h
3v9kVeNGCz+6Cvr3LucHSaHM7Y/I3saYt4V0h3c2oP+FDjJ2ywfVjd8iu1yB
xt4f1bpG65s3uf8BMnsUPQzg/sP6ntMatLb3BrQ/dSXG8W5163o/dkyYeZSE
T/BFuLl4FGs0YLD98eSX15+yf04bDkIvjtMHyqCnH/PeB7WMVSnMypX022s8
2z+P/cwPU4YjGV5HaD2xtJp9eeXTm3O4/WPlG/sndS6tNYQwQsLNFab5V3ti
F3j2tZHGi5GvcBv67jx0NJXzV3lmLGPD0oIerzVWf0M/Oab+yT1HZBuN9f70
cPQ8gbRLddYYSf6PdTcmU3mOOWnviunm9pBd/SZ99E3abXYPx1/r20Yx2IoZ
fF7f6yOMn1iTcpzW3g91/pK0KMDxTx8UNNa1cIz20I93V7E/9LJI+0jLhnK7
gNdn6YqpQQfWkVagYxvUPuRdj3mkG+Py2iHGFthJ+jPK2B0az+92td1S34sT
SQkjPUZrfH5OcS21zC+g9bD2LlZ0sf+UfAzlQ/Ut75qttpYeJng/WphWwhIU
jqD8Y87z7HHkdoy0THsa6EIy/SwX42vfTGOJVaLdfulsTGHZxObTnrPoC8V7
un+qb24e5HjfDOHroHsJlPFIPfsktBJ+RH/vmWge0XwijFatnWeVtW+hfLHl
X7iB9J72OElHh5sLryTfQUX72TfuKP3wXnvjq+Qj75E8d0t21KHGmRLPTEnk
vDzUmN2RyGkbdV5D2YL4htnMu7oydmzhWLaJccdO5rf/m3zfLiKnG/T7pVr7
Nvf79F75472Avqypbex5zQXyO9V8IH758HRjIQlL+3Iv42lHDTGmn7D9EpHX
AcpbkvtO0cZZ6M/ogo4f+aK5MVR3CA+COkQkGo9mTUdzoHShr45DZjH0y16F
vO9/ua2/AQvk93dgAGUs3c/8W/IxlK9hZl779cu/X/787RhXJ1KGskGe9wqR
5w36Q4sU+17L71qxqTcG2AYelO0DUi/aPq/ns/0lblQ3r6D4BcWX1Zj3xiUZ
A28D7ba+qteyWtM+oF2C0dODHL+j/L+WM3+QeIRkg/sl2w7XL8w8l304/kie
x3nPMdIl+dSgX2XCzZf53EjzZ9aqaL/ts8i2HmNwscr2oz+GznSnPK2bGh/u
eZ45XcxxjGG0+/Lu9qsVFqFwCIXJtzCPcS7FnZ1MW1zvZ95QcSOJF+nvLPNd
daA9a5HvP5pXIo1rJz40YdtVJd/q2j9CZs0Y33NRztAO9tET7tceysptOc4z
Pj1S2H74icXthxfJf5/I5kX5+iXapnWGb4U+9NNt8ikmz8IR9is7Qf3my5ZF
+pd83i/mWIYQnqtKWabqO7Gm4zvm1HSMx9/CJ2Ce/ofj/7SXgszyojN3aZMz
1OvvofbHXFfTPpnyBZNP2J1h5rAWN0YzxsXKlLF8hrFuhO8nbBxh/D0qfzD5
ylC2drz/C/T/Fv0kEvns1L5jou17BZBZP/K7xZqgFH1pcE/7U/yHNdXCbdWY
MWlBsnnmPxlirnlhGwnjqHo+YyNoftY8/X8xg7qH247fEL1fjYxPdDBugHBc
C6CXNynP3SzHI98v5Zhk2ZUWVrHtSrognXgVmd+u472XoZnG+4mgPs37ey9P
nANrGdMHp9qPXz78sdT/b+T2S2v7BMofMKiE913ExSQclaeQXZrWdM0cx1Yp
wLFs8vv4KntO6VnUe1PtSjrOUvGWsxJsKyiF/ItybEn9+7MmmpPs+MpX8zvG
UhwM4pMQl0RYlrnoxEMnv2L58Ym/TjwY3/H8Ktr3WvZR13+haweYg1LJ67b8
QIoZI3JeMWOrPMfxuuyulGUf7w6hTapT1nvIL2ek8QqEW9CdMaIbKTLZMcfi
KVXccQVkvZp3VeR4BP1riW4d5biI8gcVMhbmHPTnS+GXZTluUrGeBZHJcer2
PH3ndqCxhR5pZHyhbuHGhRI+lLgVKg42v8IXXFcd5Liq/MivPHmVZs46prgU
6vAiOtmmrdfQbduaL3QA40gcqVZx4yQLL1l8m+sp579Z9i1pXdD+JRV7OmZM
8WKBmeb9FeevOGiFGyn8yO0h5reR/eVd5BKPzhyO9Ddddf5vH2IuwfJ5zSeY
jlxTNM8gg+n0p6La26Y9hiKfEujZMI4hHKuEOh7zaer3FXk/7Go7iHx4ZQsR
Np8w+qYWtL/CV33sIziP81NDbUeTH+VbvHsH6XN9F9AX/ixljFjZZWWTFXau
fADFaSQ/3sVD7Ms7qYwxFXJGGYdeMbNyvy1Pe4yiTBUambNKGAiK597NnLWN
dt/D8THZ19DhUY2M8TG1njE/tObW2rsKaT/ynaMxsLh5fsXx+wX3rERv5tGW
q1o4rkExDf+kG8ctQn7qfcznuwxd71bKe2vHSIeLGzu8HLJ9nPzOMNafREbp
HFN6Om7lkWIeP2Ygv/e0riW/hVw/L5sI8ljJc2soWyCy6iUsmqIuSw2eXRdn
7FPZiY/k9HzVB32ewDu7U68iwklAVt3I5zj12NTCccNj0MnJjOlnahnPWLjG
C+t4XtecLj8u8S4K/yiWtgykrCOi7TclDjr5To3QPjf3XKrpvdc3ezp+Ob64
Md+Pj/BR+6g6r0Q5f0L/AjluRb+31HZMwkWt7+k/f/H+nrRZrzq2iV0hz6uk
vdT1OvpwXbgfshkg5+vobDL16yQbUWOve65S5qdZH7xE+Y4J5whZJmmcQGfb
sZYcX8LxUMJmqZzieN1EyamnMXeFvbtStnJkmV7Ktj/hazXrbN+sr6j7Ktpm
WLK5TrWvrT1t+Yh9WMo4NfLBki+W8KmnjzC/iXhOdpawLUzYL3vrWx+nUc68
tNkgjvk4xtGHAmnnP5HpFfJ7McLfJRpvNO5IbxVX/E6a44yFRSMcmg/Q9TK5
bGuXnV1jbL78Hldlo/uCtJE+sYJnSvOej6jzdvlA0deH88wzvY0/N4/0FOvs
uBHGpYtGLr82NH6i9kRz865kno1AHnO1t8C7cmTaf3EOfesZ3vku7x5LGcPI
s45ibanvOPnMlPj/z+uoa+FmPZc9vrdjPtuFTNoI84Hy9tc3TQHjGwir82PG
4Uzk2JM5dar8IbWv2M77/fKtvZ29Z6R9N+2/iU9PPHvCOfuEdJO6r6AfVGWO
X07bH+Ndb9Gm9WjjCcy3zcu7zCpvp1TblWRTEkb4P6nGVQgh/8/4bYdsc9Xt
M7yf33LVMifMbMbzrpT/iUTjU0TE2D9QvoHyn92FLiVzzzD67yHmuxPk+zrv
O1jUelyRPLpSpjDacgBlyaK+E/jtyDBjj2TRL8ahHzXpw3klC46DkPU5+vJn
pK3dHSt3kzRcvrXU/5+69k+Wb7J8TiS/XOTZi2MG7+zBb8UoS1Pe0YN7Hqba
z3ki9X6Esn4YZ1u17NSX0emJPPNLV6+5DhczJmFiLWNDCBdC3H/i/Wspny7e
0Q+5fV3De8/yo9b+s2x/0lnZ/7bRX+eE2MdO9jPxA0UNtI1Xtt7l6EthZFqI
dBwZfF3W8Zjy8bqMrBrTbl9z/1zkkYE+5M1lHsCp1OEm40Nn8uxHusd7X29p
XsL17Y0VEUdaLh8jZHQz3VjU14o63r0r9//T33gKdzkOkB81MtpS17FbilWt
ONx2Qu1jylb4K3pRGtlvaO7z+2183RI9OEg+83kmJd02vK+Qc41mxiUWPrF4
DvMNcxzr0Gj7ecrfczRj20XySWWcWZFmHLFwZD843ZzpwqpI479hlOkR7m1Y
xeukRpHG5ttJ+kM4QhHej9W+7L8htpMIxyIYGTemz3eJNf/me91sKygda64u
cXYJY1pY04U4lmR+yeKZ4tnH7SV9Lr9++fd3STauzrgI2xSEmSvs3KkDzR9y
m2d+yj7+GuBzfd8rflU4UjeCjSfxHzZgKX/fNmHsSh7mtcI36MMCZPka67VZ
hWwflp24A21egnK8HecyJuQylvZU8tiVjSFZQ/GK9PdznR1fE4XODucb8X6W
4yTFu7axr+MJFFfwKW2zjDHtE61T5ANAv6nW3mOIxjqNc4rhm0bKTz2Lsf4L
55lofl9L+8fT9v37Oh4qhLG4H23yd6b9y6r2sY/ZRMqyGP1c2sXncwb4uiNl
PkA9O8U6hqJ0S/t03aH+DyhvJX7Lol/Nkd9DJ/tIN0+1n3R0CfucdynhuEjF
RE7paux5+VjK17IIfaMRbVKMuTFihLESroXb11P8F9eZJ/oVtn5KT5MpdzNk
uBVZ19ZeAeNnCXRlJjKdTXoBnWuF3OuigyvpD20b2Sd2A/PwTs5/4P+RHHPx
3DJ06QT9OY7x7Bfa8GfSLxnGfVOM/Vze/2kV70vHU68KpPA0f2Ok1DGWy5vy
tUV3KgSZm+HjNvYnFubGm83tkya+2uOB5qwVZt7wgcbNm5zDMVGKhxKvijhV
fqKd1gSZ+0wcaO9w/2108Id4f+s9jyyyOOYfYO54cciLb+l6ts3yIm31uNaN
jAlFBpofU7ySOdoY8/RGtLFItBbROkTjfMd6HutPCMc7p7Gwi9E3s9DF4lq/
j3Csm2LexKFXj3fUJ9WMM15xs0z7su4baX9W7VWejvd+Zb10x6ueRZdack89
3lk42v4IVxLtk1AlOy5Y8cFHKepxUu4BHocUV6+xaBrjTf0YY42Je/Y5ZL6B
d+3r773pgfTzXbTXTtLjtF1e+klh+u/33NcBmUWShpPPD71s3783whhVv/Hc
VuS5jHm0SgXHXU9FVtvSvdcje4zsMsKur9zQ3JDihdT5jBRfy7dBvHfivBPH
hrg22jJ+F6U/NEQPnhziGFitwxQHOx/Z5+e+fKR9tH+h3Lbv6FtVccZZLY0r
2UtjBO84Qv+qxni0r4B9OuXbmbeB/Se0bpE/xW+sT8sgw+uKz0IG+yn3n5nW
Hx11/SDC2J7fU96vtR9Ofu0CzAMfSFsUj3efV99/g98LN/F6S2sl+ec0ymk+
2ofo1f4R9g9W/KviYD+TTVi+c8h0Vrz9RYSZLv+RwshgITq1vIx5acVJ+wjr
mpmdbLuXDV86Jd2arbU4758W7/NA6lRPtkne0WWA+Q03RZnbcD+yOEDK6G67
QBgyf7uHfXfkt/NQNmPKG0/ZTqMrY0hnmIfmk+evtPV1UtuW9s9rx3FWgOOK
FF90K9Df2qvRoxmMIy9ShveQRzByLxTg+Ka3GLv78uw6ZLCYdxRi3O1FOefT
t3kkxy5+S5HvIn2xBO2SB50pQB0+jzDvTYlK5r55m7JORJ5X23hfXPvjd/PY
R+sY6W3Fdml8451f9TYmXr4uxsXLR3lXoDtFuzvWPi8yP5nueFTFpQovvA3t
NCXNuHexlY35WEo2UXTqDnm9yJywj3F3f7Q5jZsjv3M8+yCH4zsmFnaMh/xX
r9DXKqTZD+FBXfsiCCtpCO0yPsx8obJpyrYp33HpyIqCxs+LRp9zjDI/07/o
9N0abvfzlHEI+QXncnyr4lwXokv3Sd8zxk9BNsHUbW0x64jGHvF4CiNcfoqf
Mqa8wz0bqEd6gPHm5sv+hFyqpbsvqR/NaWmbo2yPsp2Jv1X2M61h4vh/Df1x
A+9YTwph7J2XYL8x+Yy9yHy1SD4iDYwZU66TcWPk+xCR/Q0ySmtl0rV486UJ
H3Qx+e9FjxMZnz9HPk/r+5210mSOB0qb/zsd3foB+ZRNd8yQYoUUD1OT/vl2
qDlKW1HedGHBkHe/ofYJrMI7VnczX6B4A7tx/SzlSaMtcso/sLe50/4p7XhK
cRh+QJkKojvPoaDRPNueZ2exrtka4W9C4Q5fLmr8V+HAttQ+W3f7j8p3tE+i
sW6EeSMsOPFrCVskuJ35pMQr9Tvj42i1Jf81ZiwaNdTYsPo+/1ZzQaJxjIRn
tJ7jEHRvMOnvMvYvkZ9J+QL2EWjEumhTLWP3af/sIcf65DeH/PqxTuo60L4/
y5sYg1F+ii+SbvGOWz3M9Sd8kFxNzQ0tH8VE5PsUc8Qq8vlpqPE1hVkgLrUI
8i+EPL7n3WXbGz8vMBtDT/6OJwrY/1E29uPZdvY+st1Rjs2pjs3Q3rBiNeZF
2+9ZPs8lGeNWkUbSTqMoXynaZnkX75WkyucwpzEnhTcp+/8D2qt/mPf/5VOp
cqvM8n3uz38VaKNSvLsM8jtS1TiQ8gcVFuSJNPu2a38xi+M4xqXqvGMdbVmH
suXgXbORdy3aNFTrW+p+p4Ix6bVWSM6wr7Y4OcXNOUR4Yp2MmSy7rrA8tZbQ
muJl8kxmjIiTLzfy/Vr7uYxhbXnvUu0NUdfLxb3ml3+mfNblux7S2PaxzGK2
ke0MsZ9352KOJ6/KPcEcv6EO9YRpVtJ7BG+V8Z6B1hYxlW0P3RFkbrKBpD/j
HPOn2D/x0zZjbGhdwmOUfDKF3b6f30NTvce7F90Op18X5/ffSfNlb+D+/9Gm
AZRpsHyaW9nuIPvDz2GOU1C8Qgyyq619HGTzFWNNS8o1RL7FI43lcjLR81We
OvZ3F2aVsKs2U6eMcsbVEqaWYn/upDj+R/OtfL+0N6GyalxV2VtT5ia0bdmh
xt1WzNHyHOZFkV1Z3GXifhCHnLggDjHGrGHcvkBegynHOO7JOcqY+OLe2UPf
qB5vjldxvd5DBo/RR4qQVjCuH6Ov3Y+23UOcnOG9vNa8EOE5THggF1OMCfJC
PXODXqWfHo80vtl7kY7FVhy2eCB0bBjr825JxiqoU8Lr0xGx5nDXeVJs9jXl
+4EyVxlqPD7h8lXgWIox/j3a+31S7iT7C3cnhaJPXXi+muKYqMNqyjWJunWj
LEup30by+xJ59KGMZ0LcXwaVdp+5G2HuxaWJ9kNpw/1TQozLI3+Ao0OMvSxM
eNlQ9B2nb7jX2jlW9AdSb+o/PXvfVPun19s6tllxzWVCjPdXVvvgyK4l7bgS
/XgXub1P/f4Yad8n+T2N5ri3p2XUXd9E5PsvbXY+yd+C8/r4ezBhhLEshGnR
h/pfZlyaz3xau6Nx0uUPt6yPv8v0fSb/hwm97Wuv+NPIcMegbqCcZehzyZ2M
uzYfeS1mnO6k70zqsbKfceP7Iqu7lHlEb69BtBbpwphyhvr1YWw8SdnnIJ/r
aZa/ZN+KY2AH+7PX094+Zf043TYCYSpU6W57jH5vk+j/3kBn+tYypoF0Uvo4
k/6zJcbx0b9Qzv3o4iJ0MY5nWyU4XvYVdHV7mL/nAwZ4vr3Y2XNuLXQigLz/
TXKM7d/ZY538NvPE2Xfz2T7GT9pOn3qcfjqBNJ1xchJj7ERSW+bwbcKiYp6v
T9lvMTe8z7ML441VIcyKgDyOGd9RnnrR14aRXwLv3DPEsl1a07h2OpeMdX2T
9k0gr4+H2x4qWyiq+h9vqLh1/uG/QMbNL5FPZY7dkXs1yl8nw/jLwrUVvq3O
Bw/z9WT0bDFrrpzMj5Oow8vIcXJOc+6Ke/dR8qrBb1XJJ4hUDBnO4bfz+mas
aw6w7uR/t6V5NNYUdDyV4qryojMPyxtHSHhCfXmmIn2yAunHdGNR/YosMtC7
L2u7r3wuexzj417S6+hMBOV4t5HXaVqj1UeGQxQzTp/eWtNjzwLqvbar1w6y
xWj98KjiLCnH9obeM9P33gT0LhcyrSXdr2EMhzGRxnEQlrZiu8Rlrlj144nm
8nmuv32TNJe9WMu+oOKinUH9xvW3X6j2bpoV8d5SZBX7ETSWXQ+ZbOWeeT1t
s58v2z33FeW+4drryvD+z3/rdvTjVdkehGNQz7bLotmxTrJLyT61CvkvqWT/
APkGiG/pekvzL4kbUhyRozh2R0a/IJuYcvZXlY1MtjLxjs9lzdKKul+gzitZ
m3xL/r8jn460ZaTs6+jRX/zfE3k/WcSxhdrzERfxZs43kTpUdTxjUAvzDohz
4GIZ+47Kb7ThMM/7wvIWV4pihxRD9FZ5Y1AKS0U4Kv0GOq72+bLm5u3Z1vy8
04PN5Su/cfHFPAw2Z8xF8isu+19bc7rLfiKO96Bh3hPOPco2MsXFz2UsWtbc
+J2bSBO1L8jY0zzB62etnRVrLzvcD8iUZsiRLF9LOtQwZFKAPEtzb0CC21vY
hlNLmHNTfJtHY713M6OB48Gf7uo9Qfn+vEPdWlPH6tQvib6zm/LnGWU+04wi
5jTt3tl8dS+nmx+4WXFzup1CDlfr+Vv7O3RnOGX7Hf1ewPsuo3OvM9adijbn
yl3y2oWOVmS83RFq/nntoYuDflOM8SE0Dl6mTcejM19xHIQuNyTPeoHGnBPv
qThP/0RW/ehvgYxftfuYH0txdfFx5iiTf464S0fXMJfpSN7Tkf5zpYjjCPKO
cizBD1UdqyKc/o8zvBarSx8Mo1+UamLeKsV6jqlu7JqL9IPaMY4d6Euf20Nd
9pW2P0kP3jGN8q2g3/VGBi/XMvd44bzmH1cclOKhSpJyU458lKEmMvg+n+Mr
h6Y5PlE4qTODjQ0uXPCS1KEb73pB/tiR5imYpf2Yft6/07yuOb0z5fuW8aVj
f9uSZVMW34E4V0bIJyDD3PHijX9Y175W8rkqzjGIdqyjdYH21HluZ6C51Lag
u1OZG7plmEf+QmtjijxkHMxP+QuM8nnt4b4W3r7wcYSNo32IgcJGqOT93lIJ
3h/5b1+BeWkPY+gLmcbVKs3/m3nPV4zB15jTQpPMNzSG/xsxng5CHuH03+FJ
tlHKVjmHOm1jDHl3sP0lm2TYZ1KcZ2eYa8azbrqBDlwnfcT48wLlfJF0nXx3
aA+DNKWTMTtlr326nL+DD9T0t3Al2ZfoPzWQRVfZd0ubB/GXIuYG+qarbWOK
g5GtTLZwcRsJ31y8buJ3e6SCx6ZnNfb1tY/tTfrNn6Rn6BufpJg3WWO3xvA4
jneRcXnqdob/36csZ2Xjp59fp23D5JuAfkxGxpmUfQrHWPKYFm1cD/EitUo0
n4S+uV9QzAd9NyPD7+tJ+aZRp4Zcz+M99ROMTdSA43V+/037Wu39LadvulWd
jAX5eqaxIXV+Kt3XLbqbB/xv7j9Qx2O7xvgy6Fce2qwx+Z+izp/TFm/SD+4x
vqBaOTq0sAyE3XqQNAb9n93Utm5xW4jXQpzZaYz3j9LuRXj2fFNjzhbOrQ8D
r18eoLfvU6et/H821nHOmhcL8u7RpFvIMLSg/dXlq14Q/XyLeoegM9sYs/LV
M7+muDWfIf8s/ltOP5iRZaynfcj7Ofr5aMowJtj2mZ8SbKPJzT0ByLm2/GUp
V03GkT/Qo0r0oSro5/8o02rGid/JI5O8n2d8fYTfaxb0eeXhvh5KXtvRzbe0
v0V/6M4YkVnZseGKC5cf08HWjoPROrYpbTk42+9GuiQZSpZnkf0H/Na8jH0f
5QNZNdD2PNn1LtIXcvL/9+T5cz2f347y9UvU7QvKdDnC/pv3g+zDWZ0xYgDv
bN3avBSKwX+BY1Rf+5eKK3IN94+kz3WhL3wT6m/BQch0Ie/cxfj8dBPbGV/R
/gZt+7Cz50O9fz91fYa+9ChlnYqcK2WZv24IMtqH7IYWtA1kSUXbQeRzP598
A3r4fHWKr+XT/yrzS8kEY44162EsJ+0fau+wEXJuy30FWRMXIHVKdqxBYpR5
0P+iXj0SvWeu/fJ97f+DJ83RlOcpQo5vGWO/IYXF22dSvB+P1DOmh3CmhTct
THfxgArXfZr2zxt63XCT5x6gF6+SUd8B9qvtx/Ez7h3DN9ajMcYbEzaQMIJC
qlqXpFPNBnuvplO08RLl5xtUzTjw4qroUM3+w8I0FGfhzeYe8y/Snysir0Hk
1zPE3+yKWdN3u/h9xfO7sY9jHY4MdbxDbvJpzv1ZyGvmQGPzyk9Uvs3ya1b8
WTl0qwB1LVPGPMeJtM319saaSEPHQznGMOd/it58kmQbqOyfwvBXTMcQxt3U
3uY5HkmZduQz9kkKZa3Pby9XNt+v+Gfk/1xolH2ghQMn26BshPe7Go/tAcc/
qffOZPfDbTW9xv4zyGtf7ee8hf79w3jdh/l3Zm77KshPoVBec9DrnauivRem
eMxy7W1rW9jQ/NQbGZcLMM7kl50u1lwcitH5P0y9d3hVxff9T++9E2oSamih
BAg1hBIIIQQCCaSQkEJ61Dd2UEBRQREVRbGhFAUbigUVFFRUig1FEREsgAKC
iAqKBfytF+t8nu/vj3nOPfeee86cmT0ze/Zee+2u3ZyHYWm0uQh66p0eGet8
5eRpJmc53ANwEESxp1L73SKZXzjMeWQf0L3btHcO6etVBukeV6jes1WaFjrP
7ju6f40M26Iea2HfVo9C92u2ZP2bIcYJgxeOCbBnYNAGpTh2khhKOGrgp6EO
YySv8/qYlxlMDXk7wCyeUp2e0ecLmj8m61mPqs+/1Brwop5xp+5fIcKYGDBd
fTU2SyUb0/We/XR+k/rlhC45TvyP5KkMn5mOf6oeNSQv+6V7pGk83EnMl47J
2eYOgzeM2EniJr/Q/HCLzifrfe+qbD5TeE37NHL+CfCRdVRyJVe1JQ95Vexv
xO94l2S9jr57Xs85WGIc7gP9jMVdJXkI1/oRqnE/UWO0XU9z2GBbJtZ8d4l9
a/jYzsPFpXZ4UZ+TJN+7qxgjBFYIO9uABra1kbuJHMbEkMHbCla8dkLgI1Nb
VMa3Mtz5EcEu1lXdGqifu5WYOwQ+NtpskK4/ov++r+umRNiOjw2/Q2AbfF/z
xiD11beSteqSnYZqh2Fqr7QS9yn9md3GsSWdVOrpOS8HnI1wjzEXRLdzjNjI
utYLR081txi8YvVaOEasimQiV31cBYyxnrVIY61gluUC+bhW7TQ03hwf5C2+
IsZ5jOumGS/9W4DNxW+L/3Z4rPl14dl9T/W4Ru+xM/DbRem6K3XdA1Wtl6Gf
3SsZnqjnHmKuruoj57cGPKPwjW6NN3cyuXPn4L+WXM2e4dilZVM9Z26u5bzo
5Ecn7oOYj5v0v2njzIGVoHZZp3pdO8MxPMyrxF4ztz6tOf1Zlbbq/4MTjecH
1/+gjkOIOZ9mTOhctcV0teWyLOu8m/s7PzW5qYn5mRltXwY+DbgK4CwAz0Je
DvJzDJX8v6rnfqF5ZH+hx2Vr/f85Hevrfj30n2s7+3Nxrs/hl+IariW27DbJ
xJzx3u8lao37WPX/n9ooVN+9XGxcOkfOH9MzxoCL72zeBfgXFqstZnZ3vj/y
/r3T1nnvtxOrqbqN1lhpTqx9trmk4ZF+Bd+zytND7ZPAN3GH3uGMrtmpsf6i
5o1zw83dibzfK9lsON59CeaZ+DL47sDjsQd5ZpLz8jSXDBQVmpOIPq4V48/0
NedwPIDV5Tvyehap70p1vBBi//U09eMKLdIhusfyTHMmjVBZUWQM9s/TjMOO
VT+9rbZ/LDzIN6q2jVZd52cbH47PZYTG6F3sDVgHCs3JxnwGluKs6jJQx5GB
jR9bf3XNj7WlF9XQ8Tv1+7OqW4zWxBvV3pGad5p2tJ0bLils3Vfr/lepHMcn
rbHRFTyR3usJtc8TWru2Rju3zCPqkxj93r6T+fzjVPcv8W9jb9Z1t8Xb1tNE
paXqO0JrTgfNxbeoXc8SS6L73KTzjyXL85ubCxlO5O9CzBN3UX01OtU4d/Du
5Lmdq/5ZpWcc1/teXmodoEGRj9np/nwUzIPuNUPtuESytBQ9GR+E3idG++VY
lc81Z+5TeRPbtObgOSpfR1snA1v27SRjh+F8hfuVz+CJOf9T75GntXaWSk+9
+5uSnx7YsTUnnNY790s2l2I6mCxwhapDmcbChUjzHm2MMyYTvsiv4MzQOn+j
ZPo+/Tevt3mG4Rh+upIxEuAjXkmwnW+XxsN3+m6Z5qKktp6T4JaGY/rMKOfb
AQNGzh24kRlfGyRv9cBjqA33qV3zdV4W77i+B/XdQl2XWM34M3Bo8EjsUJ98
qXlqn8q9mnv3SIfYrXqHU0fdK7eZdaH5w6wPXa8+miYZ+FHv+6rWpNNq+zMq
/0hGK4LLiPMeGx7a9ZKH59RXA+AdSHROp1d0bZsIy2OzQCaJ2YRT9oDm47Ga
F/6nun0nGb1SMvEy+oLa/XSKcw91UHlX77pJ9bpd7XOP+nGp2nJhgvfY7LWP
w6WmNv1S81uSrn9Dbfae2uLTKs7lN7uT8/nBNwXXVBPVfbpkopr6v2qhear6
zXScwDqNw5ISYxDm6BkrC8xJsl7/rTzDsWJwlb+sa4+FOfcMOWhmd3Au1GPS
CRr3Mv75p1bGQF/dw/h7bPH4mMYQx6X2rKHfqrcyZwWYLnhywXXdoTpOVP2q
qx/Oa408qHnka5Wnchx7TQz2DZLJuSoXJWNdNJ62SLbuByvMWqr/FaqE6jnt
VVKJk9U9l2puSB1qjsuDGnN7Z3nMPZ3ncfeKrlut/v6EfZ2uGa5SYbLvd7/q
G6vjFTNtCwnTeViqc0NdrXmhTM+9hfiIHs5FAE4CjMTben6+5KGX2mWkvivX
b6MyXPh8WT/LKfL6UrF5H4ndJ4b/rxzrqOiq+HNvU/mv0Ec4H/g8rJY5oFLV
D09r3o2VPH0nmT6r99zewlhPxlB7jYMmcc7xSa7PC72di4GcDMvUB/1Vz63q
25ZTzcWbmmo+3o6tnC+4aS9/Bi/N+d565nIHF9BU7XhCc+6HaeYzgOsLTgN8
icmaS7ro96H63KeF9acOuna05Lumvl+jembT1tj11I436p6vaR5qo3niZr1T
Kx3fqmHOHfh24HL+JN98zmCAFtEnKrvG+Mg582eFYA4FswSnLbilde2t5xMr
Rx6pPzKcV4ocL7XqGH+TBxeL3nvAaMeUN+hqTt53sV33s/yv0295qm9umPFv
21LsUyS+NVpzwCLJ517NiXOG2J/+jurUQGvydh3rTTEO9RM9u6/aK1fvvB2b
RYj3ZL+EmMceDvvEnpa9TwJ5vra6MXzg9xjr7xHnhD6X7fbcTcyL5qT6Wtce
0Xvm6T9DNWc8pN/PaOxdaGoO/dg0c2XAmYF8/CJ5+X2oY3NY61nz4XSD2y28
yHkkijWfDBziOeMq3acqOF99f1Jy8r9pHqdw8zbINkaxs9pjVYj7u6uO+/S8
fpOMv+X9yTV3QX14czPntCFfOBg85hbigmfqPt+yRqivp2B772megeM9nR+5
nubmJ/T/vXp+lP6zV+2ZIFn7t5s59bH/ERdDjtAwjZWSNO87zunzCMnV2nHu
n7FgVyWvW3qYe6iu2m29xsbb6uPwRPN8XJ9lG/PRes6hTP4nclGQk6K+ZPkK
6Q97pIP0GuCcyuRWJsfOg9M8FzAPwBsPZ3zDMrcV81lZHcc9LIx37MMO7FBq
3xdUtqm/tkguTuu/S3Xfm8DQgHnFj8w63df22+e724ZbS99nqT1CdE21PO9d
2bcuGmc+uW/ynSM6mlhFydc7hdY9mpc49qBUMvNzvv1u+Nye0n2H6x3u19z/
jtaREbrPPbpPgsbIP5of71UdfprhOHrWXdZccqB/ofOVOt+l9hlc3/mo1kpm
t0Y5h+puyU6s7v9fhHH+5BcF60/M0J5cxw3h05yu/niN2BK9/0jdM1Zlh+pa
pa7zzi+VTNytMiDBXAZwGkyIdc4dbOPYyMObOqcJuU3uhGtDdRgrOaiqfnhf
/XJabTxb8rhEv43Jco4q4qLJF/iR2v5DlYsa/3eDIwczO8HjnbEOjqDTDMfD
d9P1J7Vu/gT+WqUmtg9d11jzygLWDbXverXHwRbG4TG+icuGxy5K5RPNwWlp
/4/TgSPnVTSeF6nNclMc90gOIzALb2k+WtTe9hn4IOCF+FvH+mG2h16JfxA/
rMZPfc35x/X/y/T5fcnJIb1nL8lNb5VYXVNNbf2U5GRkC+tfo1p4L/1NQ++t
L5O8l6tUKPb7wcXzwHTvqRpKBp+t5vzBQ1SfWnrnKerzFJXmuv/YAsc2Mm7q
qG61Vfp3dx538rnvxX+qMfBukedGuLzJ3QsXNnEYPRqZNxC+hinwNui5+9Vu
GZKZ/Sn2HWHbx38EB3aWxk9uD+cRJJ/gcR0/lZzdIDl+R+UI9gu19elYx9rs
Gux8onzeMdjn12kN3yd9opfG02vEjuu5yWrnN/X9VTpvk2Z+lY6SvdwEc+7U
ACc+07x38N/NURv/NsbvThuQqypF8vmrnn1ZsfOHkke0sdbrJpL5Z/o5Twc5
Ooi/B1PaqMy4Uj4TI8I5nCK/Bbwi8OvxvLUqafq9heSka5xj+olNTsj0u8al
+33nNXXeLvJ3HdD3t7R0XuudGhtfqT23JztfOjx4j0hf/ElycVHfT9F1QyXH
Idp3tFK5qPk6VPI2Jt25k2tkOZcy6zbrd2iG46IZS+TeXK5n36+yspNjhLeq
/q9ovFaSDLfLM1cZ+QmP1nSOws9am0NsqubqRpKDUWO9x2K/Rbzyw6n2D/8U
+Igbq12aqDRVaabSXKWFSoxkOVrt309z+F+So9slz3/qeELff697Hp/onN/E
0n6uNntb6/oT6ud1Kucl17fEmZOIfKl90p0zlTyz89Wf8Tpeqfe5UTJ4lY5P
6NoK+Ks1dtumOO6OmDuw93MrGH8/ur35aiqptFT92kom2qtM1js/qnkoMsWY
MfBixAYvQyfU8ftC+1ln93eeLz5f2d/n/zZ0buMUlStyHZNJPGZvydpXev41
KuOG2k+Hv+4hvevD+P9yzMFNrj44EGupH2qofFpiHmKOnBNLBe/ibZL1ezQ2
GrN3V1mqd/1S9WokGfuynX1+8L9VCeZdchw80ddx72v7Os/dx+AXE42PA2tG
zlNiyBaq3FHTnJv1QszBCQ9t5URz0R7Ssw4WmTMNnxI4C3KXN9JYKdZcVDzR
emfzWc7puVHj9HO98wGwhJLV15sZr4PP6s3h9luFlDmPcqsy56tlX8/+/gPN
HSHTzGl+SjI9T218o0p/9e84lQf6muv915n/bx/PkfP7pBtnqe2XY7thLVTd
Z2uurqJnTkHXVB2nTXX7P8T+I9m2ZuzM4PXB7RM7OTXVcQXEFJAznLy65Ndt
H2G+bPKJ3iuddmc18/3+Jxm9qJKRYd48sA9gIG4kjqmbOZHvCTDObSUvfXS+
tKMxl3z+tdjnbfVuw1S/dn297j0FjlBt17rMed3I6QbGG3w3Oc3Jr8v4Jq/u
1FDnc8vSfHgb/C3qh9PSoxeqHtvVDttybFchdy+2lVdUPovwnFwaZd4xOMfg
q2YvA68t+cQ3lAZ5ZzXGGo11Lml4+Lt2NBc/XPfw3BO3CzYFjMokzVlnJIuP
6F03DXA+xQldHZdILGyXVI9N1txB+u4jHRePcm5ScpSS6xJcMrb1t1Wf+yUb
/ww0F/ddapf20R5HjKFecc4Jf+9E76+ZI74qcm7l5zTOn1fpHG/bCPHh5I7p
GOk8tOSvJdca+gn514jb/kTy/1GIxy3jF1vtR3rXCbrPYs0tnbX3HaH++aaq
47GIP93aw3kL5qidKyU6H+cD0pG+0rFluDm2Q8LN10DcNTH8CzqZP7O/rnuu
gjm64eqGQ2ZeQ8s88ygxEE9jqx5t7lnynRdVD9biNHPf5lYz/+0u5nhde4Xu
uaWR89aTsx68990TjfkmngnbPjZ+9CBydaELESP+idbrYs39kUn2GYEFJrZx
U7TjG8FEwTsILupDtUEz3WuY3vlt1begkTnRGvd2nPrV8R7vc4IxP5J1TqW2
5GCs5pB4lQOjPO9eG+O593W1c7Laubfa5eXK5k+HO/1V9UGp6nJactFC9ftr
rLmOFklvuUdtcFRj8Xb9Z6vaIlX92TXd+jx6/YS+9vUsUHlCetUQ4nskL+di
zEkKH2mMZGqZ6vOrvquqNqyisj7HeQXIL/BMjvNT0Mf074vas32F3UbP+UD/
2QLOT2P9i5reQ8Dp1LXE/CrwrPSKMAcf/Hvk0358lHNqP6B2/EH9dlSlh+6x
R2Nls/pgZIp5fODweWiQ/WkN2lp+4IAgr84ZzTdr1E83qA8eK3Wubu4JN8KV
M82vArf1nyqT2hk3D28bOHo4muFqvkZlutbnw2rbNB3LCxzDDr/Ebo2T9zVm
blc9joOR071PRJv/u5X6MERlqMbDMbXVvZLdZySb0d2djxT/EPHWxGHjE8Y3
TK6HjyQH27WXebu3OTPI/XEpB0ipcwrAM1sh1bxYKZKlu9TfEQWOh4UPFR7G
iHR/vjo4x27xqz4vTXdcVZsyx1bBdUCs70ZKMK4Z3+2LHXccquMHktndKoez
vPdiD5ZSw7Fr9fBVNnBO+7FaTxtyrebf2Q0c279Xff29+vbfYdZR90tfegpf
g8biELXHcZ2H40/UOP6ms/PZwv+VrPveGWE9ZWmEcwjeWc35obYWWM+prOuv
lzycGeNcx+fwN4+z3+RRza0r85wD6SL7d8nSbbrXaR07qJ92DDU2/LOKxoeD
0zyZbKxmM71jW3Q1HX/U+yyq6Vzh5EbY2dn5EUICzAbYDfJRw72/U+MjRv3+
fifbVtvpHkc0J7fXMUv9uURjbLnmiXO6Zo7kcLyOofotTCVc5QP100nNtwMa
m0seTvkYledU70fxv+r3Drqup2TzQpFzUg+Q7HTUd1H6/Co4FX3urFJRa2yX
LOcobq5x01KljeaED/TcJLV/Ct/r/Tqpjbro+ut1/43R/vxdrs/npBuD3FXf
Xab7z5bYtexsfFGEvuuna84mm/OJ3FhPSNYfUkmpaHwGMfkr1a/ddG1/3ece
bDUaZ/M0BrrpuFN9U18yslwy97uu/Z/u31fPbqV+WaE+X6Ax213/PYRvS8ct
mvM2q3xf5PPJkrGe4OE0ZtckO3+qXrHCRtXvh9rOzfebrn0LHLDauinYTf3n
bcnPq6pLT8nUXM0T6exLVD4lpp7xqXr14rm6R5Heo6Gub6W1P1ntG1nmOvVW
2ab22a/xcwXcWNhYJVOPSfcboXpMVxsU6vlXFbmt9ujeT+rZdbUO1NVY+1vz
4bMZzvmNPb1PmXMkPltqH8GLKksynDPkF5VynV+m0kwy94HqMkb9ObqD83/O
HuMcoMmq9/OSnSm9zE+5qb45KvE9grPrq3Ku0GvqHzr2KzNX1TnNbzt1frPG
0C0q6/AXl11KW3Hpc/8yny+a5nh1YtWn6V2WdfJatEFtNov4KZWvtT4USh4G
0E7YayXzPXTso34+jQ9wkn0/ocPsC2Itb5XvtV23vSRrYN/JwTVQn0fq9x81
Hx9s7DzQLxc6R0S0+mSyKnilxu7F8Y7pPBa0GXiQ1VrD/lAf3Kf5YJ2uuVky
8LLmoXdU/35q57Oqa5Teba7uH63n1FXf9dX/83WfPJV/WZf0Wx+NuVwwIJo3
xqjfRqvESKZXSm7+UL2Xac85SP8/pjmrl9o7A5xDiD8nRPt8hf77odasaMlL
eE+1mdojFByI/jeE91V5TM+7Sc8bVuY8NR3UDw/P8mfy1RA3PEfPPad5tqfW
oSc1TwxTOzyhYwixRWrTB1XCdZ+JKsORUT13pcZ5DPOQZOIKlRf1zmHD7MMn
p9wI/faS7l1F7VpX5RGNg1h9d1z3aKJnXR7rzx3yfP6W1qkI1ekf1hu1awPN
Z9cxZ+r9L8sz92uI5Kmv2ndkmfukXlP3yyidP6V5dL8+F6ktrlJ/J+jZiRrf
l+m7YUOcy5ScppcR2661PF+lRzvnPOina89JBurT1nr2SY2L0brnGJX16r84
HceWOYcSn8cF52CoxqpeO0o9rsljC58f+bLgBTicbF6JV6VDbFLJVpvF67qt
qdaN27CPl8xMUnt+pndrLpkfX+Z8s/slw/P1/+c0n7XSnLVM903QbxPKzHvD
HMhcGKv6/aUx84Le+8N85xm8Gh9Zbf92l47lSY6ZHKX6zdc1P6jtZkiWVuq8
HBme7DWZtRm88vdqp+p6RhXJ1jGVZI314zouU/3eVbvdrWsrq/9Wq99XqaSr
/UaoXND9EtV/sZKDkSoTNUZ26F5bmXc1b8zVevOS5Doky76NROZvnU/U8dXA
ZoftDhxjUpnHRyvVb5I+Z2guSFeZqXWglnScbXqPOkM9xp7U+x7McUwj8YxN
S+wbwUcS0c74psm6rpLqXEff/a36VIz1O9TUO7WWPpms32/R+HlBk8VGfI5a
I2prjlks2T+oey1QX709wpxaeY38P/7/LfY+1gy1y/JatvmOxw4RYlw9+Pp0
zaeJatexGldtdf2NGgtjJB9luj5b/TqVtVH3CkPPGGv7+D9wGzK34kfHPqR7
/iA9O1Xf7VB/Z0ou8rX2F85wHoaRkq1uWguW6NrxGY6FJW4nDJu52nG12nyv
5tBp+v889ed0HefrOFLXlUr2P8AnrP/NUX2n6J53SG5GaZ9TUet6gto3Tdef
1bycXmYMzooCz1uN9OyTeq9t0819AS9sbb37ReYWvetz6suMMvNGYVtaoPpk
Mv82dD7dGegVkr/XJSvv9PLzqceK8cYANZS+9rne4we191GVv7CLaH6eoTat
lGa//aF4++7BHrFOsEaQ74i8R/MTPMefUJ9HwSPVwvzNcXreHZq39ZgKG9S3
W3SfzSpZ+m+2SjvVv4LmwKa67i3NM9tUXtf7PKGvH9A9UzLN8fq0nrtM9b6b
PTB8CQWeT5hXSvOcl/eadI+pkaM8rmZiT1A7JWlvk4Pc6beFKrnY8FSn3/K8
DrAeZI+0rek/veNFlc+IfdBckqdrn8v2fzarHX5SG4Xo3qtmGB+ITD6d7c/I
Jufwf8L92UXX5et8lkpBmbEsXfWslqrTXRWtX6JbVtFaMwZ7nt73Ba03hzS2
fsP3IWXopNq/q2SyvuaFevqugY4bNbb+1LWF+u9rqlMH8Ab9bT/ZpPa5Sm2z
Tv8p0Vr5q87/0xw2ERB2uOMd0tUGG/X5dfpuuvkp53V3287XcbrG3V7V4ZTu
8Uq+xwfcyz3BUWqOPxZhXE3/PsbWLOntHDV98xwvfqa7Y8Y36PNbacbrt5tl
Ds7I+o6Pul8yP6Kb9VX01heItw1wkCM0lxTp+1jiFzQWzqi/l+v7o3HOPUHc
LPkn4DR7Vu3VHL+72n+aym3EDakeSZM97xWrlJSZx5jPr47y+eWS7btqOH/C
ffpfKbKicX6aeV11vQbMtNo/Gb4wyWOtYs8v89W3czWHzEDfYg5R+02WLNSt
a7tsVonXLuz6Z1X+GGxfJH7Ijex1NHe8oHtW7euYYuKJn5rkOZW5tazM7TBb
971KpaneZYDavb9Khurwo8bVDyrp+vyA5voh4xxDAucjMSXEv+/ROOjHnk7f
t9F7RBV4Hfsi0OfJnQ4mrai2c5aTq7yfZKGZ3i9O331bYlwbeX6I0+eaogz7
YG9Quz6hfl+nUq66jmArW+g58EwrxzIO0hyXrOcP1vEdtel23SOzqXkqU6uY
t/Ihte1OzbM7VNapD9fouxqSy6k6Jkk/+gcOvyzrCBMkc+f1jD+1JrXN81xf
WGyet8dVx5+0xk3Cr6g2LVEZkGv9/rIy6/vXaP7/XnPSN7r24UluK9rs6HTz
6sZo3D490PMq8+vPksVWgywDYJzgWLwtxe2xd6DzIL2IzV2/Z2Rblw0rtW47
T+9/SN/Pkw4zVd+X6fcy7E+alz9U3ftqjvwYW95k+27qxXn8MHbIg0BOYnIh
zJVstSgxv9Ddeu/L9R5XqLzV3FxFIer3RPXJUc1TE3X8TefRks38Nv4+Jcm/
bdD5823cxuPADuoe14b58/Z+Pr8uzroTOhSxZHdnWm/nefCqwq/K5yOzfM78
yjy7XGN5rfppTaL11dnMc5rjr0OH17tkJ5mrZEKgU6FboTNfWWY/wAn161+S
j56qX1PNLzPUTi/r/lfp96tVUrUvq9Hdegj6CDH+O+Ara2Vs61B8xRp34/Tf
m1WfPTpforp+oHbYrXJMc89e/RYd7XZbgz9U6+wzutc3zIfMP5LDa/SsZurj
l/HjSh7nt7SvDh/dbpUNQ/wb3/9OzEhVcy/HqA2LOzvfWt8qzkFELiL4U8jt
Cp/KefXBVD0/qat1BvSFCWAAqzq/4FuSxVeHelwzvg9V8F7i2jLbAoi7fVNz
Wox01duIvwpisIi9+lxtsDfT6wLrQ13NlYuLnO8F3atvonWxRpLdXfr9qN53
h+aeqTHmVLxO97lepW0z62LbJGu9i8x9GN/bPHKV1NYPanzMYV+j/16tOq/U
cc0Y87bdpQlgbpn50B6Q/J+WvrFL694N+i5U7/GGvvtb10xOdi7YDB2HaX5f
mOw8sVs1nq7DnpJifZU5e5LGxugsz4U3lnmPc7id9znzNTf8q3dvqOe9pbY8
qGcdKTb29XHGn659p7dtbxN0/4tBnBrxah+pHhMnOB8aMVH4dIkLPBroj8Rm
gjcGYwDWALzgfMZdieuFLh2mtWid2r2V6n2z2vfAANt/sANdn2n9ZoE+r9Wz
1qh8pj7pQpysnt91pLnbG+ldCvX/K1SXm9AziclRPx0FFzHFe/P/6nl/3kZy
crOuGaj/9Kxq+w92oJXqm9tKrdcuSg50kDLr4ejgC1UWSD/8UeMsXu05frI/
Z4GfU5s9KfnunOZ5bJzq8q0UtPqaJ8N13wa1bFd6Q7LcQufr4LnQ9U/oOBz7
geQlVnV9Zqpxy+CXm0gGI9UWkSW2hdzXwPaQo3qfW3T+A/zuGi83p9t284T+
9xt+1Vyvr7NV/z/1++9qs8Oqyzqt8z+rre5Tn9eU/lamcZ2ua29lX1jiI+dr
9bl3lvf+52fa5oGt42GNvX8pRdbF52g8zE3yXpV9KvEs12ls19N7fdzUsofc
peZY96+v58WHGceNXRKbJPYm6t5GbTB0vNs8Mcy2F+wuhzTGu0yxzRDdbtlM
76nZW3fU/NxE88MP6rPzesa3kpWPWDsk9wNVCnSPVXrflj3NCdJW1xWqfW/T
fbZJTj7TusRi+4O+S1S7LirzWsSaxDr3j8bj93r+4jLb0pAxZO2jkdZH0UXZ
P99e5v00n+vn+PxLyURvsK+ap1aEOr8dfNjhGvtpOt6tvt6seh3T/Lelp3PN
xeqe/yXa/gIudGSx7XArNOYydFwtGV2rcgf6sf7zvdrhmGRta4THLWMWGy22
2nL1Ubmev0f3uk3vcFrrxxL99jh9Lxk+peMa9dWd+u5HtW8tXbey1Hw0+vrS
PnmF5rPdeq/e6Laqw4Zw3w87LDbYGZL1SPXj0jLnn5qpfrurzHmmsAlgG2hT
4j3EB7rH3frtHmQt05+LU3y+TOfDJRM7VO+EdI9/xj5cWFnjzCWSqjH6P91/
mo5/617vMNepHXfh01TbLtP179Y0xg58HdeOVX1/1D2nS4+5l/FT5uO5BH9u
zD5Ia1OY2nG5zsdK9/tYY/9+9lF6r5vVxrdq/ByQfJxQnaqonR7QbyvY90jm
Z0teo/TMB8v8/bxkfz6Q7PNI6X2LNO4fKvN6hH65Sceaus9fIzyPV5IMvQiu
oJLtTQ/r2lVTfGwU489zVPbBsaVnFWu9/kXr2phxtgldI5m5SuUhtf/DKo+g
M6jd/qeSqn5aMMNcBXAW8HlOqc/7sg/Tmpar0g3cbqnzJvKZ+Z3zNkne698g
2btF69M2tcGjZbYV1wnsxfPQsdTPMRrr23TdQ4XmoG060faxH9Jtc0KHr1tq
+83RLO/N7sTOqvE6YpZtodhB+8bbN/G75q+8ad73gC/8tbvtKeTFO6mySPL1
rOaWtlpHW0jXuVz7+VWq36pMx2i0Ub8f0rpxv/r0pI579d13VZ0fbh46t2Tq
eXxecIfo2qc1RtuoL+6VnrGyzLY47HAF8LroPEd9t1xj7XL1yeM6n6tnn9Tn
n8Az670P5ns9f1/z4Nv63yp9fibEnwtKfY6Mvq3Pp5vZpoht8b1Cz/klwT7q
RJxzdT6g8bpTffwePleNk0Zqk0WS99tVFugeq8tsG83v59yz5KDdiy1OZU2Z
/RL4DvAhwDfxk+qxv63tqmvV/vdJfmvmO79bgtrjpVmu76pgjlirY/s82zKb
6PwJ5rhSxxr+19Z1Jx6L+hNXis+C2NJ/9fy3NW820bh6QHrFGdX7jxnW79Dz
3pUcP4luQ4zZKHM9wfN0q2TtvRL7b/Dd4K95BvuvdPxy9cG6MnOStmN8Sw7W
M8emOi8aOdGwV8ER/JS+D9OziyTXfXSvwWAwdf/b9N/4Qf6e35+r5P0Se6UP
9V5ZksMhOi/AT6zzp3Wfb/XdcbXLnHHWH58pc9s/XGhZz29tnxJ1XdDFNvsN
FWy3L51i3b12N+vu6PCzUs2TzPdwJbOesK6Ql726nvusvn9liJ87ZrqfPWOS
bbJZOn4c6FroXPDRP6frN6gc72eOvhM6Pl9mzPk8tVm55rmv1V611f6Tuts3
P6ix9+LsydepL28O9bq8MNT2aezUC/ElT/A5n8k5eZ/KHK2hheOsk3xSx74t
/FprdNwW2MCxhRMzTOxwbz23INF2fuz99DF93bGvfWj4NPBtVFMbXKzimNfN
arcXmPs1d4eWuq1oS3SOjfr8Ypnne+b93pK3j/ScPwvtu3lpgo//aj49orlw
ncZ9W43PbqrDDvXN+ypD9P1wOEvTzJ/M/gz79kHNE59qLLxU5j0xe+Muko2G
krUe6sO+uu7INOOAeqitr9F3jTU+Ngz3HpW6Us+X9f8zebb7kQuBnAjV1bYH
1afFOr+3xHYVbCq3hpubAfsxdmR8AfDqLMmyjewVlcp5tgljD4Z7ANsw51sk
P+vxW6l+gzU3b9K1HSWPa9Q26xKcL2mP1qfP4syr+qp+f00lXn0+TmUea3OH
ChW6q28Spxl/94/6Y81M4/HA5eHzeb3MtvHHG5rLe1VD701uBjcsnWVuivOo
kl+d9YZ1B8xIf/0WNdY6xXzNB0M0Zy/Q8byuu1LXZ+Q6Hze5uJtrjF6m9/hJ
cnhS5Qu9wyuq24O6Pkv3Gqf1O7PI68RErX0LZxpjRR9V0/ExnW9WnTbHmcN1
S5l5XG/q65jx39q67fFN4KNo1ME6HPpbF7XvRv22bohtlNn5xsa9pedFqv9H
SK96A91V4+dNHXtortskeXou0n6orWX2S0XmuV3Yr23T8VdsNyqL1Me7+ksn
05zQU/IxSu9d0NX7+/DAJ3VQbXJA73xSsvWy5qctap+3WHMKHHsAvhbO+ZcK
zDu/VvV+RXLwcrrttdhtl9S1DWMbuCf99x30HNXxz0jLFXYT+Jq2oyepXF1i
2/OfWse+jbR/61/JaqbaYmiJ85M2U2kZZT9vqOo9U3V4jzVOZYDquABZVJ1P
ZXptODfSvrRHVDYzZ2u879C1hwrta2SPFKbyr971YclgRJptki1TbZdER0BX
wNbHGhGKvTjDNo2/K9muUaD+bNLbeOHBJV7//mpqu8a5obZz9FZbvKj6zlG7
Lomz3+oO9WO81vk4zUlji63LzQv0NPwJo/X7IL3DTn1+T78/288cARUhCmrg
tqMN56u9J+t514BRaur4z61dPe/tUn126f+7A12wWzvrg4el21ZSv3TJtE/y
kOqxApxWqeX69AgfkXM+48PAlzCtvX2hrNes2x/QNnq3QRojL6nt3tczTk73
kfMlGmMf6pqPkP/+5oH8WJ+PaBx+omNVPSNUcpqZZt19op6To3b4HE7jKZaZ
wgLLDfixK2YYi4sNrCp6puaKe4Y7Byx2YfTV8kBXxU4Zr34cp3K15p6rErzP
TZSc/Ky+eg6cg+TrL8n9Ee3Bx6eZ86JLrm1h2OOwh+HjwL+BjrtE9T6GPU3j
LFHtW0vn59SWvSLNFbxH139a5px+5Pb7Rc/aIzm4u5ExuivUZ8P0/8cCvAVY
i0s+62L7f1iTWV+Yu7vqvItKUh/bHLA3fFZm2yvvxnsVFNin0WyW8VWPE+Or
Y53AZ4TvaAp7C2zpNRzbDM5gXx37afDXwAtVVGT721KtVxPVFtfovlO0Ln9a
y5gI9jpHhzsvUJT+1zPRcczYBYrbmwuv2kS3HW2ILwN7K3ZXOMhaSe5CVGZp
7LxfX+uE2ueC9KQrx3oeHqwSwpgjXkNz+mr1817Vc7va4Rv11V79/qdk+0r9
dkB1/lO6zlu59qNhG8jV2pfTzTa+Y9K9P9fxsZHOt1M+0Dl36krev0VPm+ix
HaMx9IPetb36+Q/Nq6v1rNfVju9pn/yuSlZ782hm6zhc195bbHl5KNC10Lmu
V5vF6h1maQ6s3slz/hcqZ9U21zOXTLSNGhwMGJg9nW0726fPkZqAL9c1vXU8
retv1/O3aNzU1Xvt1nOvYE/S3Zx5cOfxeUdIcF7VNvb1bbyOfCH5+EJryZdl
xqBUyvEehP3Hmi5eN+GeZ+38P1w740iiVUFTV4U+6pfX1c9Xax3anOI2pW3H
T/RcxZy1X8ff9KzaObaFr1E9DxSa25c5/hr996syr4UHyrw2Zgzy+hKvex5D
b1RZofFwWHU72tZ2+AE1rQOh/yyMNY4HDM/XZeaDmx3h9RfuMtZg5Ab5Waj3
LZpuWws2F2yp6MRgMx5PNAbh7CT7WOE7wM+KTfqgysBuruOhMu/59gU2TGyZ
+LaIHWOPRx7jzSovDLN9FdvqEZUxI80bBWcU61cNvWuvfNvHDmgMhY6yzz2Z
50iuB6TZ756lsX/zEO9h2cviy/tJn2Mlg+/purdUKmVbB8euA1YKHgC47FfW
8hqwQWWsdNzGmgOGSJ6atDI/66d6j380/nepfSNZdztYvpHzx9Ltl8M/93ms
+4k1mX4Ln2UuRXBPofmOQ0X3G5lt/XO6xt1NnazTTh3gOeVUYLPZEGm945VE
25SPqL0LNB8uT7TugT4G5vorteFXar/RatNfmhhD8Y1+P6959dcZ3qvmqx4L
KhtzAW8YuAv2Pex/8rPtj/8+0/75vBzHuxLrekUN20du0hjcCJaDOSLLtokY
1XG4Shf9v6K+75pt/blbN+vQYGVmhBs/87/hxp2AOemgQbFLMtqgisfOhQBr
9Hee8wb8o2OuxkRjME/dbT8Cj4efEy5N7PnY9fFvDAFLXmzsERik4/pvI7Vl
Q5VDuldWprFPYKDAFeRIVr4ts00cXO4tkrErpe+s0zz9VKh9Pfh58KNh/8IO
9qtk46jasb/eMXm89wz0HTwP6G0nqlqPY4wyxr9jHlBbJcCd1N5jiLH0Pett
kv3iO2fY/r+hu/O2rFW9Duv3NTrO0bvcGGP/1WzpQEf0/TC15wnd8x3NNyl6
j/V6r4oaBzNnee2qHOP1i/UcbgLW9LBM26+xXS/VnHugl/Onrhpnf+nqEPuK
0EvmqTSPs28bHr+oBNuQ+f5T4hh0/aks+3v6ZzgPJdfyH3zhFfR7ddX3jOR0
D76Ajo6hxQ7zfVXbYnppjdqgPn9Jnz8dZftFUabjHq+p6TjIo/rPQ2D4p3q9
n9na63+InlsmGeg6zdglZAlc4k16/j4dx+i5x9W2p+KMnUAekUs4Eu/QOL5O
7/MK9nn1+dtJ5nFDV0Nnw84PxmG/dLwv421bbp5m+/IYfS7SGjJYumYlOMBZ
33VtlP7XT2WMyqMBngx9/byeeaPmmRp6XkSo5Rm5Xqtx9I/K6hq2KWydYbsU
XALY+sE/7tbePbO9c+aCRwSXSC7NH/X7Mr3D5lTj2DqoPuHNnAeaOZ35/KQ+
90Gni7YPtMsQ+0HhWMWfwD4eXMnxAFsCBg/83Xlde6zM/Jhg9tAR0BXACFYY
Yz0GHeb3Jvbf47vH/47v/Q3Vsar655De9Vrdq4/m1Y3q2/e19hxnfLEfld4/
Ve/6oerxgcoJfd9LcjxPnyeoXj/p/OliXzNSZVyW8aDgQp/JML4I/ATxuDnV
zKmKfYtjU63bTVpaJ0K/hE+NPcB2vcPiGv7MvoBzbP/4AO6uZz0V7C/+mZPs
u8Y5fxx5YMkB+6WOH6YGOXOjjMPCBwgOC/xVqwCDhR5FTk90qXumes/I3vEd
6TEFGqfTpAC0133j9NwLM+w/3Rb4njvM8L6T/efdkt1lRZ4f5ku+H1G9p2mO
b60+X6Y2WMx+b5L7KV3//0NtfU4lLdY2GHIXgUXENlSvvXMY9tF8UEH9cVcV
z+k1co276tvPe5y2ofb/Lk+zD3iC5PxvMBUaZ91Ur/v0Dqd0v5P6/K3qsa2h
sSYvqG8W6Flfs/efEcSb6JrPkAvdK1X1/7nM1yXoutPoB6nOnfaF9JVXio2B
AAtxKtV4FHAplbMD/1eJ1/iKcN6pfjfMNMfqiSzzrGJ7A9ONrRCc9ZSKtkmd
jrZein5KXnOuSciyXxD/IPmpyfc+oNBYjqWSzVd0fKqnxwW4KzC23/bx/oV9
zE1qg5Oq84Qw7+PgVz0UZywh8oBv+JcyY8bAjl2n8XeDSkFjYyrm6LuTPZ1r
mbm9AdhRPbOSynWFtr9ic8BmjD8Wv+zz6d4DsBeoqrbKg3dC+kGY5sfmxfax
z1GdzpR5rwxuIWeWsRfbAjsZdmdszuwNl6ktonT/X/Xuz+i6THBa6u9N2Fb0
nGWac34t817nHV0TMtp5LcB0sffhe/SK8gCTuVfjvb3aI0wlo6mxKeBSmGe7
q/0+yDfWBSwMfQx+7jb99na+9/Ds5Zv1NofthSHmsa3X1/jOBar7V8yPkuFn
9d2r8cacna7kz2DPOAeXiI43VWNiKLh2zc1p/Y3PDA30K/gLI1PNYYgcXUSW
tDcaJJmIBlOqtvqtzPgQ1tkvNNeNlTx1zvDnz4NzfFv4tZJUciWLBexfy2zn
wt6F/ww7wNBJtgXQ7r1Vh1+a2adxKe5C5XnNsy+MtK4L3gysGdy64MzQUS/h
zlTnD1TfBWOt3x8I9GdkHFl/SeNwONh5tfNtetfektFb9V0fHQfoP69NM+4P
XP3HmZ5DseNsUX+GJNt2jw0fjog71AZPq++LhnvfwZ4DTPldaqe5zI/NrSet
yrLexOe/wn2OfetffQ7rYLsHtpUbk+0LwSeyQvN/nQ62nzEnout9XMH6HnM3
fgnm8pp17FP7prE5RyJbaF9XZPswtuHxVWyjOKtyTmVUumM2id2cLBlpoecu
1BjrK/1goN7hqVjbPMAlwNm6FZ6UVsZ7gD0Az4Z/GqwZmLOS2o4ZARvyhsq9
us996IqRxlnMV9mgNmo41XhZsLLbehlPCZYSfWis6n9M7/1cI+PPwFuwL2V/
+lyKdXviDS7ZrMu8b2D/AJYdWyI2RfyE+AvBrrDfxGbZoNi60MMjrA/xOT/d
57dqjBxRn/6n8qHG4wPq+2Z6p9rwa0jGFmqPUCnMOATwCPjSL7Q3ThLsGf4s
8GfTJXfDwcar7J9mLvMTFZ3rY6r+W6WZ87GFaQ3cqLZtHGUcJnhM9vm3jPW+
/x715Yf4sprZloZN7V+tMy+rDnum2M+brzrlSnbPaizfDPcKtmwdZ+r+f/K+
atMrdP/zZdbDx6sunaqbu32pZPOsdI0BcNixd9R9z6oUB759fPx8bjXd5+fa
2v/1cTv7fs8G/t/3A38TfidsfXBLwjHJZxQgzj8N4nqI71mj8fBeqHFIwzUf
/BrtnM34SfoE2H78tOyD2A/VV9/2Uvv1VPmrzDZ48pzBdU2OnL+D8cy+GJws
OiC6IH4mYhi3a4w3TLbu3DbQn4nPABsARoB9PPv56k2D3LqlzrUL7pjzRjpu
zbR/Gz/362r7qBL7V/5RyU4xn/pxYuR0/+GaT+upzV7QHPC8ynhwPGrrI/p9
ntrjX9ZavXPtaI+3mzXWXtfnLdG2V6A/gB2DKzE9zXbGJL3TO5rDtqlsT3Vc
64P6PXmU/cYcOf9O69UIjY0Jes4r0hlroLMOs+8RHyRxFeRNIf4wh2c28Wfi
EJ/SuLvA2JG81dN7jFaf5Gjv/MVM7+su7eng+VTpofe5WGb8HFyGYI/AIMER
Xxrn2JZlasd/VY/7wJWw79S82RFso+TzG8nrtQnmTEPHRdcFL3u7Po9Q2z6s
Z/6oueMOff9JZftSsP9gB+of+EPg83krwNmAsTlGDg7d94FS83L+oH7Ir2LM
F/6Y+FKPJ8ZVn0Tb71dOc55AdIddDa0/4Of6uat9XW00h76ntfsVteFU3etH
1efYSI8jxtDRbOMERun5yWM8/1+e4DUgLlj3WO8e0bUNNC/eXeg4t9mBTxm/
VFy3YN+aYT8U/ihkeWcPY75nq93PqA4rSl3fFuqvaZNtW0ZPxL5MfDg2C+wp
yBDxJdjAwP2D/782y/6qU6X2X2FzBrOG3flryWeW2up/ksV/1F+FGe6z/3Rd
1gjjL8DxgefbUSfw16GzqtyPn12lQrn9KzPq2N+Cjr9Pz52U4TzS7AfYC/yX
bezECl33VLBO0lYdZ3h/y9jsKPnbGev1CP90ouRiebL1LGzP6F7L9f8dut/9
Ot6hOp7VPQ9Oc4wb8W3DNJYn9XX83OS+thNjLyZm5ILGQcMI7bN7236KHbWi
6v+f1t+Oqm+FAdZf0WPBB4HNZI8BrhW7KNgmcE1rSix72Bvx7d6rtvxCY/kL
1ePJScYdMG6IUcYmMiTF+3P25mdU53DJSb7u9Z3u3V7zT6fpxteDs09SfVvq
fxNV6id4n94y2Ks/Veq5m3m7n2ToSb1LlI6Vym1Lx6b+hfqsu9aiv9vZd4QP
qZX6dluGeYuGldrWgr0sVuW+TvaXYW+hDWiLcPRMyc9fmqtbdzWmv3K5Mf58
vjXW55sDLkTsKeSlwP6F7auKfquqkpNnOwAxD9V0XlRgvQO/O74z/GbVy72f
+Aus6ij78SK0Z3xectlMes5J1WG91oEKocZrDO/iOZ69PhgO4v6JDX9H96uh
e4VLf1icbvwh2MOa+i5Pc8ss4qfLjcNHd2Hews+Mv7lJhvF84PpeL/JYwv6H
ffIa9rWaj2qXe4/CXoXYnxaaN79R21+eY/wJeEMwKJu1fixS+y8LsR0Ce0RO
hnWyJ9Tnh3Q8rL6eB1apyDi+bqpHhanO404+90m1jBcEXw1+kM/9g3Ns2Niy
Y9sZr4x/C/wy8ZxrMxyziP96nsZMHdX5TKHXRdZEcIbrazou7sR4rwnE2SUE
8znzOjFwxMKt1DWvavw+qXZ9d5TxTnV1v+3dbVvCpox9ic/gF66taVtNvXLb
a/h8PNPnLQbZN42PGhs5tnLypmBnzxxku3vXwBezaqDbY08P89Cx3wNLz/4P
2yQ2SnyUxAARCzRJMpWk42a9zx+aT66aZCwxmGJsANgKsQM8pjZ4P8oxMqH6
z0vYutQ22zW/1tZ5/XJj6j8gPlY64G2ZXk9YV4gvQk73Fvozsss5uEcwjw3K
vQ9BvjYMsy+OfqO/hjWwTRsfDuMUGzf2bfyL+COzcx2by/wFhyc5JNEr0C/A
fBL3BbakYfml9OvQUF06Nio35uWpVuYmhaO0cbnj2LCl/KOLfk/yuD+bY58B
/oKbNe/epNJnrO1s2NiG1bBugF5AjjUwjetijGsEAwsWlpgT9IJf1C+lkv3X
4bfR9+mtjZUcE+bn46dnH/N7deMam5TbV8pndF/OyRcGvy85wyapndro/zdo
vL+m/cqrKo/oultVeuo5V4Nz0Hgbov9s1vExzRNdVN+mus+0fs6/tHG6bdlg
IrFt85nYHc7rEzekfep3ox3jTHwzeXub6f+PBng87CsvqR6lYKUk6/U0Fk4V
GkfUeoSxRBfzHANCLAh2LWxazcvtp8RfSZ3Yx7Kf/WC88bXE9RHT99FM+wLx
A2IGTNcafr/atjjNvHxNMq3/tCi3DtSq0H78ljq/P9d1pK5vFxq/s7WJjxuD
z+xr8WPdHPiy0B/QI4ghI554sMbqikLjiMAT9W3gmBziccCA/9faOHDWe7CW
rP/tCv1e+GNfHGnbC2NwT19j78Hgg5Vknn8owE1WHeDzLHR3vVN2TeumD9W1
rho3yr5afLYhum6w1rUI6RBvN/F78D7Y6Paqn+6R3I7QM6P139Pqr6ptfcTP
yVpMvDx+yqggnghbFLZhbMTEhhNDMTXCPtaodPvx+gdYSnCUtO1zekac3rOD
7nFCa3YrfddFY6WynvGn5DB0gsd062Bc85l1hPNviIlrbq5CeLSJXfp8knWC
pSnWEbBZzlIZ0s5xBcQXsAdmLwTPAflUwNGHJRlLz5oGppJ17fIAF4Cedl1g
AxuoYxs9+7T65MwU+xnJj4SvEfvIYsnnSw2Nu4SLBewl+iN65Gkd+8Tax/pG
vDH9YPvDC20Tpd1pc3AsYCvBsmCbwEZBHllyYhB30A5dvqH1ug26bpzO/9Z9
ug0yVqDTFGMH3tH79u9rrAt7UOyW2C/5zL6Uc+y+4K2Zr1invq3mtYpYtpdK
g3i2psay18tzLC/YPDB67EW/kkw8pzZdUDHggKhoXw/2IzAkU6U/jJGMj27g
+G3itt/Q2vSl/hei69qWG/MIrz24R3we+D7I5wt+EUwzeOZmmi8/V5/VrGc7
IdgabIXh6u/fJMMPZJp7ICnE/APYl7AtkVuqXbnjM1l3mqpt2pd7zp6l9s0f
7blvruRslsbqnBneD4BdY3/AZ3xbnGOryW5kew3zIft25kTiYrAvYWdCfpHj
0ZKnl/TuT082xjcq2rnf66rU1hyRo7k6S+W+lhUqpOj9QsttywDvCNaRz9g3
OJ9QzTbZ8dW8hrOWk/uHnFuPSQe/OtE+e+QK+ULHu4SdQo707DUdrN+/OsX9
f02q43SJ1yVnwBb14w1aR7bqHrlqw22THBPM2sUaNra77S5VVN85ocZ3zA4z
xqNprnPbkuOWuYc5qNoAx7Vj/2wg+Rs60vZY7LJp8G5JDuaozuc1X9ykdwnT
u7fUO7+OrzvWWIQfNCdNDneMDTKP7C+KMFYBzAIxX8R7kdt1aCPv28AQ0hf0
A3FKR/UOWXrfg8XGmtIu6L2P679HelivhRsRbkj4VLHrZjW0bResBJgJYhK/
Vbt9G2WdOlxyGDbcuZ6GSUaf1P+H6lhd7zimvTFG+IHA6OMXIr84ecbPNDO2
E1znyzp2R3ZZh9XGD49yzk9i0jqUW5f5qoE/vzDL56EdndcirKMLn+9FJ2Q/
rfJZjmMgqw0znhCfNXjPfqWe75j3nlf7l+l/P48zbuTOdvbH44sH2wmuE7wh
fY2tjf4Gs/yB7hGve3QsN+8M714/wKD2U/tcLDDeHNz5CbXfT/hyNK4qDPMa
hf0U/lu4b8m9QSzh2TTHE+KHqpvvmJgWkrMwtc1QteNAjckWkoUn9P4XiIkP
vrte4/uobn1YZUioxwfj5Bb1/xH9d7HuE6F6VZPMr5I8fDzauO8K+f6MHYZz
uBSID7m3o+MB6QPa/7523qezX8c+x16vk967nq5ZrP/e1MaxbiumON6NcQY+
EXvuCukpX5V6P0/uaI6c3yXZWqrymsqqVvY3TFFbfKlnZjNe9R5H1HZx4BM0
Dr9WXfdNc9wZ45Lx2buD40EYc4y9vcPtl8Q/ybpODMNk5EjP7az6rpxhDhPm
FTAEv2Z77M2dafwDcfVgIPCTE18Jdo84jz9LrH+ASYJvJKHYMRldyj22D4+x
/ejycHNsjJCcjcPXle/YHXjiiUEAvwqOdYrqeRE7G3juyeaY6NrFfhL8Jf8M
sZ0Pex+2v38CmxW2K+rN/jmkgf32Lwc+/eIAO9ZtoPfA7IW/ifdcha7N/rqP
5tkreMfBtqnU6OP75sV4X8qeFHlGlhnPnceYT4nvWLfhUmPtBiMMLgVsbF39
d63mjdtzHCceP8Wx4v2nmB8DzM6foxwDSCzgPs0Fv2ksLa1l3zfyhCyhZy4J
dM101S1adW2uefDR+j5fWd84ePDw5K7/RPXpqmtPpRtL8ZjmvEYJ9j/Uq2If
xMVS43NiBvsz/ljOiVclVvUfzTNVNDYX656r9S43pTvmjhgYOGfgAlhcamwS
uNpO+Y5hfbKR41gfYdzoPp+l2ucHtmN0sTGOYB2J5Wmsex+UjPXua18WuCX8
WatDbUPHfk4MJbGU5G15McDYwmEDfhVeDLgwwLFyDjfGPn23Qu344MhgfI5y
3C72zRfH2d7J5wm1fD5/nP1Jl3xJRY5dBWNE3nt0VGLfl4MPxP6WZ6xWXmCX
YD05m+o1BT0FPZV9ADEYMeq7/YOsf6CHNKxruyi2zdUz7U8+r/KdysJEx4CG
DLTP/oaB9tuzL8PPxN4MvF5Wc2P2GumeT+v7xhw1Bx5UuzXJt13zNWxrGh/R
zRxXs1v9eHu65yLmJDiC4Ad6PsE5yVIaOkYjU3PMaXztmoOa6H2/KDGG/Rq9
w3/qz4sqtRLNOw4mZbzuF61xPVDlmQDPAq4F/ht4cPjum0DXhh98iMbjGfXl
2GTHaDM2idGsprrv1OenVY8Kmm9jJcsNI83JAB/DxG7mh4jKMkcEvuifA380
GG8wysQP1Ct1bCacKcSBoHOC1Y7Uc18kVjvTsTSsT+d1/RLJ1h39zP+JDwpf
FDED8EixHwGvcr/q/ZvarLXG2P+kf1ZW3b+MtN34sgTbjo/o/rP1+0DirCQ7
/6oOHYcYIw0+GkzC/lL7PfB/8PmPLJ8305wYU9Xxg2ebGF/y5kTfE+wR9wW/
DXab+fQKvc//1P571Vbb9D6t9N+6uuctyJDKYOzBmjMfU3tFlBsnAV4C7qlX
a7rPzlY2D0/dgItn+yzjyS7xxU02pws6XWRfj0/GZlod+9Wwu+NDbRlg4zel
mfuBfRS41OHBOvBwQ8cOEkM4V7K1Cx29j2NMDkiuvxpoWy+cab8M9P9YO/gv
OPzfNY6fau24UOJDR8cbF/+o6v5IZeO/DoFDUztWnOj7wMEGxvVnlW9zzZUD
tv2VAHuGXenYLOPGpuJ/ULvdluCY8N/S7X+EA4NYxW7lxg2CH8QOiD3wrpm2
QfVU3/ZXe2IU2FbBOQDxyeCbwRYDtprYJ2KdwJiBL1uj8o7+s0Pjcntz613P
gitSO20O1mrWbHCJkzQ/Jqmc1BpTUc/IlSys0W/d0fMSjGNET0JHIg52fU/b
vVdrrDTMcE6UXzUHT1e7/NbIazYxnWAXiTuam24+P3h90F3RYa+XzJ5U2yQn
2S6Offx+3Sd5guMsrxxp/RbejWlVvM/Cbry6wFxk8JDtHGlMIHjAH6SD/KTf
l0gn+qSdeYjA+u7Xc99INgbsTdbUQd7n19LxU62TJfgV9c7JKdZRn8t0nDrx
6pHBGGYsL0g2z8rHk821gk6Qq7H6ezP7dfHvEqu4ZKRtUudjzR1yY2/jNJI0
DjLVBxkR3ousy/R4ArcKfvXmAC//6xhj5ont/qSp47uTphgjGkEcb4HtENgj
KrW3DWK7rl2r+/dQf/VUWav6XpQeXV5iLk+wImBG4IjKSzRP1K7pPnKOjaht
jjmAV2ML1buNkwzUqmx7N7bu6hpbM3V9CVxWGvfJKqd0z0VpHnPE725S/fO1
PiR0sg3nWGDHuV5j9w6Nrdtbe68fpXKwgjl+ygY6jp54tNeDmDT8v7Gj7QPG
L4/eDxaceGCwgOAe4PiAo6+mvh/Q3hjLqPaO6WQNYi26Ts/+V/c+pnY7W83x
FXCNwJHSepB5Uq6UXMxWKalh/B04/Q56hx/VT9t1j6MRxpKBJamf7VjEgtbG
ycNLTuwDdgz2BD9ne19wKjhyzjxPXt6w1vaPY4/AFtGxs/EM4BrQV9Bbdle2
3+x6zVvPd/P7rajvd2SPwV5jREX7+Z8N8NL4hPAN7Up1zAGxB8R//dTY6wFr
ARiP//T5Ypb1dnR27Bi9JCsv5zonJbxQr+mdJvQzRxw45d567wHSN3Zpzdgd
bo7Jy8ExTDbfJxiOpKG2fxK7eYPKyhTzQMIHia8ZP/P3Az0Xjmnr+RC+GWJB
iOcjPol55qFqxil+FOYcu+FaU4eqrbb39voXpf/uizSnDTm7sMG3U11XV7W8
g0sE2wI2EV4IOCFKWlt/QHeonWgf+1e6d1Yr22Swx1xVbGwWvkP8hvBwgkVI
auaYxqNpjnFsojVnvfS3dbXMs0lb0A6PZXveYc55O9KYKLBRzMNwJIH3bax+
W6C6/hhqP/0M3eO85u6Lmm/3T3FcMDHCHDnHB7Ejyn4IPpMXgHNsGmAkqCPx
mP8XixkRxJITU36sruMtibV8cpZ5A1KibNtgfQZXBlcAPAHPFxsfXy/b3KCl
ql+JypIp5piAa6JZU3NZnqvofBp3TXC8I3GPrGdhXQm2cXwusbl1GpljB36d
B+p7vYA/gbkTvulTSfajgVOqF2CVNgR+NPxpo1QiNU6vm25uCTgC4ZcAq7qp
1PzKnaPNSQtnCmsta+7DE6wPwOnD2n5A9RiRZYw+3xO7yG8T9H7fqZ7zexrT
j94NRob5EE4S5kTwPkeDdQs7Hli/IU38mXhq7HqfRDnmeU+U5Rc5Jt6OOLCj
Yx0LBm8+tmts2E/oXdd1sD0UfblWqnVmPtdJ9TlrOLrxVDhKJVv19M4HUoxn
QU8E0zJK8+9irdUv1TGH6rlgv3aojX1CjVT+lH6+Efys1v3xlTx+GcfE9hHj
d1y6QYraYLzkvHFTzwnMB+TrhIOJeXJwoX01o1X65phnfN4IxzaDbVlb7Lma
eJWSao5fadzdumjD7sZH/KGxcErH+6qbMw3utNqVvLeCo+bPYD8C1hUu1ryJ
ju3G1sa+hT0LNjVsyW0zrKeir4KFpv5PaIw2Hmp7EHYhYlCJs904wXG3M9q6
X0KqeSwTp0zOoj9nOF5+S7E//xGcE2MMdgHcwqVx1tFjDSwyeIWEePvW8auv
YY0LN4cGXBqL1D6RxKVr7HTXWtJNZXhj9zt9ji2cfUp8srk6kV1kGM6fARMc
w00sN3FFMZo7r80znidX/b1+rO3DqwLf5L7xxot9qePa+sYNgBlAt0evJ8YQ
m0Nxqn3xa4IYh+6jHN/8cRDjzB6d3/h+r+bAByW/V7exr3xKQ/Ooo/8h38g2
PElDJjn29oDa+i/d5+sc45XALd2qetaQnEbouat0TUcd89Q2r9U1ByicmPjE
iVUiZgl/dAu1xV8azwvVt08lmsP6eR0Xa47sDa4k1zazo/quzWjj/sD/wUe3
oYbt4tjHwc+vH+j1m30GuB8wP/BSjg+4KXu0cGxG5GTbaOEzxo6LHs/eADzI
ion2VeCngPMKvqtVLRz72Aj/3mT7otDV0dnx0TXLsp8OPxIxe/iSJo+3zwa+
a2I0iM+4Wu8Wp+ePV9uM1fFhtV8M9r2hxp3fpjJ/gnmVM7IcWwBevWGmMevY
36LVH3d2dKxrltp8hso9eo+b1BaRNYP40zLjMcFpTMs3XoXYJeKWilWiMsz1
djHReXvm6b1uVOkdZ90PHZA1Am5KOGWYs8FmMW9HqH694s1jiU6+qsD+D46c
o5+j++G7O6e5e5jG//XTjesA64jsRpZ7r0GOLvYbxBfDrUGM8Xxde49kczHY
9Rjzimwb7n1w90rWA2hXeKRoW46XzqUDtCbuW9fOm2B+vyMzzfHHHgedhn3O
p5KpCWrX/sXeTxJzfSk2r9Tx1SdVbsDHjU+pl21N2JmIhbtX9evFfJRrXv1N
ml+vTPD6cTjbOEvwJeBMyMsKVoYYpeNVbdPFttu6n+0Q2DOxa8ITtRGsUb71
CHjm2cOwLvZWO23Osi8FTERT9M8sjy1shuxj2YfukczfG2I8yUmepXbur+uj
cmzPWDzANg32Jp0l5y1zvJ//rKH393DwsGfD3grXMDznp+oZvwuON0b98Iv+
217X/qwjXJw3YycjvhJeJZXJ8a477wBPPpxgcAjBCxTOGhVprmDiTO+dae6a
mzqYXwuerQnogpLl6wvty8FO2lh1rtLW/l18unw+W8vn5Br8XiWjt7ExcF2B
BSHe8V/14QW11aO63zd632Zqo0L12ZQiy0SL6eahYO+IzQ1725qEgAMjy1wi
8G5h18G+Q+4sxtVles9PdO89Km+N954a+wK2BbCC4ASxS07u5DgNsHfghuCo
wHYMxxNcT1eNtW8HvNIl3FJNY24+T3P8Gfh4sPHo52dzraP/n/0X2+/SfPtl
iN3Ddgj/3Q+TjPsH/1+cYRvMsVaOL1pTwfj0nZN8LB7hz3DZ09f0OZh59jjE
zBBngP0fP8CnauvvdF2nro7De3aYY/HYlzev6r35MP3nx6nGt+4PtY799kRz
gBM3RcwU8o2cvxBhvRUeePxM2HWw79ScaR/ckMAPB48BPG9wGWBDUNNd0sfA
5H2oEtbHPjr27vjp4FxvSixPtn0W+Ct6hxhzgt8Y/zG2pz7q3+HgD3vYJ0eu
9Y9080cnG49IzlK4QohleCbP8wcyA24KzBRc4lWHG/cO/h3+SbhNrtfxeo33
2Zrj53d2nMbFBLfjQo2LWzWXpEmu/tBzLlNb3tjHvA/D1WZnI4wRWTnBmJHj
zb2XZh+NXxYOJvy0V6vdxqvOK/SM29H3VbmIEbYVNYy2vShFv9+jNokf5bwJ
8JyDJSXWmzjv7qPNDQcXzeBqxsCGVTAOFt8CvjNk7FHd44zW+wMqjTQ+O+p+
90n3+kJtPRGe0xTj1rBVwZdHbrc1kqGaOu7We/fRPXYl2A+T0MS+GLBFJzQf
NKFRs70nrTjN2DBiEcGH4XuB2xv/C1gpbN/YveF7hOux91j7zw5I9+5Z31jR
K1TSVa+7WWd0n0fDzBXxdhfbQ5+ub98T3FnYlrEr/57r/T/8PHClnu3qHFhb
mjlembjlt1PNGwxnMHYAcGDY4rDJgdk5HGs+bmIneBf22Z2GWAdGF8avgH/h
piGOg8eviU8TnyI5BrBhkD/hHb1P8RjLJ7IJVznXDA6ug7ceuzN8NfPVvzPV
ptmV7PPCVoudlj093Ezo8WvJA6HrzmuPU9bSXBQbppmTmngV5gBiHULV/yWs
l3rm1+iyKnF6/wTJ8uhm1usKVYdvZ5jThfgg4oTgMnlK+ud6lVv1+7XY7MeY
uxvb3qO9zYMMH/K4Jo7rhce1qKV1BXigcrKdh4N8HNvbWJ9DryPe9Q2NH20X
KqSMcDzIM9PNvTkviAvhHF4z+M3gnUY3Ri/+uLJtzveE2u7MuGf8gzdbHeAL
wBmQjyREpUWS49PAla7LNs6N3ATElGJ7oe2XFzvvATbHl6IdN9m3/P/tRzly
vktz2TrtyYaneo6hL9E/4Zq5dYK5Z9B/0NvRgX4cYl0LnYuxs3qaxw/7oW+D
PdENaeZSgFNhYI559fEJzw32pzekOxdXe9XvplxjAYkz6K/njk/yGsFaAdcU
MRNgUdENWctY034kDkJjoAGYmjD/znUJUxx3h9+GvIjkR+xX7jhEYhBjuxlL
H1toPecS50uZeXNHqz7vS2fOlj7wpcZUvD4nqIxV24RoLO2LN28PnD37Co2p
AE+RpM9v67fdksdBFc1rSAzY3rqeE/DLNggzxwLxduTkIa8LfCN/FDt2f+1g
cy2+KT3jZ8n5S9OcTwVfNPs4/NXwpTJWsN0WJ9l+W2OA7ZvYNldL5vZrvviy
vrHtYNy+0vj5UXL8ap5xlsTSwY/zZIq5tgpqm18NjoXygGfhs3hjjMEawwFA
jFa3aPs+8HtgP0OnKw/0ugZBrCI+S/ZQ6HjoeuD0wOuB1SO2mji/pVrXQgYY
3w7OHZ8v/t64mV7rnwjW+wOtbJuGSw9cSWGAuYEPiH1xZluvi3+0cL4h7Afk
rgNXemnNCtYtYlGYC5gHmMOXVrSOtWyi+UiI/wQHhz36XAvv89jv1ZMMndJ4
bVLdcRHkpYkZ59w0xIARC7ZI4/Zy6R8TNV/cWM0+DWJNtg3y+sjaiG+GNZr1
mfjgTzWeknT/OzO8F2Mfho0FHYzYB2Ig4COFixS+dewuxBqzDyc+Bz7KjCbm
DrmslflD4PCFY+v9gdadiMnGh4XdgphaZB/bBzYQuN0eH+RcHcRRkEODXBrk
2CAWkZjE35qYN+sS3kV9k5DqGHFixS+XbFSVHAyrZGwHGA90Q/yR+CUX638R
4213XDve/gDyJ8TVMR9P7cCm+YBk93Ndv7KVsdJwirRQG3+taxvqt+UZtsXg
W2+i4wbpzjvVDwnS3X9o6zge4nku5bCIdh4L1uUjet/mGY5VQ34e0fs82sW2
aOZF/OGrWLN6Bc/QfRo0M98KvCunIqxbheo5bXuaC+OXSd73sz580dprxFu6
/leNi9+HmLttc6i53BoFsejEoX8IR4rk7KfpxqB9U2i8CHY2eJfA1TN3MW8R
GwYWg9/hwrpf61lJB8dI8x1YE7Bsbch3wPjq5Dw2YAvAFeCnwGaBrwKcMXg7
cMf4B5FF5LCr1peJ6u8IHaeqb29Qu8zrYozdnVojZsw0zrqS6no+0vI0N+Bt
A9cNppsYDHB18LjC57o1sO9tamjsMbhjdD1ySMW0cx4p/FL4p/Ats08j10St
ep5js9VWoYMcS0RMUZcMx9HGd3VsETg98HrkbQCXAialuL7Xbdbv74c4Bgec
JmME3RBMOXhysD/o0/1ynE9kT2/nFAEXCiY0qtx8a3CtzepqDAf6D35p4s2J
NSf3Ob4C5j1iPp+L8n6fff/fUV5XWV/xp4M3AXeCP2dp4NPZWMuxZcTIwIcF
Lxa8fhzhybpdc2LzQnPRkP8FHzFzMn7iz4Ybh1QFXHfQd9Vr2waDLaZ3gf1R
z5XaJ8XnacU+Z16oH2KeFOIwyFt3n/p3kto7AlvTGNud4Gwgv9Ogqb5vgvrp
WslZlObCAS2MX2WOZa69TvWeo5Iww/afVaNsA/o/frFBtcyHMSewmSAb+I7g
vmN9GDHB9jr85I3+f1iWTN0zI9yf+Y5zdBl0ms+TPI5ZDxjLC3W/mbrHhV6O
s5oT6M/tq9v+kSEZa6z3yZf85kWa82RAO/ssrw633ZA6MPYYgy3reu2HL3+J
xkjftsZSgalq0dn7EGLasBv1DGxH4LzYt4H1Ih6SuMiuA+wfyahlHwn+eMZc
iq65Xe1xlebea0Z4n8N+p3G01yz0Heze+HbhY8K/+73G3wsTPS74vJyY9AzH
0sCveUZjP7rUe7lUPfMUPnbwS+PdJrRH/Y7O7wUvTpN+nu95T3Qd8PkDVBdV
4ZK/d3F/+3zhbP19pDn60GO3BLps7TzH3RHDWXOE7QjYEC7v6v0g+0J0Nfb0
5EkqCPDgcFkQT8FaT6wl9g3WYNZfcFJDVM9repoHGw7s5ArWRdFDO3UwHw28
NMxFzHPkUgFH1QQfsT43rer5gzairZif4Qxgjl4JfjWIJ31f/Raretef7rgX
4l++y/beNDXT+9PbKzkehliYC2rDTLigZpozn7kMfCfYY3DHD6bY5kZ70VZg
4veqLJpq/ya+zT2SgduD2D1i+H4scj/QH9ghyflC7hf2E3DK5gR+LHItkueO
vETkJ9qkNuzb0jZR4tOZY5lf2UeDV/wxsFWxDyC2jL0AeyL2Q2A44WrCtgnG
Oy7ZuCIwRcyR7KXJtYQt/6o82/OxpzFHMz/f0MmxJ8SgxKg/3lcdivHd5Hm/
iE/21inm09sw0HrNJs0VE3vZ3or9CL8ZOTy+qGL/J740fGpgERqONBcQ3EFw
ruztZN4V/sN/yfVKLsEuMebt6aY5/d6+zo9HDHb7BMdh4+NIirJ+BWbiE7i3
GpojIVPvkVHPfi+4hMHERIwxhwQYSfYZ5K5DdjcPMQ4EPAhcH8RJVuvuOAZ8
KuQkjNectEDPKptsPOWSto6nxh44oNw2wTeKnD8Engh4pLAFYRMiRga/0ciJ
PrJP4vOewB83qL11AGIZwWRiv21SYt2QMfeg6pQfZaw1vC1wtsQHeyX2TLQX
7Ya9Dk4r8J3ch76Ht/yNit5DXcrBUOQ4GTh3F9d1LE9Ktm0D8wM/T0iEfdWX
YsVSjHMj5xn5zg6DaVL7HImynQEbQ0GGeZnJrXmxjXV+OD7Q+9nLs3djP7+e
OAPJWZTkahCcE/r8na59MuCnYs5mbMEjXVhonkvyZd2VaHnb1MUyB7cVnMLg
m8A9gnk8HOq959pk7z87pBsnA17m3aA90bPJobEk03k0iE0iRgkMdaHqXqDy
QaLzaDXrZfxldzj/JZePxtr+QP46bBCDNB8f0jgaEO0cSejul/IklRsrHFrd
saZd1d4dMpx/oXWJczAQi0h8+Zhcc/hMC3wo+GCuG2TeFj7Do8g5nKfEeMSr
bNL7L1S/7S427zP8z+TjA0uTkGI8zddR3uPBpYyOAuYot671YXThlcEROwGf
mwbz6oQC54hsOtX4PjhCloyz3kysCnEq5BgF5wbGbVod5/rDJos9dqvG0Xr1
44MVjWe+NrClgTFYp/JLrH25J0Lsz0UPQjdaqDlLHy/ZLbFfXtvacY7EOxI7
/Pso5+f6paY5t55uZTsduRzwsxN7+vUkx5+iy6DT4KtqJVlsqnmmyizH4DJX
kgPkh8HuczDzA8s9f//dzFgnME9/Z1nngztudrj5/IeOMv/I/ukeJ4yRjmPN
wUtsOPFr4JHAJV2pNa+tnjmqg/fRYNHYS38gWRk52vhR8pV3SnXO8s0x/p7f
4SyC1xxcAnkUyGk7KcV2dvANNXTP5onGLrVIND4f2yJ2RXD5j6tMBhdcyZ+/
7uIcF8hni56Ob3h+lGMcaOPUGOemeaaW7enY0q/RO/WXTESpHEz0OGW8YieA
MxBbwcD25lWDqw9sJnsC/LjohOiDn45zvPXv4R4H22s6/wJ5GN4LuBXbDLA8
kI8oUmVQkv0++H/gY4DP7RIng/onv645ecgL92y288nx+blsn4/JNq6aHEHo
S+i8YPMmBX5WdN0G/czLDyc/+jJ686GG9jmwf4Y3C15IdPKJkoFztR0fSp6U
9VON7Q5L91pGDrOTTcwpA7fM8gq2aYWqbMo1p993Y83rF13u9Y11js+31fA5
vnl8fuTzApcNJgQ85lStMfXBMqod7lTfPJtnngQ4rMGFwG8KroW8reBcyD9G
zCNrMfgTclWCQVke8LLTDvDag7cGaw2X8Pga5hOO1O+NVc/y7o5tALcDfoe8
TXAEDKtv3QIdY3l/+x7YJ7NHJqaB2IZ/xhtbSNwBNqrZzZ2H68rm9ln80cNx
RGCciSts0NK2YfKawpscEexxptcyXx3+l/5RfvclwfvDoUos1touzgE2W223
cbLjXIhxIf/S/AzjWPrk2M/WvIt9bT00l3+j7z/qaqw+OP3DOt830ftI9pPU
91K9i4z3AOtRp5JtFNgnNmfYP048I75b/NFwG5J7LCo44p+G940cmndMse8I
Xyl4xA2ar16VLOyRfO1U2YHfWHPidrXJUOxisxxf8RN26+aODUY/R0//u435
hpZFmr/rmYHm8Fqh5/4omTgeZ3zQ/kbGCKHXoBsQCwXuHCwztuUVnRy/Sxwv
NgpyEZKTEHsmtsxGsY7HvDHgJpshWZqq9rhbbTNedRxUbl0HXAK6FjrXdwEe
pqyLeWqIzYXfA/5PuD/h1ITnCL4IeCPYn2K/Yo9anG9+RnS8j5s4d9+5wcZu
gOUFX0dsA7o1ejUca+DZv2xsHjjyFH462H7ETS3tV2RMgt9ijGK/gH9+fZH3
Dh+p/S7M8h66drb30fjpNMQv+ergkyN/AfyH2N/BEBFzXl/Pu6OOeYzI6URu
J3gySzQmBqttBxWaUwlupeYzPDeivzI/fhrttnhhpjmQuAf3Yq39pKbXXvyA
+AAZy5c4hGPsuyCWfYues7iH8aVwC5HrDH4d5h04duDDebWqOXHg7DudbX7W
EXqpg3rOs609N91Xwf8hTn5HpuPmiYcgLuJ4ouu5N6gr633JCK//xMSzl4M7
55U859klxy751G7u6pxqcJZf4i6Pc66Gz7qbkwvOanRnMIBwL4we4vyCV2pv
86TabHC588Az12ILIeci+efIwfhLuOcA5oLRet51kusN48zVBCYVXjA40Jp3
Nw8aOWVeC+Lr4d6Bd4fYiDUtPE+tbWF+UXK8NMjy+sA6gY0EjgC4AuDRxz6O
nfy8ZOuWTPMrwMcKdwtxqvC3EKuP7Qy72fulxruBewMP/Vms8dH42fYWe066
Xdd2UBs31fiL0L3uVN1jhtqPRGwvMb7glNv2tT0fbqNp0rM2DfT6AI4LLAB+
IHy+2JXh7iLWAF2MvcOgwIaYE+c8j+Qv+TjNelELPX+L5OImPfM/yVWS6rUC
e32pOe7gt5uj73uNMpaxxyjjf7HjYN/DXoGfBpvFD6Nt5wK/zJzWp57nNWLC
sP2D8UBu8NmhOxI/RBxRYi3nzYULvaeO/2aYz5K8Cth1sen+2NZ5c+PRPRPN
GbMx4I25ebA5JOCSGB/E7cKjCH80NlpstW/Gma8V3lbyXhE3R/zcn+qneySr
cwsdgzp6uu0FTQvM3Qj/PLZTcFngs+Cg+7CC48DYP7J3JK6C/L3w7/9UwZwI
cAjA1UAuzlvGmAuez/ATcc6+n/3/HUXGGrHnx5dI3BvYJrBpT0hWr1abzsZe
GWWbObmH8WfBIcm4mpfvPGtwhK9u6Dwbv3ZxnmXyD5F7CI4luJaa5dnWTZ4F
xvHRHMe+wzvQR/drpT65I98xMWD5W+t4uX67Uvcaone5Ntm4HzA/2AGwAaT2
c456uBXhVCT+jti7v1SWJjmOHs4/+FvgblksHaOv5ClPsjmLmJh2tqsRs8h6
BqYHPM8ryGeyc2IRN078ODZocobivydvKDaN7/Xe3xTY/wM+Eh8QsT/EEq2X
Tlmia+cVOV8B9hT2vLQz+aFOdHRuXDCXYC8bqd26633W65ondJ+v1NfTsZ/2
NU8tuWIHZNk+DKYRbONFyeDkBuZkAI+n6egSJg+bFrgAfEtwRcN9CAaHWENi
Dok/BFcChhu+tIRSY03AmUxWPe8E+xhu/yL1o241pjtfKblKwcudz3J+CPB9
t0eYj4Bc1Ic1HurPtJ8K7i58VfgX4O0pG2d+Pny3I9paB2Suu6QHZrr+cD0n
6Z3y9awN7Vy3OJXOfZ2ndYiu76J36h2Mb8Z5nOp4TM8dHud8TeTk3N3XnLTM
k8yXQ9E79Nx3iA0d5Zzp6KO/av5+SWNm7STHcJPv/UQwZ+EfwfexSu24RmXY
ZOsH5F/Hjs3Y/zzC45+5kDkR3Xmu3rGy3rtxY8eIEiuK7g7uA/lBjuC/3ad7
/lnq+ZV5dthUtzdYYjC5PI/n3jHLeK6s0cZ0Eddaq4953oj3xxcPp9df6rud
xJxkWq9FH0bPvSywdWDzYH/CvuT36Z538DExD+EXI16GMU48IdhpMNRgCchZ
XG+KdVt0XPLdwq9wosSxDosmm3MSXfBdHT/S2PtSfbsMHj3V8Vrde0WmeRuu
auY1lPVzpdpm/hTH6RGjx16DeFDiQDdJTo9Ipv7WfLRb7bFLZaza9VZ9P1Py
n93LugXrEevS9zneD5PbjthKYiybjLPOh793h8pVSeb+w3YMZgpOS7gtsafD
D/dbmOt2OljjI3XfT7Ff55i75JpSx4cS28F78/7ECZCDLkr7wCtUpx2jHeeK
fwHOXHwMN2req6F611L5eLr9b3BLX9Dc3yDHuWHBmsCJAW6c+DQ4EAc093t9
F7wb8w3zDnZUZI21FzwVXBWzBjv3Ep/JV845earhu05Un13s7hyO5HLE/zC6
qufYl6rZdoyvAj8o8aHsb9er3depvDzWfj18evityCNFPqkX9J4jtJ7fVds+
2+oa77/r+4pZtidhVwL3Slw48eHwBYApQ6dE54HTpVoD87qAScZeAC55WZZz
kJyNsU+EeYP5Az4cuHBuCTFOu0aWsdrwz8M9j/0svLrtXNi4pqbbf4Mfh1i3
KT2Mp2WOIr8z8xR6Mdyj3XLtz6ub5Xyd5JInNwQ5IhgHxNke1nx1UYOlrf67
Xu/VqJ/XUdbQXZLhcbnmVl2mZ3ZKMR8O9tJLOR9K7OMA14yf48FS+7/Q8cA5
kEeCNeHmOHPBw4lyiadrqrm6hoHxLfGY4/PsZJ+/r3ceKDlvo3o+pOv2aM2o
p+PxNuaQBk+wWe1zm9qiQifzs8yNMV8Ln3NyfN6SWKNEx+4Sqw4f5CqNwa2S
m7/Ab83wOGA81OplHmv4rDt2MTblXY31MZ3Ne9lY5fcS6/jo+uTrQo+Dr3g4
NkD150J8sFqjT6v9QmdYrtp3NM9FDfVLjK47TuwO+0LpDS/qc5Tu10d9cr3m
j1v0/0c1l4ZpHpoY7vwFr6m9Xle7PiaZek333FRoXlY4WeFGGqGx+Kq+31bk
WGv2GHsS/x+HMlhReM7IwzBCz/9cY3OA3u1DyWbvJH8uyPKR31omGSeD7riA
vVuCMeNT2zlmAJvTDfruKo2JbX393q/pHQ5r3Fxo7hzYrDXTtPa8JhkMlYA8
oncv17y+U+NyvOaTQ7rPNr3/LcXOj0QeJfjL3koy9z86ZQvWT/XR7WDs1N87
dd+FQ80F9ct480F9ob45o7XoN5W8VubC/lv/jy13n0zKdVuSu4i8RayTrJe8
F/G1j09xjO0A7NEaR1MKzAf12UDzM2ZrXHRTe+7Su7VoZL41/PPwEBGjOLLc
+aXbNTPusK3m9Xrq/4qq21zi8yRn09RuS9VH7Uqdu5vPtxb6nDiqiR0dSwV/
FJzQo3TP+8CUqOQXuL69VO/52Dc1Hxfq2ub4VvHRq7yUbhzoU7mOq5ytdeN/
3RwPdGVw5JwxwFgghn1fmrmu4nXfKqpDbdWlvcZvZ/0+Ws9rpnffmWuuBrAW
fIazgfNf1Qe9sKsPdZvRdkska+t1ze36fxf1XW/9/p76rKPes6P+X09zaWXJ
yBjaS+f71LeVJNdZqtObkt1YtVdPPX+f7ne4xG0M/2ScjvHp5u+PVJ3u1f1q
dTZH8dhy8xT30Ty2Rferq3lmdXePCziLIyTTx7WPeFR1+1rPKNR9bmFtk1xe
pXbbWtP3YNwx/saVm3+P3MN8bj7Q5xs1J/2MfUN9+4fG0vd6z5U8E+yIxuSi
QufcXB7ivJu5etbUeo4DeXmq+4X+Ieb0gGQpu8jzSsEgzy1j9ew48IylXl8e
CnwWfI8tDDsY88c0/V5N4+gxPftajZeZYE01vwzTtbvrGh8ATmCd+mV/tOcJ
5ov/NM5e0z2K9bmDrnmlv/nNuQ/vwr1ohxz1z0yVt9SHGWqnBzo4Z++z+i4e
v1e55z/mQT6/1sDnlXXtrMaWY9qDdnlY7z1Q35/XcwsTbLdHj8N2z/hmnN8x
xNzdCbrXgSLzIVYnlkrH10c6r/I9XYz5fiHUGHDmAuaELP13WBBrR8wdOTiY
45jf8sCb6J0Hq68yRpl7cmyhxzLj+BNiudW2K4a4zcEKD88xdpj3n9PMMjGh
3ByVTw/3Z7gqOWf/lajj4EGWP9oO+cG+vV5zwr5sj2vahTYhPgmZQ95u1W+D
VafXM6x3sE6wRrAudA7WBuYu/JnM3SO7+7k8/3bd/wqNiUfHOPcvXGTwDs5M
c33YD72W7PaMV79u1rO3qOwf4PkO3CPzOv0APy59MSWY94pVJmh9PiW5KGpi
uyz4tzHx5oqbFfDFpeV5LDAmJpY79+EtqtNA1e0xPWOW1tHhaosk/bZxlmU4
Kc1yDA52dqn9aPQR/TOw0GOFMZOs4yLpT8skvzU0Rz1DTF25dSn4+SJVJpd7
nlkXzDX9qmgeVp1yVM/D7TynH2G+JV5Hz39Pc/Aovc/eeK9DveAS0D2mlNsf
w5hibD2m4/Oqy2H1xS7J3E6VR0e6X1mTPwi1LO9Re4V39bhLhtdnmONMeQ7P
m6r7Ts9w/t57O1sukckiycVfjJN25iU+CW5C9/9GY/c76Sgt9OwUxlQFc4OR
S4acMnX0W6q+/6OW9xQdgrmUOVUicomzc4PkeGpsENMX5njSkgzHlCL3TSTf
7ce6T+nPOLA1+t806pXsz91n+pzf6Xc4yt9S+7yn534Xbl5f2gxuX9YM8nSM
nWr9IYXxkOHck1EpzkWJLoJO8oDmlp/VFvN1bVovz1HMT08O9VrNmr1csldR
db5f/ZM209wo3GO+jn9onn5K8rJH8rf7/2PqvON9Lt8/bm8OJ2TPY+TY2zk2
h4PDweEcZy9nf85HiaaU0qAhLe1F0aDSUKhQRqWhHWmIomGrpPJ7Pb3ePb6/
P+7Hfd3nvD/v9z2v+9pXTcednVrieIjvcp+GnLPkZX1juM5YT/1+k/qxRn36
fIjPDed3DzZ46uM8la2dHPcRXyHgtBy3iY2SEW+btD0VfLdj6/UM+gDR3U9F
Oscnd+7rqs/TXD+R4zuJ2KbVqjtvO7FciUVcpYp1DIyL8eGv2kTrnar6Hs3L
3SqlrZ0PeYb+/ivxTMLOx0o+0WqjPceX5TqHzdsXOAY9MHltaGNfh21dkvrw
XZntztPD9j8eKfw0OcH4PK+1cXpWvumsRkn+H8/ExjlX5BGtxX2a54pa6446
Pyv1/ddDxi/EMMfPjNxd5O0iT3yLVMdHJYZP9yTH8YEWgyZrqn5N0Nm4U9+r
X892/sipiDVMH+kruGBpQ+tmvkBWLVqgkfoyJsK2lXUFL1I9X2v5iM7h1ZOd
23Gg5upsifm/mgEPuEprPabc+4oa/AGcpLMyVaVXR9Msv1Uw3VImHNpT81dH
7/1Q98IU7fsheb5TmDvulTma++XaI3NVt4PmbefcSOT8vlGlUPP3lXDrNcIf
jXVXnqlqPAIOAQfDM4GHoW8HlJjGZU6Yj4h6xpP4k4ErwQ1FrY0ffhP8k/q3
u6Pzk5B3/d/RvtPP17eeGeA9T76elwp9rjhfHzVwno/K07yXgImBQXunvpOn
Nf57ULAe+lux9vF3OhtztE8vS/VeZE/Ox2+puvFhtVbGm+BPaHjwSjONp6nm
fC68j3DVFj1/qc7G5ZGO6wBtBi3BvfhuJX27knE0vAl8SSPVRzVXx1VaJxof
vyR6/lCRczYx5+xv8NbSKcZdB5pZHrRF83ez1nO98O26HPtVj2lv+iQ+qGlz
n/+p/VJpnHkseK2D9e130yHwvVmh9yxXeVZz85K+PVvvi0kyjr9UeySnvXnF
mweZd4T27j/K9Dc0OfI26HJoDeh06PVtwrn99J7tqhfpbDyqvXVPS+eRyQjb
RupxzWVT3X1Nhvusch4yofG1Zlnww9r/WVr72RrbwXyvN7Qc679Uc/GRvntW
axkBX6X53tfIdD287hJ4gRY+w3/UMY8Er5Q4w/wgPBF0Bedtu/q5BNuCFL+X
d4I7P9D7N6v+Wu3rNGevjDMPCP+Xgo4w0/wOfA98Ojz6AfwkRTu8ofLeSPNr
0AQ7gv2Z2sP3ADQTtAp4JU7PXKW/TxeuaVXD9rLYyvaB5x3hPK0Jac4d1kB7
Yo/+P1Xj+GymxwQfWB5vHhianzb0y8PxpmF4z7oRfhc48CN9LynK+VRPNXJO
1d8am88kLxN44Vfhh5ND/B2+99lg8/nw+8QMYP5qNTNfCQzvT5vxQv8wZnJ2
3VjsvF3QdfD6D3c0TI2+H54Z3hl5Abw184t/NvQIdAk027U6g29q31xT3XOG
vD8voPWgQWn/qm+u0VhXN7SMrFhju/V88/ppY017PBTrmvb7GabJ4ClOqkTp
vG+sHfBR+nuvKT5j0IjQ7OAlaJePqnifZoe9V6FfTtY2DQNdh28T+JxnLg7a
sQ1NK0IzlmOHN9D5xiP17klpXlv47CnaYx8NNE8FPwJfwliqzHTc2pX6bbL2
xYOJxsOcec45eBYcBa6qqN8t0PztmGD+vXvAw3OmOE/EDIN/5M7mvj6R7t/w
PHBO2G1otjsCug3+lPxm8yIsC9ilckB9vS7Z55rzDf8AH/HhYM8zv2euwafg
1bmiI1OEL5ppzdcN93eIY8+34IugKaEnuSu4M+CH3hhh/Q26m2uLvL6sM3uR
Pfl0hmkQaBF4/4zAV2WgzstTWuNSlfnRtsmHt0AO9S+6OeGvfSo36TexQ02/
wlvDY+fMMD0GLYa90UOR3p/IeKD3oEO2aa2j0MfMtD6RNeBOZE2A57dzG/kB
8V6/rG84dpLbs3WubkdWo7lbKTw4q6Nzp12l794sHPBUnOPXQ59ApzTKM94j
dhTx10uTHYN9Lraemtu7Ovs+/zW408eqj5u0n7/rYBycqTFmDPVdAI/HfYAM
DnofProCsph4x3Ljfn54su/oXeeZ3oTunKK1T9W8p6l01nw+pXW4QHWJ5vQC
4ZqQcONirccZ7b2/Utwf6Ix3GxvnwEODd9oKzz1b5HwR0PxDepnu5/5NruK9
cnuhc/W+gG1VvL+FrpPvUtNuN9D3MXK1I+g7tbeeHuG9dWSE9xpr1TLd6/VT
d98HHSJ8z8L/cNcyLsY0Y7TnbXNdzx33GnIm+MWkgC8ryDJd0yXO54374f3g
jtin//2Q5fyr/O+CONMM0L3Y2ED7ElM2N+y4soe0118SL9Wnt2UEyAqqTDJd
D31P3O579a4d2nuJk2yvw10FjThfc9dJ790w2bgBHAGu+y3ZcsRBE03DQcul
CO+c1fmape9fpPv3jr7OJ3ky3fPI/I5VSU73nQueIDYCv+H50HTH4puabdzf
bYDxP/0pTXKfkDMWNDcPU1xqn8GZWuM9em9lzXGlCaZzoHGmJFnOBT4Br/TV
mj6mO+/+UT738O0jJ1qOhjxtjL6b0dF0ADTANchL1L89mqPSOMtPGTN3RMtU
3xMb400nT80zbQSNVH2CaTVotqdzrUdAxoCs4RbhmPjejpvMmKAHGFcVnbWj
GvMFWf7O14Gs9kn08YFMAfwAbiB+8AP63Vj15Yyez9eZ+Ew4YGZ2wBOk278R
+gg6Cb4/T3t/TkPLY/rhBySaoP9k006c2XP0U4771CXGtFvjwabfyEmaHdBM
69mXOmeDc5xDrEqS84jt1Xh+HWOc+3muf4+MHf6L3E/EDFpf1f2mz7101vuc
52ebww+otFCZN8nySdaLuWKeiDPNerFWyKyQd22sZxlgtVLzNdB0yHAOFVqO
U7ui+0hfkd0gw/mxk+V/hYEMEHoBumGjznBdzW207sDzkt2XQ9HuD/wedPFF
wvV52vf9sNE837E8Hq3svbuotcfP2CtoznM090+3dj85b43rey1Z075a48kp
PpOcxxUtLG9D7jY34EHhRaHDkSPUjncuXnLydmlt2wHONecbn9FSlcfKzL/A
u/xS4r0Pnd9L+K2GzmSG8Hwh9Hhs4C8Qth4C3QOyBOSgfQJZKLwY/Cn82INt
PYfMJXQjNOM/scbRyAgOj7JOAhkIshDOY+tMn0nkLdAp2BN9X2x+DzwBziFn
OvKEPztavo/sGdkw8rqDNSxrhD6ETkSf9l6gUzuieX9Iffy1r886+By8zrpD
G7L24xJMN0E/IfMGz4BvkB0hN0JuC36G1wZHLx7jO5L7salw6GWauw0627/q
+eYaR3lrwy1Hu80+eUvrszndc/9omecfWf01yZbXf51u+gnaCTlcfDC3F8fb
bhz7cWLIED+G3LjI05Cl9aviuWBOkMWDp8BX+X28huBo8DP3CHfI1Aif6Ysb
Wl8CbYmcDvqysvrSSuPoM9R7tMJE42XoshnisUK1jcMe1DdO6Hd5+l6W5qBN
qnUC3QK9ADIFZAs19Y4twbgZ/6rAFw+74skzveb4cCNDP5bt+JHInPB7JV8Q
cr1XO1nOB70G3TZbfz+Br6vw69tVjSfAF8hq1rS1/Bk5dE/tqTPah6nZ5uvP
0Sr4c061zPp3wXfVsGwX/6lY/C7U/+/Vx+URlnGg3y3Uuo/UN4tU54lGWIOs
WOfzvenmqeCn0OshR0uZahl27eAcwtfAG9UoN/8HH9i7rfk9+L42Ha3fQQeD
bIGY/esSHLd/axAXr6PKQ1rHa7W+vRo4nxC6rf0dHds9P+xY78B/j3Ebu1fO
K7ws+thVKdbJpkw3vYzMcqX620N9eqOH8f+5+M7pPpucy/kJluEgv8EuDd8r
7il4eu4uZD0PIRep57ueOx/9LLrZkfrdI8hWRes83sjjQ8bMGJFtIePKR94U
6Tw95OhZqbVdUEnnoZJ1vXsGWffLGZxW3zQwMklkRXcNsa4GnQ15/bh7Lojx
XcR+Z9+Dw2bqe4fVx97jLZtGRo2uf0GkdVHMJ3I8cjTfGWc9EDJuYoIhp0Ne
Nw7agXushnPGvVbovLRbQpaZISdKyzLtCw2MDKCk3OtzfqTpOOSxyGV/COTe
xAwmdy3yYeTE6BHRJ5JrlvsEfMGZQUeObhy98JOBrJ2xowNGlgseZvzMA3kO
96RaloRMaVxv0wzch6cauu/kvWOPnAn2CfTqnQlBTqUa1gWnBrZ70F38nXMO
zcK5hz8gN0RUIDtHhl4Ytm6DnCvYcgKj76ANfigKcATwj5Xchj/4Od2ySWwt
21xge0vO3PJAtggOJFcY+gj0mviSgy+x684I9ji8DTwOumL0QeiC4gPZLTiB
PB/DgjseWQrrhTwNudrIbpbP7NM3soosN0Z+/J8u9uOxpr3OyQKyLKe4/gLr
XpKwgRJ6FOo9x8OEokybw5+h/9wY8Fno4+C12P+cc/SsnEH0X5zDccH6LIsx
3bsxoH15lrOCzBF8xT0PzsKeG5nIN3nW/7Ie8G3IiMFvMYk+6xExPu+cRewl
jmU6NxFyeOTx69Sv7+NsCwCMDIM2cmNkxtwxrNWBYL3Ys+SPRAfP/mfvb+3h
umlDw8g6kD+/Huxn9nKJ1uUVvau+xrRO9U0NfMdx16HnR9+PDQWyFXjYyInG
KeCWqjrL92l+jiBvmeQ7uVilW65108Dc1eBI9Dn4a4LnydVNnm70DMheXwps
CdgnyAG5N98N5JzzMwJdpt5Vwr5kzzQ2HJnvNuuPHIg9MCfD+xUbYfSp5PRo
GNia/DvCbWh96DZ4HPDoH1WNSwvhjdXf0xPMQy8O+Ohb0H3pt5OQbejMjNZZ
uUzveF6/Hapnvm5l/NULWaS+NU73XgXt37o1vc/Har3L1McPp/mOZn6YK2Du
7WHjHIdmqPb72+r7Wu3hrcS9wLZaJZ/9GzatDs3eWOc8Wnhmse7HherrvibC
Q9qDr+q961S2ag1zhNOXCQfmqv6h0Pbq/RtZhv+q3reusmWOi+pZBgm+ZN8Q
T5Oze2WG6UpiqdyA32yCx7q3lceLnAL5ffty94P+JOi7L3EnlzoWx8XCiTO0
72trXmtpfH1jHHPj5SzrPsr17hVaw4s1npeLLbNvpb1S0No45IfJ7gfjZx5S
W1tnzZ3BPM8Q/PVI82T8rXcw/0n621SVeQleW2raN6GfinQO8WvUzwra343V
5zPo+2ppH1WxLS02tV+qROn7r+g3m7t4TVnPfXruAc3hHnzZGnlMxBNhXGdq
e4+0UonRXBXouwP7eTyM65kcxyrtGcz1paXeT+yl3zItz0J+Vl6tQoWw4DeK
3R/6Ao3NnHw/2fPC9zvWcR+Y48RgnlkraITD3bxPIkd5baL17ep1HR8Bu/HD
6nPFSl5j5vgKlU2tvE6DRbPHVrHMtY722z70gDoHNUc6N/tAzccDqiNnOnbr
pdEe7yCVoRrzZu3J3ep3O+wMyryf2dd5xITvYnnA49N8xpBXcf+mTrEshb4x
dvrH3NIf+rUnxe9q09Lrzbof0h4rbOzv8a1QcD6enO53HOng91yte/1TdJGR
3s/s5fuxsZlm25kFBc4v36XI+4JcYLPC5snKArqVc9xb+/l3zQMO/3xvXi1/
n7zDUdWdwxtb673oqnK8FnyP9aD/zANjuE5jqiF82VX9aN7IvhfEHibXeFKw
b8sC/jo12AeMh7nBDgLbAWwIirA7KPVvZmvMF3JWRdc10p6+oZPHxBpdHu38
INSRwXo9M8q5ivkOOYLpB3mC2WNXBvc388d32Y/8nz7yTK/g/HB2YhO89kOD
szY96H/7AD9gI808zgr4W3SXnHnOO/3kXbyHfb0M/7fJPuMlaT7T7BdkR+wZ
zg0xf8mlB966KcBd3DHcNeBU5h87d9YA/xzwHviP8wd+QQbPmeI8IdfCLoJn
sYkghhD4C9xFv8m9yjjA/5xrzvfKQv+e3+IHxDfI/wouzwruPua1cTC30cW2
7eha7DuEdw0b/b/1IGZ+h6k+n5xN1oXfcWcgg7o60Nfummp70sYa60nt9++0
B/9SeXSEa9qMBZsOaGju3xnBHXyd9mq1CMeYeVzPlOi7J6v6ff20p/uq3N3T
NjvEFeVeoM0c3yO6Y5zWvIL6MU900lrN/fl6ZvdYv4f3fak1itT8zB7r314e
/H5if//+3gHuP31n/qj5Nt/lezyPXPlK7Z0nS51fkDyDtIHBkXnBvcv/mff+
gf0KY2bt+A7fo6/Y3/J+vkmf5wf9Zj+xrwao35v0zFr1sain+z8722OAF+E5
nqHwfD/VX3UJnhvr3/K7Z4d5Dk5V9XzyDb4FTUnfz/mJqb+nEpz7jb5cpHff
rTX+VrhttuCcQsdATxZumK49+ie26cIPhdrvd4wxvHua2xdDr2rO7tHvF2vM
E/S7pBTnlCEGFvv2Ep3FMcIT8dmud7YzTE7Ud6Ic83Kb9kGRzsk6vX8aZ1v7
earqOcH7+Q4w9T96tovO5QLN5+16/uUc5+eGV1neQrDK3ijnL79U8/E6MWPC
jiWPP1Rr/e5C7f3Xu1mXeYn+ty7Qa54qdbu/1nAjNl0ql6q9WfTwpqGOS0R8
os/wndUYVmQ7pzJxXnvouzu1JzP0ruM6l8fg09TXHTp/r2nc2zrrXuUsRDlH
HXw0OYHAPVeVmuZYpPb7WvNGjQ1/f4HbyDDQ7z2s+nK9Y6O+0V7f/DjW9P3x
Hoapj6t+Sc9eLLx6s9biPT37lNbnXdVd9Z3X1efTevfmVr7HuFvDon9e1rwk
5Nu+9Ap4Xu2nS4p8Tjmv9+vvD6p8NNa5tcmxPVTvuVLPzlPJCOCtTdweLJ5z
uvbKVWHXxCK+KuDtPkbX2Msw/AJt4szvVZ/Hqm6f5Zr2jfr+fNZEfdk/xHk1
DqhuLlx0r+6JZ7WWV4ede/KnIsPU2do336qvt2jvZ6pco7+PQrYkXLcg7L7S
5wVBn2nnE39G+3DmFMPX6m95IdebWxq+q8j/L5ji3KvkGGc+wG3c39hcMZeF
GsOIXNcFAVyz3PXMoI3+BThFZ7qh3tEoZJtw7LCwC78WO3rhjN/bGT4z0e0P
kXmHHIcZ+JkObl+nPpzScyenG15f4Hb0FNvRPK5+lanU0l0dpb2yVr95VLTI
Ffp+c3wgerqP0P7wALO1X7ro+Zaquw02XK2a27doPT/QXC0M224yX/Dt8YbJ
/027kvb5/frOWzo7lQWnqr/hqY4984XuiaWqq2lflqsPW/vZL/V+ffuy7o7l
R0y/u7Qn2+rvP2jex+mMxKe6pn2d1vValftKHX+/bbljgDyguWup8f4gPLGl
zLlNpgmvTRHf3ru+9rX2xWf6/nHiDGkfH9PZ/1jv64wtWIZr2uixh2lNJ6re
rHNzPWMTXj+NbFf9vGuG6+ixhntqfWaCi7T3nhrpmvaVxY43gN/9F/gvppnG
+1k4qIJ+W1F/26A1WaW9tFH1DpX92GRGOV8Xebtq6z6/gX2ufXMKeyf9/190
PWpv1HMbVFbhy6jzcpvG2V9nP6nEeTXHdzE8N8btm5D/q75R79vSyTXt80Rf
R6rk6tlF+l71IuMPYuSgD48Qrtil8b+l9XlzhvMV7NE8Rod8F+6obt5hmtZi
lMafxB2sdzyh/j8l3PiyxtxA70pWqSjcvUN76Dz8HfTbF0ULvawyVHh0oc7a
cNWFeu50yDkupuKDJ37qUu2xSPzJ+W1QX55seE9rx+lM1bzUE219vMjvTdBY
nii13+canaXv9f+tWoPdmrvP9dtD+t5mfMRFx4zReJYQR0jfvR1emr8N1B0h
XH4TOEQ4sEd7wx1z3F4kuJfel4lPlXDMYvCF6utTfAeRp3OazlZyT8c6rEbs
Efwj0xzfe/lMx/juNcD7i31WoN/8qLHdDN2reqHGcV1r+2bO0XsvVjmsOboF
XmCQ4SplblPuj/ffuWO4a8g9R7wdYv3Wh2bRHTNKZ/RQN+PZGrnGu7t1Vi/V
vXeR9sEUzd+tetfAmYYr9XWbAnxFinNGnJ8Y5I1I9Z3HfVdf6/2Evjk21nB6
odtXa+7m6DeLy5wv7XOV1/GP17d7og/TuBf3cpzR5ax/kWMkECthrvq1UOO/
VuWsnsvVe0fNMEzcOdrMNXPO/b8Fva/27GbVr4o3+hddpub8pRmuaY/ROn2v
sYxWHRthn6j7anvvse/gadKxLdA636Y+9NRePq5ztkM4qbXWI1H9bKO6pd5R
Uftrl/5/Ybnp8Ivgn6o5dzR0DTD5pGm30rO34JtOLG/dP5dj+676YMgxdZep
HqP2KWK46BvROnNdVH7SvCWp71drPmfrjN0ueLq+PSjT8O+T3Z5C/Bh95/ag
AEdwBvT3Y1qn1v0Nf9HW7ev13i2JzqELzsvlfledE9S05yB/Uv2m5mraNPs3
7w3Z15ma9vPq85+Cn44y/pwU/Jb6uzqGbyt3XqKRIcPkJ6IdXVf7trVjLtEH
fs/zX2Gfp/atWv+fxacuznTMcnIpxmPrqGeOagyf6+x+UmTcDU5fp5Ko87RU
75s8wAU4WfU8fecd/f4HjfsOzrX6cF+a8TV06jvCE49oP8zV3inXnd5AeDpT
a1R/rOOzXqffjcxy/xnH0ZDxCvglp7ppqsKArqL8d/+TdyJd++vOsH1s7wo7
LysF+MsRlqEjY+9d08+0+X//o6Y9XO+upbPVSmM5pnVdKhrgNpVT2psndIZ/
V303dJz+dkh7rlTf3qR91QK9pujyw/hACq9lTPLvbu9gXH9Te+P+msLdlfS9
Z/TcQf3uLb1vVsh+jv9oPs4mOdYTcZ6In/HODN/LB7BNZy+HHbcJX6i3J9gf
qr3uoQ4q72WZfhgpvFJNZ3Cc7r14lWs0jiMqzfWeZqmmC6EPy4WfH9U99YjK
25MMUy/Rb6bpG82F+5bpe/tKTdtD4x9Qf9/QMz81cA7db2fYHxsbp2ohy3aB
nyp2m9jwxIg/IZxYmG5/IvyKfitxDAzu7HChfYeGpxu+p8Rt4geRQ/KQaJ39
6LNEY9ZUOUkMDa13D/FhbVv7vGXWMvx5W7e/0btnw6vUMnx5O7e3a1wP6h13
il5K1l5oo37emO/8JMRKzNKcVhVez9O7CzXnzVu7pv20+vWA2g+pbNdvyvXe
apGGybFBe2Ngz4ldZ7bOVW4N+73N1f8+0NmtoTEuEz5uqu9dqLEmiy+ervIW
fvesqea4aq7haoPcjgvZh+yGcsciuK/cNgWzdce8qX3yidZjqtqf9PHfJ2v/
1UMvpn4dTPNY71DJLbfuBx0x8OTKbsPvwfdVKLecofkgyxrm6T3L9O4edQ3v
zHS7aYrjmncSrrhrunVsW9Ndo2cD/gCd4iCPY5Hm+R69f6vG1SzSNe0+2rOt
tedaqRzW367KtA038PzMoK0+fouNiMqfOn9/DHUMP+xysM+Zq/KxvveJyhHt
yaPauzXVv3vDrjMLDXMXHsYWLNswOQO4J/FXwCcRn4VGouO2aJ4SdTZKNM7f
waHpzi90ONo5hsjp2Gigc5p9qzk+oHHUG2A+A/7oxQzD8B60iXl+wSTHPUfe
SL4eZGR/1rZejDxc/dElq183YHOg+XlXY6ik+2a/+rdO7fUqi7QvvxEt1Uhn
cmWp42xAd+3Xs/1Es1ZLsY/KlYmODdVCe+1L3Rn3cUaFz/J0x9wv+GHddUvU
30dU79PvbhPe/Vl9qK53n+nkOFPEASAOyfFc20gQ35yYjgfhWfSOPcMNH05w
e5/+P1w0WMwUw1tz3MZPamFv7W31d2606fRLVB9XH0+o1BCuekQ4NEM0Zk/N
WRuN4ajWIBE5subpiMrWVMMbg3aW5vdizdV27Z1VWp/p+DKcb/hQntvct8gC
3gvkB1OER3qqHlVkveBG/b64zPzNA2HXB2IM3xyybm4+9jNq99N7Jqpfj6V7
Pz+Ta5j8vLSR+yCjYk0iRRu+pLVeq3ILcvBG2i+NfHY5w+hO38EHS/toaa7h
nRXdvlXfeyjs/EjcI+317h3aMy+rry+ppGtM2ydbhvBwUICRKzyr/l1f4DYF
GDmDulShDTZUYev+0NNih1AnZFoSGQpwsxy3mwqXz8bOQz8cqDMf1v+2dXK9
c5Jh7kp4TO7VEym2aU/u6LzZ25r7b4PV16Eqj3Lf6rt3q4zT3FTSOytSpjpe
34PYLUw2jtyk/m7VPO7Kt087eSeAE5u7PbuecIv6URU7O+2PffU9Z51mOk5M
deHQx/Rcbb0jv4rhO9Ldhqa6LMV01KwZ9gMn1xc2e4/rbw8McAG+b4DzPSwa
7fwPR9Tv5fp7LvJlfXeS5mYFfct1TXua9l9X4a1DdV03CHvOW+jeWj1Ee56Y
P1HGJ9xvK+Hd1I/r8hwfknwuxIjM0r0Yr+fP6Ju/6jebkHfobDTV+GZojd5u
bJi4R7Rj1J/79b0hDV1j+wV8veb3U413/gzTD9AO8O7EcoM+m6/ynL71hOah
OnhVc9xH79sEryecsFvlibBtnNDdoYteLt7hX+GGT9X/9EHmBcnf0BWbO31v
r+7HuiHHdyA2xm3CWS217k+oHjjC9jyf6E55XufpAp3Fq7JtK/lk2PNOAS4Q
7uqncVVR//uoLr3ANe3H4BuQzwhnzNZcb0JmVewcLdW417nfkTdrL6xDnhhh
e5ZPIhxvjLhjI7EXFN3zvObx3srmzQeqX6V6zwb1aWu+8QO8Ojz7yrDrDuMM
Q5vg4wx9ckg0xUGV+zWOizQnF7KfOlr2igw2T/TeH1rjUyoH1LdJ+Ktp7M30
3BnB2zRvP+juWaXnf9P/U2YYfjHX7R8110OL/d2HUlzTvhLfI5WFqbY5uVRn
46mw60sCmP7ye34D/gUP31zsM1ZXa7dFOPxNnaFH9a2/Vfoie9Fzh9S/Mu3P
CRrnvjTDxOinTSyM87SOnacZJj4G7WbYSui31TQvM9DjiiZ4THjviSG2IcN+
7I7AVgi7mfGiG24ULpqgerHwzf1aq/vVvzrq637NRz/0xtrjDVROa788HbYs
HHk6tip3qTwTdg7mT9SvG7DZEt94Bfy06h3aH5eLJ7yymu+nb0f6ziLHzTSt
9YeC9+o+/AbeSXWE8E91zc1HaY7VuUH1+gA+PtPtJaK17tEd/JrG9q7e+y86
V93hZ3TnTlef/x7vfGjEOyXu6XD1YaTKvlQX4Ez8KdpYDo4MvLP68Qo8tMp9
/UyjQqseCH7D84f1zd9Ung27AJ+qbhlBFc37lSn2a8bW56Fyx2R9WvNxNsLy
/i+wzdNd+RDxdvpYP4rsBbkL+ayplyUZ7si6pjnn8q66tqMsVn+eh2bQuH5Q
PXWY7h49t7al45mRU50cFNhqzCi2vQY2J9ibwCMhV9iF/5BKBH4Vk63TIAcq
uVDnqu/bQ9Y98H/8A2P1m0HQStMsQ0hIMK6qgY2lxrtPfXhae3e1vvOo6P1T
6udy1VP0v3d0thI1t5P0/fP0nUYqLdW/e7UH7lPZq/3aK9/ytfxxzl3yrPZT
LT2XIzopMeS4x+0DveAZnY0mqi/SO9Zhk6BxDNXvC/S9VHSiJda9IafGHxh+
mzymIwPcSr+rlhr3Dyo0/r9M98oqvS9Cf1uj332iffMZcXQ03mf0v1raV3eJ
f7hT5Uf9/kutV6bWdNsM+wNcifwZWltjjdA61exn+1zsdKeo/lj78zr95hqV
BI1pjfqbMdC8HDwd8ZbX6DfPqX3RQPOf8KH/VNW64WubY90O9eWBnucrrc1c
vXccvlfY3RXapxRceY6mAn/VcNx/Yv7PKTGverHqDN036diCa78/pu/HaF9c
V8Vwg9puAy8P2uj3n61vO5gTqo+rTNId0FjrP1Rr9ZPwxis6lxfiT6b2DM3N
G8In12is9QQP0Vw+HzZMPUnPXlvFdtrYayOfPHGeZZTkXmItWUdg8jHRHqX+
xqnEan5e4F1h220AJxe5DY1eZbLfVzfKfC550F4v8dy+UeL1/QYbvtqGWWfa
b2ie1oYt1wSeF+N2H635Jp3HOprPSwSfFb9zGX8rcAy96citI0z7VKljP4cL
dEZeDFsmj9wTuTzw4JDb2Bd+kG7b1HT9Lx9+W/9/W335Tb99arr5j9W6q59T
GYSvmeZpYgvHj7xY+zdWdWig7ZOxU+6s330G36N57E7fNbcvqoxXeTbXcgdk
r8hgHxDev1F/eznfvH837fEe0JVxhqlf1/g2C26u967KtSwD3csL0w0j36D9
ksaSJJy1QOd3uuir1sIFbYd5LQ8Pcpyjy+HztF+LZ1jeQsBuZC7DRRfU0P08
QvWjulseUfkAnZtwc5RwW/vuhhN6uo3ce7dKiwTbO2L3yN85e/izrWYt9K27
8KsJuw9HBrkfD0zwvcT9tEfffFBnLkL4J9TG8pOLy8y3nuNZG9i/A3k9svoH
dOZOxhpuiH4Tu1zN8Rrxpa+E/fyn/V2/EvC2yHvhb3sIzxepnY2djs7MOv3/
wBjH+6Cm/Y7ovcdFmxwlfl2R800vV3mv1Hz013p2TaT3Q5z2xXc6b1v1roo6
p83Vr6ax9lO4XuN+Ve/bm2w4+jy3t0a5pg38TfL/nqOmXVt1BPR6keGO7d3+
I9/8Yddol+MBn4h+Gj31v6rvHGOdObpy9NcR2huvhQ1Trx5umPrZ4T5jnC30
B5wzatrLkS1yDicajurpdkWd6UtKrXNp3Ni64p/U5wPJrmmX6JkKekfsWMNj
ot3emOV3bOBOLHBN++ppjmtHfDv4zP2cmamGqUszHYv9Hj1/l8rl+s0pnZs/
VJ4Rjh+jPfWU6o/1v/X6TXmc4V1Bmz03ZIzzhT2ET1P8//Ti1LSJmQrfAP+A
HrEg0C0ij8e+CJn8Nq3tPO2/SWO9N9gXHbVX79LdF6n/7yw1nJboNvVLwwz/
Au+s+/QdzWeqfp8+1rp86BBoEGwPyCmxuYHzSjwdsp3vpzqnX6DbGmG++++Q
dQJjxhpGT0B7jWiwDaqfU/3KRO/LCh1s03oFsURU/zzZ+fyaaJwb9eyKkOMN
ANds5Tb8O3x8hHBNjsZaV3NQL95whP7XEr8tjWOcTQcr9MFHGrtk/eZ1rcd1
esdC1lTlIa1JP+2vM7r7WulsP45/ms7GPyW2139Rv52p77bUHP2d7/3EHvq8
smVfyMCeFj6I0N6r19P8E3xUVsg6d/TtWcNN80DvbAj0N+SO/GS0YXQ6tHme
eLPo7IH5HXp44AXB/6rovffpHu2abZh6wHTLJGdp/6Wozz+LDsgts94okru4
3DFTgHOL3KYAf6P+h7X3L1T5WzT/VZrDzpr/O+B30HVr7RsR3w9/8L6mn+jz
x+r7Tb3MK8Mzw0O30/cWYY8qHLtdd89joofzWljuh8yPnB0/aq8c0zOzROe/
REwR7tmw6305hg+Jhq2gdRyIvZyef6PM+bKA5zV3G935VYIvCmgqbNagq5C9
IrtEbrlF/3tK7/ylq3A4Nmz49IVdZ2YbvlTf2gTu0bd65ZiPhp8mXtTGQA78
kOZjiUr2eNPFzTqYNn5T99cnar+reW+a5pp2b9HFC7Q32uo8fB1j3zDw7TTx
30kq8cRMFF0fpW8drWb7E2xPupY4R/EPWtfN4CK9/yLt5drQA+AIfeO0xt5J
v39LczgRXJDjPFqxUy1vRPZ4R6TjBiW1sO1Vbqzp4yR8sLS/F+gebJ5lvXW9
NtZjk1eGGPEHNDcXQTNmO87umEqWRQ/rZBiZNG1yToGf3wobJ43MsHxjhfbM
lTobp4rsj46fOz7pb+u5fjrvbc6zznx1cAdv1d+f0LinRlqnx9wc7OG8Zis7
ObfZnHLHX+6v8pDW4xGVZzTXS1TS1P+MNvahwH8ik3gdIeeT3ah5f0TzvE1/
T0txAX4Ynkl3+nbBO3XPx3ZzTRsdM+vxoN79QE/rI9BLjNeYClQmqGziTtUe
f0P1n8QCUb+ztU5F2pNf6O8Hm3pspwJaf4vm/Vbt/RfyLAt+LdLy3ldF065X
KdJdcF2qdfvo+LFRwFbh1q7OSfKq3v2K3rUjbP8F/Bjy9J36wl1DNfYNKt9p
zIc1j9uwFRJ92V5rNVZzVyXC9kp9hSO+xG5luvVu6NxeUT1Ia/ym9uvfWpvd
CbZB2BPUGzMMf41tg95bt8i5bqhpU/oO9N+A09u6/Y76uU3j/6rIfMX6gM+A
T/tS++4Z1X9hB6+xrm9pmPrPqbZ/uzbT8hfo0RdUftSea6J5Xphof1XOMmf3
qwY+x18F7W6ie94NG9fjw0nchd8HOlYFMSvwwXqxwLIx8hUPRu+uvVtXc3++
vr9Iv9ugcaxCp6Fv1dW3W+r32/W3zZq3rcIL21WOdHFuSezmiCe+Qe9dpjVf
OtP2BOds2LQW32if7u3vXIDvhR0baaHW9MoY8wznaz3mZbumfYXe005zsEbf
uFn77BH16RbVH+p/F2p9WumdcfreTaLlftecfCacO0j32XDh5WtS7VeFf1W+
4Ca6b5oOMzwn0+0Y7audYeshsdXBNqfJCOfUPKbxLi62/GhYseVJnPPqtXz2
ewb8InHc8fGoVWyfD9amak+v1d1JtoPCHmrTeOvs3xtmGN097SmiCaaqrNI8
XKIyVHPxg749UuPqo2e+TrMci+8P7G3bQuwK8RNZrT7UrKc7R/v+35DvO+KM
zyBeivD3wCzHOz+qeTmmclr3z+CIwBZIazVW47lcV8tzwjHXiZ/7HtuHIscB
Jp4tcvLlDSwrR5e2ZIx1a6nCFWkqd8I3ax88q3nuo/oXre3UKNNmxP+FXyce
MDA8PO1W0dZNoKOAJkTvBV2IHJt4jciywcfXqpxUuZw7T/uoHF/Gka5pYw+O
LTK+P4/ptx01L7eh2xF+uDDV64eNJX6ZxJNgnpEF3NPYuSTP8bLiKc7qLF8h
vP21xvN2yHpseKudM+1vjt84Z4yzho/4hADvzdUaVICHUDmh0lrz96TW5/4q
Xj/WcaX2wKta7zPq0yvDrE9Ar/C26uEZXvO6VUyjvR82nUZNvCPgK9TPS4ln
EXIOaHQDPw12HlliPJMnkNhXx7W2UVrLncXWa6Pfri36uRZyWZ29XWW2Q8UG
FbjbFLej+liGgvyEs7qmmc8u9vhp6nPqaN9jzBv9RS5BnhBkE320l3qrfNbK
uQYe0jNrtfdeVd/Wh2xfcaHgbOGLXJWvh3p//KbysPD7bP3mzlLzA3umeS/k
RtkPFh9Ycrx8U+j8Lj21nr1Uru3pfJMdNdcdVD7UOtwsfLw4wfcCd8JybP50
7n4QHjuIb7++kaL1X6KzsF1r+4zugdUqOcxFuXHJJbrvlmkvNKlqO2TsjvGf
aqHfj1b/6qmdjX+7zu1e9XtOlnPV1Kpk+5xuKq0LPNdfFnvuTyaZf/gg7Boe
AhjecFNAZwHHjXW7vfbfkSLbVlOAkY0AU2NvfVrv/FPlxkLr7dHfvy1cdnOs
84HeEmv7TMZWQf2dpfoefftIoeVwyOMiEy1LnBjIE+GB4YWJK/BtmeU5tbSm
U7Ff1X6vVGDZ6ZX634eq/9T5/VV37bvZ5jHgS+7SOwr62yaaHNvIyo8mWnb+
ls7sMfVtNOPJsO4aHTY0FfTUn3quotYoRvM8SvTAU3r/WZ3r61Q3UJ8rar4r
q2wDf+jdL2utP0RmoLV4ebL3GnsOWeaP2mM/qZzQ+44F/ozYOx8LamyeoWew
0Tww2XVxtOG9w7zGOSpfaUw11X5O7/6h5H/6sTL17yPo83jD8ye5/bD69/xM
0ywDNJ6foFV0b50KWeaALKrdeNvZ/Ky53a2/faX3rdH/m2tceZrjptUMr2jt
dpnotEug+USLDNV8rtU7JjbwfmYv5+q5VQnWMaBfAF4ZtJvoDH+qs5jdw3Ff
by5z7FfijVLTPqNx79Kzp1Uvra6zom+9kGX9yPk51pFg7866zlQ5pvv8KvXr
4zrCfZqjbzW+swWOtftoV8feYi+wJ+qo/JZqHhFesa2+MQs7qDLD1Dm5znO0
RL/JTjY+qaCz/7H69Bi8rsoi4eVZwte/axzr4SmKzTdjYwd8S2BrN0l8V6LO
3C/wARO939h3m7V2vYusY3td7/i1iZ8hrzg+i8NV6mlPvQsPUcnw1aVu44uy
Zqh9uutONx5onmNbA2wObh/gnLvYP5CDd/v5ztMwRmV/BdMu0C0V9b/K4+0f
UDGo8REgpyn+rfi53qs+/q6742PodOG0KI2nvUpVnbcqda0DvJv9HHZOmU9V
j9R6deNsa4wRjRxvCD0sOlh4R+r8HMNVNVfb9N69mpfsfN+L3InA+CDQJs8y
9yJ3IjmkF+pOuK6P1623vlO7g+GYbm4T+3BRX/sJTgzZtqCt5i4b+kF9X9zS
MPXXpbbLwz4vJFrhPb2nHFsx4fJd+v5JveNj1Td199n+Unt23hTzc1eUGu7c
xG3sKm8ZY9vKiCjfGdwX8OrTtA//aWQY/p32Ge2/LdoTT2gv3aw9FyOcklJm
v3VoQ/xBLi60DK+gi+Gvk90G5m+/BjD16GzbwC1ReV7fXd3duIh+Y//7lcb0
qnDA7TpnvbVHLtA6HKpqe/1PsMPQWGrONO8GH0dNm793CRk+OsX2y9gxL9Qc
jtY5W6nnaoGf9Z3L2xiu389t9vyRJO/7OP2+gd7z+BTDxzPcxn4G25l39b7W
GcalW4Vvdmget2Ffq//tLjP+vTbaNqQxhbYjLSyzfQG0GXbw+6aZF8KP/Vxs
cb0jWnu6m0pFzf3SkPMOkX+IPtAXZBdvi9Z5S6VXJdvsDym33T60JjQnenbi
9uMXROz+T/TbHVq3T8QzP6vfjdf4VqvepzX4XiU/ZPoIOuk7vWc29PwM2zyD
t9d0tu/GzmzrbD7VMye0Z48I15zsaxnmrXmWY9bT72qLtopQfav2yUX65lfC
h1O0Dkt1PyTGG66Q73aS+tZIZ7J1N9sn/iH8crqH9aLpfazrzIS+Jo5Ud9tD
YgtJvI5KgY7lgN71gtp/q693h5zD8oGubgO3znN7RCBLgBbDPjxe/WpZ0zB2
4rTxDcBH4OwY6y/O8Yoa37EZtjnH9hw7uts0rnW6129R3/7Cpy3WeuYni6xr
niN8c7HK0Xbm4/HnqawxfsseyjJNDnxHc7er8z9ip06xTwYyI/wynsNmA5sD
+CR9N1V8R58S24lMEn395Azvy/fP9/7gLknRs0kFzv1ADogV2Llor1yqMl7z
UKA76Po8y4OGaz+t1Z5sqTncrPPQSPdPrmiYbYXm6eDtgIm5S7uN5u4LcFSG
7QCSo3zXEfMOO6q+er6ZcM0u8XvrhSu/DLtv9ZG3Cm5VZl8ZYOrriyzvRb6F
3Osj7NN0N15UaDkhMsKtvRybGBusnWXWCTUeZB3RnA62EyBXBvII5BL4UOED
EqU7f47Gvq7QcvGQyrea08U6X301r70zbSePvfzr6vNGtTsI53TQHrtK4x0f
cmz21+o7PvvORNseFky3ThjZFzKwsM7Z4/rebj370DTXtKHboN+eGWO+epHG
ckMTyyKRSe6bYlso6LWReZZ5YpuFjdC7WpMqeveQ7vbBgrcZovW5T++qJ3pp
5zjrdnoGdmzzhMOuVJnW2bonbMgmB/D7Fd3O0z5fqedXT7X8EjnmZnyPsq2n
REe5QmPqrXuszUzD2fXc3qM+FWksxSr/DAv0ubqDPtN6l6vvUYXWc99BfJRc
P8+zX4cNU5/Q91tqja7Xntyr9kHNT0yR9YDYNQ3QGdyv934Xa9tE7BKr6f9X
CS9u1vnYqt+11r2QlmC+Av5inMrCMo/jH/Wlpp5vp3aXXMNx+W6jm4fGhb79
WPO3C35+umWKfcXzDO1ieTKyZHR9+Ges0zmbqe817uY1g0Zlzc7RrioJWqxf
tGd/VumldclWHz6vartk7JP5O8/8HLQ7YUeq93aMsR0t9rQV0+x/gewbufem
ABd30nq/LJqoqeYwUaWO8EdIY93A3aj5f0JrPUC0TnKk44sQH3JIgfHPS3p2
i4YxX+uTluk9/EOq9zEwubFo3yb8lRVpPeLHuabNsVtbHdAPfwbyVOSqyHLJ
L3WwsfNNYX+GHdp6lTeDmja0MDQxOoQXdC6KNX8lGuc+4ZQ9+v32XrbPeVX7
LzzT8L/V3SYPIfkI8T+EBkZfc4fOdxuN4xtwTg37pmH3jv3a8+XWUVZtLzpP
+7eDyopk7y3OPjjgRvX9JpVwqfdIw1Lv/QS9e5XO/Uj8fXV+WmguYtANpLum
fRi8VOg9Wcw5SjPtCB31pPp91RSP7VRLj5V6bUPDRwNZAjKFT6fYdh9+Fj4Q
fhD7RvRzV4wyboI2iEkwfdBe/fxFZ+FPjf0a9XOl1qNPN/tvLdR+vUk4vLdw
fyfBH2nfXq3f3yac93MX+7fOybaP61m9+1+VE5qnG4kRpfm+bLThneluEwe/
12jHxeeuPqr9NYd90tb22L0623aadcRu+u4E05/jhOfKhX9D8MMh67bGhKzf
ulB3Wq+hjmvDuBk/OaqZc/zSmHdgfNVoR+ssPp9g+cVInYtVmqNynaNHVHdC
vltq23xs9LcNMA9Ifhf4QGRB8NAttS8/1ndax9pvD7/hT1paxjco8B3AxoYY
c7+d75hz5GtjL2uo5/Y7fDA0M3cd9incd9+qHNbaHFH5XX0chp2PSu0x1kui
n3xVd/w4ndEI9e1r9EYhx7dH/8B+gecAn7xSYpzSRR+sqHf9OcI+NPDdyHnw
g0Fucs4XppVtn9O07rUKXdPeP9gyhX2qi5PMe5Fz4LuwfRfxWwRe19Dti6fZ
F5Kz0Dxsfmmz2t/rHd+HLbO+prHttIilM67INPHbfQ3X6+f2g6KJhmnfdSqy
ncv8FNu6XKb/1Rhn/L9M33tO++le1fvVt11Jtu08rG8vQD5RaPiubLcPae4T
9Lef0Ttoz33Q1/4bIe3lASrTSs0zwi/+lGH/dmLLnCA+Q0XnCHxTuONy/ebK
fI9nc6ZxJLgSHwR8DtDnHtA+3a+yQLi4Tp79vzkj5LOeEOec1jX0u31q1xxo
eTi2vcjEgYmJTxs/6RWq49oZThnh9lliMWof/aP1D2l+64vevlBz/0PYPh3f
ae7S4Luz7esPf04+2qOtvWcvyvW+/aaBY++FiC2mPXKBzvSTFS1DQ362ocx2
TkP0/02jDGP7RHt1sn2L8TEuzXZOLuKzfSP8MVhnKbbAvor4LVZVH9upfSjf
387Ve0ZggwvPqLG+Dp2CvnyG7b+x/WYOsN3E9nmLxvCW8MBm1Vt0xt4XTsvU
Xmwrev0mnc8qI+yfh5/eB3G248WuGtvex7SWa4c79lzFdOtk0c2+M9j4AP9V
4KzRbtfVc0uxR+lmW/i8YtvD4xdKjj18Q/F/x999yBAXYHzgr9P/WxRZXkAB
Jr7AHu513cOnq/nuJF7aV/VNa0Nzzyuybwk5j/A1eQn/MrXnlxkeONHtjuA8
fWNyyDgUXErOm6cC24x4lVWF9oe/fpTzKOEri5/sWd3jA0Ompf4KOU7Js42c
n7GG1v5z3e87tW9ugBfWd7ej+0uxfz91vzzD6L3xi0b3gj3AfzYmV+v+mIQ+
RfWDWbanq1/bcGwHt5dmW6e2P2yflcdr2W/lZ/XlBa3pM01dvxjAxZqbYzoP
g0f5Gf62VLihd65l4MjCobXQ6cfkmfaHB8B3fVmgx0SfuV7vWaq/vT/YdunY
pP+qPXDLdNs+/WdzRE0bP6UHNLc/6Zk0zemX2qtfZBpODdrIuZCXIfeiPtDb
MH4UL06yb8UDIevySmMMD+niNvQx/4dmnqH5XtDa8Q6Q8SPr/6jMdy737VX4
Ben/37Q2PqeGTgTGpx6+jXzPhzTXeZrrn1TX1JhfFJ5cqr9v1pjKym3r+bRo
pThkUkPtCwnux5f9Px0e9vBx4oee1zsqqX/btLfO6hv/NrOPB7HwDqj/XYW/
vtP5mDrFNnj4quGfhv6fGBSfp7j+IsXwBo0jn5g7WdY7gx/QPf+ub3TXnjml
enWgx0CfwV3JPXlS9eM6Xw/rfnq0le/i9irL9e0BwoE/t3A8e2hxdIB7upse
+LieaYKHkA9Mtb4MvxF0Ym+rXqG/Hxd/+pLe+aXO9XrkBqqHd/d3h0w1/Qgv
CA15ica2F5+NeMeJIF4E8ozGTWxb8na6c0JfpfLPOM8R494x2fW2yYY/1bPP
aY66t3HsBmI4XK89Vt7VdwF3QnN963bNU2v86AR/qf9908vwV13dJt/GcK3j
Zr2ro/r1jN7XsJ59337Msm8cNlS7dV99Wd34/2x73wHT1f9VpdYbYwdGjlP8
OQqJT6O5/VHPPlvge4k+XatxdkuxjUSi9u0d2hNPF9k2BxudF9DZZ1omg2zm
Mp2Bd7RuO1QaZduXYMYMw6nJbsfAd2sfL6vqb/0U3IPkOMWWYppw1s3YzAg3
NMk0zgP3tdP9vl99fEPff6/Ia8xa79YcPql3vqv5v09rvF7v+ktr8hsxCtTP
ESNMQ+EjuqTMPqM7NBe3a72XdLctFvc293e8+jgu2bHcQ21sI/lrYIPXKLDD
I449Mew3hDwfhzp7TrCTxz6e++5y5NPQhWXGj9jfYdv3XLTtxFZp/AN1HwxQ
uaie5cbIWKupfn6EY4hjV5uK7g+5udZ2S6CDRhddrdy2EMSMWaZz3EPn9l7V
uXp3vsr8LqZx0dVB8+K7jw8/MgfyhaMjJn/4GMErickyyf5M3HnY9UbHOW78
e+pDda3TF9rzNVUP1TiTsMEULv5J4/kRH69e1iujX769l/04saXHpv5ZzeGj
GlNJnuMCzBnlOAFrdfc8rPX7UP27SX9/Dr/GUYZ/S3ObXPQf5Dg36/Rxxu3I
dpDTfJPh81kc45x85Pwsgbbhvtcdcat++7We/Uhlov62UPPzVXXXwwYbZi+Q
yzld5aDeHdI6ftTJd3BCW/t81hc+ORS2rA+5HzVtdAjDL7AfJX6kN+kOfT/k
+PnQ9Mix2FtfaG2biA7sq3n8UHP3R7Z9cfH5xDf3yrHud1ms7b943+nB9jXE
55AYR39xDojTnGubLXgR/Bs4BztH+CxEaT916OH4L2XnW8eLrjdO/z+t/ZB4
vm1zFhD3BHu2dOuM0RfDKxAn4uuZhuEfaDcTfm+s8kKR/cnxK59T2/Lm6wKZ
MzYkqzSmh5vbXw4/OXLCfhhlf+MDHQx/ELR/U/2RvrFLZes08zzwOy9pLYdo
3uslGX45aMNXvqdztXeUbf9fKLP9P/CcoI08dVOGZapfCn6FOzXeejDsrPLQ
iWnfr9GeatjA8Gulbj8ZyDZran/9pfG9rPV4LMX1LSmG4buwCcUns1h7rxoy
gV6W9RO7BHtD5BHIleDfkQcgF+gwynT0xN6mpb8qMQ9b1sm6VPSos1XP0Llp
PtN2BtAY0BrE5XjhfK/hFwXWMxF38wX9feAM8+3w7MDjz3cbXxlij/dIN52B
rSh2RNDki4ZaHvlynvvPOICv7uX2Ffnmbci3TRywlaovR8el/2Wkm6bs1Nv5
1S7T/j2m/20Rnl6SaDlpaqlt1j7Ns68SPkudSxxTn7wzr2mMn2kOH40x/GNL
t6/vbb8w/HQv050xW3O6Xnfz/VrDGlqX30LODd8t2TogbITQAS0tdb3gPMOZ
IdveYIOzSO/+R+t/Nt40AbQBdkJ9azkPdmJT6zPQa/RW3aLc9rv4p+Kz8qf6
s0D1Et3ZHTXG/l0cT4i4QsSieFx/u0Z7r18D+0ARLwU/qLr6/lcae3SZaRXo
lLHFzqm8Ps9yY/gmeCb89E4LZ3yrM3AmwTaOF462DvPNCo6JlaD1e6jANhJ1
tbc/0/o/obOb39NyWex3sd1lLg8E8wm/Ag5/cIxtahYHdlHAr49xO0s4uSJ2
XyG/v0MLf+Pfofb1wE5rmPZgivBqqspUrdnP4Dz1p63620397ZEW+E+2MP2I
D+mLOttro5yXlnx65KYlZjb2Y+OxbxlovQI6BfK5ztWa3JRrv1D8Q4nr9M4Q
17ShlYgp0LKNYegn2h11L12r9zQRzvtFeHOa8FCSyp4Y26o2DfwDgLFZRYeC
zSd6FHx62Jf49XTV2rUVHK369mjPI3uzfmDLj01/XXhWjfOGKMej4v7gPsGX
fHJVy5iRCWFf0TPetvTYSmFbP7uN44UQN2SL9teN0C1RtoNGx4UtNDaUnCV8
6CuNceykD7R3HtM8r8f2UXflpW2sM0Rmgt8Y/mO98+3PiV/n5/jp6Rz8oz0Z
1hn6VN+Yo7vlH9UT8V1Taap57tbX8jTkavhUfKa/HdPcP6L3P6099VRP6/Dh
Y7YLD9eaaX0n+s2ZM+03j/88fmFV4I1nWjY8qLflw0NVhqicreQCPJi26LIO
mqtf8hzTjNhmbYRTuov3WKF7stMo62TQzWCHn61v/oA8qZLh9b3chpeFpyUv
cMsZjnNwNs96W3S21fX3NaPty7ZU7+zV3z5MX5cZ7hO0hwTyeXhH9BHECMbH
+AudqdXap5WzDS8JuX2sr30HP1b5Jez4O7N0V9TWN57XPDVLMFwraN9S2/6f
cVr7GzTOfdiqpdp+D14EnuQbrfHvWust+m2h+p6g301SuVy4/HOd0aNltpnA
Pga7iYbNbO+FjSZ6u1/D1uMBTw7aa7WPbtR9VL+iZS3IeJC3EEersnBAsta6
TmPTucTIqBjIQkL6/3NF1iVzp0PLQNMQMyNC5+GU+rSI+BM6U/20nmv0jo7q
/wTd+QuxqdU61lG5bKR1h8hSkaNiJ439If4SX82wnnVEK8PoW2kTryRX7ZIo
w1cUu41yCr4KG6NXNZ4bVd+AH4qeWyi8/GyU7yrurMiQcTXxe4jjAwzOpo0+
o6POfE4ANw3axKPpmuj4NMvV79Van+iajllA7IKFBba7Xavx3j3C/Bs8MLzd
g5nmW+CPiMNCPDTsuuDbWvYx73ZrIDfCPw7fFeKpEUuNvDnEayNuG3IE7Dyw
8cA3b2m+/fPI0UruLvJ8E7MY/RO6J3gzeLSS8ZZN1grkk1erXyeEc6+JdiwS
bDOx0cRuEjtAfCe3RToWAHEAlunu797HsamwXUTfh97vmL71bYbln9Dqc3Ve
ovSNw3pHf+Re+Y7zl65SabxtVfYF9irw8Fs1vje1JhPwu1XZPcTwlnS3KxU6
Pi95Z9BnoINAF0GsJWIunU70ubtvlM/eEf19DbyBSmXtgcnCseN1Hr7Rml2D
LUgj2yVzv3DPEJ9r/QTLAalHVzMMPQJdAk4Dpv50hG3tsLPDz+DaNNuDTUyy
nnhr9v/0xuiR4dVfD2hy4o+Nr+aaNvFCiBuSnWHZVo7wz60a77Ycy6/x1+Q+
5F6srPKazuF3+u0lUYbJB0H7ryL/lncUpzl/IvEJX9EZfFmlneigFpqbrlq7
hzvYn5q9yD5sEuxr9jf0CzQ/8e6e6GN5Xgut4yx8wZB9qe6ncX9VYHr+Uu3H
NI07VeUb/W56NftJLYq3Dc+Nqk/qLFyLbnCQ8x2T6/gL9bko0r5Umxr4PsHX
AXvqqCTfZ+TtJVYgZ4SzElYfayO3rm97vFBgk5cz2fQLcd6g4+ApsaPGFwef
nGnF1l/vKLMOG5j4HrTBv+uSjGtv0144qL3x9Vj7GKEbREdITBJilxCnhDPO
+W7Z0/qLVXrm1YaGr89x+waN+V2N53HxXfM0xkydwSuI557jPArkUKiQ5bwW
KS3NTyJvgTaYyhzNsJ/oHfrGXSojKjnuFXGyjpbaBwZfGPjdZ7AZRz9V1XB+
hNvYwr+cY3unEen2KahYbN+LVyNNf/+oOd6GP3FF26XW6mfbVPgEZBnp5c6B
kKl5uaPMuT6IP4s/LjU+ucDQhDkBXche7j/D+7ku80WMH811jO6tTupDlMo1
WsuVOmOrVF5U6ab2zuqOB4H/x3UtrcNDl4eO8mXNyVu6D+prn3QVj5avd140
xXwGPmnwGm9qDe/TOO5VydMcddC+eA//XmJqlpsWoN7QyzAyK3DiD7qXUsZb
BoH8ARoCnz50Yw3DjuFHLD/gF0a6HdLYivS7dTGGr8l2G30weuH0LMdNWqHy
nN77W9hxI8hRjJ/Ml8QG0bgaqu/n6d6IrGk5G/aQyNo2jHRcr40jDRPfi/bN
msMk3adTuecnmQa/d5Thyclug2tb6m7/dYLh7fFux2utcvXu58c7PsmORMck
2R7UtLGxfq6N4xBtCHALOKamcMfTOpu/66y31RrV17srxds2CJsg7Pdf1hrc
pr9X7WY+AxsOeA3glUGb/bAh13uC2F3kBSF+Fz5YdZmbVMP1gzb2sfcHNrJT
e1vfit4VHhVeldhWP+c5PiCxAYGpE5Itd0P+9ovqGsJjtbQWJ9THTZ0c7wM/
7Y/yHYf+kmzHR8POOjfO8OnA7vrmTMcW/Lmj4cVB+x59e5l+f3e64UFJbtcS
njipZw70N7xzpNvEQSAeAnFOicWKjxNxBPFBb3Se/dCxAcdPHvtvfO+Qz73e
376H+Ligq0CXc1uZ9Tv4U8NX4UONLQV2XW2GOm4L3ySOCwX44YmOiYn/K76u
K7RvqnBf57u+YbphcMBfOltTtN8+q+iYBfhInad+VRD9GF/NdjzEpSK+dXIf
xw8hjsg5G6fetnPqIFzQSevZQyVO7xld0bYRxAiF751B7Cn4XJ31t0dbj876
3ql5mK71i6xvvT9xHInnOEX9vijwIcCXALhbnNvwuvC8nLsOAW0JjXlY3xqj
cc0sNU8UOdx80XGtSSvthwfb2M8QG7Mb86y/Jq8nOuyW6I70zru4l/o4dtkm
ZNXYw2ADMMNxrhH6/wy/M0znWvg2Z4R11cQgQnf9aa7vNu419IjkskKvGBfM
R7uW9lkBx4Jrh+jbVzJe0T+/V3eslMl9raNEP1mhwHadyLKx7QRfs1b4bwKz
frQP5zhW0JGgvrKWYWJOrNT6TMs3TBwK2sQRJ38wPs8RGdY3oXfaqu9dVmQ/
ze/6Op4JcU2wP8UO9aksx1DBthMbz3f0m1j17YTqsdgjhK1rI64f8f2I/8fY
srt5rODflq2MI+BH0FHs7moYO0PazCnycuTmGSHndeJuXYQvjfqyWPUgzeN7
6tu7fQ0PDNpL2Euat9uTXYAbxjnGD/nE8F0gtyuxTLuojh7pmjZ6LPRZa1Vm
En8GOyP1ZfoY89xLEx3z+L4Cxz0+Utl9urmKfdmH8hx23zqTVyArSTd8dTW3
oXmZa+YZWwdsHrAPPxvYwiC7JD48skVkiedyKE9z/FPkSCsCWdJynteYEtva
5o/4AsQW4NvdYmwfCk83MdDd4+ePv/+bYx3Lh5g+16Q77seXnR37A7oc/2Rs
zC+Fp1T7Bp3t5UWOo0M8HeIlETepU+n/YjwRdyqr2PkQCqC79Jv2whv1NW8H
ejn2U9QE0/BPBrZExIq4aHSQIzTLfjaF2qtJCY7HW1n3Y6uRrmlPa2Z73Kmq
W2mc3cfYx/lS0Zu76on3UH0sbHth7IaBPz3f7a0THLvoX+2NR1Mca4D4Akma
1ze6mq9Gx3SX8FH7wW7zd3htaC78kLEtJQYRMYfOxaVFBqM9MmewZSvECD6v
n2HiVNPeGviz4NeCby7yTuSe6wIfa/IMhNMd84/YzBlZjqdGLLWMoEYPskBz
da3K0+LPHqzl2BwR+fbj36d98IDqY8Ves61x9k3AL6GomeXVyKqxhUEORN/o
Y70oyzKQY/yj++hePVc41PHEwa0L29h2AfvcjlqXZcJdT412blhgckrSvivB
8iFiJvfU93OKLbN+K2T5PbFDgfdNdLuCfl9FY+0gPvdh3RP3az2m9nJ8PWxg
JjdwzHB8XfB52VFiW4N3Suy/ih3NMPWvQRXHPytONXxe0L5Cd8zo2o6xglwS
+eRV51tfAt2G/iSjr/ltYtIcGG+8Cn7Fxg96rnSAY9M0Fj6frW/dN9RxFYiv
ML2WfY3z9P57hcOu1FjuU92h1PYz2NEQP/0VnfVxeYZ3T3KbeBX4MOLLiEwI
2RCxmKmJxwyMjSX4dH99w9ha0sbmNpziuHvoc7AxQ6dDvE7idhJzAd0AfDEy
DWD4Y9pD1OdZGv+/eubJsY7TQLyGr4XvT+rsLNHcr9WYBut8vhjh+I5r4oMY
j6n278MfZXeWY+EQEwe7oiWag1sSDN8+zG30YsSBQzcG/Hy22+ib0Ts/rTJc
OGvWJNsDEEfsNZXSAsdQgH+7s63jezBXzFmZcHA7fWO4yn3YxmvvjFdZrTPd
U7jgOdUdZjrOwuYyx1mgpv19mX3a8G0jVgsxW6rV9nxERXhOugy0Tnlvln2N
8Dkijgc+tMTVP1tkmBr/2l/1u+rBb+Aza0137KIfNIah6m9TbJz0t9uLHb84
cYpxUZsc67eIY46OK67Iv+H5F3Q230qyHvcL9aNtsv3GiU1AjAL0hOis0H3t
C7kuqG64u97/EOenmXHAsQB336s7oKXwaodhjtc7erJj9sLPXhRt+dTFwk2f
aq8VVfW55fxiM0ksbOSvyGGBq4xyG90U9rTop7DhxZa3UopzmL6i/q5TGaD9
9op43oGqX4jzXfH9QMO1Et1G53KTyt+Fjl1Gvgbil6HbIDfAXwl+fu4Y/wYb
Pmz5sOl+Id04GZ54i+iJCOgS1a/DC+hvhYWOpUlMTfTSxN/cVubYxNhA/5fr
4EBgc4cOZH9fy22PIvOeZDtU7FGJ3bu1zLE8iAl+POwY4RTgkyW2w8P+bpHq
q/s4fiKy9hP6fzk6kDqOQ4FN/neFlqkUDLVc5ZHA/y460Fd8Eugsjmlte6sv
x1V/lmi6NivX8mVkXMi61mov78V3Mc12xtgbE/+mNMs+gP/FLKSmjb1ZbIbt
zLBXw24NnRNxZYgLSwyRo/r+IO3Fj5Ms46uGzSjjneKadvdAv3K11mG8fvec
zvqySNvYYF8T1dj6EvQm6PLwm8d/nngA1MQEAI7U87OKLE8dq71QQ+dqfrrh
mhFuE3+893Tnn7gk5Jo2uUOJqfmrSn5H25M1E76OwmdH89Uw0bwUuXFOqe4Q
1LSxu8f+npwm8MbwyJeKPg1p3S8WvTG3pu35Y7V/Y2oZxq6fNu5BK8f5Ltil
cV6kcrzMvvH0j77hk49v/ma951316R2VAei6smzvz/eJeQIfguw+npgNYecw
/lO4aof6cbqudYDwV+gBidGLndjcBtbNzQr0c8jgPyy179gjolnK4+2riT/G
YJUmgo9k2B7kcIZhbERoRwZ2oNiDEt+vm95/SSfH7SeeBbH7iWdBTfsu7ePy
uo5JAHxP0J7cyXHYHx0YlE6Oxw5OejDAS/hK4xt9SnVt4aGftOfnaK0+He34
1NeWmCaD9oXuRX7UHHv0ROfMS4xyLCF8pdt2tC81MPmpaD+HnSk2IPrbeXGu
aUfoW29AD4uebjzQPgnj9c2JWu+EIZZv4IOCLwox3IjnekrwyULDi3q53Vhj
moMdu85SViBnmDPa8C9BG/y9WWXHAMf8J7Z/Wm3bMDJ/yGmpkdsCx6rP92p9
n9A6Ngt4lYMDDbcI2seFu1fofU8OsA3E4SjbROBj/2Bj+9zjv/KnyoRcw+Ac
2uTpIT/P2hzfL2tVtqh/TXLNi8GTEXfzpWTH3gw3+9/9SZ6jzzNsu3Yu99EU
t8cPMe0NDX6fvv+a9s6G4Y5LT04ichPlhBx7hVxTxCwiXhH5f+BvDqk/+bmG
sf+nDS0FTUUcF+hC6MPTqudpX1ylEp7k+LXYwNYPW8a3E5q12LYhyDgbphtG
7kmbZ5AHzurg+L2dWlj3jB/BxSpTulv+jRy8U337rZ/S3kjOsO8P/nT41cVF
ObbZnSpz0h0X5bp0+3vi64k92+4kx7eHz4U2I8cCPuB7NB9NtEfOH+0cRfiH
tFcpVD8KWjj+3liNa/Ekn/+xAR4AH6DrflN44/UIyyXAAftKbPdB7quO6Gam
O38FeSyAqclx0Vu0zQjd0zeWmXa6QbioWO/4UOOKFd443NWxs4jlTzyRPYE/
G/ZRyHfIXTZb430HfQR3Y5rXc9Uoryk0F3gO3FwSsr4OvR0wcc5oE4/6kemO
SQ2dRgwRfgf8bNAmlsDvpb778Bf7NvAZQzZRMi6QV2i8GzTWCNGELTX+ZO2d
wjjbs3UJ4vsAV67jNvcGcWuqR9j2GBoQ+2N83vCFI+5qDeHFG6c6zjX2atAK
0YHt2rpUt2uNtR0EcWKQHyI7JNYj8Zr6dHceFuS32MgfQLaqvfMh+rwelo8Q
ZwR5CTU+qcDgm8Qi45w/9MwGeMEC50MkXxjxWNHHo5fvn2o/S+JyYbN7Q4Fj
G+FHeGl/2+7OF01ZK9pySvwE4oQ75+g+vniQ9ZX4aKGzxI/qMZ3xjEjD+FbR
rq55ulp32rhRrsePMkx8CXKRNUx1TV5zYP5OfTrs+rwAJk4dcSWIKQHcOMpt
nuf/xKog9iMyy8/6+267TPN/v/ZGnYrOhU1O7BE9HYdzmOrZGkOinpk7yHwB
PMHO7s7bhm0RNkbk5zqd4Rxd8LHk7SXuN3po/IPwE/pAc/aw2mvH2x4LP038
NYmpiX9c0SDbB2KXi30uMeSx/R1U1zLfv/S+M0MNk2eGdiXt8Xuj7TPL2pGn
lfX7vaVlGidVN9X835Ho2IbA1MiHyONDvC/2ETgnJYiXQf14A8PERdze2c/P
ynJ+GO4S4EOpbpcW2k4aG2lsvMkXRN6g70VT1Qw5JjO2/dhjMV/4+9YeZp/f
t/Wbm9X30wWOlUFsDOJ/EYedmJvE2xwS1MTjBE/gJ4K/yOOVLd9bXtn5tYg3
SqxRYlRuGeM4leiPfyuzPhmYmFG0KwlfNNX+e3KQY5FPquf8KfhAEWuY/BVn
Cx1r4LYc21bjA4V99TLhsMHsC41vi37/0xD7eBBDu+1Qy8GhCYm3Dl0I/GKh
2+SERC82vMx6MvRlJ1Ltr0asKHzWyMsxuNT6cPTab5Zbtw2OIhckeIo438Te
+C/nEjVtcixVa+u8S+QAQ17yGd/RnLTS3O7SvFyfYV84/OCuUL1N4249ynHC
iRFO7k1g6iZjHeMonGpaj/gdO3SXvzvYvnn46JGL4KZy34vcib8V2a7tqjGG
F6W4DU8Ln4r9ATESlsQ4TgJ2EMiqsYXAP5p4yPhIkwcB2xBsRJBhY/czv9xr
Ql4JYkDUS7ddBXmdyE9EbqJHqliGiCyR+Myf5DpHA7kayDVIDCN8DoEn5biN
vRV5U4gVCDziAreb63sxpV6PM2HP5Vtxtmsh7kulsYaxdTkR2I1w57wdFGDi
bqKjQ+aD7If2TbH+P7FA0Ym8qPdc2M85Fv4OuybnAjDyP/JYXVzLMLJC2sTJ
ji10HKqromxni70t8VrxiSCmWXRgJzYo0J2/me24ebm6o/Lr2BcHngU/Tvw7
sR3DXp7YgsDYk9Eub2vZLzJg4O/ruI1+BD3cqba2Gcd2PDbftkB7upiniJnm
mORDEmyXjm6svI3t8Q5Wt00eds1fVLcuer/2zbTJjrdL3TrFMHpt5O7/hF2v
CGDwEfmrWtR2vEByh5HDCJ4RPhE7EXhGatrYTGM7vTnRfmHol9AzAROLjzY+
8/jOd+8U2PqOtL0vvrYzsaVoZbutF8uce/RDrecd6NvGuAC/p/polm1AuF+J
N4sPK372H4717/ktNu7bCuzbeWMX+y0w79isYq+Kfgf958SAR0A3jI4Y30nW
n31A3PSs4c4Zio0e9h/4NGH/8a1+//EE5z5+VOdjNX5DcfbNIPYo/hljxzg2
IjZ95FcgzwK5+/BtxueTWCnkUCGXCnG58GvbpPJzvmm5DwJ6DjkxOTj+jrf/
GPw9NP6sqY5D80APy8CRf6MDI5/CkJBzKgCTx4T2cNHKh3V2LxPN8fkQyzPI
I5KaZXk6cnXyiWLvgp3LjU0cNyBO+7wyMc+QBTWz7puYAsQTAKZGF45utUhn
pXCAYeJc0SbOCjnLiJuNDBpZ9EDsufIcwx5adLv2/iealyVR9oEi52tsb8P4
QtFup7PUcKD5u87FtvkmBjwwci7afwjP9Na6f1PsHEbLI61X+QecRMyTYvsr
3xr4LL863vaG2B0CPzHMbfIYkUeSHDrT9bvXE5wLjxi/X4D70SMMcK7Gh3Os
h/5Q56NGsQu5G7BXJv4QNrzY8hKnlxi9NRNdgN8odf1aumEKfBr/P1zPdlzY
c+EzDB8KP5qmPdRSfTl7gWW7+EIj0yOuObHVibFOPAN8yLE/fz/X9Ba0I7Yo
2KFcO8Lxyqlpk7tisXB7C+230XmWISNL/j3Gc8p8kp+K+KPoOtDjos9FhkbM
qZVpjkHF2rBG8OLwV531zn/DhqnhvdboG8+nWs9XT+/bp3N+NmyY+vve9kvB
P4XYGDWamjbZo++mQRvmOxYm8J1xbuOTUGGWfRSAnw/a7DH2FzzPJZqzJnp2
Y1/rhqEB/pPRUNMmx+3KZMeC6ZFk3RY2LMS03tzQfvPktJqX6LxWmys4bzG6
6nM4Wn18Zaz9nYk3TNzhRwebtm2qvl4kHFdZ752tun9vx4Psl22bavhU7Ko7
BXwrMDIL+Eh4E3hKatrEk8TOFrsN4tESl3Zqfee2IHfm7Br+LXIPnkfGQYyH
E4WGkXvQJrcNchDkIeSwJJclvqDEdUCWwjri70VsXO4s4gBAT5HLtbyKa9rk
k/qwzPngJmH7qbO+YKZ9YvCNGXqBY7cs0PMPlzlnCblLXp3u/HbkuTupcrjc
9zP3NDD3N218kfFJviLBPBG+01+2MQxvRLu23l2n2PEWiH1K3NM20cZf+Pvj
939E++OyeMdnYl6Ikw+/npluGRDyH/JxEruBdxHzjphM0EQXaF7yscUYalki
csQ78g1Tl09yDF9kvks1xtrI91Lt8/1zjnN2QkMCXzrO7Vi9v4++1y3a8PYS
txd3sF4hq4NtyvEfwcac88c5JL5+e+3jbTpvUX0dn5Hcn8RrpACPqmUcAa4g
ZwCxgIkR3Ey/eVp44zWtf2Zl21VjU4UNFXo/9H/YXb0o/POUvj21hWMIca9W
7OZ8KuTMJXcuMDlWaG/H5kZ4qt8Uw/2mu41/MWMjZj4wfsa04eGRudRSjQM7
8YGIE4TNBbYXxPDjvsY3Cj+Tz/XsSe3JKM1RBz3bvqvjT7+v5xqV2DeM3IL4
UGKfOUL9SlafV6ifX5V5DxLvjZh6xNaboDlIHuZ41A/WNTwjaDfDf1O4as9M
x5wGf+OTgb9Xg+b2AwMn4VsPXiLPTVet//WRhu/Jdxt76FEzbbvSYrpr2sQF
eW6Y9+o3Uc5jTyxkzgv+Xvh9EV8NH8Bl0bYLRFeNL9y2ZsYpzeOcM5GxMa5W
RY5/N0CltsZTS2XWdOsSoJegm5gLbPSJ44JNSpLupD2DbO+EfpW8U8C7p7r9
u87kx+LrJja2/ONwcLcgB8F+GDvieZUdw2aYynujnP/zz1LbzOL/Dd00P/AH
B56s8/5eVfE7VS0LIrYPcXqAqZENEeMFPRT6KOawWo7njdhP4BH8tanBJcCD
A18xfMTYq8S9ekB1on5Trvvl0xjnnmpV7HxVUTm2g8EGBntf7H5ZZ+wo7oa3
HWsYewra+Pvi9/ttpn2YYphzjbHirCD/aYlh8qDSxp4AHRZ93BLgPWDsL4kV
iD0m7yAfT7WAFiKvD/TQ+gjLjtG/Izumpr1EXbpNZUcd23YSe5RcFfyOnELk
BEKXje7itM7pxHLnCzpUblsBbAZWq6wRfshSP3/JsH0H83GwheUa5+QbsbaP
3hj4fWAPjC1wJY1vbFDTRs+AvqHKRMv+kV0jwwamRhcwqYlzOFbXedqsMa/R
PC/U2bhVfbpMz6wcbnhXptstgz2FvO2ucsd5Sq1hfRp8FvzWKe2JSI3/yiTD
1MszLR9HJ3ewyPYX2GG81N/8MfpcfIrJHbVaY9w9yDlnyD0D/YDv59iAhyHW
I7o0Yjag2yNXDzl70E1+GsScwk6BuB/YKhAfk9zdBa0Mk1+BNvH42BPE5wMm
lwZtbKtiA/sqYrQQ2+eDNNOM+LdBNwKTA4w2+diQTSCPIFchdhTYU8B/kBsV
HoQ8vdiYD0kxTGwF2uwz9hv+gh/rbJ7We+9pbx9AYnJcleezmqY7+9Qgw9T1
0+2Xz3P45mOvht0aub6wIfxG//+8omNoQeM1zHUuA/IXkM/ggTa2ycMer3kg
e0EGgyx8Zf7/9GHUtMlfUUN4oFfIcSDqDHAsiB/SrRtFRwqM7R9t8sT9Vuhc
cfAwiwId7cBAt4mOE/6V2JSf1Ha8m+i2jn+Dvy180ZbhpqOgwaCl6DMxNuk3
ftrEZIP+JI8eMTmIzfG08GbdsHOUdJto3nKVvl1V752mOZo6zXGbQkNMe2Ov
ha3WB1qHQyNsr9emrW33qGnf0cZ5y+9sYzhyotvggdcCXNAmZB8pYq5Ch7w5
xbQIeBn8vKCr9wp7pkEN54aDxjoaaV6VPH/sF3RT6KjQARIjrTzQKWGziO3i
m9NsW4CNwbYMx0YnlgFxDJbiO6FyR1/Djw13m/OLHwNnuL/m66Bonr6ltmvH
vp1cSbXVv6X6RquOzqdWkGD5BfKS32tZZkIuS+L0blffGmuvZWkdMkfargL+
lNh0xwJ+FRjZNzJw/HjYA8SGGQVNUO4c0Pj1499H7i5ys1XW2bsTPXGJ4U39
3CauJXFgiHM5b7jjVhK7AVqAPBXQA1PyHXO/psreQB6LXLa6vjUP/XC54U+n
uw3PCL/4Z7kLMPnUifeHzpL4f9Gan+3NfJ9js4IsDBsWauRhwH3Vv7naPw3y
7JdDPpjNreyzjO70WMjxo9l/7L3yqc47Sf7JXYHuekWG/VTxVyXmE/KWj7It
cyGP8LEhziVMzKiFaY43hm08NvJZacar6Bv/s3egpr1uhMfNeJE1npM5hp0T
DJtnbPa7tbfMlDFRI+sDPqg+/6l13Y/uTjj6C+G0pTVt60f8BuI4lJU4/xl5
0IglQuwM/K34HnpFvg88a7zbxCslbunuFOeweGuy6QD8PMhNuyOosYsBxsad
3CEDa9ifCpsP/KuAyRFPm5zCe4bb7gBeDt9ufLyJq5Kic3qwtnMWYMuNTXd8
ECuCe574qsRZJd8Eenx0+PjKI69YWdV2OcCjJ7iND8rqaMeEwPYDu4/H06xf
Qc9CrHN0MruCNvHUs7VHL1X98PmO50IsF3L1ESv86U6OL0uMLfxFidELPuxX
6lhXxLwiXzk+5b0Cv3Jyj72Lbi9kmHxktCsK7q7fLa9jeH6+29jTwf9iU4e+
Db0bPmWsHXYX+Cjs198uGOVYwsTleqW1cXSFYttlYpMJTAwQ2vSznf52KrB7
JqbV3JGGsWOnDU0GbYYcvH2WY2EREwu5NDLp//JFUdM+qb1VRWd+eK4LcMEo
//32mv9rU9NGLkmezqNBTAJklbRba9zXgJOC+kyGYeIDYNML77+th2UoyE/G
Rtsul3xc6PLJrUAMfey6iE+AzRfwoWluY9OCHQs6T2xaqGlXn2m/W+ILd8x0
zvv9DayvJU4lOnniVFLTxi4P+7wFRZZbEKNifVDOxavQ7wbo+UPaq/262fef
GABFTaxzfT3wVUBmT95z5PbEmm0Y63izERXtX4pvKTHhiC1IXLgvYiwHfU59
G5nuGN7w0FVnOV7WoTLTDn+ETD8A7w3a0EnnaOgSx+uAryRmB3uOvUaM4+Mh
89Tw1vipEMN2aXPH1IaWgo46GeB38Dz3Jncm8cqJ+4Wd/mSNuUup8S481A+B
rzkxRrDThG+Gf8Z/c3yufTihaYn/D427uotjzxCDpnLYdsSlKYbx46WNHxX+
VMSI+UT15dNtJ0tcaXJp/JxqmFjTtMmZSjxO4nLCX2BbBX8QO8m52p8vtG8M
PjLo0cgLhC02uYGAsc+mzR2OXwbxKrF5b6fSNrB/p+480jFStjZynBTiTaal
W09Bfijsp/BTAY4KuU1Mx+X5zp/EOLD1ZSzEktqkb5YiNxNtfbPmsGue76wJ
XezTSl7ur1SW9nF9Rx/D5A5EV50ZafiyQHeN3y32YtiNTettvzD8hMjrTH5n
dJLE/K1W4Bj3i4XDSttaf0IBDrV1zthWac4bS1xE5PrEa0LvRpwpdG/k490u
nHMEGV2JbaaIO9sk1rEDiBnQZ4D9yZ9Ksf8xfsjokanDYwyTsz46w3nrDzd3
rmNyHgOTC5n2e/19Ljmv6IKRZaAPBk4O2o2m2D+2v+b4Ha3HA5rbIvFly/SO
D3WGe9S1n8KBzvZVgH6KTbAOiDwvVbi3GjiOy4Qi+0Fdrnmqq/59lmwfBWD8
FPpoPF3b2H8T35yXRlqei08GvhnIYCLH2U8cf/H3gv7Qr88DPdNn0K3qW/tO
9kcl/j82E9hLwMPDyxN3lxwg5AKpEG3dNjQitDkwtCJtcvGRF3ir6hvhx/W3
ViHD2NjSRjd/dbL19QsKrJf/osR+T/ck2ueJAnxIZ3joCNuVr2jjAjwvxTzj
meHmIb9Nd96/0Yn2u0Lm+p8dAzVtfCKwacVOddi4IO/AOMeRIg4nsaTwqyAu
L/F6yZ9EDBxi4RBTZm3IsRGb6pmftN/6aP836mw7DuwfkMFjs4FsfnOq5eCL
kwxH5LqNHRL2SCsH29eueeCDSYw0YqU1a+ZcIOQEIXY0MPVy9K1JzgWNTxd5
wYidQ26wOJV2+tuqqvYNJsbJn4Gf8E0T3F4bjIH4OKOEh58Szqgz2r58xDY5
NcwwMU5os1d36r5oi5+Cnj+mbx2oY7jmaLfXj7dPLzFagH8P2uTQJmYSuggK
MDqJB8ULdNRa3V/dfC22dfC25I4kF3BqjnMyolv/NsbwtLFukw/pu1rOj0Te
A8aPHHRNFc1ZVcekZx9id8FebNfUueivau14vcTtJcYzNhZbRjuOIrYL/RNs
y9Ax23fs55qDB/XsBN0PCfn2v8UP95WpjgFG7EvigAHfH+82+cqwv8GOhlzC
5BRe1tn6/5gY2wDg00s8kP/yq70WtJHFvRmyPG5vrnPkkSsPXyr8lA8WmyeD
N8PXnHj1PFN5snXvxOzHLwy4Wdht4hYuGu6cH8gvHtI4C0KGkWnQJmYEOAF8
QQxk7JKJSYLcEfkjuTeokUEu1D3xY7J9eckvSY6z3SrkXCK+DDngiGODD9Hl
VaxrwZ7ib/3//4o6zzAti2QNkxRQRKKiEgUEBMlhCeKQk+Qh54GBAWYQ87Ki
rAFUlNU16xoxp7O7illBRXSNoB4j5oAJXbOuGM59+3x7nR99dfcX3re7urq6
u7rqqce1o+CdL/C7iiaRid7riD9l+ehFqRt/w72Wey7l74XMxU/nJRarvsRi
F4mn/uS8zAftvScMic23597fdUbiD5QHh0E8huX8vmfhLuSJ+bEXH10WX3Rx
dfS5nNAy/u5VSmKvOaBgn3jDktwb6iulr4u6mh1t4hMqNqK4iMOVaTzvsg4p
mz84Jfuaowv3Beq81N+dT7q6I/tw0uQusWF7bUbs2IxBKq/L8609W8PPzXdL
fF+xrcW4Nj6gsQGr9U9urEDtJIwhaOxC6+baTTxeSI8VflPGOXMR6dsuWSe9
53StND+tsG4a//aigp2LZXPj4Z5V8FFQhyDmt9jf9RcH8/5h8utp37e9s+9b
sDDl7wt196tiq7lP9Qzmfs5zmfai2orO2Tu4LmK6nE9q3TkxVI2lqj+2mLne
S5t7T/15Yd3Yk/p5M+JfoD5Wvaz2xU9Oi42xNuPXTo3d+PHwyIu8axP7twrG
7Zt9g3vi/eufGMsrymPzre33H9TdF3LrxoM3vrpx1rVbe6gi/lhfFu6ejAvy
ZXl8zz1ne1egXbb3BVf2TZxasT+ND3cNvxugnrh27LK1xzbGhjFZjbmxpGnG
6fsuwbgQ80If0/OYI9tYj58oyn5XexXxjcQoWDvp/3EKKprnM/dwHzPv74Gu
j42KPlBd4Hp46xV48do+sYfT190ztWV93q0b82HZYYn74DlMXyF9hrSB0Wa/
ccHPShxD/a7MxTK0rM3HZtK55Yk3XLY0mEn6/neZkbjjxgFZuSy6oZUF/ZBl
MZOs+72xkY2RLM7EBzOyZ3fvbrnPfqlPZG37hLWmyP6xF1mDzJjRPjj1NfeJ
r4vYJO7B3IupR1bva+z2+8bH90d/Hn2v9cfWH7w9n/+btv/UOli6xicQW7fx
wpyxvx2b+NHGjZ5SM3o04w6qVzP2oDHrjcmr74d6zbPLkuvfbFkcoIOLgtNX
qo8HvHgKc/lZ+GlUr9geb2A+HDo+Pl6/iBXn/OK5i2fFlkebHn1bPBPp02Ky
7Lz6dEbW2r9WJFnWBkBsc2NDimXlOcnzkvoqffH1j9RPUnsp7aaKi+PPaHyS
WbNTXlKSuj4Aa7S5GJuY8epMtG/1Xk+8Q+/21LFL5//q7s2ta9upXec/Rwb7
8VrG/TLaeHZJ7umN2WLuXb1lbQu0MVAnba5e2rI22erZhiJnr+qR5y6rmfH7
qODTr327tu1iMnQu2D6z1fndh/OpgbER9B5kKOPRExm7tDTxSR9g/ozlXe35
386KlM2vm5d9+FGTEofP+B9iooqNqj2RPCzvvsua93Lj6Ea1sbq0YN+pbaL2
CNop7EMf/pf0deXokPQHMaaQ+Jf2/7kCzrF2C9b13zO2/e6MccuFya2v6JZ4
ejc0T8y8I0bHh9JcndJRZSn7nfV3odMb0GHL9JRPPzB19arelywoip+f+L/6
+rkGb+mUNfl68utIJ8/Pvc5qZMXO8pTNz4eH2vBdKX1e0CLlaYenrg2Mfgra
wdiWZoujA6sK7ZZNiK9BlUL5sk65z/Iu6yzWgpXjYvOl7dfQ+fE70//sUuj8
T9p/PW1dNz6+jmdrA8nYTqTfw2bHRkwbB+3E2vHdY4x1xwWhpzS8rk7oaW5d
bA7xUcTr2FUcHAjxIPRP1U91VI/Yl/+rPPbma5H7Nw4Pjs6DyMSb4M+OhyZ2
QauKxC/Qr7W4U/5fbWLkiXdgu3jvTtryxYLoNdRb628k9pMxDcfAQ1e3iB28
NvCWdw5PXWxBMQbX6/s7I3Qxjqu2GiOg85Dy2Ptq96t/v/tK95fewWkjMKM0
mGvKWOWr9+LOwxm9cy4Xt02bKXV8xm79iTVqXXHK6katG6fbeNrG5z6yR+w6
tO8Qu1o9urbNYjWK8SNuonhUh5CuLQ5ukBh4YgdtLeTWxcbT/sTy1u7JrXun
Jb6ld1cb+e0N3ikhYyZBkznwRnX44BnW2W2M0+B50e+p5zPWwl/H/79t4/28
fyhzpfqgxGrTR1bbCnN9Zi2rL9K/93ZotBjaLpwR/trN/X6vYOL9rSJ+WPpj
aQfnvYh3Iuouqs2LzsJkeWmLfO4difXBBXueIcXx+RDrVIxT7UO1EzWO094V
wfMW11sZq0/0L6Tj4c0VTYPVqw3TqQUsHuWYd7jKMu9zhxbudOsV2qQeRQy3
/8Zr3auA5WZdfaW2m/qnaqf1u71WwX5LOy7L10yIjZfYCb347XTW1pneU6n/
XRS7/vrsAfZivjUYEB2/euJhM1JWd2z9tYpgW4trrV7LWCzeT7mWeXfjGvZG
4S7VO9URS4L7Jbak8YXED9CXSWxsY8j/Wjh/eY/pGUz8e9fqykU54+woyR2u
+PziLonRb3nB3qlrg9iU3+0/POXbylJXdivDvdsy/pT4CGIjWDYOlXVj7zxi
Ys5M5bN29OGnbrHL1D7zce8F+c8/5gZvWvxA322MAMuvj0rdOefccy3c2S+x
WsRhU6cg7lL3bjkPT52b87F3kv+ekLsh42MYJ0N/pl95l7gj11fEJrVR79io
bpkfO3FjWxt/vePcxGNfwZz5I+koft+GNaJOWWLAuoc1prgYSsa6PJ60uXvw
EPXHeb0wN/4bn+qIwmf/nTPm1i9AvrwJvf7ZNLpX7Zn0oX+Ed20iVRqQWNhi
54tlqz5Z/AJ1ypbFMbB+RQH/TAx1baaM9yTurrqT+0g39UvZWH7Wldve0xgb
XDwA96QNCtg9ltt1j12R9kXiTuv/oh+MZ42xByTGmRjH3vd5z3c4tDumJDFW
vGs2LtUhpDJ+04U14Fqes/+IYHCIM2wstUcOz/nTs+d7vOO0UYm74N2Cdwy/
8v5Vhdy6WAy/Y3aSrirKXax3EObnF8riU+rv3JA5fWpx7AL/+5m+0OfXyFrg
OiBmnnFSN9CX9RXBFzf2lrpQdX0fdo++T56dAu8+VD1+rq4/rkP6ZuqPKQ5L
vSH/76O50+cPiV2g+2OxicUo7l+FMWM9mzwyftTGbNGv2nKV4tTFL+nUPBgm
6sbF01U/XmV6cuviRnZeFuxIy68W6tq8XV8tdrKPsu9cvTR26fK/7/H5xm0Q
a1HMxafFQCHN2jNYRmIui7dsWUwj62KbVef/Z7puVyQuuDHBLZs3qx5bkoqx
idFu/E1jb4ovZL66UNb/2ruve5rFjucvsPZFnE8eKQo299/p8xP07UnSSn6z
Y2RwvcWwkM+NqyevW/Yuxbp3fi/0zx2gMYT1Z9avWRxF9x3uP1bz/NNIN03L
Xc/SacF6fth7ENo6cX50NiUFvY3lsrqpi8HvvbD3w/o4eFdvnJFqyIfv4NH7
W+Z+3Xt2fXjN9em1rP5UW1b1qdqpaa/WfFrit88v+Og86b5rSXQGw5fkDtv7
68nliU9Qe1r28O7f9bPUH0l7Ru0aywpnHM86ln+uSF1sDjE59L8TG1CfF31f
LBvvzvoQ+v8vxm1wl/gD6Bcg/pO2D81o60OHxI5fe37jkW4T04bxv7VP/GaM
C1xREQwg9eynLcz9pP7W3lGObxlsRPVExuHzbsx7sZYNEtPkjvrBVDK+s9iT
rgViQ34+K2XXBOv/9Y03Fp0YLOKGd+OdvdynaO9Ykfg5xtGZPzr3us+SOg/J
XZy+Cb53FfzRdHEBLwUaT4Hv3qR/x9D/ItaZxYzFLubaltmJ36NOqaRp9Erq
FNUt6iNiDMeNS2Pn8/XU2HZ71vPM93Wh7DjoW+JYaKuo7bN3ba+p54A3r6sU
e8dZE2L/aHn2hNRv0B9xTuJEqPNXb6P+xvKCaqn3YE6ug46tkLGPIlP2mRB/
ilXQYQJjWUzajTY/tjT6PnWAxlZUX2vMSmOqThwR2x73xb/b94xIvDPjnolv
u9dBwbuVz1eMCa/vLPCPWLvqdIxdKM6Oe5WJy7JfeQX59jLpUebp9fBIE77v
NzS2G8ZW3gRNK9Hmd0YndvfufD++JPFm9K/R/1ccBvOWw1M+sJBb93P9hC17
N+UdlXFq75oTf5IXDs5cEkddHZw2E8Zq0YZic7vc4Xknqa/eAfUKevcR6bex
3vQV1GfQmC3m69umPG2/+CCJRawtpGui9pDSVP23NBajfmkBp37CgPjFfXxw
kmV9LowpIw7Xc5yLP2VO7STdCY3vahbbQzGjjC9mbLHFBdslbZj0n3mjQegl
rZ6dm/fbDuM8LJyeWA+W/1GeuuU/DUtdTO97D0qce+13vQNXx2hsFOOiaCtw
d+EeX1t+45noB+7di3o4/QvVxX1TltiYJ4+PL4g+IY6nPiHWH6beArrtz3PX
ViRZHsUzpngHTDq6c+IQm1v37O+5/6tpsQHXPlo7abG4xDbUR9my+X8W5vne
U/rciciVB+DPsyfHv9R7RePmuS80DsCIfVN2r2jddvi/A/rGP2no0NwdeIfs
XbKYG32nxs9NH7f3FsVHZHKhPHFs6ocV/HlHto2MUyeuzJs4KJiRZ7aPj+vv
eGm0vdn+sRXWTnhrcWJ1biO/mL639r65Z2SjcnEVvHZkv8R3upW2XVT4jb81
9pOf+30Xxn/P2il7dp7UKefnfvDfV/DUdbTnfebKlXxfwefvQ7ferCMnwBct
GKct7IMerZFzdf/xOWefCn/+WiPY7u9wdn2Zfm8vDc6JuCY7JyTG2Ub4bzT9
G8Xnd/C8w/VBOiSY9Zvo+3j+eyc07Ez7GsO/Z7C/WEt6lbn2CmkrbavKs19i
Hp/IOHTifw9Bm2f0jZ4SX8zR5DfSlxtID/LMsyckjvFyWG539gq7kT7jWa+y
/nfyPMAz+0KjC2tCa3j9EuTl8Xx2IGNyA+08BplwXNfEDdwPmfE4NBgCj/di
7vUg7QHPtSbfk/xH1vRD9YOfFfy7M0hXsybU51lvIkN2754+2r8J5DeRbiQN
hm6HQotrGI+Z7IU+p20Nadue6p8Z39/qx09VfMmfSJcwvlv57bV8/9xhKZdO
S32Dfgik60hDaOtq2lCb9r0C/eszjvVI2+lXkTpUnnUl+7QVrL9/LEo8uDNH
Jiac5eaFumP4+YSMo+XTOqT+vvb5zK+O8Oty1oyvaMcdyKizafP+0GsWbV7N
e6+AJkOhz1T3TLSxjfjBU0Mn6bUXvNIAXu1HWzcwX/ow9k27xKdPbIZ/k3br
nNjOxnjeCI06q8tgHDsVcuvOoytGBId1A2NxN+kn78t4VyPoc2dFYtUZs07f
4TUFea/cH87YDCO1g9b3IYe30/d/wyvP84xdzMGbesTewb2++3x9cOaQds7K
3sx4Jo3of13kXH3SUL4bx+fP8P7RvHs7c/dqxrkJ+4Gz+GyEtokM7y74vxbv
XQ+9mkKv15BFs+ZEr96wPLjfd/PcXdC1K3xci+eeT3v2JK/JHPiefD5zZMmo
YL/eXJRyu71S/4p5/6I+1+Piy6QP0ws8axj9r8mzf2COXFGY6855Y0YaO7I/
6QzmxQHIwl+Kg0XSkjW6GY3eDE/8h/H/kXQ1z/8KOfUlqYj1ownnsWn89nH+
15/3PbZvsCNvoc9043dcw1qky2nbKMb9cBPzqkuv+N5fvjC/H1KW/7x1UOJP
GL+7Bzz0KGtad21xCnsY9zKXL4oPYzfSQfBQa9Kt0GYG9J85K7gZ1RiD7+Uj
8rrwyBreV0Z/H4IW/0t/Hhwc2XD2/MiHnvDjOeJ89Ex5VpPUd/GO0+HLPZG3
A6i3Ytz+xO//yJg1YX14a2h827TzE4t1tfZ3+jjR1ob9Mw/36R+sXHFjxcu9
F966n9SCZ83rkVjKJeQn6r/WOP0+h3FbQJvXka/2LMZ43s78exu51ZvnzOqe
Z+0qyAfLPt/6kbT/EnjyMtLL0HMJNFvDWLzCmv4a6Uzm1BOs0/fAb3cydo2Q
DWuZp/tpF8a8/su8YJf8QH/fof97Q6tjWPPWwgu76yMCD0+k7+fT1178tgH9
f1Q8Cfq/AD5eCZ/94jzn93uTWsKb1ehLdX77Au2r4R0J49Je2yp+dwF9Phke
uJF5uIr8AcbyFPp8Mukx3rOZdB80fIffL0f+HEE6kf5M5b0H0sa7WRO6IvOG
a8eHDDyN9n1M3g++a0j7+5Dfzvp/G+mv+qvznub0vwXpJfanN7G3WQg992Q8
9iB9wXObDaQdMPBXtO1Z6DgEHhih/0zfrIGuhUuYexug11z6uI62HtUm9gni
Ug9qG/33PfDNGOi3DvrMhBcOnJn5rr5N7Bl1bj3gyw84L+4gVeZ5L/Cc3siF
ZYzpAfDXWcPje6cP3pQ6iVN2Cd+v4L/T4eFzeM4NzOt36Mt5yJyzyauwn+hL
/gjrTClzdAGp27jEDDsG+myFLhuow3aVTmGutUQWbaXPrch3klfnv59Cl2YL
svfspF5GX0zm2jmkzXxXh3a0gS/GUP6Bz34k3a+9D/1rMS/3P5u8r+O/FX2C
kbyW9/eB1v3YZ59KG3t7z8l3o2uF31/XVhK67vK+SDwbbV3ZTzWHLrW0u+FZ
a3j+6aSe2iMsji+hGKJiiVZoTwu9nkNmVzBP65A3hf8387tdPO9Ev+ezUfBd
GWOxC3r24r+/ToxvyMjC+dpz9mFl8YdaBH3HwbeVGPPjJsd3Vexa/Venkx52
fa6b85cYKZ7BdrJn+Ix0BjR7kzm8CV66iPQ839/NWIzrVMAF7xl7pSHwwGj3
J4zJYG1EGddnSVfx/ytJB3tO7hzf2B7QfBfj0pN+76Bfd9Gvj5G7H5G+mp07
dP04jQVqTFD/632Z8XqNVXEm7zzOOzDvYrSJ4X2LGI9K0PgR+O1n+HUe4783
qSP7im7I7vo8Yyhz43h+Xx/5VK9h8J2NX/D7Ws0c+GNJ7LqNPaz9+lzPucyL
Eug6uTj3fnfNyN2fesLXegUr5/n5iYX2XNX49p1QmthuU6ckLod8fiDt+4jy
Lub6Y4dz7qHvh3fN+X9uQSdgHBTvF1dPTrlDWerfMA7facvUPmem82ZF76iN
p/E3Hm8Y/JWHaMumVjlve84Wz6u04EOgfddq8lVzEwvSsrmxIY1vWEF+I+P+
cXn8YmeWpnxxoS4m3+WU65OPq4gd/vyhKWuPb724V+K01p0Z+4mbJyUmtvdf
N5flDsy4z+qZjf0s7neN5sH+FiOrXXnwuydq71ASHEYxDo2pJc6hsTDeZa/7
BfO7F2N8EbS8kFR3cdYg16K5yLefWUfG8qyn3D+RvkWuttVXGJq2mBq9d69G
iW9QiXe1RD7+6H1ScWJ0LecZP/C/I/jt0tmJsWmsTWM+n8se/hzSnWODGSp2
qP749ah/z/+/bhlbR+NqGFPjZfXAyIZxtRKz4r2ixK2w/E5R6p5ZPbsai0r9
ovd26lSPax7s8jeKgutrDHKxoDeUBHPNPc5RrE0flgUfSD2p+tHHtW+gb70n
B2+2St/YTtVfFJxzfTjE4l3RPH4Dx5OXtAhum/i+l8EHN9D+fkWxW9V+Vb9c
/Vn1a1Vvpx+kttz6vOnHqz9vzcPi42Uscf289APR70UfkRbtY593hOvWkpx9
PAOp9685I/cA/8P4bVwcHBqx4p9kvfvPmJSXF+r6B+kvJB7rpMJZ1jOtPPBO
3/CBMWbF6Bar++Vm8T0YtCS25R/1jx2WPhPG17L/8+pEp2ac8C0FO1Ux2M7g
P8/zfY8O4Wl521jE3jsY81x/7T17Jw79BGjYfE70Wuq3LH9ZJ3X1pOIfGjtZ
3xvt2NW1vtoouKJiF6sT1i7x5M6xKzBeoza+L6rbYK9aPCg6mC/qRg+jznZC
vcRONYaofsSb2UevKg+mtNjSR0Obw4qCSXAqa9wE+txrXOLFGfvTmHHGx9IO
5++DU364YJfjOfAs5Nla7wPm5+5Y7KhrkAsPdMvdqXSWxsYCehT5dOqI6NDE
6hOzTx2DMV60qdO2brdaiY9knKQ36iYeuevrP2jr30nXMzbb64dH7yxNLENx
H70XEudZOkmvodCqGbS8YkBw6m2bbdRG4FHodd7s4A/Kzy9NSyxRbSe0oVgN
79ynLcHSxChfTj6W3/1lWu59DylPeV2hLlaw/qViDIuRL5azmM7Ge9APqmKP
4MKKuys2bJUqOQ/c6r6Ddz7E/16Ab486JPZmk2vEv/3quplb2luIS6wNhuUz
D0xdrGjnsPP3sLa5t/H+Rjxx9bDa4IiP1qVtYpf+s0n20Z63xWErIm2hr32W
BatYzGLL2hVZ1/bo/oGxSzLGivgAVYuiN7ifNGJs7J680/Fux3Kvqal7VyD/
Gb93xEFZy1zT9NkRu+riYSnru2O94ZDg/6tfntE4dzeuNdqTHUs7fyuNbtWY
SMYv0Zdc3/ITW8dm57sDY7cjjrK6cHXi2puJh6mtmW0Tl+r2eSlrs2XdsTbG
z54tgxfyKP8XM2RlefyP9EMyJq6xcbWvt2yujb06SHWRY3rnrs5Y6d7d7fKe
eVEwAtQRVusbPaFz7iT++wXtKWf/ciFjvYR8KnunK5l708QhhQ+3wCN9+d+9
9H8RdPkOeTMbnl/eOLiBe/eK3sZxGMmeuQIZczufr+T/WxivI6dExr86KnLe
8sujUrf/YnT5/nfhib48sw9pB3L5Q1LTMYmf03t2YjhY1q7E+g/wa2fkTxfS
U4zJrfT1dmhUG16uXCv4jOp+BtaK/me2+lF45ALPBM2DmftwzehGleXqSl9j
bmzQRpF2fyi+EakN+8aeyJpXmF9TagXL2XlyBmki87oB4z2BvP7Q+NjfDH1O
4Hknjg5O+Ares505NVF/CfZUVaB9Z/JZyLOR0H6btGc/dAGpIf8dC43O4LO5
tG12zeTWr2G8fqCN68kbib0D/V5sH32Heo/R0GcTz3uE9IlYIfTlI2i6g9SR
eduI9g2iHZv1iWAOvsDYToJu2+C58XNT3rxH6nV4ZyX2qn3oQ3X+NwCa10NO
HAgNW5Dec99Cex/inQ+SbpVP9o0uQjxh7Wu0s3mN/x/nnSb5jYz1RYxNQ95z
Hrw5gPErgid/mpLY6cZDqTQ/Z6ZXjQvFOe7H/ROPS3u1Z1g3niNdyJzfiz1y
Hei6CrrPbhGfyXbw0Tm8q15pyu5jrKtDGCQOEs/uTL87kS5kjnwIz+4gHcac
PVfbA+g5m+edSZvOIH0C712F3PkIObHj8MThOJd0pPGG4O1baP/VzNlf+H9X
xvZdxuJpxqkPY9SefCxr113Qszf8cxftf421eR1jdxj8so80pl/LaOfZPKeh
eg2+/5zyj95Dk/8JPllB+gfvuKFL3vkBfZ6ofoq9zrHSifl/9rDc43mf9yXt
64/saML71/HsWxm3TdB844LY5f+wJL7gnitHM5/71c+Z0rPlo6Ra8Pu7zOH3
Sbt4Zif4sSfvKW0QnNWDKH8HL9WBtt9qGyO2EXQdSt6bZ29WlkLzustiX0XT
fy9rZ2VdG82LWROuYy4NZA6c0DWxbSt1jk3dTXvEnkN7De02jmO8n0DmNGad
nUe7VzAOZ7UJBtjgqcHRMf7UzoLNSUvoeDc8PsW9W0liGT2rDVrj3OeJaWL5
rIrUB8GThzIm59H3veHJvzI2dcir8owh/K4y+dvUX+F5L7fPuc6z4SL6ua9n
He/JeNZq5stjrOvf9Ih9/Crm2He0td784NGISzON9p8O366pnHLrSamLD3kb
/PA/c1MWJ9L6u/T7AXjrFdIXS3Jv612G5Xsrpe75bNKcnNGWQuz7+iW+tvHo
3OcbK0A/sBvh+Qfq5w5LP6GiQxKrwZgNxnj23vaUgv3ugobhLflKDAQxwtwj
30Z+Ev8dtlv0KGfp80P9/fLENhKvSuxZsWhvbZB12/XbZ4pjrj1l7z1S1q7S
untxcSgu4j8nzkpMGWPL6EuvT30H6s8sC35J3ykpH7049cUFG0PXhGfhj+dI
MybFZlzb8ca05QDo05n3vE0/n2Yefqe+uFMwNksLeBzOQeO8nLUg+F2emS8Y
krJnZ+viOus7rg+5/gJdF8VnoGt5fHfEL7LsecG65wlpZqynj/nuE9KAkYU4
KgMTS8Wz3XbmaRXm82bG7+2uOYPdOyexPe6bk/JfCnXjSBtP+rsGiS9hnAl9
HZW14tpq39i6d/Zp7tcGM3duqRt7T/0SjNtp/E7Lxp+17h7LvYnj75lZjCnx
f47neccOjl+vmEX3lAS3yHKHpak/xdi/VB57Ru+0jXVgzIOv4c11zOe/wsOX
Lw02tnEBLb/SM/UK5Hs56YjJWb876YO2e+5kVi/IvUyFPk/q/z07wo/XQM/W
zMeWyLOPXdtIHaBJR9IO+PsY2nIC6Tfeu55+vUa7LoH+FyLnLiKtbBr99dez
o8/+wHWI3z7CvG7UPzrjV6H1tmmJ7aaMqooMPL0252TGdRe81g76XfOHxAIf
xm97LUr8vRcY17G1o7NSX/Vl+5xRPa8pA34Zm1jNxyyL3dtT8NffmsUnVWwt
71cfHpy1d8seKW8q1LU1mVTQfVTfL9i44jyJlyZOWjv6Mx8a/Uy6sVvkyy3Q
8ULadyW0/CN9vhKeP5fn/sTcaMHath9r+TzW1kvYgx+MPG3Fb9uT/8b/f+0W
rNhboOtt9YMzt4S2Hs4cWEx+NGeqY0ij2HP8izFvxjPOb5+94cLC/vB5ZMRb
vG8reVv48DrGrx15Oz57SRsZ5Fhd6HMYc+DPHYLzvmly5rF7AfcE65E3dZBF
t/jbwn3EvhNyJ9GV9eQt+vg2aZa8ytgsZyyaImuuhQ5FtLka/LoBXhvZPOWq
hfoQ2jscWn5K+cu6wYl+gf7O9v18Nomx+BpanM4c+Wzf4IGLxSXmxsf85nH6
2AS6bOD7u5dEF9iGfuxgjO+g76PpTwfo05815T76ei+pyfzch3gv8nKvnM89
pxv78zvGpxdpm5gk8M9RyM1jSBcoA7SLVL88L3eIt9LOavTn2E65S7kU/tgO
vd5nbC6jfSW863ro8B7yfyOyZZtrL2O7Cvo+ra0e69Ipntfg61/o0xvQbtde
8dnR/mqxtC8NDelCpa+Yk8czxl8UJ8bJesblA2h9/qTEyHyOZ21kjB9W38c+
tAnf96Dt9/KM56Fxv4rE6HZuOEcOZQxXtUusmUvHRP86mDSqX+593S++zLP/
OD53aiNp90j3hYzJMPV2XePncH/zxJQy/lUJbdhdvdzI+DeNh0Z30OaaJcHb
1f5Cu4tBjPNA0lXwU1fql8FfLx6afaK6rtXQ/wn483b68C/yx2zfqMSVUK9f
xhj0axWbSP3If4aGbRmHb6fE9uVnxvT48py3jF8h1oA4A5bNxS7Wr1H/RvGH
xGsRt+VS8haMW3NSx+k5/xnr9R7Swp555wm0rS5yrwj67E1eylicwgCdTGoM
fW7jeW8dnPJd/VLvdHh8zg9i7JrSlg3892f+265Ozo03zEt5ZEnq+kXWaBDf
SO3rL0a+XEo6iTGozri96D6+V/Yk7k0qwZvfk++hXSj77we9U2Zcnu4X7Gh1
UVdyVriGVJM5+8OcxHUzptsTtHUZbZs9Mzgv4r18o23+mMRXNr75l39I7IR1
8xLf9MNJwRxYDf9ciQy7cU5sP7UB1X55Os89d2HsldXrqXvQhtR7Qe8HH6NP
r8GjY2jv6+RPIQcGKJv4vpW2AvBT23HZi7uHrn5E4hNp26aN278LvnbqiY+A
njVoZ9sZOWt9KIYi6VLP7OwF34KOa5jrq0lX0Z5BvPsS7cvI1y8LxuWl6iM9
W0KfXvsER9097xL+Pw5+eo823b4oukvXAHWZxsWYPz6xMdYhb54dmNgmExi7
5xnv0wcGv0UMWjFcOjZPzJxOzYNVJWZV3/1if60d9mTS3ciyu7Qvdszgn9NJ
WyYEY/LLicGZbNgtcXRvGJU49/JF//YpyyvWX4RWzWjH3dDxX/xvJXPqP+w1
epTm3OiZ0TVp6sKsUVfD0/sxtlfOzt6tmPmzvH3O13Om5oxt2fhJ1rXT7s7/
elbOXvEZ+vIR+8OPef7+PHMg338+ILHp1G0o8z4cFrmnL+J3pK/gqRWz4ser
D+/39KtYOybovm5k9gLuCU7lmR1zLKm0P/S8msKF2vHx4XrGfRjrZxPaUZXv
/jA6d9vDkUPtRyYuRaWKxKb4x5Lk1psjS3uxJjzJmO/JeF8FD3xwYMp7FOr/
1F6JOfqe90P8ZyLjWUp+65DYLxtfRvyQrQuCvWX5ttapN2Rs9iFdIx/y2bHM
kWPrR6e0pqBDfAo6beT9m0jHQKeZnaOPfwN+2W1GbEcXSX9oNZv0unxH/z6b
Hr9n9W1+t5p3nMOcO3dxYs5W4z8XIKuO4Hc1h0fPMY++zuG/bzHGnzAOF2t3
Nyx3b97B/Q9kqVywQX6rKLLcvq6Ej0vUCc9JLEWxLMXu7Dk+ZfEtrdeDTr/S
vprI0O+pv+rdz4DIHeWP6+vFvL8n8rMt47J74U7nT3z/yczESC2ZlPic5tYb
iKE1M/EZxPuaMSqYX2KSPNUruCSWexfqi/jtAO/5qgWP3zkl7pW+ZfqV/Y4h
uCQ2vfqCGhPFuHLGSLH8w+Gp6z9gLNSf5uWdvrth9cREHo2smsB8fBdZ2IZ5
VW9izvae8WHzSjWQm/fx/u1jY7NvPATjIljWjt96CevmPO80B8RPW59jY47c
y3h0R65s4vmDoNFHg3NeqUv7V8Ej9Vsn7rNy2Tv2D2nbDtKZ43Lferp4KLvF
p+TBgl/JZYvjP6of6XBos4M+VUXmXMHcu5M2X/WHtM02biyNf5y+cfPhneeR
lzuZiwN4/0euu4zrx23jw22MAv2434H/1rCfWF07vi76vBTvHr94Y6jpG295
t3qpfyyOiDqxgSk3apH67rx/DuNwAe/8UB9d0qylwVx1v6ccUVZVXpjzunmr
SSmrq1unX3PTrIEXjs066Jrh2uH41ORZ2xn7lotSrlGoL6T/Pehr831jXzm7
b2ws74Y2L/L51cNzF+OdjLYXM5nba/nftbTnFPpeiXf9uUtwpdUNNyjLHtG9
4nbm0DnQ/EHeeRX/K0aW1+yZs9A8ZMpM8i+hzdOeveh/ZZ7bhLH5lvJAZNtV
PGsVfDmVMXi7R3zGnNsvDoxs2zkoPoD6/4mFub5D7h0/Kc+cM26E884YTu7p
PY973/qZNqHtUz6gJPXXp8YfQv16O9pxMTx56GF5p+++DFq8TZrM/C0mVeV/
E7ULKg3mhpiS50kn+PUhZPEBjMX/cqb5mWffRv8q8fs24hCQ+sCb48RfoN1F
pCr6yNTIOcm1aDXpP+Is8PlW0v3QZAPy80Lk42r2rfsiR0+jfXOQo9csyrly
Of/5GZodSb4vc/NWr2aRG5dDw+ORf88x3m/Uzp6gWDtR2naWdnKzUvZMZN35
v608sSYtn94udeMKetb+Gdpctyhj6tg2046N1Jb0dnHGRxn84r6FvUF54iYa
P/GGCcHI2KNxcDOUWcouY1kd0Ci2ZNqUGftrHu/Zwty5AJ55lz4tgn8+Y/x+
Y33eAA3qIUtqDQr+Ww3mfE3SCuh639y8537yTuNz/zxM21O+K2asRldNuXRB
6odB3wET4/fehzEZ3SIxhd9lTr43IL5559GGgdC448KsIduh2SUDYgNgHEdj
OFr+ZXjqPyAr/0Hbz6JN7aQRY/4mz17QKjrA/vB8bb7ba7ffp0+lPzOXHtV/
q2nuA5zn7k0qcW5YiNyYDj3uGRg/718OD663eN4vQoeTkReX8NkaZMADnvv5
7/0HZS7uuzTz0bJ3N9bPUd8Jbc5jjdvMc/fi+cdx7rxmWvb17u/dZ+01I3ut
I2jHCHUXNPSisvhon1gnd03a9B/fKmXvn6y7LzYei3vjk0mHaIcxNXvNDwuy
2jl97ILM6xORV0dOjkxx3jp/HbMrtA1ZFiyGN91vMKbbhyQGhPEfnEf30p/r
u+Vu6R33wmLUVE35xb1TP4R59db0zNky+P5V5H8RcuzzxrGXr6NPErRbzvrd
jN+ciqz/W0nsFb1XmkW6Tn01dHhiePS76i2aHRDdRQdo3wB670P6G6TeD56r
R3/v470tPDczJ+6andigxmc6jc/WkI6cE12vOt9tE4NF5/20WDmWt7VJvRK0
/yf0eZv0Hn0fsyQ4oE27BbdhqXtR93Ztcj94f+e02za7jp5O/Uj4ZiV7xJNI
rUmPQNsj4c8f1cmWR+elvqt588xD5+D8gk+nvp2P0KabkB2/TE/55tqpnwYf
nErq3CIxCNwTPa/dOGeGlqRXoelceGs6tDiWNhzLs1bAU515dyP4bwptXs/n
L8P3q9gz/L1p7m8uLs19jrq2e5gvTQbHd1qcRH2p18O/37Dm3FY188HYlfrN
GrNqC8/8QqwF5mAx8nBt9ehW1LF8w/OOOzAyUXmoPuKkMcGkqsz8u5T/TW+W
/fGIudkvL9J+p25iKu3jnT80e4D2XAodq9DmyqQ6rOvF0G55ee71VnTK3d6B
nnmLc5beqL6bvi+aEewl9w/iLz3BWFaDd6qSHvdsxTvfgz/e7JF1R5m6grEv
Jv2JtBRZ3R363Mn61a1+9iXqG1+Dt3/ifw8znyez7/kLfVpGG98cHXv/v9dP
XFRjofYo+BFsYL1pRX7WrMQJqNk+ZeOpWXff4J4Oklf6FBl8AuP5Fnw3jP5/
xxlp6ODYlGhb8vSY7Pm7wsuPu/YxVhvoS3M+q8K4zFJnzbufVTcIDb5flP3J
2aXBS7Ts+6xfD+9uXRgetuwaYP0gePRGaN2GvIz/3MU4LSS/jmceNjt6tqnu
ZZGrW0si516aH1l3DW18n85cRb6aZz0If91DH0+ARs/pv0S+RQxcz4uM5V+h
dXWe8Qr0+WXP6CpOhi414Lk9SJ/VyHP24TcPNYzdxVr4/436iZmsPYJ2CDcx
xlOmxlfrznmpT5scPN7RyxJnxrK4vNanVmTvWTI9Zfej1n9D9rwBPdc2id5V
natzztgtPeomlos4t+pz1eWKkXpzs2CmKgM2TogcUPYpA58fnFgfx8Kbh9OX
ixmz/rT3AJ75OnvC7+HLo5G352k3xDMv3CO6CMfJ8XIv5z5O3fa0wl7UO6Rf
2v8OFVyJJleawhydUzVnXHUPn5ZH//Al4zEb2VkEnRcvjH9lEbw7Ddnbkf+3
bx+ZcJt8NCt3MuJbei9jWZxL6+JwGpfRu8wHKmff5f7ree1PhkV3/q+CrsO1
R18uMdP05/qc1IEzTntSVdrSEPpX1jaafctm5kd5rZRLa6bueriCZ582LlgY
+tJrIzqQcRlAWtQxGHnaLLlffhi+eQQ5s5H80FGxxyv2zFgltjva7Rh3rPuU
6ApHMEc/h/Zbu2U9aABd6i9M2TXCuphlynrl/M3TIreV35fx/+OZEx80C3as
54dXeGcH+L0B7R/TI773+uC/RGrF542REccwrj+5L4AHeiHDW5Ymlvs22vBs
RWxrey0OXt/Nc4LZt3pUsOTFlK9POmhi5LFYAZUZ15sRFldPSSxb49gqjx8j
TZ+bGE3GTzVO0yv0fQ2yeTXpJOh2Bf2/nHQUNF7GOFSQTm2VGKInk78LzY6D
H//OnqhGvfhAlJBqQd9xnHH2MqefZazNa/SPhd/uQUb9sF/KV1dK/S98dzFj
8Cxt3co87Em7P+bZs9Vb0caDaU8j9YSM7ZHI2kE1s8dtwrMPUY/Ou4tIU6HF
dsZgJ7T6QVsI2vm2thDLgkulH9wbtG8z328hdWdCtJ0cvOzx3jOyzu7XPncK
n9L2Mt5TwWej+eybDvG13U6b3yTN5vNZpNq0/1DPXuq+SdfD+2tZU4+BprdN
DyZoXdo5AZn5ELQcK14YfdpL2wHa8Fv70Hotc3cx77tgfGz4H+A3vxVl73wd
7RvQLHim9eCruqSxhbL5LYsSb2UcMvYkZNGpExJfwjgTTXln+2GJN6oNqDHM
T4OWk/ndkDqJb/B6SeIvGnvxkNLcx7QhVeOz0/qHRtpxuP6fSBuLGYNJ+6c/
f+Y3vzGWT7mmQJ87oMnRjP2D5BtJbWj/HWXxoXifdPeivKcx790DefYwbdlE
ms7zppFeZg8zS9uZgxLb+Bnm2QHw2hHa9PL5hewJ7izIip8K8sI1+ETSysnB
eG4Iv9YfnH1AVdJNyKCBE3OuEJd1JWvfCaShfeODvro1fEtbqyNzW6ufId8K
32yhresZ65X0+UnGaL59gmYPKU9KYxcyunbuLh6Bf9+Fz+vol90755bvhgS/
33PL+Yz1/wF8Xi+u
"]]]},
Boxed->False,
ImageSize->{247.7409798905339, 265.},
ViewPoint->{1.3, -2.4, 2.},
ViewVertical->{0., 0., 5.055106146575966}]\);Chargez le progiciel d'éléments finis et créez un maillage d'éléments finis.
In[2]:=
Needs["NDSolve`FEM`"]
mesh = ToElementMesh[DiscretizeGraphics[gr], "MeshOrder" -> 1]Out[2]=
Spécifiez l'opérateur de contrainte tridimensionnel.
Afficher l'entrée complète de Wolfram Language
Précisez les contraintes de manière à ce que la limite du vilebrequin soit maintenue fixe à ces positions.
In[4]:=
Subscript[\[CapitalGamma], D] =
DirichletCondition[#, {y <= 0.1, y >= 890}] & /@ {u[x, y, z] == 0.,
v[x, y, z] == 0., w[x, y, z] == 0.};Trouvez cinq valeurs et fonctions propres.
In[5]:=
{vals, funs} =
NDEigensystem[
Join[stressOperator[10^9, 33/100], Subscript[\[CapitalGamma],
D]], {u, v, w}, {x, y, z} \[Element] mesh, 5];Inspectez les valeurs propres.
In[6]:=
valsOut[6]=
Visualisez la cinquième fonction propre du vilebrequin par rapport à sa position au repos en utilisant le progiciel d'éléments finis.
Afficher l'entrée complète de Wolfram Language
Out[7]=