Résolvez le problème à valeurs propres d'un opérateur d'onde
Trouvez les quatre plus petites valeurs et fonctions propres d'une équation d'onde généralisée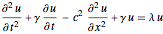 
sur une région 1D.
Mettez en place un opérateur d'onde généralisé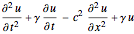 
.
In[1]:=
\[Gamma] = 1.3; c = 1.1;
op = D[u[t, x], {t, 2}] + \[Gamma] D[u[t, x], {t, 1}] -
c^2 D[u[t, x], {x, 2}] + \[Gamma] u[t, x];Trouvez les quatre plus petites valeurs et fonctions propres sur une région 1D.
In[2]:=
{vals, funs} = NDEigensystem[op == 0, u[t, x], t, {x, 0, \[Pi]}, 4];Inspectez les valeurs propres.
In[3]:=
valsOut[3]=
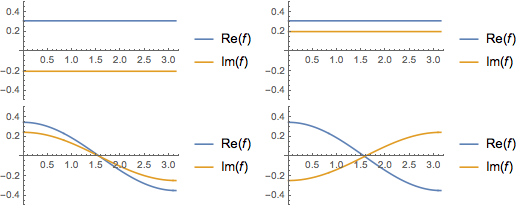
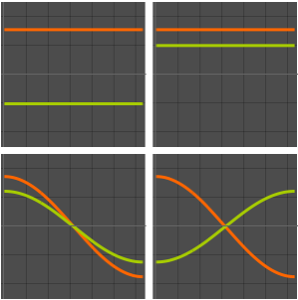
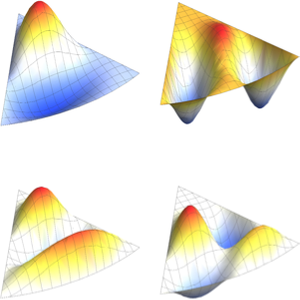
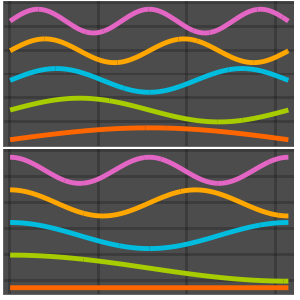
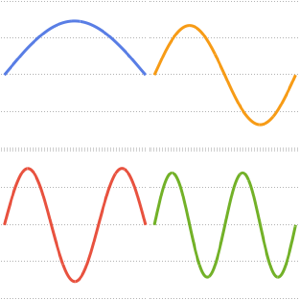
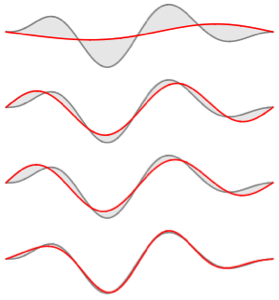
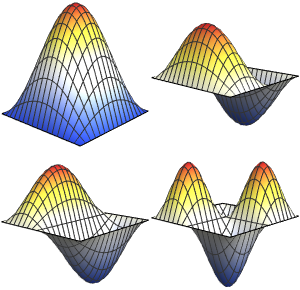
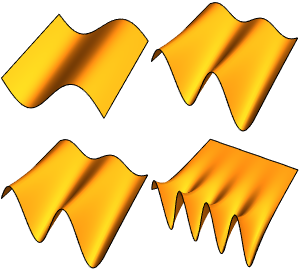
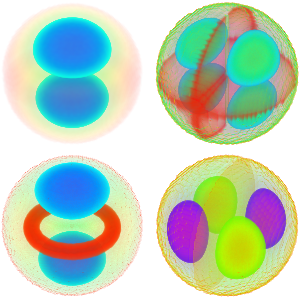
Visualisez les parties réelles et imaginaires des fonctions propres. Remarquez que les fonctions propres se présentent sous forme de paires conjuguées, comme les valeurs propres.
In[4]:=
Grid[Partition[
Plot[Evaluate[ReIm[#]], {x, 0, \[Pi]}, PlotRange -> .5,
PlotLegends -> {HoldForm@Re[f], HoldForm@Im[f]}] & /@ funs, 2]]Out[4]=
