Générez un développement de fonctions propres

Calculez le développement de la fonction propre par rapport à la base fournie par un opérateur Laplacien avec des conditions aux limites de Dirichlet sur l'intervalle .

In[1]:=

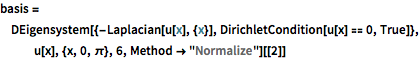
basis = DEigensystem[{-Laplacian[u[x], {x}], DirichletCondition[u[x] == 0, True]}, u[x], {x, 0, \[Pi]}, 6, Method -> "Normalize"][[2]]

Out[1]=

Calculez les coefficients de Fourier de la fonction .

In[2]:=

f[x_] := E^(-x) x^2 (\[Pi] - x) Sin[4 x]

In[3]:=

coeffs = (Table[Integrate[f[x] basis[[i]], {x, 0, Pi}], {i, 6}] // FullSimplify);

Définissez 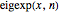en tant que ^ème somme partielle du développement.

In[4]:=

eigexp[x_, n_] := Sum[coeffs[[i]] basis[[i]], {i, n}]

In[5]:=

eigexp[x, 3] // N

Out[5]=

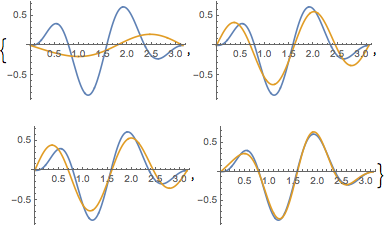
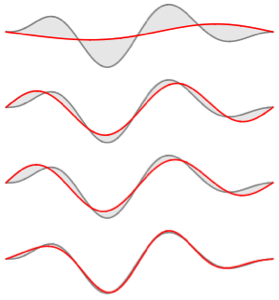
Comparez la fonction avec son développement de fonction propre pour différentes valeurs de .

In[6]:=

Table[Plot[{f[x], eigexp[x, i]} // Evaluate, {x, 0, Pi}], {i, 3, 6}]

Out[6]=