Wolfram Language™

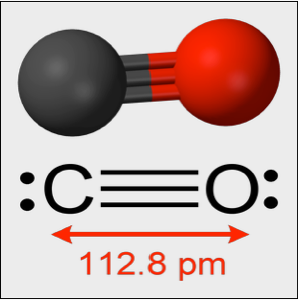
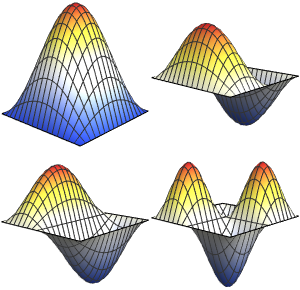
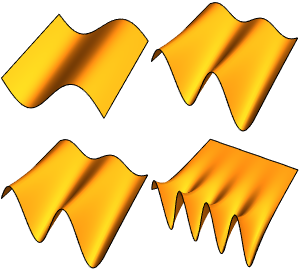
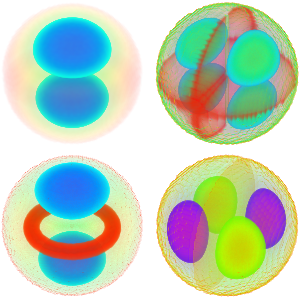
Modélisez de petites oscillations dans une molécule de monoxyde de carbone

De manière expérimentale, une molécule de monoxyde de carbone oscille autour de sa longueur à l'équilibre avec une constante de rappel effective de 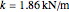. Les oscillations sont régies par l'équation de l'oscillateur harmonique quantique. Dans ce qui suit, 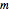est la masse réduite de la molécule, 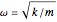est la fréquence naturelle, 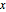est le déplacement depuis la position d'équilibre, et 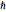est la constante de Planck réduite.

In[1]:=

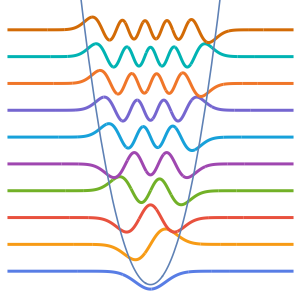
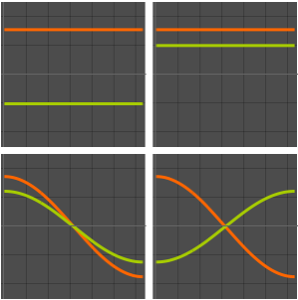
qho = -(\[HBar]^2/(2 m)) Laplacian[u[x], {x}] + (m \[Omega]^2)/ 2 x^2 u[x];

Calculez les quatre premières valeurs et fonctions propres normalisées.

In[2]:=

sol = DEigensystem[qho, u[x], {x, -\[Infinity], \[Infinity]}, 4, Assumptions -> \[HBar] > 0 && m > 0 && \[Omega] > 0, Method -> "Normalize"]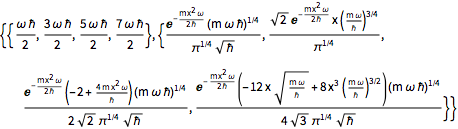

Out[2]=

En supposant que la particule se trouve dans une superposition égale des quatre états, la fonction d'onde aura la forme .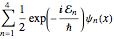

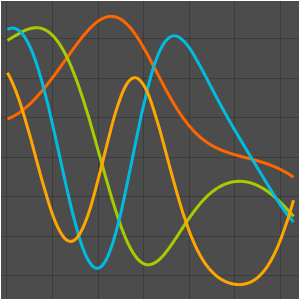
In[3]:=

\[Psi][x_, t_] = Total[MapThread[1/2 Exp[I E t #1/\[HBar]] #2 &, sol]]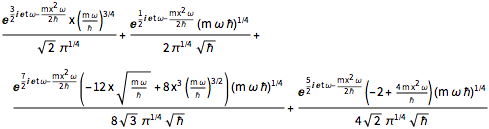

Out[3]=

Calculez les trois paramètres 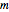, , 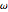et 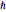en utilisant les unités de base des unités de masse atomique, femtosecondes et picomètres, car les valeurs obtenues seront proches de l'unité d'ordre.

In[4]:=

m = QuantityMagnitude[( Entity["Element", "Carbon"][ EntityProperty["Element", "AtomicMass"]] Entity["Element", "Oxygen"][EntityProperty["Element", "AtomicMass"]])/( Entity["Element", "Carbon"][ EntityProperty["Element", "AtomicMass"]] + Entity["Element", "Oxygen"][ EntityProperty["Element", "AtomicMass"]]), "AtomicMassUnits"]

Out[4]=

In[5]:=

\[Omega] = Sqrt[QuantityMagnitude[Quantity[1.86, "Kilonewtons"/"Meters"], "AtomicMassUnit"/"Femtoseconds"^2]/m]

Out[5]=

In[6]:=

\[HBar] = QuantityMagnitude[Quantity[1., "ReducedPlanckConstant"], "AtomicMassUnit"*"Picometers"^2/"Femtoseconds"]

Out[6]=

La fonction de densité de probabilité du déplacement est donnée par .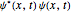

In[7]:=

\[Rho][x_, t_] = FullSimplify[ComplexExpand[Conjugate[\[Psi][x, t]] \[Psi][x, t]]]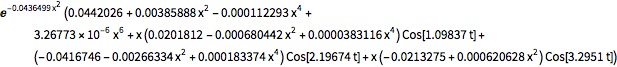

Out[7]=

En tant que loi de probabilité, l'intégrale de 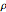sur les réels est de 1 pour tout .

In[8]:=

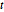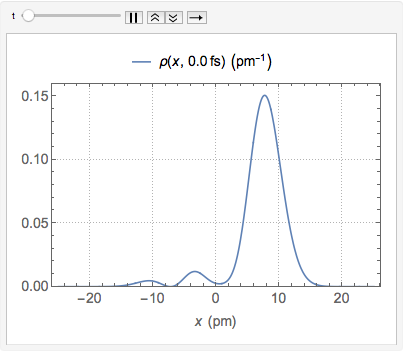
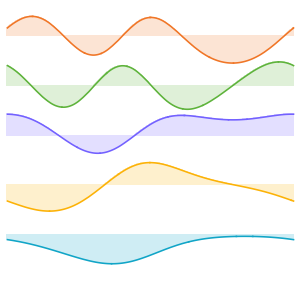
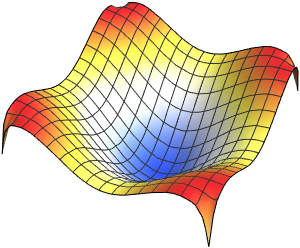
Chop[Integrate[\[Rho][x, t], {x, -\[Infinity], \[Infinity]}]]

Out[8]=

Visualisez la densité de probabilité au fil du temps.

In[9]:=

Animate[Plot[\[Rho][x, t], {x, -25, 25}, PlotRange -> {0, .16}, PlotTheme -> "Detailed", FrameLabel -> {Row[{x, RawBoxes@RowBox[{"(", "\"pm\"", ")"}]}, " "], None}, LabelStyle -> Larger, PlotLegends -> Placed[{Row[{HoldForm[\[Rho]][x, Quantity[NumberForm[t, {2, 1}], "Femtoseconds"]], RawBoxes@RowBox[{"(", SuperscriptBox["\"pm\"", -1], ")"}]}, " "]}, Above]], {t, 0., 5.7, ImageSize -> Small}, AnimationRate -> 1, SaveDefinitions -> True, Alignment -> Center]

Jouer l'animation

Arrêter l'annimation