Wolfram Language™

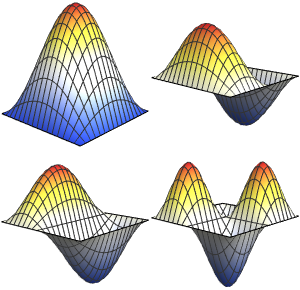
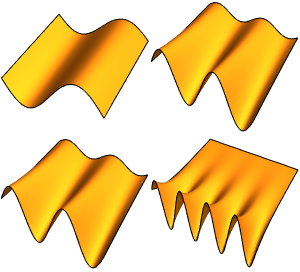
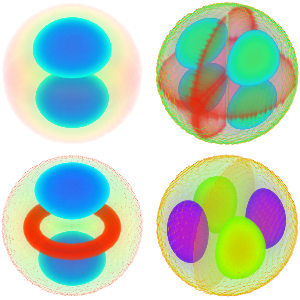
Créez une galerie de fonctions propres pour le Laplacien dans une balle

Définissez un opérateur Laplacien 3D.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x, y, z], {x, y, z}];

Spécifiez des conditions aux limites de Dirichlet homogènes.

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y, z] == 0, True];

Trouvez les 16 plus petites valeurs et fonctions propres dans une balle.

In[3]:=

\[CapitalOmega] = Ball[{0, 0, 0}, 2];

In[4]:=

{vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x, y, z], {x, y, z} \[Element] \[CapitalOmega], 16];

Les valeurs propres sont données en termes de BesselJZero.

In[5]:=

vals[[1]] // TraditionalForm

Out[5]//TraditionalForm=

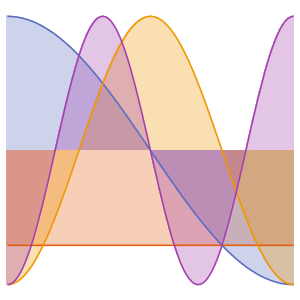
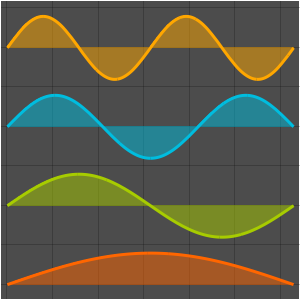
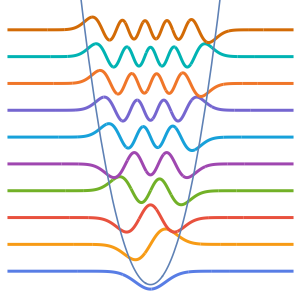
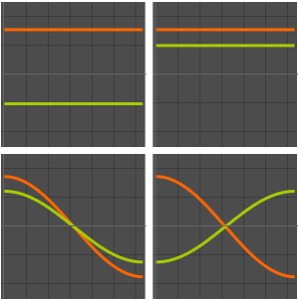
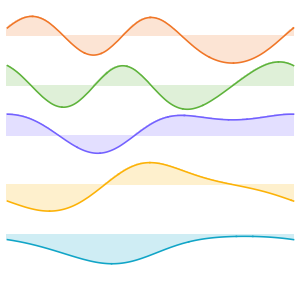
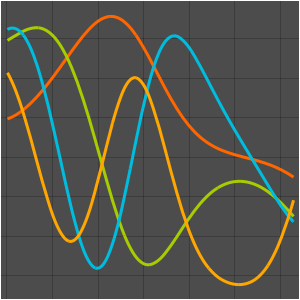
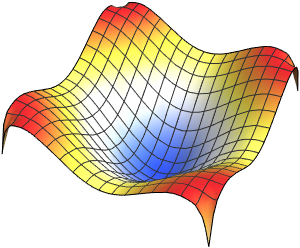
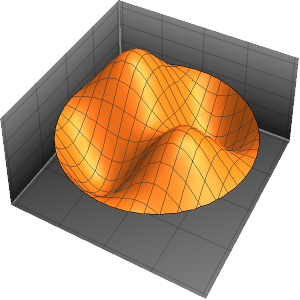
Générez une galerie de fonctions propres.

In[6]:=

Grid[Partition[ ParallelTable[ DensityPlot3D[ funs[[i]] // N // Evaluate, {x, y, z} \[Element] \[CapitalOmega], Boxed -> False, Axes -> False, ColorFunction -> Hue, Method -> {"ShrinkWrap" -> True}, ImageSize -> 125], {i, 16}], 4]]

Out[6]=