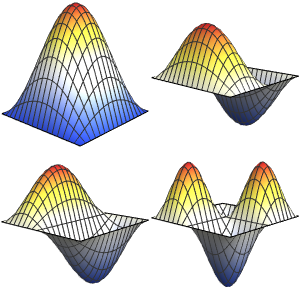
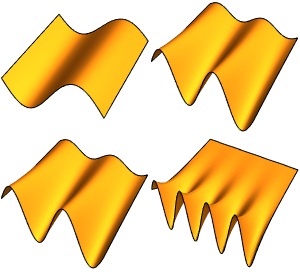
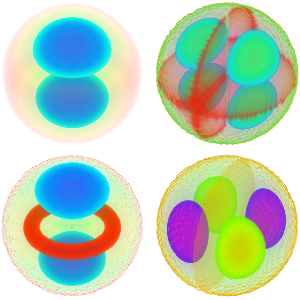
求某个区间内的特征值: Wolfram语言 11 的新功能

求某个区间内的特征值

指定区域.

In[1]:=

\[CapitalOmega] = 
  ImplicitRegion[(x^2 + y^2 + 2 y)^2 < 4 (x^2 + y^2), {x, y}];

设定拉普拉斯算子.

In[2]:=

\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}];

设定狄利克雷边界条件.

In[3]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];

用细化网格求特定区间上的特征值和相应的特征函数.

In[4]:=

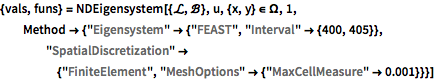
{vals, funs} = 
 NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, 
  u, {x, y} \[Element] \[CapitalOmega], 1, 
  Method -> {"Eigensystem" -> {"FEAST", "Interval" -> {400, 405}}, 
    "SpatialDiscretization" -> {"FiniteElement", 
      "MeshOptions" -> {"MaxCellMeasure" -> 0.001}}}]

Out[4]=

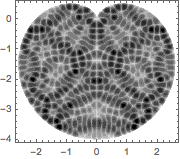
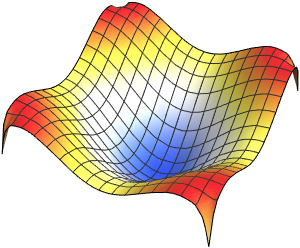
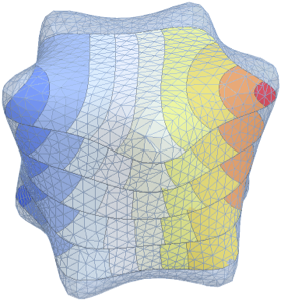
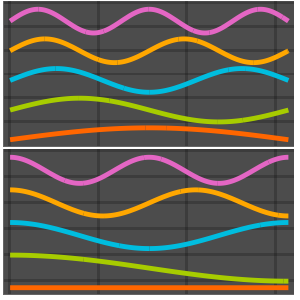
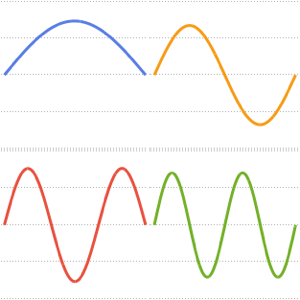
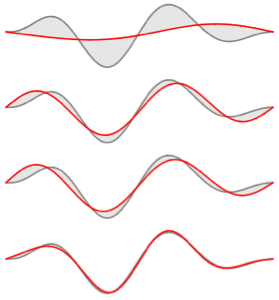
可视化求得的特征函数.

显示完整的 Wolfram 语言输入

In[5]:=

ContourPlot[
 Evaluate[Abs[funs[[1]][x, y]]^(1/2)], {x, y} \[Element] 
  funs[[1]]["ElementMesh"], PlotPoints -> 200, 
 ColorFunction -> (GrayLevel[1 - #] &), AspectRatio -> Automatic, 
 ContourStyle -> None, PlotRange -> All, MaxRecursion -> 0]

Out[5]=