トーラス上のラプラス方程式を調べる: Wolfram言語 11の新機能

‹›

トーラス上のラプラス方程式を調べる

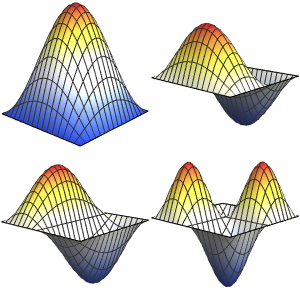
ディリクレ条件付きの正方トーラス上のラプラス方程式の固有値と固有関数を小さい方から5個求める．

1辺の長さが1の正方形上で周期的境界条件を指定する．

In[1]:=

torusBCs = {u[0, y] == u[1, y], u[x, 0] == u[x, 1]};

原点における値を指定する．上の周期的条件によると，この値は正方形の他の3つの角における値でもなければならない．

In[2]:=

constraint = DirichletCondition[u[x, y] == 0, x == 0 && y == 0];

固有値と固有関数を計算する．

In[3]:=

{vals, funs} = 
  NDEigensystem[
   Join[{-Laplacian[u[x, y], {x, y}], constraint}, torusBCs], 
   u[x, y], {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], 4];

固有値を調べる．

In[4]:=

vals

Out[4]=

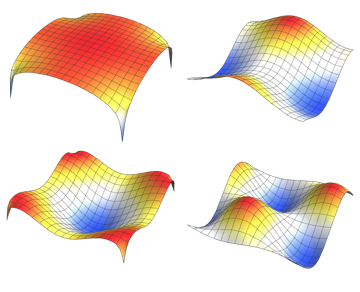
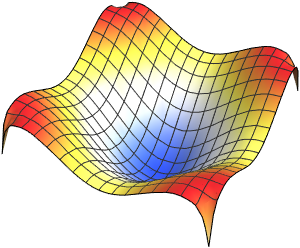
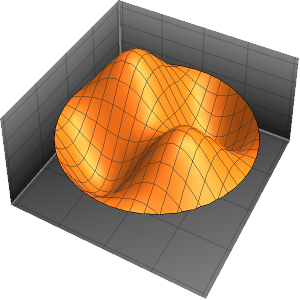
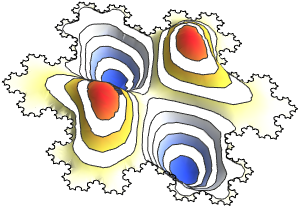
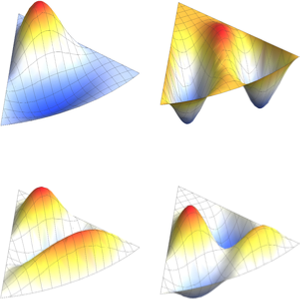
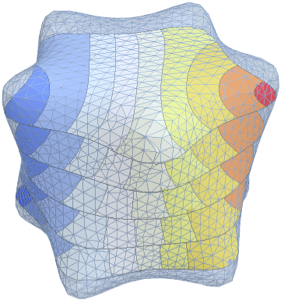
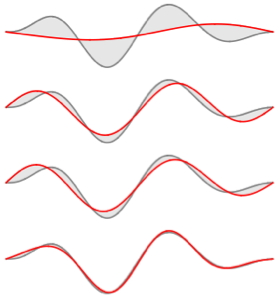
固有関数を可視化する．

完全なWolfram言語入力を表示する

In[5]:=

ImageCollage[
 Plot3D[#, {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], 
    ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> None, 
    PlotRange -> All, PlotStyle -> {Specularity[White, 20]}] & /@ 
  funs, Background -> Transparent]

Out[5]=