Wolfram 语言™

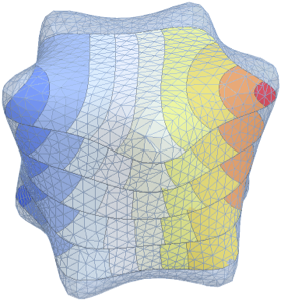
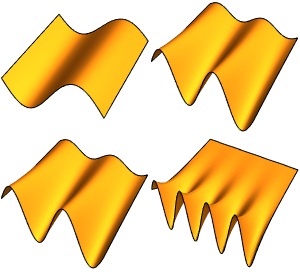
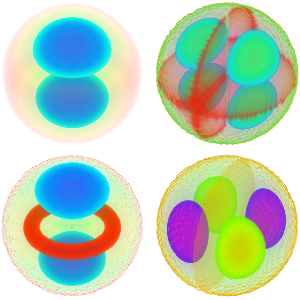
探讨环面上的拉普拉斯方程

在狄利克雷约束下求拉普拉斯方程在一个矩形环面上最小的五个周期特征值和特征函数.

在边长为 1 的矩形上设定周期性边界条件.

In[1]:=

torusBCs = {u[0, y] == u[1, y], u[x, 0] == u[x, 1]};

在原点设定一个值. 根据周期性条件，这也必须是矩形其他三个顶点的值.

In[2]:=

constraint = DirichletCondition[u[x, y] == 0, x == 0 && y == 0];

计算特征值和特征函数.

In[3]:=

{vals, funs} = NDEigensystem[ Join[{-Laplacian[u[x, y], {x, y}], constraint}, torusBCs], u[x, y], {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], 4];

查看特征值.

In[4]:=

vals

Out[4]=

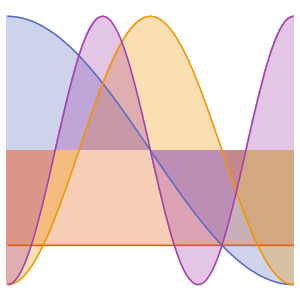
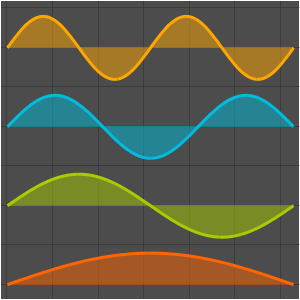
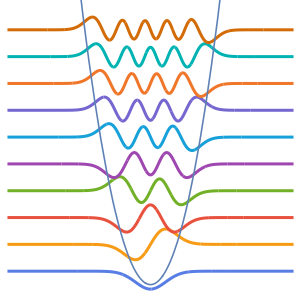
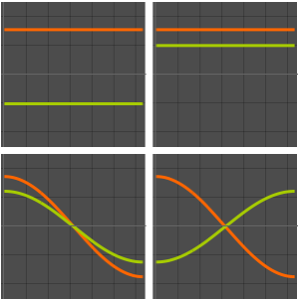
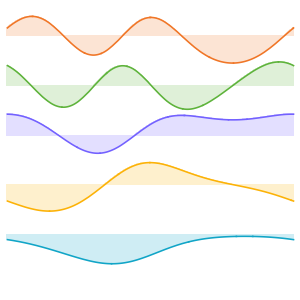
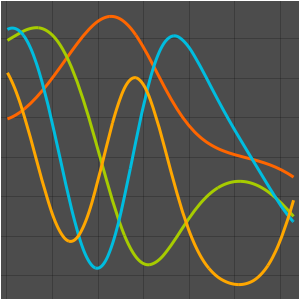
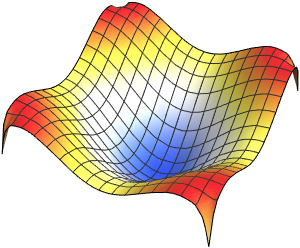
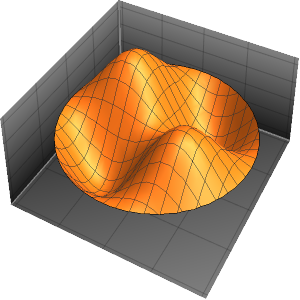
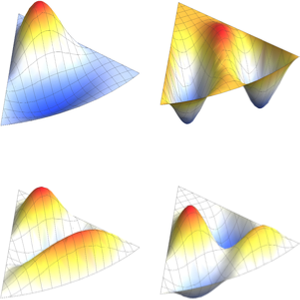
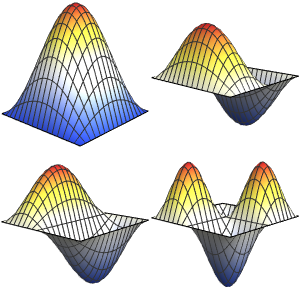
可视化特征函数.

In[5]:=

ImageCollage[ Plot3D[#, {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> None, PlotRange -> All, PlotStyle -> {Specularity[White, 20]}] & /@ funs, Background -> Transparent]

Out[5]=