Examinez une équation de Laplace sur un tore

Trouvez les cinq plus petites valeurs et fonctions propres d'une équation de Laplace sur un tore carré avec une contrainte de Dirichlet.

Spécifiez les conditions aux limites périodiques sur un carré de longueur 1.

In[1]:=

torusBCs = {u[0, y] == u[1, y], u[x, 0] == u[x, 1]};

Spécifiez une valeur à l'origine. D'après les conditions périodiques, cette valeur doit également être celle des trois autres coins du carré.

In[2]:=

constraint = DirichletCondition[u[x, y] == 0, x == 0 && y == 0];

Calculez les valeurs et fonctions propres.

In[3]:=

{vals, funs} = NDEigensystem[ Join[{-Laplacian[u[x, y], {x, y}], constraint}, torusBCs], u[x, y], {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], 4];

Inspectez les valeurs propres.

In[4]:=

vals

Out[4]=

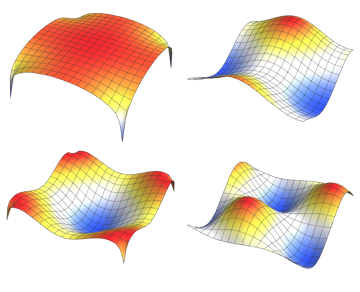
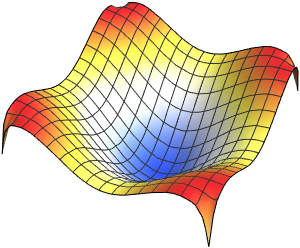
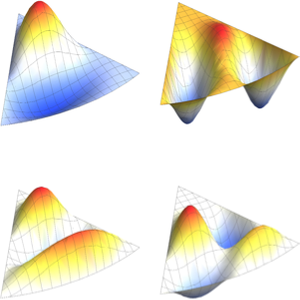
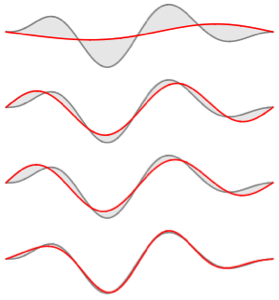
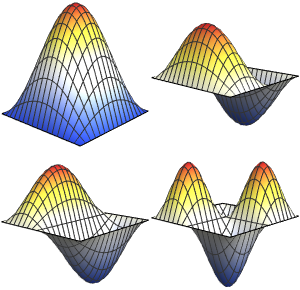
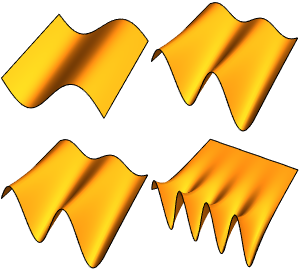
Visualisez les fonctions propres.

In[5]:=

ImageCollage[ Plot3D[#, {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> None, PlotRange -> All, PlotStyle -> {Specularity[White, 20]}] & /@ funs, Background -> Transparent]

Out[5]=