波動演算子の固有値問題を調べる
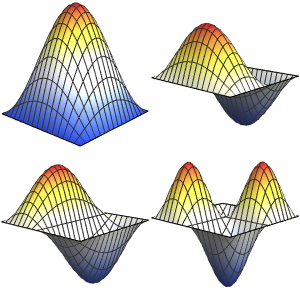
一次元領域上で，一般化された波動方程式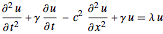 
の固有値と固有関数を小さい方から4個求める．
一般化された波動演算子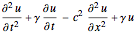 
を設定する．
In[1]:=
\[Gamma] = 1.3; c = 1.1;
op = D[u[t, x], {t, 2}] + \[Gamma] D[u[t, x], {t, 1}] -
c^2 D[u[t, x], {x, 2}] + \[Gamma] u[t, x];一次元領域上で固有値と固有関数を小さい方から4個求める．
In[2]:=
{vals, funs} = NDEigensystem[op == 0, u[t, x], t, {x, 0, \[Pi]}, 4];固有値を調べる．
In[3]:=
valsOut[3]=
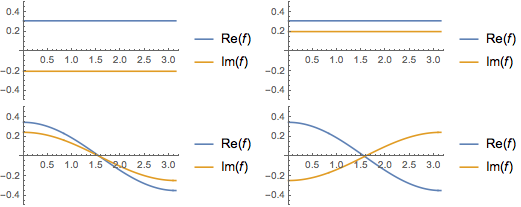
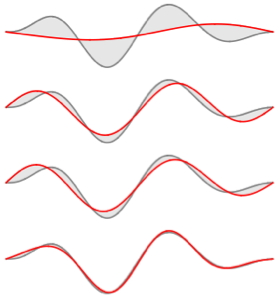
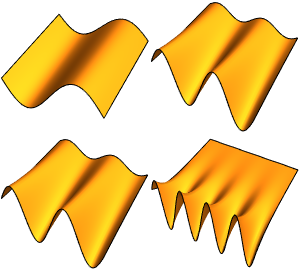
固有関数の実部と虚部を可視化する．固有関数は，固有値のように共役対になっている点に注目．
In[4]:=
Grid[Partition[
Plot[Evaluate[ReIm[#]], {x, 0, \[Pi]}, PlotRange -> .5,
PlotLegends -> {HoldForm@Re[f], HoldForm@Im[f]}] & /@ funs, 2]]Out[4]=
