探测解波动算子的特征值问题

在一维区域上求广义波动方程 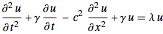最小的四个特征值和特征函数.

设定一个广义波动算子 .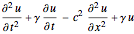

In[1]:=

\[Gamma] = 1.3; c = 1.1; op = D[u[t, x], {t, 2}] + \[Gamma] D[u[t, x], {t, 1}] - c^2 D[u[t, x], {x, 2}] + \[Gamma] u[t, x];

在一维区域上找出最小的四个特征值和特征函数.

In[2]:=

{vals, funs} = NDEigensystem[op == 0, u[t, x], t, {x, 0, \[Pi]}, 4];

查看特征值.

In[3]:=

vals

Out[3]=

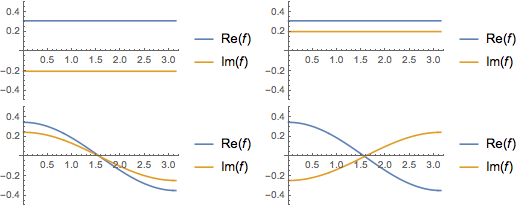
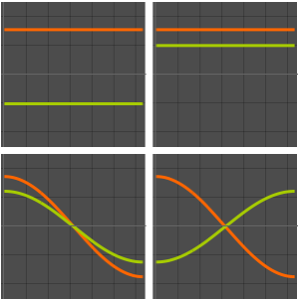
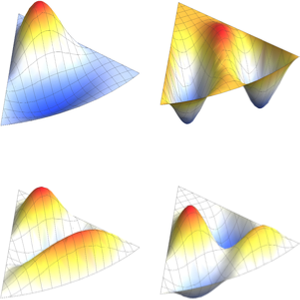
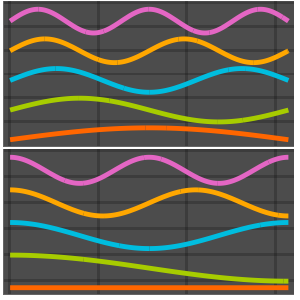
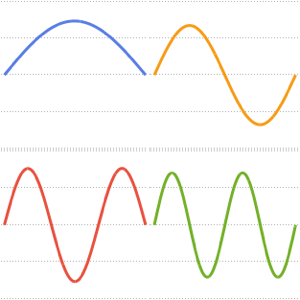
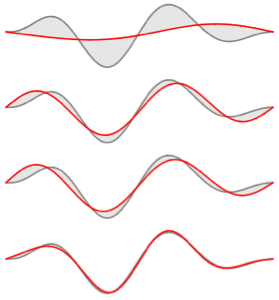
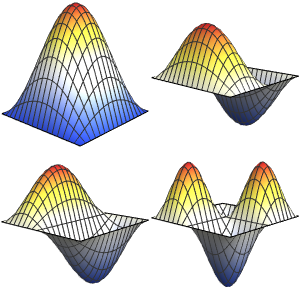
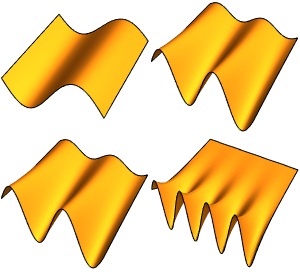
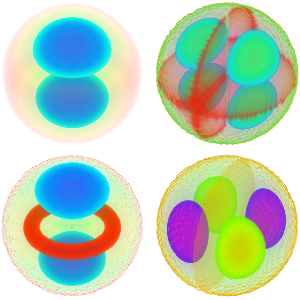
可视化特征函数的实部和虚部. 注意，特征函数像特征值一样是以共轭对形似出现的.

In[4]:=

Grid[Partition[ Plot[Evaluate[ReIm[#]], {x, 0, \[Pi]}, PlotRange -> .5, PlotLegends -> {HoldForm@Re[f], HoldForm@Im[f]}] & /@ funs, 2]]

Out[4]=