Язык Wolfram Language™

Более быстрый анализ распределений

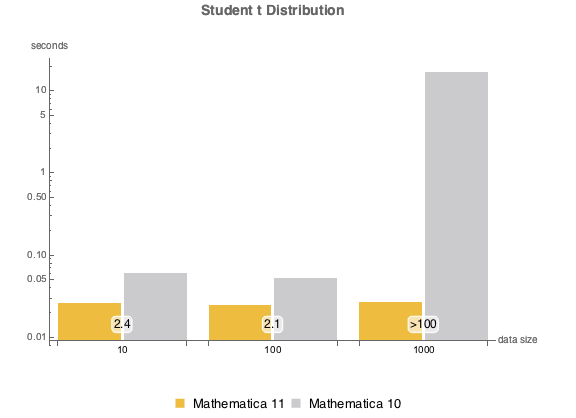
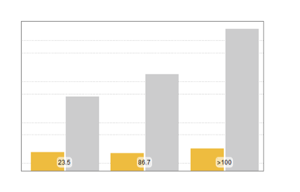
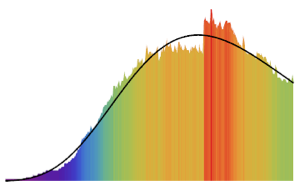
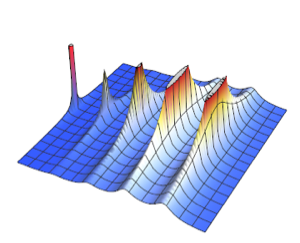
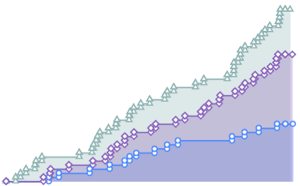
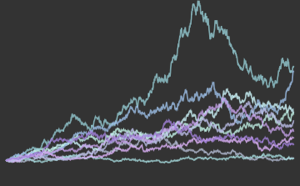
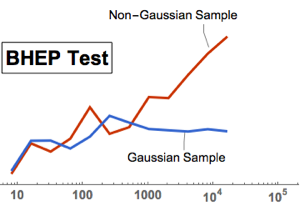
Версия 11 предлагает множество усовершенствований для анализа распределений, в том числе, его более оперативное исполнение. Следующие диаграммы показывают время, затраченное на оценку нескольких распределений с различными размерами выборки. Эксперименты проводились на основе системы Windows 10 с процессором Intel Xeon E3-1245 v2 3,40 ГГц. Приведенное ниже численное выражение показывает, насколько быстрее версия 11 выполняет данные операции по сравнению с версией 10.

t-распределение Стьюдента.

In[1]:=

dist = StudentTDistribution[loc, sc, df]; ndist = StudentTDistribution[-1, 1, 2]; Table[ sample = BlockRandom[SeedRandom["MarketingExample"]; RandomVariate[ndist, n]]; Mean[Table[ First[AbsoluteTiming[EstimatedDistribution[sample, dist];]], {5}]] , {n, {10, 100, 1000}}]

Out[21]=

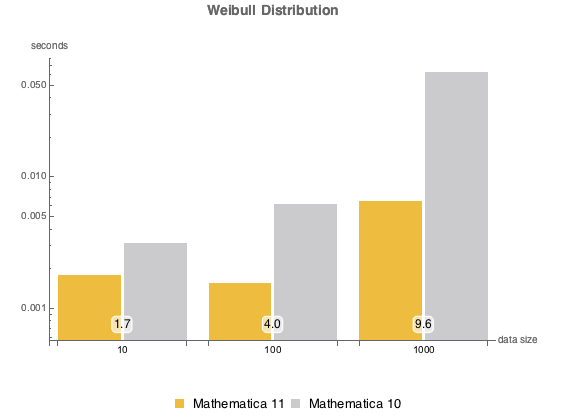
Распределение Вейбулла.

In[2]:=

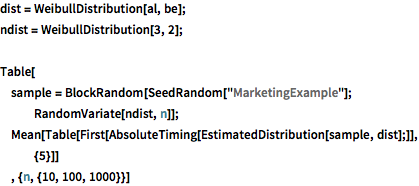
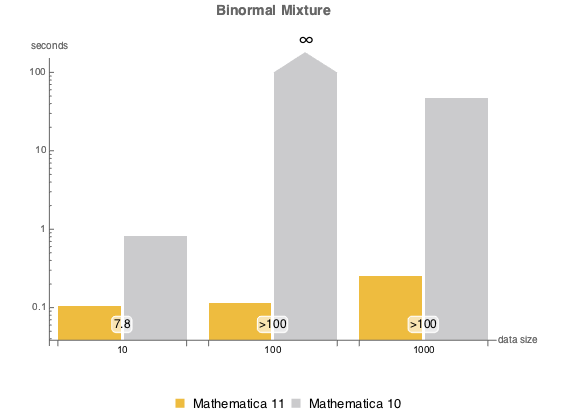
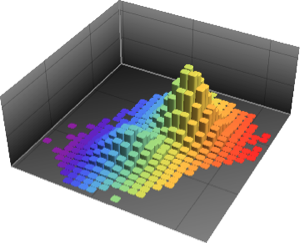
dist = WeibullDistribution[al, be]; ndist = WeibullDistribution[3, 2]; Table[ sample = BlockRandom[SeedRandom["MarketingExample"]; RandomVariate[ndist, n]]; Mean[Table[ First[AbsoluteTiming[EstimatedDistribution[sample, dist];]], {5}]] , {n, {10, 100, 1000}}]

Out[23]=

Cмесь двух нормальных распределений.

In[3]:=

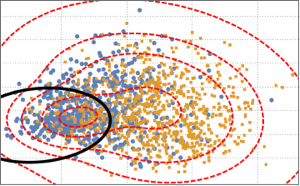
dist = MixtureDistribution[{w1, w2}, {BinormalDistribution[{m11, m12}, {s11, s12}, \[Rho]1], BinormalDistribution[{m21, m22}, {s21, s22}, \[Rho]2]}]; ndist = MixtureDistribution[{0.3, 0.7}, {BinormalDistribution[{0, 1}, {0.5, 0.25}, 0.7], BinormalDistribution[{-0.5, 0}, {0.5, 0.25}, 0.1]}]; Table[ sample = BlockRandom[SeedRandom["MarketingExample"]; RandomVariate[ndist, n]]; Mean[Table[ First[AbsoluteTiming[ TimeConstrained[EstimatedDistribution[sample, dist];, 100]]], {5}]] , {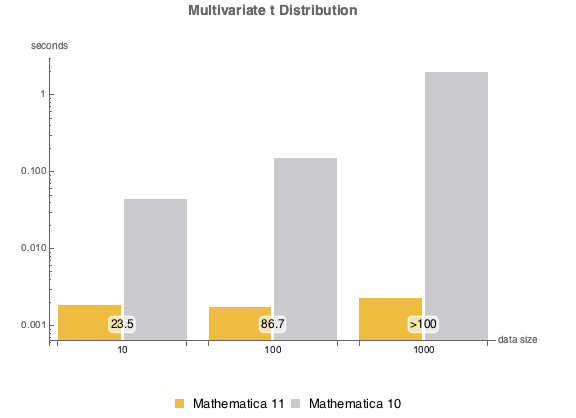n, {10, 100, 1000}}]

Out[117]=

Многофакторное t-распределение.

In[4]:=

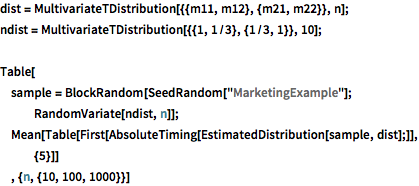
dist = MultivariateTDistribution[{{m11, m12}, {m21, m22}}, n]; ndist = MultivariateTDistribution[{{1, 1/3}, {1/3, 1}}, 10]; Table[ sample = BlockRandom[SeedRandom["MarketingExample"]; RandomVariate[ndist, n]]; Mean[Table[ First[AbsoluteTiming[EstimatedDistribution[sample, dist];]], {5}]] , {n, {10, 100, 1000}}]

Out[27]=